1 Introduction

Quantum estimation theory (QET) is a field of study in physics that deals with the estimation of unknown parameters in quantum systems. In quantum mechanics, there are limitations on the measurements that can be made on certain quantities, either due to fundamental principles or experimental constraints. This makes it necessary to devise estimation methods that rely on indirect measures or a set of observables. In quantum metrology, the primary goal is to estimate physical parameters with high precision. After estimating these physical parameters, one can then analyze the quantum state to compute properties like purity and entanglement based on the known parameters of the state. The quantum estimation theory builds upon the works of pioneers like Helstrom and Holevo [1, 2], who made significant contributions to the theory. One of the key concepts in QET is the Fisher information, which measures the amount of information that a given measurement can provide about the unknown parameter. The Fisher information determines the ultimate limit on the precision of the estimation process. The QET aims to find positive operator-valued measurements (POVMs) that maximize the Fisher information [3], this approach aims to reduce the variance of the estimator while keeping the parameter’s value fixed. By optimizing the Fisher information, QET provides a framework for designing precise measurements in the quantum regime. This is particularly relevant in quantum technologies such as quantum computing, quantum communication, and quantum metrology. The parameter estimation plays a crucial role in the advancement of high-precision devices across various technological domains [4, 5].

Recently, significant attention has been devoted to quantum metrology [6, 7], where quantum effects are harnessed to push the limits of precision and develop novel methods for accurately measuring physical parameters, surpassing the capabilities of classical metrology [8, 9]. Now days, there are many applications of quantum metrology. One may mention the optimal estimation of the temperature [10,11,12,13], the estimation of space-time parameters [14,15,16,17,18], the obtention of the bounds on the optimal estimation of phases [19, 20], maximizing the sensitivity of gravitational wave detectors like LIGO [21], measuring magnetic fields [22,23,24,25], quantifying squeezing parameters [26,27,28,29,30], the time [31, 32], and the frequency [34, 35]. The estimation precision can be considerably increased by the quantum metrology protocols precision by making use of quantum correlations which are in a multipartite system:the entanglement [36,37,38] and the quantum discord [39,40,41].

In the field of quantum metrology, the quantum Cramér–Rao bound [42, 43] is frequently employed to establish the limit of measurement precision for a set of parameters. This bound is encapsulated by the inequality \(\textrm{Cov}\left( {\hat{\theta }} \right) \ge {\mathscr {F}^{ - 1}}\), where \(\textrm{Cov}\left( {\hat{\theta }} \right) \) represents the covariance matrix of an estimation vector comprising the parameters to be estimated. On the other hand, \(\mathscr {F}\) denotes the quantum Fisher information matrix (QFIM) [44]. This inequality serves as a fundamental principle, indicating that the precision of parameter estimation is constrained by the inverse of the QFIM. In quantum parameter estimation, the choice of an optimal estimation protocol is central to achieving maximum precision, as characterized by the quantum Fisher information (QFI) and quantum Fisher information matrix (QFIM). For QFI, a well-designed single-parameter estimation protocol, with optimal probe states and measurements, is key. The inverse of QFI sets a lower limit on estimator variance, as dictated by the Cramér–Rao Bound (CRB). When dealing with multiple parameters, the QFIM introduces complexities due to incompatible measurements. The estimation protocol must navigate challenges in jointly optimizing measurements for multiple parameters to overcome QFIM limitations. In essence, the protocol choice, intricately linked to the CRB, plays a crucial role in quantum parameter estimation, dictating the precision achievable in quantum measurements. For this, the multiparameter quantum metrology has attracted great interest to generalize certain conditions to saturate the quantum Cramér–Rao bound, therefore, to achieve maximum precision.

Several reviews have recently been published on quantum parameter estimation and quantum metrology, offering comprehensive insights from various perspectives. Notable contributions include the works by Giovannetti et al. [33]. on quantum measurements and advances in quantum metrology [5], as well as those by Paris [53].

The research for practical optimal measurements, which is always a central mission in quantum metrology, ultimatly independent of the parameter that needs to be estimated. The most researched measurement strategies today involve individual and simultaneous measurement. Recently, studies on multiparameter estimation have attracted a great deal of interest. In this context, our research paper focuses on investigating both simultaneous and individual estimation strategies. We employ the density matrix vectorization method to achieve the highest precision in estimating the desired parameter. This approach allows us to explore and compare the effectiveness of different estimation strategies and optimize the precision of parameter estimation.

In this study, we focused on investigating the influence of an external magnetic field on the precision of parameter estimation using a two-spins XXZ Heisenberg model. Our findings demonstrate that the presence of a magnetic field has a significant impact on the (QFIM) in this physical model Eq. (10). Interestingly, we observed that this effect is not continuous but rather manifests in specific regions, which aligns with the previous research conducted by Ozaydin and Altinas [54]. Furthermore, our results indicate that the simultaneous estimation of parameters can achieve the highest precision when the magnetic field is considered. This implies that the magnetic field enhances the precision of parameter estimation compared to individual estimations without the magnetic field.

The paper is structured as follows. In the next section, we deal with the basics of QFI matrix for multiple parameters estimation theory and the important mathematical instruments, the determination of the optimal quantum estimator in terms of the symmetric logarithmic derivative, as well as the ultimate bounds to precision in terms of the quantum Fisher information. General formulas for the symmetric logarithmic derivative and the quantum Fisher information are derived. In Sect. 3, we investigate the precision of the multi-parametric estimation relying on QFIM in Heisenberg XXZ model. We derive the corresponding symmetric logarithmic derivatives and conditions for saturability of the quantum Cramér–Rao bound which provides the final precision. Furthermore, we analyze the simultaneous and individual strategies by introducing the ratio between the minimal amounts of total variances for each estimating protocol. Sect. 4 closes the paper with some concluding remarks.

2 Mathematical tools of QFIM for multiple parameters

In this section we will first derive the QFI matrix for multiple parameters, and construct the corresponding Cramér–Rao bound.

The QFI with respect to the parameter \(\theta \) is given by [53, 55, 56]

$$\begin{aligned} \mathscr {F}\left( {{\hat{\rho }_\theta }} \right) = \textrm{Tr}\left\{ {{{\hat{\rho }} _\theta }{\hat{\mathscr {L}}}_\theta }^2 \right\} , \end{aligned}$$
(1)

where \({\hat{\mathscr {L}}}_\theta \) is the symmetric logarithmic derivative. For more parameters \({\theta _i}\), the QFIM is defined [53]

$$\begin{aligned} {\mathscr {F}_{ij}} = \frac{1}{2}\textrm{Tr}\left\{ {\left( {{{{\hat{\mathscr {L}}}}_{\theta _i}}{{{\hat{\mathscr {L}}}}_{\theta _j}} + {{{\hat{\mathscr {L}}}}_{\theta _j}}{{{\hat{\mathscr {L}}}}_{\theta _i}}} \right) \hat{\rho }} \right\} , \end{aligned}$$
(2)

where the symmetric logarithmic derivatives (SLD) \({{{{\hat{\mathscr {L}}}}_{\theta _i}}}\) are defined as operator solutions to equations

$$\begin{aligned} 2{\partial _{\theta _i}}\hat{\rho }= {{\hat{\mathscr {L}}}_{\theta _i}}\hat{\rho }+ \hat{\rho }{{\hat{\mathscr {L}}}_{\theta _i}}, \end{aligned}$$
(3)

with \({\partial _{\theta _i}}=\frac{\partial }{\partial \theta _i}.\)

Applying the spectral decomposition technique of \({{\hat{\rho }} } = \sum \limits _k {{p_k}} \left| k \right\rangle \left\langle k \right| \) where \(\left| k \right\rangle \) and \({p_k}\) denoted the eigenvectors and eigenvalues of the matrix \(\rho \), respectively; to check that Eq. (2) have solutions

$$\begin{aligned} {{\hat{\mathscr {L}}}_{\theta _i}}= 2\sum \limits _{{p_k} + {p_l} > 0} {\frac{{\left\langle k \right| {\partial _{{\theta _i}}}{{\hat{\rho }} }\left| l \right\rangle }}{{{p_k} + {p_l}}}}\left| k \right\rangle \left\langle l \right| . \end{aligned}$$
(4)

Replacing (4) into Eq. (2) gets the [57,58,59]

$$\begin{aligned} {\mathscr {F}_{ij}} = 2\sum \limits _{{p_k} + {p_l} > 0} {\frac{{\left\langle k \right| {\partial _{{\theta _i}}}{{\hat{\rho }} }\left| l \right\rangle \left\langle l \right| {\partial _{{\theta _j}}}{{\hat{\rho }} }\left| k \right\rangle }}{{{p_k} + {p_l}}}}, \end{aligned}$$
(5)

the QFIM can be represented by the following integral expression for every density matrix [53].

$$\begin{aligned} {\mathscr {F}_{ij}} = 2\int \limits _0^\infty {\textrm{Tr}\left[ {{e^{ - {{\hat{\rho }} }t}}{\partial _{{\theta _i}}}{\rho }{e^{ - {{\hat{\rho }} }t}}{\partial _{{\theta _j}}}{{\hat{\rho }} }} \right] }. \end{aligned}$$
(6)

Subsequently, we rewrite the formula for the QFIM by utilizing a significant property of vectorization (see Ref. [57] and the computation of the inverse of the following matrix; see also Ref. [60]). Appendix A and B is dedicated to the details of this task.

$$\begin{aligned} \Lambda = \left( {{{\hat{\rho }} ^T} \otimes \mathbb {I} + \mathbb {I} \otimes {\hat{\rho }} } \right) . \end{aligned}$$
(7)

The characterization of the QFIM is as follows:

$$\begin{aligned} {\mathscr {F}_{ij}} = 2\textrm{vec}{\left[ {{\partial _i}\hat{\rho }} \right] ^T}{\Lambda ^{ - 1}}\textrm{vec}\left[ {{\partial _j}\hat{\rho }} \right] . \end{aligned}$$
(8)

And the SLDs are given by

$$\begin{aligned} \textrm{vec}\left[ {\hat{{\mathscr {L}}}_{{\theta _i}}} \right] = 2{\Lambda ^{ - 1}}\textrm{vec}\left[ {{\partial _i}\hat{\rho }} \right] , \end{aligned}$$
(9)

where, \(\bigotimes \) denotes the Kronecker product, and vec[.] is a vectorization of a matrix.

The issue of saturation is a crucial aspect in parameter estimation of the multi-parametric quantum Cramér–Rao bound (QCRB), which is an inequality. Understanding the conditions under which saturation occurs is essential. In the case of the single parameter estimation, the Cramér–Rao bound inequality is always saturable and it can reach its optimal quatum mesurement due to the projections on the eigenvectors of the SLDs operators \({\mathscr {L}_{\theta _i}}\), while, the matrix Cramér-Rao inequality in multiparameter estimation can not always be saturable, in fact the incompatibility of the different parameters can hinder the existance of an optimal quantum mesurement [61, 62]. Therefore, we must provide a condition that must be verified in order to saturate this inequality. By solving the Eq. (9), as a result we can have the symmetric logarithmic derivatives \({\mathscr {L}_{\theta _i}}\) that correspond to the different estimated parameters, we have to distingue between two cases, the first one is when the \({\mathscr {L}_{\theta _i}}\) operators comute, we can find a common eigenbasis for all SLDs, and this allows us to perform a simultaneous estimation to saturate the Cramér–Rao inquality, we can resume this commutativity in this relation \(\left[ {\mathscr {L}_{{\theta _i}},\mathscr {L}_{{\theta _j}}} \right] = 0\) which is a sufficient conditon and necessary to saturate the Cramér-Rao inequality provided a finite number of quantum states given, the second case is when the SLDs are not commuting, we proceed to this condition \(Tr\left( {\rho \left[ {\mathscr {L}_{{\theta _i}},\mathscr {L}_{{\theta _j}}} \right] } \right) = 0\) which is sufficient and necessary to ensure the saturation of Cramér–Rao inequality for an infinite number of quantum states are given [62,63,64].

3 Physical model

The Hamiltonian of the XYZ model with an external magnetic field acting on both qubits takes the form

$$\begin{aligned} H = B(S_{z}^{1} + S_{z}^{2}) + J_xS_{x}^{1}S_{x}^{2}+ J_yS_{y}^{1}S_{y}^{2} + J_{z}S_{z}^{1}S_{z}^{2}, \end{aligned}$$
(10)

with \(J_{x}, J_{y}\), and \(J_{z}\) the coupling constants, \(S^j_{x,y,z} = \sigma ^j_{x,y,z}/2\), \(\sigma _{x}^{j}, \sigma _{y}^{j}\), and \(\sigma _{z}^{j}\) the usual Pauli matrices acting on qubit j, and B the external magnetic field. We have assumed \(\hbar = 1\). The density matrix describing a system in equilibrium with a thermal reservoir at temperature T (canonical ensemble) is \(\rho = \exp {\left( -H/kT \right) }/Z\), where \(Z = \text{ Tr }\left\{ \exp {\left( -H/kT \right) } \right\} \) is the partition function and k is Boltzmann’s constant. Therefore, Eq. (10) leads to the following thermal state in the standard basis

$$\begin{aligned} \rho = \frac{1}{Z} \left( \begin{array}{cccc} A_{11} &{} 0 &{} 0 &{} A_{12}\\ 0 &{} B_{11} &{} B_{12} &{} 0 \\ 0 &{} B_{12} &{} B_{11} &{} 0 \\ A_{12} &{} 0 &{} 0 &{} A_{22} \\ \end{array} \right) , \end{aligned}$$
(11)

where \(A_{11}\) \(=\) \(\textrm{e}^{-\alpha }\) \((\cosh (\beta )\) − 4B \(\sinh (\beta )/\eta )\), \(A_{12}\) \(=\) − \(\Delta \) \(\textrm{e}^{-\alpha }\) \(\sinh (\beta )/\eta \), \(A_{22}\) \(=\) \(\textrm{e}^{-\alpha }\) \((\cosh (\beta )\) \(+\) 4 B \(\sinh (\beta )/\eta )\), \(B_{11}\) \(=\) \(\textrm{e}^{\alpha }\) \(\cosh (\gamma )\), \(B_{12}\) \(=\) − \(\textrm{e}^{\alpha }\) \(\sinh (\gamma )\), and \(Z = 2\left( \exp {(-\alpha )}\cosh (\beta ) + \exp {(\alpha )}\cosh (\gamma ) \right) \), where \(\Delta \)= \(J_{x}- J_{y}\), \(\Sigma = J_{x} + J_{y}\), \(\eta = 4B\), \(\alpha = J_{z}/(4kT)\), \(\beta = \eta /(4kT)\), and \(\gamma = \Sigma /(4kT)\),

with

$$\begin{aligned} a_{11}=\frac{A_{11}}{Z},\;a_{12}=\frac{A_{12}}{Z},\;b_{11}=\frac{B_{11}}{Z},\;b_{12}=\frac{B_{12}}{Z},\;a_{22}=\frac{A_{22}}{Z}. \end{aligned}$$
(12)

For this two-qubit system, we consider the estimation of the magnetic field B and the temperature T (i.e., \({\hat{\theta }} \equiv \left( {B,T} \right) \)). The vec-operator associated the density matrix derivatives, with respect to parameters B and T, are given by

$$\begin{aligned} \textrm{vec}\left[ {{\partial _B}\rho } \right] = {\left( {{\partial _B}c,0,0,0,0,{\partial _B}t,{\partial _B}y,0,0,{\partial _B}y,{\partial _B}t,0,0,0,0,{\partial _B}d} \right) ^T}, \end{aligned}$$
(13)

and

$$\begin{aligned} \textrm{vec}\left[ {{\partial _T}\rho } \right] = {\left( {{\partial _T}c,0,0,0,0,{\partial _T}t,{\partial _T}y,0,0,{\partial _T}y,{\partial _T}t,0,0,0,0,{\partial _T}d} \right) ^T}. \end{aligned}$$
(14)

The quantum Fisher information matrix writes

$$\begin{aligned} \mathscr {F}= \left[ {\begin{array}{*{20}{c}} {2\textrm{vec}{{\left[ {{\partial _B}\rho } \right] }^T}^{}{\Lambda ^{ - 1}}\textrm{vec}\left[ {{\partial _B}\rho } \right] }&{}{2\textrm{vec}{{\left[ {{\partial _B}\rho } \right] }^T}{\Lambda ^{ - 1}}\textrm{vec}\left[ {{\partial _T}\rho } \right] }\\ {2\textrm{vec}{{\left[ {{\partial _T}\rho } \right] }^T}{\Lambda ^{ - 1}}\textrm{vec}\left[ {{\partial _B}\rho } \right] }&{}{2\textrm{vec}{{\left[ {{\partial _T}\rho } \right] }^T}{\Lambda ^{ - 1}}\textrm{vec}\left[ {{\partial _T}\rho } \right] } \end{array}} \right] . \end{aligned}$$
(15)

After a straightforward calculation, the elements of the quantum Fisher information matrix are obtained analytically as

$$\begin{aligned} {\mathscr {F}_{BB}}= & {} \frac{1+e^{2\alpha }\cosh (\gamma )\cosh (\alpha )}{T^{2}\left( \cosh (\beta )+e^{2\alpha }\cosh (\gamma )\right) ^{2}}, \end{aligned}$$
(16)
$$\begin{aligned} {\mathscr {F}_{BT}}= & {} {\mathscr {F}_{TB}}\nonumber \\= & {} \frac{(e^{\beta }(-2B(2e^{\beta }+2e^{\alpha }(1+e^{2\beta })\cosh (\gamma ))+e^{2\alpha }(-1+e^{2\beta })J_{x}\sinh (\gamma )+e^{2\alpha }(-1+e^{2\beta })J_{z}\cosh (\gamma )))}{T^{3}(1+e^{2\beta }+2e^{2\alpha +\beta }\cosh (\gamma ))^{2}},\nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned} {\mathscr {F}_{TT}}= & {} \frac{G1}{2T^{4}(1+e^{2\beta }+2e^{2\alpha +\beta }\cosh (\gamma ))^{2}}, \end{aligned}$$
(18)

with

$$\begin{aligned} \begin{array}{ll} G1=(e^{\beta }(4B^{2}(2e^{\beta }+2e^{\alpha }(1+e^{2\beta }\cosh (\gamma ))+e^{2\alpha }(2e^{2\alpha +\beta } \\ \;\;\;+(1+e^{2\beta })\cosh (\gamma ))J^{2}_{x}-4Be^{2\alpha }(-1+e^{2\beta })J_{z}\cosh (\gamma )\\ \;\;\;+e^{2\alpha }(1+e^{2\beta })J^{2}_{z}\cosh (\gamma )-2e^{2\alpha }\sinh (\gamma )J_{x}(2B(-1+e^{2\beta })-(1+e^{2\beta })J_{z}))). \end{array} \end{aligned}$$
(19)

The optimal estimator, in any given quantum metrology protocol, is defined as one which saturates the quantum Cramér-Rao inequality. This bound is a lower limit of the covariance matrix of estimators \({\hat{\theta }} = \left( {B,T} \right) \) and it reads

$$\begin{aligned} {\textrm{Cov}}\left( \hat{\theta }\right) \ge {\mathscr {F}^{ - 1}}. \end{aligned}$$
(20)

The inverse of the quantum Fisher information matrix is given by [65]

$$\begin{aligned} {\mathscr {F}^{ - 1}} = \frac{1}{{\det \left( \mathscr {F} \right) }}\left[ {\begin{array}{*{20}{c}} {{\mathscr {F}_{TT}}}&{}{ - {\mathscr {F}_{BT}}}\\ { - {\mathscr {F}_{BT}}}&{}{{\mathscr {F}_{BB}}} \end{array}} \right] . \end{aligned}$$
(21)

The Eq. (20) gives, in this case, the following inequalities [66]

$$\begin{aligned} \textrm{Var}\left( B\right) \ge \frac{{{\mathscr {F}_{TT}}}}{{\det \left( \mathscr {F} \right) }}, \end{aligned}$$
(22)
$$\begin{aligned} \textrm{Var}\left( T\right) \ge \frac{{{\mathscr {F}_{BB}}}}{{\det \left( \mathscr {F} \right) }}, \end{aligned}$$
(23)

and

$$\begin{aligned} \left( {\textrm{Var}\left( B\right) - \frac{{{\mathscr {F}_{TT}}}}{{\det \left( \mathscr {F} \right) }}} \right) \left( {\textrm{Var}\left( T\right) - \frac{{{\mathscr {F}_{BB}}}}{{\det \left( \mathscr {F} \right) }}} \right) \ge {\left( {\textrm{Cov}\left( B,T\right) + {\mathscr {F}_{BT}}} \right) ^2}. \end{aligned}$$
(24)

Using the Eq. (9), the operators of the symmetric logarithmic derivative \({L_B}\) et \({L_T}\) are respectively given by

$$\begin{aligned} {L_B}= & {} 2\left[ {\begin{array}{*{20}{c}} {\varepsilon \,{\partial _B}\,a_{11}}&{}0&{}0&{}0\\ 0&{}{(r + \delta ){\hspace{0.55542pt}} {\partial _B}\,b_{11} + (s + \tau ){\hspace{0.55542pt}} {\partial _B}b_{12}}&{}{(s + \tau ){\hspace{0.55542pt}} {\partial _B}b_{11} + (r + \delta ){\hspace{0.55542pt}} {\partial _B}\,b_{12}}&{}0\\ 0&{}{(s + \tau ){\hspace{0.55542pt}} {\partial _B}b_{11} + (r + \delta ){\hspace{0.55542pt}} {\partial _B}\,b_{12}}&{}{(r + \delta ){\hspace{0.55542pt}} {\partial _B}\,b_{11} + (s + \tau ){\hspace{0.55542pt}} {\partial _B}b_{12}}&{}0\\ 0&{}0&{}0&{}{f{\hspace{0.55542pt}} {\partial _B}a_{22}} \end{array}} \right] , \end{aligned}$$
(25)
$$\begin{aligned} {L_T}= & {} 2\left[ {\begin{array}{*{20}{c}} {\varepsilon \,{\partial _T}\,a_{11}}&{}0&{}0&{}0\\ 0&{}{(r + \delta ){\hspace{0.55542pt}} {\partial _T}\,b_{11} + (s + \tau ){\hspace{0.55542pt}} {\partial _T}b_{12}}&{}{(s + \tau ){\hspace{0.55542pt}} {\partial _T}b_{11} + (r + \delta ){\hspace{0.55542pt}} {\partial _B}\,b_{12}}&{}0\\ 0&{}{(s + \tau ){\hspace{0.55542pt}} {\partial _T}b_{11} + (r + \delta ){\hspace{0.55542pt}} {\partial _T}\,b_{12}}&{}{(r + \delta ){\hspace{0.55542pt}} {\partial _T}\,b_{11} + (s + \tau ){\hspace{0.55542pt}} {\partial _T}b_{12}}&{}0\\ 0&{}0&{}0&{}{f{\hspace{0.55542pt}} {\partial _T}a_{22}} \end{array}} \right] . \end{aligned}$$
(26)

The eigenvectors of the operators \({L_B}\) and \({L_T}\) give the optimal measurement bases that will allow us to reach the bounds in the inequalities (22), (23) and (24). It is simple to verify that the optimal measurement basis is

$$\begin{aligned} {\mathbf{{B}}_B} = {\mathbf{{B}}_T} = \left\{ {\left| {00} \right\rangle ,\left| {{\psi ^ + }} \right\rangle , - \left| {{\psi ^ - }} \right\rangle ,\left| {11} \right\rangle } \right\} . \end{aligned}$$
(27)

The symmetric logarithmic derivatives \({L_B}\) and \({L_T }\) commute and a common eigenbasis can be constructed using the eigenvectors of the Hamiltonian. This basis is the optimal estimation basis to estimate the magnetic field B and the temperature T. The analytical expressions of the minimum variances that give the highest precision for the estimation of parameters B and T are

$$\begin{aligned} {\textrm{Var}} {\left( B\right) _{\min }} =\frac{A_{1}}{A_{2}},\end{aligned}$$
(28)
$$\begin{aligned} \begin{aligned}A_{1}&=(16e^{4\beta } T^2(\cosh (\beta ) + e^{2\alpha }\cosh (\gamma ))^4 (4B^{2}(\cosh ( 2\alpha ) + \cosh (\beta )\cosh (\gamma ) - \sinh ( 2\alpha )) \\&+(\cosh (2\alpha ) + \cosh (\beta )\cosh (\gamma ) + \sinh (2\alpha ))J_{x}^{2} \\ {}&+\cosh (\gamma )J_{z}(-4B\sinh (\beta ) + \cosh (\beta ) J_{z}) + 2\sinh (\gamma ) J_{x}(-2B\sinh (\beta ) + \cosh (\beta ) J_{z}))), \\ A_{2}&=((1 + e^{2\beta } + 2e^{2\alpha + \gamma }\cosh (\gamma ))^{3} (e^{2\alpha }(1 + e^{2\beta })J_{x}^2 \\&+(\cosh (2\alpha ) + \cosh (\beta )\cosh (\gamma ) + \sinh (2\alpha ))J_{x}^{2} \\ {}&+4e^{\beta }\sinh (\gamma )J_{x}J_{z} + 2e^{\beta }\cosh (\gamma )(J_{x}^2 + J_{z}^2))), \end{aligned} \end{aligned}$$
$$\begin{aligned}&{\mathop {\textrm{Var}}}\left( T\right) _{\min } =\frac{4e^{-4\alpha }T^{4}(1+e^{2\beta }+e^{2\alpha +\beta }\cosh (\gamma ))(1+e^{2\alpha }\cosh (\beta )\cosh (\gamma ))}{e^{2\alpha }(1+e^{2\beta })J_{x}^2+4e^{\beta }\sinh (\gamma )J_{x}J_{z}+2e^{\beta }\cosh (\gamma )(J_{x}^{2}+J^{2}_{z})}. \end{aligned}$$
(29)
Fig. 1
figure 1

The variances of simultaneous estimates of parameters B and T with \(J_{x}=1\) and \(J_{z}=0.25\)

Full size image

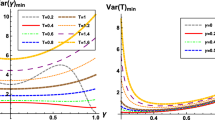
Figure 1 represents the results of the curves with minimal variances for the simultaneous estimation of parameter T and the magnetic field B for \(J_{x}=1\) and \(J_{z}=0.25.\) We notice that for low temperature the \(Var(B)_{min}\) attaints its minimum 0.24 when \(B=0.58\) which means that the optimal value of the magnetic field is \(B_{opt}=0.58.\) Furthermore, we observe that the variance of the temperature is minimal when the interval [0.5; 0.65] represents a value plage for the optimal value of T in quantum metrology. Now, if we estimate the parameters B and T individually, the Cramér–Rao inequality writes.

$$\begin{aligned} \textrm{Var}{\left( B \right) _{\min }^{Ind}} \ge \mathscr {F}_{BB}^{ - 1}, \hspace{1.5cm} \textrm{Var}{\left( T \right) _{\min }^{Ind}} \ge \mathscr {F}_{TT}^{ - 1}, \end{aligned}$$
(30)

with

$$\begin{aligned} \textrm{Var}\left( B \right) _{\min }^{Ind} = \frac{T^{2}(\cosh (\beta )+e^{2\alpha }\cosh (\gamma ))^{2}}{1+e^{2\alpha }\cosh (\beta )\cosh (\gamma )}, \end{aligned}$$
(31)

and

$$\begin{aligned} \textrm{Var}\left( T \right) _{\min }^{Ind} =\frac{2e^{\beta }T^{4}(1+e^{2\beta }+e^{2\alpha +\beta }\cosh (\gamma ))^{2}}{C_{2}}, \end{aligned}$$
(32)

with

$$\begin{aligned} \begin{aligned}C_{2}&=4 B^2(2 e^{\beta } + e^{2\alpha } (1 + e^{2\beta }) \cosh (\gamma ))+e^{2\alpha } (2 e^{2\alpha +\beta } + (1 + e^{2\beta })\cosh (\gamma ))J_{x}^{2} \\&-4 B (e^{2\alpha }) (-1 + e^{2\beta }) \cosh (\gamma )J_{z}+e^{2\alpha } (1 + e^{2\beta }) \cosh (\gamma )J_{z}^{2} \\ {}&-2 e^{2\alpha } \sinh (\gamma )J_{x}(2 B (-1 + e^{2\beta })-(1 + e^{2\beta }J_{z})). \end{aligned} \end{aligned}$$
Fig. 2
figure 2

The variances of individual estimates of parameters B and T with \(J_{x}=1\) and \(J_{z}=0.25\)

Full size image

Figure 2: the results obtained in Fig. 2 represent the evolution of the individual minimum variance of parameters B and T changes throughout the estimation protocol. From the curve we observe the behavior of these minimal variances almost similar to the results obtained in the simultaneous estimation shown in the figure, but it represents an error uncertainty in the precision of the optimal values of the parameters B and T. This uncertainty can be quantified by comparing the ratio of the minimum variance in the individual estimation scenario to the minimum variance achieved in the simultaneous scenario.

$$\begin{aligned} \Gamma = \frac{\Delta _{Sim}}{\Delta _{Ind}}, \end{aligned}$$
(33)

with \({\Delta _{\textrm{Ind}}} = {\textrm{Var}}_{\min }^{\textrm{Ind}}\left( B \right) + {\textrm{Var}}_{\min }^{\textrm{Ind}}\left( T \right) \), and \({\Delta _{\textrm{Sim}}} = \frac{1}{2}\left( {{\textrm{Var}}{{\left( B \right) }_{\min }} + {\textrm{Var}}{{\left( T \right) }_{\min }}} \right) \), we introduced a factor 1/2 into the \({\Delta _{\textrm{Sim}}}\) total variance formula because we estimated two parameters simultaneously. This factor is necessary for considering the resource reduction, illustrating that the simultaneous strategy demands two fewer resources than the individual scheme in the multiparameter estimation procedures. After some simplifications, we obtain

$$\begin{aligned} \begin{aligned}\Delta _{Sim}&=e^{-2 \alpha } (2 e^{\beta } + e^{2 \alpha } (1 + e^{2\beta }) \cosh (\gamma ))(4 B^2 (2 e^{\beta } + e^{2 \alpha } (1 + e^{2\beta })\cosh (\gamma ))+e^{2 \alpha } (2 e^{2 \alpha +\beta })\\&+(1 + e^{2\beta })\cosh (\gamma ))J_{x}^{2}-4 B +e^{2 \alpha } (-1 + e^{2\beta }) \cosh (\gamma )J_{z}+e^{2 \alpha } (1 + e^{2\beta }) \cosh (\gamma )J^{2}_{z} \\ {}&-2 e^{2 \alpha }\sinh (\gamma )J_{x}(2 B (-1 + e^{2\beta })) - (1 + e^{2\beta })) J_{z})), \end{aligned}\\ \Delta _{Ind}=(2 (1 + e^{2\beta } + 2 e^{2 \alpha +\beta }\cosh (\gamma ))((e^{2 \alpha } + e^{2 (\alpha +\beta )}) + e^{2\beta }\cosh (\gamma ))J_{x}^{2}+4 e^{\beta }\sinh (\gamma )J_{x}J_{z}+2 e^{\beta }\cosh (\gamma )J^{2}_{z})). \end{aligned}$$
Fig. 3
figure 3

The ratio between the minimal total variance of estimating the parameters B and T with \(J_{x}=1\) and \(J_{z}=0.25\)

Full size image

In Fig. 3, we represent the ratio \(\Gamma \) (33) in the case where the coupling parameters \(J_{x} = 1\) and \(J_{z} = 0.25.\) As it can be seen on the curve, the minimum variance for the simultaneous strategy is consistently smaller than the minimum total variance achieved through individual strategies; in other terms, \(\Delta _{\textrm{Sim}} \le \Delta _{\textrm{Ind}}\). These results validate that when simultaneously estimating the parameters B and T in the XXZ model with a magnetic field, we achieve higher estimation accuracy compared to individual parameter estimates.

4 Concluding remarks

In this study, we have focused on exploring the multi-parametric estimation strategy in quantum metrology within the Heisenberg system. To ensure realism, we have chosen the anisotropic XXZ model, allowing us to investigate the effects of the magnetic field and temperature on the QFI and more importantly, on the precision of parameter estimation. We have mathematically analyzed the multi-parameter quantum Cramé-Rao bound for both simultaneous and individual estimation of the temperature and magnetic field parameters. This bound is mathematically linked to the concept of the quantum Fisher information matrix. Our findings demonstrate that as the values of the magnetic field increase, the local minimum for the variance of the individual estimation \(\textrm{Var}\left( B \right) _{\min }^{Ind}\) tends to be suppressed. Consequently, we have concluded that the simultaneous estimation of the parameters B and T in the XXZ model offers better estimation accuracy compared to individual estimation. These results highlight the advantages of considering multiple parameters simultaneously for more precise estimation. Furthermore, it is important to note that this research focuses on two-qubit systems. To broaden the scope of our study, future investigations can be extended to include multi-qubit cases, allowing for a more comprehensive analysis of the topic.