1 Introduction

Superoscillatory functions were discovered by Yakir Aharonov et al., and later by Michael Berry independently in different contexts [1,2,3,4]. The faster than expected oscillations of this class of functions are physically close to the phenomenon of weak valued pointer shifts [5]. The usual property of interest in these functions is that fact that although these functions have a Fourier spectrum that is bounded by a largest frequency Fourier component, it is possible to find a small region of the function that locally oscillates faster than that fastest Fourier mode. While counter intuitive, this is a straightforward mathematical fact that can be seen in quite simple functions. One such function is [2, 6]

$$\begin{aligned} f(x) = (\cos x + i a \sin x)^N, \end{aligned}$$
(1)

where a and N are real constants. It is easy to see that while the largest wavenumber in the Fourier series expansion of this function is \(k_\mathrm{max} = N\), if we expand the function around the position \(x=0\), the function locally oscillates with a wavenumber of aN, which can be arbitrarily larger than N. There are two trade-offs that must be made to achieve this fast oscillation. First is the fact that the position x, must be approximately in the range \(\left( -1/\sqrt{N(a^2-1)}, 1/\sqrt{N(a^2-1)}\right) \), to obtain the fastest oscillations, and outside this region the function behaves very differently. The second is that the magnitude of the function at this point is in fact very small. Its value is exponentially suppressed, so that this “anomalous” feature must be greatly magnified to be of any use in a practical setting.

The physically motivating reason to consider this class of functions is to gain “superresolution” of the features of an image in an imaging system. In a conventional imaging system, the minimum feature size of an object that can be resolved is given by

$$\begin{aligned} \delta _x = \lambda /(2 {\mathcal {A}}), \end{aligned}$$
(2)

where \({\mathcal {A}}\) is the numerical aperture of the imaging tool and \(\lambda \) is the wavelength of the light (the Abbe limit) [7]. This is closely related to the Rayleigh bound for imaging by a numerical factor of 1.22 larger. This later criteria is derived from imaging the separation of two point sources, and seeing when the point spread functions of the two point sources begin to overlap, such that it is no longer possible to see if the object is a single bright point or two points of half the intensity. The resolution is ultimately set by the wavelength of the light that is being used to interrogate the object: the shorter the wavelength in Eq. (2), the more can be the resolution obtained in the image.

In recent years, several methods have been proposed to get around the Rayleigh limit. We mention optical mode sorting rather than direct imaging [8], evanescent wave imaging [9], and quantum states of light [10] as three possible methods, in addition to the one we will discuss here: superoscillations and supergrowth. Given the introduction above, the physical implementation of this idea is straightforward: create a state of light that has superoscillatory behavior (such as with a spatial light modulator [2], or a quasi-periodic array of nanoholes in a screen [11]), and use this as the point spread function for the imaging system. The light is then used to image the object of interest, and if the processing is done correctly, the image will be able to show object features smaller than the wavelength of the light used. This could be important for many applications, notably for biological samples [12]. This technique has been successfully implemented in laboratory settings, with enhanced resolution [4]. However, the technique has several drawbacks. As mentioned previously, the value of the superoscillatory function is greatly suppressed in this quickly oscillating range. In an optical context, what is usually done is to apply a pinhole filter of the light to select the very small range of superoscillatory light. This has the effect of reducing the intensity of the imaging light down by many orders of magnitude, and is consequently very wasteful of the light. This leads to several questions: Is there a better way of using the superoscillatory features of the function other than to simply filter it? What is the optimal resolution one can obtain from the whole function? If the resolution of the whole function can exceed that of the superoscillatory portion of the function, what is the optimal way to extract it? The rest of the paper begins to develop a framework to answer these questions.

The paper is organized as follows. In Sect. 2 we introduce the concept of supergrowth and demonstrate that the rate of exponential growth can exceed that of the fastest Fourier component. In Sect. 3 we review the basic theory of optical imaging and demonstrate the improved performance of the superoscillation feature as well as the supergrowth feature in comparison to just using the fastest Fourier component of the function (appropriately scaled in intensity). In Sect. 4, we give an outlook for the further development of this proposed idea for imaging.

2 Supergrowth

In this paper, we demonstrate that it is also possible to use another feature of superoscillatory functions to gain access to superresolution features. We observe that the function (1) also changes exponentially over small position scales. Importantly, the value of the function can change exponentially with a growth or decay rate that exceeds that of the largest inverse wavenumber. Our proposal is to use this feature of the function to image with. We mention that this idea is not so different from using evanescent waves to beat the Rayleigh limit [13]. In those ideas and experiments, the inventors notice that because the intensity of an evanescent wave of light, impinging for example, on a surface at an angle greater than Brewster’s angle, decays exponentially as one moves further into the sample, with a decay constant faster than the wavelength, this optical physics can be used to image finer features of the object than could be done in conventional imaging. Normal to the total internal reflection surface, the electric field decays exponentially with distance z,

$$\begin{aligned} E_\mathrm{evan}(z) = E_0 \exp (-z/d_\mathrm{p}), \end{aligned}$$
(3)

where \(d_\mathrm{p}\) is the penetration depth of the sample and is typically \(\sim 0.75 \lambda \) [14]. This idea does indeed work and because the decay rate of the light is set by physical parameters, besides the wavelength, fine structures can be resolved. The method and its relatives have been called various things, “photon tunneling microscopy” [14], “frustrated total internal reflection microscope” [13], “scanning near-field optical scanning microscopes” [15], and so on. The main drawback of this method is the fact that the imaging can only be done using near-field optics, before the evanescent waves have a chance to die away.

The great advantage the supergrowth features described below can have over the evanescent wave method is that these are far-field features of the optical field. Another advantage our idea has over the superoscillation method is the fact that the supergrowth region of the function that is to be used has much higher intensity, giving much better signal to noise in the detection process. The downside of our method is that a large range of intensity measurements must be made, which can vary over many orders of magnitude. Thus, a high dynamic range detector will be necessary to extract the finest features of the object.

If we take the function (1) and write it as \(\log f(x) = A + i B,\) we see that this form reveals the local exponential behavior. Let us define a local wavenumber k(x), and a local decay or growth rate \(\kappa (x)\), so that we can write \(f = {\mathcal {N}} \exp [\int i k(x) \mathrm{d}x + \int \kappa (x) \mathrm{d}x]\), where \(\mathcal {N}\) is a constant. Here k(x) captures the oscillatory behavior, and \(\kappa (x)\) captures the growing or decaying behavior. We therefore have the definitions \(k(x) =\mathrm{Im}\, \partial _x \log (f)\), and \(\kappa (x) = \mathrm{Re}\, \partial _x \log (x).\) For the function (1), the results are

$$\begin{aligned} k(x) = N \frac{a}{\cos ^2 x + a^2 \sin ^2 x} \end{aligned}$$
(4)

and

$$\begin{aligned} \kappa (x) = N \frac{(a^2-1) \sin x \cos x}{\cos ^2 x + a^2 \sin ^2 x}. \end{aligned}$$
(5)

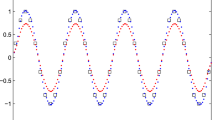
These functions are plotted in Fig. 1 for \(N = 20\), and \(a=6\). The figure shows that there are regions of k(x) that exceed the highest Fourier frequency, \(k_\mathrm{max} = N\), and also there are (different) regions where \(\kappa (x)\) exceeds the highest Fourier frequency, as well. It is easy to see that the largest local wavenumber is aN near \(x=0\). The largest growth (decay) rate occurs when \( x = \pm \arctan (a^{-1})\), giving a maximum rate of

$$\begin{aligned} \kappa _\mathrm{max} = \pm \frac{N}{2} \left( a - a^{-1}\right) . \end{aligned}$$
(6)

For large values of a, this limits quickly to \(\pm N a/2\). This value can be much larger than the fastest Fourier component of N, but still half as large as the fastest superoscillatory local wavenumber. The biggest advantage is that the function is not small near this region, but indeed exponentially rises or falls in value. If we view f(x) as the value of an electric field in an optical imaging problem, then the intensity is given by \(I(x) = |f(x)|^2\). The intensity of the function (1) is then governed by \(\kappa \) because of the consequence of the polar decomposition of f, giving \(\log |f|^2 = 2 \mathrm{Re} [\log f]\), and therefore

$$\begin{aligned} \partial _x \log I(x) = 2 \kappa (x), \end{aligned}$$
(7)

which has a maximum growth (decay) rate in position of aN, matching the superoscillatory advantage.

Fig. 1
figure 1

The local wavenumber and local rate of growth or decay are plotted versus position and divided by N. This plot takes \(a=6, N=20\). The upper and lower bounds are \(\pm k_\mathrm{max}/N=\pm 1\), the scaled largest wavenumber in the Fourier expansion

Full size image

3 Theory of optical imaging and the usefulness of supergrowth

In the theory of optical imaging, we have the concept of the object one wishes to image, which can be, for example, an intensity mask, or an optical source, together with the optical image itself. For a simple one-dimensional model, these are represented by the functions O(x) for the object and S(x) for the image. They are linked via the point spread function of the imaging system, \(\chi (x)\), which indicates the image created from a point source. The point spread function is also the optical Green’s function for the system.

Imaging theory relates these functions as

$$\begin{aligned} S(x) = \int \mathrm{d}y O(y) \chi (y-x), \end{aligned}$$
(8)

so the image created is a convolution of the object with the point spread function [16]. One way of characterizing the resolving power of the microscope is to image two point sources of small separation distance \(\epsilon \). Consider two point sources of unit intensity, whose object function is given by

$$\begin{aligned} O(y) = (1/2) \left[ \delta (y-\epsilon ) + \delta (y+\epsilon )\right] . \end{aligned}$$
(9)

In this case, the image function will be given by

$$\begin{aligned} S(x) = (1/2) \left( \chi (x-\epsilon ) + \chi (x+\epsilon )\right) . \end{aligned}$$
(10)

We wish to use the superoscillating/supergrowth function’s intensity for the point spread function of this system. The central question is for how small of an \(\epsilon \) can we still detect the difference of a double source from a single source? The intuition of why the supergrowth function gives an advantage is that as the two point sources are moved apart, the intensity as filtered through the point spread function will grow super-exponentially faster than the wavelength. This will give enhanced resolution of the object. This basic observation is confirmed in the plot shown in Fig. 2. There, we compare the log intensity from the two hypothetical images of (a) a single point source at position \(y=0\) and (b) two point sources of half the intensity at positions \(y = \pm \epsilon \), as we scan through the image plane. Using the values of \(N=20\), \(a=6\), and \(\epsilon = 0.01\), we would expect to only be able to resolve lengths of size \(\lambda \sim 1/N = 0.05\). However, it is clear that there is a much larger difference in sensitivity even on a log plot. Taking the ratio of the intensity value of the two possible scenarios at the position of maximum sensitivity \(x \approx 0.165\), we obtain nearly a factor of 1.7 ratio in intensity, which should be easily detected. This gives a basic proof of principle of the concept.

We can demonstrate this effect more clearly in Fig. 3, where we use the fastest Fourier component function, interfered with itself to yield a point spread function of \(\chi _\mathrm{Fourier} = \cos ^2(N x)\).

Fig. 2
figure 2

The log-intensity ratio of the image for a point source separation of \(\epsilon = 0.01\) compared to a point source separation of \(\epsilon = 0\), plotted verses image position coordinate. \(N=20, a=6\). Contrast is maximized at \(x = \arctan (1/a) \approx 0.165\)

Full size image
Fig. 3
figure 3

The sensitivity of a pure Fourier mode image function with \(N=20\) is plotted versus \(\epsilon \) at the point of maximum contrast, \(x = 0\). The y axis is \(\delta I/I(0)\), where \(\delta I = I(\epsilon ) - I(0)\)

Full size image
Fig. 4
figure 4

(Top) The sensitivity of the superoscillation image function with \(N=20, a=6\) is plotted versus \(\epsilon \) at the point of maximum contrast, \(x = 0\). The y axis is \(\delta I/I(0)\), where \(\delta I = I(\epsilon ) - I(0)\). (Bottom) Same as top, with a zoom into the small \(\epsilon \) region, demonstrating super-resolution

Full size image
Fig. 5
figure 5

(Top) The sensitivity of the supergrowth image function with \(N=20, a=6\) is plotted versus \(\epsilon \) at the point of maximum contrast, \(x = \arctan (1/a) \approx 0.165\). The y axis is \(\delta I/I(0)\), where \(\delta I = I(\epsilon ) - I(0)\). (Bottom) Same as top, with a zoom into the small \(\epsilon \) region, demonstrating super-resolution

Full size image

We plot the relative difference of \((S(x, \epsilon ) - S(x, 0))/S(x, 0)\) at the place of maximum sensitivity \(x=0\) for \(N=20\). The curve in Fig. 3 demonstrates the expected resolution of \(\epsilon \sim 1/N \approx 0.05\). We can contrast this behaviour with the superoscillatory behavior, using the point spread function of \(\chi _{so} = (\mathrm{Re} f(x))^2\). The plots in Fig. 4 confirm that much better sensitivity of the image function is achieved around \(x=0\), where the superoscillations occur. We see that a factor of approximately \(a=6\) improvement in resolution is achieved. Similarly, if we consider the behavior of the supergrowth part of the function, we can directly use the function itself (rather than an interfered version with itself), so \(\chi _\mathrm{sg} = |f(x)|^2\). The relative difference of \((S(x, \epsilon ) - S(x, 0)/S(x, 0)\) is plotted in Fig. 5, at the place of maximum sensitivity, \(x = \arctan (1/a)\). It is clear that we also achieve an improvement in resolution of the image function by a factor of approximately \(a=6\) compared to the pure Fourier mode oscillating with wavenumber N.

4 Outlook

In this paper, I have explored the possibility of a new type of superresolution scheme, built on the concept of supergrowth and intensity contrast imaging. A number of tantalizing initial ideas and issues have been raised and should be explored. This suggests the following research program:

  • Make a systematic study of the improved resolution using the supergrowth concept. This will involve calculating the Fisher information of the optical intensity distribution about the parameter \(\epsilon \) introduced above, and demonstrating that it vanishes more slowly as \(\epsilon \) goes to zero than a conventional imaging system. The Fisher information should contain the global advantage in optical resolution [17] and exceed the precision from either filtering the superoscillatory part of the function or the supergrowth parts of the function.

  • I conjecture that any optical wave phenomenon that exhibits superoscillations also exhibits supergrowth phenomenona. Prove it by using a Kramers–Kronig relation of the log-electric field, and relating the argument of the function to its modulus (the A and B functions introduced in Sect. 2). That is, if the local wavenumber exceeds the largest Fourier wavenumber at a given position, the local (growth or decay) rate will also exceed it at another position.

  • This would imply that any system that uses the superoscillation method for superresolution can also use the supergrowth method as well to get improved resolution. This is extremely interesting because all existing methods using superoscillations go to great lengths to filter out the growing part of the electric field intensity, but we have demonstrated here that this portion of the field is equally useful (if not more so) for imaging with superresolution. The stone which the builders rejected has become the chief cornerstone.