Two-person Bargaining with Lexicographic Preferences

Abstract

In bargaining theory a usual assumption is either that of von Neumann–Morgenstern utility functions or that of continuous preferences. In this note, we consider a bargaining model with lexicographic preferences for the two players. We show that the Rubinstein et al. (1992), definition can still be used to obtain a Nash solution. We also look briefly at the alternating offers approach.

1 Introduction

There have been and still are ongoing substantial, original developments in both the general equilibrium and game theory areas. The papers in the recent ‘Symposium on Discontinuous Games’, in Economic Theory, edited by Reny (2016) make important contributions. A main theme is that the continuity assumption of preferences and payoffs in the Nash (1950) and Debreu (1952) theories has been relaxed. The issues and the development of the theory from Nash and Debreu are explained clearly in the introduction of the He and Yannelis (2016) paper in the volume. In their work they generalize the classical equilibrium existence theorems by dispensing with the assumption of continuity of preferences.

With respect to the developments in Nash equilibrium theory, the original contribution is by Dasgupta and Maskin (1986) and it was followed up by Reny (1999). This pioneering work dispenses with the continuity assumption on the payoff function of each agent as a necessary condition for the existence of Nash equilibria in game theory. Their works were motivated by realistic applications in Bertrand competition and auctions theory.

Starting with Dasgupta and Maskin (1986) important research in generalizing the conditions of Nash equilibrium is still taking place. Generalizations of the Nash–Debreu equilibrium existence theorems have been obtained where payoff functions need not be continuous.

In this note, we make an extension of problems in bargaining theory. A usual assumption is either that of von Neumann-Morgenstern utility functions or that of continuous preferences. We break away by considering a model with lexicographic preferences for the two players.

Lexicographic preferences have not been widely discussed in the literature mainly because of the mathematical convenience of continuous and partially continuous functions. We believe there are circumstances where lexicographic preferences are important. First we look at some such examples.

Examples with lexicographic preferences

Lexicographic preferences, of course within ranges of variables, are seen in the following examples.

• (i) A Choice between quality vs quantity.

  At a higher level of income, away from Giffen goods, richer people have as their main concern the quality of goods. Beyond a particular level of consumption there is no compensation for loss of quality through larger quantity.

• (ii) A choice between unemployment and inflation. At a given level of unemployment society is better off with lower inflation. But the first concern of policy makers is unemployment and its level. There is no substitution between the variables.

• (iii) Education vs holidays. For a number of families there is no trade off between school fees and family holidays.

• (iv) Safety vs speed. It is given that the plane will reach its destination within a certain time. Beyond this, the passengers are not prepared to trade risk with faster arrival.

• (v) State security vs welfare. Beyond some elementary level of welfare covering the needs of the population, military power might be the first consideration of a regime. The expression “our first priority is” implies a lexicographic arrangement of this nature. Such issues might arise when basic needs have been met and the choice of one item is compared to the rest of the goods, without the possibility of substitution. The general idea is that more attention could be paid to integrating lexicographic preferences into the analysis. As far as we know this the first time that the idea of lexicographic preferences is applied to bargaining theory. It is the use of the Rubinstein et al. (1992) method that makes this possible.

2 The model

In the context of bargaining, it would be interesting to look at an example beyond the original von Neumann-Morgenstern utility functions, Nash (1950), and the wider continuous preferences assumption, Rubinstein et al. (1992). The assumption of ‘nice’ preferences is usual and it characterizes also the choices of an arbitrator when he is called upon to make the best recommendation among solutions. We are looking at the Nash solution in an example in which the complete preference preorderings are not continuous, Debreu (1959). In particular the preferences of both bargainers are lexicographic.

Example

Two players, P1 and P2, are bargaining over $1. P1 gets share $x_1$ and P2 gets $x_2$, not necessarily on the boundary set. In disagreement each player gets $0. We denote $x=(x_1, \;x_2)$. The (lexicographic) preferences of P2 are as follows. For fixed $x_1$, he strictly prefers more of $x_2$. On the other hand he strictly prefers a lower $x_1$ for P1 (even with $x_2=0$) to any combination with a larger $x_1$. That is P2 is happiest the less P1 gets. The bargaining set is denoted by X.

These preferences, denoted by $\succeq$, are not continuous. If a feasible sequence $(x^n_1,\; x^o_2)$ with $x^n_1>x^*_1$ and constant positive $x^o_2$ approaches the vertical line of $x^*_1$ then throughout the sequence $(x^*_1, 0)\succeq (x^n_1, x^o_2)$. On the other hand, in the limit $(x^*_1,\; x^o_2)\succ (x^*_1, 0)$. Lack of continuity of preferences places the example beyond the ‘if and only if’ statement in Debreu’s theorem for the existence of a continuous utility function. Moreover there is no representation in a utility function altogether, as there are too many elements to be registered. For the (lexicographic) preferences of P1 the roles of $x_1$ and $x_2$ are reversed and the argument is adapted. P1 is happiest the less P2, his opponent, gets.

An agent, (arbitrator, mediator), who is experienced and has his own preferences, is called upon to divide the $1. According to his preferences all points on the boundary are Pareto optimal. A simple and intuitively fair rule for the agent to follow would be, for example, to maximize the minimum element of $(x_1, x_2)$ and give $$\displaystyle \frac{1}{2}$ to each. The agent can be assumed to be impartial, and thus a solution to the bargaining problem could be obtained although the preferences of the players are not of the type usually considered.

We now look at whether, without the intervention of an arbitrator, the application of the Rubinstein et al. (1992) approach for characterizing a bargaining solution can be extended to produce a result in the above example where preferences are not continuous.

When we go beyond utility functions and ‘nice’ preferences it is a different world not yet fully explored. The results here are a first step in the area of bargaining theory.

3 The Nash solution

We use definitions from Rubinstein et al. (1992), repeated in Osborn and Rubinstein (1997). X is the bargaining set and D the disagreement point. The game is normalized so that $D=0$. The preferences $\succeq _i$ are not here necessarily continuous. A bargaining solution assigns to a bargaining problem a unique feasible $x^*=(x^*_1,\;x^*_2)$. We take 301.2 in Osborne - Rubinstein, p. 301:

Definition

The Nash solution is a bargaining solution that assigns to the bargaining problem $(X;D;\succeq _1;\succeq _2)$ an agreement $x^* \in X$ for which if $p x \succ _i x^*$ for some $p \in [0, 1]$ and $x \in X$ then $p x^* \succeq _j x$ for $j \not = i$.

We can also turn the definition into an equivalent form:

Definition 1

The allocation $x^*\in X$ will not be a Nash solution only if there exists $p \in [0, 1]$ such that for $x \in X$ we have $p x \succ _i x^*$ and $p x^* \prec _j x$ for $j \not = i$.

Given these definitions of objection and counter objection the Nash solution is the set of all agreements $x^*$ with the property that player j, Pj, can counter-object to every objection of player i, Pi. to $x^*$.

The approach of Rubinstein et al. (1992) is quite powerful, it rests on the rational outcome of the agents’ arguments of offers and objections and nests the Nash product of utilities approach. The argument is delicate and intriguing. The decisions of P1 and P2 are decentralized and for a Nash solution there should be a counter objection to any possible objection. Hence, $x^*$ cannot be blocked.

The investigation of the Nash solution is through the following steps. Faced with a proposed allocation $x^*$ player i objects. He makes the offer of x which has probability p that negotiations on it will be successfully completed, and $1-p$ that it will be rejected and bring about the status-quo payoffs (0, 0). Player i is threatening to press his objection to $x^*$, i.e. to take action that will lead to no agreement with probability $1- p$. So he will be expecting payoff vector px which, for him, must be strictly better than $x^*$, for the objection to make sense.

Pj makes his own calculations. He listens to x and accepts p as the credible probability of success of the negotiations. Taking into account the threat $1-p$ of a failure, if he insists on $x^*$, he will end up with expected payoff $px^*$.

Therefore, he can successfully counter-object to (x; p) if $p x^* \succeq _j x$. The interpretation is that even under the risky conditions that Pi creates with his objection, it will still be desirable for Pj to insist on the original agreement $x^*$ rather than agreeing to what is now offered, x. That is, Pj calculates conditions under which, in spite of the raised objection (x; p), it is still desirable for him to insist on $x^*$.

Rubinstein’s et al. (1992) definition of a Nash solution, $x^*$, puts together the actions and interactions of the bargainers and says that for an equilibrium to be reached any attempt by Pi to make a profitable counter offer will be frustrated by the insistence of Pj on $x^*$.

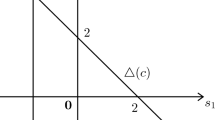
Now we look at the application of this definition to the lexicographic preferences example above, (Fig. 1a). As a contrast, at the end we also look at a conventional bargaining game (Fig. 1b).

We use $X^o$ for the open set in X and $X \setminus X^o$ for its complement. First we look at the Pareto optimal payoffs for X, with the lexicographic preferences considered here. The non-negative vertical axis shows the payoff to Pj, identified with P2, and the non-negative horizontal axis measures that of Pi, identified with P1.

It is easy to see that no allocation $x\in X^o$ is Pareto optimal. With centre $x\in X^o$ we can draw a small circle of payoffs. Changes of allocations in a south-west direction will always be feasible. This will imply that both players will be better off, as the quantity allocated to the opponent is reduced. Of course the same is true for the allocations on the boundary of X away from the axes.

Next, the two axes in X, including the status-quo payoffs (0, 0), share the property that it is not possible to make one player better off without reducing the payoff of the other. Consider the vertical axis. A movement into $X^o$ would imply that Pj’s payoff is reduced. Also any movement along the vertical axis would imply that the payoff of one of the agents would be reduced. We can argue in an analogous manner if we start from a point on the horizontal axis.

It follows that the feasible allocation on the axes form the set of all Pareto optimal points. This is due to the particular structure of the preferences.

Fig. 1

Applying the criterion of Nash solution to a lexicographic preferences and b a utility model

We shall now show that no point $x'\in X^o$ is a Nash solution. Given proposal $x'=(x'_1, x'_2)$, player i can object with the feasible counter proposal $\{(x=(x'_1-\epsilon ,\;x'_2-\epsilon , \;p=1)\}$, where $\epsilon$ small. Then $p x \succ _i x'$ and also $p x \succ _j x'$ which means that no counter objection will be raised by P$_j$ as both players strictly prefer the counter proposal. Of course the same is true for the allocations on the boundary of X away from the axes.

Next we show that no allocation placed on either axis away from the origin will be a Nash solution. Looking only at the vertical axis, this is shown on the graph in Fig. 1a with the proposed allocation placed on $x^*$. Player i objects to it with $(x; \;p=\epsilon )$, where $\epsilon$ small. It is true that $px \succ _i x^*$ but also $px^* \prec _j x$. Hence no such $x^*$ can be a Nash solution. There will always be an objection by P$_{i}$ that will be preferable to both bargainers.

We note that we do not have to consider also an objection with $x>x^*$, because all we had to do was to find a single $(x;\;p)$ for which the definition of a Nash solution is not satisfied.

Finally, we investigate whether $x^*=(0, 0)$, i.e. the status-quo allocation, is a Nash solution and consequently the only one for the bargaining game.

Suppose that Pi objects with the offer $(x=(x_1, \;x_2)> (0,\;0);\;p>0)$. Then $px \prec _i x^*$ and $px \prec _j x^*$. Therefore, $x^*=(0, 0)$ cannot be blocked through $((x=(x_1, \;x_2)> (0,\;0);\;p>0)$. No player will be making such a counter offer.

Now looking only at the horizontal axis, we argue as follows. We need to have $px \succ _i x^*$ so we must have $p>0$ and we must also have $x_1>0$. Then we come to Pj and we get $px^*\succeq _j x$. Hence Pj objects in his turn to $((x_1>0,\; x_2=0);\;p>0)$. Therefore, $x^*=(0, 0)$ is the unique Nash solution.

The application of Rubinstein’s et al. criterion for the Nash solution selects the point (0, 0) where envy stops everybody from getting any sum of money. The $1 is left undistributed.

By contrast we also look at a conventional situation (Fig. 1b). It gives an example that the Nash solution of $(X={\text {dividing a}\; \$ 1;\;\;D=\$ 0;\;u_1=x_1;\;u_2=x_2})$, (in the usual notation), cannot be blocked by a particular objection. Indeed it cannot be blocked by any objection.

Proposition 302.1 connects Rubinstein’s et al. approach with the Nash approach. It shows that the former nests the latter. Rubinstein et al. strict requirement that every possible objection to $x^*$ has a counter objection is matched up by the uniqueness of the maximum of the Nash product.

In Rubinstein’s et al. paper the preferences of P1 and P2 are assumed to be continuous. On the other hand although lexicographic preferences are not continuous they have been referred to in economic theory; for example in Debreu (1959). It is of interest that the Rubinstein et al. criterion has wider applicability. It can also produce a Nash solution in a lexicographic preference bargaining game where no possibility of a von Neumann–Morgenstern or more general utility functions is available.

4 The alternating offers approach

4.1 The utility model

Rubinstein (1982) presents a non-cooperative, sequential offers approach to bargaining which offers support, through a refinement of Nash equilibrium, to the Nash bargaining solution (NBS), and the generalized NBS. The game in which simultaneous demands are made is replaced by one in which the players at each move take turns to issue a demand which the other player may accept or reject. We consider an infinite horizon and assume no discounting. The game from $\hbox {t}=2$ is identical with that from $\hbox {t}=0$. This is the uniformity over time property of the model. Even with a constant discount factor $\delta <1$ the two games would be identical after re-scaling.

Lemma 1

For the model with $u_1=x_1$ and $u_2=x_2$, any partition $x_1+x_2=1$ can be supported as a Nash equilibrium through appropriate strategies.

Proof

• P1 adopts the strategy:

• Say $x=(x_1, x_2)$ at $\hbox {t}=0$;

• For t>0, if t is odd, say N, (reject), and if t is even, say $x_1=1$, both at any node.

• P2 adopts the strategy:

• At $\hbox {t}=0$: If P1 says x, then say Y, (accept);

• if P1 says $x'\not =x$, then say N.

• For t>0, if t is even, say N and if t is odd, say $x_1=0$, both at any node.

Fig. 2

Supporting a a Nash equilibrium in the utility case and b the status-quo payoffs in the analogous lexicographic case

We want to show that the above pair of strategies form a Nash equilibrium. Assume P1 changes his strategy and P2 stays with the same one. Either P1 changes at $\hbox {t}=0$ to $x'$ say, implying that the game never terminates, or P1 does not change at $\hbox {t}=0$ which has the same outcome as the original strategies.

Next assume P2 changes and P1 stays the same. Either P2 does not change at $\hbox {t}=0$ which implies the same outcome as the original strategies. Or P2 changes at $\hbox {t}=0$ implying either a changed response to x to N implying no termination, or no change in response to x with the same payoffs as the original strategies. Thus the strategies above form a Nash equilibrium. (See Glycopantis and Muir 2010) $\square$

Intuitively, an offer is made at $\hbox {t}=0$ which is accepted. Beyond this, each player will always demand $1 and will reject all offers. When it is his turn to play he will offer $0 to his opponent. If we look at the game at $\hbox {t}=1$, there can be no agreement following, at that point, a ‘reject’ decision by P2. So the only agreement that there can be is on x, proposed at $\hbox {t}=0$.

The development of the representative game tree is shown in Fig. 2a. Throughout, the double lines indicate actual choice at a node.

The above discussion explains that there exist an infinite number of Nash equilibria corresponding to the possible divisions of the $1. We note that the strategies described above are not subgame perfect. For consider the node resulting from saying $x'\not =x$, with $x'_2>x_2$, at $\hbox {t}=0$. If P2 alters strategy to: “If P1 says $x'$, then say Y, he becomes better off.

Finally, we consider the following strategies. Each player will always demand the whole dollar and will reject anything less. Now this is a Nash equilibrium. Given the strategy of the opponent there is nothing the player can do to improve his payoff. The strategies might not be subgame perfect, as a player can profit by saying Y to a positive offer, but they are Nash. However, the players end up with the conflict point (0, 0), which is not Pareto optimal. Also by allowing $x_1+x_2\le 1$, we obtain Nash equilibria which are not Pareto optimal.

4.2 The lexicographic preference model

In the ordinary utility problem, when we propose a division of the dollar we always have that in the case of disagreement the status-quo payoffs vector (0, 0) is available. In the case of the lexicographic preferences the structure of the game is such that the status-quo payoffs vector (0, 0) assumes special significance. We can call this ‘conflict’ point the ‘compromise’ outcome. First, taking a lead from Lemma 1 we consider the case where at all stages $x_1+x_2=1$ and ask whether any such division can be supported through strategies as a Nash equilibrium. The analysis is with the help of Fig. 2b.

Lemma 2

For the model with the lexicographic preferences, any partition $x_1+x_2=1$ with $x_2\not =1$, proposed by P1 at $\hbox {t}=0$, can support, through appropriate strategies, the status-quo, compromise payoff (0, 0), as a Nash equilibrium.

Proof

Consider the feasible strategies with $x_1+x_2=1$: P1 plays x with $x_2\not =1$ at $\hbox {t}=0$ and then P2 plays N, at all nodes horizontally. From then on the players alternate in asking, at any node, for the best possible outcome for themselves and similarly rejecting all offers made, in which case there will be no agreement. The players end up with the compromise payoff $(0,\;0)$.

This is a Nash equilibrium because no player can improve his payoff by changing his strategy unilaterally. Assume P1 changes his strategy and P2 keeps his own the same. If P1 changes at $\hbox {t}=0$ the outcome is no agreement. If at any point P1 changes his strategy and accepts P2’s offer, then the game terminates but P1 will be worse off. Assume next that P2 changes his strategy and P1 keeps his own the same. If at any point he changes his strategy and accepts P1’s offer, then the game terminates but P2 will be worse off. Also if P2 changes his offer at any stage, this will not affect the eventual outcome of the compromise payoff $(0,\;0)$. $\square$

Fig. 3

A support for the status-quo payoffs in the general lexicographic case

On the other hand if P2 is called upon at some t>0, due to a trembling hand of P1, to accept $x_2=1$ he will play Y and obtain his best outcome. Therefore, the strategies described above, although Nash, do not form a subgame perfect equilibrium. However if a responding player chooses N, at all nodes apart from when he is offered the whole dollar, where he plays Y, the Nash equilibria discussed above is subgame perfect.

In the statement of Lemma 2 we are concerned with the case of the partitions at $\hbox {t}=0$ with $x_2\not =1$. We now consider the strategies: P1 plays x with $x_2=1$ at $\hbox {t}=0$ and then P2 plays N, at all nodes horizontally apart from $x_2=1$, where he plays Y. From then on the players alternate in asking, at any node, for the best possible outcome for themselves and similarly rejecting all offers made. Then the strategies which start with the pair ($x_2=1$, Y), for P1 and P2, respectively, do not form a Nash equilibrium. P1 can change his strategy to $x_2\not =1$ and become better off through the eventual outcome (0, 0).

Of course the strategies in the proof of Lemma 2 were also available in the utility model discussed above. However, in that case they do not imply a Nash equilibrium. P2 can change his strategy at $\hbox {t}=0$ to accepting the offer of P1 and become better off.

We now turn our attention to the general case of feasible strategies {$x_1+x_2\le 1; x_1, \;x_2\ge 0$}. This is exactly what the lexicographic structure of the preferences requires. It is much easier to draw a game tree to represent the feasible division of the straight line segment $x_1+x_2=1$. For the generalized case it is harder to visualize the tree but we can still understand that a decision line with specific values $x_1>x_2$ is possible. Any straight line segment $\{x_1+x_2=c;\; 0<c \le 1\}$ of the 2-simplex of the feasible set of allocations can be divided completely. So perhaps with some stretch of imagination we can think of the graph of an extensive form game.

In Fig. 3 when referring to player Pi we place to the left of $(0,\; 0)$ the vectors with $x_i> x_j$ and to the right those with $x_j> x_i$. The vectors with $x_i= x_j$ are assumed to be very near and divided on the left and on the right of $(0,\; 0)$. So the choices at all stages is a much larger set that those in Fig. 2b. That is we do not assume that $x_1+x_2=1$ holds necessarily. The combinations with $x_i> x_j$ are ‘better’ for Pi and those with $x_j> x_i$ are ‘better’ for Pj. For example, given $x_1$, any $x_1>x_2$ will be preferable to P1 than any feasible $x_2>x_1$. We also note that the feasible allocation $(k,\; 0)$ is strictly better than $(0,\; 0)$ for P1. At the same time the feasible allocation $(0,\; k)$ is strictly better than $(0,\; 0)$ for player P2. We call these outcomes as favourable to a player.

In Fig. 3 the game starts at $\hbox {t}=0$ with P1 offering (0, 0). From then on when a player is to respond he plays N, apart from the points when he is offered a favourable outcome for himself. Then he accepts the offer and plays Y. In addition, every time a player is to make an offer he plays (0, 0). These strategies imply that the payoffs vector (0, 0) is constantly postponed in the hope that the opponent’s hand will tremble at some stage and offer part or the whole dollar without keeping any part for himself. The payoffs vector (0, 0) becomes available as a result of the non-termination of the game. The game is Nash as no player can change his strategy unilaterally and increase his payoff. It also satisfies the subgame perfect equilibrium condition that a trembling hand that brings about a favourable outcome is met with a Y response.

Another set of possible strategies is for Pi to accept ‘positive’ offers $x_i>x_j$ and also (0, 0), and reject the rest. The game starts at $\hbox {t}=0$ with P1 proposing (0, 0). From then on the players alternate accepting positive offers and (0, 0) and rejecting the rest, and when it is their turn proposing (0, 0) at all nodes. The game terminates immediately and if a player were to alter his strategy unilaterally he could not increase his payoff. Therefore, (0, 0) will be implemented as a Nash equilibrium. The strategies described are Nash but not subgame perfect because, for example, the trembling hand offer (0.4, 0.6) by P1 will be accepted by P2, but he would be better off to reject it and play (0, 0), which his opponent will accept.

Next, analogously to the case $x_1+x_2=1$, suppose now that to start with, P2 plays N, at all nodes horizontally apart from the favourable offers $(0,\; k)$, where he plays Y. From then on the players alternate in asking, at any node, for the best possible outcome for themselves and similarly rejecting all offers made. The strategies which start with the pair ($(0,\; k)$, Y), for P1 and P2, respectively, do not form a Nash equilibrium. P1 can change his strategy to $x_1\not =0$ and become better off through the eventual outcome (0, 0).

5 Concluding remarks

This note attempts to take the discussion in bargaining theory in a different direction than that of von Neumann–Morgenstern utility functions and continuous preferences. In the context of a lexicographic preferences model it identifies the status-quo payoff as the Nash solution and discusses its support and implementation through the alternating offers approach.