Divide-and-choose with nonmonotonic preferences

Abstract

I consider the divide-and-choose method for allocating fixed quantities of infinitely divisible commodities among two agents when their preferences are commonly known but need not be monotonic. First, I show that with single-dipped preferences, the outcome may not be envy-free (or efficient). Also, it may be advantageous to be the chooser rather than the divider. I then show that if preferences are single-peaked, the divide-and-choose outcome is envy-free. This establishes a significantly weaker sufficient condition for no-envy than monotonicity. Moreover, it shows that it is not the lack of monotonicity per se that may cause the divide-and-choose outcome to be envious but rather a particular type.

The divide-and-choose method is a commonly used procedure for allocating fixed quantities of resources between two agents. In this procedure one agent divides the resources into two parcels and the other chooses whichever parcel they prefer.¹ For the case in which the commodities are infinitely divisible and the preferences of the agents are known, this procedure is generally taken to result in a fair, or envy-free, allocation, that is, neither agent prefers the other agent’s parcel to its own. This is sometimes stated without condition (e.g., Young 1994; Moulin 1995; Brams and Taylor 1996) or under standard restrictions, namely, that agents’ preferences are continuous and strongly monotonic (Kolm 1994; Crawford 1977).² Moreover, it has been shown that this result extends to the case in which the chooser’s preferences are private information³, to allocating “bads” as well as “goods,” and in some cases to include indivisible commodities.⁴ It has also been generalized to include additional agents (Steinhaus 1948; Dubins and Spanier 1961). Further, in this context, it has been shown that there is a divider’s advantage , that is, given the choice of which role to play, each agent would rather be the divider (Crawford 1977; Young 1994).⁵

Here, I consider the case in which commodities are infinitely divisible and preferences are commonly known but need not be monotonic. First, I show that in this case the outcome obtained under divide-and-choose may entail envy. Clearly, the chooser would not be envious of the divider since it selects its preferred parcel. However, the divider can be envious of the chooser. Also, it may be advantageous to be the chooser. The proof of both of these claims is by way of an example involving single-dipped preferences.⁶$^{,}$⁷ I then show that if preferences are single-peaked, the divide-and-choose outcome is envy-free. This establishes a considerably weaker sufficient condition for no-envy than monotonicity. Moreover, it shows that it is not the lack of monotonicity per se that may cause the divide-and-choose outcome to be envious but rather a particular type of nonmonotonicity.

To establish the first result, it is sufficient to consider a single, divisible commodity. Thus, suppose 1 unit of a commodity is to be allocated between two people, D and C, where D is the designated divider and C is the chooser. The divide-and-choose game is described as follows. First, D divides the commodity into two portions, x and $1-x$, where x is the amount it intends to keep for itself. C then chooses whichever of the two portions it prefers. I consider the case in which D’s and C’s preferences are common knowledge. The general procedure by which D would determine an optimal proposal is the following. D would identify the set of proposals at which C would be willing to accept its intended portion, $1-x$, rather than take the portion intended for D, x.⁸D would then propose its most preferred division among those C would accept.⁹ To demonstrate, suppose both agents’ preferences are monotonically increasing in the commodity, then C will prefer $1-x$ to x providing $1-x\ge \frac{1}{2}$, or $x\le \frac{1}{2}$; otherwise, it would choose x . Among all “acceptable” proposals, i.e., in which $x\le \frac{1}{2}$, the one most preferred by D would be $x= \frac{1}{2}$. Hence, this is the divide-and-choose outcome, and in this case it is envy-free.

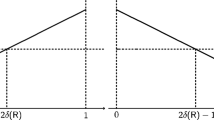
One can graphically depict this problem by considering the one-dimensional analog of the standard Edgeworth box. That is, consider a line segment of length 1, and measure the portion allocated to D to the right from the left endpoint and the portion allocated to C to the left from the right endpoint. Next, depict each agent’s preferences over pairs $(x,1-x)$ by “drawing” a curve over the segment with the interpretation that the higher the curve, the better the allocation.¹⁰ Figure 1 depicts the previous example in which agents’ preferences are monotonic. As mentioned, C will reject (i.e., choose x instead of $1-x$) any proposal in which it is offered less than $\frac{1}{2}$. Therefore, D will propose its most preferred allocation among those for which $x\le \frac{1}{2}$, namely, $(x,1-x)=( \frac{1}{2},\frac{1}{2})$.

Fig. 1

Divide-and-choose with monotonic preferences

Now, consider the example of Fig. 2 in which C’s preferences are again monotonic but D’s are single-dipped, as indicated. Then D will again propose its most preferred allocation among those for which $x\le \frac{1}{2 }$, but in this case that is (0, 1). However, D clearly prefers (1, 0) to (0, 1) and would thus be envious of C.

Fig. 2

Divide-and-choose with envy

Next, suppose the roles of D and C were reversed in the second example. That is, now C divides the resource into $(x,1-x)$ and D chooses its preferred portion.

In Fig. 3¹¹, the dotted curve is the reflection of D’s preferences across the midpoint. D would accept any proposal at which the reflection lies on or below its (solid) preference diagram and reject any proposal at which the reflection lies above. C would thus propose its most preferred division among those D would accept, namely, z. Clearly, C would be better off at (0, 1), where it was the chooser, than at z, where it is the divider.¹²

Fig. 3

Divide-and-choose with chooser’s advantage

Returning to the case in which D is the divider and C is the chooser, I now show that envy cannot occur if preferences are single-peaked rather than single-dipped. The argument is easily made for the 1-commodity case and is precisely the same with additional commodities.

First, let $X=\{z=(x,1-x)\in {\mathbb {R}}^{2}\mid 0\le x\le 1\}$ denote the set of feasible allocations. Formally, i’s preferences over X are single-peaked if there exists $z^{*}\in X$ such that for all $z^{\prime },z^{\prime \prime }\in X$, if $z^{\prime }=\alpha z^{*}+(1-\alpha )z^{\prime \prime }$ for some $\alpha \in (0,1)$, then $z^{*}\succ _{i}z^{\prime }\succ _{i}z^{\prime \prime }$, where $\succ _{i}$ denotes i’s strict preference relation. Similarly, i’s preferences are single-dipped if there is $z^{*}\in X$ such that for all $z^{\prime },z^{\prime \prime }\in X$, if $z^{\prime }=\alpha z^{*}+(1-\alpha )z^{\prime \prime }$ for some $\alpha \in (0,1)$, then $z^{\prime \prime }\succ _{i}z^{\prime }\succ _{i}z^{*}$.

FormalPara Proposition

If preferences are continuous and single-peaked, then the divide-and-choose outcome is envy-free.¹³

FormalPara Proof

For $z\in X$, write $z^{-1}:=(1-x,x)$. Now, suppose i’s preferences $\succsim _{i}$ over X are continuous and single-peaked, for $i=C,D$. As in Fig. 3, above, X can be partitioned into regions $A_{1},A_{2},...,A_{n},R_{1},R_{2},...,R_{m}$ such that for all j, if $z\in A_{j}$, then $z\succsim _{C}z^{-1}$, and for all k, if $z\in R_{k}$, then $z^{-1}\succ _{C}z$. Also, if $z\in R_{j}$ for some j, then $z^{-1}\in A_{k}$ for some k. Let $\mathbf {A=}A_{1}\cup \cdot \cdot \cdot \cup A_{n}$ and ${\mathbf {R}}=R_{1}\cup \cdot \cdot \cdot \cup R_{m}$. (Note that if C’s preferences are symmetric, i.e. $z\sim _{C}z^{-1}$ for all $z\in X$, then ${\mathbf {A}}=X$ and ${\mathbf {R}}=\varnothing$.) For any allocation z on the boundary between adjacent A and R regions, $z\sim _{C}z^{-1}$. Hence, both z and $z^{-1}$ are in ${\mathbf {A}}$, and thus ${\mathbf {A}}$ is closed. Also, ${\mathbf {A}}$ is clearly bounded.

Now, let $z^{*}=(x^{*},1-x^{*})$ denote the divide-and-choose outcome. By definition, $z^{*}$ is D’s most preferred allocation in ${\mathbf {A}}$. (Such a maximizer exists since $\succsim _{D}$ is continuous and ${\mathbf {A}}$ is compact.) Thus, $z^{*}\in A_{j}$, for some j. Hence, $z^{*}\succsim _{C}z^{*-1}$, or C is not envious of D. Also, by definition $z^{*}\succsim _{D}z$ for all $z\in {\mathbf {A}}$. Suppose, by way of contradiction, that D is envious of C at $z^{*}$, that is, $z^{*-1}\succ _{D}z^{*}$. Then since preferences are single-peaked, this means that $\left( \alpha z^{*-1}+(1-\alpha )z^{*}\right) \succ _{D}z^{*}$ for all $\alpha \in (0,1)$. In particular, $( \frac{1}{2},\frac{1}{2})\succ _{D}z^{*}$. Since $(\frac{1}{2},\frac{1}{2} )\in {\mathbf {A}}$, this contradicts the fact that $z^{*}$ is preference maximizing for D over ${\mathbf {A}}$. $\square$

Consequently, it is not the lack of monotonicity per se that may cause the divide-and-choose method to result in an unfair outcome, but rather that the divider’s preferences are single-dipped. Do such preferences have practical significance? First, preferences over combinations of goods with negative cross-effects might be single-dipped (Klaus et al. 1997; Manjunath 2014). For instance, Klaus (2001) mentions the example of a professor who would prefer to devote all of his or her time to teaching or to research rather than to allocate some to each. She also points out that in an exchange economy, preferences restricted to the set of affordable bundles might be single-dipped if unrestricted preferences and/or budget sets are nonconvex. In the context of voting, preferences are single-dipped when a voter has a least preferred candidate or position for a given ordering (Inada 1964; Gehrlein and Lepelley 2017). Or consider commodities for which it is necessary to acquire a taste (for example, beer or tobacco or opera) or activities for which it is necessary to achieve a minimum level of proficiency before enjoying them (for example, playing a musical instrument or participating in a sport). Also, preferences over the location of a public bad (such as a prison or waste facility) are often taken to be single-dipped (Vickrey 1960; Peremans and Storcken 1999; Barberà et al. 2012; Öztürk et al. 2013). Finally, as mentioned in footnote 10, it could even be that preferences are monotonic in one’s own consumption but are single-dipped due to an externality.¹⁴ Hence, there are numerous natural settings in which preferences might be single-dipped.¹⁵ In such cases, the divide-and-choose method might be unsuitable for the reasons described herein.