1 Introduction

In the high-speed cutting process, adiabatic shear fracture (ASF) is a distinctive dynamic fracture behavior of adiabatic shear band (ASB) in the last stage of adiabatic shear evolution, transforming serrated chip into isolated segment chip at high cutting speeds. The occurrence of ASF in isolated segment formation generally induces a discontinuous cutting process with inevitable influences on the machinability, such as cutting system chattering, cutting force and temperature fluctuation, and tool failure. Based on the adiabatic shear theory, most existing studies have reported on the formation condition of the serrated chip during relatively low speed cutting the materials with poor thermo-physical property [1,2,3,4,5] and good thermal conductivity [6,7,8,9]. The thermal softening effect exceeding the strain and strain-rate hardening effects in the deformation zone are the requirement for adiabatic shear evolution. Thus, with the cutting speed increasing, it is more important to investigate the ASF behavior.

Hitherto, the fracture behavior of the serrated chip in high-speed cutting has been rarely studied. The periodic cyclic fracture theory was first proposed by Shaw and Vyas [6] to illustrate the causation of serrated chip fracture in machining of hardened steel. Elbestawi et al. [7] and Poulachon and Moisan [9] found brittle cracking on the machined surface resulting from the deformation and heating effects in cutting of high-hardness steels. Wang et al. [10] found that the fracture easily occurred in the transformed band of serrated chip. Su and Liu [8] affirmed that the brittleness enhancement led to the serrated chip fracture in high-speed milling of alloy steels. Some studies have dealt with the fracture behavior of ASB in serrated chip through damage or fracture mechanical theories. Sowerby and Chandrasekaran [11] adopted a damage factor to assess the deformation, temperature and stress state of the serrated chip cracking. Marusich and Ortiz [12] developed the continuous and adaptive meshing techniques in Lagrangian model for machining AISI 4340 steel. Xie et al. [13] indicated that the ASB fracture in serrated chip could be estimated through the chip flow localization parameter, expressed by cutting parameters and material properties. The Johnson-Cook damage model was applied by Guo and Yen [14] to simulate the crack propagation process in serrated chip. Hua and Shivpuri [15] simulated the crack propagation in the formation of serrated chip by applying FEM software. Gu et al. [16, 17] found that the ASB fracture of serrated chip was of energy related characteristic. Most of these studies that applied the dynamic damage and fracture models were based on the assumption of a small scale yielding condition, which could not properly describe the ASF characteristics of high-rate deformation and heating. Therefore, the main purpose of this study is to further investigate the critical occurrence characteristics of ASF at various rake angles and feeds, which will help to understand the high-speed cutting process and its applications.

In this work, based on the saturation limit theory of adiabatic shear, the theoretical prediction model of ASF is developed by considering the dynamic deformation, temperature, stress, and energy conditions of ASB. The theoretical critical cutting speed of ASF, at various negative rake angles and feeds, is predicted and verified experimentally through chip morphology examinations during high-speed cutting of a hardened steel and a stainless steel. The influences of the cutting parameters and thermal-mechanical properties of the materials on the critical occurrence condition of ASF are discussed.

2 Prediction model of ASF

2.1 Saturation limit criterion

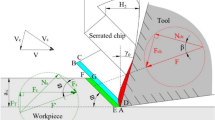
The theoretical model for predicting the critical condition of ASF is developed in this section. The ASB evolution is inevitably influenced by the stress wave propagation in a high-rate loading process, especially in a high-speed machining process [16, 18]. According to the saturation limit theory of high-speed cutting [17], the flat wave fronts in this situation are considered, while the effects of wave reflection, refraction, and superposition are ideally ignored under the continuous disturbance. The propagation of the plastic shear waves (PSW) and thermo-plastic shear waves (TPSW) in the primary deformation zone (PDZ) of serrated chip under negative rake angle is modeled, as shown in Fig. 1. The blue and red colors represent the rigid-plastic region (RP region) and thermal-plastic region (TP region), respectively. The red and blue curves represent the stress-displacement relation and the displacement-time field, respectively. The PSW and TPSW are subsequently generated, with the speeds of \(C_{\text{P}}\) and \(C_{\text{TP}}\), when the intensity of the disturbance imposed on the work material exceeds \(U_{y}\) and \(U_{0}\). As the loading continues, the propagation speed of TPSW decays and the ASB evolves until fracture at time \(t_{\text{c}}\).

Fig. 1
figure 1

Wave propagation model in PDZ during serrated chip formation

Full size image

Considering the adiabatic shear evolution in the TP region, which follows the momentum and energy conservation principles, the continuum governing equations in the Lagrangian coordinate system are given as

$$\left\{ \begin{array}{l} \rho \frac{\partial v_{\text{S}} }{\partial t} = \frac{\partial \hat{\tau }}{\partial y}, \hfill \\ \frac{\partial \theta }{\partial t} = \frac{\beta }{\rho c}\hat{\tau }\dot{\gamma } + \chi \frac{\partial^{2} \theta }{\partial y^{2} }. \hfill \\ \end{array} \right.$$
(1)

The adiabatic temperature rise due to fast heating during the adiabatic shear banding in the chip can be expressed as

$$\theta = \frac{\beta }{\rho c}\int_{0}^{\gamma } {\hat{\tau }\left( {\gamma ,\dot{\gamma },\theta } \right)} {\text{d}}\gamma + \theta_{0} .$$
(2)

The movement of the material in the TP and RP regions is related with the TPSW wavefront and the boundary velocity of the RP region. Based on the adiabatic shear gradient plastic law, the velocity distribution of the TP region can be calculated as

$$v(y) = \dot{\gamma }\left( {y - \frac{\xi }{\uppi}\cos \left( {\frac{y}{\xi } + \frac{1}{2}} \right)\uppi + \xi } \right), - \xi \le y < \xi .$$
(3)

The kinematic equation of the TPSW wavefront can be derived through the momentum theorem as

$$\frac{{{\text{d}}p_{y} \left( \xi \right)}}{{{\text{d}}t}} = 4\rho \dot{\gamma }\xi \dot{\xi } = \tau_{\text{p}} - \hat{\tau }(U,\dot{U},\theta^{*} ).$$
(4)

According to the high-rate loading experiment, the post-peak performance of TP region can be liberalized as [19]

$$\hat{\tau }(U,\dot{U},\theta ) \approx \tau_{\text{p}} \left( {1 - \frac{{\tau_{\text{p}} }}{{\Delta W_{\text{c}} }}\Delta U} \right),$$
(5)

where \(U\) is the boundary displacement of RP region and \(W\) is the boundary shear work of RP region. The compatible movement condition of the TP region is given by

$$\Delta U = U - U_{0} = \int_{{t_{0} }}^{t} {\dot{\gamma }\xi {\text{d}}t} .$$
(6)

Considering the kinematic law and boundary condition: \(\Delta \dot{U}_{0} = \Delta U_{0} = 0\), the TPSW front \(\xi\), and the stress collapsing time \(\Delta t_{\text{c}}\) are solved as

$$\left\{ {\begin{array}{l} {\xi = \frac{{\tau_{\text{p}}^{2} \Delta t^{2} }}{{24\rho \Delta W_{\text{c}} }},} \\ {\Delta t_{\text{c}} = \frac{2}{{\tau_{\text{p}}^{{}} }}\left( {\frac{{9\rho \Delta W_{\text{c}}^{ 2} }}{{\dot{\gamma }}}} \right)^{1/3} .} \\ \end{array} } \right.$$
(7)

Considering the damage weakening effect owing to the thermal softening effect in the TP region, the post-peak constitutive relation is given by

$$\tau_{\text{S}} = \tau_{\text{p}} \left( {1 - \alpha \left( \theta \right)} \right),$$
(8)

where \(\alpha\) is the damage weakening coefficient related to the thermal softening effect. The maximum temperature rise of the TP region by the energy equation is approximated as

$$\Delta \theta_{\text{c}}^{{}} \approx \frac{{\tau_{\text{p}} \dot{\gamma }}}{\rho c}\Delta t_{\text{c}} - \chi \frac{{\partial^{2} \theta }}{{\partial y^{2} }}\Delta t_{\text{c}} ,$$
(9)

where the strain energy and heat conduction components can be estimated according to Ref. [16]. Based on the minimum energy dissipation principle, the critical shear bandwidth and collapsing time are

$$\left\{ {\begin{array}{*{20}c} {S_{\text{c}} = 2\left( {\frac{{18\rho^{3} \chi^{3} c^{2} \Delta \theta_{\text{c}}^{2} }}{{a^{3} \tau_{\text{p}}^{ 3} \dot{\gamma }_{\text{c}} }}} \right)^{1/4} ,} \\ {\Delta t_{\text{c}} = \frac{{12\rho c\Delta \theta_{\text{c}} }}{{\tau_{\text{p}}^{{}} }}\left( {\frac{2\rho \chi }{{a\tau_{\text{p}}^{{}} \dot{\gamma }_{\text{c}} }}} \right)^{1/2} ,} \\ \end{array} } \right.$$
(10)

where the rate-related gradient factor \(a\) can be obtained according to the shear bandwidth model proposed by Dodd and Bai [20] as

$$a = 2\left( {\frac{{36\beta k\dot{\gamma }}}{{c\tau_{\text{p}} }}} \right)^{1/3} .$$
(11)

The saturation limit \(G_{\text{ASB}}^{\text{f}}\) can be calculated by the sum of the pre-peak energy \(G_{0}\) [16] and the post-peak energy as

$$G_{\text{ASB}}^{\text{f}} \approx G_{0} + 12\rho c\Delta \theta_{\text{c}}^{{}} \left( {\frac{{2\rho \chi \dot{\gamma }_{\text{c}} }}{{a\tau_{\text{p}}^{{}} }}} \right)^{1/2} .$$
(12)

Thus, the critical occurrence condition of ASF is defined as

$$G_{\text{ASB}} \geqslant G_{\text{ASB}}^{\text{f}} {\text{ or }}D_{\text{ASB}} = \frac{{G_{\text{ASB}} }}{{G_{\text{ASB}}^{\text{f}} }} \geqslant 1,$$
(13)

where \(G_{\text{ASB}} = \int_{0}^{{\gamma_{\text{c}} }} {\hat{\tau }\left( {\gamma ,\dot{\gamma },\theta } \right)} \text{d} \gamma\) is the energy concentration in ASB and \(D_{\text{ASB}}\) is the saturation limit.

2.2 Stress condition

The triaxiality stress state is considered on the basis of the dynamic criterion during a high-speed cutting process. The stress state of an infinitesimal element in TP region, under the mechanics conditions of plane strain, is illustrated in Fig. 2. Through the plastic mechanics analysis under plane strain condition, the principal stresses, strain, and strain rate can be solved as

$$\left\{ \begin{array}{l} \left( {\sigma_{1} ,\sigma_{2} ,\sigma_{3} } \right) = \left( {\frac{{\sigma_{y} }}{2} + \frac{1}{2}\sqrt {\sigma_{y}^{2} + 4\tau_{xy}^{2} } ,\frac{{\sigma_{y} }}{2},\frac{{\sigma_{y} }}{2} - \frac{1}{2}\sqrt {\sigma_{y}^{2} + 4\tau_{xy}^{2} } } \right), \hfill \\ \left( {\varepsilon_{1} ,\varepsilon_{2} ,\varepsilon_{3} } \right) = \left( {\sqrt {\varepsilon_{x}^{2} + \frac{{\gamma_{{_{xy} }}^{2} }}{4}} ,0, - \sqrt {\varepsilon_{x}^{2} + \frac{{\gamma_{{_{xy} }}^{2} }}{4}} } \right), \hfill \\ \left( {\dot{\varepsilon }_{1} ,\dot{\varepsilon }_{2} ,\dot{\varepsilon }_{3} } \right) = \left( {\sqrt {\dot{\varepsilon }_{x}^{2} + \frac{{\dot{\gamma }_{{_{xy} }}^{2} }}{4}} ,0, - \sqrt {\dot{\varepsilon }_{x}^{2} + \frac{{\dot{\gamma }_{{_{xy} }}^{2} }}{4}} } \right). \hfill \\ \end{array} \right.$$
(14)
Fig. 2
figure 2

Stress state under plane strain condition in TP region

Full size image

According to the Mises yielding condition, the effective stress, strain, and strain rate can be expressed as

$$\left\{ \begin{array}{l} \hat{\tau } = \hat{\sigma }/\sqrt 3 , \hfill \\ \hat{\gamma } = \sqrt 3 \hat{\varepsilon }, \hfill \\ \hat{\dot{\gamma }} = \sqrt 3 \hat{\dot{\varepsilon }}. \hfill \\ \end{array} \right.$$
(15)

Considering the relation: \(\sigma = \tau \cot \phi\), the effective stress can be expressed through the compressive stress \(\sigma\) and the shear stress \(\tau\) as

$$\hat{\tau } = \tau \sqrt {1 + \cot^{2} \phi /4} .$$
(16)

The dynamic mechanic performance of the materials influences the critical occurrence conditions of ASF. The thermo-visco-plastic constitutive model can be obtained through the split Hopkinson pressure bar (SHPB) tests [14, 21]. The general form can be given as

$$\hat{\sigma }\left( {\hat{\varepsilon },\hat{\dot{\varepsilon }},\theta } \right) = f_{1} \left( {\hat{\varepsilon }} \right)f_{2} \left( {\hat{\dot{\varepsilon }}} \right)f_{3} \left( {\theta^{*} } \right),$$
(17)

where \(f_{1} \left( \varepsilon \right)\) is the component of strain hardening effect, \(f_{2} \left( {\dot{\varepsilon }} \right)\) the component of strain rate hardening effect, and \(f_{3} \left( {\theta^{*} } \right)\) the component of thermal softening effect.

2.3 Deformation condition

According to the modified physical model of the isolated segment chip [22], the corresponding deformation of an isolated segment under negative rake angle is established in Fig. 1. Aiming at the deformation process of the segment \({\text{OABC}}\), the deformation in the RP region is influenced by the angle \(\beta_{0}\). After the geometry examination of the obtained serrated chips in the high-speed experiment, the teeth space \(L_{\text{P}}\) of the isolated segment is approximated to the boundary displacement \(U\) under the effect of the free surface incline angle. We can obtain the relation

$$2a_{\beta } \beta_{0} \approx \frac{\uppi}{2} - \phi - \gamma_{0} ,$$
(18)

where the coefficient \(a_{\beta }\) is the experimental constant ensuring the balance of Eq. (19). It shows that the free surface incline angle \(\beta_{0}\) was mainly influenced by shear angle \(\phi\) under a constant rake angle. Gente et al. [4] found the free surface incline angle \(\beta_{0}\) was about 18.7°, which could be verified experimentally. The shear angle \(\phi\) can be approximated to the angle between the ASB and cutting direction as

$$\phi = {\text{arc}}\tan \left( {\frac{{\cos \gamma_{0} }}{{\xi - \sin \gamma_{0} }}} \right),$$
(19)

where \(\xi = a_{\text{ch}} /a_{\text{c}}\) is the chip deformation coefficient and its critical value \(\xi \approx 0.8 - 1\) can be obtained through the machining experiment and microscopic measurement.

Fig. 3
figure 3

Schematic diagram of theoretical prediction procedure of ASF

Full size image

Adiabatic shear occurs when the thermal softening effect exceeds the strain hardening and strain rate strengthening effects. According to the previous work of Ye et al. [23], the shear band space \(L_{\text{S}}\) between the segments during serrated segment formation can be approximated as

$$L_{\text{S}} = \frac{{2X^{3/4} }}{{\left( {2 - X} \right)^{1/2} }}\left( {\frac{{9\rho c^{2} k}}{{\tau_{y} \alpha^{2} \gamma_{0}^{3} }}} \right)^{1/4} ,$$
(20)

where \(X \approx 1\) represents a fully mature ASB. The increase in cutting speed increases the strain rate, leading to the decrease of shear band space [24]. Thus, in the actual deformation process condition of a segment, the boundary displacement of ASB, which is dependent on the teeth space during isolated segment formation, can be calculated as

$$\left\{ \begin{array}{l} U \approx L_{\text{P}} \left( {\cot \psi \cos \left( {\phi - \gamma_{0} } \right) + \sin \left( {\phi - \gamma_{0} } \right)} \right), \hfill \\ L_{\text{P}}~=~L_{\text{S}} \sin \left( {\phi - \gamma_{0} } \right). \hfill \\ \end{array} \right.$$
(21)

Thus, the average strain and strain rate in the ASB can be calculated as

$$\left\{ \begin{array}{l} \gamma_{\text{ASB}} = \frac{U}{S} + \gamma_{\text{S}} , \hfill \\ \dot{\gamma }_{\text{ASB}} = \frac{{v_{\text{S}} }}{S} \approx \frac{{v\cos \gamma_{0} }}{{S\cos \left( {\phi - \gamma_{0} } \right)}}, \hfill \\ \end{array} \right.$$
(22)

where \(\gamma_{\text{S}} = \sin \beta_{0} /(\sin \phi \sin \psi )\) is the strain of RP region in an isolated segment and \(S\) is the ASB width which can be obtained according to Eq. (10).

2.4 Prediction procedure

The saturation limit can be deduced through the above equations of stress, deformation, and temperature conditions. The theoretical prediction results of the limit energy in ASB have been verified in our previous works [16, 17]. The schematic diagram of theoretical prediction procedure of ASF is shown in Fig. 3. With the cutting speed increasing, the energy concentration in ASB increased and attained an energy limit. On this basis, the predicted critical conditions of ASF are shown in Fig. 4. The upside and downside of the critical surface represent the unfractured serrated chip and the isolated segment chip, respectively. The prediction results show that the critical cutting speed of ASF decreases with the decrease of rake angle and the increase of feed, which will be verified in the following section.

Fig. 4
figure 4

Theoretical prediction results of ASF high-speed cutting the two steels a Hardened AISI 1045 steel and b Fv520(B) steel

Full size image

3 Experimental verification

3.1 Materials and methods

AISI 1045 steel and Fv520(B) stainless steel were selected as the to-be-cut materials. The physical and mechanical properties of the two steels are listed in Table 1. The hardened AISI 1045 steel was of higher thermal conductivity, hardness, lower malleability, and fracture surface shrinkage, and Fv520(B) stainless steel was of higher tensile strength, yield strength, and fracture surface shrinkage. These differences in mechanical and thermal physical properties lead to the different sensitivities to ASF. In order to better describe the strain rate hardening characteristic of the Fv520(B) stainless steel and the thermal softening characteristic of the AISI 1045 steel, the constitutive models of these two steels were modified based on the Johnson-Cook law through the SHPB tests [25]. The modified Johnson-Cook constitutive models of the two steels are expressed as

$$\left\{ \begin{aligned} {} \sigma_{{{\text{AISI }}\; 1045}} &= \left( {630 + 244\varepsilon^{0.15} } \right)\left( {1 + 0.0877\ln \dot{\varepsilon }^{*} } \right)\\ & \exp \left( { - \left( {\frac{{\theta^{*} + 0.005989}}{0.4415}} \right)^{2} } \right), \\ \sigma_{{{\text{FV}}520({\text{B}})}} & = \left( {426 + 564\varepsilon^{0.213} } \right)\left( {1 + 0.04905\dot{\varepsilon }^{*0.9544} } \right) \\ & \left( {1 - \theta^{*0.9} } \right). \hfill \\ \end{aligned} \right.$$
(23)

Machining tests were carried out on a Mill-Turn CNC by using PCBN inserts under a dry cutting condition. The feed was 0.2–0.5 mm/r, the tool rake angles were − 10° and − 20°, and the cutting speed increased until the isolated segment was formed. The to-be-cut steels were machined into a cylindrical workpiece and fixed with the spindle as shown in Fig. 5. The cutting width was 2 mm to satisfy the orthogonal cutting condition. The obtained chips in the tests were embedded vertically into curing denture acrylics. The chip cross sections in the curing denture acrylics were polished and etched. The morphologies of the chip cross sections were examined through the LEICA MeF-4 metallographic microscope.

Table 1 Physical and mechanical properties of the experimental materials
Full size table
Fig. 5
figure 5

Arrangement of high-speed machining setup

Full size image

3.2 Experimental results

3.2.1 The influence of cutting speed

Figure 6 shows the influence of cutting speed on chip morphology transformation during high-speed cutting of the hardened AISI 1045 steel at the constant rake angle of − 10° and feed of 0.3 mm/r. When the cutting speed increased to 700 m/min, white-color transformed bands were generated in the serrated chip (see Fig. 6a). When the cutting speed increased to 800 m/min, the cracks propagated almost to the bottom of the chip (see Fig. 6b). When the cutting speed increased to 900 m/min, the serrated chip segments were completely fractured along the band and formed isolated segment chips (see Fig. 6c). Similar results with the Fv520(B) steel can also be observed in Fig. 7, with a rake angle of − 10° and feed of 0.3 mm/r. The experimental results showed that the increase in cutting speed enlarged the deformation and shortened the deformation time in ASB, transforming the serrated chip into isolated, separated chips, owing to ASF.

Fig. 6
figure 6

Chip morphology transformation of hardened AISI 1045 steel with cutting speeds a v = 700 m/min, b v = 800 m/min, c v = 900 m/min

Full size image
Fig. 7
figure 7

Chip morphology transformation of FV520(B) steel with cutting speeds a v = 500 m/min, b v = 600 m/min, c v = 800 m/min

Full size image

3.2.2 The influence of feed

Figure 8 show the influence of feed on chip morphology transformation during high-speed cutting of the hardened AISI 1045 steel at the constant rake angle of − 10° and cutting speed of 800 m/min. The transformed bands were generated in the serrated chip at feed of 0.2 mm/r (see Fig. 8a). The cracks propagated almost to the bottom of the chip at feed of 0.3 mm/r (see Fig. 8b). The serrated chip segments were completely fractured along the band and formed isolated segment chips at feed of 0.4 mm/r (see Fig. 8c). Similar results for the Fv520(B) steel can also be observed in Fig. 9, with the rake angle of − 10° and cutting speed of 650 m/min. The experimental results showed that the increase of feed elevated the shear band deformation compared with Figs. 6, 7. Thus, the increase of feed tended to cause ASF and form isolated segment chips.

Fig. 8
figure 8

Chip morphology transformation of hardened AISI 1045 steel with feeds a f = 0.2 mm/r, b f = 0.3 m/r, c f = 0.4 mm/r

Full size image
Fig. 9
figure 9

Chip morphology transformation of Fv520(B) steel with feeds a f = 0.3 mm/r, b f = 0.4 m/r, c f = 0.5 mm/r

Full size image

3.2.3 The influence of rake angle

Figure 10 show the influence of rake angle on chip morphology transformation during high-speed cutting of hardened AISI 1045 steel at the constant rake angle of − 10° and cutting speed of 1 000 m/min. When the rake angle decreased to − 10°, though cracks were already extended in the transformed bands, the segments still connected with each other. When the rake angle decreased to − 20°, fracture took place in the ASB of the serrated chip. Similar results for the Fv520(B) steel can also be observed in Fig. 11 with feed of 0.3 mm/r and cutting speed of 860 m/min. The experimental results showed that the decrease in rake angle drove the serrated chip toward isolated segment chips.

Fig. 10
figure 10

Chip morphology transformation of hardened AISI 1045 steel with rake angles a γ0 = –10° and b γ0 = –20°

Full size image
Fig. 11
figure 11

Chip morphology transformation of FV520(B) steel with rake angles a γ0 = –10° and b γ0 = –20°

Full size image

3.2.4 Verification and discussion

By choosing a proper speed interval under different feeds and rake angles, the theoretical and experimental results of critical cutting conditions of ASF are illustrated by the solid and dotted lines in Figs. 12 and 13, respectively. It can be seen that the tendency of the predicted results is coincident with the experimental ones. When the cutting speed exceeded the critical cutting speed during the cutting process, the serrated chip would be transformed into the completely fractured serrated chip. The relative error of the prediction results for the hardened AISI 1045 steel and the Fv520(B) steel were controlled in the range of ± 12% and ± 15%, respectively, which basically meets the actual application requirements of high-speed cutting operations. There were many factors influencing the prediction error, such as the governing equations and dynamic constitutive relationship, stress and deformation in the chip, and simplified assumptions. Moreover, the defects and inhomogeneity of the material under the heat treatment would also affect the experimental data.

Fig. 12
figure 12

Theoretical prediction results of ASF in high-speed cutting of hardened AISI 1045 steel a \(\gamma_{0} = -~10^{ \circ }\) and b \(\gamma_{0} = -~20^{ \circ }\)

Full size image
Fig. 13
figure 13

Theoretical prediction results of ASF in high-speed cutting of FV520(B) steel a \(\gamma_{0} = -10^{ \circ }\) and b \(\gamma_{0} = -20^{ \circ }\)

Full size image

According to the morphology transformation of the hardened AISI 1045 steel and the Fv520(B) steel, these two materials exhibit similar critical characteristics of ASF: high cutting speed, low rake angle, and large feed drive the ASB to the occurrence of ASF, resulting in isolated segments formation. The critical cutting speed for ASF of the hardened AISI 1045 steel is lower than that of the Fv520(B) steel under lower feed (f ≤ 0.3 mm/r) and higher rake angle (γ0 ≥ −10°). The critical cutting speed of ASF of the hardened AISI 1045 steel is higher than that of the Fv520(B) steel under higher feed (f ≥ 0.4 mm/r) and lower rake angle (γ0 ≤ −20°). The temperature in the PDZ under lower feed can be easily influenced by the cutting tool. The hardened AISI 1045 steel with better thermal conductivity was rarely influenced by the tool temperature, compared with the Fv520(B) steel. The different sensitivity to pressure stress under lower rake angle can also lead to different critical cutting speeds.

According to the saturation limit theory, a material with lower thermal conductivity leads to larger heating, and plasticity enhancing. The shear band material, owing to the thermal softening effect under high temperature, attains the saturation limit with difficulty. In the cutting tests, the chip with a small thickness was heated by the tool temperature, and thus, the ASB energy converged easier in the experimental results than in the theoretical results. Theoretically, the chip with smaller cutting thickness needs more energy for the occurrence of ASF. Some studies found that the temperature and the cracking speed in the ASB increased with the increase of impact speed [26,27,28]. Moreover, the tempered sorbites with better work hardening effect in hardened AISI 1045 steel contributed to low critical cutting speed for ASF. The austenitic with poor heat conductivity and pressure sensitivity in the Fv520(B) steel can also induce a lower critical cutting speed under smaller negative rake angle.

It was found that the energy limit value of the hardened carbon steel was approximately 5.5 × 109 J/m2 and that of the stainless steel was maintained around 5.14 × 109 J/m2 [17, 22]. The increase in cutting speed enlarged the strain rate in ASB, shortened the segment deformation time, and suppressed the heat diffusion in band, aggravating the energy concentration in ASB until fracture. Thus, the cutting speed was the significant and necessary loading condition for energy converging to the occurrence of ASF. Rittel et al. [29, 30] suggested that the cold deformation energy in the fracture was a relatively constant value of approximately 4 × 107 J/m2. Therefore, this prediction model of ASF can obtain reasonable results under a wide cutting speed range, which will open theoretical and experimental ways for a deeper understanding of the effect of ASF in the cutting process.

4 Conclusions

According to the theoretical and experimental investigations, the critical characteristics of ASF behavior during high-speed cutting of the hardened AISI 1045 steel and the Fv520(B) stainless steel at various negative rake angles and feeds were revealed. The following conclusions are obtained:

  1. (i)

    Low negative rake angle and large feed contribute to an increase in sensitivity to ASF in high-speed cutting of the two steels, resulting in more energy convergence in ASB and the decrease of critical cutting speed of ASF.

  2. (ii)

    The critical cutting speed of ASF in the hardened AISI 1045 steel is lower than that in Fv520(B) steel under smaller feed, but higher than that in the Fv520(B) steel under larger feed and lower negative rake angle, owing to the pressure sensitivity.

  3. (iii)

    The thermo-mechanical performance induces different sensitivities to ASF in high-speed cutting of the two steels. The tempered sorbites with better work hardening effect and the austenitic with poor heat conductivity and pressure sensitivity contribute to a low critical cutting speed for ASF under the small negative rake angle.

  4. (iv)

    The occurrence of ASF behavior greatly depends on the stress, temperature, strain and strain rate conditions in a to-be-cut material. The prediction model of ASF based on the saturation limit theory agrees well with the experimental results in a wide cutting speed range, which will facilitate the engineering applications in high-speed cutting operations.