1 Introduction

Control of real-order systems has received much importance in design and analysis with adaptive to little calculus operators dealing with orders not limited to integers [1, 2]. Although there are many different real-order derivative operators [3], the most basic one, the Caputo derivative, enables a pathway to design many real-order control systems due to the physically interpretable initial conditions. In the design of many different real-order control systems (e.g., [4, 5]), it is very important to consider the random initial time attached to such systems instead of the ideal zero initial time. One can think that it is not possible to control the complicated or non-asymptotic dynamics of many real-order systems associated with different orders as well as random initial- times. But this is not the case, as we report at first glance in this paper with the introduction of a new linear affine control strategy.

Stability is a fundamental concept in all kinds of control systems. The problem of stabilization of random initial-time real-order systems seems crucial and a very promising topic of research in advancing scientific engineering real-order control theory. The issue of how to design suitable controllers for such types of systems may bring many different challenging and complex mathematical problems to control theory. In this context, random initial-time real-order control systems seem to be direct extensions of many investigated zero initial-time real-order systems [6,7,8]. Consequently, it can bring new importance to the formulation of new theories as good conditions to measure performance analysis of controlled responses to target control objectives [9,10,11].

In the literature, the issue of designing and controlling the dynamics of real-order systems associated with fixed zero initial time has been extensively investigated by many researchers. The main reason for the consideration of such a typical issue could be due to the fact that many mathematical methods are not known how to analyze and operate such systems when associated abrupt initial times are placed on a real number line. That is why Zhang et al. in [12] designed a form of linear state feedback controller to zero initial-time linear class of real-order systems with equal order lie in the interval (0, 2) and provided sufficient conditions. Lenka and Banerjee [8] discussed linear state feedback control strategy and provided conditions to control for zero initial-time nonlinear class of real-order systems associated with different orders in the interval (0, 2). In [13], Thuan and Huong have designed a linear state feedback controller and identified LMI conditions to control responses of nonlinear real-order systems associated with the same order in (0, 1]. In [14], Badri and Sojoodi designed a dynamic output feedback controller for a linear class of zero initial-time real-order systems associated with different orders in (0, 2) and established LMI conditions to track the non-trivial responses to zero. In [15], Peng et al. introduced a switching controller along with electrical experiments to stabilize the responses of discontinuous zero initial-time nonlinear real-order systems associated with equal order in (0, 1]. Lenka and Upadhyay in [16] designed time-varying linear state feedback control law and proposed new order-dependent conditions for time-varying nonlinear uncertain real-order systems associated with different orders that lie in (0, 1] and random initial time. In [17], Tavazoie and Asemani studied the robust stability of zero initial-time class of linear real-order systems with uncertainties and introduced new stability conditions via the Nyquist-based method. Later, in [18] Tavazoie and Asemani provided finite gain \(L_{2}\) stability and asymptotic stability to the linear class of zero initial-time real-order system with time-varying interval uncertainty. By using the linear state feedback form of the controller, Gholamin et al. [19] provided some conditions to control trajectories of zero initial-time nonlinear class of real-order systems associated with different orders. Chen et al. [20] designed a linear state feedback controller to a class of zero initial-time nonlinear real-order systems associated with different orders in (0, 1] and developed LMI conditions in order to control obtained responses. Lu et al. in [21] designed linear state feedback control to some class of zero initial-time interval uncertainty linear real-order systems associated with different orders in (0, 1] and established some LMI conditions. Lenka and Upadhyay in [22] have designed a dynamic output control strategy for some class of random initial-time nonlinear real-order systems associated with different orders in (0, 1] and established order dependency conditions to measure controlled responses. In [23], Ding et al. investigated nonlinear Mittag-Leffler stabilization of zero initial-time nonlinear real-order systems with equal order by the use of fractional Lyapunov direct method.

However, due to limited knowledge of available mathematical tools [24,25,26], Mittag-Leffler stability/asymptotic stability of random initial-time real-order control systems has become the most important problem in engineering control theory look to future potential applications. It has been noticed that measuring of controlled response of such types of systems seems very difficult and the issue has not been reported in the literature. Roughly, Mittag-Leffler asymptotic stabilization to random initial-time real-order systems associated with different orders seems very challenging. In this context, no theoretical conditions have been reported yet on how to control trajectories of such real-order systems to some target unknown dynamics.

Motivated by aforementioned important issues, it is the purpose of this paper to design a new linear affine state feedback control law to control the unpredictable or non-asymptotic trajectories of random initial-time nonlinear real-order systems to any given constant vector that may be present or absent within the system.

In short, the innovation and contribution of this work are highlighted as follows:.

  1. (i)

    The idea of designing an affine controller for real-order nonlinear systems with a random initial time has been first developed. Our motivation comes from an important no-equilibrium chaotic system proposed by Wei in [27]. The real-order extension of such a system has no equilibrium points and causes memory chaos.

  2. (ii)

    In control theory developments, the standard linear state feedback approach does not permit well-designed controllers to control systems like Wei where the target control objectives are widely unknown. A novel linear affine state feedback controller is designed in this context to control the system’s response if given any arbitrary vector that may not be present with the system.

  3. (iii)

    In order to make the control system workable, the concept of Mittag-Leffler stabilization has been introduced to achieve control performance and enable the estimation of the rate of decay associated with energy responses.

  4. (iv)

    We use the ideas of the comparison principle method [28] and establish order-dependent and order-independent Mittag-Leffler stabilization results that give sufficient conditions to conclude convergence of responses to a controlled system. In short, our results provide a distinctive approach to constructing some Metzler and nonnegative matrices under Lipschitz nonlinearity conditions to establish possible bounds for controlled trajectory to measure optimum performance.

  5. (v)

    In the demonstration, the importance of positive initial-time and negative initial-time cases is examined to control the trajectories of real-order nonlinear systems with the implementation of the proposed affine control strategy. We have shown that the theoretical results suggested are effective in taking decisions while operating control systems to achieve control goals for target vectors that may be present or absent within the systems.

Paper structure: In Sect. 2, key tools for real-order control systems are recalled. In Sect. 3, we give the description of random initial-time real-order systems. In Sect. 4, a new form of affine controller has been designed to control systems. In Sect. 5, the main control theory results are established. In Sect. 6, application to trajectory control and measurement of controlled performance are illustrated. Conclusions close to this paper are discussed in Sect. 7.

Notations: \({\mathbb {N}}\): natural numbers, \({\mathbb {Z}}_{+}\): positive integers, \({\mathbb {Q}}_{+}\): positive rational numbers, \({\mathbb {R}}_{+}\): positive real numbers, \({\mathbb {R}}\): real numbers, \({\mathbb {C}}\): complex numbers, \(\arg (z)\): principal argument of \(z\in {\mathbb {C}}\), \(Z^{T}\): transpose of \(Z\in {\mathbb {R}}^{m\times {n}}\), \({\mathbb {R}}^{n}\): Euclidean space, gcd: greatest common divisor, lcm: least common multiple, \(\Vert {\cdot }\Vert \): Euclidean norm. Let \(x, y\in {\mathbb {R}}^{n}\) and we mean \(x\le y\) the difference \(x_{i}-y_{i}\le 0\) for \(i=1,2,\cdots ,n\).

2 Preliminary tools

Here we present some basics that will be used throughout the paper.

Definition 1

[29, 30] The Caputo derivative of some n-times continuously differentiable function \(\xi :(t^{\star },\infty )\rightarrow {\mathbb {R}}\) is defined by

$$\begin{aligned} ^{C}\!{\mathscr {D}}^{\gamma }_{t^{\star }, t}\xi (t)=\frac{1}{\varGamma (n-\gamma )}\int _{t^{\star }}^{t}\left( t-\tau \right) ^{n-\gamma -1}\frac{\text {d}^n}{\text {d}\tau ^n}\xi (\tau )d\tau , \end{aligned}$$
(1)

whenever \(\gamma \in (n-1, n)\) and \(^{C}\!{\mathscr {D}}^{\gamma }_{t^{\star }, t}\xi (t)=\frac{\text {d}^n}{\text {d}t^n}\xi (t)\) when \(\gamma =n\), where order \(\gamma \in {\mathbb {R}}_{+}\), initial time \(t^{\star }\in {\mathbb {R}}\), \(n\in {\mathbb {Z}}_{+}\) and \(\varGamma (p)=\int _{0}^{\infty }\tau ^{p-1}e^{-\tau }\text {d}\tau \) with \(p\in {\mathbb {R}}_{+}\).

Definition 2

[31] We say a square matrix \(S(t)=[s_{ij}(t)]\in {\mathbb {R}}^{n\times {n}}\) on \([t^{\star },\infty )\), \(t^{\star }\in {\mathbb {R}}\) is time-dependent Metzler if the off-diagonal entries \(s_{ij}(t)\ge 0\), \(j\ne i\), for all \(t\ge t^{\star }\).

Definition 3

[32] We say a vector function

\(q=\left( q_{1},q_{2},\cdots ,q_{n}\right) ^{T}: {\mathbb {R}}\times {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}\) is of Class W if, for every \(t\in {\mathbb {R}}\), we have \(q_{k}\left( t,u\right) \le q_{k}\left( t, \widehat{u}\right) \), \(k=1,2,\cdots ,n\), for all \(u, \widehat{u}\in {\mathbb {R}}^{n}\) such that \(u_{j}\le \widehat{u}_{j}\), \(u_{k}=\widehat{u}_{k}\) for \(k=1,2, \cdots ,n\) with \(k\ne j\), where \(u_{k}\) denote the kth component of u.

Lemma 1

[28](Nonnegative comparison principle) Let \(t^{\star }\in {\mathbb {R}}\) and \(\beta _1,\cdots ,\beta _n\in (0,1]\). Consider the comparison inequality

$$\begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\beta }}_{t^{\star },t}\eta (t)\le {^{C}\!{\mathscr {D}}^{\widehat{\beta }}_{t^{\star },t}}\xi (t),\; \xi (t^{\star })\ge \eta (t^{\star })\ge 0, \end{aligned}$$
(2)

where \(\eta (t)=\left( \eta _1(t),\cdots ,\eta _{n}(t)\right) ^{T}\in {\mathbb {R}}^{n}\), and \(^{C}\!{\mathscr {D}}^{\widehat{\beta }}_{t^{\star },t}\eta (t)=(^{C}\!{\mathscr {D}}^{\beta _1}_{t^{\star },t}\eta _{1}(t),\cdots ,{^{C}\!{\mathscr {D}}^{\beta _n}_{t^{\star },t}\eta _{n}(t)})^{T}\). Then, the inequality hold:

$$\begin{aligned} 0\le \eta (t)\le \xi (t),\; \forall t\ge t^{\star }. \end{aligned}$$
(3)

Lemma 2

[33] Let \(\xi \) be a real-valued continuous function on \([t^{\star },\infty )\) and differentiable on \((t^{\star },\infty )\). Then, the “\(t-t^{\star }\)”-Caputo derivative inequality

$$\begin{aligned} ^{C}\!{\mathscr {D}}^{\beta }_{t^{\star },t} \xi ^{2}(t)\le 2\xi (t){^{C}\!{\mathscr {D}}^{{\beta }}_{t^{\star },t}\xi (t)},\; \forall t>t^{\star },\; \forall \beta \in (0,1]. \end{aligned}$$
(4)

Theorem 1

[34] Consider the system

$$\begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\beta }}_{t^{\star },t}\xi (t)= Q\xi (t),\;\; \xi (t^{\star })=\xi _{t^{\star }}, \end{aligned}$$
(5)

where \(^{C}\!{\mathscr {D}}^{\widehat{\beta }}_{t^{\star },t}\xi (t)=(^{C}\!{\mathscr {D}}^{\beta _1}_{t^{\star },t}\xi _{1}(t),\ldots ,{^{C}\!{\mathscr {D}}^{\beta _n}_{t^{\star },t}\xi _{n}(t)})^{T}\), \(t^{\star }\in {\mathbb {R}}\),

\(\beta _{1},\beta _2,\ldots ,\beta _{n}\in (0, 1]\), and constant matrix \(Q=[q_{ij}]\in {\mathbb {R}}^{n\times {n}}\). If every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( s^{\beta _1},s^{\beta _2},\cdots ,s^{\beta _n}\right) -Q\right] =0 \end{aligned}$$
(6)

lies in the sector \(\vert {\arg (s)}\vert >\frac{\pi }{2}\), then the geometric solution \(\xi =0\) to (5) is globally asymptotically stable.

3 Random initial-time real-order system

This section gives a description of a random initial-time nonlinear real-order system associated with different orders.

In particular, we consider the random initial-time nonlinear real-order system given by

$$\begin{aligned} \begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t}\eta (t)=M(t)\eta (t)+g(t,\eta (t)),\; \eta (t^{\star })=\eta ^{\star }, \end{aligned} \end{aligned}$$
(7)

where state vector \(\eta (t)\in {\mathbb {R}}^{n}\),

operator \(^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t}\eta (t)=(^{C}\!{\mathscr {D}}^{\alpha _1}_{t^{\star },t}\eta _{1}(t),\ldots ,{^{C}\!{\mathscr {D}}^{\alpha _n}_{t^{\star },t}\eta _{n}(t)})^{T}\in {\mathbb {R}}^{n} \), initial time \(t^{\star }\in {\mathbb {R}}\), order index \(\widehat{\alpha }=\left( \alpha _1,\alpha _2,\cdots ,\alpha _n\right) \in (0,1]\times (0,1]\cdots \times (0,1]\), matrix \(M(t)=\left[ m_{ij}(t)\right] \in {\mathbb {R}}^{n\times {n}}\) is continuous on \([t^{\star },\infty )\) and \(g:[t^{\star },\infty )\times {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}\) is piecewise continuous function.

Note that when \(M(t)=M\) and \(g(t,\eta (t))=g(\eta (t))\), the system (7) is called autonomous (time-invariant); otherwise, it becomes non-autonomous (time-varying).

4 Affine controller design strategy

Controlling the unstable or non-asymptotic dynamics of zero initial-time real-order systems to a target zero response vector using standard state feedback control techniques is commonly achieved in different research studies [10, 19, 20]. But in many situations, it might happen that the target objective is not present in the system under consideration. Consequently, it poses a challenging problem: how to design a control strategy to achieve control goals.

Here, suppose that the system (7) produces non-asymptotic or complicated trajectories with system inputs. In order to control the obtained trajectories for any target vector

\(v^{\star }=\left( v_{1},v_{2},\cdots ,v_{n}\right) ^{T}\), first we add a control input \(u(t)=\left( u_{1}(t),u_{2}(t),\cdots ,u_{n}(t)\right) ^{T}\) to system (7) that needs to be designed. Then, the real-order control system becomes

$$\begin{aligned} \begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t}\eta (t)=M(t)\eta (t)+g(t,\eta (t))+u(t),\; \eta (t^{\star })=\eta ^{\star }. \end{aligned} \end{aligned}$$
(8)

By using the state of (7) and control objective target \(v^{\star }\), we introduce a new variable \(\xi (t)=\eta (t)-v^{\star }\). To implement the control strategy, we introduce a linear affine state feedback control law defined by

$$\begin{aligned} u(t)=K\xi (t)-g(t,0), \end{aligned}$$
(9)

where the constant control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) needs to be identified. Substituting the affine control law (9) into (8), we define the transferred control system by

$$\begin{aligned} \begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t}\xi (t)&=\left[ M(t)+K\right] \xi (t)+g(t,\xi (t))-g(t,0),\\ \xi (t^{\star })&=\eta (t^{\star })-v^{\star }. \end{aligned} \end{aligned}$$
(10)

We introduce the below-mentioned definitions.

Definition 4

(Mittag-Leffler asymptotic stability) We say the system (10) is Mittag-Leffler asymptotically stable if the non-trivial solution satisfies

(i):

\(\xi (t)\rightarrow 0\) as \(t\rightarrow \infty \),

(ii):

the inequality

$$\begin{aligned} \Vert {\xi (t)}\Vert \le C^{\star }\left[ \tilde{C}E_{\theta ,1}\left( -\lambda (t-t^{\star })^{\theta }\right) \right] ^{k_{1}}\Vert {\xi (t^{\star })}\Vert ^{k_{2}},\; t\ge t^{\star }, \end{aligned}$$
(11)

where \(\theta \in (0,1]\), constants \(C^{\star }\ge 1\), \(\tilde{C}>0\), \(\lambda >0\), \(k_{1}>0\) and \(k_{2}>0\).

Definition 5

(Mittag-Leffler asymptotic stabilization) If there exists a control input \(u(t)\in {\mathbb {R}}^{n}\) in (9) such that the control system (10) is Mittag-Leffler asymptotically stable, we say the system (7) is Mittag-Leffler asymptotically stabilizable (ML-ASTZ) to \(v^{\star }\) via control input (9). That means, one must have

(i):

\(\eta (t)\rightarrow v^{\star }\) as \(t\rightarrow \infty \),

(ii):

the inequality

$$\begin{aligned} \begin{aligned} \Vert {\eta (t)}\Vert&\le C^{\star }\left[ \tilde{C}E_{\theta ,1}\left( -\lambda (t-t^{\star })^{\theta }\right) \right] ^{k_{1}}\Vert {\eta (t^{\star })-v^{\star }}\Vert ^{k_{2}}\\&\qquad {}+\Vert {v^{\star }}\Vert ,\; t\ge t^{\star }, \end{aligned} \end{aligned}$$
(12)

where \(\theta \in (0,1]\), constants \(C^{\star }\ge 1\), \(\tilde{C}>0\), \(\lambda >0\), \(k_{1}>0\) and \(k_{2}>0\).

Note that the objective of controlling responses of (7) to target \(v^{\star }\) reduces to Mittag-Leffler asymptotic stabilization of system (10) via control input (9). That means the basic way to conclude objective from (10) is to ensure \(\xi (t)\rightarrow 0\) as \(t\rightarrow \infty \) and satisfy the inequality (11), by identifying some suitable entries of control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\).

5 Main results

Finding control conditions for the class of systems (7) subject to control input (9) is not easy. This section introduces local and global results that give Mittag-Leffler asymptotic stabilization and is presented in two separate subsections.

We begin by introducing the below-mentioned assumptions that will be used throughout the main results.

Assumption 1

(Local Lipschitz condition) The function \(g(t,\eta )\) in system (7) satisfies Lipschitz condition:

$$\begin{aligned} \begin{aligned}&\Vert {g(t,x)-g(t,y)}\Vert \le L_{g}\Vert {x-y}\Vert ,\; \forall t\ge t^{\star },\;\\&\qquad \forall x,y\in \varOmega _{g}\subseteq {\mathbb {R}}^{n}, \end{aligned} \end{aligned}$$
(13)

where \(\varOmega _{g}\) is a compact set and \(L_{g}>0\) is the Lipschitz constant.

Assumption 2

(Global Lipschitz condition) The function

\(g(t,\eta )\) in system (7) satisfies Lipschitz condition:

$$\begin{aligned} \begin{aligned} \Vert {g(t,x)-g(t,y)}\Vert \le L\Vert {x-y}\Vert ,\; \forall t\ge t^{\star },\; \forall x,y\in {\mathbb {R}}^{n}, \end{aligned} \end{aligned}$$
(14)

where \(L>0\) is the Lipschitz constant.

We define a new time-dependent Metzler matrix by

$$\begin{aligned} \begin{aligned}&\varDelta _{E}(t)=\\&\begin{bmatrix} 2\left( k_{11}+m_{11}(t)\right) &{} 0 &{} \cdots &{} 0\\ 0 &{} 2\left( k_{22}+m_{22}(t)\right) &{} \cdots &{} 0\\ \vdots &{} \cdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 2\left( k_{nn}+m_{nn}(t)\right) \end{bmatrix}\\ +&\left[ \begin{array}{cc} \sum \limits _{j=1;j\ne 1}^{n}\vert {k_{1j}+m_{1j}(t)}\vert &{} \vert {k_{12}+m_{12}(t)}\vert \\ \vert {k_{21}+m_{21}(t)}\vert &{} \sum \limits _{j=1;j\ne 2}^{n}\vert {k_{2j}+m_{2j}(t)}\vert \\ \vdots &{} \cdots \\ \vert {k_{n1}+m_{n1}(t)}\vert &{} \vert {k_{n2}+m_{n2}(t)}\vert \end{array}\right. \\&\left. \begin{array}{cc} \cdots &{} \vert {k_{1n}+m_{1n}(t)}\vert \\ \cdots &{} \vert {k_{2n}+m_{2n}(t)}\vert \\ \ddots &{} \vdots \\ \cdots &{} \sum \limits _{j=1;j\ne n}^{n}\vert {k_{nj}+m_{nj}(t)}\vert \end{array}\right] \end{aligned} \end{aligned}$$
(15)

Assumption 3

Let the matrix (15), and suppose that there exist a constant Metzler matrix \({\mathscr {M}}^{+}=[\rho _{ij}]\in {\mathbb {R}}^{n\times {n}}\) such that

$$\begin{aligned} \varDelta _{E}(t)\le {\mathscr {M}}^{+}, \; \forall t\ge t^{\star }. \end{aligned}$$
(16)

Remark 1

In (16), we note that the entries of matrix \(\varDelta _{E}(t)\) are bounded above by matrix \({\mathscr {M}}^{+}\).

Assumption 4

Consider Assumption 1. Define a matrix \({\mathscr {N}_\mathscr {S}}\in {\mathbb {R}}^{n\times {n}}\) by

$$\begin{aligned} {\mathscr {N}_\mathscr {S}}=\begin{bmatrix} 1+L_{g}^{2} &{} L_{g}^2 &{} \cdots &{} L_{g}^{2}\\ L_{g}^{2} &{} 1+L_{g}^2 &{} \cdots &{} L_{g}^{2}\\ \vdots &{} \cdots &{} \ddots &{} \vdots \\ L_{g}^{2} &{} L_{g}^2 &{} \cdots &{} 1+L_{g}^{2} \end{bmatrix}. \end{aligned}$$
(17)

Assumption 5

Consider Assumption 2. Define a matrix \({\mathscr {N}_\mathscr {L}}\in {\mathbb {R}}^{n\times {n}}\) by

$$\begin{aligned} {\mathscr {N}_\mathscr {L}}=\begin{bmatrix} 1+L^{2} &{} L^2 &{} \cdots &{} L^{2}\\ L^{2} &{} 1+L^2 &{} \cdots &{} L^{2}\\ \vdots &{} \cdots &{} \ddots &{} \vdots \\ L^{2} &{} L^2 &{} \cdots &{} 1+L^{2} \end{bmatrix}. \end{aligned}$$
(18)

5.1 Order-dependent results

Theorem 2

Consider the system (7). Let Assumptions 1, 3 and 4. If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is locally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( s^{\alpha _1},s^{\alpha _2},\cdots ,s^{\alpha _n}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {S}}\right] =0 \end{aligned}$$
(19)

satisfies \(\vert {\arg (s)}\vert >\frac{\pi }{2}\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\le -\lambda {I}, \end{aligned}$$
(20)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

Take \({\mathscr {E}}(t,\xi )=\left( \varepsilon _{1}(t,\xi _{1}),\varepsilon _{2}(t,\xi _{2}),\cdots ,\varepsilon _{n}(t,\xi _{n})\right) ^{T}\)

where \(\varepsilon _{i}(t,\xi _{i})=\xi _{i}^2\) for \(i=1,2,\cdots ,n\). We apply governing inequality Lemma 2 along the solution to (10) and obtain

$$\begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t} {\mathscr {E}}(t,\xi (t))\le \left[ {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}} \right] {\mathscr {E}}(t,\xi (t)), \end{aligned}$$
(21)

where Assumptions 1, 3 and 4 were utilized. Then, we define a new comparison system

$$\begin{aligned} \begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t} {\mathscr {Y}}(t,\widehat{z}(t))&=\left[ {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}} \right] {\mathscr {Y}}(t,\widehat{z}(t)), \\ {\mathscr {Y}}(t^{\star },\widehat{z}(t^{\star }))&={\mathscr {E}}(t^{\star },\xi (t^{\star })), \end{aligned} \end{aligned}$$
(22)

where \({\mathscr {Y}}(t,\widehat{z})=\left( \varpi _{1}(t,\widehat{z}_{1}),\varpi _{2}(t,\widehat{z}_{2}),\cdots ,\varpi _{n}(t,\widehat{z}_{n})\right) ^{T}\). Since \(f=\left[ {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\right] u\) is of Class W, applying Lemma 1 for (21) and (22), it is immediate that

$$\begin{aligned} 0\le {\mathscr {E}}(t,\xi (t))\le {\mathscr {Y}}(t,\widehat{z}(t)),\; \forall t\ge t^{\star }. \end{aligned}$$
(23)

Note that when condition \(\complement _{1}\) is satisfied, then by using Theorem 1 for (22), one concludes that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty } {\mathscr {Y}}(t,\widehat{z}(t))=0. \end{aligned}$$
(24)

Then, it is immediate from (23) and (24) that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\xi (t)=0. \end{aligned}$$
(25)

It implies that \(\lim \limits _{t\rightarrow \infty }\eta (t)=v^{\star }\). On the other hand, when condition \(\complement _{2}\) is satisfied, one has from (22) that

$$\begin{aligned} \begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t} {\mathscr {Y}}(t,\widehat{z}(t))&\le -\lambda {I}{\mathscr {Y}}(t,\widehat{z}(t)), \\ {\mathscr {Y}}(t^{\star },\widehat{z}(t^{\star }))&={\mathscr {E}}(t^{\star },\xi (t^{\star })). \end{aligned} \end{aligned}$$
(26)

Then, we consider an associated comparison system

$$\begin{aligned} \begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t} {\mathscr {X}}(t,\nu (t))&= -\lambda {I}{\mathscr {X}}(t,\nu (t)), \\ {\mathscr {X}}(t^{\star },\nu (t^{\star }))&={\mathscr {Y}}(t^{\star },\widehat{z}(t^{\star })), \end{aligned} \end{aligned}$$
(27)

where \({\mathscr {X}}(t,\nu )=\left( \varsigma _{1}(t,\nu _{1}),\varsigma _{2}(t,\nu _{2}),\cdots ,\varsigma _{n}(t,\nu _{n})\right) ^{T}\). Subsequently, application of Lemma 1 for (26) and (27) gives

$$\begin{aligned} 0\le {\mathscr {Y}}(t,\widehat{z}(t))\le {\mathscr {X}}(t,\nu (t)), \; \forall t\ge t^{\star }. \end{aligned}$$
(28)

The explicit solution to (27) is given by

$$\begin{aligned} \varsigma _{i}(t,\nu _{i}(t))=E_{\alpha _{i},1}\left( -\lambda (t-t^{\star })^{\alpha _{i}}\right) \varsigma _{i}(t^{\star },\nu _{i}(t^{\star })),\; \forall t\ge t^{\star }, \end{aligned}$$
(29)

for \(i=1,2,\cdots ,n\). By adding the set of inequalities in (29), it follows from (23) and (28) that

$$\begin{aligned} \Vert {\xi (t)}\Vert ^{2}\le \sum \limits _{i=1}^{n}E_{\alpha _{i},1}\left( -\lambda (t-t^{\star })^{\alpha _{i}}\right) \Vert {\xi (t^{\star })}\Vert ^{2},\; \forall t\ge t^{\star }. \end{aligned}$$
(30)

Since the Mittag-Leffler function satisfies

\(0<E_{\alpha _{i},1}\left( -\lambda (t-t^{\star })^{\alpha _{i}}\right) \le 1\), \(t\ge t^{\star }\), when \(\lambda >0\) and \(0<\alpha _{i}\le 1\), for \(i=1,2,\cdots ,n\) (refer, [29]), one has

$$\begin{aligned} \Vert {\xi (t)}\Vert ^{2}\le C^{\star }\left[ nE_{\theta ,1}\left( -\lambda (t-t^{\star })^{\theta }\right) \right] \Vert {\xi (t^{\star })}\Vert ^{2},\; \forall t\ge t^{\star }, \end{aligned}$$
(31)

where \(C^{\star }\ge 1\), \(\theta \in \{\alpha _{1}, \alpha _{2},\cdots ,\alpha _{n}\}\). In what follows, the estimate:

$$\begin{aligned} \Vert {\xi (t)}\Vert \le C^{\dagger }\sqrt{nE_{\theta ,1}\left( -\lambda (t-t^{\star })^{\theta }\right) }\Vert {\xi (t^{\star })}\Vert ,\; \forall t\ge t^{\star }, \end{aligned}$$
(32)

where \(C^{\dagger }=\sqrt{C^{\star }}\ge 1\) and \(\theta \in (0,1]\). As a result, it follows from (32) that

$$\begin{aligned}&\Vert {\eta (t)}\Vert \le C^{\dagger }\sqrt{nE_{\theta ,1}\left( -\lambda (t-t^{\star })^{\theta }\right) }\nonumber \\&\qquad \Vert {\eta (t^{\star })-v^{\star }}\Vert +\Vert {v^{\star }}\Vert ,\; t\ge t^{\star }, \end{aligned}$$
(33)

where \(C^{\dagger }=\sqrt{C^{\star }}\ge 1\) and \(\theta \in (0,1]\). Thus, the system (7) is ML-ASTZ to \(v^{\star }\). This completes the proof. \(\square \)

Solving (19) in Theorem 2 seems quite challenging and remains an open problem in stability theory. We find some patterns that reduce the complexity of solving (19) to some simplified polynomial equations addressed in the below-mentioned corollaries.

Corollary 1

Consider the system (7). Let Assumptions 1, 3 and 4. Assume that there exist numbers \(N_{1},N_{2},\cdots ,N_{n}\in {\mathbb {N}}\). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is locally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ^{N_{1}},\tau ^{N_{2}},\cdots ,\tau ^{N_{n}}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {S}}\right] =0 \end{aligned}$$
(34)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2N_{k}}\alpha _{k}>0\), \(\forall \) \(k=1,2,\cdots ,n\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\le -\lambda {I}, \end{aligned}$$
(35)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

Use the transformations \(s^{\alpha _{i}/N_{i}}=\tau \) for \(i=1,2,\cdots ,n\). Then, the result follows from Theorem 2. \(\square \)

Corollary 2

Consider the system (7). Let Assumptions 1, 3 and 4. Assume that there exist numbers \(N_{1},N_{2},\cdots ,N_{n}\in {\mathbb {N}}\). Set \(\beta =\max \{\frac{\alpha _{1}}{N_{1}},\frac{\alpha _{2}}{N_{2}},\cdots ,\frac{\alpha _{n}}{N_{n}}\}\). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is locally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ^{N_{1}},\tau ^{N_{2}},\cdots ,\tau ^{N_{n}}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {S}}\right] =0 \end{aligned}$$
(36)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2}\beta >0\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\le -\lambda {I}, \end{aligned}$$
(37)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

The proof follows from Corollary 1. \(\square \)

Corollary 3

Consider the system (7). Let Assumptions 1, 3 and 4. Let \(\alpha _{i}=\gamma _{i}\delta \in (0,1]\), \(\gamma _{i}=\frac{\ell _{i}}{\rho _{i}}\in {\mathbb {Q}}_{+}\) with \(gcd(\ell _{i},\rho _{i})=1\), for \(i=1,2,\cdots ,n\) and \(0<\delta \in {\mathbb {R}}\). Set \(\varSigma =lcm\left( \rho _{1},\rho _{2},\cdots ,\rho _{n}\right) \). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is locally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ^{\varSigma \gamma _{1}},\tau ^{\varSigma \gamma _{2}},\cdots ,\tau ^{\varSigma \gamma _{n}}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {S}}\right] =0 \end{aligned}$$
(38)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2\varSigma }\delta >0\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\le -\lambda {I}, \end{aligned}$$
(39)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

Use \(s^{\delta /\varSigma }=\tau \). Then, the proof follows from Theorem 2. \(\square \)

Corollary 4

Consider the system (7). Let Assumptions 1, 3 and 4. Let \(\alpha _{i}=\gamma _{i}\in (0,1]\), \(\gamma _{i}=\frac{\ell _{i}}{\rho _{i}}\in {\mathbb {Q}}_{+}\) with \(gcd(\ell _{i},\rho _{i})=1\), for \(i=1,2,\cdots ,n\).

Set \(\varSigma =lcm\left( \rho _{1},\rho _{2},\cdots ,\rho _{n}\right) \). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is locally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ^{\varSigma \gamma _{1}},\tau ^{\varSigma \gamma _{2}},\cdots ,\tau ^{\varSigma \gamma _{n}}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {S}}\right] =0 \end{aligned}$$
(40)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2\varSigma }>0\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\le -\lambda {I}, \end{aligned}$$
(41)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

Take \(\delta =1\) in Corollary 3. \(\square \)

Corollary 5

Consider the system (7). Let Assumptions 1, 3 and 4. Let \(\alpha _{i}=\gamma \in (0,1]\), for \(i=1,2,\cdots ,n\). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is locally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ,\tau ,\cdots ,\tau \right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {S}}\right] =0 \end{aligned}$$
(42)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2}\gamma >0\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\le -\lambda {I}, \end{aligned}$$
(43)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

Use the transformation \(s^{\gamma }=\tau \) in Theorem 2. \(\square \)

Next, we introduce global Mittag-Leffler stabilization results addressed as follows. These results provide conditions associated with the Metzler matrix and nonnegative matrix.

Theorem 3

Consider the system (7). Let Assumptions 2, 3 and 5. If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is globally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( s^{\alpha _1},s^{\alpha _2},\cdots ,s^{\alpha _n}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {L}}\right] =0 \end{aligned}$$
(44)

satisfies \(\vert {\arg (s)}\vert >\frac{\pi }{2}\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}\le -\lambda {I}, \end{aligned}$$
(45)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

The proof is immediate. We thus omit it here. \(\square \)

Corollary 6

Consider the system (7). Let Assumptions 2, 3 and 5. Assume that there exist numbers \(N_{1},N_{2},\cdots ,N_{n}\in {\mathbb {N}}\). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is globally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ^{N_{1}},\tau ^{N_{2}},\cdots ,\tau ^{N_{n}}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {L}}\right] =0 \end{aligned}$$
(46)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2N_{k}}\alpha _{k}>0\), \(\forall \) \(k=1,2,\cdots ,n\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}\le -\lambda {I}, \end{aligned}$$
(47)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

Use the transformations \(s^{\alpha _{i}/N_{i}}=\tau \) for \(i=1,2,\cdots ,n\). Then, the result follows from Theorem 3. \(\square \)

Corollary 7

Consider the system (7). Let Assumptions 2, 3 and 5. Assume that there exist numbers \(N_{1},N_{2},\cdots ,N_{n}\in {\mathbb {N}}\). Set \(\beta =\max \{\frac{\alpha _{1}}{N_{1}},\frac{\alpha _{2}}{N_{2}},\cdots ,\frac{\alpha _{n}}{N_{n}}\}\). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is globally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ^{N_{1}},\tau ^{N_{2}},\cdots ,\tau ^{N_{n}}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {L}}\right] =0 \end{aligned}$$
(48)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2}\beta >0\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}\le -\lambda {I}, \end{aligned}$$
(49)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

The proof follows from Corollary 6. \(\square \)

Corollary 8

Consider the system (7). Let Assumptions 2, 3 and 5. Let \(\alpha _{i}=\gamma _{i}\delta \in (0,1]\), \(\gamma _{i}=\frac{\ell _{i}}{\rho _{i}}\in {\mathbb {Q}}_{+}\) with \(gcd(\ell _{i},\rho _{i})=1\), for \(i=1,2,\cdots ,n\) and \(0<\delta \in {\mathbb {R}}\). Set \(\varSigma =lcm\left( \rho _{1},\rho _{2},\cdots ,\rho _{n}\right) \). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is globally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ^{\varSigma \gamma _{1}},\tau ^{\varSigma \gamma _{2}},\cdots ,\tau ^{\varSigma \gamma _{n}}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {L}}\right] =0 \end{aligned}$$
(50)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2\varSigma }\delta >0\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}\le -\lambda {I}, \end{aligned}$$
(51)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

Use \(s^{\delta /\varSigma }=\tau \). Then, the proof follows from Theorem 3. \(\square \)

Corollary 9

Consider the system (7). Let Assumptions 2, 3 and 5. Let \(\alpha _{i}=\gamma _{i}\in (0,1]\), \(\gamma _{i}=\frac{\ell _{i}}{\rho _{i}}\in {\mathbb {Q}}_{+}\) with \(gcd(\ell _{i},\rho _{i})=1\), for \(i=1,2,\cdots ,n\).

Set \(\varSigma =lcm\left( \rho _{1},\rho _{2},\cdots ,\rho _{n}\right) \). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is globally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ^{\varSigma \gamma _{1}},\tau ^{\varSigma \gamma _{2}},\cdots ,\tau ^{\varSigma \gamma _{n}}\right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {L}}\right] =0 \end{aligned}$$
(52)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2\varSigma }>0\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}\le -\lambda {I}, \end{aligned}$$
(53)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

Take \(\delta =1\) in Corollary 8. \(\square \)

Corollary 10

Consider the system (7). Let Assumptions 2, 3 and 5. Let \(\alpha _{i}=\gamma \in (0,1]\), for \(i=1,2,\cdots ,n\). If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the below-mentioned conditions hold for the control system (10), then the system (7) is globally ML-ASTZ to \(v^{\star }\).

\(\complement _{1}\).:

Every root of

$$\begin{aligned} \det \left[ \mathrm{{diag}}\left( \tau ,\tau ,\cdots ,\tau \right) -{\mathscr {M}}^{+}-{\mathscr {N}_\mathscr {L}}\right] =0 \end{aligned}$$
(54)

satisfies \(\vert {\arg (\tau )}\vert -\frac{\pi }{2}\gamma >0\).

\(\complement _{2}\).:

There exists a constant \(\lambda >0\) such that

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}\le -\lambda {I}, \end{aligned}$$
(55)

where \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix.

Proof

Use the transformation \(s^{\gamma }=\tau \) in Theorem 3. \(\square \)

5.2 Order-independent results

Theorem 4

Consider the system (7). Let Assumptions 1, 3 and 4. If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the inequality

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\le -\lambda {I}, \end{aligned}$$
(56)

where constant \(\lambda >0\) and \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix, holds for the control system (10), then the system (7) is locally ML-ASTZ to \(v^{\star }\).

Proof

Take \({\mathscr {E}}(t,\xi )=\left( \varepsilon _{1}(t,\xi _{1}),\varepsilon _{2}(t,\xi _{2}),\cdots ,\varepsilon _{n}(t,\xi _{n})\right) ^{T}\) where \(\varepsilon _{i}(t,\xi _{i})=\xi _{i}^2\) for \(i=1,2,\cdots ,n\). We apply governing inequality Lemma 2 along the solution to (10) and obtain

$$\begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t} {\mathscr {E}}(t,\xi (t))\le \left[ {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}} \right] {\mathscr {E}}(t,\xi (t)), \end{aligned}$$
(57)

where Assumption 1, Assumption 3 and Assumption 4 were utilized. Then, by using inequality (56), one obtains from (21) that

$$\begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t} {\mathscr {E}}(t,\xi (t))\le -\lambda {I}{\mathscr {E}}(t,\xi (t)). \end{aligned}$$
(58)

We let an associated comparison system

$$\begin{aligned} \begin{aligned} ^{C}\!{\mathscr {D}}^{\widehat{\alpha }}_{t^{\star },t} {\mathscr {X}}(t,\nu (t))&= -\lambda {I}{\mathscr {X}}(t,\nu (t)), \\ {\mathscr {X}}(t^{\star },\nu (t^{\star }))&={\mathscr {E}}(t^{\star },\xi (t^{\star })), \end{aligned} \end{aligned}$$
(59)

where \({\mathscr {X}}(t,\nu )=\left( \varsigma _{1}(t,\nu _{1}),\varsigma _{2}(t,\nu _{2}),\cdots ,\varsigma _{n}(t,\nu _{n})\right) ^{T}\). Subsequently, application of Lemma 1 for (58) and (59) gives

$$\begin{aligned} 0\le {\mathscr {E}}(t,\xi (t))\le {\mathscr {X}}(t,\nu (t)), \; \forall t\ge t^{\star }. \end{aligned}$$
(60)

The explicit solution to (60) is given by

$$\begin{aligned} \varsigma _{i}(t,\nu _{i}(t))=E_{\alpha _{i},1}\left( -\lambda (t-t^{\star })^{\alpha _{i}}\right) \varsigma _{i}(t^{\star },\nu _{i}(t^{\star })),\; \forall t\ge t^{\star }, \end{aligned}$$
(61)

for \(i=1,2,\cdots ,n\). Since the Mittag-Leffler functions

\(E_{\alpha _{i},1}\left( -\lambda (t-t^{\star })^{\alpha _{i}}\right) \) tends to 0 as \(t\rightarrow \infty \) (see Theorem 1.6 [29]), one gets from (61) that \(\xi (t)\rightarrow 0\) as \(t\rightarrow \infty \). On the other hand, by adding the set of inequalities in (61), it follows from (60) that

$$\begin{aligned} \Vert {\xi (t)}\Vert ^{2}\le \sum \limits _{i=1}^{n}E_{\alpha _{i},1}\left( -\lambda (t-t^{\star })^{\alpha _{i}}\right) \Vert {\xi (t^{\star })}\Vert ^{2},\; \forall t\ge t^{\star }. \end{aligned}$$
(62)

Since the Mittag-Leffler function satisfies

\(0<E_{\alpha _{i},1}\left( -\lambda (t-t^{\star })^{\alpha _{i}}\right) \le 1\), \(t\ge t^{\star }\), when \(\lambda >0\) and \(0<\alpha _{i}\le 1\), for \(i=1,2,\cdots ,n\) (refer, [29]), one has

$$\begin{aligned} \Vert {\xi (t)}\Vert ^{2}\le C^{\star }\left[ nE_{\theta ,1}\left( -\lambda (t-t^{\star })^{\theta }\right) \right] \Vert {\xi (t^{\star })}\Vert ^{2},\; \forall t\ge t^{\star }, \end{aligned}$$
(63)

where \(C^{\star }\ge 1\), \(\theta \in \{\alpha _{1}, \alpha _{2},\cdots ,\alpha _{n}\}\). In what follows, the estimate:

$$\begin{aligned} \Vert {\xi (t)}\Vert \le C^{\dagger }\sqrt{nE_{\theta ,1}\left( -\lambda (t-t^{\star })^{\theta }\right) }\Vert {\xi (t^{\star })}\Vert ,\; \forall t\ge t^{\star }, \end{aligned}$$
(64)

where \(C^{\dagger }=\sqrt{C^{\star }}\ge 1\) and \(\theta \in (0,1]\). Thus, the system (7) is ML-ASTZ to \(v^{\star }\). This completes the proof. \(\square \)

Theorem 5

Consider the system (7). Let Assumptions 2, 3 and 5. If there exists a control matrix \(K=[k_{ij}]\in {\mathbb {R}}^{n\times {n}}\) in (9) such that the inequality

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}\le -\lambda {I}, \end{aligned}$$
(65)

where constant \(\lambda >0\) and \(I\in {\mathbb {R}}^{n\times {n}}\) is an identity matrix, holds for the control system (10), then the system (7) is globally ML-ASTZ to \(v^{\star }\).

Proof

One gets the result by following the proof strategy of Theorem 4. \(\square \)

Remark 2

In Theorem 4 and Theorem 5, it is not needed to verify additional conditions on orders as found in Theorem 2 and Theorem 3. The merit of Theorems 4 and  5 provides convergence directly from the Mittag-Leffler function. On the other hand, in Theorem 2 and Theorem 3, one required an external system to conclude convergence associated with system orders.

6 Applications

In this section, we illustrate the novelty of the proposed control method approach by applying some theoretical results. In contrast to the demonstrated performance of control systems [10, 19, 20], the below-mentioned discussions sharpen improved performance with the inclusion of random initial time and selected control objective.

Example 1

Consider the random initial-time real-order extension of Wei system [27]:

$$\begin{aligned} \begin{aligned} ^{C}\!{\mathscr {D}}^{\alpha _{1}}_{t^{\star }, t}\eta _{1}(t)&=-\eta _{2}(t),\\ ^{C}\!{\mathscr {D}}^{\alpha _{2}}_{t^{\star }, t}\eta _{2}(t)&=c\eta _{1}(t)+\eta _{3}(t),\\ ^{C}\!{\mathscr {D}}^{\alpha _{3}}_{t^{\star }, t}\eta _{3}(t)&=a\eta _{2}^{2}(t)+\eta _{1}(t)\eta _{3}(t)-d, \end{aligned} \end{aligned}$$
(66)

where \(\alpha _{1},\alpha _{2},\alpha _{3}\in (0,1]\), a, c and d are real parameters.

The system (66) is known to give rise to zero equilibrium chaotic Sprott-D system when \(t^{\star }=0\), \(\alpha _{1}=\alpha _{2}=\alpha _{3}=1\), \(a=3\), \(c=1\) and \(d=0\). The Wei system (66) is also known to be chaotic with no equilibrium when \(t^{\star }=0\), \(\alpha _{1}=\alpha _{2}=\alpha _{3}=1\), \(a=2\), \(c=1\) and \(d=0.35\). Here we consider a case when \(t^{\star }=-50\), \(\alpha _{1}=0.995\), \(\alpha _{2}=0.999\), \(\alpha _{3}=0.997\), \(a=2\), \(c=1\), \(d=0.35\).

Fig. 1
figure 1

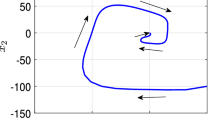
Memory chaos in real-order Wei system (66) where \(t^{\star }=-50\), \(\alpha _{1}=0.995\), \(\alpha _{2}=0.999\), \(\alpha _{3}=0.997\), \(a=2\), \(c=1\), \(d=0.35\)

Full size image

The simulation [35] shows that the system (66) has memory chaos presented in Fig. 1 starting from initial values \(\eta (-50)=\left( \eta _{1}(-50),\eta _{2}(-50),\eta _{3}(-50)\right) ^{T}=\left( -1.6,0.82,1.9\right) ^{T}\). Suppose we wish to control the memory chaos of the real-order Wei system (66) by using the proposed affine control strategy discussed in Sect. 4 to a target vector \(v^{\star }=\left( -100,50,100\right) ^{T}\) that is absent in the system (66). First, notice that the system (66) can be represented in the form (7), where \(M(t)=\begin{bmatrix} 0 &{} -1 &{} 0\\ c &{} 0 &{} 1\\ 0 &{} 0 &{} 0 \end{bmatrix}\) and

\(g(t,\eta (t))=\left( 0,0,a\eta _{2}^{2}(t)+\eta _{1}(t)\eta _{3}(t)-d\right) ^{T}\). Let \(\xi (t)=\eta (t)-v^{\star }=\left( \eta _{1}(t)+100,\eta _{2}(t)-50,\eta _{3}(t)-100\right) ^{T}\). By adding the linear affine controller (see (9)):

$$\begin{aligned} u(t)=K\xi (t)-g(t,0) \end{aligned}$$
(67)

where entries of \(K=[k_{ij}]\in {\mathbb {R}}^{3\times {3}}\) needs to be determined, to the system (66), we obtain (see (10)):

$$\begin{aligned} \begin{aligned} \begin{pmatrix} ^{C}\!{\mathscr {D}}^{\alpha _{1}}_{t^{\star }, t}\xi _{1}(t)\\ ^{C}\!{\mathscr {D}}^{\alpha _{1}}_{t^{\star }, t}\xi _{2}(t)\\ ^{C}\!{\mathscr {D}}^{\alpha _{1}}_{t^{\star }, t}\xi _{3}(t) \end{pmatrix}&=\begin{bmatrix} k_{11} &{} k_{12}-1 &{} k_{13}\\ c+k_{21} &{} k_{22} &{} 1+k_{23}\\ k_{31} &{} k_{32} &{} k_{33} \end{bmatrix}\begin{pmatrix} \xi _{1}(t)\\ \xi _{2}(t)\\ \xi _{3}(t) \end{pmatrix}\\&\qquad {}+\begin{pmatrix} 0\\ 0\\ a\xi _{2}^{2}(t)+\xi _{1}(t)\xi _{3}(t) \end{pmatrix}. \end{aligned} \end{aligned}$$
(68)

Here we wish apply Corollary 1 to the system (68). First, we set \(\varOmega _{g}=\{\left( \eta _{1},\eta _{2},\eta _{3}\right) ^{T}: \vert {\eta _1}\vert ^{2}+\vert {\eta _2}\vert ^{2}+\vert {\eta _3}\vert ^{2}\le r^2<\infty \}\). Then, based on the boundedness of attractor shown in Fig. 1, we set up \(\vert {\eta _i}\vert \le 5\) for \(i=1,2,3\). Note that

$$\begin{aligned} \begin{aligned} \vert {g_{1}(t,x)-g_{1}(t,y)}\vert ^{2}&\le \Vert {x-y}\Vert ^{2},\\ \vert {g_{2}(t,x)-g_{2}(t,y)}\vert ^{2}&\le \Vert {x-y}\Vert ^{2},\\ \vert {g_{3}(t,x)-g_{3}(t,y)}\vert ^{2}&\le \left( 100a^{2}+50\right) \Vert {x-y}\Vert ^{2}. \end{aligned} \end{aligned}$$
(69)

Consequently, Assumption 1 holds with Lipschitz constant \(L_{g}=\sqrt{52+100a^{2}}\). Set \(\varOmega =\{\left( \eta _{1},\eta _{2},\eta _{3}\right) ^{T}: \vert {\eta _1}\vert ^{2}+\vert {\eta _2}\vert ^{2}+\vert {\eta _3}\vert ^{2}< 25\}\). Next, we define the Metzler matrix (15) by

$$\begin{aligned} \begin{aligned}&\varDelta _{E}(t)\\&=\left[ \begin{array}{cc} 2k_{11}+\vert {k_{12}-1}\vert +\vert {k_{13}}\vert &{} \vert {k_{12}-1}\vert \\ \vert {k_{21}+c}\vert &{} 2k_{22}+\vert {k_{21}+c}\vert + \vert {k_{23}+1}\vert \\ \vert {k_{31}}\vert &{} \vert {k_{32}}\vert \end{array}\right. \\&\qquad {} \left. \begin{array}{c} \vert {k_{13}}\vert \\ \vert {k_{23}+1}\vert \\ 2k_{33}+\vert {k_{31}}\vert +\vert {k_{32}}\vert \end{array}\right] \end{aligned} \end{aligned}$$
(70)

Then, we let the Metzler matrix

$$\begin{aligned} \begin{aligned}&{\mathscr {M}}^{+}\\&=\left[ \begin{array}{cc} 2k_{11}+\vert {k_{12}-1}\vert +\vert {k_{13}}\vert &{} \vert {k_{12}-1}\vert \\ \vert {k_{21}+c}\vert &{} 2k_{22}+\vert {k_{21}+c}\vert + \vert {k_{23}+1}\vert \\ \vert {k_{31}}\vert &{} \vert {k_{32}}\vert \end{array}\right. \\&\qquad {} \left. \begin{array}{c} \vert {k_{13}}\vert \\ \vert {k_{23}+1}\vert \\ 2k_{33}+\vert {k_{31}}\vert +\vert {k_{32}}\vert \end{array}\right] \end{aligned} \end{aligned}$$
(71)

Since \(a=2\), the nonnegative matrix (17) becomes

$$\begin{aligned} {\mathscr {N}_\mathscr {S}}=\begin{bmatrix} 453 &{} 452 &{} 452\\ 452 &{} 453 &{} 452\\ 452 &{} 452 &{} 453 \end{bmatrix}. \end{aligned}$$
(72)

Here, we select a control matrix

$$\begin{aligned} K=\begin{bmatrix} -1000 &{} 1 &{} 0\\ -1 &{} -1000 &{} -1\\ 0 &{} 0 &{} -1000 \end{bmatrix}. \end{aligned}$$
(73)

Then, one gets the matrix

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}=\begin{bmatrix} -1547 &{} 452 &{} 452\\ 452 &{} -1547 &{} 452\\ 452 &{} 452 &{} -1547 \end{bmatrix}. \end{aligned}$$
(74)

Set \(N_{1}=13\), \(N_{2}=17\) and \(N_{3}=19\). Then, the equation (34) reduces to

$$\begin{aligned} \begin{aligned} \tau ^{49}&+ 1547\tau ^{36} + 1547\tau ^{32} + 1547\tau ^{30} + 2188905\tau ^{19} \\&\qquad {}+ 2188905\tau ^{17} + 2188905\tau ^{13} + 2569428643=0. \end{aligned} \end{aligned}$$
(75)

Solving (75), one has

$$\begin{aligned} \min \{\vert {\arg (\tau _{1})}\vert ,\vert {\arg (\tau _{2})}\vert ,\cdots ,\vert {\arg (\tau _{49})}\vert \}\approx { 0.1692}. \end{aligned}$$
(76)

It can be observed that the obtained estimate in (76) is greater than the below-mentioned estimates:

  1. i)

    \(\frac{\pi }{2N_{1}}\alpha _{1}=\frac{\pi }{26}(0.995)\approx {0.1202}\),

  2. ii)

    \(\frac{\pi }{2N_{2}}\alpha _{2}=\frac{\pi }{34}(0.999)\approx {0.0923}\),

  3. iii)

    \(\frac{\pi }{2N_{3}}\alpha _{3}=\frac{\pi }{38}(0.997)\approx {0.0824}\).

Therefore, the condition in \(\complement _{1}\) of Corollary 1 is satisfied. On the other hand, one gets \(\lambda _{1}=-643\), \(\lambda _{2}=-1999\) and \(\lambda _{3}=-1999\) are the eigenvalues of \({\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\). Set \(\lambda =643\). Then, one has \({\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {S}}\le -\lambda {I}\). Thus, the condition in \(\complement _{2}\) of Corollary 1 is satisfied. As a result, it is immediate from Corollary 1 that the system (7) should be locally ML-ASTZ to \(v^{\star }=\left( -100,50,100\right) ^{T}\) in \(\varOmega \). Thus, the controlled trajectory must obey the bounds given by

$$\begin{aligned} \begin{aligned} \Vert {\eta (t)}\Vert&\le C^{\dagger }\sqrt{3E_{\theta ,1}\left( -643(t+50)^{\theta }\right) }\Vert {\eta (t^{\star })-v^{\star }}\Vert \\&\qquad {}+\Vert {v^{\star }}\Vert ,\; t\ge t^{\star }=-50, \end{aligned} \end{aligned}$$
(77)

where \(C^{\dagger }=\sqrt{C^{\star }}\ge 1\) and \(\theta \in (0,1]\).

Fig. 2
figure 2

Controlled memory chaos of real-order Wei system (66) to \(v^{\star }=\left( -100,50,100\right) ^{T}\) under action of affine control law (67) with (73) where \(t^{\star }=-50\), \(\alpha _{1}=0.995\), \(\alpha _{2}=0.999\), \(\alpha _{3}=0.997\), \(a=2\), \(c=1\), \(d=0.35\)

Full size image

The simulation is shown in Fig. 2 with the implantation of control law (67) to (66) with the selection of control matrix (73). It illustrates the convergence part of the effectiveness of the theoretical result to control the trajectory to an achievable target goal: \(v^{\star }=\left( -100,50,100\right) ^{T}\).

Fig. 3
figure 3

Euclidean norm measure (ENM) and Mittag-Leffler estimate (MLE) of controlled trajectory shown in Fig. 2, where \(t^{\star }=-50\), \(C^{\star }=4\), \(C^{\dagger }=2\) and \(\theta =0.5\). It demonstrates ML-ASTZ to \(v^{\star }=\left( -100,50,100\right) ^{T}\)

Full size image

Let ENM denote the Euclidean norm measure of controlled trajectory obtained in Fig. 2. Let MLE denote the Mittag-Leffler estimate on the right-hand side of (77). The simulations for ENM and MLE are presented in Fig. 3. It illustrates that ENM cannot exceed the Mittag-Leffler estimate. Hence, Figs. 2 and 3 show that the system (66) should be Mittag-Leffler asymptotically stabilizable. This closes the demonstration.

Remark 3

The new design of practical applications (e.g., [4, 5]), including hardware implementation, is out of the scope of the current research facility at present. It is suggested that engineers practice making circuit designs to demonstrate the feasibility of the performance of systems owing to theoretical validations.

Remark 4

A bifurcation diagram may not give new information about the structure of solutions when it comes to real- or fractional-order systems. For instance, it is known that the existence of periodic solutions in real-order systems seems impossible [36, 37]. Thus, a bifurcation diagram may not tell anything new even if one obtains similar-type phenomena (e.g., [38, 39]) corresponding to ordinary differential systems counterparts. The occurrence of observed visual periodic motions like orbits may not be actually periodic. A question of thought we address here for potential researchers is as follows: Is it possible that the period-doubling route to chaos is actually possible in real-order systems? On the other hand, computing Lyapunov exponents for fractional-order systems seems quite challenging. Although there is no rigorous theory available so far in the current literature, the sign of Lyapunov exponents may not give exact information about system behavior. The basin of attraction of fractional-order systems is not easy to compute due to the involvement of a long memory of system behavior. The boundaries of classifications of various types of solutions in fractional-order systems remain unknown to date. We believe that these useful discussions might bring new challenges and light in the direction of the achievement of surprising phenomena in the field of the theory of real-order systems.

Example 2

Suppose we wish to control the non-asymptotic trajectory of a real-order system

$$\begin{aligned} ^{C}\!{\mathscr {D}}^{\alpha _{1}}_{t^{\star },t}\eta _{1}(t)&= \frac{11}{2}\eta _{1}(t)+\sin ^2(t-t^{\star })\eta _{1}(t)\nonumber \\&\qquad +\sin ^{2}(\eta _{2}(t))+u_{1}(t), \nonumber \\ ^{C}\!{\mathscr {D}}^{\alpha _{2}}_{t^{\star },t}\eta _{2}(t)&= \frac{11}{2}\eta _{2}(t)+\cos ^2(t-t^{\star })\eta _{2}(t)\nonumber \\&\qquad +\sin ^{2}(\eta _{1}(t))+u_{2}(t). \end{aligned}$$
(78)

with \(\eta _{i}(t^{\star })=\bar{\eta }_{i}(t^{\star })\) for \(i=1,2\), where \(\alpha _{1}, \alpha _{2}\in (0,1]\), \(t^{\star }\in {\mathbb {R}}\) and \(u_{i}(t)\) needs to be designed for \(i=1,2\).

When control inputs \(u_{i}(t)=0\) for \(i=1,2\), the system (78) can be represented by the form in (7), where \(M(t)=\begin{bmatrix} \frac{11}{2}+\sin ^{2}(t-t^{\star }) &{} 0\\ 0 &{} \frac{11}{2}+\cos ^{2}(t-t^{\star }) \end{bmatrix}\) and

\(g(t,\eta (t))=\left( \sin ^{2}\left( \eta _{2}(t)\right) , \sin ^{2}\left( \eta _{1}(t)\right) \right) ^{T}\). We let \(t^{\star }=50\), \(\alpha _{1}=0.9\) and \(\alpha _{2}=0.7\). The simulation [35] shows that the system (78) has a non-asymptotic response indicated in Fig. 4 starting from initial values

\(\eta (50)=\left( \eta _{1}(50),\eta _{2}(50)\right) ^{T}=\left( 50,-100\right) ^{T}\) with input \(u_{i}(t)=0\) for \(i=1,2\).

Fig. 4
figure 4

Non-asymptotic (unbounded) response of system (78) when inputs \(u_{i}(t)=0\), \(i=1,2\), where \(t^{\star }=50\), \(\alpha _{1}=0.9\) and \(\alpha _{2}=0.7\)

Full size image

Suppose we wish to control the obtained response to a target vector \(v^{\star }=\left( 0,0\right) ^{T}\) that is present in the system (78). Based on the affine control strategy discussed in Sect. 4, we design the control law

$$\begin{aligned} u(t)=\left( u_{1}(t),u_{2}(t)\right) ^{T}=K\xi (t)-v^{\star } \end{aligned}$$
(79)

where entries of \(K=[k_{ij}]\in {\mathbb {R}}^{2\times {2}}\) needs to be selected and \(\xi (t)=\eta (t)-v^{\star }=\eta (t)\). Then, the control system becomes

$$\begin{aligned} \begin{aligned}&\begin{pmatrix} ^{C}\!{\mathscr {D}}^{\alpha _{1}}_{t^{\star },t}\xi _{1}(t)\\ ^{C}\!{\mathscr {D}}^{\alpha _{1}}_{t^{\star },t}\xi _{2}(t) \end{pmatrix} =\begin{pmatrix} \sin ^{2}\left( \xi _{2}(t)\right) \\ \sin ^{2}\left( \xi _{1}(t)\right) \end{pmatrix}\\&\quad +\begin{bmatrix} \frac{11}{2}+\sin ^{2}(t-t^{\star })+k_{11} &{} k_{12}\\ k_{21} &{} \frac{11}{2}+\cos ^{2}(t-t^{\star })+k_{22} \end{bmatrix}\\&\begin{pmatrix} \xi _{1}(t)\\ \xi _{2}(t) \end{pmatrix}. \end{aligned} \end{aligned}$$
(80)

Here we wish to apply Theorem 5. Note that the function \(g(t,\eta )\) satisfies global Lipschitz condition in Assumption 2 with constant \(L=2\). In view of Assumption 3, we take the Metzler matrix

$$\begin{aligned} \begin{aligned} \varDelta _{E}(t)&=\left[ \begin{array}{c} 2\left( \frac{11}{2}+\sin ^{2}(t-t^{\star })+k_{11}\right) +\vert {k_{12}}\vert \\ \vert {k_{21}}\vert \end{array}\right. \\&\qquad {} \left. \begin{array}{c} \vert {k_{12}}\vert \\ 2\left( \frac{11}{2}+\cos ^{2}(t-t^{\star })+k_{22}\right) +\vert {k_{21}}\vert \end{array}\right] , \end{aligned} \end{aligned}$$
(81)

and set the constant Metzler by

$$\begin{aligned} {\mathscr {M}}^{+}=\begin{bmatrix} 13+2k_{11}+\vert {k_{12}}\vert &{} \vert {k_{12}}\vert \\ \vert {k_{21}}\vert &{} 13+2k_{22}+\vert {k_{21}}\vert \end{bmatrix}. \end{aligned}$$
(82)

Then, we let the nonnegative matrix in Assumption 5 by

$$\begin{aligned} {\mathscr {N}_\mathscr {L}}=\begin{bmatrix} 5 &{} 4\\ 4 &{} 5 \end{bmatrix}. \end{aligned}$$
(83)

Here we select the control matrix

$$\begin{aligned} K=\begin{bmatrix} -15 &{} 1\\ -1 &{} -20 \end{bmatrix}. \end{aligned}$$
(84)

Then, one gets the matrix

$$\begin{aligned} {\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}=\begin{bmatrix} -11 &{} 5\\ 5 &{} -21 \end{bmatrix}. \end{aligned}$$
(85)

Since \(\lambda _{1}=-16-5\sqrt{2}\) and \(\lambda _{2}=5\sqrt{2}-16\) are the eigenvalues of \({\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}\), one has \({\mathscr {M}}^{+}+{\mathscr {N}_\mathscr {L}}\le -(16-5\sqrt{2})I\), where \(I\in {\mathbb {R}}^{2\times {2}}\). Therefore, the condition of Theorem 5 is satisfied.

Fig. 5
figure 5

Controlled response of system (78) when implemented affine controller (79) with (84), where \(t^{\star }=50\), \(\alpha _{1}=0.9\) and \(\alpha _{2}=0.7\)

Full size image

It can be concluded that the system (78) should be globally ML-ASTZ to \(v^{\star }=\left( 0,0\right) ^{T}\). The simulation shown in Fig. 5 illustrates the effectiveness of the theoretical results owing to the proposed control method. This closes the demonstration.

7 Conclusions

Mittag-Leffler asymptotic stabilization of random initial-time incommensurate nonlinear real-order systems has been developed to control the complicated or non-asymptotic trajectories arising in such systems for any target constant vector in Euclidean space. The approach provides new tools to obtain precise theoretical measurements of the performances of automatic controlled responses under the action of the linear affine control law that has been implemented in such class systems. New results introduce order-dependent and order-independent local and global stabilization results, which provide Mittag-Leffler decay associated with an external order lie between (0, 1]. The results show that if there exists a suitable control matrix associated with the aforementioned control law such that one finds a scaling bounding constant to the sum of a constant Metzler matrix and a nonnegative matrix, then it is possible to conclude the introduced Mittag-Leffler asymptotic stabilization.

In the demonstration, at first glance, we discover complicated memory chaos in a no-equilibrium real-order Wei system that has been controlled to a vector \((-100,50,100)^{T}\) under affine control law when the initial time is \(-50\). Secondly, a nonlinear real-order system gives a non-asymptotic trajectory controlled to a target vector \((0,0)^{T}\) under the proposed control methodology. We have successfully demonstrated applicable theoretical results and shown that the method is effective and practically convenient and could apply to many different real-order systems whenever the initial time is not limited to 0.

The key advantage of this method is that it provides a way to control any target constant vector via a linear affine state feedback control law, although the original system may not have any equilibrium solutions. In the absence of any other simple methods, the current demonstration method provides a new way to investigate the stabilization problems of real-order systems associated with random initial time acting like an ultimate intrinsic parameter. It has been discovered that the limitations of the current demonstration are different. For instance, the use of Theorems 2 and 3 in engineering control technology remains an open exercise problem. It is suggested that control engineers should practice the results to such an extent in the direction of the achievement of developing real-world stability theories for advancing control design systems.