1 Introduction

The evolution of research in the automatic control field has given rise to the development of several effective synthesis methods over the last few decades [1]. The resulting robust controllers can guarantee good reference tracking dynamics, good closed-loop robustness against model parameter variations, good load disturbance rejection, good sensor noise suppression dynamics, and a good trade-off between them [1, 2]. These targets have previously required the availability of an adequate mathematical model that describes the actual behavior of the process as accurately as possible. This last must maintain its accuracy and good performance, regardless of undesired exogenous effects that often have not been introduced during the modeling stage of the real process [1,2,3]. Unfortunately, a perfect model is rarely available in most real-world applications. This is due to the existence of nonlinear and un-modeled dynamics that are inherent in the real process. It is also due to the existence of several uncertainties that occurred in the mathematical model [3]. As a result, all these effects considerably complicate the synthesis step of the desired controller, leading to the failure of many conventional controllers such as the proportional–integral–derivative (PID) controller [4]. To overcome these drawbacks, several synthesis methods such as robust H∞, neural networks, and fuzzy logic have been employed for imprecise models. In this study, the controller design is carried out using the FLC-based method. It is known that the key to the success of all synthesis methods is the availability of the set of states constituting the mathematical model [5]. In fact, the absence of one or more of them often causes a considerable degradation of the performances, provided by the chosen synthesis method. Sensor and sensorless speed control of actual DFIM systems, that will be discussed and analyzed in this paper, are one of the most existing cases in the literature where the corresponding mismatch model has many inaccessible states [5, 6]. For this reason, the FLC strategy equipped with a proposed state estimator will present the main contribution of this study. Furthermore, the given closed-loop performances will be significantly enhanced over those provided by the existing PI controller in terms of reference tracking dynamic as well as closed-loop robustness, regardless of model parameter variations.

The DFIM system is one of the most popular AC machines, used in many domestic and industrial applications such as: in power generation from either wind or water sources, in aerospace and naval applications, in fan drives, and water pumps [7]. These wide applications are mainly due to several properties such as high operating speed range, significant drive power especially when it is used as a generator, flexibility of its actual behavior where the controller design is quite easy as compared to other existing synchronous and asynchronous machines, reliability and the repair cost which is comparatively reduced.

The DFIM system was first conceived in 1899 [8]. Their actual behavior is often characterized by nonlinear dynamics due to the strong cross-coupling that occurs between their flux and electromagnetic torque. The RFOC strategy is the most commonly adopted principal for decoupling the flux from the electromagnetic torque, where each one can be controlled independently from the other. It is worth mentioning that the corresponding imprecise DFIM model often has varying parameters, each one depending on the state of the actual behavior and its operating point. Furthermore, a slight variation in any electrical or mechanical quantity of the DFIM system can significantly deteriorate the performance of the feedback control system, resulting in instability in the responses of the process to be controlled [9].

Therefore, the robustness of the closed-loop is also paramount, presenting another challenge for designers. In this regard, the rotor speed control of the DFIM system has often motivated a lot of work in the control community over the past decades. Among them, Hopfensperger et al. [10] described the stator flux-oriented control structures for a DFIM system with and without a position encoder. Experimental results are given by applying the power-control method on a wound rotor induction machine [10]. Jovanovic [11] examined various aspects of voltage/frequency scalar control, vector control, and direct torque control (DTC) of the doubly fed brushless reluctance machine (DBRM) [11]. Lacchetti [12] handled the adaptive tuning of the stator inductance in a rotor-current-based model adaptive reference observer (RCMO) for the sensorless DFIM control where mismatched model parameters are taken into account. Xu et al. [13] proposed a new high-frequency injection method to identify the rotor position for sensorless DFIM control. The given results have shown that the system states estimation becomes enough to determine the controller parameters for the rotor speed regulation [13].

Recently, Bhuvaneshvari et al. [14] synthesized a fuzzy controller for sensorless rotor speed regulation of a DFIM system where its actual speed is estimated through measuring both stator currents and stator voltages. Rani et al. [15] applied a versatile closed-loop method to compute the rotor speed of a DFIM system. Accordingly, the R-PLL with the q-axis stator flux is used as the reference signal whereas the rotor speed is computed as feed-forward input [15]. Cherifi and Miloud [16] developed two adaptive reference observer models for speed sensorless control of a DFIM system. The first model is used as a reference model wherein the second one is used to estimate the two components of the rotor flux through the measured stator current and rotor voltages [16]. Bahloul et al. [17] proposed the Luenberger multi-objective adaptive fuzzy observer for sensorless asynchronous drive motor [17]. Luo and Huang [18] estimated the rotor speed for sensorless direct RFOC induction motor drive using the particle swarm optimization PSO algorithm [18].

Considering all the existing works on this topic, the robust FLC synthesis equipped with Luenberger observer, designed for the rotor speed control of sensorless DFIM system, has not been explored yet by any researcher. The proposed methodology combining the three concepts: RFOC principle, Luenberger observer, and FLC technique will be the main contribution and the success key to improving the performance of the feedback control system based on a standard PI controller. The novelty lies in the manner of setting the low-order Luenberger observer to estimate the mechanical speed of the sensorless DFIM system. The parameters of the three stages, fuzzification, rule bases, and defuzzification, are self-tuned by the Luenberger observer. Indeed, they become indispensable in the design of the proposed robust FLC controller.

To reach this goal, the RFOC principle is employed to mitigate as much as possible the cross-coupling between the rotor flux and the electromagnetic torque of the DFIM system, leading thus the DFIM system to operate similarly to a DC machine. Therefore, the good rotor speed control is preserved by the proposed robust FLC, providing thus the accurate orientation of the rotor flux. The proposed control configuration improves significantly the trade-off between reference tracking dynamic and closed-loop robustness. The validity of the proposed control scheme has been verified by a comparison between its performances and those provided by the conventional PI controller. The simulation results show that the proposed robust FLC has the ability to improve the trade-off provided by the PI controller, without the need of any unnecessary mechanical sensors, subject to the condition that the Luenberger observer successfully estimates the missing states of the DFIM model.

The paper is organized as follows: In Sect. 2, the modeling step of the DFIM system is presented. Afterward, the design optimal decoupler based on RFOC strategy is detailed in Sect. 3. In Sect. 4, the design of the proposed robust FLC equipped with Luenberger observer is detailed and the rotor speed control of the sensorless DFIM system is then presented in Sect. 5. Section 6 presents the simulation results. Finally, Sect. 7 concludes this study.

2 Modeling of DFIM system

In the DFIM system, the stator is connected directly to the grid while the rotor is fed by a voltage source inverter, which is controlled using the pulse-width modulated (PWM) method. Moreover, the three-phase wound rotor induction motor is doubly powered when the stator windings are supplied with three-phase power at the rotation frequency \(\omega_{{\text{s}}}\) and the rotor windings are supplied at the rotational frequency \(\omega\) [8, 9, 19]. The electrical model of the DFIM is expressed, in d–q synchronous rotating frame, by Eq. (1) [10,11,12]

$$\begin{aligned} & u_{{{\text{ds}}}} = R_{{\text{s}}} i_{{{\text{ds}}}} + \frac{{{\text{d}}\varphi_{{{\text{ds}}}} }}{{{\text{d}}t}} - \omega_{{\text{s}}} \varphi_{{{\text{qs}}}} \\ & u_{{{\text{qs}}}} = R_{{\text{s}}} i_{{{\text{qs}}}} + \frac{{{\text{d}}\varphi_{qs} }}{{{\text{dt}}}} + \omega_{{\text{s}}} \varphi_{{{\text{ds}}}} \\ & u_{{{\text{dr}}}} = R_{{\text{r}}} i_{{{\text{dr}}}} + \frac{{{\text{d}}\varphi_{{{\text{dr}}}} }}{{{\text{d}}t}} - \omega_{{\text{r}}} \varphi_{{{\text{qr}}}} \\ & u_{{{\text{qr}}}} = R_{{\text{r}}} i_{{{\text{qr}}}} + \frac{{{\text{d}}\varphi_{qr} }}{{{\text{d}}t}} + \omega_{{\text{r}}} \varphi_{{{\text{dr}}}} \end{aligned}$$
(1)

where the stator and rotor fluxes are expressed by [11,12,13]

$$\begin{aligned} & \varphi_{{{\text{ds}}}} = L_{{\text{s}}} i_{{{\text{ds}}}} + Mi_{{{\text{dr}}}} \\ & \varphi_{{{\text{qs}}}} = L_{{\text{s}}} i_{{{\text{qs}}}} + Mi_{{{\text{qr}}}} \\ & \varphi_{{{\text{dr}}}} = L_{{\text{r}}} i_{{{\text{dr}}}} + Mi_{{{\text{ds}}}} \\ & \varphi_{{{\text{qr}}}} = L_{{\text{r}}} i_{{{\text{qr}}}} + Mi_{{{\text{qs}}}} \end{aligned}$$
(2)

Moreover, the electromagnetic torque \(C_{{\text{e}}}\), associating the two rotor currents \(i_{{{\text{dr}}}}\) and \(i_{qr}\) with the two stator flux linkages \(\varphi_{{{\text{ds}}}}\) and \(\varphi_{{{\text{qs}}}}\), can be expressed by [11,12,13]:

$$C_{{\text{e}}} = p\frac{M}{{L_{{\text{r}}} }}\left( {i_{{{\text{dr}}}} \varphi_{{{\text{qs}}}} - i_{{{\text{qr}}}} \varphi_{{{\text{ds}}}} } \right).{ }$$
(3)

In parallel, the mechanical equation of the DFIM system is defined by [11,12,13]:

$$J\frac{{{\text{d}}\Omega_{{\text{m}}} }}{{{\text{d}}t}} = C_{{\text{e}}} - C_{{\text{r}}} - f\Omega_{{\text{m}}} .$$
(4)

Table 2 summarizes the meaning and value of each DFIM parameter used in the simulation part of this study (see “Appendix”).

3 Decoupler design based on RFOC strategy

In general, the RFOC strategy is used to ensure a good decoupling behavior between the flux and the magnetic torque. This can be done by orienting the d-axis along the rotor flux vector. Hence, the rotor flux \(\varphi_{{{\text{dr}}}}\) is kept at the constant flux \(\varphi_{{\text{r}}}\), i.e., \(\varphi_{{{\text{dr}}}} = \varphi_{{\text{r}}}\) while the rotor flux \(\varphi_{{{\text{qr}}}}\) is set at zero value, i.e., \(\varphi_{{{\text{qr}}}} = 0\) [18, 20]. Therefore, the resulting stator and rotor flux, given in Eq. (2) can be substituted in the state-space representation, given by Eq. (1). This yields the two stator and rotor voltages, given by [11,12,13]:

$$\begin{aligned} & u_{{{\text{ds}}}} = R_{{\text{s}}} i_{{{\text{ds}}}} + \left( {L_{{\text{s}}} \frac{{{\text{d}}i_{{{\text{ds}}}} }}{{{\text{d}}t}} + M\frac{{{\text{d}}i_{{{\text{dr}}}} }}{{{\text{d}}t}}} \right) - \omega_{{\text{s}}} \varphi_{{{\text{qs}}}} \\ & u_{{{\text{qs}}}} = R_{{\text{s}}} i_{{{\text{qs}}}} + \left( {L_{{\text{s}}} \frac{{{\text{d}}i_{{{\text{qs}}}} }}{{{\text{d}}t}} + M\frac{{{\text{d}}i_{{{\text{qr}}}} }}{{{\text{d}}t}}} \right) + \omega_{{\text{s}}} \varphi_{{{\text{ds}}}} \end{aligned}$$
(5)
$$\begin{aligned} & u_{{{\text{dr}}}} = R_{{\text{r}}} i_{{{\text{dr}}}} + \left( {L_{{\text{r}}} \frac{{{\text{d}}i_{{{\text{dr}}}} }}{{{\text{d}}t}} + M\frac{{{\text{d}}i_{ds} }}{{{\text{d}}t}}} \right) \\ & u_{{{\text{qr}}}} = R_{{\text{r}}} i_{{{\text{qr}}}} + \omega_{{\text{r}}} \left( {L_{{\text{r}}} i_{{{\text{dr}}}} + Mi_{{{\text{ds}}}} } \right). \end{aligned}$$
(6)

Finally, both derivative stator and rotor currents are expressed through Eq. (5) and then replaced in Eq. (6). This yields the simplified electromagnetic torque, which is computed through one of the two expressions, given by Eq. (7)

$$\begin{aligned} C_{{\text{e}}} & = - pMi_{{{\text{ds}}}} i_{{{\text{qr}}}} \\ C_{{\text{e}}} & = - p\varphi_{{\text{r}}} i_{{{\text{qr}}}} . \end{aligned}$$
(7)

Also, the two simplified rotor voltages \(u_{{{\text{dr}}}}\) and \(u_{{{\text{qr}}}}\). can be given by [11,12,13]:

$$\begin{aligned} u_{{{\text{dr}}}} & = R_{{\text{r}}} i_{{{\text{dr}}}} + L_{r} \frac{{\text{d}}}{{{\text{d}}t}}i_{{{\text{dr}}}} + \frac{M}{{L_{{\text{s}}} }}\left( {u_{{{\text{ds}}}} - R_{{\text{s}}} i_{{{\text{ds}}}} + \omega_{{\text{s}}} \varphi_{{{\text{qs}}}} } \right) - \frac{{M^{2} }}{{L_{{\text{s}}} }}\frac{{\text{d}}}{{{\text{d}}t}}i_{{{\text{d}}r}} \\ u_{{{\text{qr}}}} & = R_{{\text{r}}} i_{{{\text{qr}}}} + L_{{\text{r}}} \delta \frac{{\text{d}}}{{{\text{d}}t}}i_{{{\text{qr}}}} + \frac{M}{{L_{{\text{s}}} }}\left( {u_{{{\text{qs}}}} - R_{{\text{s}}} i_{{{\text{qs}}}} + \omega_{{\text{s}}} \varphi_{{{\text{ds}}}} } \right) - \omega \varphi_{{\text{r}}} \end{aligned}$$
(8)

where \(\delta = \left( {1 - \frac{{M^{2} }}{{L_{{\text{r}}} L_{{\text{s}}} }}} \right)\) denotes the dispersion coefficient. In the next section, let us consider the two compensated rotor voltages \(u_{{{\text{dr}}}}^{{\text{c}}}\) and \(u_{{{\text{qr}}}}^{{\text{c}}}\), defined from Eq. (8), as follows [11,12,13]:

$$\begin{aligned} & u_{{{\text{dr}}}}^{{\text{c}}} = R_{{\text{r}}} i_{{{\text{dr}}}} + L_{{\text{r}}} \delta \frac{{\text{d}}}{{{\text{d}}t}}i_{{{\text{dr}}}} \\ & u_{{{\text{qr}}}}^{{\text{c}}} = \frac{M}{{L_{{\text{s}}} }}\left( {u_{{{\text{qs}}}} - R_{{\text{s}}} i_{{{\text{qs}}}} + \omega_{{\text{s}}} \varphi_{{{\text{ds}}}} } \right) - \omega \varphi_{{\text{r}}} \end{aligned}$$
(9)

and the remaining parts of the rotor voltages \(u_{{{\text{dr}}}}\) and \(u_{{{\text{dr}}}}\), defined from Eq. (8), as follows [11,12,13]:

$$\begin{aligned} u_{{{\text{dr}}}}^{{\text{c}}} & = R_{{\text{r}}} i_{{{\text{dr}}}} + L_{{\text{r}}} \delta \frac{{\text{d}}}{{{\text{d}}t}}i_{{{\text{dr}}}} \\ u_{{{\text{qr}}}}^{{\text{c}}} & = \frac{M}{{L_{{\text{s}}} }}\left( {u_{{{\text{qs}}}} - R_{{\text{s}}} i_{{{\text{qs}}}} + \omega_{{\text{s}}} \varphi_{{{\text{ds}}}} } \right) - \omega \varphi_{{\text{r}}} \end{aligned}$$
(10)

where the two rotor voltages \(u_{{{\text{dr}}}}\) and \(u_{{{\text{qr}}}}\) can be computed by \(u_{{{\text{dr}}}} = u_{{{\text{dr}}}}^{{\text{c}}} + u_{{{\text{dr}}}}^{{\text{R}}}\) and \(u_{{{\text{qr}}}} = u_{{{\text{qr}}}}^{{\text{c}}} + u_{{{\text{qr}}}}^{{\text{R}}}\), respectively. In this paper, the desired decoupler design problem consists of imposing two rotor current references \(i_{{{\text{dr}}}}^{*}\) and \(i_{{{\text{qr}}}}^{*}\) such that the where \(i_{{{\text{dr}}}}^{*} { }\) is kept at zero value, i.e.,\(i_{{{\text{dr}}}}^{*} = 0\), ensuring thus a good attenuation of the cross-coupling that is occurred between all electrical components presented in d-axis and q-axis. Consequently, the rotor speed control depends only on an accurate setting of \(i_{{{\text{qr}}}}^{*}\). Accordingly, the compensation system between the torque and electromagnetic flux can be performed using the following procedure, described below. Assume that the inner loops that ensure proper rotor current regulation in the d-axis and q-axis are well guaranteed at \(\varphi_{{{\text{dr}}}} = \varphi_{{\text{r}}}^{*}\). This involves also \(i_{{{\text{dr}}}} = i_{{{\text{dr}}}}^{*} \approx 0\) and \(i_{{{\text{qr}}}} = i_{{{\text{qr}}}}^{*}\). Therefore, based on Eq. (7), the optimal rotor current reference \(i_{{{\text{qr}}}}^{*}\) is given by [11,12,13]:

$$i_{{{\text{qr}}}}^{*} = - \frac{1}{{p\varphi_{{\text{r}}}^{*} }}C_{{\text{e}}}^{*}$$
(11)

where \(C_{{\text{e}}}^{*}\) denotes the optimal control signal, which should be provided by the proposed FLC controller. The estimated flux and electromagnetic torque can be computed through Eqs. (12) and (13), respectively [11,12,13].

$$\widehat{ \varphi }_{{\text{r}}} = \frac{M}{{1 + T_{{\text{r}}} p}}i_{{{\text{ds}}}} { }$$
(12)
$$\hat{C}_{{\text{e}}} = \frac{{pM\varphi_{{\text{r}}} }}{{L_{{\text{s}}} }}i_{{{\text{qs}}}} .{ }$$
(13)

The block diagram of an indirect RFOC of a doubly fed induction motor is shown in Fig. 1. Usually, the conventional RFOC control strategy has three PI controllers. The first two PI controllers are implemented in the inner loop to control the electromagnetic torque and flux. However, the last PI controller is implemented in the outer loop to control the mechanical rotor speed of the DFIM system. Therefore, the success of this method is heavily dependent on a good choice of the two unknown parameters of each PI controller. Each one of them is commonly found directly from the machine parameters using classical analytical methods, often available in the literature. Unfortunately, it fails when either the corresponding closed-loop system has an inappropriate decoupler or the parameters of the DFIM model are affected by uncertainties. To overcome this drawback, the inner loop control of the conventional RFOC strategy is retained while replacing the corresponding outer-loop control with the proposed robust FLC controller. This last allows ensuring a good reference tracking dynamic, regardless of any undesirable effects caused by mismatched decoupler and the DFIM model.

Fig. 1
figure 1

Block diagram of an indirect RFOC

Full size image

4 Robust fuzzy logic design controller

In this study, the proposed robust FLC controller has two inputs: the speed error \(e\left( t \right)\) and the corresponding variation (derivative) \(\dot{e}\left( t \right)\). They are, respectively, given by [12, 15]:

$$\begin{aligned} e\left( t \right) & = {\Omega }_{{\text{m}}}^{*} - {\Omega }_{{\text{m}}} \\ \dot{e}\left( t \right) & = \frac{{{\text{d}}e}}{{{\text{d}}t}} \approx \frac{{e\left( {t + \Delta t} \right) - e\left( t \right)}}{\Delta t} \end{aligned}$$
(14)

where \(\Omega_{{\text{m}}}\) and \(\Omega_{{\text{m}}}^{*}\) are, respectively, the rotor speed and the reference rotor speed. It also has the electrical torque that serves as the desired optimal command, which is injected into the DFIM system. Figure 2 depicts the outer-loop system used for the rotor speed regulation [14, 15].

Fig. 2
figure 2

Outer-loop system based on the robust FLC

Full size image

The three previous controller input–output are normalized using the weighting signals, given by [12, 15]:

$$\begin{aligned} & e_{n} = K_{e} e \\ & d\dot{e}_{n} = K_{de} \dot{e} \\ & dC_{{e_{n} }} = K_{du} C_{e} \end{aligned}$$
(15)

where \(K_{e}\), \(K_{de}\), and \(K_{du}\) are positive factors that penalize the signals \(e\), \(\dot{e}\), and \(C_{e}\), respectively. These normalizations have a decisive impact on the static and dynamic performance of the control system. Also, the design of the proposed robust FLC controller consists of three main steps: fuzzification, rule bases, and defuzzification. Figures 3 and 4 show the membership functions that are used for the fuzzification step of the two inputs and the output of the proposed robust FLC controller.

Fig. 3
figure 3

Membership functions used for the FLC inputs

Full size image
Fig. 4
figure 4

Membership function used for the FLC output

Full size image

According to Figs. 3 and 4, it is well to mention that the fuzzy sets are assumed using the following labels: Negative Big (NB), Negative Medium (NM), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Medium (PM), Positive Big (PB). Also, it can be seen that all the given membership functions are asymmetrical. They are given near to the origin, i.e., steady-state value, in which the fuzzification step of each FLC controller inputs and output is ensured with more accuracy. Here, there are 7 fuzzy subsets for each input variable, giving a total of \(7 \times 7 = 49\) of inference rules, illustrated in Table 1. In this paper, the defuzzification step is performed by the Center of Area COA where the inference step is carried out using the Mamdani algorithm [12].

Table 1 Fuzzy rules used in the design of the robust FLC controller
Full size table

5 Design of the Luenberger observer

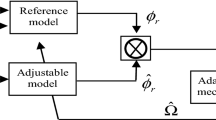
The Luenberger observer is used to estimate the mechanical rotor speed \(\Omega_{{\text{m}}}\) and the load torque \(C_{{\text{r}}}\) using the measured rotor currents and the constant rotor flux \(\varphi_{{\text{r}}}^{*}\). For this reason, the corresponding state-space representation can be derived by combining both Eq. (4) and Eq. (11). Here, the load torque is assumed to be constant over the sampling time used in the simulation. It yields [15, 21]:

$$\begin{aligned} & \frac{{\text{d}}}{{{\text{d}}t}}\hat{\Omega }_{{\text{m}}} = - \frac{f}{J}\Omega_{{\text{m}}} - \frac{{p\varphi_{r}^{*} }}{J}i_{{{\text{qr}}}} - \frac{1}{J}C_{{\text{r}}} \\ & \frac{{{\text{d}}C_{{\text{r}}} }}{{{\text{d}}t}} = 0. \end{aligned}$$
(16)

Let us consider \(\hat{\Omega }_{{\text{m}}}\) and \(\hat{C}_{{\text{r}}}\) the estimated mechanical rotor speed and the estimated load torque, which are regrouped into the state vector \(\hat{X} = \left( {\hat{\Omega }_{{\text{m}}} \hat{C}_{{\text{r}}} } \right)^{{\text{T}}}\). Also, let us consider \(L = \left( {L_{1} L_{2} } \right)^{{\text{T}}}\) the gain matrix of the Luenberger observer and \(\xi_{{\text{m}}} = \Omega_{{\text{m}}} - \hat{\Omega }_{{\text{m}}}\) the discrepancy value occurred when the mechanical rotor speed and its corresponding estimated speed is compared in each sampling time. The state-space representation of the Luenberger observer can be expressed by [15, 21]:

$$\begin{aligned} & \left( {\begin{array}{*{20}c} {\frac{{{\text{d}}\hat{\Omega }_{{\text{m}}} }}{{{\text{d}}t}}} \\ \\ {\frac{{{\text{d}}\hat{C}_{r} }}{{{\text{d}}t}}} \\ \end{array} } \right) = \underbrace {{\left[ {\begin{array}{*{20}c} {\left( {\frac{ - f}{J} - L_{1} } \right)} & {\frac{ - 1}{J}} \\ { - L_{2} } & 0 \\ \end{array} } \right]}}_{{A_{{\text{L}}} }} \left( {\begin{array}{*{20}c} {\hat{\Omega }_{{\text{m}}} } \\ {\hat{C}_{{\text{r}}} } \\ \end{array} } \right) + \underbrace {{\left[ {\begin{array}{*{20}c} {\frac{ - p}{J}\varphi_{{\text{r}}}^{*} } \\ 0 \\ \end{array} } \right]}}_{{B_{{\text{L}}} }}i_{{{\text{qr}}}}^{*} + \underbrace {{\left[ {\begin{array}{*{20}c} {L1} \\ {L2} \\ \end{array} } \right]}}_{L}\Omega_{{\text{m}}} \\ & \Omega_{{\text{m}}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {\hat{\Omega }_{{\text{m}}} } \\ {\hat{C}_{{\text{r}}} } \\ \end{array} } \right). \end{aligned}$$
(17)

According to Eq. (17), the rotor mechanical speed \(\Omega_{{\text{m}}}\) must be calculated and then replaced in its derivative. The main goal of the Luenberger observer is to mitigate, as much as possible, the estimating error \(\xi_{{\text{m}}}\) over the simulation time range \(t \in \left( {0 t_{\max } } \right)\). This requires selecting a proper gain matrix \(L\) that ensures the asymptotic stability of the matrix \(\left( {A_{{\text{L}}} - LC} \right)\). In other terms, all eigenvalues of the preceding matrix must be located in the left-half plane (LHP) of the s-plane. In this study, the above goal can be reached when the observer poles \(\lambda_{{{\text{Lo}}}}\) are chosen to be proportional to the induction motor poles \(\lambda_{{{\text{im}}}}\) with a constant gain \(k_{{\text{p}}}\) greater than the unit value, i.e., \(k_{{\text{p}}} > 1\) [16,17,18]. It yields [15]:

$$\lambda_{{{\text{Lo}}}} = k_{{\text{p}}} \lambda_{{{\text{im}}}} .$$
(18)

Figure 5 shows the block diagram used for the Luenberger observer to estimate the mechanical rotor speed \(\Omega_{{\text{m}}}\) and the load torque \(C_{{\text{r}}}\). The observer's efficiency depends heavily on the proper setting of its parameters as well as on the accurate measurement of its electrical inputs. These requirements are rarely available in most real-world applications due to the existence of exogenous disturbances and sensor noise, resulting thus in an imprecise estimation of DFIM parameters. For this reason, the implementation of the proposed robust FLC controller becomes indispensable to attenuate as much as possible all previous undesirable effects during the DFIM system operation.

Fig. 5
figure 5

Block diagram of the Luenberger observer

Full size image

6 Simulation results

In this section, the indirect RFOC strategy is simulated in MATLAB/SIMULINK R2013a (Version 8.1) environment, in which the toolbox of MATLAB fuzzy logic is performed for the FLC design. The parameters of the PI controller as well as those of the observer's gain are mentioned in Table 3, available in “Appendix”. The validity of the improved RFOC strategy including the proposed robust FLC, which is implemented in the outer loop of the closed-loop system, is verified for the speed control with mechanical sensor of the DFIM system. The performances provided by the FLC-based RFOC strategy are firstly compared with those provided by the conventional PI controller-based RFOC strategy for the mechanical speed sensor control. Afterward, the given reference tracking dynamics by the FLC-based RFOC strategy are compared by those provided by RFOC strategy based on the FLC equipped with the Luenberger observer for the mechanical speed sensorless control of the DFIM system.

6.1 Speed control with mechanical sensor of the DFIM system

In this subsection, the speed control with mechanical sensor of the DFIM system is presented in which a constant gain of the reference input is used and a sudden change in the sign of this last input is then performed. Figures 6, 7, 8, and 9 show, respectively, the rotor speed, the corresponding electromagnetic torque, the corresponding rotor currents, and the corresponding rotor flux, provided by the conventional RFOC strategy.

Fig. 6
figure 6

Reference tracking dynamic provided by the conventional RFOC strategy

Full size image
Fig. 7
figure 7

Electromagnetic torque provided by the conventional RFOC strategy

Full size image
Fig. 8
figure 8

Rotor currents provided by the conventional RFOC strategy

Full size image
Fig. 9
figure 9

Rotor flux provided by the conventional RFOC strategy

Full size image

According to Fig. 6, it is easy to see that the conventional RFOC strategy is able to provide an acceptable tracking dynamic of the reference rotational speed. This is characterized by a reduced steady-state tracking error, especially in the time range [1.35, 2] seconds. It is also characterized by a fast rise time, which is less than 0.2 s, and a very small overshoot, which is close to zero. However, this dynamic is unfortunately accompanied by the presence of an undesirable tracking error in the transient state, especially in the time range [0.2, 0.6] seconds. Removing this error is the main target of the proposed control strategy.

From Fig. 7, it is seen that the control effort, provided by the conventional RFOC strategy, becomes very smooth and invariant throughout the time range [0.22, 2] seconds. The presence of a fluctuation in the transient state reflects the presence of a cross-coupling between the electrical quantities occurring in the two axes d and q. This last one decreases as the time increases from the time t = 0.2 s.

The shape of the control signal will predict the two shapes of the two rotor currents and flux, which are, respectively, given in Figs. 8 and 9.

Now the validity of the preceding RFOC strategy is demonstrated in the presence of a quick change in the reference input. It should be noted that this choice is only performed in simulation, because a sudden change in the reference input often requires a very short time interval. As a result, the resulting tracking error becomes extremely large, requiring a lot of attenuation effort in a short time scale, which leads to providing some undesirable peaks in the control signal. Recalling here that the preceding reference tracking dynamic is characterized by the existence of a tracking error, appearing at time t = 0.2 s and requiring other 0.4 s before being totally minimized. For this reason, the choice of changing the gain of the reference input is performed at the time of 1 s, which includes the last 0.6 s plus another 0.4 s that ensure the total stabilization of the system output. The purpose of this verification is to define the exact period of time needed to perfectly minimize the tracking error in the presence of a sudden change in the reference input. Figure 10 shows the reference tracking dynamic when the reference rotor speed input is kept at the positive gain \(\Omega_{{\text{m}}}^{*} = 157\) radian per second within the time range \(0 \le t < 1\) seconds and then changed to a negative gain \(\Omega_{{\text{m}}}^{*} = - 157\) radian per second during the remaining time of simulation. Figures 11, 12, and 13 show, respectively, the control effort (electromagnetic torque), rotor currents, and rotor flux needed to ensure the preceding tracking dynamic for the quick change in the reference mechanical speed input, mentioned before.

Fig. 10
figure 10

Tracking dynamic of conventional RFOC strategy provided for a sudden change in the reference input

Full size image
Fig. 11
figure 11

Electromagnetic torque of conventional RFOC strategy provided for a sudden change in the reference input

Full size image
Fig. 12
figure 12

Rotor currents of conventional RFOC strategy provided for a sudden change in the reference input

Full size image
Fig. 13
figure 13

Rotor flux of conventional RFOC strategy provided for a sudden change in the reference input

Full size image

According to Figs.10, 11, 12 and 13, it is easy to see that the change in gain of the reference input leads to the generation of a tracking error, which is completely eliminated after the time t = 1.37 s. This also leads to providing a strong electromagnetic torque, requiring thus to implement a saturation block at the controller output in order to secure the closed-loop system against inadequate peaks occurring in the control signal. It is also noted that the rotor flux reaches its reference value, i.e., 0.85 Wb, and its appearance reveals the conservation of the decoupling principle of the electrical quantities of the DFIM system. As a result, the main drawback of the RFOC strategy using the PI controller lies in the persisting presence of tracking errors at the DFIM system output, which decreases the settling time of the desired response, especially in the presence of a quick change in gain of the set-point input. To enhance the given reference tracking dynamic in terms of settling time, rise time, and steady-state error, the preceding PI controller is replaced by the proposed robust FLC for the speed control with mechanical sensor of the DFIM system. The given performances by the enhanced RFOC strategy are compared by those provided by the conventional RFOC based on the PI controller. Figure 14 compares the evolution of the rotation speed, given by the PI controller-based and FLC-based RFOCs. Figure 15 verifies the two preceding dynamics in the presence of a fast change in sign of the reference input.

Fig. 14
figure 14

Assessment of reference tracking dynamics for both FLC-based and PI controller-based RFOCs

Full size image
Fig. 15
figure 15

Verification of the preceding dynamics in the presence of a sudden change in the reference input

Full size image

From Figs. 14 and 15, the proposed FLC-based RFOC strategy provides better reference tracking dynamics than those provided by the PI controller-based RFOC strategy. The superiority of the proposed control strategy is exhibited for a constant gain as well as for a sudden change in the gain of the reference input. This better reference tracking dynamic is characterized by the total suppression of the tracking error in the whole-time range, improving thus both the rise and settling times. Another considerable benefit of the proposed control strategy is its Degree-Of-Freedom (DOF), which is higher compared to the PI controller-based RFOC strategy, since it has multiple tuning parameters, which allows to meet a lot of imposed requirements as well as to satisfy rigorous objectives.

6.2 Mechanical speed sensorless control of the DFIM system

The main drawback of the proposed method is the availability of all states of the DFIM model. In sensorless speed control case, the FLC design can be failed so the implementation of the Luenberger observer ensuring the correct estimation of the missing states becomes indispensable during the FLC synthesis. In the remaining part of this study, the reference tracking dynamics provided through sensorless speed control will be discussed. Figures 16 and 17 compare the reference tracking dynamics for the sensorless speed control of the DFIM system. These dynamics are provided by the basic FLC and the FLC equipped with the Luenberger observer for a constant and sudden change in the gain of the reference input.

Fig. 16
figure 16

Comparison between the tracking dynamics given by both basic FLC and FLC equipped with the Luenberger observer

Full size image
Fig. 17
figure 17

Assessments of tracking dynamics for the two preceding controllers for a sudden change in the reference input

Full size image

Figures 16 and 17 show that the implementation of the Luenberger observer allows to extend the application of the proposed robust FLC-based RFOC strategy even in the absence of any information on the mechanical speed of the DFIM system. These two figures also show that the system output is a little more improved, especially in achieving a smooth output in the transient state, improving the rise and settling times, accompanied by the presence of a tolerable overshoot.

7 Conclusion

This paper has addressed the sensor and sensorless mechanical speed control of DFIM systems, in which the reference tracking dynamics, provided by the PI controller-based RFOC strategy, have been improved. The required improvement has been achieved by implementing a robust FLC in the outer loop of the feedback control system based on the RFOC strategy where the model states must be assured in advance. The validity of the proposed control strategy has been proven by simulation for a constant and sudden change in the reference inputs. The reference tracking dynamics of the proposed control strategy become better than those provided by the conventional PI controller-based RFOC in terms of the rise and settling times as well as the steady-state error. The simulation results also confirmed that the proposed control strategy can be extended even in the absence of mechanical sensors where the Luenberger observer becomes essential in the FLC synthesis. It is built with lower maintenance costs and operates with increased reliability.