Analysis of a stochastic mathematical model for tuberculosis with case detection

Abstract

In this work, we investigate some qualitative properties of a stochastic dynamical model for tuberculosis with case detection. Using appropriately formulated stochastic Lyapunov functions, we derive sufficient conditions for the existence (and uniqueness) of an ergodic stationary distribution of the positive solutions of the model, guaranteeing persistence of the disease in the presence of case detection. We also obtained conditions that will allow for the eradication of the disease from the population. Using numerical simulations, we were able to illustrate the analytical results obtained herein.

1 Introduction

Tubersulosis (TB), an airborne disease, continues to pose serious health burden on several countries, especially developing countries, in the world. According to the World Health Organization (WHO), about one-quarter of the world’s population are latently infected with TB and only about 5−15% of such individuals go on to develop active TB during their lifetime [1]. Conditions such as a compromised immune systems, infection with HIV, and diabetes, increases an infected person’s chance of progressing to active tuberculosis [1].

In 2018, the WHO reported that 30 high burden countries accounted for about 87% of new TB cases globally, with 8 countries accounting for two thirds of the new TB cases, namely, India, China, Indonesia, Philippines, Pakistan, Nigeria, Bangladesh and South Africa [1]. Also, in 2018, about 10 million people fell ill with active TB worldwide, with approximately 5.7 million men, 3.2 million women and 1.1 million children [1]. However, the good news is that TB can be treated effectively [1].

Increased TB case detection rates have resulted in quick identification of active cases and subsequent treatment. In fact, about 58 million lives were saved through effective TB diagnosis and treatment between 2000 and 2018 [1].

Mathematical models have become very useful tools used in gaining insight into the dynamics of infectious diseases, such as cholera outbreaks [2], malaria [3], co-infections in a target population such as HIV and Sphilis [4], and HPV [5]. Mathematical models for Tuberculosis are in abundance in literature, such as those found in [6, 7]. The work in [6] investigated the effect of case detection on the dynamics of TB in a population where the direct observation therapy strategy (DOTS) is being implemented for effective TB control. In [7], a TB model was formulated to investigate the role of key parameters on improving the TB case detection rate; it was shown that parameters such as quick identification (and reportage) of likely TB cases and very low testing and treatment costs can affect TB case detection.

Studies have shown that the spread of infectious diseases, such as tuberculosis, are always affected by environmental noise, especially in a small population and during the initial stage of an epidemic [8] and deterministic mathematical models do not take into cognizance the effect of these fluctuations on disease spread. To take into account the effect of environmental noise on the dynamics of infectious diseases, stochastic models have been formulated and deployed in infectious disease modelling. For example, the work in Liu and Jiang [8] investigated the dynamics of tuberculosis using a stochastic mathematical model for a population where vaccination and treatments are available, while in [9], the authors formulated a stochastic TB model for a population that has incidences of antibiotic resistance. The work in [10] provides some theoretical results to a formulated stochastic model for SIR diseases with vaccination and vertical transmission while Zhao and Jiang [11] formulated and analyzed a stochastic model for SIS diseases whereby vaccination is present in the population. Few articles, such as those in [8, 9], have shown the existence of an ergodic stationary distribution for stochastic tuberculosis models. Hence, this work seeks to add to such body of knowledge as it strives to investigate the existence of an ergodic stationary distribution for a stochastic tuberculosis model with case detection as well as derive conditions for disease eradication. Moreover, it will be interesting to investigate the impact of low and high intensity stochastic noise on the dynamics of TB in a population with case detection efforts.

This work is organized as follows. In Sect. 2, we will present the stochastic mathematical model for TB with case detection while, in Sect. 3, we will provide the sufficient condition required for the existence and uniqueness of the global positive solution of model. Section 4 will provide the proof of the existence of a unique ergodic stationary distribution under certain conditions. In Sect. 5, we will derive conditions for disease eradication and in Sect. 6, we will give some numerical simulations to illustrate the analytical results in this work. Section 7 will give some concluding remarks and future directions.

2 The TB stochastic mathematical model

In this work, we will analyze a stochastic version of a modified mathematical model from the work in [6]. As stated above, the work in [6] mathematically assessed the impact of case detection on the dynamics of TB in a population where the direct observation therapy strategy (DOTS) is being implemented. We obtain the modified version of the model in [6] by assuming insignificant treatment failure and fast progression rates, in the light of improved detection and sustained treatment rates observed in several countries in recent times [1]. Hence, the modified deterministic mathematical model for tuberculosis with case detection is of the form:

$$\begin{aligned} \frac{dS}{dt}= & {} \Lambda -\beta S(I_1+\gamma I_2)-\mu S,\nonumber \\ \frac{dE}{dt}= & {} \beta (S+\alpha T)(I_1+\gamma I_2) -(k+\mu ) E,\nonumber \\ \frac{dI_1}{dt}= & {} (1-\omega )kE - (\mu +d_{1}+r_{1})I_U,\nonumber \\ \frac{dI_2}{dt}= & {} \omega kE - (\mu +d_{2}+r_{2})I_D,\nonumber \\ \frac{dT}{dt}= & {} r_1 I_1 + r_2 I_2 - \alpha \beta T(I_1+\gamma I_2) - \mu T. \end{aligned}$$

(2.1)

In the model (2.1), $S(t), E(t), I_1(t), I_2(t)$, and T(t) are the number of susceptible individuals, the exposed (latently infected) individuals, the undetected infectious individuals (in the presence of the DOTS programme), the detected infectious individuals (under the DOTS programme) and the treated/recovered individuals in the population, respectively, at time t, so that $N =S+E+I_1+I_2+T$ is the total population.

Let $\Lambda$ be the recruitment rate into the susceptible class. We assume that $\mu$ is the per capita natural mortality rate for all individuals in the population. Let $d_1$ be the TB-induced mortality rate for the undetected infectious TB cases (with the DOTS programme in place) and $d_{2}$ being the death rate for the detected TB cases. Also, let $\beta$ be the disease transmission rate with $\alpha$ being a modification parameter which accounts for the relative susceptibility to re-infection by treated individuals. We further assume that k is the rate of progression of the individuals in the latent stage to active tuberculosis. We assume that $\omega$ ($0<\omega <1$) is the fraction of infectious TB cases that are detected and treated under the DOTS program while the remaining $(1-\omega )$ is the fraction of the infectious individuals who are not detected under the DOTS programme. In this formulation, we assume that disease transmission occurs with a bilinear incidence rate. We further assume that infectious individuals recover at the rates $r_1$ and $r_2$ (for those in the $I_1$ and $I_2$ classes, respectively).

It is easy to show that the region

$$\begin{aligned} {\mathcal {D}} = \{(S,E,I_1,I_2,T)\in {\mathbb {R}}_{\ge 0}^{5} \left| N\le \Lambda /\mu \right. \} \end{aligned}$$

is a positively invariant set and a global attractor of system (2.1).

The model (2.1) has a disease-free equilibrium (DFE), given by $E^* = (S^*,E^*,I_1^{*},I_2^{*},T^*) = (\Lambda /\mu ,0,0,0,0)$. Following the next generation matrix approach in [12], we have that the effective reproduction number of the model (2.1) is given by

$$\begin{aligned} {\mathcal {R}}_0 = \frac{\beta \Lambda k}{\mu (k+\mu )}\left[ \frac{1-\omega }{\mu +d_1+r_1}+\frac{\gamma \omega }{\mu +d_2+r_2}\right] . \end{aligned}$$

By virtue of Theorem 2 in [12], we have that the DFE is locally asymptotically stable whenever ${\mathcal {R}}_0 < 1$ and unstable if ${\mathcal {R}}_0 > 1$. Using similar approaches in [6], we can show the existence or otherwise of the endemic equilibrium when ${\mathcal {R}}_0 > 1$.

We will now include stochastic perturbations (motivated by the work in [9]) in the base deterministic model (2.1), by assuming that the perturbations are of the white noise type and are directly proportional to the sub-populations, $S,E,I_1,I_2,T$, influenced on the derivatives ${\dot{S}},{\dot{E}},\dot{I_1},\dot{I_2}$, and ${\dot{T}}$, so that we now have the stochastic version of (2.1) as follows:

$$\begin{aligned} \begin{aligned} dS&= [\Lambda -\beta S(I_1+\gamma I_2)-\mu S]dt + \sigma _1 SdB_1(t),\\ dE&= [\beta (S+\alpha T)(I_1+\gamma I_2) -(k+\mu ) E]dt + \sigma _2 EdB_2(t),\\ dI_1&= [(1-\omega )kE - (\mu +d_{1}+r_{1})I_1]dt + \sigma _3 I_1B_3(t),\\ dI_2&= [\omega kE - (\mu +d_{2}+r_{2})I_2]dt + \sigma _4 I_2dB_4(t),\\ dT&= [r_1 I_1 + r_2 I_2 - \alpha \beta T(I_1+\gamma I_2) - \mu T]dt + \sigma _5 TdB_5(t), \end{aligned} \end{aligned}$$

(2.2)

where $B_i(t)$, $i=1,\ldots ,5$, are mutually independent standard Brownian motions with $B_i(0) = 0$ and $\sigma _i^2 > 0$, $i=1,\ldots ,5$, denote the intensities of the $B_i$’s.

3 Preliminaries

In this work, let $(\Omega ,{\mathcal {F}},\{{\mathcal {F}}_t\}_{t\ge 0},P)$ be a complete probability space with filtration $\{{\mathcal {F}}_t\}_{t\ge 0}$ satisfying the usual conditions as discussed in [13, 14]. Consider the n-dimensional stochastic differential equations (SDEs)

$$\begin{aligned} dx(t) = f(x(t),t)dt + g(x(t),t)dB(t) \end{aligned}$$

(3.1)

with initial value $x(t_0) = x_0\in {\mathbb {R}}^n$, $x\in {\mathbb {R}}^n$ (with $x \ge 0$) and B(t) is the m-dimensional standard Brownian motion defined on $(\Omega ,{\mathcal {F}},\{{\mathcal {F}}_t\}_{t\ge 0},P)$. Let the family of all nonnegative functions V(x, t) defined on ${\mathbb {R}}^n \times [t_0,\infty ]$, such that V(x, t) is continuously twice differentiable in x and once in t, be denoted by ${\mathcal {C}}^{2,1}({\mathbb {R}}^n\times [t_0,\infty ];{\mathbb {R}}_+)$. Then, the differential operator ${\mathcal {L}}$ of (3.1) is defined by

$$\begin{aligned} {\mathcal {L}} = \frac{\partial }{\partial t} + \sum _{i=1}^n f_i(x,t)\frac{\partial }{\partial x_i} + \frac{1}{2}\sum _{i,j=1}^n[g^T(x,t)g(x,t)]_{ij}\frac{\partial ^2}{\partial x_i \partial x_j}. \end{aligned}$$

If ${\mathcal {L}}$ acts on $V\in {\mathcal {C}}^{2,1}({\mathbb {R}}^n\times [t_0,\infty ];{\mathbb {R}}_+)$, then

$$\begin{aligned} {\mathcal {L}}V(x,t) = V_t + V_xf+\frac{1}{2}\text {trace}[g^TV_{xx}g], \end{aligned}$$

where $V_t = \frac{\partial V}{\partial t}$, $V_x = \left( \frac{\partial V}{\partial x_1}, \frac{\partial V}{\partial x_2},\ldots ,\frac{\partial V}{\partial x_n}\right)$, and $V_{xx} = \left( \frac{\partial ^2 V}{\partial x_i \partial x_j}\right) _{n\times n}$.

By Itô’s formula [14], if $x\in {\mathbb {R}}^n$, then

$$\begin{aligned} dV(x(t),t) = {\mathcal {L}}V(x(t),t)dt + V_xgdB(t). \end{aligned}$$

Let X(t) be a regular time-homogeneous Markov $\{E_x\equiv {\mathbb {R}}^l\}$ process in an l-dimensional Euclidean space, $E_l$, described by the following SDE

$$\begin{aligned} dX(t)=b(X)dt+\sum _{r=1}^k g_r(X)dB_r(t). \end{aligned}$$

The diffusion matrix is defined as

$$\begin{aligned} A(x)=(a_{ij}(x)), a_{ij}(x) = \sum _{r=1}^k g_r^{i}(x)g_r^{j}(x). \end{aligned}$$

Then, we have the following as in [13].

Lemma 3.1

[13] The Markov process X(t) has a unique ergodic stationary distribution $\pi (.)$ if there exists a bounded open domain $Z\subset {\mathbb {R}}^d$ with regular boundary $\Gamma$, having the following properties:

$\text {H}_1$:

: there is a positive number M such that the diffusion matrix A(x) is strictly positive definite $\forall$ $x\in Z$ i.e., such that $\sum _{i,j=1}^{l}a_{ij}(x)\xi _{i}\xi _{j}\ge M|\xi |^2$, $x\in Z$, $\xi \in {\mathbb {R}}^l$.

$\text {H}_2$:

: there exists a nonegative ${\mathcal {C}}^2$-function V such that ${\mathcal {L}}V$ is negative for any ${\mathbb {R}}^l\setminus Z$.

4 Existence and uniqueness of positive solutions

Since the variables $S,E,I_1,I_2$ and T in (2.2) represent human sub-populations, we expect that they be nonnegative for all time. Following the same line of reasoning and methodology in articles such as [8,9,10] and [15], we claim the following.

Theorem 4.1

For any initial condition $(S(0),E(0),I_1(0),I_2(0),T(0))\in {\mathbb {R}}_{+}^{5}$, there exists a unique positive solution $S(t),E(t),I_1(t),I_2(t),T(t)$ of (2.2) on $t\ge 0$ and the solution will remain in ${\mathbb {R}}_{+}^{5}$ with probability one, almost surely(a.s.).

Proof

As the coefficients of (2.2) are locally Lipschitz continuous, it follows that for any initial condition ($S(0),E(0),I_1(0),I_2(0),T(0))\in {\mathbb {R}}_{+}^{5}$, there is a unique local solution ($S(t),E(t),I_1(t),I_2(t),T(t)$) on $[0, \tau _e]$ where $\tau _e$ is the explosion time [14]. For this solution to be global, it is required that $\tau _e = \infty$ a.s. Let $z_0$ be sufficiently large such that $S(0),E(0),I_1(0),I_2(0)$, and T(0) all lie within the interval $[\frac{1}{z_0}, z_0]$. For each integer $z \ge z_0$, define the stopping time

$$\begin{aligned} \begin{aligned} \tau _z&= \text {inf}\bigg \{t\in [0,\tau _e]:\text {min}\left\{ S(t),E(t),I_1(t),I_2(t),T(t)\right\} \le \frac{1}{z}\\&\qquad \qquad \text {or max} \left\{ S(t),E(t),I_1(t),I_2(t),T(t)\right\} \ge z\bigg \}. \end{aligned} \end{aligned}$$

It is clearly discernable that $\tau _z$ is increasing as $z\rightarrow \infty$. Now, let $\tau _\infty = \lim _{z\rightarrow \infty }\tau _z$, so that $\tau _\infty \le \tau _e$ a.s. Now we need to show that $\tau _\infty = \infty$ a.s. to conclude that $\tau _e = \infty$ a.s. so that $S(t),E(t),I_1(t),I_2(t),T(t)\in {\mathbb {R}}_{+}^{5}$ a.s. for $t\ge 0$. If this assertion is false, then there is a pair of constants ${\hat{T}}$ and $\epsilon \in (0,1)$ such that ${\mathbb {P}}\{\tau _\infty \le {\hat{T}}\}>\epsilon$. Hence, there is an integer $z_1\ge z_0$ such that

$$\begin{aligned} {\mathbb {P}}\{\tau _z\le {\hat{T}}\}\ge \epsilon \quad \text {for all} \quad z\ge z_1. \end{aligned}$$

(4.1)

Define a ${\mathcal {C}}^2$-function $U:{\mathbb {R}}_{+}^{5}\rightarrow {\mathbb {R}}_{+}$ by

$$\begin{aligned} \begin{aligned} U(S,E,I_1,I_2,T)&= \left( S-a-a\ln \frac{S}{a}\right) \\&\quad + (E-1-\ln E) + (I_1-1-\ln I_1)\\&\quad + (I_2-1-\ln I_2) + \left( T-b-b\ln \frac{T}{b}\right) , \end{aligned} \end{aligned}$$

(4.2)

where the positive constants, a and b, will be determined shortly. Note that the nonnegativity of U is guaranteed since $v-1-\ln v\ge 0$, for any $v>0$.

Applying Itô’s formula to U yields

$$\begin{aligned} \begin{aligned} dU(S,E,I_1,I_2,T)&= {\mathcal {L}}Udt + \sigma _1(S-a)dB_1\\&\quad +\sigma _2(E-1)dB_2+\sigma _3(I_1-1)dB_3\\&\quad + \sigma _4(I_2-1)dB_4+\sigma _5(T-b)dB_5, \end{aligned} \end{aligned}$$

where ${\mathcal {L}}U:{\mathbb {R}}_{+}^{5}\rightarrow {\mathbb {R}}_{+}$ is given by

$$\begin{aligned} \begin{aligned} {\mathcal {L}}U&= \left( 1-\frac{a}{S}\right) \\&\quad [\Lambda -\beta S(I_1+\gamma I_2)-\mu S]\\&\quad + \left( 1-\frac{1}{E}\right) \\&\quad [\beta (S+\alpha T)(I_1+\gamma I_2) -(k+\mu ) E]\\&\quad + \left( 1-\frac{1}{I_1}\right) [(1-\omega )kE\\&\quad - (\mu +d_{1}+r_{1})I_1] + \left( 1-\frac{1}{I_2}\right) \\&\quad [\omega kE - (\mu +d_{2}+r_{2})I_2]\\&\quad + \left( 1-\frac{b}{T}\right) [r_1 I_1 + r_2 I_2 - \alpha \beta T(I_1+\gamma I_2) - \mu T] \\&\quad + \frac{a\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _4^2 + b\sigma _5^2}{2}, \end{aligned} \end{aligned}$$

which, after several calculations reduces to

$$\begin{aligned} {\mathcal {L}}U= & {} \Lambda + a\beta (I_1+\gamma I_2) \\&+ a\mu + (k+\mu )+(\mu +d_1+r_1) + (\mu +d_{2}+r_{2})\\&+ b\alpha \beta (I_1+\gamma I_2)\\&+ b\mu + \frac{a\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _4^2 + b\sigma _5^2}{2} - \mu S - \frac{a\Lambda }{S} \\&- \mu E - \frac{\beta (I_1+\gamma I_2)(S+\alpha T)}{E}\\&- (\mu +d_1)I_1 - \frac{(1-\omega )kE}{I_1}-(\mu +d_2)I_2 \\&- \frac{\omega kE}{I_2} -\mu T - \frac{r_1 I_1}{T} - \frac{r_2 I_2}{T}\\\le & {} \Lambda + a\mu + k + 3\mu +d_1+r_1 +d_{2}+r_{2} + b\mu \\&+ \frac{a\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _4^2 + b\sigma _5^2}{2}\\&+ [(a + b\alpha )\beta - (\mu +d_1)]I_1 \\&+ [(a + b\alpha )\beta \gamma - (\mu +d_2)]I_2. \end{aligned}$$

Now, choose

$$\begin{aligned} a= & {} \text {min}\frac{\left\{ \frac{\mu +d_1}{\beta },\frac{\mu +d_2}{\beta \gamma } \right\} }{2}\quad \text {and}\quad b = \text {min}\frac{\left\{ \frac{\mu +d_1}{\beta },\frac{\mu +d_2}{\beta \gamma }\right\} }{2\alpha } \end{aligned}$$

such that $(a + b\alpha )\beta - (\mu +d_1) \le 0$ and $(a + b\alpha )\beta \gamma - (\mu +d_2)\le 0$. Then, we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}U&\le \Lambda + a\mu + k + 3\mu +d_1+r_1 +d_{2}\\&\quad +r_{2} + b\mu + \frac{a\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _4^2 + b\sigma _5^2}{2}\\&:= W, \end{aligned} \end{aligned}$$

where W is a constant. Hence, we now have that

$$\begin{aligned} \begin{aligned} dU(S,E,I_1,I_2,T)&\le Wdt + \sigma _1(S-a)dB_1\\&\quad +\sigma _2(E-1)dB_2+\sigma _3(I_1-1)dB_3\\&\quad + \sigma _4(I_2-1)dB_4+\sigma _5(T-b)dB_5. \end{aligned} \end{aligned}$$

(4.3)

Integrating both sides of (4.3) from 0 to $\tau _z\wedge {\hat{T}} = \text {min}\{\tau _z,{\hat{T}}\}$ and taking expectation results in

$$\begin{aligned} \begin{aligned}&{\mathbb {E}}U(S(\tau _z\wedge {\hat{T}}), E(\tau _z\wedge {\hat{T}}), I_1(\tau _z\wedge {\hat{T}}),I_2(\tau _z\wedge {\hat{T}}), T(\tau _z\wedge {\hat{T}})\\&\quad \le U(S(0),E(0),I_1(0),I_2(0),T(0))\\&\qquad + W{\mathbb {E}}(\tau _z\wedge {\hat{T}}). \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned}&\quad {\mathbb {E}}U(S(\tau _z\wedge {\hat{T}}), E(\tau _z\wedge {\hat{T}}), I_1(\tau _z\wedge {\hat{T}}),I_2(\tau _z\wedge {\hat{T}}),T(\tau _z\wedge {\hat{T}})\\&\quad \le U(S(0),E(0),I_1(0),I_2(0),T(0))\\&\qquad + W{\hat{T}}. \end{aligned} \end{aligned}$$

(4.4)

Now, let $\Phi _z = \{p\in \Phi :\tau _z(p)\le {\hat{T}}\}$ for $z\ge z_1$ and according to (4.1), we have ${\mathbb {P}}(\Phi _z)\ge \epsilon$. Since, for every $p\in \Phi _z$, there exists $S(\tau _z,p)$, or $E(\tau _z,p)$, or $I_1(\tau _z,p)$, or $I_2(\tau _z,p)$, or $T(\tau _z,p)$ equals either z or $\frac{1}{z}$, it follows that $S(\tau _z,p)$, $E(\tau _z,p)$, $I_1(\tau _z,p)$, $I_2(\tau _z,p)$, or $T(\tau _z,p)$ is no less than either $z-a-a\ln \frac{z}{a}$ or $\frac{1}{z}-a-a\ln \frac{1}{za} = \frac{1}{z}-a+\ln (za)$ or $z-b-b\ln \frac{z}{b}$ or $\frac{1}{z}-b-b\ln \frac{1}{zb} = \frac{1}{z}-b+\ln (zb)$ or $z-1-\ln z$ or $\frac{1}{z}-1-\ln \frac{1}{z} = \frac{1}{z}-1+\ln z$. Hence, we have that

$$\begin{aligned} \begin{aligned}&U(S(\tau _z,p),E(\tau _z,p),I_1(\tau _z,p),I_2(\tau _z,p),T(\tau _z,p))\\&\quad \ge \left( z-a-a\ln \frac{z}{a}\right) \\&\quad \wedge \left( \frac{1}{z}-a+\ln (za)\right) \\&\quad \wedge \left( z-b-b\ln \frac{z}{b}\right) \\&\quad \wedge \left( \frac{1}{z}-b+\ln (zb)\right) \\&\quad \wedge (z-1-\ln z) \wedge \left( \frac{1}{z}-1+\ln z\right) . \end{aligned} \end{aligned}$$

Following (4.4), we get that

$$\begin{aligned} \begin{aligned}&\quad U(S(0),E(0),I_1(0),I_2(0),T(0))+ W{\hat{T}}\\&\quad \ge {\mathbb {E}}[1_{\Phi _z(p)}U(S(\tau _z,p), E(\tau _z,p),I_1(\tau _z,p),I_2(\tau _z,p),T(\tau _z,p))]\\&\ge \epsilon \left( z-a-a\ln \frac{z}{a}\right) \wedge \left( \frac{1}{z}-a+\ln (za)\right) \\&\quad \wedge \left( z-b-b\ln \frac{z}{b}\right) \wedge \left( \frac{1}{z}-b+\ln (zb)\right) \\&\quad \wedge (z-1-\ln z) \wedge \left( \frac{1}{z}-1+\ln z\right) , \end{aligned} \end{aligned}$$

where $I_{\Phi _z}$ stands for the indicator function of $\Phi _z$. Letting $z\rightarrow \infty$ leads to the contradiction

$$\begin{aligned} \infty > U(S(0),E(0),I_1(0),I_2(0),T(0))+ W{\hat{T}} = \infty . \end{aligned}$$

Therefore, we must have that $\tau _\infty = \infty$ a.s. This completes the proof. $\square$

5 Disease persistence

We will now derive conditions that will guarantee the existence (and uniqueness) of an ergodic stationary distribution of the solutions to the model (2.2), which shows that the disease will persist in the population for all time; by persistency in this model, we mean that the disease will remain perpetually in the population for all time i.e., there will be TB infected individuals in the population for all time.

Define the parameter

$$\begin{aligned} {\mathcal {R}}_0^s= & {} \frac{\beta \Lambda k}{\left( \mu +\frac{\sigma _1^2}{2}\right) \left( k+\mu +\frac{\sigma _2^2}{2}\right) }\\&\quad \left[ \frac{1-\omega }{\left( \mu +d_1+r_1+\frac{\sigma _3^2}{2}\right) } +\frac{\gamma \omega }{\left( \mu +d_2+r_2+\frac{\sigma _4^2}{2}\right) }\right] . \end{aligned}$$

We claim the following:

Theorem 5.1

For any initial value $(S(0),E(0),I_1(0),I_2(0),T(0))\in {\mathbb {R}}_{+}^{5}$, the system (2.2) has a unique ergodic stationary distribution $\pi (.)$ if and only if ${\mathcal {R}}_0^s > 1$.

Proof

To prove Theorem 5.1, all we need to do is to ensure that the two conditions in Lemma 3.1 holds.

The diffusion matrix of (2.2) is given by

$$\begin{aligned} A = \left( \begin{array}{*{5}c} \sigma _1^2 S^2&{}0&{}0&{}0&{}0\\ 0&{}\sigma _2^2 E^2&{}0&{}0&{}0\\ 0&{}0&{}\sigma _3^2 I_1^2&{}0&{}0\\ 0&{}0&{}0&{}\sigma _4^2 I_2^2&{}0\\ 0&{}0&{}0&{}0&{}\sigma _5^2 T^2.\\ \end{array} \right) \end{aligned}$$

Obviously, the matrix A is positive definite for any compact subset of ${\mathbb {R}}_{+}^{5}$.

Now, choose

$$\begin{aligned} M = \min _{(S,E,I_1,I_2,T)\in {\bar{D}}_\sigma \subset {\mathbb {R}}_{+}^{5}}\{\sigma _1^2 S^2,\sigma _2^2 E^2,\sigma _3^2 I_1^2,\sigma _4^2 I_2^2,\sigma _5^2 T^2\}. \end{aligned}$$

Hence, we have that

$$\begin{aligned} \begin{aligned} \sum _{i,j=1}^5 a_{ij}(S,E,I_1,I_2,T)\xi _i \xi _j&= \sigma _1^2 S^2\xi _1^2 + \sigma _2^2 E^2\xi _2^2 + \sigma _3^2 I_1^2\xi _3^2\\&\quad + \sigma _4^2 I_2^2\xi _4^2 + \sigma _5^2 T^2\xi _5^2 \ge M|\xi |^2, \end{aligned} \end{aligned}$$

where $(S,E,I_1,I_2,T)\in {\bar{D}}_\sigma$ and $\xi = (\xi _1,\xi _2,\xi _3,\xi _4,\xi _5)\in {\mathbb {R}}_{+}^{5}$. Therefore, condition $\text {H}_1$ in Lemma 3.1 is satisfied. Next we prove condition $\text {H}_2$ in Lemma 3.1.

Now, we need to construct a ${\mathcal {C}}^2$-function ${\bar{V}}:{\mathbb {R}}_{+}^{5}\rightarrow {\mathbb {R}}$ in the form:

$$\begin{aligned} \begin{aligned} {\bar{V}}(S,E,I_1,I_2,T)&= MV_1(S,E,I_1,I_2,T) + V_2(S) \\&\quad + V_3(E) + V_4(I_1) + V_5(T)\\&\quad + V_6(S,E,I_1,I_2,T) \end{aligned} \end{aligned}$$

(5.1)

where each $V_i$, $i=1,\ldots ,6$, is uniquely obtained, and $M>0$ is a sufficiently large number satisfying the following condition

$$\begin{aligned} -M\psi + B \le -2, \end{aligned}$$

(5.2)

with B and $\psi$ to be determined.

Note that ${\bar{V}}(S,E,I_1,I_2,T)$ tends to $\infty$ as $(S,E,I_1,I_2,T)$ approaches the boundary of ${\mathbb {R}}_{+}^{5}$. Hence, it must be bounded from below and this is achieved at a point $(S^o,E^o,I_1^o,I_2^o,T^o)$ in the interior of ${\mathbb {R}}_{+}^{5}$. Then we define a ${\mathcal {C}}^2$-function ${\tilde{V}}:{\mathbb {R}}_{+}^{5}\rightarrow {\mathbb {R}}$ as follows

$$\begin{aligned}&{\tilde{V}}(S,E,I_1,I_2,T) = {\bar{V}}(S,E,I_1,I_2,T) \nonumber \\&\quad - {\bar{V}}(S^o,E^o,I_1^o,I_2^o,T^o)\nonumber \\&= MV_1(S,E,I_1,I_2,T) + V_2(S) + V_3(E) + V_4(I_1) + V_5(T) \nonumber \\&\quad + V_6(S,E,I_1,I_2,T) - {\bar{V}}(S^o,E^o,I_1^o,I_2^o,T^o). \end{aligned}$$

(5.3)

Define

$$\begin{aligned} \begin{aligned} V_1(S,E,I_1,I_2,T)&= -a_1\ln S \\&\quad - a_2\ln E - a_3\ln I_1 - a_4\ln I_2 - a_5\ln S,\\ V_2&= -\ln S,\quad V_3 = -\ln E,\quad V_4 = -\ln I_1,\quad V_5 = -\ln T,\quad \text {and}\\ V_6&= \frac{1}{\nu +1}(S+E+I_1+I_2+T)^{(\nu +1)}, \end{aligned} \end{aligned}$$

where $\nu$, a sufficiently small constant, satisfies $0<\nu <\frac{2\mu }{\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2 \vee \sigma _4^2 \vee \sigma _5^2}$ and the $a_i$’s, $i=1,\ldots ,5$, in $V_1$ are positive constants to be determined.

Applying Itô’s formula to $V_1$, we have

$$\begin{aligned} \begin{aligned} {\mathcal {L}}V_1&= -\frac{a_1\Lambda }{S} \\&\quad - \frac{a_2\beta SI_1}{E} - \frac{a_3(1-\omega )kE}{I_1} \\&\quad + a_1\mu + \frac{a_1\sigma _1^2}{2} + a_2\left( k+\mu +\frac{\sigma _2^2}{2}\right) \\&\quad + a_3\left( \mu +d_1+r_1+\frac{\sigma _3^2}{2}\right) \\&\quad + (a_1 + a_5)\beta I_1 - \frac{a_2\beta \alpha I_1T}{E} - \frac{a_5\Lambda }{S} - \frac{a_2\beta \gamma SI_2}{E}\\&\quad - \frac{a_4\omega kE}{I_2} + a_5\mu \\&\quad + \frac{a_5\sigma _1^2}{2} + a_4\left( \mu +d_2+r_2+\frac{\sigma _4^2}{2}\right) \\&\quad + (a_1 + a_5)\beta \gamma I_2\\&\quad - \frac{a_2\beta \alpha \gamma I_2T}{E}\\&\le -3\root 3 \of {a_1a_2a_3\Lambda \beta (1-\omega )k} \\&\quad + a_1\left( \mu +\frac{\sigma _1^2}{2}\right) \\&\quad + a_2\left( k+\mu +\frac{\sigma _2^2}{2}\right) \\&\quad + a_3\left( \mu +d_1+r_1+\frac{\sigma _3^2}{2}\right) \\&\quad + (a_1 + a_5)\beta I_1 - 3\root 3 \of {a_2a_4a_5\Lambda \beta \gamma \omega k}\\&\quad + a_5\left( \mu +\frac{\sigma _1^2}{2}\right) \\&\quad + a_4\left( \mu +d_2+r_2+\frac{\sigma _4^2}{2}\right) + (a_1 + a_5)\beta \gamma I_2. \end{aligned} \end{aligned}$$

Now, choose

$$\begin{aligned} \begin{aligned} a_1&= \frac{\Lambda \beta (1-\omega )k}{\left( \mu +\frac{\sigma _1^2}{2}\right) ^2 \left( k+\mu +\frac{\sigma _2^2}{2}\right) \left( \mu +d_1+r_1+\frac{\sigma _3^2}{2}\right) },\\&\quad a_2 = \frac{1}{\left( k+\mu +\frac{\sigma _2^2}{2}\right) },\\ a_3&= \frac{\Lambda \beta (1-\omega )k}{\left( \mu +\frac{\sigma _1^2}{2}\right) \left( k+\mu +\frac{\sigma _2^2}{2}\right) \left( \mu +d_1+r_1+\frac{\sigma _3^2}{2}\right) ^2},\\ a_4&= \frac{\Lambda \beta \gamma \omega k}{\left( \mu +\frac{\sigma _1^2}{2}\right) \left( k+\mu +\frac{\sigma _2^2}{2}\right) \left( \mu +d_2+r_2+\frac{\sigma _4^2}{2}\right) ^2},\\ a_5&= \frac{\Lambda \beta \gamma \omega k}{\left( \mu +\frac{\sigma _1^2}{2}\right) ^2 \left( k+\mu +\frac{\sigma _2^2}{2}\right) \left( \mu +d_2+r_2+\frac{\sigma _4^2}{2}\right) }. \end{aligned} \end{aligned}$$

Then, we have that

$$\begin{aligned} {\mathcal {L}}V_1\le & {} -3\left\{ \frac{\Lambda \beta (1-\omega )k}{\left( \mu +\frac{\sigma _1^2}{2}\right) \left( k+\mu +\frac{\sigma _2^2}{2}\right) \left( \mu +d_1+r_1+\frac{\sigma _3^2}{2}\right) }\right\} \nonumber \\&+ 2\left\{ \frac{\Lambda \beta (1-\omega )k}{\left( \mu +\frac{\sigma _1^2}{2}\right) \left( k+\mu +\frac{\sigma _2^2}{2}\right) \left( \mu +d_1+r_1+\frac{\sigma _3^2}{2}\right) }\right\} \nonumber \\&-3\left\{ \frac{\Lambda \beta \gamma \omega k}{\left( \mu +\frac{\sigma _1^2}{2}\right) \left( k+\mu +\frac{\sigma _2^2}{2}\right) \left( \mu +d_2+r_2+\frac{\sigma _4^2}{2}\right) }\right\} \nonumber \\&+ 2\left\{ \frac{\Lambda \beta \gamma \omega k}{\left( \mu +\frac{\sigma _1^2}{2}\right) \left( k+\mu +\frac{\sigma _2^2}{2}\right) \left( \mu +d_2+r_2+\frac{\sigma _4^2}{2}\right) }\right\} \nonumber \\&+ 1 + \beta \frac{1}{\left( \mu +\frac{\sigma _1^2}{2}\right) }{\mathcal {R}}_0^s (I_1+\gamma I_2) \nonumber \\= & {} -3{\mathcal {R}}_0^s + 2{\mathcal {R}}_0^s + 1 + \beta \frac{1}{\left( \mu +\frac{\sigma _1^2}{2}\right) }{\mathcal {R}}_0^s (I_1+\gamma I_2)\nonumber \\= & {} -({\mathcal {R}}_0^s - 1) + \beta \frac{1}{\left( \mu +\frac{\sigma _1^2}{2}\right) }{\mathcal {R}}_0^s (I_1+\gamma I_2)\nonumber \\:= & {} -\psi + \beta \frac{1}{\left( \mu +\frac{\sigma _1^2}{2}\right) }{\mathcal {R}}_0^s (I_1+\gamma I_2),\quad \quad {\mathcal {R}}_0^s > 1 \end{aligned}$$

(5.4)

where $\psi = ({\mathcal {R}}_0^s - 1) > 0$.

Next, applying Itô’s formula to $V_2$, we have

$$\begin{aligned} \begin{aligned} {\mathcal {L}}V_2&= -\frac{1}{S}(\Lambda -\beta S(I_1+\gamma I_2)-\mu S) + \frac{\sigma _1^2}{2}\\&= -\frac{\Lambda }{S} + \beta (I_1+\gamma I_2) + \mu + \frac{\sigma _1^2}{2}. \end{aligned} \end{aligned}$$

(5.5)

Applying Itô’s formula to $V_3$, we have

$$\begin{aligned} \begin{aligned} {\mathcal {L}}V_3&= -\frac{1}{E}(\beta (S+\alpha T)(I_1+\gamma I_2) \\&\quad -(k+\mu ) E) + \frac{\sigma _2^2}{2}\\&\le -\frac{\beta S(I_1+\gamma I_2)}{E} + (k+\mu ) + \frac{\sigma _2^2}{2}. \end{aligned} \end{aligned}$$

(5.6)

Next, applying Itô’s formula to $V_4$, we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}V_4&= -\frac{1}{I_1}[(1-\omega )kE \\&\quad - (\mu +d_{1}+r_{1})I_1] + \frac{\sigma _3^2}{2}\\&\le (\mu +d_{1}+r_{1}) + \frac{\sigma _3^2}{2}. \end{aligned} \end{aligned}$$

(5.7)

Applying Itô’s formula to $V_5$, we have

$$\begin{aligned} \begin{aligned} {\mathcal {L}}V_5&= -\frac{1}{T}(r_1 I_1 + r_2 I_2 - \alpha \beta T(I_1+\gamma I_2) \\&\quad - \mu T) + \frac{\sigma _5^2}{2}\\&= -\frac{r_1 I_1}{T} - \frac{r_2 I_2}{T} + \alpha \beta (I_1+\gamma I_2) \\&\quad + \mu + \frac{\sigma _5^2}{2}. \end{aligned} \end{aligned}$$

(5.8)

Next, applying Itô’s formula to $V_6$, we have

$$\begin{aligned} {\mathcal {L}}V_6= & {} (S+E+I_1+I_2+T)^\nu (\Lambda - \mu (S+E+I_1+I_2+T) \nonumber \\&- d_1 I_1 - d_2 I_2) \nonumber \\&+ \nu (S+E+I_1+I_2+T)^{\nu - 1}\times \nonumber \\&\frac{\sigma _1^2 S^2 + \sigma _2^2 E^2 + \sigma _3^2 I_1^2 + \sigma _4^2 I_2^2 + \sigma _5^2 T^2}{2} \nonumber \\\le & {} (S+E+I_1+I_2+T)^\nu \{\Lambda - \mu (S+E+I_1+I_2+T)\} \nonumber \\&+ \frac{\nu }{2}(S+E+I_1+I_2+T)^{(\nu +1)}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2) \nonumber \\= & {} \Lambda (S+E+I_1+I_2+T)^\nu - \left\{ \mu \right. \nonumber \\&\left. \qquad - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right\} \nonumber \\&\times (S+E+I_1+I_2+T)^{(\nu +1)} \nonumber \\\le & {} A - \frac{1}{2}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \nonumber \\&(S+E+I_1+I_2+T)^{(\nu +1)} \nonumber \\\le & {} A - \frac{1}{2}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \nonumber \\&(S^{\nu +1}+E^{\nu +1}+I_1^{\nu +1}+I_2^{\nu +1} +T^{\nu +1}), \end{aligned}$$

(5.9)

where

$$\begin{aligned} \begin{aligned} A&= \sup _{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+}\bigg \{\Lambda (S+E+I_1+I_2+T)^\nu \\&\quad - \frac{1}{2}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \\&\qquad \times (S+E+I_1+I_2+T)^{\nu +1}\bigg \} < \infty . \end{aligned} \end{aligned}$$

(5.10)

Hence, using (5.4) - (5.9), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le - M\psi + M\beta (a_1+a_5)I_1 \\&\quad + M\beta \gamma (a_1+a_5)I_2 \\&\quad - \frac{1}{2}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] (S^{\nu +1}\\&\quad +E^{\nu +1}+I_1^{\nu +1}+I_2^{\nu +1} +T^{\nu +1})\\&\quad -\frac{\Lambda }{S} -\frac{\beta S(I_1+\gamma I_2)}{E} -\frac{r_1 I_1}{T}\\&\quad - \frac{r_2 I_2}{T} + \beta (I_1+\gamma I_2) + \alpha \beta (I_1+\gamma I_2)\\&\quad + 4\mu + k+d_1+r_1 \\&\quad + \frac{\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _5^2}{2} + A, \end{aligned} \end{aligned}$$

(5.11)

which can be written as

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le - M\psi + M\beta (a_1+a_5)I_1 + M\beta \gamma (a_1+a_5)I_2 \\&\quad -\frac{\Lambda }{S} -\frac{\beta S(I_1+\gamma I_2)}{E} -\frac{r_1 I_1}{T} - \frac{r_2 I_2}{T} + B. \end{aligned} \end{aligned}$$

(5.12)

where B is defined by

$$\begin{aligned} \begin{aligned} B&= \sup _{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+}\bigg \{- \frac{1}{2}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \\&\qquad (S^{\nu +1}+E^{\nu +1}\\&\quad +I_1^{\nu +1} +I_2^{\nu +1} +T^{\nu +1}) + \beta (I_1+\gamma I_2)\\&\qquad + \alpha \beta (I_1+\gamma I_2) + 4\mu + k+d_1+r_1\\&\quad + \frac{\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _5^2}{2} + A\bigg \}. \end{aligned} \end{aligned}$$

(5.13)

Recall that, as stated earlier in (5.2), M must satisfy $-M\psi + B\le -2$.

Let us define a bounded close set

$$\begin{aligned} \begin{aligned} {\mathbf {Z}}_\epsilon&= \bigg \{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+: \epsilon<S<\frac{1}{\epsilon },\\&\quad \epsilon ^3<E<\frac{1}{\epsilon ^3}, \epsilon<I_1<\frac{1}{\epsilon },\\&\quad \epsilon<I_2<\frac{1}{\epsilon },\epsilon ^2<T<\frac{1}{\epsilon ^2}\bigg \}, \end{aligned} \end{aligned}$$

with $0<\epsilon<<1$, sufficiently small. Then, in ${\mathbb {R}}^5_{+}\backslash {\mathbf {Z}}_\epsilon$, we can choose $\epsilon$ such that

$$\begin{aligned}&-\frac{\Lambda }{\epsilon } + C \le -1, \end{aligned}$$

(5.14)

$$\begin{aligned}&\quad M\beta (a_1+a_5)(1+\gamma )\epsilon \le 1, \end{aligned}$$

(5.15)

$$\begin{aligned}&\quad -\frac{\beta }{\epsilon } + C\le -1, \end{aligned}$$

(5.16)

$$\begin{aligned}&\quad -\frac{\beta \gamma }{\epsilon } + C\le -1, \end{aligned}$$

(5.17)

$$\begin{aligned}&\quad -\frac{r_1}{\epsilon } + C\le -1, \end{aligned}$$

(5.18)

$$\begin{aligned}&\quad -\frac{r_2}{\epsilon } + C\le -1, \end{aligned}$$

(5.19)

$$\begin{aligned}&\quad - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \end{aligned}$$

(5.20)

$$\begin{aligned}&\quad \frac{1}{\epsilon ^{\nu +1}} + C\le -1, \end{aligned}$$

(5.21)

$$\begin{aligned}&\quad - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2 \vee \sigma _4^2\vee \sigma _5^2)\right] \end{aligned}$$

(5.22)

$$\begin{aligned}&\quad \frac{1}{\epsilon ^{3(\nu +1)}} + C\le -1, \end{aligned}$$

(5.23)

$$\begin{aligned}&\quad - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _ 3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \end{aligned}$$

(5.24)

$$\begin{aligned}&\quad \frac{1}{\epsilon ^{2(\nu +1)}} + C\le -1, \end{aligned}$$

(5.25)

where C is a positive constant to be determine later.

Next, to complete the requirement of condition $H_2$ of Lemma 3.1, we show that

$$\begin{aligned} {\mathcal {L}}{\tilde{V}} \le -1, \quad \text {on} \quad {\mathbb {R}}^5_{+}\backslash {\mathbf {Z}}_\epsilon . \end{aligned}$$

To do this, we divide ${\mathbb {R}}^5_{+}\backslash {\mathbf {Z}}\epsilon$ into 11 domains, thus

$$\begin{aligned} \begin{aligned} {\mathbf {Z}}_1&=\{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+:0<S<\epsilon \},\\ {\mathbf {Z}}_2&=\{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+:0<I_1<\epsilon ,0<I_2<\epsilon \},\\ {\mathbf {Z}}_3&=\{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+:0<E<\epsilon ^3,S\ge \epsilon ,I_1\ge \epsilon \},\\ {\mathbf {Z}}_4&=\{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+:0<E<\epsilon ^3,S\ge \epsilon ,I_2\ge \epsilon \},\\ {\mathbf {Z}}_5&=\{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+:0<T<\epsilon ^2,I_1\ge \epsilon \},\\ {\mathbf {Z}}_6&=\{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+:0<T<\epsilon ^2,I_2\ge \epsilon \},\\ {\mathbf {Z}}_7&=\bigg \{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+: S \ge \frac{1}{\epsilon }\bigg \},\\ {\mathbf {Z}}_8&=\bigg \{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+: E \ge \frac{1}{\epsilon ^3}\bigg \},\\ {\mathbf {Z}}_9&=\bigg \{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+: I_1 \ge \frac{1}{\epsilon }\bigg \},\\ {\mathbf {Z}}_{10}&=\bigg \{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+: I_2 \ge \frac{1}{\epsilon }\bigg \},\\ {\mathbf {Z}}_{11}&=\bigg \{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+: T \ge \frac{1}{\epsilon ^2}\bigg \}. \end{aligned} \end{aligned}$$

Clearly, ${\mathbf {Z}}_\epsilon ^c = {\mathbb {R}}^5_{+}\backslash {\mathbf {Z}}_\epsilon ={\mathbf {Z}}_1 \cup {\mathbf {Z}}_2\ldots \cup {\mathbf {Z}}_{11}$.

Now, proving that ${\mathcal {L}}{\tilde{V}} \le -1$ for any $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_\epsilon ^c$ is equivalent to proving it on each of the eleven domains ${\mathbf {Z}}_1,\ldots , {\mathbf {Z}}_{11}$.

Consider the case where $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_1$. From (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le -\frac{\Lambda }{S} + M\beta (a_1+a_5)I_1 \\&\quad + M\beta \gamma (a_1+a_5)I_2 + \beta (I_1+\gamma I_2) + \alpha \beta (I_1+\gamma I_2)\\&\quad - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \\&\quad (S^{\nu +1}+E^{\nu +1}+I_1^{\nu +1}+I_2^{\nu +1} +T^{\nu +1})\\&\quad + 4\mu + k+d_1+r_1 \\&\quad + \frac{\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _5^2}{2} + A\\&\le -\frac{\Lambda }{S} + C\le -\frac{\Lambda }{\epsilon } + C \le -1, \end{aligned} \end{aligned}$$

(5.26)

which follows from (5.14), where

$$\begin{aligned} \begin{aligned} C&= \sup _{(S,E,I_1,I_2,T)\in {\mathbb {R}}^5_+}\bigg \{M\beta (a_1+a_5)I_1 + M\beta \gamma (a_1+a_5)I_2\\&\quad + \beta (I_1+\gamma I_2) + \alpha \beta (I_1+\gamma I_2)\\&\quad - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2 \vee \sigma _4^2\vee \sigma _5^2)\right] \\&\quad (S^{\nu +1}+E^{\nu +1}+I_1^{\nu +1}+I_2^{\nu +1} +T^{\nu +1})\\&\quad + 4\mu + k+d_1+r_1 \\&\quad + \frac{\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _5^2}{2} + A\bigg \}. \end{aligned} \end{aligned}$$

(5.27)

Next, we consider the case where $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_2$. From (5.11), we have that

$$\begin{aligned} {\mathcal {L}}{\tilde{V}}\le & {} - M\psi + M\beta (a_1+a_5)I_1 \nonumber \\&+ M\beta \gamma (a_1+a_5)I_2 \nonumber \\&- \frac{1}{2}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \nonumber \\&(S^{\nu +1}+E^{\nu +1}+I_1^{\nu +1}+I_2^{\nu +1} +T^{\nu +1})\nonumber \\&+ \beta (I_1+\gamma I_2) + \alpha \beta (I_1+\gamma I_2)+ 4\mu + k+d_1+r_1 + A \nonumber \\&\frac{\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _5^2}{2} \nonumber \\\le & {} - M\psi + B + M\beta (a_1+a_5)I_1 + M\beta \gamma (a_1+a_5)I_2 \nonumber \\\le & {} - M\psi + B + M\beta (a_1+a_5)(1+\gamma )\epsilon \nonumber \\\le & {} -2 + 1\le -1, \end{aligned}$$

(5.28)

which follows from (5.2) and (5.15).

Next, we consider the case where $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_3$. From (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le -\frac{\beta SI_1}{E} + M\beta (a_1+a_5)I_1 \\&\quad + M\beta \gamma (a_1+a_5)I_2 + \beta (I_1+\gamma I_2) + \alpha \beta (I_1+\gamma I_2) \\&\quad - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \\&\quad (S^{\nu +1}+E^{\nu +1}+I_1^{\nu +1}+I_2^{\nu +1} +T^{\nu +1})\\&\quad + 4\mu + k+d_1+r_1 + A \\&\quad + \frac{\sigma _1^2 + \sigma _2^2 + \sigma _3^2 + \sigma _5^2}{2}\\&\le -\frac{\beta SI_1}{E} + C\le -\frac{\beta }{\epsilon } + C\le -1, \end{aligned} \end{aligned}$$

(5.29)

which follows from (5.16) and (5.27), for sufficiently small $\epsilon$.

Now, consider the case where $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_4$. From (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le -\frac{\beta \gamma SI_2}{E}\\&\quad - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] (S^{\nu +1}+E^{\nu +1}\\&\quad +I_1^{\nu +1}+I_2^{\nu +1} +T^{\nu +1}) + C\\&\le -\frac{\beta \gamma SI_2}{E} + C\le -\frac{\beta \gamma }{\epsilon } + C\le -1, \end{aligned} \end{aligned}$$

(5.30)

which follows from (5.17) and (5.27).

Now, if $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_5$, then using (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le -\frac{r_1 I_1}{T} \\&\quad - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] (S^{\nu +1}+E^{\nu +1}\\&\quad +I_1^{\nu +1}+I_2^{\nu +1} +T^{\nu +1}) + C\\&\le -\frac{r_1I_1}{T} + C\le -\frac{r_1}{\epsilon } + C\le -1, \end{aligned} \end{aligned}$$

(5.31)

which follows directly from (5.18) and (5.27).

Next, consider the case when $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_6$; then using (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le -\frac{r_2 I_2}{T} \\&\quad - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] (S^{\nu +1}+E^{\nu +1}\\&\quad +I_1^{\nu +1}+I_2^{\nu +1} +T^{\nu +1}) + C\\&\le -\frac{r_2I_2}{T} + C\le -\frac{r_2}{\epsilon } + C\le -1, \end{aligned} \end{aligned}$$

(5.32)

which follows directly from (5.19) and (5.27).

Now, consider the case when $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_7$; then using (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le - \frac{1}{4} \left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] S^{\nu +1} + C\\&\le - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2 \vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \\&\quad \frac{1}{\epsilon ^{\nu +1}} + C\le -1, \end{aligned} \end{aligned}$$

(5.33)

which follows from (5.21) and (5.27).

Now, consider the case when $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_8$; then using (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le - \frac{1}{4} \left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] E^{\nu +1} + C\\&\le - \frac{1}{4}\left[ \mu - \frac{\nu }{2} (\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \\&\quad \frac{1}{\epsilon ^{3(\nu +1)}} + C\le -1, \end{aligned} \end{aligned}$$

(5.34)

which follows from (5.23) and (5.27).

Considering the case when $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_9$, using (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] I_1^{\nu +1} + C\\&\le - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2) \right] \\&\quad \frac{1}{\epsilon ^{\nu +1}} + C\le -1, \end{aligned} \end{aligned}$$

(5.35)

which follows from (5.21) and (5.27).

Considering the case when $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_{10}$, using (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] I_2^{\nu +1} + C\\&\le - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \frac{1}{\epsilon ^{\nu +1}} + C\le -1, \end{aligned}\nonumber \\ \end{aligned}$$

(5.36)

which follows from (5.21) and (5.27).

Finally, consider the case when $(S,E,I_1,I_2,T)\in {\mathbf {Z}}_{11}$. Therefore, using (5.11), we have that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}{\tilde{V}}&\le - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] T^{\nu +1} + C\\&\le - \frac{1}{4}\left[ \mu - \frac{\nu }{2}(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)\right] \frac{1}{\epsilon ^{2(\nu +1)}} + C\le -1, \end{aligned}\nonumber \\ \end{aligned}$$

(5.37)

which follows from (5.25) and (5.27).

Clearly, from (5.26), (5.28) - (5.37), we have shown that, for sufficiently small $\epsilon$,

$$\begin{aligned} {\mathcal {L}}{\tilde{V}}(S,E,I_1,I_2,T) \le -1,\quad \forall \quad (S,E,I_1,I_2,T)\in {\mathbb {R}}_+^5\backslash {\mathbf {Z}}_\epsilon . \end{aligned}$$

Hence, condition $H_2$ of Lemma 3.1 holds. Therefore, it follows, that the model (2.2) is ergodic and has a unique stationary distribution $\pi (.)$ $\square$

Note that Theorem 5.1 shows that the model (2.2) has a unique ergodic stationary distribution $\pi (.)$ if ${\mathcal {R}}_0^s > 1$. Recall that the expression for ${\mathcal {R}}_0^s$ is the same as that for the control reproduction number for the deterministic version of (2.2), ${\mathcal {R}}_0$, when we do not take into cognisance the effect of white noise (with $\sigma _i = 0$, $i=1,\ldots ,5$). Basically, when ${\mathcal {R}}_0 > 1$, the deterministic model (2.1) will have a unique endemic equilibrium, so that disease persistence is guaranteed.

6 Disease eradication

Now, we derive necessary and sufficient conditions for eradication of tuberculosis in a population where case detection is being implemented. Of course, this results in a disease-free state for the stochastic system (2.2). At this stage, we will define

$$\begin{aligned} <y(t)> = \frac{1}{t}\int _0^t y(s) ds. \end{aligned}$$

To derive the sufficient conditions for disease eradication, we will be making use of Lemmas 2.1 and 2.2 in [11]. For convenience, we restate them as follows:

Lemma 6.1

[11] Let $(S(t),E(t),I_1(t),I_2(t),T(t))$ be the solution to the model (2.2) with initial value $(S(0),E(0), I_1(0),I_2(0),T(0))\in {\mathbb {R}}_{+}^{5}$. Then,

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{S(t)+E(t)+I_1(t)+I_2(t)+T(t)}{t} = 0\quad a.s. \end{aligned}$$

Moreover,

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }\frac{S(t)}{t}&\!=\! 0,\lim _{t\rightarrow \infty }\frac{E(t)}{t}\!=\! 0,\lim _{t\rightarrow \infty }\frac{I_1(t)}{t}\!=\!0,\quad \lim _{t\rightarrow \infty }\frac{I_2(t)}{t}\!=\!0,\\ \lim _{t\rightarrow \infty }\frac{T(t)}{t}&=0,\quad a.s. \end{aligned} \end{aligned}$$

Lemma 6.2

[11] Assume that $\mu > \frac{(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)}{2}$. Let $(S(t),E(t),I_1(t),I_2(t),T(t))$ be the solution to the model (2.2) with initial value $(S(0),E(0),I_1(0),I_2(0),T(0))\in {\mathbb {R}}_{+}^{5}$. Then,

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }\frac{\int _0^t S(s)dB_1(s)}{t}&= 0,\lim _{t\rightarrow \infty }\frac{\int _0^t E(s)dB_2(s)}{t} = 0,\\&\quad \lim _{t\rightarrow \infty }\frac{\int _0^t I_1(s)dB_3(s)}{t} = 0,\\ \lim _{t\rightarrow \infty }\frac{\int _0^t I_2(s)dB_4(s)}{t}&\!=\! 0,\lim _{t\rightarrow \infty }\frac{\int _0^t T(s)dB_5(s)}{t} \!=\! 0,\quad a.s. \end{aligned} \end{aligned}$$

Lemmas 6.1 and 6.2 can be proven using the same approaches implemented in [11]. Now, using the information in Lemmas 6.1 and 6.2, we claim the following.

Theorem 6.1

Let $(S(t),E(t),I_1(t),I_2(t),T(t))$ be the solution to the model (2.2) with initial value $(S(0),E(0),I_1(0), I_2(0),T(0))\in {\mathbb {R}}_{+}^{5}$. If

$$\begin{aligned}&\mu > \frac{(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)}{2}\quad \text {and}\quad \hat{{\mathcal {R}}_0^s}\\&\quad = \frac{8[\beta \Lambda (1+\gamma )-\mu ^2]}{\mu (\sigma _2^2\wedge \sigma _3^2\wedge \sigma _4^2\wedge \sigma _5^2)} < 1, \end{aligned}$$

then the disease will die out exponentially with probability one, i.e.,

$$\begin{aligned}&\lim _{t\rightarrow \infty }E(t)= 0,\quad \lim _{t\rightarrow \infty }I_1(t)=0,\\&\quad \lim _{t\rightarrow \infty }I_2(t) =0,\quad \lim _{t\rightarrow \infty }T(t)=0,\quad \text {a.s.}, \end{aligned}$$

with

$$\begin{aligned} \lim _{t\rightarrow \infty }S(t) = \frac{\Lambda }{\mu } \quad \text {a.s.} \end{aligned}$$

Proof

From the equation describing the rate of change of S(t) in (2.2), we have that

$$\begin{aligned} \begin{aligned} S(t) - S(0)&= \Lambda t - \int _0^t\beta S(s)[I_1(s)+\gamma I_2(s)]ds \\&\quad - \mu \int _0^tS(s)ds\\&\quad + \sigma _1\int _0^tS(s)dB_1(s). \end{aligned} \end{aligned}$$

(6.1)

Dividing (6.1) through by t and taking limits results in

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }<S>&= \frac{1}{\mu }\lim _{t\rightarrow \infty }\\&\quad \bigg [\Lambda - \frac{S(t) - S(0)}{t} - \beta <S(I_1+\gamma I_2)>\\&\quad + \frac{\sigma _1}{t}\int _0^tS(s)dB_1(s)\bigg ]\\&\le \frac{1}{\mu }\lim _{t\rightarrow \infty }\\&\quad \bigg [\Lambda + \frac{\sigma _1}{t}\int _0^tS(s)dB_1(s)\bigg ]. \end{aligned} \end{aligned}$$

(6.2)

Hence, it follows that

$$\begin{aligned} \lim _{t\rightarrow \infty }<S>\quad \le \frac{\Lambda }{\mu } \quad \text {a.s.} \end{aligned}$$

(6.3)

Define

$$\begin{aligned} W(t) = E(t)+I_1(t)+I_2(t)+T(t). \end{aligned}$$

By applying Itô’s formula, we have that

$$\begin{aligned} \text {d}\ln W= & {} \bigg [\frac{1}{E(t)+I_1(t)+I_2(t)+T(t)}\nonumber \\&\bigg \{\beta (I_1+\gamma I_2)S - \mu (E+I_1+I_2+T) - d_1I_1 - d_2I_2\bigg \}\nonumber \\&- \frac{1}{2(E(t)+I_1(t)+I_2(t)+T(t))^2}\nonumber \\&\bigg (\sigma _2^2E^2 + \sigma _3^2I_1^2 \nonumber \\&+ \sigma _4^2I_2^2 + \sigma _5^2T^2\bigg )\bigg ]dt\nonumber \\&+ \frac{\sigma _2 E}{E(t)+I_1(t)+I_2(t)+T(t)}dB_2(t)\nonumber \\&+ \frac{\sigma _3 I_1}{E(t)+I_1(t)+I_2(t)+T(t)}dB_3(t)\nonumber \\&+ \frac{\sigma _4 I_2}{E(t)+I_1(t)+I_2(t)+T(t)}dB_4(t) \nonumber \\&+ \frac{\sigma _5 T}{E(t)+I_1(t)+I_2(t)+T(t)}dB_5(t)\nonumber \\\le & {} \bigg \{\beta S(1+\gamma ) - \mu - \frac{1}{2(E(t)+I_1(t) +I_2(t)+T(t))^2}\nonumber \\&\bigg (\sigma _2^2E^2 + \sigma _3^2I_1^2 + \sigma _4^2I_2^2 + \sigma _5^2T^2\bigg )\bigg \}dt\nonumber \\&+ \frac{\sigma _2 E}{E(t)+I_1(t)+I_2(t)+T(t)}dB_2(t)\nonumber \\&+ \frac{\sigma _3 I_1}{E(t)+I_1(t)+I_2(t)+T(t)}dB_3(t)\nonumber \\&+ \frac{\sigma _4 I_2}{E(t)+I_1(t)+I_2(t)+T(t)}dB_4(t) \nonumber \\&+ \frac{\sigma _5 T}{E(t)+I_1(t)+I_2(t)+T(t)}dB_5(t)\nonumber \\\le & {} \bigg \{\beta S(1+\gamma ) - \mu \nonumber \\&- \frac{\sigma _2^2\wedge \sigma _ 3^2\wedge \sigma _4^2\wedge \sigma _5^2}{8(E^2+I_1^2+I_2^2+T^2)}(E^2 + I_1^2 + I_2^2 + T^2)\bigg \}dt\nonumber \\&+ \frac{\sigma _2 E}{E(t)+I_1(t)+I_2(t)+T(t)}dB_2(t) \nonumber \\&+ \frac{\sigma _3 I_1}{E(t)+I_1(t)+I_2(t)+T(t)}dB_3(t)\nonumber \\&+ \frac{\sigma _4 I_2}{E(t)+I_1(t)+I_2(t)+T(t)}dB_4(t) \nonumber \\&+ \frac{\sigma _5 T}{E(t)+I_1(t)+I_2(t)+T(t)}dB_5(t)\nonumber \\\le & {} \bigg \{\beta S(1+\gamma ) - \mu - \frac{\sigma _2^2\wedge \sigma _3^2\wedge \sigma _4^2\wedge \sigma _5^2}{8}\bigg \}dt\nonumber \\&+ \frac{\sigma _2 E}{E(t)+I_1(t)+I_2(t)+T(t)}dB_2(t) \nonumber \\&+ \frac{\sigma _3 I_1}{E(t)+I_1(t)+I_2(t)+T(t)}dB_3(t)\nonumber \\&+ \frac{\sigma _4 I_2}{E(t)+I_1(t)+I_2(t)+T(t)}dB_4(t) \nonumber \\&+ \frac{\sigma _5 T}{E(t)+I_1(t)+I_2(t)+T(t)}dB_5(t) \end{aligned}$$

(6.4)

Integrating (6.4) from 0 to t and diving by t gives

$$\begin{aligned} \begin{aligned}&\frac{\ln W(t) - \ln W(0)}{t} \\&\quad \le \frac{\beta (1+\gamma )}{t}\int _0^t S(s)ds - \mu - \frac{\sigma _2^2\wedge \sigma _3^2\wedge \sigma _4^2\wedge \sigma _5^2}{8}\\&\qquad + \frac{\sigma _2}{t}\int _0^t \frac{E(s)}{E(s)+I_1(s)+I_2(s)+T(s)}dB_2(s)\\&\qquad + \frac{\sigma _3}{t}\int _0^t \frac{I_1(s)}{E(s)+I_1(s)+I_2(s)+T(s)}dB_3(s)\\&\qquad + \frac{\sigma _4}{t}\int _0^t \frac{I_2(s)}{E(s)+I_1(s)+I_2(s)+T(s)}dB_4(s)\\&\qquad + \frac{\sigma _5}{t}\int _0^t \frac{T(s)}{E(s)+I_1(s)+I_2(s)+T(s)}dB_5(s). \end{aligned} \end{aligned}$$

(6.5)

Taking the superior limit of (6.5), and using (6.3), we have that

$$\begin{aligned} \begin{aligned}&\limsup _{t\rightarrow \infty } \frac{\ln W(t)}{t} \\&\quad \le \frac{\beta \Lambda (1+\gamma )}{\mu } - \mu \\&\quad - \frac{\sigma _2^2\wedge \sigma _3^2\wedge \sigma _4^2\wedge \sigma _5^2}{8}\\&= \frac{1}{8}(\sigma _2^2\wedge \sigma _3^2\wedge \sigma _4^2\wedge \sigma _5^2)\bigg \{\frac{8[\beta \Lambda (1+\gamma )-\mu ^2]}{\mu (\sigma _2^2\wedge \sigma _3^2\wedge \sigma _4^2\wedge \sigma _5^2)} - 1 \bigg \}\\&=\frac{1}{8}(\sigma _2^2\wedge \sigma _3^2\wedge \sigma _4^2\wedge \sigma _5^2)(\hat{{\mathcal {R}}_0^s} - 1) < 0\quad \text {a.s.}, \end{aligned} \end{aligned}$$

which shows that

$$\begin{aligned}&\lim _{t\rightarrow \infty }E(t)= 0,\quad \lim _{t\rightarrow \infty }I_1(t)=0,\quad \lim _{t\rightarrow \infty }I_2(t)=0,\\&\quad \lim _{t\rightarrow \infty }T(t)=0,\quad \text {a.s.} \end{aligned}$$

This completes the proof $\square$

Remark 6.1

It is imperative to note that the threshold parameters, ${\mathcal {R}}_0^s$ and $\hat{{\mathcal {R}}_0^s}$, for determining the existence of an ergodic stationary distribution (and therefore provides the basis for concluding that the disease will persist for all time) and the condition for disease eradication, respectively, are not ”reproduction numbers” of the model (2.2) in the classical sense of the derivation and use of reproduction numbers in epidemiological modelling using deterministic nonlinear ordinary differential equation models. They are simply parameters that are derived from the direct application of the techniques used in determining the existence of a stationary distribution and for investigating conditions that will result in disease eradication in the target population.

Remark 6.2

It is interesting to note that the parameter for determining the existence or otherwise of the stationary distribution, ${\mathcal {R}}_0^s$, is a function of the case detection parameter, $\omega$; hence, the case detection parameter plays a role in the condition that allows for the persistence of the disease. However, for the parameter used for determining condition for disease eradication, $\hat{{\mathcal {R}}_0^s}$, we see that this parameter is not a function of the case detection parameter, $\omega$; hence, regardless of what the value of $\omega$ is, the disease will be eradicated as far as the conditions in Theorem 6.1 are satisfied.

7 Numerical simulations

Using the Milstein’s Higher Order Method (MHOM) [16], we carry out some numerical simulations of the model (2.2) to illustrate the analytical results presented herein. The convergence of the MHOM is well discussed in [16]. The MHOM has a strong order of convergence, which is higher than the Euler Maruyama (EM) method, a well known numerical method for solving stochastic differential equations, due to the addition of a correction to the stochastic increment in the EM, which then gave rise to the MHOM [16]. The correction is due to the fact that the traditional Taylor expansion must be modified in the case of Itô’s Calculus [16]. By virtue of the Milstein’s Higher Order Method [16], we obtain the following discretization form of model (2.2):

$$\begin{aligned} \begin{aligned} S_{i+1}&= S_i + [\Lambda -\beta S_i(I_{1,i}+\gamma I_{2,i})-\mu S_i]\triangle t\\&\quad + \sigma _1 S_i\chi _{1,i}\sqrt{\triangle t} + \frac{\sigma _1^2}{2}S_i(\chi _{1,i}^2 - 1)\triangle t,\\ E_{i+1}&= E_i + [\beta (S_i+\alpha T_i)(I_{1,i}+\gamma I_{2,i}) \\&\quad -(k+\mu ) E_i]\triangle t + \sigma _2 E_i\chi _{2,i}\sqrt{\triangle t}\\&\quad + \frac{\sigma _2^2}{2}E_i(\chi _{2,i}^2 - 1)\triangle t,\\ I_{1,i+1}&= I_{1,i} + [(1-\omega )kE_i - (\mu +d_{1}+r_{1})I_{1,i}]\triangle t\\&\quad + \sigma _3 I_{1,i}\chi _{3,i}\sqrt{\triangle t}\\&\quad + \frac{\sigma _3^2}{2}I_{1,i}(\chi _{3,i}^2 - 1)\triangle t,\\ I_{2,i+1}&= I_{2,i} + [\omega kE_i - (\mu +d_{2}+r_{2})I_{2,i}]\triangle t \\&\quad + \sigma _4 I_{2,i}\chi _{4,i}\sqrt{\triangle t}\\&\quad + \frac{\sigma _4^2}{2}I_{2,i}(\chi _{4,i}^2 - 1)\triangle t,\\ T_{i+1}&= T_i + [r_1 I_{1,i} + r_2 I_{2,i} - \alpha \beta T_i(I_{1,i}+\gamma I_{2,i})\\&\quad - \mu T_i]\triangle t + \sigma _5 T_i\chi _{5,i}\sqrt{\triangle t}\\&\quad + \frac{\sigma _5^2}{2}T_i(\chi _{5,i}^2 - 1)\triangle t, \end{aligned} \end{aligned}$$

(7.1)

where $\triangle t > 0$ is time increment, and $\chi _{j,i}$, $j = 1, 2,\ldots ,5$ are the independent Gaussian random variables which follow the distribution N(0, 1).

For the simulations, we use the following initial condition$(S(0),E(0),I_1(0),I_2(0),T(0))$ = (0.2, 0.2, 0.3, 0.2, 0.2). Note that the choice of parameter values that follows are made simply to illustrate the analytical results herein.

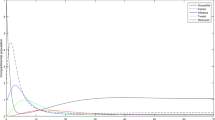
To numerically prove the existence of an ergodic stationary distribution, we choose the following parameters, $\mu =0.02042$, $\Lambda =0.8$, $\beta = 3.9$, $\gamma =0.5$, $\alpha =1$, $k=0.008$, $\omega =0.41$, $d_1=0.365$, $r_1=0.2$, $d_2=0.22$, $r_2=1.5$, $\sigma _1^2=0.2$, $\sigma _2^2=0.2$, $\sigma _3^2=0.2$, $\sigma _4^2=0.3$, $\sigma _5^2=0.3$. Using these parameter values, we have that ${\mathcal {R}}_0^s = 1.7394 > 1$. Therefore, as seen in Fig. 1, Theorem 5.1 holds as we observe that the model 2.2 has a unique ergodic stationary distribution $\pi (.)$ which implies that, for all time, the disease persists in the population.

Fig. 1

The paths of $S(t), E(t), I_1(t), I_2(t)$ and T(t) of model (2.2), when $\mu =0.02042$, $\Lambda =0.8$, $\beta = 3.9$, $\gamma =0.5$, $\alpha =1$, $k=0.008$, $\omega =0.41$, $d_1=0.365$, $r_1=0.2$, $d_2=0.22$, $r_2=1.5$, with noise intensities given as $\sigma _1^2=0.2$, $\sigma _2^2=0.2$, $\sigma _3^2=0.2$, $\sigma _4^2=0.3$, $\sigma _5^2=0.3$. The red plots represents the solutions of the perturbed system (2.2) while the blue plots are for the unperturbed system (2.1). (Color figure online)

To numerically show the possibility of disease eradication, we choose the following parameters, $\mu =0.85$, $\Lambda =0.6$, $\beta = 0.7$, $\gamma =0.5$, $\alpha =1.5$, $k=0.005$, $\omega =0.11$, $d_1=0.365$, $r_1=0.2$, $d_2=0.22$, $r_2=1.5$, $\sigma _1^2=0.8$, $\sigma _2^2=0.6$, $\sigma _3^2=1$, $\sigma _4^2=1.2$, $\sigma _5^2=1.4$. Using these parameter values, we have that $\hat{{\mathcal {R}}_0^s} = -1.4510 < 1$, with the condition $\mu = 0.85 > \frac{(\sigma _1^2\vee \sigma _2^2\vee \sigma _3^2\vee \sigma _4^2\vee \sigma _5^2)}{2} = 0.7$. Therefore, the disease will be eradicated from the population in this case.

In Fig. 1, we observe that the disease persisted (for all time) for small noise intensities. However, as seen in the calculated threshold in this section, the disease will be eradicated for all time, for larger white noise intensities.

8 Discussions and conclusion

This work presents some qualitative study of a stochastic mathematical model for tuberculosis with case detection. Using appropriately constructed stochastic Lyapunov functions, we derived sufficient conditions for the existence and uniqueness of an ergodic stationary distribution of the positive solutions of the model, thereby guaranteeing the persistence of the disease in the population for all time. We also derived sufficient conditions that would result in disease eradication for all time. From the analytical results, we observe that the condition for disease eradication is independent of the case detection parameter ($\omega$) whereas the condition for disease persistence is a function of the case detection parameter, showing the effect case detection has on the overall stochastic dynamics of the model. Using some numerical simulations, we illustrated the theoretical results obtained in this work. We also demonstrated, using the numerical simulations, that small noise intensities will lead to the existence of the ergodic stationary distribution, which eventually allows for the disease to persist in the population, whereas for large white noise, the disease was eradicated from the population for all time, hereby showing the significant effect environmental noise can have on the dynamics of tuberculosis in a population where efforts are in place to increase TB case detection. This agrees with the conclusions reached from the numerical simulations in [8].

It will be nice to investigate the effect of intrinsic fluctuations or noise on some other tuberculosis models. For example, what would be the effect of white noise on the dynamics of tuberculosis in a population where genetic heterogeneity (susceptibility and disease progression) affects the disease burden? Also, it is imperative to investigate the effect of intrinsic fluctuations on the impact of awareness, by the susceptible and latently infected individuals, on TB control. We leave these for future work.