1 Introduction

An equilibrium of a two-dimensional system of ordinary differential equations can be seen as an intersection between two curves. These curves (or more generally nullclines) are defined by the zero set of each of the components of the vector field. It is assumed that the vector field depends smoothly on one or two parameters. Consequently, the two previously mentioned curves will vary smoothly in \({\mathbb {R}}^2\) as the parameters are being varied. In particular, fold bifurcation corresponds to the situation where the system has two equilibria which coalesce with each other and disappear when the parameter is being varied. This phenomenon can be observed in the neighborhood of a point where the two curves have a tangential intersection. Such a point can be found using the classical Lagrange multiplier method.

In practice, finding fold bifurcation points can be accomplished numerically by using numerical continuation software such as MATCONT [5], AUTO [6], or XPPAUT [7]. This involves fixing all of the parameters and then computing the equilibria in the system. In this paper, we will refer to these initial values for the parameters and the corresponding equilibrium as initial condition. By varying one of the parameters, we compute a branch of equilibria for the system and look for fold bifurcations in that branch.

By way of illustration, in Fig. 1, a particular situation where there are three branches of equilibria are presented, i.e. a solid black curve, a dashed black curve, and a dotted black curve. We present also three different initial conditions, which are labeled as I, II and III. Choosing the initial condition I, one might be able to compute three equilibria for the system. By varying the bifurcation parameter, two branches of equilibria are obtained (the solid curve and the dashed curve) and thus, the fold points \(F_1\), \(F_2\) and \(F_3\) will be detected. However, we will not be able to compute the curve of equilibria for the system which is plotted using dotted line (and consequently, we will miss the point \(F_4\)). The situation is similar if we start the process at initial condition III, but we will miss the fold point \(F_1\) instead of \(F_4\). A worse situation is when we start at initial condition II. Thus, using existing numerical continuation software, one need to choose the initial condition carefully. However, in practice, it is not always clear how to choose the initial conditions.

Fig. 1
figure 1

Three branches of equilibria in different line style

Full size image

Another approach is using a (semi) analytical method. This is conducted by solving a system of equations which consists of equations for the equilibrium, together with taking the determinant of the Jacobian zero, while requiring the trace of the Jacobian as nonvanishing. In most cases, it is not very easy to solve this system of equations analytically and numerically computing the determinant of a matrix can be quite demanding even when the vector field of the system is polynomial. The advantage of this new method in comparison with the traditional continuation method is that we are immediately solving a system of algebraic equations for fold bifurcation instead of the one used for general equilibrium.

Indeed, the theory of fold and cusp bifurcations has quite a long history. However, interest in the so-called backward bifurcation in epidemiological models has emerged (see for example in [8] and the references therein). This bifurcation is related with the fold bifurcation and analytical computation of the bifurcation point can help in providing a more accurate prediction for backward bifurcation.

In [16] an alternative method for computing fold bifurcation points using the Lagrange Multiplier Method is described. The method itself has been previously applied in a dynamical system in [9]; however, the method was not explained clearly there. The method is extended in [17] and [21] to include computation of cusp bifurcation points.

One of the goals of this paper is to prove the relation described above by providing the conditions on the (local) maxima or minima of a constrained optimization problem to correspond to a fold bifurcation in a particular system of ordinary differential equations. It is also demonstrated how the method in combination with the Newton method can be extended to compute cusp bifurcations by varying two parameters. By varying the third parameter, the bifurcation diagrams are generated for some values of the third parameter which indicate the occurrence of swallowtail bifurcation.

1.1 Outline

We start in Sect. 2.1 with studying a system of two ordinary differential equations which depend on one parameter. Assuming the existence of a fold bifurcation point, in the neighborhood of that point we derive a particular constrained optimization problem where that fold bifurcation point is either a maximum or minimum. Conversely, starting from a maximum or minumum of a constrained optimization problem, two conditions are derived so that the system undergoes fold bifurcation. See Theorems 1 and 2.

In Sect. 2.2, we are concerned with the situation where one of the conditions in Theorem 2 is violated. We assume that the system now depends on two parameters. This extra parameter allows us to generate the curve of fold bifurcations if the Implicit Function Theorem applies. In the case where the Implicit Function Theorem cannot be applied, some conditions are provided for cusp bifurcation in Theorem 3.

In Sect. 3, two examples are discussed, i.e. : Bazykin’s system (see [3]) and the predator–prey system with non-monotonic response function (see [9, 20, 21]). These two examples are known in the literature to exhibit fold and cusp bifurcations. In Bazykin’s system, the explicit formula for the coordinate of the fold bifurcation points as functions of the bifurcation parameter can be explicitly computed. Then, the cusp bifurcation points are computed numerically from those explicit formulas. This is not the case in the predator–prey system. Applying a standard continuation method to the equation for one of the coordinates of the fold bifurcation, in combination with the Newton method for root findings, the cusp bifurcation point is computed.

In Sect. 4, the method is applied to a two-dimensional dynamical system which is derived from the so-called tritrophic food-chain model (see [4]). This system belongs to a class of predator–prey type of dynamical systems which has been studied extensively in the literature. For example, in [12, 13, 22] there is a predator–prey type of dynamical systems of dimension higher than two while in [10, 11, 15, 24] there is a two-dimensional system but with various response functions.

As for the functional response, in [18, 19], the Holling type IV is employed to accommodate the group defence mechanism. A combination of response functions of different types might bring much more interesting dynamics and bifurcations; see for example [1, 2]. In this paper, we assume that the predator has a group defence mechanism to protect them from the top predator, while the prey has not. This implies that we use the Holling type II response function on the prey–predator subsystem, and the Holling type IV for the predator–top predator subsystem.

Our results are compared with those using the continuation software AUTO. Furthermore, our result is extended by providing an evidence for swallowtail bifurcation.

2 Main results

2.1 One-parameter family of dynamical systems

Consider a one-parameter family of systems of ordinary differential equations in \({\mathbb {R}}^2\) with coordinate (x, y), i.e.

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}} = \phi (x,y) \\ {\dot{y}} = \psi _1(x,y) - \beta \psi _2(x,y). \end{array} \right. \end{aligned}$$
(1)

We assume that \(\psi _2(x,y) > 0\) for all x, y. Then the System (1) can be rewritten as:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}} = \displaystyle \psi _2(x,y) \frac{ \phi (x,y)}{\psi _2(x,y)} \\ {\dot{y}} = \displaystyle \psi _2(x,y) \left( \frac{\psi _1(x,y)}{\psi _2(x,y)} - \beta \right) . \end{array} \right. \end{aligned}$$

Thus, System (1) is orbitally equivalent to:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}} = F(x,y)\\ {\dot{y}} = G(x,y) - \beta , \end{array} \right. \end{aligned}$$
(2)

with:

$$\begin{aligned} F(x,y) = \frac{ \phi (x,y)}{\psi _2(x,y)} \text{ and } G(x,y) = \frac{\psi _1(x,y)}{\psi _2(x,y)}. \end{aligned}$$

The equilibrium of System (2) is a solution of system:

$$\begin{aligned} \left\{ \begin{array}{l} F(x,y) = 0\\ G(x,y) = \beta . \end{array} \right. \end{aligned}$$

Let us assume that at \(\beta = \beta _0 \in {\mathbb {R}}\), System (2) undergoes a fold bifurcation. Without loss of generality, suppose that for \(\beta < \beta _0\), System (2) has two equilibria. Then, these equilibria collide with each other at \(\beta = \beta _0\), and disappear when \(\beta >\beta _0\). This means that the curve: \(G(x,y) = \beta \) has two intersection points with the curve: \(F(x,y) = 0\). Furthermore, at \(\beta = \beta _0\) the two curves are tangential to each other while for \(\beta > \beta _0\) they do not intersect with each other. This implies that \(\beta _0\) is a local maximum of G(x, y) on the level set \(F(x,y) = 0\) in the neighborhood of \((x_0,y_0)\). The following theorem if found.

Theorem 1

If System (2) undergoes fold bifurcation at \((x_0, y_0)\) for \(\beta = \beta _0\), then \((x_0, y_0)\) is a local maximum or minimum point of G(x, y) on \(F(x,y) = 0\).

Let \((x_0, y_0, \lambda _0)\) be a solution for: a constrained optimization problem:

$$\begin{aligned} \left\{ \begin{array}{l} \nabla G(x,y) = \lambda \nabla F(x,y) \\ F(x,y) = 0, \end{array} \right. \end{aligned}$$
(3)

with: \(\lambda _0 \not = 0\) (see Remark 2 for \(\lambda _0 = 0\)). By setting \(\beta = \beta _0 = G(x_0,y_0)\), it implies that the point \((x_0,y_0)\) is an equilibrium for System (2). Furthermore, the linearized vector field of System (2) at the vicinity of the equilibrium \((x_0,y_0)\) is:

$$\begin{aligned} \left( \begin{array}{cc} F_x(x_0, y_0) &{}\quad F_y(x_0, y_0) \\ \lambda _0 F_x(x_0, y_0) &{}\quad \lambda _0 F_y(x_0, y_0) \end{array} \right) , \end{aligned}$$

with eigenvalues: 0 and \(\eta = \lambda _0 F_y(x_0, y_0) + F_x(x_0, y_0)\).

Let us denote by A and B, the Hessian matrices of F and G at the equilibrium \((x_0, y_0)\), i.e.:

$$\begin{aligned} A= & {} \left( \begin{array}{cc} F_{xx} (x_0, y_0) &{}\quad F_{xy} (x_0, y_0) \\ F_{xy} (x_0, y_0) &{}\quad F_{yy} (x_0, y_0) \end{array}\right) \text { and }\nonumber \\ B= & {} \left( \begin{array}{cc} G_{xx} (x_0, y_0) &{}\quad G_{xy} (x_0, y_0) \\ G_{xy} (x_0, y_0) &{}\quad G_{yy} (x_0, y_0) \end{array}\right) , \end{aligned}$$
(4)

and by J, the matrix:

$$\begin{aligned} J = \left( \begin{array}{cc} 0 &{} -1 \\ 1 &{} 0 \end{array}\right) \end{aligned}$$

The following theorem is found.

Theorem 2

If

$$\begin{aligned} \eta = F_x(x_0, y_0) + \lambda _0 F_y(x_0, y_0) \not =0, \end{aligned}$$
(5)

and,

$$\begin{aligned} \left( J \nabla F(x_0, y_0) \right) ^T \left( \lambda _0 A - B \right) J \nabla F(x_0, y_0) \ne 0, \end{aligned}$$
(6)

then at \(\beta = \beta _0 = G(x_0,y_0)\) System (2) undergoes a fold bifurcation.

Note that the condition in Eq. (5) implies that \((x_0,y_0)\) is a degenerate equilibrium of System (2) with a single zero eigenvalue. The proof for this theorem is produced by the center manifold reduction of System (2) in the neighborhood of \((x_0,y_0)\). Then by checking two nondegeneracy conditions for fold bifurcation (see Theorem 3.1, pp. 85-86 in [14]) the condition in Equation (6) is derived. The detail of the proof can be found in Appendix A.

Remark 1

A fold bifurcation point in System (2) can also be computed by considering the following system:

$$\begin{aligned} \left\{ \begin{array}{l} F(x,y) = 0 \\ F_x G_y - F_y G_x = 0, \end{array} \right. \end{aligned}$$
(7)

and subsequently computing \(\beta \) from: \(\beta = G(x,y)\). One also needs the condition in Eq. (5) which is equal to the nonvanishing of the trace of the Jacobian in the solution of System (7).

System (7) consists of two equations with two unknowns while System (3) consists of three equations with three unknowns. However, the system: \(\nabla G = \lambda \nabla F\), is a priori simpler than \(F_x G_y - F_y G_x = 0\). For example, when F and G are cubic, then \(\nabla G = \lambda \nabla F\) is quadratic in (x, y), while \(F_x G_y - F_y G_x = 0\) is quartic.

Remark 2

We have to avoid the situation where \(\lambda _0 = 0\) in System (3). The reason for this is that when \(\lambda _0 = 0\), \((x_0, y_0)\) corresponds to a critical point of G. In that case, the level set of \(G(x,y) =\beta \), locally in the neighborhood of \((x_0,y_0)\), either for \(\beta < \beta _0\) or \(\beta >\beta _0\) is empty. In other words, \(\beta _0 = G(x_0,y_0)\) is not a regular value of G.

2.2 Two-parameter family of dynamical systems

Consider a two-parameter family of systems of ordinary differential equations, i.e.:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}} = F(x,y,\alpha )\\ {\dot{y}} = G(x,y,\alpha ) - \beta , \end{array} \right. \end{aligned}$$
(8)

Let us fix a value for \(\alpha = \alpha _*\in {\mathbb {R}}\), and assume that \((x_*, y_*, \lambda _*)\) is a solution of

$$\begin{aligned} \left\{ \begin{array}{l} \nabla G(x,y,\alpha _*) = \lambda \nabla F(x,y,\alpha _*) \\ F(x,y,\alpha _*) = 0, \end{array} \right. \end{aligned}$$
(9)

which corresponds to the fold bifurcation in System (8). We set the value \(\beta _*\) by: \(\beta _*= G(x_*, y_*, \alpha _*)\).

We define a function: \( {\varvec{H}} : {\mathbb {R}}^4 \longrightarrow {\mathbb {R}}^3\) by:

$$\begin{aligned} \begin{array}{lccc} {\varvec{H}} : &{} {\mathbb {R}}^4 &{} \longrightarrow &{} {\mathbb {R}}^3 \\ &{} (x,y, \alpha , \lambda ) &{} \longmapsto &{} \left( \begin{array}{c} \nabla G(x,y,\alpha ) - \lambda \nabla F(x,y,\alpha ) \\ F(x,y,\alpha ) \end{array} \right) . \end{array} \end{aligned}$$

If the partial derivative of \({\varvec{H}}\) with respect to \(\alpha \):

$$\begin{aligned} {\varvec{H}}_{\alpha }(x_*, y_*, \alpha _*, \lambda _*) \not = {\varvec{0}}, \end{aligned}$$
(10)

then by the Implicit Function Theorem there exists a neighborhood U of \(\alpha _*\), so that the curve:

$$\begin{aligned} \alpha \longmapsto \left( x(\alpha ), y(\alpha ), \lambda (\alpha ) \right) , \alpha \in U, \end{aligned}$$

satisfies: \({\varvec{H}}\left( x(\alpha ), y(\alpha ), \alpha , \lambda (\alpha ) \right) = {\varvec{0}}\). Furthermore \(x(\alpha _*) = x_*\), \(y(\alpha _*) = y_*\) and \(\lambda (\alpha _*) = \lambda _*\). Using this curve, we can define:

$$\begin{aligned} G\left( x(\alpha ) , y(\alpha ), \alpha \right) - \beta = 0, \end{aligned}$$

which provides us with a fold bifurcations curve in the parameter space \((\alpha , \beta )\).

In some cases, there are N solutions for System (9) satisfying Eq. (10). Let:

$$\begin{aligned} \left\{ (x_i(\alpha ), y_i(\alpha ), \lambda _i(\alpha )) \; | \; i=1,2, \ldots , N \right\} \end{aligned}$$

be a set of those solutions. Then, each of these curves:

$$\begin{aligned} G(x_i(\alpha ) ,y_i(\alpha ) ,\alpha ) - \beta = 0 , i=1, 2, \ldots , N \end{aligned}$$

defines a fold bifurcations curve in the parameter space \((\alpha , \beta )\).

Consider the equation:

$$\begin{aligned} G(x_i(\alpha ) ,y_i(\alpha ) ,\alpha ) = G(x_j(\alpha ) ,y_j(\alpha ) ,\alpha ), i\not =j, \end{aligned}$$
(11)

for some fixed i and j, and let \(\alpha = \alpha _0\) be a solution of Eq. (11). Then we define: \(x_0 = x_i(\alpha _0)\), \(y_0 = y_i(\alpha _0)\), and \(\beta _0= G\left( x_0 , y_0, \alpha _{0} \right) \).

In the following theorem it can be concluded that under certain conditions, System (8) is topologically equivalent to the normal form of cusp bifurcation in the neighborhood of the point: \((x_0, y_0)\).

Theorem 3

Let \((x,y) = (x_0,y_0)\) be a solution for

$$\begin{aligned} \left\{ \begin{array}{rcl} \nabla G(x,y,\alpha _0) &{}=&{} \lambda \nabla F(x,y,\alpha _0)\\ F(x,y,\alpha _0) &{}=&{} 0, \end{array} \right. \end{aligned}$$

for some \(\lambda _0 \not = 0\), such that:

  1. 1.

    \(\displaystyle \eta = F_x + \lambda _0 F_y \not =0\) evaluated at \((x_0, y_0,\alpha _0)\),

  2. 2.

    \(\displaystyle \left( J \nabla F \right) ^T \left( \lambda _0 A - B \right) J \nabla F = 0\), where A and B are the Hessian of F and G, respectively, at the equilibrium \((x_0,y_0,\alpha _0)\).

  3. 3.

    \(\displaystyle c_1 - 3c_2 c_3 \not = 0\) where:

    $$\begin{aligned} \begin{array}{l} c_1 = \eta ^2 \left. \left( \left( J\nabla F \right) ^{\scriptscriptstyle T} \left( \lambda _0 A_2 - B_2 \right) J\nabla F \right) \right| _{(0,0,0)},\\ c_2 = \displaystyle \left. \left( \left( J\nabla F\right) ^{\scriptscriptstyle T} \left( \lambda _0 A - B \right) \; {\varvec{p}} \right) \right| _{(0,0,0)}, \\ c_3 = \displaystyle \left. \left( \left( J \nabla F \right) ^{\scriptscriptstyle T} \left( F_{x} A + F_{y} B \right) J \nabla F \right) \right| _{(0,0,0)},\\ A_2 = \left( \begin{matrix} F_y F_{xxx} &{} 3 F_y F_{xxy}\\ -3F_x F_{xyy} &{} -F_x F_{yyy} \end{matrix}\right) , \\ B_2 = \left( \begin{matrix} F_y G_{xxx} &{} 3 F_yG_{xxy} \\ -3 F_x G_{xyy} &{} -F_x G_{yyy} \end{matrix}\right) , \text { and } {\varvec{p}} = \left( \begin{matrix} 1\\ \lambda _0 \end{matrix}\right) ; \end{array} \end{aligned}$$

    all evaluated at \((x_0, y_0, \alpha _0)\),

  4. 4.

    and, lastly:

    $$\begin{aligned} \left. \left( J \nabla F \right) ^T \left( \left( \begin{matrix} G_{xx\alpha }\\ G_{yy\alpha } \end{matrix}\right) - \lambda _0 \left( \begin{matrix} F_{xx\alpha }\\ F_{yy\alpha } \end{matrix}\right) \right) \right| _{(x_0, y_0, \alpha _0)} \not = 0. \end{aligned}$$

Then at \(\beta = \beta _0 = G(x_0,y_0)\) System (8) undergoes a cusp bifurcation.

As in the previous theorem, the proof follows from the center manifold reduction of System (2) in the neighborhood of \((x_0,y_0)\), and from checking four conditions for cusp bifurcation (see [14]). The detail of the proof can be found in Appendix B.

3 Two examples

In this section, two examples are presented which are well-known in the literature: the Bazykin’s system (see [3]) and the predator–prey systems with non-monotonic response function (see [9, 20, 21, 24]). It is known that both systems undergo fold and cusp bifurcations. In the first example, the solutions for System (3) as a function of the parameter can be obtained explicitly. For the second example, the fold bifurcation curves are obtained numerically by applying the Newton method. The numerical results are presented in ten-digit accuracy.

3.1 Bazykin’s system

Let us consider the system

$$\begin{aligned} \begin{array}{l} {\dot{x}} = \displaystyle x - \frac{x y}{1+\alpha x} - 0.01 x^2\\ {\dot{y}} = \displaystyle - y + \frac{x y}{1+\alpha x} -\delta y^2 \end{array} \end{aligned}$$
(12)

where x and y are densities of the prey and the predator, respectively. The parameter \(\alpha \) is the saturation parameter of the predator functional response and \(\delta \) is the predator rates of competition for external resources. In [14] it is shown that System (12) exhibited two cusp bifurcation points in the parameter-space \((\alpha ,\delta )\). These two cusp bifurcation points will be reconstructed using the procedure which has been described in the previous sections.

From the second equation of System (12), we derive:

$$\begin{aligned} -\frac{\alpha x - x +1}{y (\alpha x + 1)} = \delta . \end{aligned}$$

Hence, we set

$$\begin{aligned} G(x,y,\alpha ) := -\frac{\alpha x - x +1}{y (\alpha x + 1)}, \end{aligned}$$

as the cost function. As a consequence, the constraint is:

$$\begin{aligned} F(x,y,\alpha ) := x - \frac{x y}{1+\alpha x} - 0.01 x^2 =0. \end{aligned}$$

Appying the Lagrange Multiplier Method, two curves of solutions are derived : \(\alpha \longmapsto (x_k(\alpha )\), \(y_k(\alpha ), \lambda _k(\alpha ))\), \(k=1,2\). The explicit formulas for these solutions are:

$$\begin{aligned} x_{1,2}(\alpha )= & {} \displaystyle \frac{100 \alpha ^2 - 103 \alpha \pm \sqrt{10000 \alpha ^4 - 19800 \alpha ^3 +10601 \alpha ^2 - 792 \alpha } }{4 \alpha (\alpha -1)} \\ y_{1,2}(\alpha )= & {} -0.01 (x_{1,2}(\alpha )-100)(\alpha \, x_{1,2}(\alpha ) +1)\\ \lambda _{1,2}(\alpha )= & {} \frac{-8 \cdot 10^4 \alpha (\alpha ^4 - 4 \alpha ^3 + 6 \alpha ^2 - 4 \alpha + 1)}{x_{1,2}(\alpha ) A(\alpha ) + B(\alpha )} \end{aligned}$$

where

$$\begin{aligned} A(\alpha )= & {} 10^6 \alpha ^6 - 2.99 \cdot 10^6 \alpha ^5\\&+ 2.8999 \cdot 10^6 \alpha ^4 - 8.35901 \cdot 10^5 \alpha ^3 - 76052 \alpha ^2 + 1972 \alpha \\ B(\alpha )= & {} 10^6 \alpha ^5 - 9.9 \cdot 10^5 \alpha ^4\\&- 7.601 \cdot 10^5 \alpha ^3 + 9.70299 \cdot 10^5 \alpha ^2 - 2.15222 \cdot 10^5 \alpha + 396 \end{aligned}$$

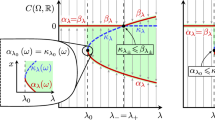
These two solution curves define fold bifurcations curves: \(G(x_k(\alpha ),y_k(\alpha ),\alpha ) = \delta \), \(k=1,2\). In Fig. 2, the two fold bifurcation curves \(G(x_k(\alpha ),y_k(\alpha ),\alpha ) = \delta \), \(k=1, 2\) have been plotted in \((\alpha ,\delta )\)-coordinates.

Fig. 2
figure 2

b The two fold bifurcation curves of equilibria in System (12) in \((\alpha ,\delta )\)-coordinates are plotted. The coordinates of the two cusp bifurcation points are \((\alpha ,\delta ) = (0.0887673081, 2.7983226350)\) and (0.9012326919, 0.0035631988). a and c are the magnification of two cusp bifurcation points

Full size image

Instead of solving Eq. (11), \(x_1(\alpha ) = x_2(\alpha )\) is solved to derive two cusp bifurcation points. This is clear since \((x_k(\alpha ), y_k(\alpha ))\), \(k =1,2\) correspond to degenerate equilibria at fold bifurcation, for every \(\alpha \) where they are defined. Thus, at the cusp bifurcation the coordinate of these degenerate equilibria is the same. Solving \(x_1(\alpha ) = x_2(\alpha )\) for \(\alpha \) we have:

$$\begin{aligned} \alpha = 0.0887673081, \alpha = 0.9012326919, \text { or } \alpha = 0.99. \end{aligned}$$

Note that we have to exclude: \(\alpha = 0.99\) from our consideration since \(y_{1,2}(0.99) = 0\); hence G(x, y) is singular there. Thus, it can be concluded that there are two cusp bifurcations at \((\alpha , \delta ) = (0.0887673081,\) 2.7983226350) and (0.9012326919, 0.0035631988).

Table 1 In this table, the coordinate of the bifurcation points with its value of \(h_{uu}, h_{uuu}\) and \(h_{\beta } h_{u \alpha } - h_{\alpha } h_{u\beta }\) is presented
Full size table

3.2 Predator–prey systems with non-monotonic response function

In [24], Zhu et al. introduce a predator–prey systems with non-monotonic response function, i.e.

$$\begin{aligned} \begin{array}{l} {\dot{x}} = \displaystyle x \left( 1-\kappa x - \frac{y}{\alpha x^2 + \beta x +1}\right) \\ {\dot{y}} = \displaystyle y \left( -\delta -\mu y + \frac{x}{\alpha x^2 + \beta x +1}\right) \end{array} \end{aligned}$$
(13)

where x and y are the prey and predator densities, respectively. The parameter \(\delta \) measures the mortality rate of the predator while \(\kappa \) and \(\mu \) measure the intraspecific competition between the preys and predators, respectively. The predation factor is measured by parameters \(\alpha \) and \(\beta \).

Following Harjanto et al. in [9, 20], we fix the parameters \(\delta = 1.1, \kappa = 0.01, \mu = 0.1\) and describe the local bifurcation diagram of equilibria of System (13). Let us define:

$$\begin{aligned} \begin{array}{l} f(x,y,\alpha ,\beta ) = \displaystyle 1-\kappa x - \frac{y}{\alpha x^2 + \beta x +1}, \\ g(x,y,\alpha ,\beta ) = \displaystyle -\delta -\mu y + \frac{x}{\alpha x^2 + \beta x +1}. \end{array} \end{aligned}$$

Assuming that \(\beta ^2 - 4 \alpha < 0\) we have \(\alpha x^2 + \beta x +1\) which is positively definite. Solving \(g(x,y, \alpha , \beta ) = 0\) for \(\alpha \) yields:

$$\begin{aligned} \alpha = \frac{-\beta \lambda x^2 +(\beta - \kappa )x + 1-y }{x^2 (\kappa x -1)}. \end{aligned}$$

Hence, we define

$$\begin{aligned} G(x,y,\beta ) = \frac{-\beta \kappa x^2 +(\beta - \kappa )x + 1-y }{x^2 (\kappa x -1)}, \end{aligned}$$

as our cost function. Then, the constraint is defined by:

$$\begin{aligned} F(x,y,\beta ) = f(x,y, G(x,y,\beta ), \beta ) = 0. \end{aligned}$$

Using the Lagrange Multiplier Method, a family of solutions is derived that satisfies

$$\begin{aligned}&H(x, \beta ) = 2 \beta ^2 x^6 + (-600 \beta ^2 + 8 \beta ) x^5\nonumber \\&\quad + (59395\beta ^2-9000\beta +8008) x^4 \nonumber \\&\quad + (-1879000\beta ^2+1337580\beta -1215600) x^3\nonumber \\&\quad + (-6050000\beta ^2-49519500\beta +45622580) x^2 \nonumber \\&\quad + (-157300000\beta +29477000) x -290400000 = 0, \end{aligned}$$
(14)

and

$$\begin{aligned} y(\beta ) = -5.5 + 0.1 \sqrt{-10 {x(\beta )}^2 + 1000 {x(\beta )} + 3025 }, \end{aligned}$$
(15)

with x is a solution for Eq. (14). The expression for \(\lambda \) is rather complicated, so it is omitted. Unlike the previous one, in this example explicit solutions for System (3) cannot be achieved. We proceed with constructing the fold line by the following procedure.

First, a value for \(\beta \) is fixed, for example: \(\beta _0=0\). Then Eq. (14) reduces this to a fourth-degree polynomial, which can be solved numerically. In this case it produces four positive roots. We can then eliminate two of them using the expression in Eq. (15) since all of the solutions should be positive from a practical point of view. Up to this point, we have \((x_k(\beta _0),y_k(\beta _0))\), \(k=1,2\) as a solution for Eqs. (14) and (15). Then we can define:

$$\begin{aligned} \alpha _k(\beta _0) =G(x_k(\beta _0),y_k(\beta _0), \beta _0), k=1,2. \end{aligned}$$
(16)
Fig. 3
figure 3

a The fold bifurcation curve \(H(x,\beta ) = 0\) in Eq. (14) in \((x, \beta )\)-coordinates. The maximum point of \(H(x,\beta ) = 0\) occurs at \((x,\beta ) = (13.19432911, 0.5500793819)\) and it is equivalent with the cusp bifurcation points of System (13) occurring at \((\beta ,\alpha ) = (0.5500793819, -0.0042066960)\}\). b Bifurcation diagram of System (13) in \((\beta , \alpha )\)-coordinates. The two fold curves coalesce in one cusp bifurcation point at \((\beta , \alpha ) = (0.5500793819, -0.0042066960)\)

Full size image

Next, we turn to the Newton method for computing the cusp bifurcation points. Suppose \((\beta _*, x_*)\) is the local maximum of the function \(\beta (x)\) which is implicitly defined by \(H(x,\beta ) = 0\). Then, this point corresponds to the cusp bifurcation point since for \(\beta = \beta _*- \delta \), \( 0< \delta \ll 1\), System (2) has two fold bifurcation points which collide with each other at \(\beta = \beta _*\), and then disappear when \(\beta = \beta _*+ \delta \), \( 0< \delta \ll 1\). The same applies when \((\beta _*, x_*)\) is the local minimum. Thus, the cusp bifurcation point can be found at the local extremum of \(\beta (x)\).

Since \(H(x,\beta ) = 0\), then \(0 = dH = H_x dx + H_{\beta } d\beta \) which implies:

$$\begin{aligned} \frac{d\beta }{dx} = - \frac{H_x}{H_\beta }. \end{aligned}$$

Furthermore:

$$\begin{aligned} \frac{d^2 \beta }{d x^2} = \frac{H_{\beta x} H_{\beta } - H_{xx} H_\beta }{{H_\beta }^2}. \end{aligned}$$

We want to look for \(\beta ^*\) so that \(\frac{d\beta }{dx}(x,\beta ^*) = 0\). Starting at \(\beta _0=0\), and taking one of the possible solutions of \(H(x, \beta _0) = 0\), say: \(x(\beta _0)\), for \(i = 0, 1, 2, \ldots \) we define a recurrence formula:

$$\begin{aligned} \beta _{i+1} = \beta _i + \left. \frac{ H_x H_{\beta } }{ H_{\beta x} H_x - H_{xx} H_\beta }\right| _{(x(\beta _i),\beta _i)}, \end{aligned}$$

assuming: \(H_{\beta x} H_x - H_{xx} H_\beta \not = 0\) at \((x(\beta _i),\beta _i)\). Note that at every level i, the value of \(x(\beta _i)\) is updated by computing (numerically) the solution of \(H(x, \beta _i)\) for x. The iteration is terminated when the difference \(| \beta _{i+1} - \beta _i|\) is less than some tolerance. The result of this procedure is then substituted into Eqs. (15) and (16).

For System (13), the cusp bifurcation point occurs at

$$\begin{aligned} (\beta ,\alpha ) = (0.55007938196, -0.004200565504) \end{aligned}$$

The result of Eq. (16) in System (3) is plotted and this result is in agreement with the result in [9], see Fig. 2 page 191.

Table 2 In this table, the coordinate of the bifurcation point is presented with its value of \(h_{uu}, h_{uuu}\) and \(h_{\beta } h_{u \alpha } - h_{\alpha } h_{u\beta }\)
Full size table

Remark 3

In Tables 1 and 2, it can be seen that the values of \(h_{uu}\) at the cusp bifurcation point are quite large. This is due to the numerical approximation of the coordinate of the bifurcation points. These results can be improved by increasing the accuracy of the approximation.

4 Subsystem of the tritrophic food-chain model

Let us consider a system of ordinary differential equations in \({\mathbb {R}}^3\), i.e.:

$$\begin{aligned} \begin{array}{l} {\dot{x}} =\displaystyle x\left( 1-x-\frac{y}{\alpha + x}\right) \\ {\dot{y}} = \displaystyle \zeta y \left( \frac{x}{\alpha + x} -\delta _1 - \sigma _1 y -\frac{z}{\beta _2 + \beta _1 y + y^2} \right) \\ {\dot{z}} = \displaystyle \zeta \varepsilon z\left( \frac{y}{\beta _2 + \beta _1 y + y^2} -\delta _2 -\sigma _2 z\right) \end{array} \end{aligned}$$
(17)

where x, y, z are the population densities of prey, predator, and top predator, respectively. This system is also known as the normalized tritrophic food-chain model (see [4]). We assume that y only consumes x and z only consumes y. This implies that there are an intraspecific competition both in the predator and the top predator (measured by \(\sigma _1\) and \(\sigma _2\)). As for the response function between x and y, we have chosen the Holling type II response function with parameter: \(\alpha \). The parameters \(\beta _1\) and \(\beta _2\) are the parameters that measure the group defence mechanism. This corresponds to the Hollng type IV response function between y and z. The parameters \(\delta _1\) and \(\delta _2\) are the mortality rate of predator and top predator, respectively. Parameter \(\zeta \) represents the ratio between the growth rate of x and y while parameter \(\varepsilon \) represent the ratio between the growth rate of y and z.

We will focus on the situation where \(\varepsilon = 0\). In this case, \({\dot{z}} = 0\), which implies that \(z(t) = z_0\) at all times. Consider the dynamical system:

$$\begin{aligned} \begin{array}{l} {\dot{x}} = \displaystyle x\left( 1-x-\frac{y}{\alpha + x}\right) \\ {\dot{y}} = \displaystyle \zeta y \left( \frac{x}{\alpha + x} -\delta _1 - \sigma _1 y -\frac{z_0}{\beta _2 + \beta _1 y + y^2} \right) \end{array} \end{aligned}$$
(18)

Apart from being a subsystem of System (17), it is also interesting to see that the second equation of System (18) can be regarded as:

$$\begin{aligned} {\dot{y}} = -\zeta \left( \delta _1 + \frac{z_0}{\beta _2 + \beta _1 y + y^2}\right) y - \zeta \sigma _1 y^2 + \zeta \frac{xy }{\alpha + x}. \end{aligned}$$

Thus, System (18) can be considered as a type of the predator–prey model with the Holling type II response function, where the mortality rate of the predator is non-constant.

4.1 Numerical continuation using AUTO

Let us fix some values for the parameters, i.e.: \(\alpha = 0.0675\), \(\beta _1 = 0.2360\), \(\beta _2 = 0.5850\), \(\delta _1 = 0.1580\), and \(\sigma _1 = 0.1000\). For these values of the parameters and \(z_0 = 0.2\), an equilibrium is computed for System (18), i.e. \((x,y) = (0.064, 0.123)\). We follow this equilibrium, as we vary \(z_0\) using the numerical continuation software AUTO (see [6]). Two fold bifurcations point are found, i.e. at \(z_0 = 0.4543905251\) and \(z_0 = 0.4668738180\).

Let us now let another parameter free, i.e. \(\sigma _1\), and follow the loci of the fold bifurcations. This gives us two fold curves (the curve where fold bifurcation occurs) in \((\sigma _1, z_0)\)-plane. These two curves of fold bifurcations coalesce with each other to a point which is a co-dimension two bifurcation known as cusp bifurcation at \(C_2 = ( 0.4720339157,\) 0.4476167091). As we follow one of the branches emanating from \(C_2\), another cusp point is found at \(C_1 = (-0.5682189318, 0.3658528382)\), which then provides us with the third fold curve.

Fig. 4
figure 4

Bifurcations diagrams computed using the numerical continuation software AUTO (diagrams a and b) and computed using the Lagrange Multiplier Method (diagrams c and d), for \(\alpha = 0.0675\), \(\beta _1 = 0.2360\), \(\beta _2 = 0.5850\), \(\delta _1 = 0.1580\), and \(\sigma _1 = 0.1000\)

Full size image

In Fig. 4a the one-parameter continuation of equilibria is plotted for System (18). These equilibria are represented by the x-coordinate. There are two fold points in the \((z_{0},x)\)-plane, i.e. \(F_1 = (0.4543905251, 0.9554454984)\) and \(F_2 =\) (0.4668738180,  0.6567319592) . In Fig. 4b, we have plotted the two-parameter continuation of the the loci of the fold bifurcations. Diagrams (a) and (c) are branches of equilibria as a function of \(z_0\). The fold bifurcation points are labelled by \(F_j\), \(j =1,2,3\). The diagrams (b) and (d) are the bifurcation diagrams in the \((\sigma _1, z_0)\)-plane; thus the parameter \(\sigma _1\) is now a free parameter. The cusp bifurcation points are labeled by \(C_k\), \(k= 1,2, 3\).

4.2 Computation of fold bifurcation using the Lagrange multiplier method

Let us consider the system of equations for the nontrivial equilibrium of System (18), i.e. :

$$\begin{aligned} \begin{array}{l} f(x,y) = 0\\ g(x,y, z_0) = 0. \end{array} \end{aligned}$$
(19)

where:

$$\begin{aligned} f(x,y) = \displaystyle 1-x-\frac{y}{0.0675 + x}, \end{aligned}$$

and

$$\begin{aligned} \begin{array}{l} g(x,y, z_0) = \displaystyle \frac{x}{0.0675 + x} - 0.1580 - 0.1000 y \\ \displaystyle \quad \quad \quad - \frac{z_0}{0.5850 + 0.2360 y + y^2}. \end{array} \end{aligned}$$

Note that by considering System (19) instead of looking for the zeroes of the vector filed in System (18) we disregard the equilibria at \(x=0\) or \(y=0\).

Since \(g(x,y, z_0)=0\) is linear with respect to \(z_0\) with a non-vanishing coefficient, there exists a unique function

$$\begin{aligned} G(x,y)= & {} \displaystyle \left( \frac{x}{0.0675 + x} - 0.1580 - 0.1000 y \right) \\&\quad \left( 0.5850 + 0.2360 y + y^2 \right) , \end{aligned}$$

so that \(g\left( x,y, G(x,y)\right) = 0\). This implies that system:

$$\begin{aligned} \begin{array}{l} G(x,y) = z_0\\ F(x,y) = f(x,y) = 0. \end{array} \end{aligned}$$

is equivalent with System(19). Thus, choosing G as the cost function, and \(F=0\) as the constraint, the Lagrange Multiplier Method can be applied with \(\lambda \) as the Lagrange multiplier, as described earlier.

By solving System (3), three fold bifurcation points are derived in the \((z_0, x)\)-plane. Those points are: \(F_1 =\) (0.4543905466, 0.9554454889), \(F_2 =\) (0.4668738384, 0.6567319636), and \(F_3 = (0.7463729068, -0.2801091825)\), see Fig. 4c by way of illustration. Let us concentrate on \(F_1\) and \(F_2\). In Table 3, the comparison is presented between the coordinates of the fold points computed by using the Lagrange Multiplier Method and by using AUTO. The table shows a remarkable agreement between the two methods.

Table 3 Comparison between the computation of fold bifurcation points in \((z_0,x)\)-plane by using the Lagrange multiplier method and by using the numerical continuation software AUTO
Full size table

Let us now look at fold bifurcation point \(F_3\). Comparing the bifurcation diagram in Fig. 4a and the diagram in Fig. 4c, it can be seen that the the numerical continuation software AUTO did not produce the branch of equilibria containing point \(F_3\). This is due to the fact that AUTO starts at the generic equilibrium \((x,y) = (0.064, 0.123)\) and follows it as we vary the parameter. The branches of equilibria containing \(F_1\) and \(F_2\) are connected to the initial generic equilibrium while the branch of equilibria containing point \(F_3\) is not. As a consequence, one would have needed to to choose other values for the parameter, for example \(\sigma _1 = 0.1\) and \(z_0 = 0.8\), to be able to find the branch of equilibria containing \(F_3\).

Our proposed procedure, on the other hand, computes the fold points directly. Thus, it immediately produces all fold points in the system, and hence the branches of equilibria connected to those fold points. It will, however, miss the branches of equilibria that contain no fold point. Thus, our method produces a more complete description of the fold bifurcation in System (18).

Fig. 5
figure 5

a The branch of continuation equilibria as a variation on parameter \(z_0\) for \(\sigma _1 = -0.5\). The five fold bifurcation points are \(F_1 =(0.4149094356, 1.537457058),\) \(F_2 = (0.3850176356, 1.272747424),\) \(F_3 =(0.6348137918,\) 0.5311964085),  \(F_4 = (0.6133043890,\) \(-0.6744081460),\) and \(F_5 = (0.5617187782,\) \(-0.4105314359)\). b Bifurcation diagram of System (18) in \((\sigma _1, z_0)\)-coordinates. The fold bifurcation points \(F_1\) and \(F_2\) coalesce at \(C_1\) as we decrease parameter \(\sigma _1\). The fold bifurcation points \(F_2\) and \(F_3\) coalesce at \(C_2\) as we increase parameter \(\sigma _1\). The fold bifurcation points \(F_4\) and \(F_5\) coalesce at \(C_3\) as we decrease parameter \(\sigma _1\)

Full size image

4.3 Cusp bifurcation

Let us consider \(\sigma _1\) as another free parameter apart from \(z_0\). Redefining the cost function G which is now dependent on \(\sigma _1\), as

$$\begin{aligned} G(x,y,\sigma _1)= & {} \left( \frac{x}{0.0675 + x} - 0.1580 - \sigma _1 y \right) \nonumber \\&\quad \left( 0.5850 + 0.2360 y + y^2 \right) , \end{aligned}$$
(20)

it is found that the x- and the y-components of the solution of System (3) satisfy

$$\begin{aligned}&147.7058643\sigma _1 x^7 - 324.3990044 \sigma _1 x^6\\&\quad + (167.8849471 \sigma _1 + 82.91222515) x^5 \\&\quad + (27.79293779 \sigma _1 - 109.7653975) x^4\\&\quad + (13.31369504 \sigma _1+11.13900450) x^3 \\&\quad + (-12.81549081 \sigma _1 + 9.231941878) x^2\\&\quad + (-1.898133469 \sigma _1+ 0.9504178198) x\\&\quad -0.06594893214 \sigma _1 +1 = 0 \end{aligned}$$

and

$$\begin{aligned} y = - x^2 + 0.9325 x + 0.0675. \end{aligned}$$

Numerically, we derive five fold bifurcation curves that are defined by \(z_0 = G(x_k(\sigma _1),y_k(\sigma _1),\sigma _1)\) for \(k = 1,2,3,4, 5\). There are two fold curves (dotted-curves in Fig. 4d) which are intersecting with each other non-transversally at a cusp point: \(C_3\), at

$$\begin{aligned} (\sigma _1, z_0) = (-0.5843125907, 0.5278605980). \end{aligned}$$

Another three fold curves (solid curves in Fig. 4d) are also intersecting with each other non-transversally at two cusp bifurcation points \(C_1\) at \( (\sigma _1, z_0) = (-0.5682189267, 0.3658528580) \) and, \(C_2\) at (0.4720339081,  0.4476167308). See Fig. 4d by way of illustration.

Table 4 Bifurcation diagram of system (18) in \((\sigma _1, z_0)\)-coordinates
Full size table
Table 5 Comparison of the Matlab program running time (measured in seconds)
Full size table

4.4 Swallow–tail bifurcation

Let us consider another example, at \(\sigma _1 = -0.5\). Using the Lagrange Multiplier Method, there are five fold points, i.e. :

$$\begin{aligned} F_1= & {} (0.4149094356, 1.537457058),\\ F_2= & {} (0.3850176356, 1.272747424),\\ F_3= & {} (0.6348137918, 0.5311964085),\\ F_4= & {} (0.6133043890, -0.6744081460), \text{ and } \\ F_5= & {} (0.5617187782, -.4105314359). \end{aligned}$$

See Fig. 5a for the illustration for the location of these fold points.

Fig. 6
figure 6

Four sections of fold bifurcation surfaces in three parameter \((\sigma _1, z_0, \beta _1)\)-space, for several values of \(\beta _1\)

Full size image

We remark that the distance between the two cusp bifurcation points on the solid curves in Fig. 5 become smaller, as parameter \(\beta _1\) becomes smaller. This behavior gives a very strong indication of the swallow-tail bifurcation. We choose several values of \(\beta _1\), i.e.: \(\beta _1 = 0.1\), \(\beta _1 = -0.5\), \(\beta _1 = -0.8\), and \(\beta _1 = -1\). For each value of \(\beta _1\), we repeat the procedure as is added done in the previous sections; see Fig. 6.

In general, by varying \(\delta _1\), a dimension is added to the bifurcation diagram plotted in the diagram (b) in Fig. 5. Thus, the fold curves become fold surfaces and the cusp points become cusp curves. In Fig. 6, four two-dimensional sections are plotted in \((\sigma _1, z_0)\)-space, of the three dimensional bifurcations diagram in \((\sigma _1, z_0, \beta _1)\)-space. These sections are for \(\beta _1 = 0.1\), \(\beta _1 = -0.5\), \(\beta _1 = -0.8\), and \(\beta _1 = -1\). From these four diagrams in Fig. 6, it can be observed that the two cusp bifurcation points collapse into one swallow-tail bifurcation point as \(\beta \) decreases.

5 Concluding remarks

The procedure for computing fold and cusp bifurcation points for equilibria of system of two ordinary differential equations using Lagrange Multiplier Method has been introduced in [16, 17]. This is an alternative method which has some advantages. One of them, as explained in Remark 1, is that the set of equations to be solved is relatively simpler than using a direct approach. We also created a Matlab program to compute the running time needed to calculate fold bifurcation points using the Lagrange Multiplier Method and the direct method through the determinant of the Jacobian matrix, see Table 5.

Another advantage is the following. In a standard continuation method, we usually start at a non-degenerate equilibrium of the system and follow it (by means of continuation) as the parameter change. There is no a priori reason to expect that a degenerate equilibrium will be reached as the parameter change. In fact, in Fig. 4 we show an example where the traditional continuation method fails to compute some branches of degenerate equilibria. This is due to the fact that those branches are not connected with the initial equilibrium we started with.

Extending our result to higher dimensional system poses an interesting question. For example in a three-dimensional system, one could reduce the dimension to two by writing one of the coordinates in terms of the other using one of the equations, see [16]. What we have in mind as an extension of our result is to study the relation between the optimization problem with two (or more) constraints and fold bifurcation. This may be a subject of future investigation.