1 Introduction

For over a decade, the attention of robotics researchers worldwide has been drawn towards unmanned aerial vehicles (UAVs) due to their numerous applications. Among different types of multi-rotor UAVs, quadrotors are considered the most preferred platform for critical applications, especially where safe performance in complex and cluttered environments is required [1,2,3,4]. This is thanks to their great dynamical maneuverability, vertical takeoff/landing ability, lightweight and, most importantly, their simplicity in design. However, the quadrotor advantages come at some cost. Specifically, their control challenges including system underactuation, model uncertainties, and subsystem coupling complicate their stabilization and trajectory tracking, significantly. Furthermore, other aspects such as actuator saturation, disturbances, noises influence control performance. For a control system to have acceptable performance, these challenges need to be taken into consideration. The work represented here mainly aims to tackle these control problems by designing a globally robust tracking controller.

The main shortcoming of a quadrotor system is its lack of enough independent control inputs i.e., the quadrotor is an underactuated system. In other words, the lack of adequate control actions in the quadrotor’s configuration space prevents them from following unrestricted flight in full vector space. Consequently, different techniques have been developed to deal with this challenge. One of the most practical and simple strategies is known as the cascade feedback strategy [5,6,7,8,9,10] that uses the dynamic inversion scheme [11]. It is based on dividing the system into two subsystems including an outer-loop and an inner-loop that form the position dynamics and attitude dynamics, respectively. Afterward, the subsystems are connected after designing a feedback control for each loop separately. Even though applying this technique has simplified the control problem, one still needs to guarantee the stability of the internal dynamics as they may lead the system to instability. Hence, one needs non-traditional control algorithms to deal with the underactuation of the system and the underlying internal dynamics. More recent attempts for controlling quadrotor involve the use of backstepping control (BC) [12,13,14]. Basically, the BC approach is developed for designing stabilizing controls and for a special class of nonlinear dynamical systems (systems with cascaded and coupled dynamics). The BC design is a recursive process that involves stabilizing the system states step-by-step to guarantees the stability of the entire system. However, the use of BC can be problematic because of the “explosion of terms” in its control law. Despite this challenge, BC is one of the commonly used approaches for quadrotor control in the literature. Another approach is the incorporation of discontinuous solutions through a hybrid control architecture or a switching mechanism [15,16,17]. In the last decade, the interest in the use of discontinuous solutions has increased, especially for cases in which a suitable solution cannot be provided using traditional control algorithms [18]. However, the use of this approach can also lead to other challenges such as chattering of the input signal due to switching that may excite some unmodeled dynamics and consequently destabilize the system. Furthermore, proving the stability of the overall system may be nontrivial, as there may exist a specific switching sequence that can cause system instability.

Through the literature, numerous control systems have been proposed for quadrotors with different representations of the UAV attitude. In some cases, the control design is based on local coordinates for simplicity [9]. However, this restricts the ability of the control system to achieve complex maneuvers, which is critical for multi-rotor vehicles. In most cases, the control systems are based on Euler-angles as their attitude representation [6,7,8]. This allows the control system to achieve better stability and performance than that based on local coordinates. Nonetheless, the control system still suffers from singularities in their attitude representation. Furthermore, the control law will involve complicated expressions with trigonometric functions, which cannot be linearized for complex maneuvers. Other control approaches are based on quaternion for their attitude representation. Quaternion-based control systems are preferable over Euler-angle based ones, as they do not suffer from singularities in their representation [10]. Still, quaternion representations can cause ambiguity, as one attitude can be represented by two different representations. Unless this ambiguity is resolved by the control system, it will lead to undesired behavior where the quadrotor unnecessarily intends to rotate a large angle. Recently, the focus of researchers is shifted towards designing control systems based on the special Euclidean group, SE(3) to represent the attitude [19]. Although the latter is not as compact as the quaternion representation, it has been favored in recent work since it is a globally valid expression even for complex maneuvers while avoiding singularities and ambiguities without complex mathematical expressions.

In general, traditional control methods are based on model approach, as they start with a mathematical model that describes the system operation. However, the developed mathematical model is usually inaccurate in capturing the process dynamics leading to model uncertainties. For example, a quadrotor carrying unknown payloads in the package delivery application is subject to a large parameter uncertainty attributed to variations of mass and inertia [3, 20]. More generally, uncertainties can be attributed to unknown parameters, external disturbances and unmodeled nonlinear dynamics e.g., wind. Thus, solutions with adaptive features are required to overcome potential model uncertainties and control the real plant [9, 16]. These control solutions can be interpreted as online techniques capable of controlling systems with bounded uncertainties in their dynamics model. However, using only an adaptation technique in the control system can still destabilize the system in the presence of small disturbances. This is because typical adaptive mechanisms work only with structured uncertainties while performing poorly with unstructured and non-parametric ones. Consequently, adaptive controllers need to be enhanced with robust features to effectively tackle unmodeled dynamics or external disturbances [21, 22]. On the other hand, several researchers investigated the integration of artificial intelligence (AI) techniques into an adaptive controller to improve the overall performance [6, 23]. One of the main advantages of AI techniques is their use of complex learning models, unlike most adaptive approaches that can take simple models with only a limited number of control parameters into consideration. The drawback is that AI techniques typically require high computational power and prior training.

Table 1 Review of the method, approach and challenges of recent control systems
Full size table
Fig. 1
figure 1

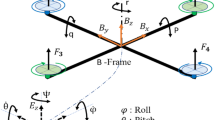
Quadrotor’s structure and reference frames. The body reference frame (B-frame) is a right-handed frame where its origin \(\left( o_B\right) \) is selected at the center of mass of the quadrotor. Its axis points toward the front \(\left( x_B\right) \), left \(\left( y_B\right) \) and up \(\left( z_B\right) \). The earth inertial reference frame (E-frame) is right-handed frame selected in North-East-Up configuration

Full size image

Literature about the control of quadrotors is vast. A great review of the recent work in the quadrotor system can be found in [24]. Table 1 summarizes a review of recent work on control systems describing the general framework, proposed method, challenges and drawbacks, robustness, attitude representation as well as the verification and demonstration of each method. In this work, we utilize an alternative control technique called dynamic surface control (DSC). Similar to the backstepping control (BC) method, this technique uses a step-by-step recursive process utilizing multiple sliding surfaces to stabilize the dynamic system. However, it avoids the drawback of BC that is the “explosion of terms” when it is applied to highly complicated systems. Specifically, it does that by incorporating a series of first-order low-pass filters into the recursive process [25]. The proposed control scheme combines the second-order sliding mode controller with the DSC technique to enable the globally robust tracking control of a quadrotor. The contributions of the control system proposed in this paper compared to other studies [6, 16, 26] are as follows. First, it is developed directly on the nonlinear configuration manifold to enable robust tracking with a region of attraction that covers the entire configuration space. Also, it is developed for the full six degrees of freedom (DOF) dynamic model of a small-scale quadrotor without any simplification or assumptions except omitting the motor dynamics. Second, the control system combines a second-order sliding mode controller for high accuracy tracking the performance of the translation dynamics and the dynamic surface control (DSC) technique that handles the coupling effects between the transitional and rotational dynamics. Third, the proposed attitude controller is based on DSC and developed directly on the special Euclidean group with a region of attraction covering the configuration space globally. This will allow the controller to maintain both dynamics stability and tracking performance while avoiding the singularity associated with orientation representations. Fourth, a combination of a robust adaptive technique based mainly on radial basis function neural network (RBF-NN) is proposed. This will guarantee the asymptotical convergence of tracking error in the presence of external disturbances and uncertainties in unmodeled dynamics and system parameters including mass and inertial matrices as well as motor coefficients. Fifth, the proposed algorithm is validated with simulation for agile maneuver and further examined using a testbed subjected to high disturbances. The testbed has 3 DOF for the attitude dynamics and another 3 DOF implemented in simulation for the translation dynamics since the testbed rotates around 3 axes, but its position is fixed. The numerical simulations are carried out using MATLAB SIMULINK\(^{\textregistered }\). The illustrative results prove that the proposed control approach outperforms similar approaches in terms of both accuracy and convergence rate.

This paper is organized as follows. The dynamic model of the quadrotor system is described in detail in Sect. 2. The problem statement and proposed control system are described in Sects. 3 and 4, respectively. The results are discussed in Sect. 5. In Sect. 5.1, the numerical simulation results are illustrated to highlight the overall performance and the effectiveness of the designed controllers. Section 5.2 describes the testbed and experimental results. Concluding remarks are provided in Section 6.

2 Quadrotor dynamic system

In general, quadrotors are preferable UAV platform for applications with cluttered and complex environments due to their unique features. A quadrotor has 6 DOF with only four actuators. Typically, the four actuators have fixed and parallel axes of rotation and they form a multi-rotor cross-platform. Its symmetry allows the control system and payload to be centralized. Moreover, it uses fixed-pitch propellers that allow the rotors to create a downward push and lifts the vehicle. In contrast to helicopter UAV which requires a tail rotor for stabilization, quadrotor eliminates that need by configuring the rotation directions of its rotors in a certain way. In particular, the rotation direction of the left and right rotors are in the opposite direction of the rotation of the rare and front rotors. The altitude and attitude of the vehicle are controlled by changing the rotational speed of the rotors to generate and forces and torques along and around the axes of the vehicle. This section starts by outlining the reference frames and followed by describing the nonlinear dynamical model of the system.

2.1 Reference frames

The first step in modeling mechanical systems involves defining proper reference frames to simplify the procedure. In this work, two right-hand reference frames were selected to describe the motion of the quadrotor’s rigid body as shown in Fig. 1. The frames are body reference frame (B-frame) and earth inertial reference frame (E-frame).

The system configuration is represented using its position and attitude with respect to the E-Frame. The distance vector between the origins of the E-frame and B-frame is known as the linear position vector \(p=\left[ \begin{array}{c@{\quad }c@{\quad }c}x&y&z\end{array}\right] ^T\). The linear position \(p=\left[ \begin{array}{c@{\quad }c@{\quad }c}x&y&z\end{array}\right] ^T\) represent the distance from E-frame to B-frame. The vehicle’s attitude angles can be defined as the rotation angles between the B-frame and E-Frame represented in the E-frame. These angles are known as Euler angles and donated by \({\Theta }=\left[ \begin{array}{c@{\quad }c@{\quad }c}\phi&\theta&. \psi \end{array}\right] ^T\). However, the angular velocity denoted by \(\omega =\left[ \begin{array}{c@{\quad }c@{\quad }c} p&q&r \end{array}\right] ^T\) is described with respect to B-Frame. In addition, all the control inputs are defined in the Body frame (B-Frame), including torques \(\tau \in {\mathbb {R}}^3\) and thrust \(F\in {\mathbb {R}}\) signals. The rotation matrix \(R\in {\mathbb {R}}^{3\times 3}\) is a special orthogonal group SO(3) used to map a vector from the B-frame to the E-frame and has the following properties:

$$\begin{aligned} R^TR=I_{3\times 3},\ \ \det {\left( R\right) }=1 \end{aligned}$$
(1)

Using R, the direction of the i th axis of the B-frame is represented by its i th column and is given by:

$$\begin{aligned} \begin{array}{l} b_i=Re_i,\ \ i=\left\{ 1,2,3\right\} \\ e_1=\left[ \begin{array}{c}1\\ 0\\ 0\\ \end{array}\right] ,\ \ e_2=\left[ \begin{array}{c}0\\ 1\\ 0\\ \end{array}\right] ,\ \ e_3=\left[ \begin{array}{c}0\\ 0\\ 1\\ \end{array}\right] \end{array} \end{aligned}$$
(2)

There are different types of forces acting on the vehicle body, however, we are going to focus only on weight and thrust. The vehicle weight acts along the direction of z-axis in the E-frame and denoted by mg, where \(m\in {\mathbb {R}}\) represents the quadrotor’s mass in (kg) and g is the gravitational acceleration in (\(\hbox {m}/\hbox {s}^2\) kg). The thrust forces are denoted by \(f_{i}\) and generated by the rotors which act in the direction of the B-frame z-axis. Additionally, a reaction torque \(\tau _{i}\) is generated by the rotation of the propeller and acts on the vehicle body in the same direction of rotation. The thrust and torque generated by each rotor are directly proportional to its rotation speed of \(\varOmega _{i}\) and defined as follows:

$$\begin{aligned} f_i= & {} K_b{\Omega }_i^2 \end{aligned}$$
(3)
$$\begin{aligned} \tau _i= & {} K_df_i \end{aligned}$$
(4)

where \(i=\left\{ 1,\ 2,\ 3,\ 4\right\} \) represents the number of rotors, \(\varOmega _i>0\) is the speed of the i th rotor in (rad/s), \(K_{b}\) represents the rotor’s thrust factor in (\(\hbox {N}\,\hbox {s}^2\)), \(K_{d}\) is thrust to torque ratio. The total thrust acting on the body F is equal to the summation of all thrust forces generated by the rotors. Additionally, the overall moments acting upon the body, which consist of the reaction torques and the moments due to the rotor forces, are expressed as follows

$$\begin{aligned} \left[ \begin{array}{c}F\\ \tau _p\\ \tau _q\\ \tau _r\end{array}\right] = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c}1&{}1&{}1&{}1\\ 0&{}l&{}0&{}-l\\ -l&{}0&{}l&{}0\\ K_d&{}-K_d&{}K_d&{}-K_d\end{array}\right] \left[ \begin{array}{c}f_1\\ f_2\\ f_3\\ f_4\end{array}\right] \end{aligned}$$
(5)

where l represents the arm distance, the distance between the center of each rotor to the center of mass in (m). It was found that the dynamics of the rotors have a low influence on the resultant system behavior. Hence, it was omitted from the system dynamics. For simplicity, the following assumptions were made:

  1. 1.

    The speeds of the propellers are controlled by high bandwidth motors.

  2. 2.

    The motor speed is unaffected by the quadrotor motion.

  3. 3.

    The propeller’s rotational inertia is much smaller than the vehicle inertia.

Through the literature, various research articles are focusing on the modeling of the quadrotor system [27, 28]. Due to the different assumptions and simplifications used by these studies, different models have been proposed. Here, we are adopting one of the most common dynamical models in the literature. The dynamic equation is described using the Euler-Lagrange approach as follows:

$$\begin{aligned}&{\dot{p}}=v \end{aligned}$$
(6)
$$\begin{aligned}&m{\dot{v}}=-\,mge_3+FRe_3+d_v \end{aligned}$$
(7)
$$\begin{aligned}&{\dot{R}}=R\omega _\times \end{aligned}$$
(8)
$$\begin{aligned}&J{\dot{\omega }}+\omega \times J\omega =\tau +d_\omega \end{aligned}$$
(9)

where \({J\in {\mathbb {R}}^{3\times 3}}\) represents the inertia matrix in \((\mathrm{N}\ \mathrm{m}\ \mathrm{s}^2), d_v\in {\mathbb {R}}^3\) and \({d_\omega \in {\mathbb {R}}^3}\) represent the modeling error and uncertainties in the translation and rotation dynamics, respectively, The second term of the dynamic equation of angular velocity expresses the cross-coupling of the angular momentum in the system.

The times map \(\bullet _\times :\ {\mathbb {R}}^3\rightarrow SO\left( 3\right) \), known also as skew matrix, is defined by the condition that \(a_\times b=a\times b\) for all \(a,\ b\in {\mathbb {R}}^3\), the matrix \(a_\times \) is given by:

$$\begin{aligned} a_\times =\left[ \begin{array}{c@{\quad }c@{\quad }c}0&{}-a_3&{}a_2\\ a_3&{}0&{}-a_1\\ -a_2&{}a_1&{}0\\ \end{array}\right] \end{aligned}$$
(10)

where the inverse of times map is denoted by the vee map \(\bullet ^\vee :\ SO\left( 3\right) \rightarrow {\mathbb {R}}^3\) that is \(\left( a_\times \right) ^{\vee }=a\).

3 Problem definition

In general, quadrotor systems suffer from uncertainties in their parameters and models which may cause inaccuracy or instability for the control system. Thus, the control systems require having some robustness to overcome the uncertainties effects and adaptation mechanisms to improve the system response with time. Consider a nonlinear system described by (6-9) and rewrite it as follows:

$$\begin{aligned}&{\dot{p}}=v \end{aligned}$$
(11)
$$\begin{aligned}&{\dot{v}}=F_v+\theta _v\ G_v\ u_v+D_v \end{aligned}$$
(12)
$$\begin{aligned}&{\dot{R}}=F_R(R,\omega ) \end{aligned}$$
(13)
$$\begin{aligned}&{\dot{\omega }}=F_\omega +\theta _\omega u_\omega +D_\omega \end{aligned}$$
(14)

where

$$\begin{aligned} \left. \begin{array}{c} F_v=\ -g\ e_3,\ \ G_v=\ Re_3 \\ F_R\left( R,\omega \right) =R\omega _\times \\ \theta _v=\frac{K_b}{m},\ \ D_v=\frac{d_v}{m} \\ J=J_0+\Delta \mathrm {J} \\ J^{-1}\left( d_\omega -\ \omega \times J\omega \right) =F_\omega +D_\omega \\ F_\omega =\ -J_0^{-1}\ \left( \omega \times J_0\omega \ \right) \ \\ D_\omega =\triangle F_\omega +J^{-1}d_\omega \\ \theta _\omega =J^{-1}\left[ \begin{array}{c@{\quad }c@{\quad }c}K_b&{}0&{}0\\ 0&{}K_b&{}0\\ 0&{}0&{}K_d\end{array}\right] \\ u = \left[ \begin{array}{c}u_v\\ u_\omega \end{array}\right] = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c}1&{}1&{}1&{}1\\ 0&{}l&{}0&{}-l\\ -l&{}0&{}l&{}0\\ 1&{}-1&{}1&{}-1\end{array}\right] \left[ \begin{array}{c}\varOmega _1\\ \varOmega _2\\ \varOmega _3\\ \varOmega _4\end{array}\right] \end{array}\right\} \end{aligned}$$
(15)

where \(u\left( t\right) \in {\mathbb {R}}^4\) is the input vector, \(y\left( t\right) =\left[ P^T,\ \psi \right] ^T\in {\mathbb {R}}^4\) is the output vector, \(x\left( t\right) =\left[ P,\ \ v,\ \ R,\ \ \omega \right] ^T\in {\mathbb {R}}^{18}\) is the state vector, \(F_v\in {\mathbb {R}}^3\) and \(\ F_\omega \in {\mathbb {R}}^3\) are the state function, \(\theta _v\in {\mathbb {R}}\) and \(\theta _\omega \in {\mathbb {R}}^{3\times 3}\) are the system’s uncertainties and \(D_v\in {\mathbb {R}}^3\) and \(D_\omega \in {\mathbb {R}}^3\) are the lumped uncertainties in the system model including unmodeled dynamics and external disturbances. The goal of this research is to design a robust adaptive nonlinear motion controller for a 6DOF UAV to achieve a proper path tracking in presence of external disturbances and system underactuation. Here are the main considered assumptions:

  1. 1.

    All of the state variables, x(t), are measurable.

  2. 2.

    \(\theta _{v}\) and \(\theta _{\omega }\) are unknown constant parameters with known sign and lower threshold \({\bar{\theta }}_{v}\) and \({\bar{\theta }}_{\omega }\), respectively.

  3. 3.

    Upper bounds for the vehicle uncertainties \(D_{v}(t)\) and \(D_\omega (t)\) are assumed \(D_{v}(t) \le D_{v_{max}}\) and \(D_{\omega }(t) \le D\omega _{max}\). This assumption can be achieved by using a nonlinear model with a good level of accuracy.

With the above assumptions, the system stability can be guaranteed using the proposed control systems.

4 Control system development

In general, the purpose of the developed control system is to guarantee system stability and achieve proper tracking for the desired command signals selected as a position in 3 DOF \(\left[ x_d,y_d,z_d\right] \) and heading angle \(\psi _d\). However, quadrotors are an underactuated system. In this research, a cascade feedback strategy is adopted by the control system using a dynamic inversion technique to control the 6 DOF quadrotor [11]. This strategy involves splitting the UAV dynamics into two subsystems; attitude dynamics and position dynamics. Then control each subsystem separately by designing two feedback controllers. Each of these controllers is based on a different control technique suitable for their individual control challenges. Finally, the controls are connected together to control the overall system. In particular, the control signals of the outer controller (position controller) is used to provide a reference signal to the inner controller (attitude controller). Figure 2 illustrates the block diagram of the overall control system.

Fig. 2
figure 2

Block diagram of the control system. The outer-loop assigns a command rotation \(\left( R_c\right) \) and control signal \(u_v\) from the command signal of position and heading angle. The inner-loop control the underactuated dynamics \(u_\omega \). The rotor control takes the input signal and controls the rotor speed by generating a proper signal command \({\Omega }_c\). The adaptive laws estimate the disturbances \({{\hat{D}}}_i\) and unknown parameters \({\hat{{\Phi }}}_i\)

Full size image

4.1 Position flight control

The outer-loop dynamics are introduced using the feedback linearization technique and given by the Eqs. (11–12). The outer-loop includes the internal dynamics of the translation motion in, x and y axes along with the altitude motion in, z-axis. The control system must stabilize the linear dynamics (internal dynamics) to guarantee the stability of the overall system. The position flight control is divided into two controllers, planner control and altitude control.

4.1.1 Planar control

The goal of the position control is to produce a suitable attitude command signal \(R_c\) for the attitude controller to track. The command signal is developed in the \(SO\left( 3\right) \), therefore it avoids singularities of Euler angles and unwinding quaternions. Let us start by assuming a smooth desired position tracking command signals \(p_d=\left[ \begin{array}{c@{\quad }c@{\quad }c}x_d&y_d&z_d\end{array}\right] ^T\in {\mathbb {R}}^3\) is given. Define a tracking error signal for position states as

$$\begin{aligned} e_p= & {} \left[ \begin{array}{c}e_x\\ e_y\\ e_z\end{array}\right] = \left[ \begin{array}{c}x-x_d\\ y-y_d\\ z-z_d\end{array}\right] \end{aligned}$$
(16)
$$\begin{aligned} e_v= & {} {\dot{e}}_p=\left[ \begin{array}{c}{\dot{e}}_x\\ {\dot{e}}_y\\ {\dot{e}}_z\end{array}\right] = \left[ \begin{array}{c}v_x-{\dot{x}}_d\\ v_y-{\dot{y}}_d\\ v_z-{\dot{z}}_d\end{array}\right] \end{aligned}$$
(17)

Now, define the sliding surface for the sliding mode control of uncertain nonlinear systems as [19]

$$\begin{aligned} s_p=\left[ \begin{array}{c}s_x\\ s_y\\ s_z\end{array}\right] = e_v+\lambda _p \ e_p \end{aligned}$$
(18)

where \(\lambda _p\) is a design positive diagonal matrix defined latter. Calculate the dynamics of the sliding surface using the nonlinear system defined in (11)-(12) yields

$$\begin{aligned} \begin{array}{l} {{\dot{s}}}_p=({\dot{v}}-{\dot{v}}_d)+\lambda _p \ e_p \\ {{\dot{s}}}_p=(F_v + \theta _v\ G_v\ u_v + D_v + -{\dot{v}}_d)+\lambda _p \ e_p \end{array} \end{aligned}$$
(19)

Using the relation between the rotation matrix and sliding surface dynamics, one can utilize the sliding error to construct the direction of the third axis of the command attitude signal as follows

$$\begin{aligned}&q_p={{\dot{v}}}_d-{{\hat{D}}}_v-F_v-\lambda _p\ e_v-K_p\ s_p \end{aligned}$$
(20)
$$\begin{aligned}&R_c\ e_3 = b_{3c} = q_p/\Vert q_p\Vert \end{aligned}$$
(21)

where \(K_p\) is a positive diagonal matrix and selected later with \(\lambda _p\) to represent a stable Hurwitz polynomial. \({{\hat{D}}}_v\in {\mathbb {R}}^3\) denote the estimate of the disturbance signal \(D_v\) defined using the RBF-NN as

$$\begin{aligned} {{\hat{D}}}_v={\hat{f}}\left( e_v,{{\dot{e}}}_v\right) ={{{\hat{W}}}_v}^T\ h_v\left( s_v\right) \end{aligned}$$
(22)

where \({{\hat{W}}}_v\) is the estimated disturbance weights.

The component of unit vector \(b_{3_c}\) is constructed to resemble the weight of the correction term \({q_p}_i\) of each translation axis. The direction of the first axis of the command attitude signal can be chosen to specify the desired heading direction of the quadrotor in the horizontal plane. This is done using the command heading angle \((\psi _c)\) as follows

$$\begin{aligned} b_1{_{ideal}}= \left[ \begin{array}{c@{\quad }c@{\quad }c} \cos {\left( \psi _c\right) } &{} -\sin {\left( \psi _c\right) } &{} 0 \\ \sin {\left( \psi _c\right) } &{} \cos {\left( \psi _c\right) } &{} 0 \\ 0 &{} 0 &{} 1 \end{array}\right] \left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] \end{aligned}$$
(23)

However, we need to ensure that the attitude command signal \(R_c\) is defined properly, that is \(R_c \in SO(3)\). Practically, the direction of its first column need to be orthogonal to the third column. This could be done by find the projection of the of the ideal first axis on the third axis as follows

$$\begin{aligned} \begin{array}{l} {b_1}_c\ ={Proj}_{b_{3_{c}}}\left( b_{1_{ideal}}\right) \\ {b_1}_c\ =\ b_{1_{ideal}}-\left( b_{1_{ideal}}^T\ {b_3}_c\right) b_{3{_c}} / \Vert b_{3{_c}}\Vert \end{array} \end{aligned}$$
(24)

It is worth to mention that, using the projection function, the first axis of the attitude command signal as \(t\rightarrow \infty \) converges to the projection of \({b_1}_c\) not \({b_1}_{ideal}\). Then the full construction of the attitude command signal is found as

$$\begin{aligned} R_c=\left[ b_{1_c},{b_3}_c\times b_{1_c},\ {b_3}_c\right] \end{aligned}$$
(25)

4.1.2 Altitude control

The purpose of this part is to develop a control system for the altitude motion in the z-axis. To design a proper tracking signal of the altitude desired command signal \(z_d\), we need to calculate the value of the input signal \(u_v\). We can reuse the chosen sliding surface defined in the previous step to build a proper input signal. The time derivative of the third element of the sliding surface defined in (19) is rewritten as follows

$$\begin{aligned} {\dot{s}}_{pz}= & {} {\dot{v}}_z-\ddot{z}_d+\lambda _{{p}_{z}}\ e_{{p}_{z}} \end{aligned}$$
(26)
$$\begin{aligned} {{\dot{v}}}_z= & {} {F_v}_z+\theta _v\ R_{3,3}\ u_v+D_z \end{aligned}$$
(27)

where the z-subscript indicates the third element of a corresponding vector, \(R_{3,3}\) is the third element of the third column of the current attitude rotation matrix. Define the estimation of the parameter \(\theta _v\) and its error as

$$\begin{aligned} {{\widetilde{\theta }}}_v=\theta _v-{{\hat{\theta }}}_v \end{aligned}$$
(28)

where \({{\hat{\theta }}}_v\in {\mathbb {R}}\) is the estimation of the unknown parameter \(\theta _v\) and \({{\widetilde{\theta }}}_v\) is the estimation error. We can now define the input signal \(u_v\) using (19) as follows

$$\begin{aligned} u_v=\left( R_{3,3}\ {{\hat{\theta }}}_v\right) ^{-1}q_{p_z} \end{aligned}$$
(29)

By substituting the input signal into the dynamics of the sliding surface defined in (26) yields

$$\begin{aligned} {{\dot{s}}}_{p_z}= & {} -K_{p_z}\ s_{p_z}-{{\widetilde{W}}}_{v_z}^T\ h_{v_z}+\epsilon _z-{{\widetilde{\theta }}}_v\ R_{3,3}\ q_{p_z} \end{aligned}$$
(30)
$$\begin{aligned} {{\widetilde{W}}}_{vz}= & {} W_{vz}-{{\hat{W}}}_{vz} \end{aligned}$$
(31)

where \({\widetilde{W}}_{vz}\) is the estimation error of the disturbance signal. With \({K_p}_z>0\) and \({{\widetilde{W}}}_{vz},\ \ {{\widetilde{\theta }}}_v\rightarrow 0\) as \(t\rightarrow \infty \), then \(s_{p_z}\rightarrow \epsilon _z\). Proof: using the following Lyapunov function:

$$\begin{aligned} V_z=\frac{1}{2}s_{p_z}^2+\frac{1}{2\gamma _v\ } {{{\widetilde{W}}}_{v_z}}^2+\frac{1}{2\eta _v}{{{\hat{\theta }}}_{v_z}}^2\ \end{aligned}$$
(32)

where \(\gamma _v\) and \(\eta _v\) are positive constants represent the learning rate of the estimated weights and parameters, respectively. The derivative of the Lyapunov function can be expressed as

$$\begin{aligned} \dot{V_z}= & {} -{K_p}_z\ {s_p}_z^2+\epsilon _z\ {s_p}_z +\ {{{\widetilde{W}}}_{v_z}}^T\left( {s_p}_z\ h_z-\frac{1}{\gamma _{v_Z}\ }{{\dot{{\hat{W}}}}_v}_z\right) \nonumber \\&-\,{{\hat{\theta }}}_v\left( R_{3,3}\ {s_p}_z\ q_z+\frac{1}{\eta _{v_Z}}{\dot{{\hat{\theta }}}}_v\right) \end{aligned}$$
(33)

Let us choose the following adaption function to to avoid the singularity and guarantee the stability of the control signal

$$\begin{aligned}&{\dot{{\hat{W}}}}_{v_z}=\gamma _v\ s_{v_z}\ h_{v_z} \end{aligned}$$
(34)
$$\begin{aligned}&\alpha _z={R_{3,3}\ s_p}_z\ q_z \end{aligned}$$
(35)
$$ \begin{aligned}&{\dot{{\hat{\theta }}}}_v\ =\left\{ \begin{array}{cc}-\eta _{v_z}\alpha _z&{}\alpha _z>0\\ -{\eta _v}_z\alpha _z&{}\alpha _z\le 0\ \& \ {{\hat{\theta }}}_v>{\bar{\theta }}_v\\ -\eta _{v_z}&{}\alpha _z\le 0\ \& \ {{\hat{\theta }}}_v\le {\bar{\theta }}_v \end{array}\right. \end{aligned}$$
(36)

Here, \({\bar{\theta }}_v\) is the lower limit of the parameter \({\theta }_v\) where the initial value of estimated parameter must follow the condition of \({{\hat{\theta }}}_v\left( 0\right) >{\bar{\theta }}_v\). Thus, the derivative can be represented as:

$$\begin{aligned} \dot{V_z}=-{K_p}_z {s_p}_z^2+\epsilon _z{s_p}_z \end{aligned}$$
(37)

The adaptive algorithm RBF-NN guarantees that the approximation error \(\epsilon \) is adequately small enough and limited that makes \(\left( \dot{V_z}<0\right) \). As a result, the filter error \({s_p}_z\) has an exponential convergence rate and, in return, guarantees the convergence of tracking error \(e_p\). Using the Barbalat’s extension so does \({{\dot{e}}}_p\). Hence the altitude tracking is achieved. Similarly, we can generalize the adaption law of the disturbance weights \({{\hat{W}}}_v\) for all position dynamics as defined in (34)

4.2 Attitude flight control

The inner-loop subsystem represents the UAV’s attitude dynamics. It considered a fully actuated system as it has 3DOF and 3 input signals, i.e. \(u_\omega \in {\mathbb {R}}^3\). Here, the controller system’s main objective is to guarantee the exponential convergence of the attitude, represented by a rotation matrix R, toward the rotational command signal \(R_c\). Furthermore, the control system has to guarantee the system’s stability and performance in the presence of external disturbances and model uncertainties. This will be accomplished using Dynamic Sliding Control (DSC) technique. The DSC method is a recursive procedure which basically composed of multiple sliding surfaces and first-order low-pass filters. In particular, the employment of the filters manifests to overcome the mathematical difficulties of an “explosion of terms” , which is a major drawback of similar techniques, such as integrator backstepping technique.

4.2.1 Attitude tracking control

To ensure the smoothness of the attitude command tracking signal \(R_c\) generated by the position control, we will introduce the following first-order low-pass filter and its augmented error as

$$\begin{aligned}&\tau _R{{\dot{R}}}_d+R_d=R_c \end{aligned}$$
(38)
$$\begin{aligned}&\zeta _R=R_d-R_c \end{aligned}$$
(39)

where \(\tau _R\) represent the time constant of the filter and will be determined later, \(R_{d}(3)\) is the filtered signal of the command attitude. For a given desired attitude tracking \(R_d\) and the current attitude \(\left( R\right) \), we define first error surface vector for attitude dynamics as follows

$$\begin{aligned} s_R=\left( {R_d}^TR-I_{3\times 3}\right) ^\vee \end{aligned}$$
(40)

With its time derivative is calculated using (12) as

$$\begin{aligned} {{\dot{s}}}_R=\left( {{{\dot{R}}}_d}^TR+{R_d}^TR\omega _\times \right) ^\vee \end{aligned}$$
(41)

At this step, the objective is to ensure the stability of the first sliding surface, that is to drive \(s_R\rightarrow 0\) as \(t\rightarrow \infty \). This is done by designing a suitable forcing term for the angular velocity defined as:

$$\begin{aligned} {\omega _c}_\times =\left( {R_d}^TR\right) ^T\left( -{{{\dot{R}}}_d}^TR-q_R\right) q_R=\left( K_RS_R\right) _\times \end{aligned}$$
(42)

where \(K_R\) is a positive diagonal matrix defined later. When the angular velocity converges to the forcing term, that is \(\omega \rightarrow \omega _c\), the dynamics of the error surface becomes

$$\begin{aligned} {{\dot{s}}}_R=-K_R\ s_R \end{aligned}$$
(43)

Thus, guarantee the exponential convergence of the first error surface \(s_R\). Angular Velocity Tracking Control Similarly, we can choose the second first-order low-pass filter for the command angular velocity and its augmented angular velocity error as follows:

$$\begin{aligned}&\tau _\omega {{\dot{\omega }}}_d+\omega _d=\omega _c \end{aligned}$$
(44)
$$\begin{aligned}&\zeta _\omega =\omega _c-\omega _d \end{aligned}$$
(45)

where \(\tau _\omega \) represent the time constant of the filter and will be determined later, and \(\omega _d\in {\mathbb {R}}^3\) is the desired angular velocity. For a given desired angular velocity \(\omega _d\) and the current angular velocity \(\omega \), we define the second error surface vector as follows

$$\begin{aligned} s_\omega =\omega -\omega _d \end{aligned}$$
(46)

With its time derivative is calculated using (13) as:

$$\begin{aligned}&{{\dot{s}}}_\omega ={\dot{\omega }}-{{\dot{\omega }}}_d \end{aligned}$$
(47)
$$\begin{aligned}&{{\dot{s}}}_\omega =F_\omega +\theta _\omega \ u_\omega +D_\omega -{{\dot{\omega }}}_d \end{aligned}$$
(48)

At this step, the objective is to ensure the stability of the second error surface, that is drive \(s_\omega \rightarrow 0\) as \(t\rightarrow \infty \). This is done by designing a suitable input signal \(u_\omega \). First, let us define the estimation error \({{\widetilde{\theta }}}_\omega \) as the difference between the unknown parameter \(\theta _\omega \) and its estimation \({{\hat{\theta }}}_\omega \) and write it as

$$\begin{aligned} {{\widetilde{\theta }}}_\omega =\theta _\omega -{{\hat{\theta }}}_\omega \end{aligned}$$
(49)

Using this relation, we can now define the control signal as

$$\begin{aligned} u_\omega= & {} {{\hat{\theta }}}_\omega ^{-1}\left( q_\omega \right) \end{aligned}$$
(50)
$$\begin{aligned} q_\omega= & {} {{\dot{\omega }}}_d-F_\omega -{{\hat{D}}}_\omega -K_\omega s_\omega \end{aligned}$$
(51)

where \(K_\omega \) is a positive diagonal matrix defined later, \({{\hat{D}}}_\omega \in {\mathbb {R}}^3\) is the disturbance estimation defined using the RBF-NN as

$$\begin{aligned} {{\hat{D}}}_\omega ={\hat{f}}\left( s_w\right) ={{{\hat{W}}}_\omega }^Th_\omega \left( s_w\right) \end{aligned}$$
(52)

where \({{\hat{W}}}_\omega \) is the estimated disturbance weights. Substituting the input signal \(u_\omega \) into the dynamics of the second error surface defined in (48) yields

$$\begin{aligned} {{\dot{s}}}_\omega= & {} -K_\omega s_\omega +{{{\widetilde{W}}}_\omega }^Th_\omega +\epsilon _\omega +{{\widetilde{\theta }}}_\omega u_\omega \end{aligned}$$
(53)
$$\begin{aligned} {{\widetilde{D}}}_\omega= & {} D_\omega -{{\hat{D}}}_\omega ={{{\widetilde{W}}}_\omega }^Th_\omega +\epsilon _\omega \end{aligned}$$
(54)

where \({{\widetilde{W}}}_\omega \) represents the difference between the estimated weights and their desired values. One can easily prof that the approximation error \(\epsilon _\omega \) is limited and sufficiently small. As the estimation error signal of \({{\widetilde{W}}}_\omega \) and \({{\widetilde{\theta }}}_\omega \) goes to zero, the angular velocity error surface will go to zero, i.e. \(s_\omega \rightarrow 0\).

4.2.2 Neural network-based adaptive controller

Similar to the work in [29], this paper approximates the uncertainty in the nonlinear functions using neural network technique, namely radial basis function neural network (RBF-NN). In brief, this technique is defined as:

$$\begin{aligned} h_j= & {} e^{\Vert x-c_j\Vert ^{2}/2bj^2} \end{aligned}$$
(55)
$$\begin{aligned} f(x)= & {} {W^*}^Th\left( x\right) +\epsilon \ \end{aligned}$$
(56)

where h function defines the output of the Gaussian function, signal x defined as the input signals of the neural network, parameter j represent the number of hidden layer nodes in the network, the function f defines the overall output value of the network, the neural network’s ideal weights are denoted by \(W^*\), finally, the parameter \(\epsilon \) defined as the approximation error. To estimate the nonlinear function of the dynamic system \(f\left( x\right) \), one must estimate the ideal weights \(W^*\) of the NN as:

$$\begin{aligned}&{\hat{f}}\left( x\right) \ ={{\hat{W}}}^Th\left( x\right) \end{aligned}$$
(57)
$$\begin{aligned}&{\widetilde{W}}=W-{\hat{W}} \end{aligned}$$
(58)

where \({\hat{f}}\) and \({\hat{W}}\) represent the estimated disturbance and weights, respectively, \({\widetilde{W}}\) defined as the error between the estimated weights and their desired values, that is

$$\begin{aligned} f-{\hat{f}}={{\widetilde{W}}}^Th+\epsilon \end{aligned}$$
(59)

4.3 Error dynamics

Once the design procedure is applied, the closed-loop error dynamics need to be derived for stability analysis. Using the definition of the error surfaces, forcing term and input signals, the nonlinear system equations for the rotation dynamics can be described as the error equations of DSC as follows:

$$\begin{aligned} \begin{array}{c} {{\dot{s}}}_R=\left( -{{{\dot{R}}}_d}^TR-{R_d}^TR\left( {\omega _c}_\times -{s_\omega }_\times +{\zeta _\omega }_\times \right) \right) ^\vee \\ {{\dot{s}}}_R=-K_Rs_R+{R_d}^TR\left( s_\omega -\zeta _\omega \right) \end{array} \end{aligned}$$
(60)

and for the angular velocity as:

$$\begin{aligned} {{\dot{s}}}_\omega =-K_\omega s_\omega -{{{\widetilde{W}}}_\omega }^Th_\omega -\epsilon _\omega -{{\widetilde{\theta }}}_\omega u_\omega \end{aligned}$$
(61)

The dynamics of the augmented errors defined in (39) and (45) affect the overall error dynamics of the closed-loop system. By assuming fast responses of the first-order low-pass filters, that is faster than the error surfaces and system dynamics, one can simply ignore their effects when designing the control system. Thus, the dynamics of the error surfaces becomes

$$\begin{aligned}&{{\dot{s}}}_R\approx -K_Rs_R+{R_d}^TRs_\omega \end{aligned}$$
(62)
$$\begin{aligned}&{{\dot{s}}}_\omega =-K_\omega \ s_\omega -{{{\widetilde{W}}}_\omega }^T\ h_\omega -\epsilon _\omega -{{\widetilde{\theta }}}_\omega u_\omega \end{aligned}$$
(63)

Now, Let us define a Lyapunov function as:

$$\begin{aligned} V=\frac{1}{2}\left( s_R^Ts_R+s_\omega ^Ts_\omega +\ {{{\widetilde{\theta }}}_\omega }^T{\Gamma }_\omega ^{-1}{{\widetilde{\theta }}}_\omega +{{\widetilde{W}}}_\omega ^T\gamma _\omega ^{-1}{{\widetilde{W}}}_\omega \right) \end{aligned}$$
(64)

where \(\Gamma _\omega \) and \(\gamma _\omega \) are positive matrices. Driving its derivative yields:

$$\begin{aligned} \begin{array}{c} {\dot{V}}=-K_R\ \Vert s_R\Vert ^2 - K_{\omega } \Vert s_{\omega }\Vert ^2 + s_R\ R_d^T\ R\ s_{\omega } - s_{\omega }\epsilon _{\omega } \\ + {\widetilde{W}}_{\omega }^T \left( h_{\omega } s_{\omega }^T - \gamma _{\omega }^{-1}\ \dot{{\hat{W}}}_{\omega } \right) + {\widetilde{\theta }}_{\omega } \left( u_{\omega } s_{\omega }^T - \Gamma _{\omega }^{-1}{\dot{{\hat{W}}}}_{\omega }\right) \end{array} \end{aligned}$$
(65)

Similarly, an adaptation function can be used to guarantee the control signal’s stability and avoid singularity as follows:

$$\begin{aligned} {\dot{{\hat{W}}}}_\omega= & {} \gamma _\omega \ h_\omega s_\omega ^T\ \end{aligned}$$
(66)
$$\begin{aligned} \alpha _\omega= & {} {\Gamma }_\omega u_\omega s_\omega ^T \end{aligned}$$
(67)
$$ \begin{aligned} \alpha _\omega= & {} {\Gamma }_\omega u_\omega s_\omega ^T {\dot{{\hat{\theta }}}}_\omega \ = \left\{ \begin{array}{cc} -\eta _\omega \alpha _\omega &{}a_\omega>0\\ -\eta _\omega \alpha _\omega &{}\alpha _\omega \le 0\ \& \ {{\hat{\theta }}}_\omega >{\bar{\theta }}_\omega \\ -\eta _\omega &{}\alpha _\omega \le 0\ \& \ {{\hat{\theta }}}_\omega \le {\bar{\theta }}_\omega \end{array} \right. \end{aligned}$$
(68)

where the estimated parameter \({\theta }_\omega \) has a lower limit represented by \({\bar{\theta }}_\omega \). The initial values of \({\theta }_\omega \) must be selected as \({{\hat{\theta }}}_\omega \left( 0\right) >\left( {\bar{\theta }}_\omega \right) \). The derivative of the Lyapunov function can be rewritten as

$$\begin{aligned} \begin{array}{c} {\dot{V}}=-K_R\ \Vert s_R\Vert ^2 - K_\omega \ \Vert s_\omega \Vert ^2 + s_R\ R_d^T \ R\ s_\omega - s_\omega \epsilon _\omega \\ \le K_R\ \Vert s_R\Vert ^2 - K_\omega \ \Vert s_\omega \Vert ^2 - s_\omega \epsilon _\omega \end{array} \end{aligned}$$
(69)

RBF-NN guarantees that the approximation error represented by \(\epsilon _\omega \) is adequately small enough and limited i.e. \(({\dot{V}} < 0)\). This gives the surface error \(s_R\) and \(s_\omega \) an exponential convergence rate which results in tracking the desired signal, i.e. \(R\rightarrow R_d\)

Fig. 3
figure 3

Desired and actual trajectories

Full size image
Fig. 4
figure 4

Position command and response in x-, y-, z-axis; command in black, desired in red and actual in blue

Full size image
Fig. 5
figure 5

Euler-angle response in roll, pitch and yaw domain

Full size image
Fig. 6
figure 6

Tracking error between in x-, y- and z-axis

Full size image

5 Results

In this section, we demonstrate the results of the proposed controller through simulation software and experimentally using a testbed. The purposes of the simulations are to show the overall performance of the proposed controller in an ideal environment, while the experimental experiments show the feasibility of the proposed control in real-life implementation.

5.1 Numerical simulation

The simulations are carried out through MATLAB SIMULINK\(^{\textregistered }\) software. The simulation demonstrates the performance of the proposed global robust DSC controller in terms of accuracy and convergence rate under the presence of uncertainties and disturbances. The quadrotor system parameters carried out through the simulation tests are shown in Table 2 while the used control parameters are shown in Table 3.

Table 2 Plant parameters and inputs saturation
Full size table
Table 3 Control parameters in each domain
Full size table

Here, the simulation illustrates the behavior of the proposed controller in the presence of unmodeled dynamics, parameter uncertainties, and external disturbance. The desired trajectory consists of four flight behaviors: ascending (take-off), stand still (hovering), path following and descending (landing). At the vertical take-off behavior, the system is commanded to start raising until it reaches a certain altitude with a slope of 1 m/s while the system is subjected to uncertainties in its parameters and dynamics. The required performance of the system for this stage includes showing a good error convergence with proper estimations and handling of the system uncertainties. At the hovering and path following stages, the system will be subjected to external disturbances, i.e. wind gust, on all of its axes. At both stages, the performance of the system is required to show a good disturbance rejection while following the specified trajectory for each stage. This includes demonstrating a good error convergence and an adequate estimation of the external disturbances. Finally, at the fourth stage, the landing test, the quadrotor is commanded to start descending from a specific altitude until it reaches the ground with a slower sloop, 0.5 m/s. The quadrotor needs to land safely and precisely. Figure 3 shows the path of the desired and actual trajectories of the carried tests.

Figure 4 shows the position signal of the command, desired and actual signals. Figure 5 shows the Euler-angle responses. The results show a perfect tracking of the command signals. Due to the uncertainties in the system model, the designed adaptation mechanism enhances the system behavior, continuously. The quadrotor was able to perform all required behaviors despite the considered challenges.

Detailed navigational of the position and Euler angles are shown in Figs. 6 and 7, respectively. It is clearly seen that the proposed control system achieved an adequate tracking of the command signals, i.e. all tracking error have converged to zero, despite the external disturbances and model uncertainties.

Fig. 7
figure 7

Tracking error in roll, pitch and yaw domain

Full size image

To show the efficiency of the proposed control algorithm, several comparison tests have been carried out. Two algorithms have been selected for the comparison; a PID-based technique, similar to the one typically used in the off-the-shelf controller, and the control algorithm proposed by T. Lee in [16]. The comparison tests are carried out by generating a train of pulses as a command signal and then calculating the integral of absolute error (IAE) for each algorithm. Two sets of command signals are generated; one with a range between \({\pm }\,\pi /3\) and the other between \({\pm }\,2\pi /3\). For each set, the tests were carried out with and without applying external disturbances. The results of the comparison tests are shown in Table 4. In this table, lower numbers of IAE indicate better performance and smaller tracking error.

Table 4 Attitude comparison tests
Full size table

5.2 Experimental test

To experimentally validate the proposed control system, we have developed a testbed system. The testing system uses Robot Operating System (ROS) environment to smoothly integrate required sensors, estimation and control algorithms, and communication with the system. The testbed system consists mainly of five parts, a mechanical skeleton, sensors, actuators, a processor and a ground station. Figure 8 shows a graphical representation of the overall architecture of the testbed system. The testbed is developed to resemble the rotation dynamics of a quadrotor vehicle. The body frame of the quadrotor is mounted on a 3-DOF pivot joint, which allows the quadrotor to rotate about its x-, y- and z-axes. The mechanism allows the frame to have a maximum of 35 degrees in roll and pitch angles and 360 degrees in yaw angle. The platform is supported by a thick aluminum base with a 40 cm long and 5 cm thickness pipe. The system is mounted on the ceiling to reduce the ground effects generated by the quadrotor vortex. The testbed consists of four arms with 30 cm in length. At the end of each arm, a brushless DC motor is attached with a propeller and controlled using an Electrical Speed Controller (ESC) unit. To measure the vehicle states, the testbed is supported with various on-board sensors. In our setup, we use two Inertial Measurement Unit (IMU) sensors and three joint encoders. Each IMU sensor consists of 3-axis accelerometers, 3-axis gyroscopes, and 3-axis magnetometers. The reason for using two IMU sensors is mainly for improving the measurement accuracy and the system redundancy. The joint encoders can accurately measure the platform’s rotation angles which are used to obtain the orientation of the testbed with a relatively low noise level and micro degree accuracy at up to 1 kHz. In our experiments, the encoder readings are used for the purpose of estimation comparisons as they serve as the ground truth measurements. In terms of onboard computing power, the testbed contains a Raspberry pi 3®microprocessor board that runs up to 1.2 GHz and capable of running the closed-loop controller algorithm. The board is supported with an input-output extension that allows it to control 16 PWM channels with 12bit resolution used to control the ESC. We use a PC, serves as the ground station, running the ROS environment on Ubuntu 16, which generates the command orientation signals and displays the testbed states. We have connected the on-board microprocessor to the ground station through WiFi. The communication gives the user the ability to control the testbed’s orientation through a graphical user interface (GUI) and visualize the vehicle states using GAZEBO software. During this experiment, the data interchange was running at 100 Hz. Figure 9 shows the testbed fixed to the ceiling.

Fig. 8
figure 8

A graphical representation of the overall architecture of the experimental setup

Full size image
Fig. 9
figure 9

Testbed while fixed to the ceiling

Full size image

In the experimental test, we have implemented the control algorithm using the C++ language. All control processes and measurements were performed on-board. In this experiment, we have generated pulse inputs as a desired command signal in roll and yaw domains. The initial weights of the Neural-Network parameters have been randomly selected, as the proposed RBF-NN does not require any prior training for its weights.

Figure 10 shows the output response of the setup for the Euler angles. The result shows a good convergence for the yaw angle and acceptable convergence for the roll and pitch angles. The output response of the roll and pitch angles are designed to be faster than the yaw angle, as can be seen from the selected control parameters defined in Table 3.

Fig. 10
figure 10

Testbed response in roll, pitch and yaw domain

Full size image

Figure 11 illustrates the tracking errors for the Euler angles. The error signal reached zero within an acceptable time. The response of the roll and pitch domains is less smother than the yaw domain that is due to the subsystem coupling effect, where the rotation of one domain generates a disturbance signal on the other one. Figure 12 shows the input signal generated by the proposed control system for each angle. The control signals are noisy due to the usage of embedded sensors in the feedback loop. The signal limitation, seen in the control signal of the yaw domain, is a software limitation designed so the relation in Eq. (5) is fully defined. This limitation is manually designed and depends on the system configuration and parameters.

Fig. 11
figure 11

Tracking error in Euler angles

Full size image
Fig. 12
figure 12

Control signal

Full size image

6 Conclusions

A global robust control system with an adaptation mechanism is designed for quadrotors in the presence of underactuation, external disturbances and model uncertainties. The proposed attitude controller is based on dynamic surface control and developed directly on the special Euclidean group with a region of attraction covering the configuration space globally. Moreover, the proposed controller uses adaptive RBF-NN to overcome the model uncertainties and external disturbances. The RBFNN is based on a single hidden layer to reduce the computational complexity of the control system. This will allow the controller to maintain both dynamics stability and tracking performance while avoiding the singularity associated with orientation representations. The performance of the proposed controller was compared to two other approaches; a traditional PID control used typically in off-the-shelf solutions and a state-of-the-art solution proposed by T. Lee in [16]. The results show that the proposed controller outperforms those two approaches in terms of both accuracy and convergence rate. The stability of the control system is proven using Lyapunov functions, and its performance has been validated by both simulation and experiments.

The performance of the overall control system has been validated by both simulation and experiments using a 3-DOF testbed. The use of this testbed, instead of a regular UAV, has offered two very important advantages for this research. First, we have been able to use encoders to measure and record the angle and rate of yaw, pitch, and roll much more accurately than what we could have been measured using the IMU of a regular UAV, which is typically not an impressively accurate sensor in the price range of UAV applications. Second, and perhaps more importantly, we have been able to subject the testbed to much greater disturbances (for example a physical impact using a long stick) rather than what we could safely apply to a freely flying UAV. In other words, the use of the testbed made it possible for us to demonstrate the stability and robustness of the proposed dynamic surface control method in a much broader application domain without facing the risk of crashing the experimental setup over and over again.

The study of the performance of the control system in real-flight experiments will be the topic of further research. In an uncontrolled environment, the system may be subjected to unexpected conditions. Thus, one future direction can be to validate the proposed algorithm against the unmodeled dynamics in 6 DOF. Even though the attitude dynamics have more influence on the stability of the system in comparison with the translation dynamics, real-flight validation tests are still required. Another future direction can be in terms of simplifying the procedure of identifying the control parameters. Although the proposed control system uses adaptive techniques to compensate for system uncertainties, several tests are still required in order to find suitable control parameters. One solution to that could be the use of the model reference adaptive control in conjunction with the dynamic surface control in the attitude controller. This will contribute to having a consistent system behavior regardless of the actual system parameters.