1 Introduction

1.1 Antecedents and motivations

Renewable energy capacity has increased this last decade due to its main objective to alleviate the problem of pollution caused by the traditional energy source. Particularly, wind energy technology is attracting scientific community as an interesting solution to produce clean energy especially for remote and isolated areas.

The use of permanent magnet synchronous machine in generator mode especially in wind electric systems is becoming more and more popular. This fact is motivated by its considerable advantages over other types of generators, namely: the smaller weight and size in relation to power unit; higher operational reliability because of brushless construction (rotor without slip-rings); higher efficiency because of very small energy losses in magnetic rotor. Since the rotor is made up of permanent magnet there is no need to use automatic priming capacitors as in the case of cage induction generator; in addition, the frequency of maintenance is reduced. The permanent magnet synchronous generator (PMSG) is suitable for variable speed wind turbine and can be used without a gearbox, and therefore contributes in the wind power plant total cost reduction [1–4]. Another interesting fact is that a high number of poles PMSG can operate at low speed and hence becomes a good candidate for regions where the wind speed is relatively low. But the PMSG is a multivariable, nonlinear and highly coupled system with time-varying parameters. This increases the challenge level of the well known problem of power efficiency maximization in variable speed wind electric systems. A lot of research works have been devoted to this end. In [5–7], the control of PMSG associated to PWM rectifier and driven by a wind turbine has been reported. In [5], a vector oriented control based on conventional PI controller is used to regulate the machine current and the dc-bus voltage. In [6], direct torque control technique is proposed. But the stator flux estimator used needs the knowledge of the stator voltage. This may be problematic in practice in terms of voltage sensor to be used as it is well known that when the generator is connected to the converter, the voltage waveform is not sinusoidal. In [7], feedback linearization based controller has been proposed. In the above contributions, the investigation of the variation of PMSG WT parameters as well as maximum power point tracking problem have not been discussed.

Known for its robustness, fast dynamic response capability, design and real-time implementation simplicity, sliding mode control has widely been used to control a large number of nonlinear systems [8–12]. Sliding mode control originally was designed to cope with the uncertainties of the system parameters and their variations. Extensive studies on sliding mode control of PMSG wind turbine systems to achieve good performance have been reported [13–18]. Merzoug et al. [13] proposed a cascaded sliding mode control to regulate the generator current and the dc-bus voltage, but the maximum power caption enhancement problem is not addressed. The works in [14–17] have addressed the problem of the generator current and speed control as well as the enhancement of the maximum power from the wind. But the authors have not treated the problem of dc-bus voltage regulation and the control of the inverter side. In [18], power control of a wind energy conversion system integrated in a stand-alone hybrid generation system is proposed. But the proposed control emphasized only on the power maximization issue since the dc voltage is imposed by the battery bank.

Although sliding mode control used in [13–18] copes with system uncertainties, keeping a properly chosen constraint by means of high-frequency control switching, the adaptation of time-varying parameter in the equivalent control term would improved significantly the efficiency of the overall control scheme. High control gains help in suppressing parameter uncertainty but are likely to excite high-frequency un-modeled dynamics [9]. While parameter adaptation leads to high robustness with smaller control gains and hence resulting in smooth control actions suitable to interface with PWM units [9].

Fig. 1
figure 1

Control system diagram

Full size image

1.2 Main contributions

In this paper, a solution to the problem of maximum power caption and current regulation as well as dc-bus voltage regulation of a stand-alone PMSG wind turbine is proposed. The dc-bus voltage is regulated to its reference value through a single switch PWM DC–DC converter. For the control of dc-bus voltage, generator current and generator speed, a chattering free adaptive sliding mode controller is designed. The proposed control algorithm is robust with respect to PMSG WT parameters and load variations. The convergence and stability analysis of the rotor flux estimator and the sliding mode controller have been proved by using Lyapunov theory. The speed operation range includes relatively low speeds which implies that the proposed control system can be applied in remote areas with low wind speed profile.

1.3 Structure of the paper

The paper is organized as follows. Section 2 deals with the system description and modeling. In Sect. 3, the control objective is specified, the maximum power point tracking algorithm is presented and the proposed nonlinear adaptive sliding mode control design for current, speed and dc-bus voltage regulation of PMSG is described. Guidelines for load side converter control are provided. In Sect. 4, simulation results using the conventional PI control and the proposed sliding mode approaches are reported and some concluding remarks are given in Sect. 5.

2 System modeling

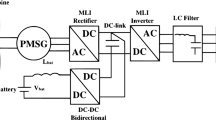
The structure of the stand-alone wind conversion system studied in this work (Fig. 1) consists of:

  • Wind turbine,

  • Gearbox,

  • Permanent magnet synchronous generator,

  • Three phase PWM rectifier (generator side converter) used to control the generator current and realize the maximum power point tracking,

  • Electronic load controller (DC–DC converter) used to regulate the dc-bus voltage,

  • Three phase PWM inverter (load side converter) used to maintain the load voltage at constant amplitude and constant frequency,

  • LC filter which attenuates the harmonics produced by the three phase PWM inverter,

  • Two loads: a main load (AC load) and an electronic load which can be a heater or a battery storage system.

2.1 Wind turbine model

The general equation of the power captured from the wind by the wind turbine is given as follows:

$$\begin{aligned} P_{t}=0.5\rho {\pi }r^{2}C_{p}(\lambda ,\beta )v^{3}_{w} \end{aligned}$$

where \(\rho \) is the density of air, r is the rotor radius, \(C_{p}\) is the power coefficient and \(v_{w}\) is the wind speed. The power coefficient is a function of the tip-speed-ratio \(\lambda \) and the blade picth angle \(\beta \). The tip-speed-ratio is defined as:

$$\begin{aligned} \lambda =\frac{r{\Omega }_{t}}{v_{w}}=\frac{r{\Omega }}{Gv_{w}},~G=\frac{{\Omega }}{{\Omega }_{t}}=\frac{T_{t}}{T_{m}} \end{aligned}$$
(1)

\({\Omega }_{t}\) and \(T_{t}\) are the blade side rotor speed and aerodynamic torque respectively. G is the gearbox ratio. \({\Omega }\) and \(T_{m}\) are the generator side rotor speed and mechanical torque. The aerodynamic torque is calculated from the power and the rotor speed as follows:

$$\begin{aligned} T_{t}=\frac{P_{t}}{\Omega _{t}}=0.5\rho {\pi }r^{3}\frac{C_{p}(\lambda ,\beta )}{\lambda }v^{2}_{w} \end{aligned}$$

The power coefficient model depends on the wind turbine characteristics. The expression used in this work has been taken from [19] and is given by:

$$\begin{aligned} C_{p}(\lambda ,\beta )=0.5176\left( \frac{116}{\lambda _{i}}-0.4\beta -5\right) e^{-21/\lambda _{i}} +\,0.0068\lambda \nonumber \\ \end{aligned}$$
(2)

with

$$\begin{aligned} \frac{1}{\lambda _{i}}=\frac{1}{\lambda +0.08\beta }-\frac{0.035}{\beta ^{3}+1}. \end{aligned}$$

The dynamic equation of the wind turbine referred to the generator side is given by:

$$\begin{aligned} \frac{d\Omega }{dt}=\frac{T_{m}}{J}-\frac{f{\Omega }}{J}-\frac{T_{e}}{J} \end{aligned}$$
(3)

where J is the inertia of the rotating parts, f the friction coefficient and \(T_{e}\) the electromagnetic torque of the generator.

2.2 Nonlinear dynamics of PMSG

The dynamic model of a surface mounted PMSG associated to PWM rectifier, PWM DC–DC converter and PWM inverter (Fig. 1) in the synchronously rotating d–q reference frame is given by [20–23]:

$$\begin{aligned}&\dot{i}_{sd}=-\frac{R_{s}}{L_{s}}i_{sd}+p{\Omega }i_{sq}-\frac{v_{sd}}{L_{s}}\end{aligned}$$
(4)
$$\begin{aligned}&\dot{i}_{sq}=-\frac{R_{s}}{L_{s}}i_{sq}-p{\Omega }i_{sd}+\frac{p\Omega {\phi }_{r}}{L_{s}}-\frac{v_{sq}}{L_{s}} \end{aligned}$$
(5)
$$\begin{aligned}&T_{e}=\frac{3}{2}p{\phi }_{r}i_{sq} \end{aligned}$$
(6)
$$\begin{aligned}&{\phi }_{sd}=L_{s}i_{sd}+{\phi }_{r},\quad ~{\phi }_{sq}=L_{s}i_{sq} \end{aligned}$$
(7)
$$\begin{aligned}&v_{sd}=S_{d}v_{dc},\quad ~v_{sq}=S_{q}v_{dc} \end{aligned}$$
(8)
$$\begin{aligned}&\dot{v}_{dc}=\frac{1}{C}(S_{d}i_{sd}+S_{q}i_{sq})-\frac{Sv_{dc}}{CR_E}-\frac{i_i}{C} \end{aligned}$$
(9)
$$\begin{aligned}&\dot{u}=\frac{3p\Omega {\phi }_{r}}{C}i_{sq}-\frac{2Su}{CR_E}-\frac{2P_i}{C},~\hbox {with}~u=v^{2}_{dc} \end{aligned}$$
(10)

In the above equations, \(\phi _{r}\) is the rotor flux, \(\Omega \) is the rotor mechanical speed, \(i_{sd}\) and \(i_{sq}\) are the stator current components, \(v_{sd}\) and \(v_{sq}\) are the stator voltage components, \(R_{s}\) and \(L_{s}\) are the stator resistance and inductance, \(T_{e}\) is the electromagnetic torque, p is the number of pole pairs and \(v_{dc}\) is the dc-bus voltage. C is the dc-bus capacitor, \(R_{E}\) denotes the electronic load resistance. S is the switching function stating the ON/OFF positions of the DC–DC converter switch. \(i_i\) and \(P_i\) are the inverter current and active power respectively.

\(\theta =p\int {\Omega }\,dt\) is the angular position of generator voltage. \(S_{d}\) and \(S_{q}\) are the \((a,b,c)-(d,q)\) reference frame transformation of the switching functions \(S_{a}\), \(S_{b}\) and \(S_{c}\) for the PWM technique. The state of \(S_{k}, k=a,b,c\) is defined as

$$\begin{aligned} S_k=\left\{ \begin{array}{l} +1,\quad \bar{S}_k=-1\\ -1,\quad \bar{S}_k=+1 \end{array}\right. \end{aligned}$$
(11)

3 Proposed control strategy

3.1 Control objective

The following assumptions will be considered until further notice.

  1. (i)

    The rotor speed, the stator current and voltage are bounded signals as well as the dc voltage.

  2. (ii)

    It is also assumed that the electrical parameters vary slowly (e.g. the rate of variation of these parameters are negligible compared to other dynamics of the PMSG states variables).

The main control objective is to control the PMSG in such a way that under wind speed fluctuations the machine current and the dc-bus voltage are regulated as well as the maximum power is harnessed from the wind energy. For this end we design a nonlinear adaptive controller that forces the d-axis current to track the desired reference \(i^{*}_{sd}=0\) and regulates the rotor speed to its optimal value \(\Omega _{opt}\). The third control action is designed to track the dc voltage set reference \(v^{*}_{dc}\) while the fourth controller design is to maintain the load voltage at constant amplitude and constant frequency through the inverter.

3.2 Maximum power point tracking

For each wind velocity, there is a maximum power that the turbine can extract if operated at a particular (or optimum) tip speed ratio (\(\lambda _{opt}\)). The power coefficient in (2) achieves its maximum value (\(C_{pmax}=0.48\)) for \(\beta =0\) and \(\lambda =\lambda _{opt}=8.1\). By solving equation (1) for \(\Omega \) we obtain:

$$\begin{aligned} \Omega _{opt}=\frac{\lambda _{opt}{Gv_{w}}}{r} \end{aligned}$$
(12)

Therefore, in order to obtain maximum possible power, the turbine must operates at \(\lambda _{opt}\) and this is possible by controlling the turbine rotational speed such that it always tracks the reference or optimum speed \(\Omega ^{*}=\Omega _{opt}\).

3.3 Direct axis current control and generator speed regulation

In order to derive the control of the PMSG d-axis current, we rewrite (4) in the following form:

$$\begin{aligned} \dot{i}_{sd}=f_{i_{sd}}+g_{i_{sd}}v_{sd} \end{aligned}$$
(13)

with

$$\begin{aligned} f_{i_{sd}}=-\frac{R_{s}}{L_{s}}i_{sd}+p{\Omega }i_{sq},\quad ~g_{i_{sd}}=-\frac{1}{L_{s}} \end{aligned}$$

By replacing the electromagnetic torque by its expression in (6) and taking the time derivative of (3), we obtain:

$$\begin{aligned} \ddot{\Omega }=\frac{\dot{T}_{m}}{J}-\frac{f\dot{\Omega }}{J}-\frac{3p{\phi }_{r}\dot{i}_{sq}}{2J} \end{aligned}$$
(14)

Taking into consideration the fact that the control algorithm needs the derivative of \(T_m\), which is a non measurable, we exploit the work in [24], and replace \(T_m\) by

$$\begin{aligned} T_{mopt}=K_{opt}{\Omega }^{2},\quad ~\hbox {with}~K_{opt}=0.5\rho {\pi }r^{5}\frac{C_{pmax}}{(G{\lambda }_{opt})^{3}} \end{aligned}$$
(15)

In order to obtain the dynamic of the rotor speed which contains the control variable \(v_{sq}\), we replace \(\dot{\Omega }\) and \(\dot{i}_{sq}\) by their expressions given, by (3) and (5) respectively:

$$\begin{aligned} \ddot{\Omega }= & {} \frac{2K_{opt}{\Omega }-f}{J^2}\big (K_{opt}{\Omega }^{2}-f{\Omega }-\frac{3p{\phi }_{r}i_{sq}}{2}\big )\nonumber \\&+\,\frac{3p{\phi }_{r}}{2JL_{s}}\big (R_{s}i_{sq}+p{\Omega }L_{s}i_{sd}-p\Omega {\phi }_{r}+v_{sq}\big ) \end{aligned}$$
(16)

Equation (16) can be rewritten as:

$$\begin{aligned} \ddot{\Omega }=f_{\Omega }+g_{\Omega }v_{sq} \end{aligned}$$
(17)

with

$$\begin{aligned} f_{\Omega }= & {} \frac{2K_{opt}{\Omega }-f}{J^2}\left( K_{opt}{\Omega }^{2}-f{\Omega }-\frac{3p{\phi }_{r}i_{sq}}{2}\right) \nonumber \\&\quad +\,\frac{3p{\phi }_{r}}{2JL_{s}}\big (R_{s}i_{sq}+p{\Omega }L_{s}i_{sd}-p\Omega {\phi }_{r}\big ),\nonumber \\&\quad \hbox {and}~g_{\Omega }=\frac{3p{\phi }_{r}}{2JL_{s}}. \end{aligned}$$

Remark 1

The control goals of the rectifier can now be viewed as a decoupling problem since \(v_{sd}\) and \(v_{sq}\) given by (13) and (17) are responsible for the d-axis current control and rotational speed control respectively. Let us denote the d-axis current and rotor speed tracking errors by

$$\begin{aligned}&e_{i_{sd}}=i_{sd}-{i}^{*}_{sd}\\&e_{\Omega }=\Omega -{\Omega }^{*} \end{aligned}$$

The errors dynamics are computed as

$$\begin{aligned}&\dot{e}_{i_{sd}}=f_{i_{sd}}+g_{i_{sd}}v_{sd}-\dot{i}^{*}_{sd} \end{aligned}$$
(18)
$$\begin{aligned}&\ddot{e}_{\Omega }=f_{\Omega }+g_{\Omega }v_{sq}-\ddot{\Omega }^{*}. \end{aligned}$$
(19)

Assuming that the rotor flux is available, let us choose the sliding manifolds [25] (\(C_{i_{sd}}>0\) and \(C_{\Omega }>0\) are tuning parameters)

$$\begin{aligned}&S_{i_{sd}}={e}_{i_{sd}}+C_{i_{sd}}\int {e}_{i_{sd}}\,dt \end{aligned}$$
(20)
$$\begin{aligned}&S_{\Omega }=\dot{e}_{\Omega }+C_{\Omega }e_{\Omega } \end{aligned}$$
(21)

and the Lyapunov candidate function

$$\begin{aligned} V=\frac{1}{2}{S}^{2}_{i_{sd}}+\frac{1}{2}S^{2}_{\Omega }. \end{aligned}$$
(22)

Computing the time derivative of V, we obtain

$$\begin{aligned} \dot{V}=S_{i_{sd}}\dot{S}_{i_{sd}}+S_{\Omega }\dot{S}_{\Omega }. \end{aligned}$$
(23)

Choosing (\(K_{v_{sd}}\) and \(K_{v_{sq}}\) are positive constants)

$$\begin{aligned} v_{sd}= & {} v_{sdeq}-K_{v_{sd}}S_{i_{sd}} \end{aligned}$$
(24)
$$\begin{aligned} v_{sq}= & {} v_{sqeq}-K_{v_{sq}}S_{\Omega } \end{aligned}$$
(25)

where

$$\begin{aligned} v_{sdeq}= & {} \frac{1}{g_{i_{sd}}}\big (\dot{i}^{*}_{sd}+C_{i_{sd}}i^{*}_{sd}-f_{i_{sd}}-C_{i_{sd}}i_{sd}\big ) \end{aligned}$$
(26)
$$\begin{aligned} v_{sqeq}= & {} \frac{1}{g_{\Omega }}\left\{ \ddot{\Omega }^{*}+C_{\Omega }\dot{\Omega }^{*}-f_{\Omega }-\frac{C_{\Omega }}{J} \right. \nonumber \\&\left. \quad \left( K_{opt}{\Omega }^{2}-f{\Omega }-\frac{3p{\phi }_{r}i_{sq}}{2}\right) \right\} \end{aligned}$$
(27)

are the unique solution of \(\dot{S}_{i_{sd}}=0\) and \(\dot{S}_{\Omega }=0\), respectively, the time derivative of V becomes

$$\begin{aligned} V=-K_{v_{sd}}S^{2}_{i_{sd}}-K_{v_{sq}}S^{2}_{\Omega }. \end{aligned}$$
(28)

Therefore, \(|S_{i_{sd}}|\rightarrow 0\) and \(|S_{\Omega }|\rightarrow 0\) exponentially and consequently \(e_{i_{sd}}\) and \(e_{\Omega }\) converge exponentially to zero.

3.4 Rotor flux estimator

In this section online estimator of the rotor flux is provided. Taking equation (15) into consideration, we rewrite (3) as follows

$$\begin{aligned} \dot{\Omega }=\frac{K_{opt}{\Omega }^{2}-f{\Omega }}{J}-\frac{3p}{2J}{\phi }_{r}i_{sq}. \end{aligned}$$
(29)

Let us consider the following observer (\(K_{1}>0\) is the positive design parameter)

$$\begin{aligned} \dot{\hat{\Omega }}=\frac{K_{opt}{\Omega }^{2}-f{\Omega }}{J}-\frac{3p}{2J}\hat{\phi }_{r}i_{sq}-v_{1},~v_{1}=K_{1}\hbox {sign}(\tilde{\Omega }).\nonumber \\ \end{aligned}$$
(30)

The estimated quantities are shown as \(\hat{x}\) while the error quantities are shown as \(\tilde{x}=\hat{x}-x\) (e.g. \(\tilde{\Omega }=\hat{\Omega }-\Omega \), \(\tilde{\phi }_{r}=\hat{\phi }_{r}-\phi _{r}\)). The dynamic of observation error can be computed using (29) and (30) as:

$$\begin{aligned} \dot{\tilde{\Omega }}= & {} -\frac{3p}{2J}\tilde{\phi }_{r}i_{sq}-v_{1} \end{aligned}$$
(31)

To achieve the design of \({\phi }_{r}\) identifier, the following additional assumption is required.

Assumption (iii) It is assumed that the following parameter identifiability condition holds: \(-\frac{3pi_{sq}}{2J}\ne 0~\forall t\ge 0\).

We now consider the following Lyapunov function candidate

$$\begin{aligned} V_{1}=\frac{1}{2}\tilde{\Omega }^{2}. \end{aligned}$$
(32)

Its time-derivative along the trajectories of (31)

$$\begin{aligned} \dot{V}_{1}= & {} -K_{1}|\tilde{\Omega }|-\frac{3p\tilde{\phi }_{r}i_{sq}}{2J}\tilde{\Omega }. \end{aligned}$$
(33)

Assuming that the estimate \(\hat{\phi }_{r}\) is bounded, let positive constant \(\xi _1\) be available such that:

$$\begin{aligned} \xi _1= & {} \left| \frac{3p\tilde{\phi }_{r}i_{sq}}{2J}\right| _m \end{aligned}$$
(34)

where \(|.|_m\) denotes the maximum value of |.|. By taking into account the above assumption and assumption (i), the following inequality holds:

$$\begin{aligned} \dot{V}_{1}\le -|\tilde{\Omega }|\left( K_{1}-\left| \frac{3p\tilde{\phi }_{r}i_{sq}}{2J}\right| \right) \end{aligned}$$
(35)

By choosing

$$\begin{aligned} K_{1}>\xi _1 \end{aligned}$$
(36)

the derivative of \(V_1\) will be negative definite \(\forall {\tilde{\Omega }}\ne 0\). Therefore, the observer error \(\tilde{\Omega }\) converges to 0 if \(K_{1}\) is chosen such that condition (36) is satisfied.

Let us now consider the following quadratic function of the rotor flux estimation error

$$\begin{aligned} V_{2}=\frac{1}{2}\tilde{\phi }^{2}_{r}. \end{aligned}$$
(37)

Its time-derivative yields

$$\begin{aligned} \dot{V}_{2}=\dot{\tilde{\phi }}_{r}\tilde{\phi }_{r} \end{aligned}$$
(38)

If we choose \(\dot{\tilde{\phi }}_{r}\) as follows (\(K_{{\phi }_{r}}>0\) is a designed parameter)

$$\begin{aligned} \dot{\tilde{\phi }}_{r}=\dot{\hat{\phi }}_{r}=-K_{{\phi }_{r}}\tilde{\phi }_{r} \end{aligned}$$
(39)

\(\dot{V}_{2}\) becomes

$$\begin{aligned} \dot{V}_{2}=-\tilde{\phi }^{2}_{r}. \end{aligned}$$
(40)

Consequently, under assumption (iii) and if the auxiliary variable \(\dot{\tilde{\phi }}_{r}\) is chosen as in (39), \(\dot{V}_{2}\) will be negative definite \(\forall {\tilde{\phi }_{r}}\ne 0\). Thus, \(\hat{\phi }_{r}\) converges to its nominal value \({\phi }_{r}\). In order to complete the identification algorithm, the implementable expression of \(\tilde{\phi }_{r}\) is required. Under condition (36) a sliding mode occurs on the manifold

$$\begin{aligned} \tilde{\Omega }=0. \end{aligned}$$
(41)

The equivalent control \(v_{1eq}\) [26] is the unique solution of \(\dot{\tilde{\Omega }}=0\). Therefore, (31) can be rewritten as

$$\begin{aligned} 0=-\frac{3p}{2J}\tilde{\phi }_{r}i_{sq}-v_{1eq}. \end{aligned}$$
(42)

We approximate \(v_{1eq}\) by using first order low-pass filter using the work of [9]. Rearranging (42), we obtain

$$\begin{aligned} \tilde{\phi }_{r}=\frac{v_{1eq}}{-\frac{3p}{2J}i_{sq}},\quad \hbox {with}~v_{1eq}=\frac{v_{1}}{1+{\tau }_1s}. \end{aligned}$$
(43)

Finally the overall control algorithm taking into account the interconnection between the d-axis current and rotor speed controllers as well as the rotor flux estimator is given by the set of the following Eqs. (44–53).

$$\begin{aligned}&v_{sd}=v_{sdeq}-K_{v_{sd}}S_{i_{sd}},~v_{sq}=v_{sqeq}-K_{v_{sq}}S_{\Omega } \end{aligned}$$
(44)
$$\begin{aligned}&S_{i_{sd}}={e}_{i_{sd}}+C_{i_{sd}}\int {e}_{i_{sd}}\,dt,~S_{\Omega }=\dot{e}_{\Omega }+C_{\Omega }e_{\Omega } \end{aligned}$$
(45)
$$\begin{aligned}&{e}_{i_{sd}}=i_{sd}-{i}^{*}_{sd},~{e}_{\Omega }=\Omega -{\Omega }^{*} \end{aligned}$$
(46)
$$\begin{aligned}&v_{sdeq}=\frac{1}{g_{i_{sd}}}\big (\dot{i}^{*}_{sd}+C_{i_{sd}}i^{*}_{sd}-{f}_{i_{sd}}-C_{i_{sd}}i_{sd}\big ) \end{aligned}$$
(47)
$$\begin{aligned}&v_{sqeq}=\frac{1}{\hat{g}_{\Omega }}\left\{ \ddot{\Omega }^{*}+C_{\Omega }\dot{\Omega }^{*}-\hat{f}_{\Omega }-\frac{C_{\Omega }}{J}\left( K_{opt}{\Omega }^{2}-f{\Omega }\right. \right. \nonumber \\&\left. \left. ~~~~~~~~~~~-\,\frac{3p\hat{{\phi }}_{r}i_{sq}}{2}\right) \right\} ,\quad ~\hat{g}_{\Omega }=\frac{3p\hat{{\phi }}_{r}}{2JL_{s}} \end{aligned}$$
(48)
$$\begin{aligned}&{f}_{i_{sd}}=-\frac{{R}_{s}}{L_{s}}i_{sd}+p{\Omega }i_{sq},\quad ~g_{i_{sd}}=-\frac{1}{L_{s}} \end{aligned}$$
(49)
$$\begin{aligned}&\hat{f}_{\Omega }=\frac{2K_{opt}{\Omega }-f}{J^2}\big (K_{opt}{\Omega }^{2}-f{\Omega }-\frac{3p\hat{{\phi }}_{r}i_{sq}}{2}\big )\nonumber \\&~~~~~~+\frac{3p\hat{{\phi }}_{r}}{2JL_{s}}\big ({R}_{s}i_{sq}+p{\Omega }L_{s}i_{sd}-p\Omega \hat{{\phi }}_{r}\big ), \end{aligned}$$
(50)
$$\begin{aligned}&\dot{\hat{\Omega }}=\frac{K_{opt}{\Omega }^{2}-f{\Omega }}{J}-\frac{3p}{2J}\hat{\phi }_{r}i_{sq}-v_{1} \end{aligned}$$
(51)
$$\begin{aligned}&\dot{\tilde{\phi }}_{r}=\dot{\hat{\phi }}_{r}=-K_{{\phi }_{r}}\tilde{\phi }_{r},~\tilde{\phi }_{r}=\tilde{\phi }_{r}=\frac{v_{1eq}}{-\frac{3p}{2J}i_{sq}} \end{aligned}$$
(52)
$$\begin{aligned}&v_{1}=K_{1}\hbox {sign}(\tilde{\Omega }),~v_{1eq}=\frac{v_{1}}{1+\tau _{1}s}. \end{aligned}$$
(53)

3.5 DC-bus voltage regulation

In order to regulate the dc-link voltage, a PWM DC–DC converter feeding an electronic load is proposed. This consists of an insulated gate bipolar transistor (IGBT) operating as a chopper connected in series with a dump load resistance \(R_E\). This dump load is designed such that when the duty cycle of the chopper is unity (during fault or over-generation), it should consume the maximum output power of the generator (Fig. 2).

Following the same reasoning as in the case of d-axis current and rotor speed control design, we rewrite (10) as:

$$\begin{aligned} \dot{u}= & {} f_{u}+g_{u}v_{u}~\hbox {with}~ \nonumber \\ f_{u}= & {} \frac{3p\Omega {\phi }_{r}}{C}i_{sq}-\frac{2P_i}{C},~g_{u}=-\frac{2}{CR_E},~v_{u}=Su, \end{aligned}$$
(54)

and derive the control signal responsible of dc voltage regulation as (\(K_u>0\)):

$$\begin{aligned} \begin{aligned} v_{u}&=v_{ueq}-K_{u}S_u,\quad ~v_{ueq}=\frac{1}{g_{u}}\big (\dot{u}^*-f_{u}\big ),\\ S_{u}&=e_{u},\quad ~e_{u}=u-u^*,\quad ~u^*=v^{*2}_{dc}. \end{aligned} \end{aligned}$$
(55)

The detailed structure of the proposed adaptive nonlinear controller (NLC) is shown in Fig. 3.

Fig. 2
figure 2

Structure of the proposed adaptive nonlinear controller

Full size image
Fig. 3
figure 3

Structure of inverter PI control

Full size image
Fig. 4
figure 4

Structure of the PI controller

Full size image
Fig. 5
figure 5

Performance under wind speed and load variations when PMSG WT parameters are assumed to be constant. a Case of the PI regulator. b Case of the proposed nonlinear controller (NLC). i—Stator d-axis current, ii—stator q-axis current, iii—turbine torque, iv—electromagnetic torque

Full size image
Table 1 PMSG parameters
Full size table

3.6 Inverter side control

The purpose of the inverter control is to regulate the amplitude and frequency of the load voltage. In this work, this task is achieved by a conventional PI controller that regulates the dq-components of the load voltage. The state equations used to design the controller in the (d, q) reference frame are given by [27]:

$$\begin{aligned}&\dot{i}_{fd}=-\frac{R_{f}}{L_{f}}i_{fd}+{\omega }_{L}i_{fq}+\frac{v_{id}}{L_{f}}-\frac{v_{d}}{L_{f}} \end{aligned}$$
(56)
$$\begin{aligned}&\dot{i}_{fq}=-\frac{R_{f}}{L_{f}}i_{fq}-{\omega }_{L}i_{fd}+\frac{v_{iq}}{L_{f}}-\frac{v_{q}}{L_{f}} \end{aligned}$$
(57)
$$\begin{aligned}&\dot{v}_{d}=\frac{i_{fd}}{C_{f}}+{\omega }_{L}v_{q}-\frac{i_{Ld}}{C_{f}} \end{aligned}$$
(58)
$$\begin{aligned}&\dot{v}_{q}=\frac{i_{fq}}{C_{f}}-{\omega }_{L}v_{d}-\frac{i_{Lq}}{C_{f}} \end{aligned}$$
(59)

where \(R_{f}\), \(L_{f}\) and \(C_{f}\) are the filter resistance, inductance and capacitance respectively. The dq-voltages controller block along with the required input signals and their associated output signals are depicted in Fig. 4. It is worth mentioning that, it is the imposed value of \({\omega }_{L}\) which helps to regulate the frequency of the load voltage through (d, q)–(a, b, c) reference frame transformation.

4 Simulation results and discussion

The effectiveness of the proposed adaptive nonlinear control algorithm has been verified by numerical simulation using Matlab/Simulink software environment. The parameters of PMSG, taken from [28], are listed in Table 1. This particular high number of poles PMSG is suitable for gearless-drive WT. However, to deal with flexible transmission which is more realistic, a gearbox ratio \(G=1.2\) has been considered in this work.

Fig. 6
figure 6

Performance under wind speed and load variations when PMSG WT parameters are assumed to be constant. i—Wind speed profile, ii—rotor speed, iii—power coefficient, iv—dc-bus voltage

Full size image
Fig. 7
figure 7

Performance under wind speed and load variations when PMSG WT parameters are assumed to be constant. a i—rotor speed tracking error, ii—dc-bus voltage tracking error, iii—stator phase\(-a\) current, b i—load \(d-\)axis voltage, ii—load \(q-\)axis voltage, iii—load \(d-\)axis voltage tracking error

Full size image

For comparison, simulations using conventional Proportional Integral (PI) control method are carried out. The structure of the PI control method is shown in Fig. 2. The control gains used for all simulations are given as follows. Direct axis current and rotor speed control: \(C_{i_{sd}}=10\), \(K_{v_{sd}}=30\), \(C_{\Omega }=190\) and \(K_{v_{sq}}=0.6\); flux estimation and dc voltage control: \(K_{1}=10\), \(K_{{\phi }_r}=8000\) and \(K_{u}=0.5\). Rectifier PI controller: current regulation \(\hbox {PI}_{sd}\): \(K_P=33\), \(K_I=3425\); \(\hbox {PI}_{sq}\): \(K_P=33\), \(K_I=3425\); speed regulation: \(K_P=11\), \(K_I=61\). Inverter control: current regulation \(\hbox {PI}_{d}\): \(K_p=15\), \(K_I=0.8\); \(\hbox {PI}_{q}\): \(K_I=15\), \(K_I=0.8\); voltage regulation: \(\hbox {PI}_{d}\): \(K_P=1\), \(K_I=0.5\); \(\hbox {PI}_{q}\): \(K_P=0.4\), \(K_I=50\); load voltage frequency: \(\omega _L=100{\pi }~\hbox {rad/s}\).

In all simulations a wind profile which starts with low wind speeds and ends with high wind speeds has been used. For \(0{\le }t{\le }4\,\hbox {s}\) the mean value of the wind speed profile is \(6.5\,\hbox {m/s}\) while for \(4\,\hbox {s}{\le }t{\le }6\,\hbox {s}\), this value is \(9.5\,\hbox {m/s}\). To test the robustness of the control scheme face to different types of loads in all simulations, the control system starts with a capacitive load (RC) at time \(t=0\,\hbox {s}\). At time \(t=1.5\,\hbox {s}\), sudden change, from capacitive load to inductive load (RL), is performed. Finally, at time \(t=2.5\,\hbox {s}\), instantaneous variation from inductive load to capacitive-inductive load (RLC) is realized. The values of different loads have been chosen as follows: \(R=250\,{\Omega }\), \(L=50\,\hbox {mH}\) and \(C=30\,\upmu \hbox {F}\).

Fig. 8
figure 8

Performance under wind speed and load variations when PMSG WT parameters are assumed to be constant. Zoom during transients on: i—rotor speed tracking error, ii—power coefficient, iii—dc-bus voltage tracking error

Full size image
Fig. 9
figure 9

Performance under wind speed, load and PMSG WT electrical parameters variations (parameters variations occurred simultaneously at time \(t=1s\) with \(+100\,\%\) for \(R_s\), \(+50\,\%\) for \(L_s\) and \(-20\,\%\) for \({\phi }_r\)). a i—Wind speed profile, ii—rotor speed tracking error, iii—power coefficient, iv—dc-bus voltage tracking error, \(v-\)Rotor flux. Zoom during transients on: b i—rotor speed tracking error, ii—power coefficient, iii—dc-bus voltage tracking error

Full size image
Fig. 10
figure 10

Performance under wind speed, load and PMSG-WT parameters variations (parameters variations occurred simultaneously at time \(t=1s\) with \(+100\,\%\) for \(R_s\), \(+50\,\%\) for \(L_s\), \(-20\,\%\) for \({\phi }_r\) and \(+30\,\%\) for J). a i—Wind speed profile, ii—rotor speed tracking error, iii—power coefficient, iv—dc-bus voltage tracking error, v—Rotor flux. Zoom during transients on: b i—rotor speed tracking error, ii—power coefficient, iii—dc-bus voltage tracking error

Full size image

The set of Figs. 5, 6, 7 and 8 shows simulation results under nominal values of PMSG WT parameters. It can be seen from Fig. 5 that the generator d-axis current converges rapidly to zero. It is visible from Figs. 6 and 7 that the rotor speed converges to its optimal reference and the power coefficient is near the maximum value indicating the achievement of maximum power transfer for wind speed variation. From these figures, one can also notice that the dc voltage tracks its constant reference \(540\,\hbox {V}\) and the load voltage amplitude is properly regulated at \(311\,\hbox {V}\). It is clearly observable in Fig. 8 that during transition periods, the proposed controller presents smaller response times and less overshoot values compared to the results obtained using PI control method.

In Fig. 9, the electrical parameters variation of PMSG is performed from time \(t=1\,\hbox {s}\). The stator resistance, the stator inductance and the rotor flux are simultaneously changed up to \(+100\), \(+50\) and \(-20\,\%\) respectively from their nominal values. It is seen on Fig. 9a that the rotor flux estimate converges to its nominal value. One can notice that the tracking errors have increased under these variations in the case of (see Fig. 9b) PI controller while the proposed nonlinear controller still presents good performance.

Figure 10, shows simulation results obtained when the WT inertia is changed up to \(+30\,\%\), simultaneously with PMSG electrical parameters variations. It is observed on Fig. 10a that these variations do not affect the rotor fux estimation. It can be clearly seen from Fig. 10b that the proposed control method provides better performance during transitions periods than the PI control method.

5 Conclusion

In this paper, a nonlinear control strategy is developed for a stand-alone PMSG WT system under variable wind speed. A DC–DC converter feeding an electronic load has been added in parallel to a three phase PWM rectifier to control the dc-bus voltage. An adaptive sliding mode control strategy has been developed to regulate the direct axis current, ensure maximum power tracking issue as well dc-bus voltage regulation. The amplitude and frequency of the stand-alone load voltage are regulated through a three phase PWM inverter. The simulation results have shown that the performances of the proposed adaptive control strategy are satisfactory given the global system convergence and robustness with respect to load variations and parameters uncertainties. The proposed adaptive control can be used in remote area where wind speed is low.