1 Introduction

Over the past few decades, the world has rapidly shifted toward renewable energy sources, recognized for their cleanliness and stability. Various technologies based on renewable sources can be employed, with solar power emerging as one of the most commonly utilized options. Solar energy has a wide range of applications, including electricity generation, heating and cooling. Solar energy is pivotal in fostering a sustainable future, providing a clean power that reduces environmental impact and mitigates the reliance on fossil fuels. Harnessing solar power is not just an option; it's a crucial step toward cultivating a more environmentally sustainable planet. Solar radiation can be converted into electricity through photovoltaic panels or into heat using thermal collectors [1]. Photovoltaic panels can achieve electricity production efficiencies ranging from 5 to 20% [2], while solar thermal collectors can reach thermal efficiencies up to 83% [3]. However, the performance of photovoltaic solar panels is notably influenced by the cell’s temperature. Raising the temperature, particularly beyond 50°C during the process of converting solar radiation into electricity, leads to a decline in the electrical efficiency of the collector. This decline fluctuates between 0.4 and 0.65% for every additional degree of the PV cells temperature [4, 5]. Hence, it is highly recommended to incorporate an effective cooling process for photovoltaic cells. This not only enhances the efficiency of solar panels by maintaining cell’s temperature at an acceptable level but also protect them from the harmful effects of high operating temperatures. Therefore, hybrid photovoltaic thermal PVT solar systems emerge as an ideal configuration to meet these criteria by seamlessly integrating both solar thermal conversion process and solar photovoltaic features. In this system, the fluid flow working as a coolant, and at the same time, it gains more heat to produce thermal energy.

Many researchers worldwide are actively working to improve the performances of PVT systems by exploring various methods to optimize heat extraction for the working fluid. This optimization is crucial for maintaining photovoltaic cells at an acceptable operating temperature, leading to an increased PVT’s efficiency. In this context, Alfegi et al. [6] developed a numerical model for a double-pass solar air collector PVT with attached fins behind the photovoltaic panel. The viability of this model has been confirmed through experimental validation using relevant data. The obtained results indicate that the incorporation of these fins resulted in a decrease in the temperature of the photovoltaic cells, thereby enhancing their electrical efficiency. Moreover, the effect of passing cold air through rectangular tubes on the efficiency of a PVT was studied by Jin et al. [7]. Their results showed that as the air flow increases, the temperature of the photovoltaic cells decreases, resulting in higher efficiencies. Moreover, they also indicated that the efficiencies of a hybrid solar collector utilizing rectangular tubes notably surpass those of a solar collector without tubes.

Boulfaf et al. [8] presented a mathematical model utilizing the finite element approach to investigate the impact of various parameters, including fluid mass flow rate, ambient temperature, solar radiation, and collector length, on the performances of a hybrid solar collector PVT. They found that an increase in received solar radiation and ambient temperature led to a decrease in electrical efficiency, while the thermal efficiency is notably improved with the increase in collector length.

To study the overall performances of a PVT collector, Pauly et al. [9] proposed a numerical model based on ANSYS-FLUENT environment and compared the simulation results with real operating data from the literature. Good agreement between the two datasets has been reached. Moreover, the incorporation of a novel design in the considered PVT system, which features a variable cross-sectional duct, resulted in a 20% improvement in the global efficiency compared to the conventional configuration.

On the other hand, many researchers have incorporated nanoparticles in the working fluid as another way to enhance the cooling proves of photovoltaic cells [10,11,12,13,14]. The addition of nanoparticles significantly amplifies the heat capacity of the coolant and augments the heat exchange rate, as indicated by Maghsoudi and Siavashi [15]. In this regard, an experimental study was performed by Sangeetha et al. [16] to investigate the effect of using nanofluids in the cooling process of the PVT system. Thus, three different nanofluids were suggested; MWCNT, Al2O3, and TiO2. The results showed a rise in both generated power and electrical efficiency of the studied system between 25–45% and 27–47%, respectively (There are three nanofluids, consequently three efficiencies). Another experimental analysis of employing nanofluids in PVT systems was conducted by Kang et al. [17]. They conducted estimations and comparisons of efficiencies between flat-plate and U-tube solar collectors utilizing Al2O3 as the coolant, with those operating with water. The analysis results revealed that solar collectors utilizing flat plate and U-tube designs, when working with this nanofluid, can achieve higher thermal efficiencies. Specifically, there was an increase of 14.8% for the flat plate layout and 10.7% for the U-tube layout compared to those operating with water. Moreover, Sardarabadi et al. [18] conducted an experimental study to examine the effects of employing water and a nanofluid at two concentrations (1% and 3%) on the performances of a PVT solar collector. Their findings demonstrated an improvement in the global efficiency of the PVT system, revealing an increase of 3.6% and 7.9%, respectively, for the two concentrations of the chosen nanofluid compared to that of the collector utilizing pure water as the coolant. Karamiand Rahimi [19] carried out an experimental comparison between the utilization of a nanofluid; Boehmite (AlOOH.xH2O) and water in a PVT system containing straight and helical cooling channels. Their results confirmed that the use of Boehmite nanofluid instead of water provides a better cooling performance of the PVT system. In particular, the electrical efficiency experienced a notable increase, with a rise of 20.57% for the straight channel and 37.67% for the helical channel. Rubbi et al. [20] introduced two-dimensional (2D) MXene (Ti3C2) and Thermino l55 oil-based mono and hybrid nanofluids designed for concentrated photovoltaic/thermal (CPV/T) solar systems. Their study centers on the experimental formulation, characterization of properties, and the performance assessment of the CPV/T system utilizing nanofluids. Thermo-physical properties, including conductivity, viscosity, and rheology, along with optical properties (UV–vis and FT-IR), and stability properties (Zeta potential and TGA) of the formulated nanofluids are thoroughly characterized within the concentration range from 0.025  to 0.125 wt. %. Numerical simulations were conducted to assess the impact of experimentally evaluated nanofluids on a CPV/T collector, employing a three-dimensional transient model. The analyses show enhancements in the CPV/T system, along with beneficial cooling effects. Specifically, under a concentrated solar irradiance of 5000 W/m2 and an optimized flow rate of 3 L/min, the most substantial improvements in thermal and electrical efficiencies were identified at 12.8% and 2%, respectively.

Besides, the incorporation of phase change materials (PCMs) can substantially improve the performance of PVT solar collectors. These materials actively contribute to the cooling of the photovoltaic panels within the system by storing thermal energy for extended durations [21]. Accordingly, many works have been presented in the literature in this direction. Hasan et al. [22] used five types of PCM in a PVT collector whose melting point ranged between 21 and 29 C°. The results indicated that hydrated calcium chloride salt had the most effective cooling performance, resulting in an average temperature reduction of 10°C on photovoltaic panels. Furthermore, an experimental study was conducted by Choubineh et al. [23] to enhance the cooling performance of the PVT air solar collector by incorporating a layer of a PCM (Salt Hydrates) with a thickness of 6 mm behind the PV solar panel. Their results revealed that the temperature of the PV panel is decreased by about 3.7 to 4.3 °C with the new layout. In another study, Hasan et al. [24] incorporated a layer of a PCM on the back side of a photovoltaic collector. Once again, adding a layer of phase change material (PCM) improved the cooling process of the cells. The temperatures of both the front and the back surfaces of the PV panel have decreased by 12.3°C and 22.6°C, respectively. Additionally, an increase in power production was noted, with peak and mean values rising by 7.2% and 5.5%, respectively. Sardarabadi et al. [25] innovatively combined nanoparticles (ZnO/water) with PCM (Parafin) in the cooling mechanism for the PVT system. They established two models of PVT system: the first model integrating nanoparticles and PCM, while the second is a comparative model employing water as a reference case. Their results show that the simultaneous use of PCM materials and nanoparticles will raise the electrical efficiency by 13% compared to the PVT reference system.

Nowadays, numerous researchers are introducing porous medium as an innovative technique to enhance the cooling process of thermal conversion systems [26,27,28,29,30]. The incorporation of porous medium enhances the heat exchange rates and increases the thermal performance of the cooling medium. In this regard, some works have been performed on the application of this technology in solar collectors. Ahmed et al. [31] introduced glass ball porous media to the bottom pass behind the photovoltaic panels in an experimental setup. They found that the incorporation of a porous medium and a glass cover can raise the global efficiency of the PVT collector by 3%, and raises the thermal efficiency of the PVT up to 80.23%. Moreover, Abed et al. [32] confirmed the positive effect of integrating the same porous medium (glass balls) on both electrical and thermal efficiencies of these systems. Two experimental units of the PVT system were constructed: one incorporating porous media, while the other operates without porous media. The experimental setup with porous media demonstrated increase in both electrical and global efficiencies of the PVT collector by 2.2% and 11.36%, respectively, compared to the setup without porous media. Rad et al. [33] presented an experimental investigation on the feasibility of integrating a porous media and a phase change material in PVT systems. The porous media is represented by aluminum shavings, while the PCM is represented by hydrated salt. A decrease in the PV surface temperature by 24 degree was recorded. Furthermore, an increase rates of 2.5% and 4.34% were reached for both electrical and exergy efficiencies of the collector, respectively. Tahmasbi et al. [34] performed simulations under ANSYS-FLUENT environment to study the effect of different variables including solar radiation, thickness of porous layer made of aluminum, and coolant flow rates on the performances of a PVT solar collector. The analysis results revealed a 4% improvement in electrical efficiency with the use of porous media. On the other hand, increasing the thickness of the porous layer beyond half of the channel height raises pressure inside the channel and enhances the thermal efficiency. However, this increase negatively impacts the electrical efficiency of the system. Mustafa et al. [35] studied numerically the impact of the positioning of porous metal foam on the performance of a PVT system. In their investigation, the porous foam was placed in three different positions: underside the photovoltaic panel, above the back-insulation wall, and in both positions simultaneously. These layouts were compared with the classic PVT system without porous foam. The results showed that the overall energy efficiency of the studied layouts varied from 61.53 to 111.49%, while the overall exergy efficiency ranged between 14.18 and 17.46%. Another study, presented by Salman et al. [36], investigated experimentally and numerically the impact of various factors, including coolant mass flow rate, solar radiation and porosity of the added porous media, on the performances of the PVT. Water is used as the working fluid, and the channel is fully filled with plastic metal beads as the porous media. The results disclosed that the use of porous media decreases the surface temperature of the panel by about 9–14 °C. Conversely, increasing the porosity of porous media and the mass flow rate contributes to a further reduction in the surface temperature of the solar panel. Furthermore, Variji et al. [37] conducted a numerical investigation on the influence of incorporating metal foam on heat transfer and electrical efficiency of PV-PCM systems. The study involved a comparative analysis of metal foam porosity ranging from 0.7 to 0.9. Additionally, various inclination angles, from 0° to 90° were examined to assess their impact on natural convection enhancement through liquid PCM. The findings revealed that an increased inclination angle improved natural convection of molten PCM and enhanced heat transfer through the PCM. Furthermore, the results demonstrated an increase of 6.8% in average temperature and 9.8% in electrical efficiency when employing metal foam with a porosity of 0.9 compared to the PV-PCM system. Recently, Khelifa et al. [38] conducted an in-depth numerical analysis on the thermal performance of a PVT solar collector integrated with flax fibers as natural porous materials. The study extensively explored the impact of porous layer thickness (5–50 mm), solar flux (50–1000 W/m2), and coolant flow rate (0.40–1.0 m/s). Utilizing ANSYS software, Navier Stokes equations, and the Darcy-Brinkman-Forchheimer porous model, simulations were performed to determine the optimized thickness of the porous material and the cooling fluid flow rate for maximizing photovoltaic panel performance. The results indicated that the best cooling approach was achieved by incorporating a 50 mm thick porous flax fiber layer with a cooling water flow rate of 0.907 m/s, showing a remarkable 173.46% improvement in Nusselt number compared to using pure water alone under similar conditions. The thermal efficiencies of the PVT system were found to be 69.58%, 50.02%, and 34.60% with water and flax fibers, pure water, and air as coolants, respectively.

Drawing from the previous literature review and to the best of our knowledge, several numerical and experimental works have sought to optimize PVT systems, aiming to improve their efficiency using various techniques centered on the forced convection of the coolant. Notably, these investigations overlooked the natural convection impact, which becomes particularly crucial when air serves as the working fluid and the solar collector operates at specific tilt angles. Conversely, it is well known that the impact of this phenomenon is not a novel concept, previously studied within cavities and channels [39, 40], where its impact notably results in a significant increase in fluid velocity within systems, thereby facilitating their cooling process. Thus, neglecting this phenomenon could introduce inaccuracies in evaluating the performance of the PVT solar collector. Consequently, the main novelty of this paper is to numerically investigate the impact of the coupling between the natural and forced convection on the PVT solar collector performances with an integrated porous layer. In this regard, this study aims to discuss the impact of multiple parameters such as panel tilt angle (α), buoyancy force (Ri), thickness of porous layer (Ep) and Darcy number (Da) on the performances of a PVT solar collector including its thermal and electrical efficiencies.

2 Data and methodology

2.1 Physical model

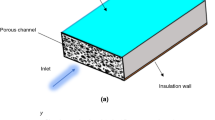
The present study concerns a numerical analysis of an inclined solar PVT system working with air as a coolant.

As shown in Fig. 1, the PVT system consists of a PV panel without a glass-cover, which is connected to a channel where air is circulating to cool down the panel and gain the heat for heating and cooling applications. To increase the heat transfer rate by conduction, a porous layer (metal foams) is added to the bottom surface of the PVT solar panel. Different specifications of the considered PVT system including its dimensions are given in Table 1. Furthermore, Table 2 outlines the main thermal properties of the materials used in the considered PVT solar collector.

Fig. 1
figure 1

Schematic of the studied PVT solar collector

Full size image
Table 1 Specifications of the studied PVT
Full size table
Table 2 Thermal properties of the studied PVT [34]
Full size table

2.2 Governing equations

In order to perform the simulations in the present study, the following main assumptions have been made:

  • The fluid flow is considered laminar, steady-state, incompressible and Newtonian.

  • Solar radiation is considered to be constant and perpendicular to the photovoltaic panel.

  • The porous medium is homogeneous and isotropic.

  • Local thermal equilibrium assumption (LTE) between the two phases of the porous medium is considered valid.

  • The thermo-physical proprieties are assumed to be uniform and constant, except the air-density, which is approximated by the Boussinesq equation (Eq. 1).

  • The bottom surface of the channel is considered adiabatic (isolated).

    $$ \rho = \rho_{0} \left[ {1 - \beta_{T} \left( {T - T_{0} } \right)} \right] $$
    (1)

Under the above assumptions, the mathematical model developed to simulate the mixed convection in the entire channel is as follows [41, 42]:

Continuity equation:

$$ u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = {0} $$
(2)

x—component of momentum equation:

$$ \frac{{\rho_{f} }}{{\varepsilon^{2} }}\left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right) = - \frac{\partial p}{{\partial x}} + \frac{\mu }{\varepsilon }\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) \, - \delta \left( {\frac{\mu }{{\text{K}}}u + \frac{{{\text{CF}}}}{{\sqrt {\text{K}} }}\rho_{f} u\sqrt {u^{2} + v^{2} } } \right) + \rho_{f} g\beta_{f} (T - T_{0} )\sin (\alpha ) $$
(3)

y—component of momentum equation:

$$ \frac{{\rho_{f} }}{{\varepsilon^{2} }}\left( {u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}}} \right) = - \frac{\partial p}{{\partial y}} + \frac{\mu }{\varepsilon }\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) \, - \delta \left( {\frac{\mu }{{\text{K}}}v + \frac{{{\text{CF}}}}{{\sqrt {\text{K}} }}\rho_{f} v\sqrt {u^{2} + v^{2} } } \right) + \rho_{f} g\beta_{f} (T - T_{0} )\cos (\alpha ) $$
(4)

Energy equation for the channel

$$ u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{k}{{\rho_{f} Cp}}\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) \, $$
(5)

Energy equation for the PV cells:

$$ 0 = \frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }} $$
(6)

where

$$ k = \left\{ \begin{gathered} k_{f} {\text{ in fluid medium}} \hfill \\ k_{eff} {\text{ in porous medium}} \hfill \\ \end{gathered} \right. $$
$$ k_{eff} \, = \varepsilon k_{f} + (1 - \varepsilon )k_{s} $$

In the fluid zone: \(\delta = { 0, }\varepsilon \, = { 1}\).

In the porous zone: \(\delta = { 1, }\varepsilon \, = { 0}{\text{.9}}\).

\(\varepsilon , \, \rho {, }\mu {, }K{\text{, and F}}\), represent porosity, density, kinematic viscosity, permeability, and Forchheimer number, respectively. Moreover,\(k_{eff} ,k_{f} {\text{ and }}k_{s}\) denote effective thermal conductivities of the porous medium, as well as the thermal conductivity of the fluid and the solid phases, respectively.

In addition, the thermal and dynamic boundary conditions of the present study are described in Table 3. Furthermore, the dimensionless form of the above equations (Eqns. (2), (3), (4), (5) and (6) is used to simplify the numerical calculations and reduce the number of parameters. Thus, the dimensionless variables which are used for the sake of writing the governing equations in dimensionless forms are below:

$$ (X,Y, \, Ep) = {{(x,y, \, h_{p} )} \mathord{\left/ {\vphantom {{(x,y, \, h_{p} )} {H, \, (U, \, V) = {{\left( {u, \, v} \right)} \mathord{\left/ {\vphantom {{\left( {u, \, v} \right)} {U_{{\text{int}}} , \, \theta }}} \right. \kern-0pt} {U_{{\text{int}}} , \, \theta }}}}} \right. \kern-0pt} {H, \, (U, \, V) = {{\left( {u, \, v} \right)} \mathord{\left/ {\vphantom {{\left( {u, \, v} \right)} {U_{{\text{int}}} , \, \theta }}} \right. \kern-0pt} {U_{{\text{int}}} , \, \theta }}}} = k_{f} {{\left( { \, T - T_{{\text{int}}} } \right)} \mathord{\left/ {\vphantom {{\left( { \, T - T_{{\text{int}}} } \right)} {Q_{U} H}}} \right. \kern-0pt} {Q_{U} H}}, \, P = {p \mathord{\left/ {\vphantom {p {\rho_{f} U_{{\text{int}}}^{2} }}} \right. \kern-0pt} {\rho_{f} U_{{\text{int}}}^{2} }} $$
(7)
Table 3 Dimensional thermal and dynamic boundary conditions
Full size table

These dimensionless variables are substituted into Eqs. (2–6) to obtain the governing equations in the dimensionless forms as:

Continuity equation:

$$ U\frac{\partial U}{{\partial X}} + V\frac{\partial U}{{\partial Y}} = {0} $$
(8)

Momentum equations:

$$ \frac{1}{{\varepsilon^{2} }}\left( {U\frac{\partial U}{{\partial X}} + V\frac{\partial U}{{\partial Y}}} \right) = - \frac{\partial P}{{\partial X}} + \frac{{R_{\mu } }}{{\text{Re}}}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) \, - \delta \left( {\frac{1}{{{\text{ReDa}}}}U + {\text{F}}U\sqrt {U^{2} + V^{2} } } \right) + Ri\theta \sin (\alpha ) $$
(9)
$$ \frac{1}{{\varepsilon^{2} }}\left( {U\frac{\partial V}{{\partial X}} + V\frac{\partial V}{{\partial Y}}} \right) = - \frac{\partial P}{{\partial Y}} + \frac{{R_{\mu } }}{{\text{Re}}}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) \, - \delta \left( {\frac{1}{{{\text{ReDa}}}}V + {\text{F}}V\sqrt {U^{2} + V^{2} } } \right) + Ri\theta \cos (\alpha ) $$
(10)

Energy equation for the channel:

$$ U\frac{\partial \theta }{{\partial X}} + V\frac{\partial \theta }{{\partial Y}} = \frac{Kr}{{\Pr {\text{Re}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right) \, $$
(11)

Energy equation for the PV cells:

$$ 0 = \frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }} $$
(12)

where;

$$ {\text{Re}} = \frac{{HU_{{\text{int}}} }}{\upsilon }{\text{ , Da }} = \frac{K}{{H^{2} }},{\text{ Ri}} = \frac{g\beta \Delta TH}{{\upsilon^{2} }},{\text{ Pr}} = \frac{\mu Cp}{{k_{f} }},{\text{ F}} = \frac{{{\text{C}}_{{\text{F}}} {\text{H}}}}{{\sqrt {\text{K}} }}{ , }\Delta T = \frac{{Q_{U} {\text{H}}}}{{k_{f} }}, \, Kr = \frac{{k_{eff} }}{{k_{f} }},{\text{ R}}_{\mu } = \frac{{\mu_{eff} }}{{\mu_{f} }} $$

Furthermore, the dimensionless boundary conditions of this problem can be expressed as:

Bottom wall;

\(U = V = 0,\) \(\frac{\partial \theta }{{\partial Y}} = 0\)

Top wall;

\(U = V = 0,\) \(\frac{\partial \theta }{{\partial Y}} = \frac{ - 1}{{Rk_{c} }}\)

Inlet;

\(U = 1, \, V = 0, \, \theta = {0}\)

Outlet;

\(\frac{\partial U}{{\partial X}} = 0, \, V = {0, }\frac{\partial \theta }{{\partial X}} = 0\)

Cell/porous interface;

\(U = V = 0, \, \theta_{{\text{c}}} = \theta_{p} , \, \left( {\frac{\partial \theta }{{\partial Y}}} \right)_{c} = \frac{{k_{eff} }}{{k_{c} }}\left( {\frac{\partial \theta }{{\partial Y}}} \right)_{p}\)

Porous /fluid interface;

\(U_{f} = U_{p} , \, V_{f} = V_{p} , \, \theta_{f} = \theta_{p} ,\)\(\left( {\frac{\partial U}{{\partial Y}} + \frac{\partial V}{{\partial Y}}} \right)_{f} = {\text{R}}_{\mu } \left( {\frac{\partial U}{{\partial Y}} + \frac{\partial V}{{\partial Y}}} \right)_{p}\)

\( \, \left( {\frac{\partial \theta }{{\partial Y}}} \right)_{f} = Kr\left( {\frac{\partial \theta }{{\partial Y}}} \right)_{p}\)

Moreover, the performances of the studied system can be evaluated considering both thermal and electrical efficiencies expressions. The thermal efficiency of this system is modeled by [43]:

$$ \, \eta_{Th} = \frac{{Q_{u} }}{{IA_{c} }} $$
(13)

where \(Q_{u}\) is the useful heat energy transferred to the coolant which could be expressed as the following:

$$ Q_{u} = \dot{m} \times Cp \times \left( {T_{Outlet} - T_{{\text{int}}} } \right) $$
(14)

With \(Cp, \, T_{{\text{int}}}\) and \(T_{Outlet}\) presents specific heat, and average inlet and outlet temperatures of the working fluid, respectively. Moreover, the mass flow rate \(\left( {\dot{m}} \right)\) can be calculated as;

$$ \dot{m} = \rho \times H \times U_{{\text{int}}} $$
(15)

With the inlet velocity \(\left( {U_{{\text{int}}} } \right)\) depends on the Reynolds number value.

On the other hand, the electrical efficiency of the PV panel can be written as [44]:

$$ \, \eta_{Et} = \eta_{ref} \left( {1 - \beta_{0} \left( {T_{PV} - 298} \right)} \right) $$
(16)

where \(\eta_{ref}\) is the electrical efficiency of the PV panel under reference states, and \(\beta_{0}\) is the power temperature coefficient which are given in Table 1, while \(T_{PV}\) is the average PV cells temperature.

3 Numerical analysis and code validation

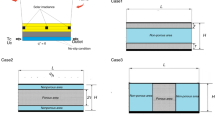
An in‐house FORTRAN computer code is developed based on the finite volume method is used to solve the equations of momentum, energy, and continuity, while the SIMPLER algorithm to handle the pressure–velocity coupling. To study the autonomy between the numerical results and the mesh, a range of non-uniform grid points, namely, 1100, 2800, 7200, 12,000, 18,000, 24,000 and 30,000, is used (Fig. 2). As shown in Fig. 3, no significant variations in fluid outlet temperature and PV cells temperature are observed for a grid size superior than 36,000 points. Consequently, the mesh of 18,000 nodes (60 × 300) is chosen to investigate the current problem. In order to ensure the accuracy of our FORTRAN computer code, two comparisons are chosen. The first comparison is realized with the numerical data of Hooman [45] for the case of forced convection in a fully horizontal porous channel. As illustrated in Fig. 4, a good agreement is observed between our U-velocity profiles and those presented by Hooman [45].

Fig. 2
figure 2

The structured mesh of the system at Ep = 0.3

Full size image
Fig. 3
figure 3

Grid sizes effect on the average outlet fluid and PV cell temperatures for Ep = 0.3, Re = 500, Pr = 0.71, and Da = 10–3

Full size image
Fig. 4
figure 4

Validation of the U-velocity profiles with those of Hooman [45], as a function of S (S = \(1/\sqrt{Da}\))

Full size image

The second comparison is performed with the numerical data of Tahmasbi et al. [34] for the case of a PVT solar collector, whereas porous foam is integrated to improve its efficiencies. The dynamic and thermal fields inside the system, illustrated in Fig. 5, show good agreement between our results and those of Tahmasbi et al. [34] for Ep = H/2, Re = 2300, and ε = 0.9. Besides, other comparisons were performed to validate the precision of our FORTRAN computer code in simulating either mixed or natural convection in composite domains which can be found in our previous works [46, 47].

Fig. 5
figure 5

Comparison of dynamic and thermal fields: results of Tahmasbi et al. [34] (on the upper), present study (on the lower) at Ep = H/2, Re = 2300 and, ε = 0.9

Full size image

As confirmed in Figs. 4 and 5, the numerical accuracy of the in-house FORTRAN computer code is verified, and the developed model is viable to establish this study.

4 Results and discussion

In this paper, the mixed convection during the air-cooling process of the studied PVT collector in the absence and in the presence of a porous layer is investigated numerically. Thus, the results are presented to clarify the effects of several parameters such as Richardson number (0.1 ≤ Ri ≤ 10), tilt angle of the PVT collector (0 ≤ α ≤ 45), Darcy number (10–6 ≤ Da ≤ 10–1), and porous layer thickness (0.1 ≤ Ep ≤ 0.7) on the performances of the investigated system. The Forchheimer number (F), the Prandtl number (Pr), the Reynolds number (Re), and the viscosity ratio \(\left( {R_{\mu } } \right)\) are kept constant, respectively, at 1, 0.71, 500, and 1. The results are presented in terms of x-velocity contours (i.e., longitudinal velocity), thermal field, average PV cells and outlet fluid temperatures, as well as thermal and electrical efficiencies in dimensional forms. Furthermore, the mentioned improvements in the studied PVT solar collector efficiencies are achieved in comparison with traditional PVT systems, specifically referring to the case without natural convection effects (pure forced convection) and without porous medium.

4.1 Effect of collector tilt angle (α) and Richardson number (Ri)

Figure 6 illustrates the effect of tilt angle of the solar collector on the dimensional velocity contours (the upper part of Fig. 6) and the thermal field (the lower part of the same figure) for Ri = 10, Re = 500 and Ep = 0 (absence of porous layer). It is apparent from the figure that in the absence of natural convection (α = 0°: pure forced convection), the velocity contours exhibit symmetrical qualitative and quantitative patterns with respect to y = H/2 (i.e., middle of the channel). By increasing α from 0° to 45°, the symmetry of the x-velocity has been destroyed, where an increase in the air flow strength near the PV cells is noticed due to the rise in the natural convection impact in this zone, accompanied by a reduction in the air-flow strength in the lower half of the channel confirming the conservation of mass flow rate. These results are confirmed obviously by Fig. 7, which illustrates the outlet u-velocity profiles as a function of the tilt angle (α). For the thermal field (lower part of Fig. 6), intensifying the fluid flow near the PV cells with α, results in an increased rate of heat removal through convection. This enhancement contributes to the improved cooling process of the PV cell, subsequently leading to a noticeable decrease in the maximum temperature observed within the system (it varies from a high value of 381 K to a low one of 361 K).

Fig. 6
figure 6

x-velocity contours and thermal field for various values of the panel tilt angle for Ri = 10, Re = 500 and in the case without porous layer

Full size image
Fig. 7
figure 7

u-velocity profiles as a function of the tilt angle

Full size image

The effects of the tilt angle (α) and the Richardson number (Ri) on the average PV cells temperature (TPV) and average outlet fluid temperature (TOutlet), are presented in Fig. 8a, b. As depicted in this figure, it can be seen that TPV and TOutlet decreases and increases, respectively, with the Richardson number, regardless of the tilt angle. Furthermore, for low value of the Ri (Ri = 0.1), where the natural convection effect is negligible, the increase in the tilt angle doesn’t impact the two average temperatures, TPV and TOutlet. By increasing the Richardson number from 0.1 to 10, both TPV and TOutlet become increasingly affected by the change in tilt angle. Specifically, as the tilt angle increases up to 45°, the average outlet fluid temperature shows a rise of 1.75 degrees, while the average PV cells temperature drops by 17 degrees. This trend can be clarified by the increase in the strength of the air-flow near the PV cells with the increasing of the two parameters, Ri and α (Figs. 7 and 9).

Fig. 8
figure 8

a Average PV temperature as a function of α and for different Ri. b Average outlet fluid temperature as a function of α and for different Ri

Full size image
Fig. 9
figure 9

u-velocity profiles as a function of Richardson number

Full size image

The relationship between the Richardson number, panel tilt angle and electrical and thermal efficiencies (\({\eta }_{El}, {\eta }_{Th})\) is illustrated in Fig. 10a, b. The electrical efficiency (Fig. 10a) demonstrates an inverse trend compared to TPV, showing a maximum increase in \({\upeta }_{{\text{El}}}\) up to 9.88%, achieved by increasing Ri and α to 10 and 45°, respectively. Regarding Fig. 10b, it is quite clear that \({\eta }_{Th}\) is directly related to TOutlet according to Eqs. (14), where the same trend of the TOutlet profile is noticed. Indeed, an improvement in the thermal efficiency is observed reaching up to 10% for fixed values of Ri and α (i.e., Ri = 10 and α = 45°).

Fig. 10
figure 10

a Electrical efficiency as a function of α and for different Ri. b Thermal efficiency as a function of α and for different Ri

Full size image

4.2 Effect of Darcy number and thickness of the porous layer

Figure 11 presents the impact of Darcy number on the x-velocity contour and the thermal field for Ep = 0.3, Re = 500, Ri = 0 and α = 0°. As established, the reduction in Da values correlates with the diminished permeability of the installed porous layer, consequently amplifying the resistance of the porous medium to fluid flow. In this case, the air penetration inside the porous zone decreases when Da is reduced from a high value of 10–1 to a low one of 10–4, which leads to an increase in the air flow strength in the clear fluid zone. For Da ≤ 10–4, the porous layer functions as a solid partition, and the air in this case is moving only in the clear fluid zone, which can be justified by the variation of the u-velocity profile in Fig. 12. In this last figure (Fig. 12), the u-velocity within the porous layer exhibits a consistent decline as the Da number decreases, eventually reaching zero at Da ≤ 10–4. Simultaneously, a notable increase in velocity is observed within the clear fluid region. Regarding the corresponding thermal field (Fig. 11 on the lower), the decrease in the infiltration of cold air into the porous layer as Da decreases reduces the cooling process of the PV cells (i.e., preventing the cold air from reaching the PV cells). Consequently, the maximum PV cells temperature rises from 352 to 364 K.

Fig. 11
figure 11

x-velocity contours and thermal field for different values of Darcy number at α = 0°, Re = 500 and Ep = 0.3

Full size image
Fig. 12
figure 12

u-velocity profiles as a function of Darcy number

Full size image

Shifting our focus to the impact of the porous layer thickness (Ep) on the dimensional velocity contours and the thermal field, as illustrated in Fig. 13 in the case of forced convection (i.e., Ri = 0 or α = 0°) for defined values of Darcy (Da = 10–3), Reynolds (Re = 500). It is observed that an increase in Ep from 0.1 to 0.7 results in a proportional expansion of the heat transfer area across a significant portion of the channel. Consequently, the thermal energy received by the PV cells is predominantly conveyed through the porous medium to the airflow. Therefore, the maximum PV cells temperature undergoes a reduction by 40 degrees as Ep varies from 0.1 to 0.7. For the x-velocity contours, it is worth noting that the impact of porous medium resistance to the fluid flow expands over a significant portion of the channel as Ep increases up to Ep = 0.7, resulting in a decrease in the fluid passage section. Consequently, the dimensional x-velocity exhibits a significant increase in the clear fluid region, as depicted in the outlet U-velocity presented in Fig. 14, where the maximum of U-velocity value demonstrates a 175% increase as Ep varied from 0 to 0.7. In addition, this figure also reveals a slight increment in the U-velocity within the porous layer as Ep increases, attributed to the gradual suffocation of the flow passage area.

Fig. 13
figure 13

x-velocity contours and thermal field for different values of Ep at α = 0°, Re = 500 and Da = 10–3

Full size image
Fig. 14
figure 14

u-velocity profiles as a function of porous layer thickness

Full size image

The effect of the Darcy number on the average PV cells temperature (TPV) and the average outlet fluid temperature (TOutlet) for different values of Ep is shown in Fig. 15a, b. It is observed from Fig. 15a that TPV decreases with respect to the porous layer thickness regardless of the values of Da. Furthermore, with the increase in Darcy number from 10–6 to10−4, the porous layer is considered akin a solid layer where heat conduction becomes the predominant mode of heat transfer within the porous zone (absence of fluid phase within the porous zone). Consequently, TPV remains invariant no matter Ep is. Beyond this value (Da > 10–4), cold air increasingly infiltrates the porous layer, reaching the PV cells (i.e., intensifying the convective impact). This, in turn, enhances the cooling process of the PV collector, causing the average PV cells temperature decreases to relatively low values, and its decrease rate increase with Ep. In fact, a decline in TPV is observed from 79 degrees at Ep = 0.1 and Da = 10–6 to 42 degrees at Ep = 0.7 and Da = 10–1.

Fig. 15
figure 15

a Average PV temperature as a function of Da and for different Ep. b Average outlet fluid temperature as a function of Da and for different Ep

Full size image

For the average outlet fluid temperature (TOutlet) presented in Fig. 15b, the increase of Da leads to an increase in TOutlet irrespective of Ep, as a consequence of the enhancement of the air penetration in the porous zone. Regarding the effect porous layer thickness, the average outlet fluid temperature takes different trends depending on Da number values. In fact, for Da > 10–3, TOutlet increases proportionally with Ep, while, for Da ≤ 10–3, this temperature shows an asymmetric variation. In this case (i.e., Da ≤ 10–3), the increase in Ep enhances of the heat transfer by conduction, and at the same time, minimizes the convection effect near the PV cells, preventing cold air from reaching the PV cells, as can be seen from Fig. 14. Thus, for Ep values ranging from 0.1 to 0.5, the decrease rate in the convection effect outweighs the increase rate of the conduction, resulting in a decline in TOutlet. On the other hand, as Ep exceeds 0.5, the conduction heat transfer rate becomes more pronounced, and in this case, TOutlet increases with Ep.

Figure 16a, b illustrates both electrical and thermal efficiencies of the PV/T system as functions of the Darcy number and for different values of porous layer thickness. As demonstrated by the previous results, an increase in the porous layer thickness enhances the cooling process of the PV cells and augments heat transfer to the fluid flow, particularly noticeable at higher Darcy number values. Consequently, the electrical and the thermal efficiencies (ƞEl and ƞTh) exhibit improvements of 26.71% and 38.16%, respectively, with the increase in the considered parameters (Da and Ep), compared to the case of traditional PVT system (i.e., at Ep = 0 and α = 0°; ƞTh = 24.08% and ƞEl = 10.93%).

Fig. 16
figure 16

a Electrical efficiency as a function of Da and for different Ep. b Thermal efficiency as a function of Da and for different Ep

Full size image

4.3 Effect of porous layer thickness and panel tilt angle

To clarify the combination impact of the panel tilt angle (α) and the porous layer thickness (Ep) on the performance of the PV/T solar collector, we examined α within the range of 0° to 45° for various Ep values (0.1–0.7) at Ri = 10, Da = 10–3, Re = 500. Furthermore, to avoid repetition and redundancy in presenting the results, only average temperatures and efficiencies curves are presented and discussed.

Figure 17 reflects the influence of the considered parameters (α and Ep) on the average PV cells temperature (Fig. 17a) and the average outlet fluid temperature (Fig. 17b). In addition to what has been found in the previous results (i.e., TPV decreases with the increasing of α and Ep), for high values of Ep (Ep = 0.7), TPV shows minimum values and becomes quasi-unaffected by the change in the tilting angle (α). This is attributed to the fact that, in this case, the thermal energy reaching the PV cells is almost totally recovered by the flowing air.

Fig. 17
figure 17

a Average PV temperature as a function of α and for different Ep. b Average outlet fluid temperature as a function of α and for different Ep

Full size image

In the contrary, the average outlet fluid temperature (Fig. 17b) shows an asymmetric variation with increasing Ep no matter α is. Indeed, it increases when Ep rises from 0 to 0.1, followed by a decrease as Ep rises from 0.1 to 0.3, and beyond this value (Ep > 0.3), it becomes an increasing function of Ep. For high values of Ep (Ep = 0.7), TOutlet exhibits a highest values owing to the expanded heat exchange area, and it remains relatively unchanged with the increase in α (rising by about half a degree as α varies from 0° to 45°). This is due to the dominance of the porous medium resistance to the air-flow on large parts of the channel.

Figure 18 depicts the effects of the PV/T panel tilt angle on the electrical (Fig. 18a) and the thermal (Fig. 18b) efficiencies of the solar system for different porous layer thicknesses. According to the variation of the corresponding average temperatures, (TPV) and (TOutlet), with the tilt angle and the porous layer thickness, improvements in both electrical and thermal efficiencies have been recorded. These improvements can attain high values of 23.39% and 28.14%, respectively, for Ep = 0.7 and α = 45° compared to the case of traditional PVT system.

Fig. 18
figure 18

a Electrical efficiency as a function of α and for different Ep. b Thermal efficiency as a function of α and for different Ep

Full size image

5 Conclusion

This numerical study is conducted to highlight the natural convection effect in a PVT solar collector performance with and without an integrated porous layer. The impacts of different parameters on the system performances are investigated, including panel tilt angle, porous layer thickness, and Darcy and Richardson numbers. These performances are presented in terms of fluid velocity contours, fluid thermal field, cell temperature and outlet average fluid temperature, as well as thermal and electrical efficiencies. The major findings of this study show that:

  • Improvements in both electrical and thermal efficiencies are observed, reaching up to 9.88% and 10%, respectively, when the natural convection is dominant, Ri = 10 and α = 45°.

  • The integration of a porous layer with an intermediate permeability (Da = 10–3) can enhance both electrical and thermal efficiencies by more than 23% and 28%, respectively, under specific values of the studied parameters compared to the traditional PVT system.

  • The impact of panel tilt angle on the PVT solar performances decreases with an increase in the porous layer thickness.

  • The decrease in the porous medium permeability (Da) has a detrimental effect on the PVT solar collector performances, especially its thermal efficiency.

Finally, a further extension of this work is highly recommended as perspective to check the case of local thermal non-equilibrium assumption inside the porous layer. In such instance, the solid and fluid phases exhibit distinct local temperatures from one another. In this case, other parameters necessitating consideration include the inter-phase heat transfer coefficient and modified thermal conductivity ratio. Furthermore, the techno-economic dimensions of the studied system are advised as part of future work to analyze the feasibility of this system compared to conventional air PVT solar collectors.