1 Introduction

Overhead conductors are complex structural components whose mechanical performance depends on many parameters, such as geometry, material properties, and mechanical loads. One of the most frequent causes of failures in overhead conductors is fatigue caused by the vibration process induced by the action of moderate winds [1,2,3,4]. Typically, this failure process occurs in the assembly conductor/suspension clamp region, the bending stress is generated due to movement restriction and Aeolian vibration. Besides the dynamic stress caused by the wind, the conductor is also submitted to static loading, due to the stretching load applied when installing the transmission lines. The primary function of this load elongation is to control the clearance (minimum distance between the ground and the maximum conductor deflection point). A prescribed axial load is applied to induce a nominal stretching load called EDS (Everyday Stress) [5]. In addition to controlling clearance, EDS also controls other parameters such as the conductor's self-damping level (the higher the EDS, the lower the self-damping), the mean stress in the conductor strands (the higher the EDS, the higher the mean stress in the strands), and the contact pressure between the conductor (the higher the EDS, the higher the contact pressure). Thus, depending on the EDS levels adopted in the transmission line design, the overhead conductor may become more susceptible to premature fatigue failure due to the wind vibration process [1,2,3,4, 6, 7]. Although the effect of the presence of mean stress is still a subject much studied by the fatigue community, as far as it is known, there are not many studies reported in the literature that seek to evaluate the effect of the mean stress produced by the stretching load on the fatigue behavior of the aerial conductors. In general, these studies present experimental results of specific conductors that prove that the stretching load influences the fatigue life and propose particular methodologies that allow considering the influence of average stretching loads on the fatigue life of conductors [2, 8,9,10, 11].

The Conseil International des Grands Électriques (CIGRÉ), or International Council on Large Electric Systems, has proposed the use of a reference fatigue curve for conductors known as the CIGRE Safe Border Line (CSBL) to ensure the safety and reliability of transmission lines subject to mechanical fatigue [12]. According to [12], the CSBL can be used when the actual S–N curve for a conventional aluminum-based conductor is not available. However, it is important to note that while the CSBL is considered a “universal” and naturally conservative curve, its use can lead to incorrect life predictions because it does not consider the level of EDS acting on the conductor, which prevents designers from consistently evaluating the effect of this important parameter on the fatigue behavior of the overhead conductor. Therefore, it is important to exercise caution when applying the CSBL and consider strategies or models that allow the influence of this important parameter on conductor fatigue behavior to be incorporated, ensuring safer and more reliable operation of electric power transmission lines.

Studying the fatigue behavior of an overhead conductor composed of strands made from Al 1350 alloy (pure aluminum) with a steel core (ACSR conductor), Fadel et al. [2] demonstrated a 50% reduction in its fatigue life when the tensile load was increased from 20 to 30% of the RTS (Rated Tensile Strength). Pestana et al. [8] expanded on Fadel et al.'s [2] experimental analysis and developed a strategy to predict the fatigue life of this conductor using artificial neural networks (ANN). Using a similar ANN structure to Pestana et al. [8], Kalombo et al. [9, 11] analyzed the fatigue behavior of an overhead conductor composed of aluminum alloy strands (Al 6201-T81) under three different stretching load levels. In a similar vein, Câmara et al. [10] complemented the works of Pestana, Kalombo, and Fadel, showing that an ANN can also be used to estimate the fatigue behavior of overhead conductors composed of all aluminum conductor strands (AAC) and aluminum conductor alloy-reinforced strands (ACAR). The study aimed to evaluate the adequacy of the experimental results, and the increase in the number of experimental data confirmed the effectiveness of the ANN approach in predicting the fatigue behavior of these conductors. However, the network trained with a single conductor did not allow for the estimation of the behavior of multiple conductors simultaneously, and a larger amount of data is required to increase the confidence level of the fatigue life behavior estimation using ANN. Additionally, the use of ANN analysis presents a high computational cost due to data processing time.

To address these challenges, other researchers have also explored, from a mechanical point of view, more sophisticated approaches to assessing fatigue life prediction in overhead conductors. One of these approaches is a numerical methodology combined with experimental tests, which allows the description of mechanical interactions during strand contact. Lalonde et al. [13] proposed an FE model approach using beam elements to describe strands geometry and contact interactions, offering a solution for internal element variations of multilayer strands through 3D simulations of different pitch lengths of strand segments from affordable computational resources. Rocha et al. [14] and Pereira et al. [15] investigated the behavior of fretting fatigue in aluminum strands and used Walker's model to improve predictions. In 2020, Matos et al. [16] conducted fretting fatigue tests on 6201-T81 aluminum alloy strands taken from conductor AAAC 900 MCM. The development of a predictive design tool enables transmission line designers to estimate the fatigue life of conductors based on different mean loads and stresses, helping to determine the most appropriate overhead conductor to use. However, the contact problem model is simplified and does not cover the entire conductor, and analysis presents a high computational cost due to data processing time.

Although the use of artificial neural networks (ANN) and numerical models, in combination with laboratory tests on strands, have significantly advanced the prediction of fatigue behavior in overhead conductors, the complexity of these methods often requires advanced and complex software, making their use and interpretation of results difficult. As a result, their practicality is limited and their use by concessionaires is hindered. Therefore, it is essential to develop a methodology for predicting the life of overhead conductors under different tensile loads that is mechanically consistent and relatively simple to use, in order to make it more practical for utilities. To provide a more practical and mechanically consistent approach, this research aims to evaluate the feasibility of developing a “universal” fatigue curve for overhead conductors. In this regard, the authors will use fatigue data available in the literature and generated by themselves to define a new “universal” curve (master curve), which will allow for the estimation of the effect of both aeolian and stretching loads on the fatigue life of overhead conductor. The proposed master curve will be developed using the Smith–Watson–Topper (SWT) and Walker models, which are commonly used to characterize the effect of mean stress on the fatigue behavior of metallic materials.

2 Bibliographic review

2.1 Bending stress

During aeolian excitation, the conductor undergoes cyclic movement, inducing bending stress in the overhead conductor. Fatigue generally occurs at points where conductor motion is restricted against transverse vibration, such as at suspension clamps (see Fig. 1). Fatigue failures can occur at contact points of strands-to-strands and strands-to-suspension clamps [1, 17]

Fig. 1
figure 1

Schematic montage of the conductor and the suspension clamp showing the measured position of the bending amplitude and the LPC

Full size image

Poffenberger and Swart developed a mathematical model to calculate the bending strain or stress in the outer layer of the overhead conductor's aluminum strand at 89 mm from the last point of contact between the conductor and the suspension clamp (LPC) [9, 18]. In this mathematical model, this part of the conductor near the suspension clamp is considered a Euler beam. Thus, the bending stress on the outer layer of the aluminum strand conductor was calculated from the vertical amplitude measured peak-to-peak at 89 mm from LPC, using the Poffenberger-Swart formula Eq. (1).

$$S_{a} = KY_{b}$$
(1)

where \(S_{a}\) is the nominal stress amplitude (zero to peak); \(Y_{b}\) is the overhead conductor vertical displacement range (peak-to-peak) measured at \(x\) mm from LPC; and \(K\) represents the Poffenberger parameter, given by:

$$K = \frac{{E_{a} {\text{d}}p^{2} }}{{4\left( {e^{ - px} - 1 + px} \right)}}$$
(2)

where, \(E_{a}\) (MPa) is the aluminum Young’s modulus; \(d\) (mm) is the diameter of the outer layer strand; \(x\). is the distance on the conductor from the LPC and the vertical displacement measuring point, (usually \(x\) = 89 mm); and:

$$p = \sqrt{\frac{T}{EI}}$$
(3)

where \(T\left( N \right)\) denotes the static conductor tension at average ambient temperature during the test period; and \(EI\) \(\left( {{\text{N}} \cdot {\text{mm}}^{2} } \right)\) is the flexural stiffness of the overhead conductor, whose minimum value is:

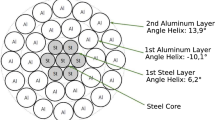
$$EI_{{{\text{min}}}} = n_{a} E_{a} \frac{{\pi d_{a}^{4} }}{64} + n_{s} E_{s} \frac{{\pi d_{s}^{4} }}{64}$$
(4)

where \({n}_{a}\), \({d}_{a}\), \({E}_{a}\) are the number, individual diameter, and Young’s modulus of the aluminum strands, respectively; and \({n}_{s}\), \({d}_{s}\), \({E}_{s}\) represent the above parameters but applied to steel strands. The conductor in this approach, different from its original helical form, is described as a bundle of individual strands that are free to move and touch one another, and the minimum value (\(E{I}_{{\text{min}}}\)) for flexural stiffness is considered.

When the overhead conductor vibrates at smaller bending amplitudes, the strands stick together. Therefore, the conductor behaves as a solid rod, increasing its flexural stiffness to the maximum. Some approaches to calculating the value of \(EI\) that consider the stick–slip between strands, which is the dynamic bending stress, can be found in Papailiou [19, 20].

Note that, when it comes to overhead conductor made up of strands with non-circular cross sections, the application of Eq. (4) for calculating the \(EI\) parameter is not appropriate. In such cases, it is necessary to use other way that allow for the precise calculation of this parameter, according to the strands’ cross section. To address the calculation issue, we have modified Eq. (4) to a generalized form presented on Eq. (5), where \(E{I}_{{\text{cond}}}\) represents the overall flexural rigidity, \({E}_{j}\) is the modulus of elasticity, and \({I}_{j}\) is the moment of inertia for each layer (including the core), calculated using the Steiner's theorem [21]. This modification allows for improved calculation of \(E{I}_{{\text{cond}}}\), considering the specific characteristics of each layer in non-circular cross sections such as Trapezoidal and Aero-Z shapes.

$$EI_{{{\text{cond}}}} = \mathop \sum \limits_{j}^{J} E_{j} I_{j}$$
(5)

where \(J\) represents the number of layers.

2.2 Stretch load control parameters

The presence of a tensile load on the conductor is important to ensure a minimum clearance between it and nearby objects, thus avoiding physical contact between the electrical conductor and these objects. However, as mentioned earlier, the presence of this load can impair the fatigue behavior of the overhead conductor. This is because the load reduces the self-damping capacity of the conductor and induces the appearance of average stresses in the wires, which in turn reduces their fatigue behavior. In 1960, CIGRE convened the Everyday Stress Panel to investigate the problem and define possible limiting parameters of the loads that could be applied for this specific purpose, while ensuring the safety of transmission line conductors against fatigue caused by aeolian excitation. The panel aimed to investigate the fatigue caused by wind excitation in electric power transmission lines and recommend possible limiting parameters of the loads that could be applied to ensure the safety of the conductors. As a result, the Everyday Stress Panel recommended the adoption of an upper limit of tension on the conductor in transmission lines to maintain its service life. The panel emphasized that to establish the maximum safe tension limit, it is important to consider, in addition to the fatigue resistance of the conductors, factors such as environmental conditions and local topography. The EDS, expressed as a percentage of the specified tensile strength (RTS) of the conductor, is defined as the maximum stretch load that the conductor can be subjected to at a temperature that will occur for the longest period without risk of damage due to wind vibrations, according to references [5, 22]. However, field observations have reported fatigue of power lines even when using the value suggested by CIGRE for EDS [1, 23, 24]. Therefore, it is known that the EDS parameter may be insufficient given the recent damages found in power lines. In 1999, CIGRE adopted the catenary parameter as a solution. This parameter represents the ratio between the initial horizontal stretching load (H [N]) and the weight of the conductor per unit length (w \([N/m]\)). The H/w [m] parameter presents some advantages compared to EDS, affecting other parameters involved in dynamic behavior, such as natural frequency and self-damping, material fatigue behavior, and wire contact conditions, according to references [5, 10, 22, 23, 25].

2.3 Procedure for evaluating the mean stress acting on the strands of a conductor

The concept presented in this paper is an approach based on a master curve that helps estimate the fatigue life of several conductors subjected to fatigue tests under different values of stretching stress \((H/w\) parameter). Each \(H/w\) value is related to the mean stress (\({S}_{m}\)) of the conductor, which is calculated according to Eq. (6).

$$S_{m} \cong g\rho_{al} \frac{H}{w}$$
(6)

where \(g\) is the gravity acceleration \(\left[ {{\text{m}}/{\text{s}}^{2} } \right]\) and \(\rho_{{al{ }}}\) is the aluminum density \(\left[ {{\text{kg}}/{\text{m}}^{3} } \right]\).

3 Strategy to evaluate the master curve

To solve the problem of predicting the fatigue life of overhead conductor considering different stretching loads, it is necessary to express the alternating and mean stress components through simple relationships. In this paper, we adopt Eqs. (1) and (6) to calculate the nominal alternating, \({S}_{a}\), and mean, \({S}_{m},\) stresses. We also define a model that allows estimating an equivalent stress, \({S}_{ar}\), that represents the pair \(\left({S}_{m}, {S}_{a}\right)\). We thus propose that a master curve that represents the effect of the stretching load on the fatigue behavior of conductors can be obtained by defining the state of nominal stresses \(({S}_{m}, {S}_{a})\) acting and through approaches that account for this pair of stresses over the life of the strand material.

To obtain the master curve, we first present the best methods for estimating mean stress effects in aluminum alloy and then look at the ability of these methods to correlate stress-life data of the various overhead conductors tested with different stretching loads. This procedure is divided in two stages: calibration and validation. In the first stage, part of the experimental data is used to calibrate the researched criteria through the technique named interpolation. In the second step, the other part of the experimental data is used to validate the models from the calibration. Thus, this process makes it possible to determine the most appropriate criteria to represent the behavior of the analyzed conductor about the impact of average stress on its fatigue life. The obtained results are then analyzed and interpreted to define a master curve for overhead conductor fatigue design, capable of withstanding various stretching loads Methodologies for the Prediction of Mean Stress Effect.

Various methodologies have been developed to account for the effect of mean stress on the fatigue response of metallic materials. These include Gerber [26], Goodman [27], Morrow [28], Smith–Watson–Topper (SWT) [29], and Walker [30], among others. According to studies [28, 31, 32], the Goodman methodology lacks precision but is safe as it predicts failure before it occurs. On the other hand, the Morrow methodology accurately represents the behavior of steel in general but is less accurate when representing the behavior of aluminum alloys. The Gerber methodology tends to be imprecise and, more seriously, is non-conservative as it predicts failure after it occurs. The SWT methodology correlates to the experimental fatigue data for most of the structural metals and appears to work particularly well for aluminum alloys [28, 33], and its generalization into the Walker formula provides even better results [34]. For this reason, only the Smith–Watson–Topper and Walker relationships will be evaluated for their ability to correlate the stress-life data of the various aerial conductors tested with different stretch loads.

3.1 Approach proposed by Smith–Watson–Topper (SWT)

This methodology was proposed by Smith et al. (1970) to predict fatigue failure in materials that fail due to crack grow that develops in planes of maximum stress and strain. For fatigue life prediction using a stress-based approach (S–N curve), the SWT relationship is calculated, as shown in Eq. (7).

$$S_{{ar\;{\text{SWT}}}} N^{k} = C$$
(7)

where \({{S}_{ar}}_{SWT}\) is the fully reversed stress equivalent according to the SWT approach (\({S}_{a{r}_{SWT}}=\sqrt{{S}_{a}\left({S}_{a}+{S}_{m}\right)}\)) and \(k\) and \(C\) are material parameters fitted from fatigue test data performed following ASTM E466 Standard [35]. In this standard, the geometry, dimensions, and surface finish of the specimens, as well as the loading conditions, are defined.

3.2 Approach proposed by Walker

In 1970, Walker independently presented an expression very much alike that proposed by Smith et al. (1970) but using a \(\gamma\) factor, which is an empirical parameter that changes between 0 and 1, representing the maximum and minimum sensitivity to the load ratio, respectively Eq. (8).

$$S_{ar\;W} N^{k} = C$$
(8)

where \({{S}_{ar}}_{W}\) is the fully reversed stress equivalent according to the Walker approach (\({S}_{a{r}_{Walker}}={S}_{a}^{\gamma }{\left({S}_{a}+{S}_{m}\right)}^{1-\gamma }\)), \(k\) and \(C\) are the same material parameters used in Eq. (7), and the quantity \(\gamma\) is a fitting constant that may be considered to be a material property.

3.3 Parameter estimation of master curves using Smith–Watson–Topper and Walker equations

As previously mentioned, the Smith–Watson–Topper equations (Eq. (7)) and the Walker equation (Eq. (8)) are characterized by the parameters C, k, and γ. To estimate these parameters, we assume that: a) The logarithms of the experimentally observed fatigue life, N, are independent of each other and that their probability distribution is approximately symmetrical and bell-shaped; b) The distribution of the residuals of the logarithm of the fully reversed equivalent voltage, \({S}_{ar}\), must be approximately symmetric and centered on zero, and that the variance of the residuals is constant over the entire range of log(N) values, and that the residuals are independent of each other. By representing Eqs. (7) and (8) in linearized form, we obtain the resulting equations presented in Eqs. (9) and (10):

$${\text{Log}}\left( {\sqrt {S_{a} \left( {S_{a} + S_{m} } \right)} } \right) = {\text{Log}}\left( {C_{SWT} } \right) - k_{SWT} {\text{ Log}}\left( N \right)$$
(9)

and

$${\text{Log}}\left( {S_{a}^{\gamma } \left( {S_{a} + S_{m} } \right)^{1 - \gamma } } \right) = {\text{Log}}\left( {C_{W} } \right) - k_{W} {\text{Log}}\left( N \right){ }$$
(10)

where \({C}_{SWT}\), \({C}_{W}\), \({k}_{SWT}\), and \({k}_{W}\) represent the constants and exponents of the master curves considering the approaches proposed by Smith, Watson and Topper, and Walker, respectively.

Upon analyzing Eq. (9), it is noted that the technique of linear regression can be directly used to estimate the \({C}_{SWT}\) and \({k}_{SWT}\) parameters that characterize the Smith–Watson–Topper relationship. On the other hand, the linearized form of the Walker relationship, given by Eq. (10), requires the estimation of three parameters, \({C}_{W}, {k}_{W}, \; and \; \gamma\), which characterizes Eq. (10) as a hyper parameterized function. To obtain the parameters characterizing the effect of \({S}_{a}\) and \({S}_{m}\) stresses on the fatigue life of the overhead conductor, \(N\), a combination of the grid search optimization method [36] and the linear regression method will be adopted in this study [37]. Specifically, given the known valid range of \(\gamma\), a simplified form of the grid search optimization strategy is employed, where only the value of \(\gamma\) is varied within its range. For each value of \(\gamma\), linear regression is performed to estimate the values of \({C}_{W}\) and \({k}_{W}\) based on experimental data. Once \({C}_{W}\) and \({k}_{W}\) have been determined, the coefficient of determination, \({R}^{2}\), is calculated to evaluate the quality of the fit for each value of \(\gamma\). After performing linear regression for all values of \(\gamma\), the \((\gamma , {C}_{W}, {k}_{W})\) set resulting in the highest value of \({R}^{2}\) is selected as the best fit for Eq. (10).

3.4 Prediction interval estimation of the fatigue lifetime prediction models

Considering that (9) and (10) can be represented in a simplified way by the statement (11) and assuming that X and Y are normally distributed and the variance of the errors of the dependent variable is the same for all sample observations [38, 39].

$$Y = A + bX$$
(11)

where \(X\) is equal \(log(N)\), \(Y\) is equal \(Log\left(\sqrt{{S}_{a}\left({S}_{a}+{S}_{m}\right)}\right)\) or \(Log\left({S}_{a}^{\gamma }{\left({S}_{a}+{S}_{m}\right)}^{1-\gamma }\right)\), \(A\) is equal \(Log\left({C}_{SWT}\right)\) or \(Log\left({C}_{W}\right)\), and \(b\) is equal \({k}_{SWT}\) or \({k}_{W}\).

For the case where the S–N relationship is described by the linear model \(Y = A + bX\) (or \({\mu }_{Y\left|X\right.}=A+bX\)), the log-normal distribution describes the fatigue life \(N\) [40]. So, considering that the parameters for A and b can be estimated by statistical method from the fit of the experimental data [38, 39, 41], Eq. (11) will take the form.

$$Y_{i} = \hat{A} + \hat{b}X_{i}^{*} \pm \Delta_{{\text{i}}} { }$$
(12)

where \({Y}_{i}\) is the true or real value of an observation of the dependent variable\(Y\), \(\widehat{A}\) and \(\widehat{b}\) are the estimated coefficients obtained from the statistical method, \({X}_{i}^{*}\) represents the observed value for the independent X, and \(\Delta\) is the measure of uncertainty or error in the prediction, which represents the difference between the real value of \({Y}_{i}\) and the predicted value \({Y}_{i}^{*}(=\widehat{A}+\widehat{b}{X}_{i}^{*})\).

In this particular application, we can calculate the measure of uncertainty by determining the standard error of the estimate for the linear regression model, whose expression is defined in Eq. (13).

$${\Delta }_{{\text{i}}} { } = \delta_{{Y_{i} }} t_{\alpha , \nu } { }$$
(13)

where \({\delta }_{{Y}_{i}}\) represents the residual standard deviation of the response variable, such that \({\delta }_{{Y}_{i}}={S}_{YX}\sqrt{1+\left(\frac{1}{n}+\left[\frac{{\left({Y}_{i}-\overline{Y }\right)}^{2}}{\sum {\left({Y}_{i}-\overline{Y }\right)}^{2}}\right]\right)}\), so that \({S}_{YX}\) is a standard deviation of the residuals, \(n\) is the total number of test specimens (the total sample size) and the \({t}_{\alpha , \nu }\) is a critical value to \(t\)-distribution such that the parameter \(\nu\) represents the number of degrees of freedom of the distribution and the parameter \(\alpha\) represents the significance level (one-tailed), that is, the probability of rejecting the null hypothesis when it is true – in the specific case: reject the condition of \({Y}_{crit}\le {Y}_{i}^{*}-{\delta }_{{Y}_{i}}{t}_{\alpha , \nu }\). Based on the representative data of \(X\) and \(Y\) and the estimated values of \(A\) and \(b\), we can calculate the values of \({\Delta }_{i}\), which represent the uncertainty or error in predicting the value of Y for each observed value of \(X\). We can follow these steps to calculate \({\Delta }_{i}\) using Eq. (13):

  1. 1.

    Calculate the mean of the \(X\) values, \(\widehat{X}\).

  2. 2.

    Calculate the sum of the squares of the differences between each X value and the mean of X: \(\sum {\left({X}_{i}-\widehat{X}\right)}^{2}\)

  3. 3.

    Calculate the residual standard deviation, \({S}_{YX}\):

  4. 4.

    Calculate the residual standard deviation for each \({X}_{i}\) value, \({\delta }_{{X}_{i}}\).

  5. 5.

    Determine the critical value for the Student's t-distribution, \({t}_{\alpha , \nu }\), such that \(\nu =n-2\) (where \(n\) is the sample size).

  6. 6.

    Calculate \({\Delta }_{i}\) for each \({X}_{i}\) value using Eq. (13).

Although the relationship between \({\delta }_{{Y}_{i}}\) (\({\delta }_{Log\left({P}_{*}\right)}\)) and \({X}_{i}\) (\(Log({N}_{i})\)) can exhibit a generally nonlinear behavior, the authors aim to determine the lower limit prediction curve for constructing a master curve based on the probability of failure. To this end, they make the hypothetical assumption that the variation of \({\delta }_{{Y}_{i}}\) is sufficiently small within the analyzed range to approximate it by its mean value. This assumption further enables them to assume that the standard error of the estimate, \(\Delta\), is constant, which greatly facilitates the construction of a curve that defines failure conditions as a function of the predicted confidence level. We will use heuristic procedures to validate the hypothesis that \({\delta }_{{Y}_{i}}\) is approximately constant and equal to its mean value, \({\widehat{\delta }}_{Y}\). This will involve presenting and analyzing a scatter plot between \({X}_{i}\) and \({\delta }_{{Y}_{i}}\), evaluating the behavior of the function that best represents this relationship, and analyzing the mean, standard deviation, coefficient of variation, and range of variation of \({\delta }_{{Y}_{i}}\) [38].

Thus, once the hypothesis is validated, to discover the equations that define the prediction bands (lower and upper bands) we apply in Eq. (12) the logarithm and power rules. Follows the sequence of rules application (Eqs. 14–17).

$$\log \left( {\hat{S}_{ar} } \right) = \hat{b}\log \left( N \right) + \hat{A} \pm \Delta$$
(14)
$$10^{{{\text{log}}\left( {\hat{S}_{ar} } \right)}} = 10^{{\left( {(\log \left( {{\text{N}}^{{\text{b}}} } \right) + \hat{A} \pm \Delta )} \right)}}$$
(15)
$$10^{{{\text{log}}\left( {\hat{S}_{ar} } \right)}} = 10^{{(\log {\text{N}}^{{{\hat{\text{b}}}}} )}} 10^{{\left( {\hat{A} \pm \Delta } \right)}}$$
(16)
$$\hat{S}_{ar} = 10^{{\left( {\hat{A} \pm \Delta } \right)}} N^{{\hat{b}}}$$
(17)

From Eq. (17), it is possible to obtain curves that represent the mean relationship between the alternating stress, \({S}_{ar}\) (based on Smith–Watson–Topper and Walker criteria), and the number of cycles until failure of the component, \(N\). The parameter \(\Delta\) in this equation represents the measure of uncertainty or error in the prediction. Hence, considering this parameter, it is also possible to obtain curves that characterize the upper and lower limits of the uncertainty in predicting the values of \({S}_{a}\). The upper curve obtained for \(+\Delta\) is the upper limit of the confidence interval and represents the maximum value that the dependent variable can assume with a certain level of confidence. Similarly, the lower curve obtained for \(-\Delta\) is the lower limit of the confidence interval and represents the minimum value that the dependent variable can assume with a certain level of confidence. In this context, choosing the lower curve as a design curve allows defining a conservative trend curve that takes into account the lower limit of the probability distribution of the predictions. This curve represents the limit below which the probability of the actual response being below that value is equal to the chosen significance level. Therefore, using this curve as a design curve implies a conservative decision, as it assumes that the actual response is likely to be above this curve. However, it is possible to control the degree of conservatism of this approach by choosing the appropriate significance level. The lower the chosen significance level, the more conservative the lower curve will be. In this sense, from a conceptual point of view, the approach proposed here is a viable alternative, as it allows obtaining curves that characterize the fatigue behavior that take into account the associated uncertainties, considering the typical test conditions adopted in fatigue tests of overhead conductor (long test time and type of test classified as preliminary and exploratory [40]) Although other approaches, such as the one used for the definition of the P-S–N (Probabilistic-S–N) curve [39, 41], can be applied to the fatigue analysis of overhead conductor, it is important to consider that the method proposed here offers a feasible and practical alternative, capable of taking into account the most different types of energy conductors subjected to the most diverse stretching conditions. Since to use the P-S–N curve a number of experimental data should be large to evaluate experimental variability and scatter, that can be unpractical due to the high duration of fatigue tests [42]. Additionally, an optimization algorithm can be required, taking a long “computational time” to estimate the design curves, for example [42].

4 Calibration of fatigue curves and comparison with experimental data

In order to test this strategy, 179 experiments were conducted to correlate fatigue life with various combinations of tensile load and peak-to-peak vibration amplitude. These experiments included tests on the following families of overhead conductors: AAC (a conductor composed solely of Al 1350-H19), ACSR (a conductor with a steel core and layers of 1350-H19 aluminum wires, which can have either a circular or trapezoidal shape), Aero-Z (a conductor with layers of 1350-H19 aluminum wires in a Z shape, with two types of core: steel or composite), AAAC (a conductor composed solely of aluminum alloy wires Al 6201-T81 or Al 1120 aluminum wires) and ACAR (a conductor with an aluminum alloy core of Al 6201-T81 and external layers of 1350-H19 aluminum wires). Table 1 present the Mechanical and Geometrical Properties of this conductors.

Table 1 Mechanical and geometrical properties of the conductors
Full size table

All fatigue tests were performed on the GFFM laboratory – UnB. The bench was previously described in other publications [2, 6, 43]. The conductor is stretched at the recommended value of \(H/w\) after the conductor was fixed on the bench and mounted on the suspension clamp. These tests were carried out according to IEEE (Institute of Electrical and Electronics Engineers) and CIGRÉ standards. Each conductor’s fatigue test was completed when the number of strands broken was 10% of the total number of conductor aluminum strands [3, 37].

The bending stress (\({S}_{a}\)) of the conductor is calculated using the P-S equation, and the bending displacement peak-to-peak (\({Y}_{b}\)), measured at 89 mm from the LPC, was controlled during all tests. A \(S-N\) diagram was generated at the end of each test (three tests by bending stress under different values of \(H/w\) parameter) for each overhead conductor analyzed. The mean stress of the conductor is calculated according to Eq. (6). In Table 2, the values of \(H/w\) parameter, the levels of bending stress (\({S}_{a}\)) considered during the experimental program, the mean stress (\({S}_{m}\)), and the Poffenberger-Swart constant (\(K\)) are presented.

Table 2 Fatigue test parameters for each overhead conductor
Full size table

5 Results and discussion

5.1 Fatigue tests

The scatter plots and the S–N curve generated using the results of fatigue tests performed with the stretching conditions described in Table 2 are shown in Fig. 2. To generate the graphs of this figure, 179 fatigue tests were considered, in the most diverse stretching conditions. The fatigue data were grouped considering the \(H/w\) parameter; that is, graphs 2.a, 2.b, and 2.c present the curves obtained with \(H/w\) levels equal to 1820, 2144, and 2725 m, respectively. A fourth graph (2.d) was constructed considering tests performed under other \(H/w\) conditions.

Fig. 2
figure 2

S–N curves of overhead conductors a \(H/w\) =1820 m; b \(H/w\) =2144 m; c \(H/w\) =2725 m; d other \(H/w\) conditions and e all the experimental results

Full size image

In the scatter plots, the fatigue life, \(N\), is plotted in abscissa on a logarithmic scale and the Poffenberger-Swart stress, \({S}_{a}\) is plotted in the ordinate on a linear scale. Each type of conductor is represented by a different mark, which makes it easy to identify. The solid line represents the best fit S–N curve that correlates fatigue life \((N)\) with the stress amplitude calculated using the Poffenberger-Swart formula Eq. (1), \({S}_{a}\). The dashed lines represent the lower and upper limits for the predicted fatigue life range calculated through the fitted S–N curve (in general, an approach used to predict fatigue life is considered to have good accuracy when experimentally observed lifes vary between one-third and three times the estimated life using the approach).

Analysis of graphs 2(a) to 232(c) indicates that as the \(H/w\) parameter increases (consequently the mean stress, \({S}_{m}\)), the experimental points shift to the left, indicating that a lower P-S stress, \({S}_{a}\), is required to induce failure in the conductor for the same life \(N\), regardless of the conductor type. Furthermore, when comparing Fig. 2a with c, it was observed that for all five conductor types, on average, an increase in the \(H/w\) ratio from 1820 to 2725 m results in a reduction of fatigue life by approximately 50%, bringing it very close to the CIGRÉ Safe Border Line. Despite the clear relationship between Poffenberg-Swarts stress (P-S stress) and fatigue life, a more detailed analysis of the graphs in Fig. 2a–d reveals that the estimated fatigue curve based on these parameters (summarized in Table 2) fails to account for the influence of the \(H/w\) parameter on the fatigue behavior of conductors. This is best demonstrated by examining graph 2(e), which presents the S–N diagram incorporating all experimental results from Fig. 2a–d. This graph displays both a) the trend curve, represented by a solid line, and b) the confidence bands for 3 lifes, shown as dashed lines, allowing for visualization of the confidence intervals for the mean life, as well as for the lower and upper lifes. While the graph indicates the existence of a trend line correlating P-S stress with fatigue life, it is important to note that its coefficient of determination, which measures the quantity of data variance explained by the fitted model [45], is extremely low (\({R}^{2} = 0.15\)), and that a relatively large amount of experimental data falls outside the region defining the 3-life prediction band. Therefore, using this curve in practice would be counterproductive, as it does not fully explain this relationship. This result emphasizes the need to explore other strategies that can show the influence of mean stress on the fatigue behavior of conductors in order to obtain more accurate and reliable results.

5.2 Adherence of the models to the experimental results

To assess the effectiveness of the proposed strategy for generating master curves that describe the fatigue behavior of conductors subjected to different tensile loads, with the SWT and Walker models as references, we used 123 sets of experimental data to fit the fatigue curves according to these models. The results of this analysis, presented in Table 3, revealed that the coefficient of determination of the \({S}_{a{r}_{*} }-N\) curves increased to 0.54 and 0.55 for the SWT and Walker models, respectively. These findings are relevant to engineering applications and can serve as a basis for further studies and decision-making processes. Notably, the use of the Smith–Watson–Topper and Walker equivalent stress parameters led to a significant improvement in the coefficient of determination for both models, compared to the use of the Poffenberg-Swarts stress amplitude parameter (\({R}^{2}=0.15\)). It is worth noting that the fitting function obtained by considering the SWT model showed slightly lower correlation coefficients than the fitting curve estimated by considering the Walker model, so we focused our analysis on the SWT model (which, in theory, should present slightly worse predictions).

Table 3 Equivalent stress-life fitting constants
Full size table

Figure 3 shows the correlation between the SWT parameter and fatigue life. The circles on the graph represent the 123 experimental data points used to calibrate the SWT curve. The plus markers represent the 56 experimental tests conducted with an H/w ratio of 2144 m. These 179 experimental data points will be used to evaluate the accuracy of the life predictions based on the master curves. The SWT model effectively captures the effect of mean stress, as all the experimental data points correlating the SWT equivalent stress with fatigue life fall within the 3-life prediction band. Even when considering only the 56 experimental data points conducted under H/w = 2144 conditions to evaluate life predictions, the results remain accurate, with all points falling within the region delimited by the 3-life prediction band. These outcomes reinforce the potential of our approach to significantly enhance the quality of the life predictions for overhead conductors under different stretching loads, making it a valuable tool for fatigue analysis.

Fig. 3
figure 3

Diagram correlating the fatigue life, to a Smith–Watson–Topper Parameter, and b Walker Parameter

Full size image

5.3 Estimation of the is a measure of uncertainty, \({\varvec{\Delta}}\), and the parameters of the master curves for predicting the fatigue life of conductors for different levels of reliability

In this topic, we will discuss the results of a fatigue life prediction analysis of conductors at different reliability levels. In the first part, we will validate the hypothesis that in the case under study the variability of the residual standard deviation \({\delta }_{Y}\) (\({\delta }_{Log\left({P}_{*}\right)}\)) is small, which allows us to assume that its value is constant and equal to its mean. Next, we will estimate and discuss the master curve parameters in relation to the implications for predicting the fatigue life of conductors.

5.4 Analysis of the behavior of the uncertainty measure \({{\varvec{\delta}}}_{{\varvec{Y}}}\) and \({{\varvec{\Delta}}}_{{\varvec{Y}}}\)

In Fig. 4, a scatter diagram is presented correlating the logarithm of life and the standard deviations of predictions for individual values of the Smith–Watson–Topper \(({\delta }_{Log\left( {P}_{SWT}\right)})\) and Walker \(({\delta }_{Log\left( {P}_{Walker}\right)})\) parameters' logarithms. This figure clearly shows the existence of a dependency relationship between \({\delta }_{Log({P}_{*})}\) e \(Log(N)\). By applying curve-fitting techniques, it is found that the best relationship between these variables is a quadratic one (see fitting equations presented in Fig. 4). However, it can also be observed that the vertex of the parabola is located at the center of the range of the analysis interval, and that the coefficients of the quadratic and linear terms are, respectively, two and one order of magnitude lower than the coefficient of the constant term. Additionally, as showed in Table 4, the difference between the maximum and minimum observed values is of the order of 6E−4 (approximately 2% of the constant term's coefficient). Therefore, based on these pieces of information, assuming that \({\delta }_{Log({P}_{*})}\) is small, which allows us to assume that its value is constant and equal to its mean, proves to be a reasonable hypothesis from an engineering standpoint.

Fig. 4
figure 4

Diagram correlating the logarithms of Fatigue Life, \(Log(N)\), with the residual standard deviation of the predictions of the individual values of the logarithms of the Smith–Watson–Topper (\(Log({\delta }_{{P}_{\text{SWT}}})\)) and Walker (\(Log({\delta }_{{P}_{\text{Walker}}})\)) parameters

Full size image
Table 4 Statistical parameter of \({\delta }_{Log({P}_{*})}\)
Full size table

Once it has been demonstrated that the variability of the uncertainty measure \({\delta }_{Y}\) is small and that its value can be assumed as constant and equal to its mean, we can now estimate the values of \({\Delta }_{Y}\) using Eq. (12), making it possible to estimate prediction intervals for fatigue life curves, and allowing the construction of prediction curves based on the probability of failure using Eq. (17). Table 5 presents the \({\Delta }_{Y}\) values as a function of the \({t}_{\alpha }\) values. This table presents the values necessary to calculate the values of the constants \({C}_{*}\) considering critical values of the t distribution associated with the significance levels of 5.0%, 2.5%, and 1%.

Table 5 Equivalent stress-life fitting constants (see Eq. 17)
Full size table

In order to visualize more comprehensively the relationship between the parameter \({C}_{*}\) and the significance level, we constructed the graphs presented in Fig. 5a, b, which show the general behavior of this parameter as a function of α, considering, respectively, the SWT and Walker criteria (represented by solid lines). Additionally, in these same figures, we present a curve that represents the relationship, \(K\), between the nominal life \(N({P}_{*}, \widehat{C}, \widehat{k}, \widehat{\gamma })\) (calculated based on the data available in Table 3), and the respective estimated life through the adjusted fatigue curves, \(N({P}_{*}, \widehat{C}, \widehat{k}, \widehat{\gamma }, \alpha )\), (represented by dashed lines). Note that this \(K\)-factor value represents the level of deviation of the curve that represents the conservative prediction factor from the nominal fatigue curve (estimated by the parameters presented in Table 3). Note that this value of the K factor represents the level of distance between the curve estimated for a specific alpha value and the nominal fatigue curve (estimated by the parameters shown in Table 3), thus representing a kind of safety factor in terms of life.

Fig. 5
figure 5

Relationship between the significance level \(\alpha\) and the constants of the adjusted fatigue curves (solid line) and the distance measured in \(k\)-lifes between the nominal fatigue and the adjusted fatigue curves

Full size image

Upon analyzing the graphs presented in Fig. 5, it is evident that the value of \({C}_{*}\) decreases as the parameter \(\alpha\) decreases. This is due to the fact that the critical value of the t student distribution tends to assume increasing absolute values as \(\alpha\) decreases, thereby directly influencing the calculation of \({C}_{*}\). Additionally, we observe from the graphs in Fig. 5 that the value of \(K\) increases as the value of \(\alpha\) decreases—a trend that was expected from a qualitative perspective. It is worth noting that the value of \(K\) is intrinsically linked to the level of conservatism of the adjusted fatigue curve for a given value of \(\alpha\). In other words, a higher value of \(K\) implies a more conservative estimate of the fatigue life of the conductor. For instance, our results show that for an \(\alpha\) value of 2.5%, the value of \(K\) is approximately 2.7, while for an \(\alpha\) value of 0.01%, the value of \(K\) is on the order of 6. Hence, the appropriate selection of the α parameter allows for a more objective definition of the safety level for the fatigue project of the overhead conductors.

Figure 6 displays the trend curves adjusted according to the SWT and Walker criteria for significance levels α of 2.5% and 0.01%, respectively. To provide a comparison, Fig. 6 also presents a) the 179 experimental data for estimating the trend (nominal) curves according to the SWT and Walker criteria; b) the corresponding trend curves and the adjusted fatigue curves considering α values of 2.5% and 0.01%; and the Cigré Safe Border Line (CSBL).

Fig. 6
figure 6

Correlations between experimentally observed fatigue life and estimated equivalent stress amplitudes according to Smith–Watson–Topper (a) and Walker (b) criteria

Full size image

Analyzing the graphs in Fig. 6, we can observe the fit of the trend curves to the experimental data. Both the trend curves adjusted with the SWT criterion (Fig. 6a) and the trend curves adjusted with the Walker criterion (Fig. 6b) show good agreement with the experimental data. It is also important to note that when using the adjusted trend curves, the values of the SWT or Walker parameters that we can adopt for a given number of cycles are dependent on the level of significance α—that is, if these curves are considered design curves, the conservatism level of the design will be intrinsically associated with the significance level. In summary, considering a specific fatigue life, \(N\), we can then admit three conditions that can be related to the selection of the values of the SWT or Walker parameters \(\left({P}_{*}\right)\) by considering the predicted value for the parameter \(\left({P}_{{*}_{adj}}\right)\) estimated by means of a trend curve adjusted as a function of the statistical significance level, α, chosen for the hypothesis test associated with the confidence interval of the SWT or Walker parameter.

If \({P}_{*}\) is greater than \({P}_{{*}_{adj}}\), it means that the selected loading condition \(\left({\sigma }_{a}, {\sigma }_{m}\right)\) is greater than the expected capacity of the conductor to resist that loading condition, considering a significance level \(\alpha\). That is, the probability of failure is higher than \(\alpha\).

If \({P}_{*}\) is equal to \({P}_{{*}_{adj}}\), it means that the selected loading condition \(\left({\sigma }_{a}, {\sigma }_{m}\right)\) induces a level of stress equal to the expected capacity of the conductor, considering a significance level \(\alpha\). That is, the probability of failure is of the order of \(\alpha\).

If \({P}_{*}\) is less than \({P}_{{*}_{adj}}\), it means that the selected loading condition \(({\sigma }_{a}, {\sigma }_{m})\) induces a stress level lower than the expected capacity of the conductor, considering a significance level \(\alpha\). That is, the probability of failure is lower than \(\alpha\).

Still considering the information contained in Fig. 6, it is important to highlight that when compared to the fatigue curves estimated in this study, the Cigré Safe Border Line (CSBL) has proven to be an extremely conservative design curve, as it is located at a significant distance from the fatigue curve corrected for α equal to 0.01% (which already has a factor of approximately 6 times the measured lives). In addition to this high level of conservatism in the CSBL, it should also be noted that such a curve was not intended to represent the effect of mean stress on the fatigue behavior of conductors, which can lead to overly conservative designs and should be approached with caution.

6 Conclusions

Based on the analyses and discussions carried out in this article, the following conclusions can be made regarding the methods that were examined to account for the effects of stretching load on the fatigue behavior of conductor cables:

  • Considering the analyzed dataset, the Walker criterion provided the best life predictions. A simple regression procedure made it possible to identify that the Walker parameter, \(\gamma\), which best represents the fatigue behavior of conductor cables is of the order of 0.42, which allowed the construction of a fatigue curve that allows explaining 55% of failures due to fatigue (\({R}^{2}\)= 0.55) [38].

  • The Smith–Watson–Topper (SWT) method provides good results in most cases analyzed. The SWT method has the advantage of simplicity and is a good choice for general use. Considering this specific criterion, the fatigue curve generated allowed explaining about 54% of failures due to fatigue (\({R}^{2}\) = 0.54) [38]. It should be noted that the SWT criterion has the advantage of simplicity and, in general terms, for the analyzed situation, it proved to be, from a practical point of view, a criterion as accurate as Walker's criterion.

  • Additionally, we also discuss strategies for estimating adjusted trend curves considering the SWT and Walker criteria. As a result, we derive equations that can be used with design criteria based on the probability \(\alpha\), where the \(\alpha\) parameter is used to define the level of conservatism of the project, based on the probability of occurrence of failures.

  • The analysis of the results suggests that the CSBL curve presents a considerable level of conservatism compared to the Walker and SWT criteria.