Numerical investigation of wind-lens combinations for improving aerodynamic performance of an elliptical-bladed Savonius wind turbine

Abstract

Savonius turbines have potential for diverse applications. Despite their relatively low efficiency, the aerodynamic performance of Savonius rotors can be enhanced. This investigation seeks to examine the impact of different wind-lens combinations on the aerodynamic performance of a two-dimensional elliptical-bladed Savonius rotor. The study accomplished independence from both mesh elements and time-step size, and numerical results were juxtaposed against relevant experimental data. Four wind-lens configurations were tested, namely, diffuser (S1), nozzle diffuser (S2), diffuser brim (S3), and nozzle diffuser brim (S4), with a notable decrease in the power coefficient being observed at all tip speed ratios. Subsequently, modifications were made to these models for the Savonius rotor (S-M1, S-M2, S-M3, and S-M4) via changes to their positions and angles, resulting in significant improvements to the aerodynamic performance of the elliptical-bladed Savonius rotor. The maximum power coefficient was observed to be 0.227 at a tip speed ratio of 1.0 for the elliptical-bladed design, whereas the S-M4 model exhibited a maximum power coefficient of 0.404 at the same tip speed ratio.

1 Introduction

Global energy consumption has been increasing significantly since the industrial revolution. For many years, fossil fuels were the primary source of electricity production. However, due to the adverse effects of global warming, governments and companies have started investing in renewable energy resources, such as solar, geothermal, and wind energy.

Wind turbines generate electricity using the kinetic energy of the wind. There are two main types of wind turbines: Horizontal Axis Wind Turbines (HAWT) and Vertical Axis Wind Turbines (VAWT). Both have their own advantages and disadvantages. HAWTs are more efficient than VAWTs but they are expensive and unsuitable for residential areas. In contrast, VAWTs are simpler in structure and more suitable for urban areas. VAWTs can be further classified into two categories: Darrieus wind turbines, which have airfoil blade shapes, and Savonius wind turbines, which usually have basic blade geometry like C-shape. However, Savonius turbines are less efficient than Darrieus turbines. Consequently, researchers have conducted studies for decades to enhance the aerodynamic performance of Savonius wind turbines.

Various techniques have been explored to enhance the performance of Savonius turbines. Alizadeh et al. investigated the impact of a quarter barrier on the aerodynamics of a Savonius hydrokinetic turbine (Alizadeh et al. 2020). Thakur et al. improved the performance of a Savonius water turbine using an impinging jet duct design (Thakur et al. 2019). Garmana et al. examined the effects of blade number on a Savonius-Darrieus hybrid turbine and found that a hybrid design with two Savonius blades and three Darrieus blades showed superior aerodynamic performance compared to a design with three Savonius blades and three Darrieus blades (Garmana et al. 2021). Zakaria and Ibrahim studied the effect of twist angle on a Savonius rotor's starting capability (Zakaria and Ibrahim 2020). Marinić-Kragić et al. optimized a Savonius wind turbine using multiple circular-arc blades (Marinić-Kragić et al. 2022). Mrigua et al. investigated a multistage Savonius turbine equipped with elliptical blades using computational fluid dynamics (CFD) (Mrigua et al. 2020). Thiyagaraj et al. experimentally examined the effect of overlap ratio and blade number on the performance of a Savonius hydrokinetic turbine (Thiyagaraj et al. 2020). Mosbahi et al. conducted a CFD study to investigate the effect of different blade shapes on the performance of a Savonius water rotor (Mosbahi et al. 2021a). To optimize the blade profile of a Savonius rotor, Gallo and Chica used response surface methodology with four parameters (gap, overlap, eccentricity, and blade radius) (Gallo et al. 2022). Chang et al. employed the Taguchi optimization method to improve the performance of a Savonius rotor (Chang et al. 2021).

Some researchers examined wind-lens configurations or deflectors on the performance of VAWT’s. Kumar Pulijala and Singh studied the effect of a single deflector plate angle on the performance of a Savonius hydrokinetic turbine with a conventional blade design (Kumar Pulijala and Singh 2020). Manganhar et al. used a wind accelerator on a Savonius rotor with conventional-shaped blades (Manganhar et al. 2019). Mohamed et al. (Mohamed et al. 2019) and Tanürün and Acır (Tanürün and Acır 2022) investigated the wind-lens configuration, but for Darrieus wind turbines. Hesami et al. have conducted a comparable study to ours, exploring the wind-lens effect on a twin-rotor Savonius wind turbine (Hesami et al. 2022). Their wind turbine model incorporated two conventional semi-circular blades, and they examined the influence of rotational directions on its performance. In contrast, our model, which is based on elliptical-blades, differs from the classic semi-circular blade design of their turbine. We investigated the impact of wind-lens models angles and their positions on the performance of our model. It is noteworthy that their wind-lens model featured a diffuser, nozzle, and brim simultaneously. In comparison, we designed four different wind-lens models, including only a diffuser, nozzle diffuser, diffuser brim, and nozzle diffuser brim. No publication has been found that investigates the effect of different wind-lens configurations, their positions, and angles on the performance of an elliptical-bladed Savonius wind turbine.

In this study, the numerical investigation of the effects of different wind-lens combinations on the aerodynamic performance of an elliptical-bladed Savonius wind turbine was conducted. Various wind-lens models were developed to enhance the performance of the Savonius wind turbine. After modeling the Savonius turbine, the independence from the number of mesh elements and time-step size was tested. After validating the turbulence model, Kaya and Acır’s (Kaya and Acır 2022) elliptical-bladed Savonius wind turbine design was modeled. The power coefficient values of different elliptical-bladed Savonius wind turbine models with and without wind-lens configurations were then compared.

2 Material and method

2.1 Definitions of main parameters

Savonius wind turbines have different aerodynamic parameters compared to other types of turbines. The overlap ratio is an important factor in aerodynamic performance and can be calculated using the formula:

$$\beta = { }e/2R$$

(1)

Here, $e$. represents the overlap distance and depicts the blade curvature radius. The power coefficient $\left( {c_{P} } \right)$. is;

$$c_{p} = {{P_{t} } \mathord{\left/ {\vphantom {{P_{t} } {P_{w} }}} \right. \kern-0pt} {P_{w} }}$$

(2)

In this equation, ${P}_{t}$ is the observed power of the wind turbine and ${P}_{w}$ is the power of the wind. The values of ${P}_{t}$ and ${P}_{w}$ can be calculated using the following equations (Sharma and Sharma 2016);

$$P_{t} = { }T{*}\omega$$

(3)

$$P_{w} = { }0,5{*}\rho {*}A{*}U^{3}$$

(4)

In these equations, $T$ is the output torque, $\omega$ is the angular velocity, $\rho$ is the air density, $A$ is the swept area and $U$ is the wind speed.

$$A= D*H$$

(5)

$D$ represents the rotor diameter and H represents the height of the turbine. The moment coefficient $\left( {c_{M} } \right)$ is calculated with the following equations (Sahim et al. 2018);

$${c}_{M}=\frac{T}{\frac{1}{4}*\rho *A*{U}^{2}*D}$$

(6)

$${c}_{M}={c}_{P}/\lambda$$

(7)

Here, $\lambda$ represents a dimensionless number, known as the tip speed ratio (TSR).

$$\lambda = \frac{\omega *D}{2*U}$$

(8)

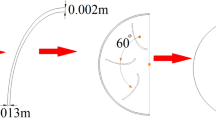
Savonius turbines operate by utilizing the difference between the drag forces acting on the advancing and returning blades (Hadi Ali 2013). Figure 1 presents a schematic view of a Savonius rotor and its working principle.

Fig. 1

A Schematic View and the Working Principle of a Savonius Wind Turbine

2.2 Modelling the Savonius rotor and the computational domain

Usually, classic semi-circular blades are used for Savonius rotors. In the present study, a two-bladed Savonius rotor was modeled in two dimensions to determine the most appropriate mesh structure, time-step size, and turbulence model, following (Fujisawa and Gotoh 1994). The modeled Savonius turbine has two classical C-shaped blades, with a diameter of 0.3 m, an overlap ratio of 0.15, and a blade thickness of 2 mm.

The inlet, top, and bottom sides were modeled at 10D, and the outlet side was modeled at 20D away from the center of the turbine. These distances were shown to be appropriate for numerical calculations (Wong et al. 2018; Zemamou et al. 2020). Symmetry boundary conditions were used for both the top and bottom sides, and an interface boundary condition was applied between the stationary and rotating domains to ensure flow continuity. Figure 2 shows the modeled wind turbine and computational domain.

Fig. 2

Modeled Savonius Turbine and the Computational Domain.

2.3 Mesh independence test

The aim was to create an optimal mesh structure that reduces solution time and provides the most accurate results. To achieve this, three different mesh structures were created, and the average ${c}_{P}$ values were calculated at $\lambda$ = 0,2. Figure 3 shows the ${c}_{M}$ values varying with azimuth angles $(\theta^\circ )$. To ensure mesh independence, a time step of 2°/step was chosen to complete the analyses more efficiently. The realizable $k-\varepsilon$ turbulence model was selected to conduct mesh independence tests.

Fig. 3

Coefficient of Moment ${(c}_{M})$ vs. Azimuth Angle $(\theta^\circ )$ for Different Numbers of Mesh Elements

The average ${c}_{P}$ values were calculated for the number of mesh elements of 39494, 90264, and 144024 as 0.108, 0.1098, and 0.1108, respectively. The difference between the calculated ${c}_{P}$ values for the number of mesh elements of 90264 and 144024 is less than 1%. Therefore, a mesh structure with 90264 mesh elements was used in the subsequent steps. Figure 4 displays the created mesh structure.

Fig. 4

Created Mesh Structure

As shown in Figure 4, the mesh density was increased near the blades. The maximum skewness value was found to be 0.61712. Furthermore, the average element and orthogonal quality were determined as 0.9624 and 0.9652, respectively. These values indicate that the created mesh design is suitable for numerical calculations (Mauro et al. 2019). Figure 5 displays the time required for ten full rotations with different numbers of mesh elements. As mentioned earlier, the mesh structure plays a crucial role in determining the solution time. All tests were conducted on a system equipped with an AMD Ryzen^TM 7 4800H processor (2.9 GHz base clock and 8-core) and 8GB of RAM.

Fig. 5

Number of Mesh Elements vs. Solution Time (min)

2.4 Determining the time-step size

The time-step size is a crucial factor in determining the solution time and can significantly impact the results. In this study, four different time-step sizes (6°, 3°, 2° and 1°) were chosen to investigate their effect on the calculated ${c}_{P}$ at $\lambda$ = 0,2 using the realizable $k-\varepsilon$ turbulence model. Figure 6 illustrates the ${c}_{P}$ values for different time-step sizes. The difference between the calculated ${c}_{P}$ values for 2° and 1° time-step sizes is less than 1%. Therefore, a 2° time-step size was used for the subsequent numerical simulations.

Fig. 6

Time Step-Size vs. Power Coefficient (${c}_{P}$)

2.5 Numerical validation and solver settings

In order to validate the methodology, it is necessary to verify all the CFD solver settings. In this study, three different turbulence models were selected to validate experimental results - namely the realizable $k-\varepsilon$, standard $k-\varepsilon$ and $k-\omega SST$. After creating the mesh structure and determining the optimum time-step size, the aim was to identify the most accurate turbulence model by comparing the numerical results with the experimental results (Fujisawa and Gotoh 1994). The ${c}_{P}$ values were calculated within the range of $\lambda$ = 0.2 and 1.4, and Figure 7 depicts the observed ${c}_{P}$ values for different turbulence models.

Fig. 7

Comparison of Numerical and Experimental Results

At lower values of $\lambda$, specifically ranging from 0.2 to 0.8, the standard $k-\varepsilon$ turbulence model yielded comparatively more precise outcomes. However, for $\lambda$ values greater than 0.8, the realizable $k-\varepsilon$ model exhibited superior performance in comparison to the other two turbulence models. Of note, the maximum power coefficient value was determined to occur at a $\lambda$ value of 0.8 with employment of realizable $k-\varepsilon$ turbulence model. At elevated values of $\lambda$, the realizable $k-\varepsilon$ turbulence model demonstrated a greater level of precision. Additionally, the realizable $k-\varepsilon$ turbulence model was deemed suitable for implementing simulations of rotating bodies (Mohamed et al. 2010), thus prompting its selection for employment in subsequent steps of the investigation.

The Second Order Upwind formulation was selected to solve the momentum, turbulence kinetic energy, and turbulent dissipation rate equations. To resolve the pressure-velocity coupling, the Coupled scheme was applied, while the Transient formulation was set to Second-Order Implicit. All numerical analyses were conducted using ASYSY FLUENT 2021 R2. The integral form of the Reynolds Averaged Navier-Stokes (RANS) equations was utilized, which can be expressed as (Ghazalla et al. 2019; Mosbahi et al. 2021b);

Continuity equation;

$$\frac{\partial }{{\partial_{{x_{i} }} }}(\overline{u}_{i} + \mathop u\limits_{i} ) \, = \, 0$$

(9)

Momentum equation;

$$\frac{\partial {\overline{u} }_{i}}{{\partial }_{t}}+{\overline{u} }_{j}\frac{\partial {\overline{u} }_{i}}{{\partial }_{{x}_{j}}}=-\frac{1}{\rho }\frac{\partial \overline{p}}{\partial {x }_{i}}+\frac{\mu {\partial }^{2}{\overline{u} }_{i}}{\rho \partial {x}_{i}\partial {x}_{j}}-\frac{\partial \overline{u}_{i}\overline{u}_{j}}{\partial {x}_{j}}$$

(10)

The continuity equation involves the average velocity (${\overline{u} }_{i}$), velocity fluctuation (úi), and flow direction ($x$) while the momentum equation includes the average pressure ($\overline{p }$), dynamic viscosity ($\mu$), and time ($t$).

Turbulent dissipation rate $(\varepsilon )$ and turbulent kinetic energy $(k)$ can be formulated as (Roy and Saha 2013; Kaya et al. 2020; Mosbahi et al. 2021b);

$$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial {x}_{j}}\left(\rho k{u}_{j}\right)=\frac{\partial }{\partial {x}_{j}}\left[\left(\mu +\frac{{\mu }_{t}}{{\sigma }_{k}}\right)\frac{\partial k}{\partial {x}_{j}}\right]+{G}_{k}+{G}_{b}-\rho \varepsilon -{Y}_{M}+{S}_{k}$$

(11)

$$\frac{\partial }{\partial t}\left(\rho \varepsilon \right)+\frac{\partial }{\partial {x}_{j}}\left(\rho \varepsilon {u}_{j}\right)=\frac{\partial }{\partial {x}_{j}}\left[\left(\mu +\frac{{\mu }_{t}}{{\sigma }_{\varepsilon }}\right)\frac{\partial \varepsilon }{\partial {x}_{j}}\right]+\rho {C}_{1}S\varepsilon -\rho {C}_{2}\frac{{\varepsilon }^{2}}{k+\sqrt{\upsilon \varepsilon }}+{C}_{1\varepsilon }\frac{\varepsilon }{k}{C}_{3\varepsilon }{G}_{b}+{S}_{\varepsilon }$$

(12)

$${C}_{1}=max\left[0.43,\frac{\eta }{\eta +5}\right], \eta =S\frac{k}{\varepsilon }, S= \sqrt{2{S}_{ij}{S}_{ij}}$$

(13)

In these equations, ${G}_{k}$ is the term of turbulence production because of the mean velocity gradient, ${G}_{b}$ is the term of turbulence production because of the average bouyancy, ${\sigma }_{k}$, ${\sigma }_{\varepsilon }$, ${C}_{1\varepsilon }$ and ${C}_{3\varepsilon }$ are constants of the $k-\varepsilon$ turbulence model. ${S}_{k}$ and ${S}_{\varepsilon }$ is the source terms and ${Y}_{M}$ is the impact of altering compressible turbulence dilatation on the overall dissipation rate.

Previous studies have shown that a minimum of 4-6 full rotations are required to minimize the impact of initial conditions (Rogowski and Maroński 2015). Therefore, ten full rotations of the Savonius turbine were simulated, and the average ${c}_{P}$ was computed by incorporating the turbine's final rotation. The time-step size (s) for 1° was determined using the following equation;

$$\Delta t (s)={(\omega *\frac{180}{\pi } deg)}^{-1}$$

(14)

3 Problem description

Kaya and Acır employed the Taguchi optimization method to enhance the aerodynamic characteristics of a Savonius rotor (Kaya and Acır 2022). Specifically, they modified the blade type, $\beta$, separation distance, and blade thickness of the turbine to optimize the value of ${c}_{P}$. Their investigation concluded that the two-bladed Savonius rotor featuring an elliptical blade, a $\beta$ of 0.15, a separation distance (s) of 7.5 mm, and a blade thickness of 2 mm demonstrated the most optimal aerodynamic performance. In light of these findings, the present study endeavors to build upon Kaya and Acır's design, seeking further enhancement of its performance. Figure 8 depicts the elliptical-bladed Savonius wind turbine created by (Kaya and Acır 2022).

Fig. 8

The Elliptical-Bladed Savonius Turbine

The performance of the elliptical-bladed design was computed, and a comparison of the resulting ${c}_{P}$ values for both the base design (refer to Figure 2) and the elliptical-bladed Savonius wind turbine is illustrated in Figure 9. Remarkably, the elliptical-bladed Savonius rotor outperformed the base design across all values of $\lambda$, affirming its superior aerodynamic performance. For more exhaustive information, readers are encouraged to refer to (Kaya and Acır 2022).

Fig. 9

Comparison of the Performance of Base and Elliptical Bladed Design

As noted in the introduction, incorporating a deflector or nozzle is a well-known strategy for enhancing the aerodynamic performance of a Savonius rotor. Tanürün and Acır employed wind-lens configurations to improve the performance of a Darrieus wind turbine (Tanürün and Acır 2022). In this study, various wind-lens combinations were implemented to evaluate their impact on the aerodynamic performance of an elliptical-bladed Savonius turbine. Firstly, the designs proposed by Tanürün and Acır were employed to examine the effect of diverse wind-lens configurations on the Savonius rotor, and geometric properties of the selected wind-lens combinations were kept constant in line with their prior study (Tanürün and Acır 2022). In Fig. 10, two and three-dimensional models of the wind-lens configurations are illustrated. Four distinct models were tested, namely the diffuser (S1), nozzle diffuser (S2), diffuser brim (S3), and nozzle diffuser brim (S4).

Fig. 10

A1) a 3D view of S1 model A2) a 2D view of S1 model B1) a 3D view of S2 model B2) a 2D view of S2 model C1) a 3D view of S3 model C2) a 2D view of S3 model D1) a 3D view of S4 model D2) a 2D view of S4 model and geometric properties

Figure 11 presents a comparison of the aerodynamic performances of the distinct wind turbine models. It is evident from the figure that the implementation of S1, S2, S3, and S4 configurations led to a considerable reduction in the aerodynamic performance.

Fig. 11

Comparison of Aerodynamic Performances of the Elliptical-Bladed, S1, S2, S3 and S4 Design

The maximum value of the power coefficient ${c}_{P}$ was calculated as 0.227 at $\lambda$ = 1.0 for the elliptical-bladed design, whereas the maximum ${c}_{P}$ was determined as 0.135, 0.12, 0.173, and 0.128 for S1, S2, S3, and S4 designs, respectively. In addition, optimal $\lambda$ values of 1.0 and 0.8 were obtained for S1 and S3, and S2 and S4 designs, respectively. Therefore, it can be observed that not only the maximum ${c}_{P}$ values declined but also the optimal $\lambda$ values were altered. Figure 12 shows ${c}_{M}$ values at $\lambda$ = 1,0 for different turbine designs.

Fig. 12

Moment Coefficient $({c}_{M})$ vs. Azimuth Angle $(\theta^\circ )$ for Elliptical-Bladed, S1, S2, S3 and S4 designs

More negative values of ${c}_{M}$ were observed with the S1, S2, and S4 models compared to the elliptical-bladed design, while the S3 design decreased the negative values of ${c}_{M}$. However, there was a considerable difference in positive ${c}_{M}$ values between the elliptical-bladed design and the other models. Consequently, the overall ${c}_{M}$ of the elliptical-bladed design was higher than the average ${c}_{M}$ of the other designs. Notably, two peak points where the maximum ${c}_{M}$ is observed correspond to the two blades of the modeled Savonius rotor.

In the subsequent phase of this investigation, four different wind-lens models were modified for the Savonius rotor with the aim of directing the wind to the advancing blade. This modification was expected to enhance the positive torque values with increasing wind speed. Figure 13 displays the four modified wind-lens models, namely the diffuser (S-M1), nozzle diffuser (S-M2), diffuser brim (S-M3), and nozzle diffuser brim (S-M4), whose geometric properties were kept the same as the S1, S2, S3, and S4 models.

Fig. 13

A1) a 3D view of S-M1 model A2) a 2D view of S-M1 model B1 and geometric properties) a 3D view of S-M2 model B2) a 2D view of S-M2 model C1) a 3D view of S-M3 model C2) a 2D view of S-M3 model D1) a 3D view of S-M4 model D2) a 2D view of S-M4 model

In Figure 14, a comparative analysis of the aerodynamic characteristics of the elliptical-bladed and the four modified wind-lens designs (S-M1, S-M2, S-M3, and S-M4) is presented.

Fig. 14

Comparison of Aerodynamic Performances of the Elliptical-Bladed, S-M1, S-M2, S-M3 and S-M4 Design.

The results indicate that the use of wind-lens models resulted in decreased ${c}_{P}$ at $\lambda$ = 0.2 for all designs. However, the S-M4 model increased the ${c}_{P}$ at $\lambda$ = 0.4, while other designs exhibited a reduction in ${c}_{P}$ at this value. Notably, for 0.4 < $\lambda$ < 1.2, all wind-lens models demonstrated an improvement in the aerodynamic performance of the Savonius rotor. At $\lambda$ = 1.2, the S-M3 design resulted in a decrease in ${c}_{P}$, whereas the S-M1, S-M2, and S-M4 models enhanced the performance of the Savonius rotor. Similarly, at $\lambda$ = 1.4, the S-M2 and S-M4 wind-lens models showed an improvement in ${c}_{P}$. Table 1 provides a detailed summary of the calculated ${c}_{P}$ values for each turbine design and the corresponding differences in aerodynamic performance compared to the elliptical-bladed design at different $\lambda$ values. Notably, the maximum ${c}_{P}$ values are highlighted for each design.

Table 1 Power Coefficient Values of Different Wind Turbine Designs

The maximum ${c}_{P}$ value of the elliptical-bladed design was found to be 0.227 at $\lambda$ = 1.0. However, the use of the S-M4 design resulted in an approximately 78% increase in ${c}_{P}$, up to 0.404 at $\lambda$ = 1.0. The S-M1, S-M2, and S-M4 designs increased the overall ${c}_{P}$ by 7.12%, 45.7%, and 44.6%, respectively, while the S-M3 design led to a decrease in the average ${c}_{P}$. Notably, the maximum ${c}_{P}$ of the S-M3 design was determined to be 0.316, 44.29% higher than that of the elliptical-bladed design.

The ${c}_{M}$ values for different models at different $\lambda$ values are presented in Figure 15. At $\lambda$ = 0.4, the S-M4 design demonstrated a significantly higher maximum ${c}_{M}$ compared to the elliptical-bladed design. However, the difference in overall ${c}_{M}$ values between the elliptical-bladed and S-M4 designs was only -4.27%. This can be attributed to the fact that the maximum negative ${c}_{M}$ of the S-M4 design is higher than that of the elliptical-bladed design. The ${c}_{M}$ values of the elliptical-bladed design were higher than those of the S-M4 design for θ values between 135° < θ < 180° and 315° < θ < 360°. At $\lambda$ = 0.6, the S-M2 modeled to maximized ${c}_{M}$ values around θ = 135° and 315°, with the maximum negative ${c}_{M}$ values being similar to those of the elliptical-bladed design. Overall, the S-M2 design demonstrated higher ${c}_{M}$ values than the elliptical-bladed and other designs at $\lambda$ = 0.6. At $\lambda$ = 0.8, 1.0, and 1.2, the S-M4 design demonstrated the maximum positive ${c}_{M}$ values, while the elliptical-bladed design had the maximum negative ${c}_{M}$ values. The S-M3 design demonstrated the maximum negative ${c}_{M}$ values at $\lambda$ = 1.4, with the minimum ${c}_{P}$, while the S-M2 design had the maximum average ${c}_{P}$ and the maximum positive ${c}_{M}$ values at $\lambda$ = 1.4. The maximum negative ${c}_{M}$ values increased with higher $\lambda$ values, reaching approximately -0.5 at $\lambda$ = 1.4, while the maximum positive ${c}_{M}$ values decreased at higher $\lambda$ values. These trends are consistent with those reported in previous studies (Kacprzak et al. 2013; Kaya et al. 2020; Asadi and Hassanzadeh 2021).

Fig. 15

Power Coefficient against $\theta$° at Different TSR Values

4 Conclusions

Vertical axis wind turbines (VAWTs) offer several advantages over their horizontal axis counterparts, such as lower cost and simpler structure. However, their efficiency is generally lower. In the context of VAWTs, the impact of wind-lens models on the aerodynamic performance of an elliptical-bladed Savonius rotor remains largely unexplored in the literature. Tanürün and Acır (2022) developed four different wind-lens models (i.e., diffuser (S1), nozzle diffuser (S2), diffuser brim (S3), and nozzle diffuser brim (S4)), and assessed their impact on the aerodynamic performance of a Darrieus wind turbine. In the current study, the same models were applied to investigate the effects of wind lens configuration on the aerodynamic characteristics of an elliptical-bladed Savonius wind turbine, using two-dimensional computational fluid dynamics (CFD) analyses. Furthermore, modified models were developed specifically for the Savonius rotor, with the aim of increasing wind speed around the advancing blade. Despite the existence of few comparable studies in the literature, as stated in the Introduction section, the impact of different wind-lens combinations and angles on the aerodynamic performance of a Savonius wind turbine with elliptical blades has not been investigated before.

Upon attaining independence from both the number of mesh elements and time-step size, the turbulence model was subjected to validation. The outcomes of the validation revealed that the realizable $k-\varepsilon$ turbulence model, particularly at higher $\lambda$ values, produced the most precise results. In this investigation, the Savonius wind turbine, featuring an elliptical blade, was modeled with due consideration given to the preceding study conducted by (Kaya and Acır 2022).

• In order to enhance the aerodynamic efficiency of an elliptical-bladed Savonius rotor, four distinct wind-lens models (Diffuser [S1], Nozzle Diffuser [S2], Diffuser Brim [S3], and Nozzle Diffuser Brim [S4]), as demonstrated in Figure 10, were implemented based on the research conducted by (Tanürün and Acır 2022).

• The results indicated a notable decrease in the aerodynamic performance of the Savonius rotor upon utilization of the Diffuser [S1], Nozzle Diffuser [S2], Diffuser Brim [S3], and Nozzle Diffuser Brim [S4] models, with maximum ${c}_{P}$ values of 0.135, 0.12, 0.172, and 0.128, respectively, as compared to the elliptical-bladed design's 0.227, as quantified in the present study.

• In total, four distinct models were modified for the Savonius rotor, as illustrated in Figure 13, with the purpose of augmenting the wind velocity around the advancing blade. This led to the creation of S-M1, S-M2, S-M3, and S-M4 models, for which the corresponding ${c}_{P}$ values were subsequently determined.

• The modified models improved the aerodynamic performance of the Savonius rotor in almost all cases. The maximum ${c}_{P}$ values were determined as 0,304 (at $\lambda$ = 0,8), 0,399 (at $\lambda$ = 1), 0,316 (at $\lambda$ = 0,8) and 0,404 (at $\lambda$ = 1) for the S-M1, S-M2, S-M3 and S-M4 designs, respectively.

It should be noted that the analyses were performed in two dimensions, which may limit the accuracy of the calculated power coefficient values as compared to experimental results. Furthermore, conducting three-dimensional studies would require more powerful computers, and investigating the effect of diffuser, brim, and nozzle angles on the aerodynamic performance of elliptical-bladed Savonius rotors could be a promising avenue for future research. Additionally, exploring the impact of modified designs on Savonius rotors with different blade structures and employing optimization techniques such as Taguchi optimization or response surface methodology could also prove fruitful.

Appendix 1

Spline Points for the Advancing Blade
Point No.	X (mm)	Y (mm)	Point No.	X (mm)	Y (mm)
1	− 7,5	− 150	29	62,622	− 74,832
2	− 2,5	− 149,83	30	62,213	− 72,784
3	2,5	− 149,38	31	61,79	− 70,837
4	7,5	− 148,6	32	61,29	− 68,826
5	12,5	− 147,5	33	60,51	− 66,053
6	17,5	− 146,1	34	59,8	− 63,775
7	22,5	− 144,28	35	59,13	− 61,775
8	27,5	− 142,15	36	58,157	− 59,243
9	30	− 140,88	37	56,664	− 55,694
10	34	− 138,7	38	55,107	− 52,416
11	38	− 136,18	39	54,124	− 50,473
12	41	− 134,1	40	52,656	− 47,764
13	45	− 131	41	51,328	− 45,53
14	48,29	− 128,06	42	49,541	− 42,665
15	50	− 126,1	43	47,628	− 39,785
16	52	− 123,57	44	46	− 37,415
17	54	− 120,76	45	44,089	− 34,86
18	56	− 117,54	46	39,786	− 29,328
19	58,01	− 113,73	47	36,273	− 25,092
20	59	− 111,55	48	31,765	− 19,9
21	60	− 109,03	49	26,39	− 14,015
22	61	− 106,12	50	21,93	− 9,391
23	62,3	101,323	51	17,178	− 4,762
24	63,15	-96,39	52	12,681	− 0,695
25	63,35	-91,62	53	7,81	3,35
26	63,65	-83,78	54	0,981	8,414
27	63,4	-80,537	55	− 3,011	11,066
28	63,075	-77,785	56	− 7,5	13,13