Study on power losses of angular contact ball bearings with and without thermal expansions of bearing components

Abstract

In this work, thermal expansions and thermal displacements of bearing components are firstly integrated into the dynamic model of ball bearings; on this basis, the contact loads, contact angles, sliding and spinning velocities of bearings are calculated to evaluate the heat generation for the heat sources of multi-node thermal network model. Then, thermal expansions and thermal displacements of bearing components are estimated through the multi-node thermal network model to adjust the dynamic model real time. Subsequently, the effects of dynamic behaviors of bearings with thermal expansions on the power loss are revealed under various rotational speeds and loads. Research results provide a theoretical basis for engineering application of angular contact ball bearings.

1 Introduction

Angular contact ball bearings, as key components of rotating machines, directly affect the performance and reliability of high-speed spindle as well as final operating accuracy and service life of rotating machines, because of sliding behaviors, thermal expansions and so on. Particularly, at high rotational speeds, too much friction-induced heat cannot be dissipated in time, leading to thermal expansions of bearing components to affect the power losses of bearings. Unfortunately, due to the interaction between mechanical behaviors and thermal expansions, the power losses of angular contact ball bearings have not been studied completely. Therefore, estimating the power losses of angular contact ball bearings is still a major issue at low and high speeds and light and large loads.

Presently, the experimental and theoretical studies on effect of frictional heat on the mechanical behaviors of bearings have been conducted by many scholars. The complete bearing load–deflection model including thermal expansion was established to study the dynamic behaviors of spindle/bearing systems [1]. A thermo–mechanical–dynamic model considering frictional heat is introduced into the spindle/bearing systems to investigate the overall spindle dynamics [2]. Also, the transient thermal network model of spindle/bearing systems was developed by considering thermal expansion and centrifugal deformation, in which power losses of bearings are calculated by the conventional estimation approach [3]. Considering the thermal expansion, centrifugal force and gyroscopic moment, a load equilibrium model of ball bearings was established to analyze the effect of structural constraints on the radial and axial heat transfers of the bearing system [4]. About the vibration-induced heat, this was also concerned to establish a multi-node thermal network model for heat generation with excitation force and vibration response [5]. To study the effects of structure and assembly constraints on power losses of high-speed angular contact ball bearings, the heat transfer model including various bearing’s sub-sources based on different heat generation mechanisms was developed [6]; on this basis, the transient heat transfer model according to local heat source analysis approach was established for accurately calculating heat generation rate of grease lubrication [7] and evaluating temperature rise of bearings under different load distributions and kinematic parameters of bearings [8]. These studies provide abundant modeling experiences for accurately establishing thermal network model of bearings, yet the prediction accuracy of power loss is still low by the quasi-static methods, which is difficult to estimate exactly tangential friction, viscous friction, differential slipping, spinning friction and elastic material hysteresis. Thus, the dynamic model of rolling bearings should be integrated into the transient thermal network model to predict the power loss. In the literature, numerous studies on the dynamic model of rolling bearings have been conducted by many scholars. The sliding between rollers and raceways, rotational and orbital speeds of rollers at various combined loads were analyzed by the established numerical model of ball bearings [9]. The dynamic behaviors of balls were revealed through the complete dynamic model including the interaction of bearing components and lubricant conditions [10]. Further, shaft speed, oil viscosity, combined loads and geometric structures were combined to study the skidding behavior of balls [11]. Moreover, an improved dynamic model according to the internal load distribution was established to analyze the sliding phenomenon in the bearing system [12]. The quasi-dynamic model was also used to study the effect of centrifugal force, gyroscopic moment on power loss despite it could not be appropriate for time-varying working conditions [13], based on which, the time-varying load conditions [14] and nonlinear contact forces and EHL offset forces [15] were adopted to improve the quasi-dynamic model of ball bearings for accurately evaluating the skidding behavior of rolling bearings. Additionally, the discontinuous contact between cage and balls, centrifugal and gyroscopic effects were considered to establish the dynamic model for analyzing the sliding friction behavior of ball bearings [16]. By comprehensively considering the effects of hydrodynamic lubrication, thermal generation, Hertzian contact and kinematics of bearing components, the nonlinear dynamic model was improved to analyze the differential slipping, spinning and elastic hysteresis behaviors of high-speed ball bearings [17]. Also, the stiffness and damping characteristics of oil film were integrated into the nonlinear dynamic model to analyze the slipping, spinning and elastic hysteresis behaviors of the ball [18]. And, the time-varying asperity friction and lubricant shearing action were employed to evaluate accurately the differential sliding, rolling resistance and hysteresis damping of ball bearings [19]. These dynamic models mentioned above generally neglected the effect of thermal expansion of bearing components induced by frictional heat on the dynamic behaviors of bearings during the process of temperature rise. Actually, the thermal expansion causes the change in contact state between balls and raceways, as well as between bearings and shaft and housing, which generate additional preload, and axial/radial displacements of bearings; accordingly, developing a dynamic model of ball bearings with thermal expansions of bearing components is essential for accurately predicting the power losses.

In this work, the power loss of bearings calculated by the dynamic model developed by Qian et al. [20] is converted into temperature distribution of bearings through the thermal network model to modify the structural parameters in real time according to the thermal expansion theory, which can attain the interaction of dynamic behaviors with temperature rise in the bearing system; thus, the accurately dynamic behaviors of bearings can be attained with respect to the previous dynamic models. Then, the power loss and dynamic behaviors of bearings with thermal expansions can be studied under various rotational speeds and loads.

2 Dynamic model of ball bearings with thermal expansions of bearing components

In this work, the macro-geometry of bearings is assumed constant throughout the analysis, with no consideration for ring flexibility, as the supports of inner and outer rings are assumed fully rigid. Inner and outer raceways and balls are assumed ideal without waviness.

2.1 Thermal expansions and thermal displacements in bearing components

Thermal expansion ϑ_ba of balls can be solved as follows [7]:

$$\vartheta_{{{\text{ba}}}} = \chi_{{{\text{ba}}}} \Delta T_{{{\text{ba}}}} \frac{{d_{{{\text{ba}}}} }}{2}.$$

(1)

For thermal expansion of inner ring and shaft, they can be identified as thin-walled rotary units. Thus, their thermal expansion can be given by:

$$\vartheta _{{{\text{ru}}}} = \chi _{{{\text{ru}}}} \Delta T_{{{\text{ru}}}} d_{{{\text{ru}}}}$$

(2)

On this basis, radial expansion ϑ_i of inner ring considering the thermal interaction of shaft and inner ring is calculated as follows:

$$\vartheta _{{\text{i}}} = \chi _{{\text{i}}} \Delta T_{{\text{i}}} d_{{{\text{ik}}}} + \left[ {\chi _{{{\text{sat}}}} \Delta T_{{{\text{sat}}}} \left( {1 + \Omega _{{{\text{sat}}}} } \right) - \chi _{i} \Delta T_{i} } \right]\frac{{d_{{{\text{ik}}}}^{2} }}{{d_{{{\text{il}}}} }}$$

(3)

Owing to the restriction of bearing house on thermal expansion of outer ring, radial thermal expansion ϑ_o of outer ring is expressed as follows:

$$\vartheta _{{\text{o}}} = \chi _{{\text{h}}} \Delta _{{\text{h}}} \left( {1 + \Omega _{{\text{h}}} } \right)d_{{\text{h}}}$$

(4)

Thermal expansion of outer ring changes the position of balls, as shown in Fig. 1a. The thermal displacement ϑ_onl of balls along normal contact direction is described as follows:

$$\vartheta _{{{\text{onl}}}} = \vartheta _{{\text{o}}} \cos \alpha _{{\text{o}}}$$

(5)

Fig. 1

Displacement of bearing components with thermal expansion: a between balls and outer ring, b between balls and inner ring

ϑ_onl acting on the ball leads to a relative displacement between balls and inner ring, as follows:

$$\vartheta _{{{\text{inl}}}} = \vartheta _{{{\text{onl}}}} \cos \left( {\alpha _{{\text{i}}} - \alpha _{{\text{o}}} } \right)$$

(6)

where ϑ_inl is the displacement along contact direction between balls and inner ring. Next, axial and radial displacements (ϑ_ix and ϑ_iz) of inner ring can be obtained as below:

$$\vartheta _{{{\text{ix}}}} = \vartheta _{{{\text{inl}}}} \sin \alpha _{{\text{i}}}$$

(7)

$$\vartheta _{{{\text{iz}}}} = \vartheta _{{{\text{inl}}}} \cos \alpha _{{\text{i}}}$$

(8)

For centrifugal expansion ϑ_icen of inner ring, it can be estimated by:

$$\vartheta _{{{\text{icen}}}} = \frac{{\rho _{{\text{i}}} \omega _{i}^{2} }}{{32E_{i} }}d_{\ell } \left[ {d_{{\text{i}}}^{2} \left( {3 + \Omega } \right) + d_{\ell }^{2} \left( {1 - \Omega _{{\text{i}}} } \right)} \right]$$

(9)

Axial and radial displacements (ϑ_bax and ϑ_baz) of balls induced by thermal expansion, as shown in Fig. 1b, are given by:

$$\vartheta _{{{\text{bax}}}} = \vartheta _{{{\text{ba}}}} \sin \alpha _{{\text{i}}}$$

(10)

$$\vartheta _{{{\text{baz}}}} = \vartheta _{{{\text{ba}}}} \cos \alpha _{{\text{i}}}$$

(11)

2.2 Ball equilibrium position with thermal expansion

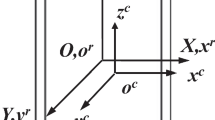
When working, the thermal expansions and thermal displacements in bearing components markedly affect the ball equilibrium position to change the interactions between balls, cage and bearing rings. To describe this phenomenon conveniently, three coordinate systems are employed, as shown in Fig. 2.

Fig. 2

Definition of three coordinate systems for bearing dynamics

The first coordinate frame (o- xyz) fixed at the bearing center is the global reference system, in which inner ring is deflected around y and z axes and translated along x, y and z axes. The second coordinate frame (o- x′y′z′) is positioned at the center of ball, and it rotates along the x axis of the global reference system (o- xyz), in which angular velocity components ω_x′, ω_y′ and ω_z′ around x′, y′ and z′ for the ball can occur. The third reference system (o- x_cy_cz_c) is defined with major axis x′′, minor axis y′′ and z′′ axis perpendicular to the contact patch between balls and raceways. On this basis, the new equilibrium position (X_1j, X_2j) of balls with thermal expansions can be expressed by the Pythagoras’ theorem from Fig. 3.

$$\begin{gathered} \left( {Bd_{{{\text{ba}}}} \sin \alpha ^{{\text{0}}} + \delta _{{\text{x}}} + \Re _{i} \theta \cos \psi _{{\text{j}}} + \vartheta _{{{\text{bax}}}} + \vartheta _{{{\text{ix}}}} - X_{{1j}} } \right)^{{\text{2}}} + \hfill \\ \left( {Bd_{{{\text{ba}}}} \cos \alpha ^{{\text{0}}} + \delta _{z} \cos \psi _{j} + \vartheta _{{\text{i}}} + \vartheta _{{{\text{icen}}}} - \vartheta _{{{\text{b}}az}} - \vartheta _{{{\text{iz}}}} - X_{{2{\text{j}}}} } \right)^{2} = \left( {\left( {f_{o} - 0.5} \right)d_{{{\text{b}}a}} + \delta _{{{\text{oj}}}} - \vartheta _{{{\text{b}}a}} } \right)^{2} \hfill \\ \end{gathered}$$

(12)

$$X_{{1{\text{j}}}}^{2} + X_{{{\text{2j}}}}^{2} = \left( {\left( {f_{o} - 0.5} \right)d_{{{\text{b}}a}} + \delta _{{{\text{oj}}}} - \vartheta _{{{\text{b}}a}} } \right)^{2}$$

(13)

where B = f_i + f_o −1, f_i = ƛ_i/(d_ba + ϑ_ba), f_o = ƛ_o/(d_ba + ϑ_ba).

Fig. 3

Ball equilibrium position with thermal expansion and thermal displacement

Considering this equilibrium position of the ball with thermal expansion, the dynamic model of ball bearings can be improved to calculate the dynamic behaviors (contact loads, contact angles, sliding and spinning velocities) of bearings for accurately predicting the heat generation.

2.3 Heat generation

Friction heat of ball bearings is closely associated with these time-varying factors (shearing action and viscous effect of lubricant, differential slipping and spin motion of balls, elastic material hysteresis of raceways and so on) at temperature rise. To describe the temperature domain of bearings in detail, the five kinds of power losses are predicted and distributed to the thermal network model of bearings according to various heat generation and heat-induced objects. Power losses caused by various inducing factors are formulated as follows [21,22,23]:

Tangential friction loss P_L caused by the shearing action of lubricant is given by:

$$P_{{\text{L}}} = {\text{n}}_{{{\text{b}}a}} \omega_{{\text{m}}} {\text{d}}_{{{\text{b}}a}} \int_{ - a}^{a} {\int_{{ - b\sqrt {1 - \left( {x^{\prime\prime}/a} \right)^{2} } }}^{{b\sqrt {1 - \left( {x^{\prime\prime}/a} \right)^{2} } }} {\eta \left( {p\left( {x^{\prime\prime},y^{\prime\prime}} \right),T} \right)} } \frac{{\Delta u\left( {x^{\prime\prime},y^{\prime\prime}} \right)}}{{{\text{H}}\left( {x^{\prime\prime},y^{\prime\prime}} \right)}}dx^{\prime\prime}dy^{\prime\prime}$$

(14)

Viscous friction loss P_v generated by the oil–air mixture is obtained by:

$$P_{{\text{v}}} = {\text{n}}_{{{\text{b}}a}} \omega_{{\text{m}}} {\text{F}}_{v} d_{\ell } /2$$

(15)

where F_v is viscous drag force imposing on balls, d_ℓ is bearing pitch diameter.

Differential slipping loss P_t induced by the differential slipping between balls and raceways is described by:

$$P_{{\text{t}}} = {\text{n}}_{{{\text{b}}a}} \int_{ - a}^{a} {\int_{{ - b\sqrt {1 - \left( {x^{\prime\prime}/a} \right)^{2} } }}^{{b\sqrt {1 - \left( {x^{\prime\prime}/a} \right)^{2} } }} {\mu \left( {x^{\prime\prime},y^{\prime\prime}} \right)p\left( {x^{\prime\prime},y^{\prime\prime}} \right)\Delta u\left( {x^{\prime\prime},y^{\prime\prime}} \right)} } dx^{\prime\prime}dy^{\prime\prime}$$

(16)

where μ_{(x’’,y’’)} is asperity friction coefficient.

Spinning friction loss P_s created by the spin motion of balls can be calculated by:

$$P_{{\text{s}}} = {\text{n}}_{{{\text{b}}a}} \omega_{{\text{s}}} \int_{ - a}^{a} {\int_{{ - b\sqrt {1 - \left( {x^{\prime\prime}/a} \right)^{2} } }}^{{b\sqrt {1 - \left( {x^{\prime\prime}/a} \right)^{2} } }} {\mu \left( {x^{\prime\prime},y^{\prime\prime}} \right)p\left( {x^{\prime\prime},y^{\prime\prime}} \right)\sqrt {x^{{\prime\prime}{2}} + y^{{\prime\prime}{2}} } } } dx^{\prime\prime}dy^{\prime\prime}$$

(17)

Rolling friction loss P_ɩ produced by the elastic material hysteresis is represented by:

$$P_{\iota } = {\text{n}}_{{{\text{b}}a}} \left( {\frac{{{2}\varepsilon Q_{{\text{i}}} a_{{\text{i}}} \left( {d_{\ell } - 2\delta_{{\text{i}}} } \right)}}{{3\pi d_{{{\text{b}}a}} }} + \frac{{{2}\varepsilon Q_{{\text{o}}} a_{{\text{o}}} \left( {d_{\ell } + 2\delta_{{\text{o}}} } \right)}}{{3\pi d_{{{\text{b}}a}} }}} \right)\omega_{{\text{m}}}$$

(18)

Due to the heat transfer between bearing components, these friction heats can induce the thermal expansions and thermal displacements in bearing components real time; for this, establishing the thermal network model of bearings in Sect. 2.4 is essential for accurately predicting the temperature rise of bearing components.

2.4 Thermal network model

2.4.1 Node planning

For the heat transfer of bearings, some investigations on the thermal network scheme are conducted by many scholars [3, 4, 8,9,10]. Global and local methods on the layout of heat sources in the bearing system are employed and compared, indicating that local method comes closer to the truth. Also, heat conduction, heat convection and thermal contact resistances between bearing components are considered for the heat transfer of bearings. Furthermore, assembly constraints are integrated into the seven-node thermal network to constitute the multi-node model, in which axial conduction is emphasized to further improve the prediction accuracy of heat transfer in the bearing system. Particularly, cooling units and coolant passage are modeled to facilitate the thermal estimation. These experiences provide references for the establishment of thermal network model in this work, and the proposed multi-node network model is detailed, as illustrated in Fig. 4.

• (1) Due to lubricant shearing friction, differential slipping friction and rolling friction caused by elastic material hysteresis which are inseparable with balls and raceways, nodes 44 and 45 are planned to represent the accumulation of their friction heats (P_L, P_t and P_ɩ). Thus, these friction heats can be transmitted to raceways and balls through resistances R_44-19, R_45-7, R_44-17 and R_45-13.

• (2) Node 43 denotes heat source P_v induced by oil–air viscosity, which is transferred to balls and oil–air through R_43-16 and R_16-15. Additionally, node 15 is set to represent spinning friction loss P_s.

• (3) For calculating heat convection between bearing components, bearing cavity and oil–air, inner surface of outer ring, outer surface of inner ring, outer surface of cage and oil–air in the chamber are represented by nodes 10, 22, 18 and 43, respectively. Owing to friction heat transferring to balls and outer/inner ring, it is also necessary to plan nodes 13, 7, 17 and 19.

• (4) For thermal contact conduction, the paired nodes 2–5, 4–8 and 11–31 are arranged to predict the temperature variation between bearing and housing. The paired nodes 24–29, 21–27 and 12–37 are employed to characterize the thermal contact conduction between bearing, retainer and shaft.

• (5) Because it is inevitable for heat transfer along axial direction, nodes 11 and 12 are planned along axial direction of outer ring, as well as nodes 25 and 26 along axial direction of inner ring.

• (6) The substructures outside of bearings are simplified to facilitate the development of multi-node network model. Oil–air channel and return line are neglected because of their less influence on heat transfer. Additionally, more details are described in Table 1.

Fig. 4

Thermal network model considering five kinds of heat sources and assembly relations

Table 1 Description of nodes’ planning

2.4.2 Thermal network analysis and development

To express heat conduction and heat convection for high-speed bearings and other accessories under oil–air lubrication, one-dimensional thermal conduction, thermal contact transmission and thermal convection in [4] are referenced to build the thermal grid model. Here, convective heat resistances depend on Nusselt number N_u, and thus, N_u is discussed for its utilization and selection according to engineering practices.

Because of oil–air taking away heat from bearing chamber, the equivalent resistance is given by [6]:

$$ER = \frac{1}{{\rho_{{{\text{eff}}}} q_{{{\text{eff}}}} C_{p} }}$$

(19)

where q_eff is flow of oil–air, and C_p is specific heat.

For each node before thermal balance, its temperature variation obeys to Eq. (20), as follows [31]:

$$qhf_{\lambda } = C_{{p_{\lambda } }} \rho_{\lambda } V_{{N_{\lambda } }} \frac{{dT_{\lambda } }}{dt}$$

(20)

where qhf_λ is net heat flux, ρ_λ is material density, V_Nλ is specific heat, dT_λ/dt means temperature rise rate at the _λth node. Thus, according to the principle of two-dimensional heat transfer system, the transient thermal balance equation can be expressed as follows [4]:

$$\frac{{T_{0}^{k + 1} - T_{1}^{k + 1} }}{{ER_{0 - 1} }} + \frac{{T_{0}^{k + 1} - T_{2}^{k + 1} }}{{ER_{0 - 2} }} + \frac{{T_{0}^{k + 1} - T_{3}^{k + 1} }}{{ER_{0 - 3} }} + \frac{{T_{0}^{k + 1} - T_{4}^{k + 1} }}{{ER_{0 - 4} }} = qhf_{0} - C_{p0} \rho_{0} V_{N0} \frac{{T_{0}^{k + 1} - T_{0}^{k} }}{dt}$$

(21)

By importing these equations to the entire thermal network mentioned above, the transient thermal analysis can be conducted. The flow chart for solving the dynamic model with thermal expansions of bearing components is illustrated in Fig. 5. This novel model converts the power loss into temperature distribution of bearings through the thermal network model to correct the structural parameters in real time so that the accurately dynamic behaviors of bearings can be attained with respect to the previous dynamic models.

Fig. 5

Flowchart of dynamic model of angular contact ball bearings with thermal expansions

3 Model validation

In this work, 7008C angular contact ball bearing is considered as the study object to validate the reliability of proposed dynamic model, and its partial structural parameters are listed in Table 2. Material properties of components are listed in Table 3, and relevant calculation parameters are presented in Table 4. Ambient temperature of node 0 is assumed to be 26 °C, and heat convection of nodes 28 and 30 between hollow shaft and air is presumed to be thorough and T₂₈ = T₃₀ = 26 °C. The temperature at nodes 38, 40 and 42 at retainer is considered as the ambient temperature. Air flow rate is 1 × 10^–3 m³/s, and oil flow rate is 0.4 ml/h.

Table 2 7008C ball bearing structure and lubrication parameters

Table 3 Material properties on parts [4]

Table 4 Heat transfer calculation parameters [4]

To validate the reliability of the proposed model, the rotation speed of inner ring ω_i is set as 15,000 r/min. Radial force F_z is defined as 0 N, and axial force F_x is varied from 50 to 1000 N. Temperature of outer ring on node 5 calculated based on this proposed model is compared with the tested results. The experimental rig of high-speed ball bearings is as shown in Fig. 6, and its technical data are shown in Table 5. Temperature sensors are assembled away from the nozzle and contacted with outer surface of outer ring. Thus, the comparison of temperature between calculated and tested results can be conducted, as shown in Fig. 7.

Fig. 6

Experimental rig of angular contact ball bearings

Table 5 Technical data of experimental apparatus

Fig. 7

Illustration of a calculated results at various axial forces and b comparison of temperature between calculated and tested results

Temperature rise of outer ring during the iterative calculation is presented in Fig. 7a, and its variation in convergent state with increasing axial force is described in Fig. 7b. It is shown in Fig. 7b that the variation trend of calculated results is consistent with that of tested ones. The deviations between calculated and tested ones are attributed to the higher oil temperature during operation compared with room temperature in the thermal network model, and they are less than 5% at various axial forces. This suggests that the proposed model is reliable.

During the process of temperature rise at different axial loads, angular velocities ω_x′, ω_y′ and ω_z′ for the ball of j = 1 with varying time and axial loads are shown in Fig. 8. In convergent state, angular velocity ω_x′ is gradually reduced with increasing axial force until it has no obvious change, while angular velocity ω_z′ is increased gradually when F_x < 300 N; then, it has no markedly fluctuation, and angular velocity ω_y′ is decreased gradually with increasing axial force until it is reduced to 0 rad/s. These variation rules are in good agreement with the research results of Han [17]. The different original values cause the discrepancies of the iterative calculations between these proposed results and Han’s ones. Besides, the difference in the variation of ω_x′, ω_y′ and ω_z′ with thermal expansion (TE) and without thermal expansion (WTE) is caused by the thermal expansions of balls and inner and outer rings. Therefore, this proposed model is believable for the study on the power losses of ball bearings.

Fig. 8

Variation of angular velocity components with time and axial loads a ω_x′, b ω_y′ and c ω_z′ and d variation of ω_x′(absolute), ω_y′ and ω_z′ in the convergent state with thermal expansion (TE) and without thermal expansion (WTE)

4 Results and discussion

4.1 Light and large loads

According to the variation rule of three angular velocities shown in Fig. 8d, light loads {50, 100, 150, 200} N and large loads{400, 600, 800, 1000} N are selected to study the power losses of angular contact ball bearings with and without thermal expansions; at this moment, rotation speed of inner ring ω_i is set as 15,000 r/min, and radial force F_z is defined as 0 N. Figure 7a describes the temperature rise process at various axial loads. With temperature rising, thermal expansions of ball and inner and outer rings at light and large loads are represented in Fig. 9. It is observed that at any load, thermal expansion of inner ring is larger than that of outer ring in the initial phase of temperature rise, yet in the later period, thermal expansion of outer ring exceeds that of inner ring, while very small expansion of the ball is generated in this process of temperature rise. Importantly, at any load, the difference of thermal expansion between outer and inner rings is maximized near iteration step of 900 during the iterative calculation, which indicates that the ball is extruded by inner and outer raceways, inducing significant increases in contact loads of inner and outer raceways near iteration step of 900, as shown in Fig. 11. Moreover, in the initial phase, the difference in thermal expansions of inner and outer rings causes the increase in radial distance A_2j between groove curvature centers of inner and outer raceways; at this moment, inner ring is shifted by the increased contact load along negative axial direction to balance the axial force. In the later period, thermal expansion of outer ring exceeding that of inner ring leads to the decrease in radial distance A_2j and in extrusion of balls by inner and outer raceways; as a result, inner ring is moved along positive axial direction by the axial force to achieve the force balance of bearings. Thus, the locus of raceway groove curvature centers can be obtained, as shown in Fig. 10. Additionally, in the convergent state, thermal expansions of ball and inner and outer rings at light loads are decreased gradually when axial force is increased, while at large loads, they are increased gradually with increasing the axial force, which is depended on temperature rise at different axial forces.

Fig. 9

Thermal expansions of ball and inner and outer rings at light and large loads: a light loads and b large loads

Fig. 10

Axial and radial distances between groove curvature centers of inner and outer raceways: a light loads and b large loads

From Fig. 11, it can be seen that at a certain axial force, contact load is small when starting iterative calculation (at room temperature) relative to that at other iteration steps. Subsequently, inner ring is thermal expanded rapidly to compress the ball, leading to significant increases in contact loads. Until the convergent state, thermal expansion of outer ring exceeds that of inner ring to relieve contact loads Q_o and Q_i. Moreover, at light loads, no obvious difference in contact loads of inner and outer raceways appears between room temperature and temperature rise (as shown in Fig. 11), yet at large loads, contact loads with thermal expansion are markedly larger than that at room temperature.

Fig. 11

Contact loads between a ball and inner and outer rings during iterative calculation: a outer ring, b inner ring and c contact loads at initial (WTE) and final (TE) iterations

From Fig. 12, it can be found that at beginning of iteration step (at room temperature), large contact angles between balls and inner and outer raceways are needed to decompose much contact load to equilibrate the axial force, so contact angle is large with respect to that at other iteration steps. When temperature rises, extrusion of balls by thermal deformation of inner and outer rings produces larger contact loads in the initial phase so that contact angle is reduced to attain the equilibration between axial component of contact loads and axial force. In the later period, the relaxation in extrusion of balls leads to the decrease of contact loads, causing the appropriate increase of contact angle to equilibrate the axial force.

Fig. 12

Contact angles between balls and raceways during iterative calculation: a outer ring, b inner ring and c contact angles at room temperature and at final temperature rise

From Fig. 12c, it can be found that for light loads at room temperature (WTE), contact angle of outer ring is markedly reduced by centrifugal force of balls, as a result of which contact angle of inner ring is obviously increased to intensify axial component of contact loads to balance the axial force, and contact angle of inner ring is gradually reduced with increasing axial force, yet contact angle of outer ring is gradually increased. For large loads, contact angles of inner and outer rings are gradually increased with increasing axial force for equilibrating the axial force. At final temperature rise, thermal expansions of ball and inner and outer rings induce extrusion to enhance contact loads, causing the increase in the axial component of contact loads to equilibrate the axial force; thus, contact angle of inner ring is gradually decreased when axial force is intensified gradually. For contact angle of outer ring, it is obviously increased by the improved contact loads at light loads, yet at large loads, no significant increase occurs when axial force is increased, which is attributed to thermal expansion improving the axial component of contact loads rather than contact angle. Additionally, contact angles of inner and outer rings at room temperature are larger than that at final temperature rise.

As shown in Fig. 13, total power loss P_T without thermal expansion is larger than that with thermal expansion at light loads, yet it without thermal expansion is less than that with thermal expansion at large loads, which is closely related to five kinds of power losses.

Fig. 13

Variation of power losses with and without thermal expansion when axial force is changed: a total power losses P_T, b differential slipping power loss P_t and tangential friction power loss P_L, c spinning friction power loss P_s, d Rolling friction power loss Pɩ and viscous friction power loss P_v

For differential slipping power loss P_t, it is mainly depended on sliding speed and contact loads. At light loads, sliding speed at room temperature is larger than that at temperature rise, but at large loads, microscopic sliding of balls occurs so that sliding speed is very small, as shown in Fig. 14a. Combining with the variation of contact loads (as shown in Fig. 11c,) it can be deduced that P_t without thermal expansion is larger than that with thermal expansion at light loads, and yet, at large loads, extrusion of balls induced by thermal expansion significantly enhances contact loads resulting in P_t being increased relative to that at room temperature.

Fig. 14

Illustration of: a sliding velocity△u, b spinning velocities ω_si and ω_so, c oil film thickness H_o and H_i

For tangential friction power loss P_L, it is closely associated with sliding speed and film thickness. Oil film thickness at room temperature is almost the same as that at temperature rise, as presented in Fig. 14c. Thus, macroscopic sliding of balls induces tangential friction power loss P_L at light loads, but at large loads, no tangential friction appears due to microscopic sliding of balls so that P_L is almost 0.

For spinning friction power loss P_s, it is mainly attributed to spinning velocities and contact loads. When F_x is 50 N, the contacts between balls and raceways difficultly build enough drag moments so that angle velocity ω_x′ is slightly reduced relative to that at F_x = 100 N; thus, P_s at F_x = 50 N is smaller than that at F_x = 100 N according to spinning velocities (as shown in Fig. 14b). Moreover, spinning velocities are gradually reduced with increasing axial forces resulting in that, P_s is being firstly reduced and then increased gradually.

For viscous friction power loss P_v, its slight variation is mainly depended on rotational speed of cage. Thus, almost no difference appears between without thermal expansion and with thermal expansion.

For rolling friction power loss Pɩ, it is gradually increased with enhancing axial force and rotation speed of inner ring, which is mainly attributed to the contact loads of balls. As a result, a difference appears at large loads between without thermal expansion and with thermal expansion.

According to these descriptions mentioned above, the difference of total power loss between without thermal expansion and with thermal expansion is mainly depended on differential slipping power loss and tangential friction power loss at light loads, and it is significantly attributed to differential slipping power loss and rolling friction power loss at large loads.

4.2 Low and high speeds

To study the effect of low and high speeds on the power loss of bearings at room temperature and final temperature rise, light axial force of 100 N and large one of 1000 N are selected and rotation speed ω_i is varied from 2000 r/min to 16,000 r/min. Radial force F_z is defined as 0 N. The final temperature of outer ring on node 5 is shown in Fig. 15a. It is clear that the temperature without thermal expansion is larger than that considering thermal expansion at 100 N, and yet, it is just the opposite at 1000 N, which is closely related to five kinds of power losses without and with thermal expansion.

Fig. 15

Temperature of outer ring and five kinds of power losses at varied rotation speeds for F_x = 100 N and 1000 N: a temperature of outer ring, b tangential friction power loss P_L, c differential slipping power loss P_t, d spinning friction power loss P_s, e Rolling friction power loss Pɩ and f viscous friction power loss P_v

For power loss P_L, it is mainly affected by sliding speeds because film thickness without thermal expansion has little difference relative to that considering thermal expansion (as shown in Fig. 16). At light loads, sliding speed of inner ring at room temperature is larger than that at final temperature rise, and their difference is improved gradually when rotation speed of inner ring is increased gradually, despite no obvious difference occurs for sliding speed of outer ring between room temperature and final temperature rise, as shown in Fig. 17a. Thus, P_L without thermal expansion is larger than that considering thermal expansion at 100 N light load. At large loads, sliding speed of inner ring at room temperature is smaller than that at final temperature rise through it is significantly restrained by contact load; as a result, P_L at final temperature rise is larger than that at room temperature at large loads according to Eq. (14).

Fig. 16

Center film thickness at varied rotation speeds without and with thermal expansion for F_x = 100 N and 1000 N

Fig.17

Sliding speeds and spinning speeds at varied rotation speeds for F_x = 100 N and 1000 N: a F_x = 100 N, b F_x = 1000 N, c F_x = 100 N and (d) F_x = 1000 N

For power loss P_t, contact loads at final temperature rise are larger than that at room temperature at light loads through sliding speeds at final temperature rise are smaller than that at room temperature (showing in Figs. 17a and 18a), resulting in no obvious difference appears for P_t between room temperature and final temperature rise, as described in Fig. 15c. At large loads, contact loads at final temperature rise are evidently large with respect to that at room temperature and sliding speeds at final temperature rise are slightly smaller than that at room temperature (as shown in Figs. 17b and 18b), leading to a distinct increase of P_t with thermal expansion relative to that without thermal expansion.

Fig. 18

Contact loads at varied rotation speeds without and with thermal expansion for F_x = 100 N and 1000 N: a F_x = 100 N, b F_x = 1000 N

For power loss P_s, at light loads, thermal expansion of bearing components induces a slight enhance in contact loads and makes a slight restraint in spinning speeds (as shown in Figs. 17c and 18a), so that P_s has little change at final temperature rise compared with that at room temperature. At large loads, thermal expansion greatly strengthens contact loads through it restraining slightly spinning speed, which induces a remarkable improvement in P_s with thermal expansion relative to that without thermal expansion.

For power loss Pɩ, thermal expansion plays little role on contact loads at light loads, yet it greatly enhances contact loads at large loads. Thus, Pɩ at final temperature rise is significantly increased relative to that at room temperature due to its dependence on contact loads at large loads, and thermal expansion has little influence on Pɩ at light loads. For power losses P_v, it has hardly changed because of their main dependence on rotation speed of inner ring.

According to the analysis mentioned above, it can be concluded that thermal expansion significantly affects the power loss of bearings at high speeds and large loads, yet at low speeds and light loads, it has little influence on the power loss.

Figure 17a shows that at light loads, relative sliding speed of inner ring is gradually increased with increasing rotation speed of inner ring, yet relative sliding speed of outer ring is firstly improved and then weakened. This is because that contact angle (as shown in Fig. 19) of inner ring is gradually increased with increasing ω_i; at this moment, centrifugal forces of balls are improved to alleviate contact load (as shown in Fig. 18) of inner raceway so that a more pronounced macro-sliding appears between balls and inner raceway. For outer ring, centrifugal forces reinforce contact load of outer raceway to weaken the macro-sliding between balls and outer raceway at high speeds, despite the increased rotation speed of inner ring intensifies macro-sliding. Moreover, macro-sliding with thermal expansion is smaller than that without thermal expansion at light loads. At large loads, micro-sliding with thermal expansion is slightly enhanced relative to that without thermal expansion, which is attributed to the obviously reduced contact angle (as shown in Fig. 19b) relative to that without thermal expansion.

Fig. 19

Contact angles at varied rotation speeds without and with thermal expansion for F_x = 100 N and 1000 N: a F_x = 100 N, b F_x = 1000 N

For spinning speeds at light loads shown in Fig. 17c, when movements (ω_x′ and ω_m) of balls are strengthened with increasing rotation speed of inner ring which are shown in Fig. A1 in appendix A, spinning speed ω_si is gradually increased with the slow increase in contact angle of inner ring, yet spinning speed ω_so is firstly increased and then is reduced, which is attributed to that the intensive movements of balls, which mainly contribute to the increase in spinning speed ω_so at low speeds, and the reduced contact angle (as shown in Fig. 19a) of outer ring which mainly influence ω_so at high speeds. At large loads (F_x = 1000 N), movements (ω_x′, ω_z′ and ω_m) of balls are intensified with increasing rotation speed of inner ring; at this moment, a slight change in contact angle of inner ring occurs, resulting in a slow increase in spinning speed ω_si. For outer ring, the increase of ω_z′ and the decrease in contact angle of outer ring slow down the increase of spinning speed ω_so at high speeds. Moreover, spinning speeds are slight reduced with thermal expansion relative to that without thermal expansion, and they at light loads are significantly larger than that at large loads.

5 Conclusions

In this work, transient thermal expansions and thermal displacements of bearing components are integrated into the nonlinear dynamic model of angular contact ball bearings. Based on this proposed model, time-varying factors (shearing action and viscous effect of lubricant, differential slipping and spin motion of balls, elastic material hysteresis of raceways and coulomb friction between rings and cage) are calculated to evaluate the five kinds of power losses. Then, a multi-node thermal network model of bearings is established to estimate thermal expansions of bearing components for adjusting real-time structural parameters of bearings. The obtained results were presented as follows:

• (1) During temperature rising, thermal deformations of ball and inner and outer rings extrude balls to induce a significantly increase in contact loads of inner and outer raceways, so that the movement locus of balls is changed real-timely to influence the rotation accuracy of bearings.

• (2) Thermal expansion significantly affects the power loss of bearings at high speeds and large loads, yet at low speeds and light loads, it has little influence on the power loss.

• (3) The difference of total power loss between without thermal expansion and with thermal expansion is mainly depended on differential slipping power loss and tangential friction power loss at light loads, and it is significantly attributed to differential slipping power loss and rolling friction power loss at large loads.

• (4) At light loads, macro-sliding of inner ring is gradually increased with increasing rotation speed of inner ring, yet macro-sliding of outer ring is firstly improved and then weakened.

• (5) At large loads, micro-sliding with thermal expansion is slightly enhanced relative to that without thermal expansion.

• (6) At light loads, when movements (ω_x′ and ω_m) of balls are strengthened with increasing rotation speed of inner ring, spinning speed ω_si is gradually increased with the slow increase in contact angle of inner ring, yet spinning speed ω_so is firstly increased and then is reduced.

• (7) At large loads, a slight change in contact angle of inner ring results in a slow increase in spinning speed ω_si, while for spinning speed ω_so, the increase of ω_z′ and the decrease in contact angle of outer ring slow down the increase of ω_so at high speeds.

Appendix

See Fig. 

Fig. 20

Variation of ω_x′(absolute), ω_y′ and ω_z′ in the convergent state with thermal expansion (TE) and without thermal expansion (WTE): a F_x = 100 N, b F_x = 1000 N

20.