On dynamic response of double-layer rectangular sandwich plates with FML face-sheets and metal foam cores under blast loading

Abstract

In this paper, the dynamic response of fiber-metal laminate (FML) double-layer sandwich plates under blast loading is studied through theoretical analysis and finite element (FE) calculation. The membrane mode solution is obtained for the dynamic response of the clamped FML double-layer sandwich plate under blast loading, and the so-called ‘bounds’ are obtained through circumscribing and inscribing lines of the exact yield locus. The FE model is established, and the analytical model is proved by the FE method. The influences of geometrical parameters and material properties on the dynamic response of FML double-layer sandwich plates are researched based on the analytical model. Finally, it is found that FML double-layer sandwich plates have better anti-explosion performance with equal mass by comparing with the metal sandwich plates.

1 Introduction

With the rapid development of modern economy and the popularization and application of the new technologies, the safe operation of the engineering structures has posed unprecedented challenges. Vehicles, spacecraft, aircraft, nuclear power plants, ships, offshore platforms, large bridges, weapons and equipment, protective structures are inevitably encountered with impact and explosion accidents, causing damage to personnel, equipment and economy. Thus, the investigations on the plastic dynamic response of structures under explosion and impact, and the evaluation of the bearing capacity of structure, have been the focus of the engineering field for a long time. Researchers always attempt to design excellent protective structures to enhance the crashworthiness, impact protection and energy absorption. The sandwich structure is a kind of excellent protective structure for blast resistance. Sandwich structures are usually composed of strong and stiff face-sheets and low-density core. Due to the advantages of sandwich structures, i.e., high specific strength and stiffness, strong energy absorption capacity, sandwich structures are generally applied to aviation, aerospace, navigation, transportation and other fields. The core material can usually choose honeycomb, foam, corrugated core, lattice and other materials [1,2,3,4,5,6,7,8,9,10,11,12,13,14] for different applications. The face-sheets are usually made of metal and composite materials; also FML [15] can be used as face-sheet, combining the advantages of metals and high-performance fibers. So that the face-sheets have strong plastic deformation capability, strong resistance to fatigue, high specific strength and stiffness. Compared with single-layer sandwich structure, the designed multilayer sandwich structure can further improve the performance and provide more choices for the structural design [16, 17]. Combining the multilayer sandwich structure and FML, taking FML plates as panel, a kind of multilayer FML sandwich plate is designed. To explore the better blast resistance of the structure, it is very essential to study the dynamic response of multilayer FML sandwich plate under blast loading.

In the last few decades, the dynamic response of single-layer sandwich structures with metal or composite face-sheets under blast loading has been studied widely. Analytical models for the dynamic response of clamped sandwich beams under uniform blast loading were developed by Fleck et al. [18] and Qiu et al. [19]. Qin et al. [20] and Zhang et al. [21] used the membrane factor method and plastic-string model to establish the theoretical model of the dynamic response of the metal sandwich beams under impulsive loading. Cui et al. [22] established a theoretical model for the dynamic response of clamped metal square sandwich plate with honeycomb core under blast loading based on the energy conservation principle and obtained the ‘bound’ solutions. Feng et al. [23] also made similar research on the sandwich plate with foam core under blast loading. Qin et al. [24] established the theoretical model for the dynamic response of fully clamped rectangular sandwich plate under impulsive loading based on the yield criterion. Zhu et al. [25] studied the structural response of sandwich plates with honeycomb core and metal foam core under blast loading by experimental and theoretical methods, and divided the deformation process into three stages: front-face deformation, core crushing and overall structural bending and stretching in the analytical model. Zhu et al. [26] studied the deformation and failure modes of square aluminum foam sandwich plate under blast loading experimentally and numerically, and the FE model well captured the deformation/failure modes observed in experiment.

For the better impact resistance, investigations on the dynamic response of multilayer sandwich structures have been done. Rezasefat et al. [27] studied the pulse impact resistance of single, double and multiple metal plates through experimental and finite element methods, and the results show that the double metal plate has the best performance. Mostofi et al. [28] studied the large deformation of double-layer rectangular plates under air burst loading, and found that the deflection of front and rear panels was approximately equal when there was no gap between the layers. Ziya-Shamami et al. [29] experimentally studied dynamic response of monolithic and multilayered circular metallic plates under repeated uniformly distributed impulsive loading. Zhang et al. [30] predicted the dynamic response of double-layer rectangular sandwich panel under impulsive loading theoretically and numerically, and obtained the so-called ‘bound’ and membrane mode solution. Cai et al. [31] studied the dynamic response of multilayer aluminum foam/ultra-high density polyethylene laminate core sandwich panel under air blast loading experimentally and numerically, and results show that increasing foam core density is beneficial to reduce the panel deformation. Liang et al. [32] studied the influence of multilayer core on the dynamic response of sandwich cylinders under blast loading, and revealed the multilayer core may reduce the maximum deflection of the sandwich cylinders by reasonable core distribution. Wang et al. [33] conducted a FE calculation to study the dynamic response of multilayer honeycomb sandwich plates subjected to explosive loading, and the results obtained by multi-objective optimization design can significantly improve the protection capacity. Cui et al. [34] studied the energy absorption performance of double-layer sandwich plate under ballistic impact experimentally and numerically, and established a modified analytical model. Selvaraj et al. [35] researched the dynamic response of double-core sandwich beams by experiment and FE calculation, and they found that double-core can enhance the stiffness of the sandwich beam. Zhu and Sun [36] conducted the low-velocity impact experiments of sandwich plates with single-layer and double-layer core, and found that the anti-impact properties of the multilayer structure is stronger with the identical mass. Al-shamary et al. [37] carried out low-velocity impact tests on composite sandwich plate with different layers through drop-hammer experiment, and found that the energy absorption capacity of three-layer sandwich plate is best.

In order to further explore the better impact resistance, the sandwich structure consisting of FML panel and core is designed and prepared. Zhang et al. [38] predicted the dynamic response of FML sandwich plate under blast loading theoretically and numerically. Ma et al. [39] studied the dynamic response of graded aluminum honeycomb sandwich panels with FML face-sheets under blast loading experimentally, and the results show that FML as face-sheet can obviously enhance the blast resistance. Baştük et al. [40] combined compressive experiment results with custom blasting date, predicted the dynamic response of sandwich plate with FML face-sheets and aluminum foam core under blast loading, and the main failure modes are observed, i.e., core shear and crushing. Zhang et al. [41] studied the dynamic response of aluminum honeycomb sandwich panel with FML face-sheets under the impact of metal foam bullet by experiment and FE calculation. Liu et al. [42] tested the dynamic response of sandwich plates with aluminum foam core and metal FML face-sheets by high-speed impact experiment, revealing the effects of impact angle and projectile geometry on impact characteristics of sandwich plate. Reyes [43] tested sandwich panels made of thermoplastic FML shells and aluminum foam cores under low-velocity impact, and the results show that a large amount of energy was absorbed by sandwich structures due to contact and bending effects. Liu et al. [44] studied the dynamic response of the sandwich plate with FML face-sheets and aluminum foam core under low-velocity impact, and revealed that increasing the thickness of FML panels significantly increases the energy absorption capacity.

The analytical investigations on the dynamic response of FML double-layer sandwich plate under blast loading were few. The research objective of this research is to study the dynamic response of fully clamped FML double-layer sandwich plate under blast loading. In Sect. 2, the research problem is described. The theoretical model for the dynamic response of clamped FML sandwich plate under blast loading is established in Sect. 3. In Sect. 4, the FE calculation is executed. In Sect. 5, the theoretical analysis results are compared with FE calculation ones. The influences of metal volume fraction, metal-composite layer strength, foam density and foam strength on the dynamic response of rectangular FML sandwich plate are discussed by theoretical model. The conclusion is in the last section.

2 Description of the problem

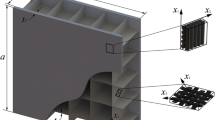
Consider a clamped double-layer FML sandwich plate with metal foam cores under blast loading, in which the length and width are 2L and 2B, respectively, as shown in Fig. 1. The blast loading is imposed on the FML sandwich plate, resulting in impulse of I per unit area. FML sandwich plates are composed of three layers of FML face-sheets with the same thickness and two layers of metal foam cores with the thickness c by perfect bonding. The FML panels consist of n layers of metal layer and (n-1) layers composite layer, and the thickness of the two material layers is h₁, h₂, respectively. Thus, the thickness h_f of FML panels is

$$h_{f} = nh_{1} + \left( {n - 1} \right)h_{2}$$

(1)

Fig. 1

Schematic diagram of a fully clamped FML double-layer sandwich plate under blast loading

Define the metal volume fraction f of the FML panels as

$$f = \frac{{nh_{1} }}{{h_{f} }} \times 100\%$$

(2)

3 Theoretical solution

According to the previous research, the dynamic response of FMLs can be predicted by rigid plastic analytical solution when plastic behavior is the dominant factor in structural response [45]. In this paper, the simplified analytical approach is extended to analyze the dynamic response of the clamped double-layer FML sandwich plate under blast loading.

Zhang et al. [30] developed the theoretical model for the dynamic response of clamped double-layer rectangular sandwich plate with metal face-sheets and metal foam core under blast loading. To make the theoretical analysis process more complete, the theoretical solutions of dynamic response of sandwich plate under blast loading are briefly presented here. The sandwich plate is composed of three layers of metal plates with thickness h_f and two layers of the metal foam core with thickness c. It is assumed that the face-sheets and metal foam obey rigid-perfectly plastic material and rigid-perfectly-plastic-locking (r-p-p-l) material, respectively. The yield strength of face-sheets is σ_f, the plateau stress and densification strain of metal foam core is σ_c and ε_D.

According to Refs. [18] and [30], the response time of the structure is much greater than the compression time of the core, and the whole response process can be decoupled into core compression stage and structural bending and stretching stage. During the first stage, it is assumed that the momentum is transferred from top face-sheet to the rest of sandwich structure.

3.1 Core compression stage

When an impulse I per unit area is imposed on the top face-sheet, the velocity of the top face-sheet is

$$V_{0} = \frac{I}{{\rho_{f} h_{f} }}$$

(3)

The foam core is then compressed. For simplicity of analysis, the foam cores are assumed to be compressed layer by layer. First, the top foam core is compressed, and on condition that top foam core fails to absorb all energy when the strain of the top foam core reaches densification strain, the remaining energy is absorbed by the bottom foam core until the strain of the bottom foam core reaches the densification strain. When $\overline{I} \le \overline{I}_{0}$, the top foam core is compressed, while the bottom foam core is not compressed. And the strain of the top foam core $\varepsilon_{c1}$ is

$$\varepsilon_{c1} = \frac{{\overline{h} + \overline{\rho }}}{{2\overline{c}^{2} \overline{\sigma }\overline{h}\left( {2\overline{h} + \overline{\rho }} \right)}}\overline{I}^{2}$$

(4)

where

$$\overline{I} = \frac{I}{{L\sqrt {\sigma_{f} \rho_{f} } }},$$

$$\overline{I}_{0} { = }\sqrt {\frac{{2\overline{c}^{2} \overline{\sigma }\overline{h}\left( {2\overline{h} + \overline{\rho }} \right)\varepsilon_{D} }}{{\overline{h} + \overline{\rho }}}} ,$$

$$\overline{h} = \frac{{3h_{f} }}{4c},$$

$$\overline{\sigma } = \frac{{\sigma_{c} }}{{\sigma_{f} }},$$

$$\overline{\rho } = \frac{{\rho_{c} }}{{\rho_{f} }},$$

$$\overline{c} = \frac{c}{L}.$$

When $\overline{I} > \overline{I}_{0}$, the top foam core reaches densification, the strain is $\varepsilon_{c1} = \varepsilon_{D}$, the bottom foam core is compressed to the strain $\varepsilon_{c2}$

$$\varepsilon_{c2} = \frac{{\overline{h} + \overline{\rho }}}{{2\overline{c}^{2} \overline{\sigma }\overline{h}\left( {2\overline{h} + \overline{\rho }} \right)}}\overline{I}^{2} - \varepsilon_{D}$$

(5)

At the end of this stage, the final velocity of the sandwich plate can be written as following by the law of momentum conservation

$$V_{f} = \frac{I}{{3\rho_{f} h_{f} + 2\rho_{c} c}}$$

(6)

3.2 Bending and stretching stage

After both top and bottom foam cores are compressed to densification strain, the first stage ends, and the bending and stretching stage begins. In this stage, the remaining energy is consumed by plastic bending and stretching of sandwich plate. In this paper, an approximate theoretical method proposed by Jones [46] is adopted for the dynamic response of the rectangular plate considering finite-deflection effect. Assume that six rigid regions can be separated by r straight hinge lines of length L from the rectangular double-layer sandwich plate, and six regions shown in Fig. 2 can be obtained by dividing the sandwich plates with nine straight hinge lines, the double-layer sandwich plate is divided into six regions by nine straight hinge lines. Then the governing equation can be given as follows through the principle of energy dissipation balance

$$\int\limits_{A} {\left( {p - \mu \ddot{w}} \right)} \dot{w}dA = \sum\limits_{j = 1}^{r} {\int\limits_{{l_{i} }} {\left( {Nw + M} \right)\dot{\theta }_{j} dl_{j} } }$$

(7)

where p is the external pressure applied on the plate, A is the plate area, u is the mass per unit area, w, $\dot{w}$ and $\ddot{w}$ are the transverse displacement, velocity and accelerate, M is the bending moment per unit length, N is the membrane force, $\dot{\theta }_{j}$ is the relative angular velocity across the hinge line $l_{j}$. It is assumed that the transverse displacement profile is linear, and the transverse displacement fields can be given by

$$w = \left\{ {\begin{array}{*{20}l} {\left( {1 - \frac{y}{B}} \right)W_{0} ,} \hfill & {{\text{Region }}{\rm I}} \hfill \\ {\left( {1 - \frac{{x^{\prime}}}{B\tan \varphi }} \right)W_{0} ,} \hfill & {{\text{Region }}{\rm I}{\rm I}} \hfill \\ \end{array} } \right.$$

(8)

where W₀ is the transverse deflection of the center of the sandwich plate, φ is defined as $\varphi = \arctan \left( {\sqrt {3 + \left( \frac{B}{L} \right)^{2} } - \frac{B}{L}} \right)$[47] through the upper bound theory, $x^{\prime}$ and y are the x-coordinate and the y-coordinate, respectively. A detailed explanation was given in Ref. [24, 26].

Fig. 2

Plastic hinge line pattern and transverse displacement fields for FML double-layer sandwich plate under blast loading

Using the similar method [46], combining the governing Eq. (7), circumscribing yield locus [30], the dimensionless maximum deflection of the bottom center and structural response time of the rectangular double-layer sandwich plate can be written as

$$\overline{W}_{m} = \frac{{W_{m} }}{L} = \frac{{\alpha_{1} \overline{I}}}{{2\beta \overline{c}\sqrt {3\alpha_{3} \alpha_{4} b_{1} b_{2} } }}\left( {\frac{\xi }{{\sqrt {1 + \xi^{2} } }}} \right) - \frac{{2A\alpha_{2} \overline{c}}}{{b_{1} \alpha_{3} }}\left( {1 - \frac{1}{{\sqrt {1 + \xi^{2} } }}} \right)$$

(9)

$$\overline{T} = \frac{T}{L}\sqrt {\frac{{\sigma_{f} }}{{\rho_{f} }}} = \frac{1}{\beta }\sqrt {\frac{{\alpha_{4} b_{2} }}{{\alpha_{3} b_{1} }}} \arctan \xi$$

(10)

Combining governing Eq. (7) and inscribing yield locus [30], the dimensionless maximum deflection and structural response time of the rectangular double-layer sandwich plate also can be written as

$$\overline{W}_{m} = \frac{{W_{m} }}{L} = \frac{{\alpha_{1} \overline{I}}}{{2\beta \overline{c}\sqrt {3\vartheta \alpha_{3} \alpha_{4} b_{1} b_{2} } }}\left( {\frac{\xi }{{\sqrt {\vartheta + \xi^{2} } }}} \right) - \frac{{2A\alpha_{2} \overline{c}}}{{b_{1} \alpha_{3} }}\left( {1 - \frac{\sqrt \vartheta }{{\sqrt {\vartheta + \xi^{2} } }}} \right)$$

(11)

$$\overline{T} = \frac{T}{L}\sqrt {\frac{{\sigma_{f} }}{{\rho_{f} }}} = \frac{1}{\beta }\sqrt {\frac{{\alpha_{4} b_{2} }}{{\vartheta \alpha_{3} b_{1} }}} \arctan \left( {\frac{\xi }{\sqrt \vartheta }} \right)$$

(12)

where

$$\beta = \frac{L}{B},$$

$$\alpha_{1} = 3\beta - \tan \varphi ,$$

$$\alpha_{2} = \beta + \cot \varphi ,$$

$$\alpha_{3} = 2\beta + \cot \varphi - \tan \varphi ,$$

$$\alpha_{{4}} = 2\beta - \tan \varphi ,$$

$$b_{1} = 2\overline{h} + \overline{\sigma },$$

$$b_{2} = 2\overline{h} + \overline{\rho },$$

$$\xi = \frac{{\alpha_{1} \overline{I}}}{{{4}\beta \overline{c}^{{2}} A\alpha_{2} }}\sqrt {\frac{{\alpha_{3} b_{1} }}{{3\alpha_{4} b_{2} }}} .$$

As the deflection continues to increase, the influence of the bending moment gradually decrease, and the deformation is dominated by the membrane force. The membrane mode solution is further obtained, when $M = 0$ and $N = N_{p}$. The dimensionless maximum deflection of the bottom center and the structural response time of the double-layer metal sandwich plate in membrane solution are given by

$$\overline{W}_{m} = \frac{{W_{m} }}{L} = \frac{{\alpha_{1} \overline{I}}}{{2\beta \sqrt {3\alpha_{3} \alpha_{4} b_{1} b_{2} } \overline{c}}}$$

(13)

$$\overline{T} = \frac{T}{L}\sqrt {\frac{{\sigma_{f} }}{{\rho_{f} }}} = \frac{\pi }{2\sqrt 3 \beta }\sqrt {\frac{{\alpha_{4} b_{2} }}{{\alpha_{3} b_{1} }}}$$

(14)

Define the metal-composite layer strength q

$$q = \frac{{\sigma_{1} }}{{\sigma_{2} }}$$

(15)

where the yield strengths of metal layers and composites layers are σ₁, σ₂.

A lot of studies have been conducted on FMLs, among which the study in Ref [45]. shows that the rigid plastic model is suitable to predict the dynamic response of FMLs when the plastic behavior plays a major role in the structural response under blast loading.

By the definition of metal volume fraction Eq. (2), the density ρ_f and yield strength σ_f of FML face-sheets can be obtained

$$\rho_{f} = f\rho_{1} + \left( {1 - f} \right)\rho_{2}$$

(16)

$$\sigma_{f} = f\sigma_{1} + \left( {1 - f} \right)\sigma_{2}$$

(17)

where the densities of metal layers and composites layers are ρ₁, ρ₂.

Thus, the dynamic response of FML double-layer sandwich plate under blast loading can be obtained theoretically by using Eq. (16) and Eq. (17).

Substituting Eqs. (2), (15)-(17) into Eqs. (9) and (10), the upper bound solution of the dimensionless maximum deflection of the bottom center and structural response time of the FML double-layer sandwich plate can be written as

$$\begin{gathered} \overline{W}_{m} = \frac{{W_{m} }}{L} = \frac{{\alpha_{1} \overline{I}}}{{2\beta \overline{c}\sqrt {3\alpha_{3} \alpha_{4} \left[ {2\overline{h} + \frac{1}{{f\overline{\rho }_{1} + \left( {1 - f} \right)\overline{\rho }_{2} }}} \right]\left[ {2\overline{h} + \frac{1}{{fq\overline{\sigma }_{2} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]} }}\left( {\frac{\xi }{{\sqrt {1 + \xi^{2} } }}} \right) \hfill \\ \, - \frac{{2A\alpha_{2} \overline{c}}}{{\left[ {2\overline{h} + \frac{1}{{f\overline{\rho }_{1} + \left( {1 - f} \right)\overline{\rho }_{2} }}} \right]\alpha_{3} }}\left( {1 - \frac{1}{{\sqrt {1 + \xi^{2} } }}} \right) \hfill \\ \end{gathered}$$

(18)

$$\overline{T} = \frac{T}{L}\sqrt {\frac{{\sigma_{f} }}{{\rho_{f} }}} = \frac{1}{\beta }\sqrt {\frac{{\alpha_{4} \left[ {2\overline{h} + \frac{1}{{fq\overline{\sigma }_{2} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]}}{{\alpha_{3} \left[ {2\overline{h} + \frac{1}{{f\overline{\rho }_{1} + \left( {1 - f} \right)\overline{\rho }_{2} }}} \right]}}} \arctan \xi$$

(19)

Substituting Eqs. (2), (15)-(17) into Eqs. (11) and (12), the lower bound solution of the FML double-layer sandwich plate can be written as

$$\begin{gathered} \overline{W}_{m} = \frac{{W_{m} }}{L} = \frac{{\alpha_{1} \overline{I}}}{{2\beta \overline{c}\sqrt {3\vartheta \alpha_{3} \alpha_{4} \left[ {2\overline{h} + \frac{1}{{f\overline{\rho }_{1} + \left( {1 - f} \right)\overline{\rho }_{2} }}} \right]\left[ {2\overline{h} + \frac{1}{{fq\overline{\sigma }_{2} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]} }}\left( {\frac{\xi }{{\sqrt {\vartheta + \xi^{2} } }}} \right) \hfill \\ \, - \frac{{2A\alpha_{2} \overline{c}}}{{\left[ {2\overline{h} + \frac{1}{{f\overline{\rho }_{1} + \left( {1 - f} \right)\overline{\rho }_{2} }}} \right]\alpha_{3} }}\left( {1 - \frac{\sqrt \vartheta }{{\sqrt {\vartheta + \xi^{2} } }}} \right) \hfill \\ \end{gathered}$$

(20)

$$\overline{T} = \frac{T}{L}\sqrt {\frac{{\sigma_{f} }}{{\rho_{f} }}} = \frac{1}{\beta }\sqrt {\frac{{\alpha_{4} \left[ {2\overline{h} + \frac{1}{{fq\overline{\sigma }_{2} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]}}{{\vartheta \alpha_{3} \left[ {2\overline{h} + \frac{1}{{f\overline{\rho }_{1} + \left( {1 - f} \right)\overline{\rho }_{2} }}} \right]}}} \arctan \left( {\frac{\xi }{\sqrt \vartheta }} \right)$$

(21)

$$\overline{\rho }_{1} = \frac{{\rho_{1} }}{{\rho_{c} }},$$

$$\overline{\rho }_{2} = \frac{{\rho_{2} }}{{\rho_{c} }},$$

$$\overline{\sigma } = \frac{{\sigma_{1} }}{{\sigma_{2} }},$$

$$\overline{\sigma }_{1} = \frac{{\sigma_{1} }}{{\sigma_{c} }},$$

$$\overline{\sigma }_{2} = \frac{{\sigma_{2} }}{{\sigma_{c} }},$$

$$\xi = \frac{{\alpha_{1} \overline{I}}}{{{4}\beta \overline{c}^{{2}} A\alpha_{2} }}\sqrt {\frac{{\alpha_{3} \left[ {2\overline{h} + \frac{1}{{f\overline{\rho }_{1} + \left( {1 - f} \right)\overline{\rho }_{2} }}} \right]}}{{3\alpha_{4} \left[ {2\overline{h} + \frac{1}{{fq\overline{\sigma }_{2} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]}}} ,$$

and $\vartheta^{\prime}$ is the inscribing coefficient factor. See the details in Appendix A. It should be noted the coupling effect of axial force and bending is considered, and the specific derivation process was described in Refs. [18, 48].

As the deflection increases, the effect of bending moment gradually decreases. In membrane mode solutions, the influence of bending moment is ignored, the dynamic response of the structure is mainly determined by the membrane force [49, 50]. The dimensionless maximum deflection $\overline{W}_{m}$ for bottom center and structural response time $\overline{T}$ for FML double-layer sandwich plate can be written as

$$\overline{W}_{m} = \frac{{W_{m} }}{L} = \frac{{\alpha_{1} \overline{I}}}{{2\beta \sqrt {3\alpha_{3} \alpha_{4} \left[ {2\overline{h} + \frac{1}{{fq\overline{\sigma }_{2} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]\left[ {2\overline{h} + \frac{1}{{f\overline{\rho }_{1} + \left( {1 - f} \right)\overline{\rho }_{2} }}} \right]} \overline{c}}}$$

(22)

$$\overline{T} = \frac{T}{L}\sqrt {\frac{{\sigma_{f} }}{{\rho_{f} }}} = \frac{\pi }{2\sqrt 3 \beta }\sqrt {\frac{{\alpha_{4} \left[ {2\overline{h} + \frac{1}{{fq\overline{\sigma }_{2} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]}}{{\alpha_{3} \left[ {2\overline{h} + \frac{1}{{f\overline{\rho }_{1} + \left( {1 - f} \right)\overline{\rho }_{2} }}} \right]}}}$$

(23)

4 Numerical analysis

ABAQUS/Explicit software is used to study the dynamic response of FML double-layer sandwich plates under blast loading numerically. In ABAQUS/Explicit software, the common methods for applying blast loading include coupled Eulerian–Lagrangian (CLE) approach [51], Arbitrary Lagrangian–Eulerian (ALE) method [52], ConWep blast function code [53, 54] and pressure pulse shape loading [55, 56]. In this study, the blast loading is applied on the sandwich structure by uniform impulsive loading.

The length of the sandwich plate is $2L = 2{\text{m}}$, the thickness of metal foam core is $c = 0.02{\text{m}}$, the thicknesses of metal and composite layers are $h_{1} = 0.0008{\text{m}}$ and $h_{2} = 0.0004{\text{m}}$, the number of metal layers in FML face-sheets is $n = 2$, respectively. Two cases of the width of FML double-layer sandwich plates are considered, i.e., $2B = 2{\text{m}}$ and $2B = 1{\text{m}}$. The symmetric boundary conditions are adopted, and a quarter of finite element model is conducted in calculation, as shown in Fig. 3, in which $2L = 2{\text{m}}$ and $2B = 2{\text{m}}$. As can be seen in Fig. 3, the displacements in all directions of ends of the sandwich plate are set zero in the clamped boundary, which is an ideal clamped boundary condition different from the study of Behtaj et al. [54]. The symmetric boundary conditions are adopted in two other edges, which are symmetric along the Z-axis and the X-axis, respectively. The velocity V₀ is imposed on the top face-sheet in Y direction, which V₀ denotes the velocity in Eq. (3). The blast loading with different impulse is simulated by setting different initial velocity V₀.

Fig. 3

The diagram of FE model

The metal layers in FML face-sheets obey J₂ plastic flow theory and Deshpande-Fleck model [57] is used to describe the crushable performance of foam. Aluminum alloy is used as the metal layers, with Young’s modulus $E_{1} = 70{\text{GPa}}$, density $\rho_{{1}} {\text{ = 2800kg}}/{\text{m}}^{{3}}$, yield strength $\sigma_{1} = 200{\text{MPa}}$, Poisson’s ratio $\upsilon_{1} = 0.3$ and linear strain hardening modulus $E_{1t} = 1 \times 10^{ - 4} E_{1}$. It is assumed that the glass fiber fabric in the woven glass composite of FML is quasi-isotropic and the material is linear elastic when the FML is stretched [58]. The composite layers are made of glass fiber with Young’s modulus $E_{2} = 3{\text{GPa}}$, density $\rho_{2} {\text{ = 1000kg}}/{\text{m}}^{{3}}$, yield strength $\sigma_{2} = 600{\text{MPa}}$ and Poisson’s ratio $\upsilon_{2} = 0.3$. In addition, the foam core choices aluminum foam with Young’s modulus $E_{c} = 1{\text{GPa}}$, density $\rho_{c} {\text{ = 540kg}}/{\text{m}}^{{3}}$, plateau stress $\sigma_{c} = 2{\text{MPa}}$, densification strain $\varepsilon_{D} = 0.7$, elastic and plastic Poisson’s ratio $\upsilon_{ce} = 0.3$ and $\upsilon_{cp} = 0$, and linear strain hardening modulus $E_{ct} = 2 \times 10^{ - 4} E_{1}$. Two adjacent layers are connected by ‘tie.’ The ends of FML double-layer sandwich plate are set zero. The interaction is frictionless general contact. The velocity of the impulsive impact is applied to the top face-sheet. The three-dimensional eight-node and linear brick elements (Type C3D8R) with reduced integration are adopted to model the FML double-layer sandwich plate. The mesh sensitivity was checked, and the results showed that further additional mesh did not change the numerical results significantly.

5 Results and discussion

Figures 4 and 5 show the comparisons between analytical and FE results for maximum deflection versus impulse $\overline{I}$ curves of clamped double-layer rectangular sandwich plates with FML face-sheets under impulsive loading, in which $\beta = 1$ and $\beta = 0.5$. The comparison shows that the analytical results agree well with the FE calculation ones. The small difference may be caused by neglecting the elasticity and strain hardening of materials, as well as the shear force of FML double sandwich plate in the analytical model. Figures 6a and 6b show Mises stress distributions of FML double-layer sandwich plate under impulsive loading $\overline{I} = 0.0017$. It is seen that the top metal foam core is obviously compressed.

Fig. 4

Comparison of theoretical and FE calculation results for the maximum central deflection $\overline{W}_{m}$ of the bottom face-sheet versus impulse $\overline{I}$ of fully clamped sandwich plates with FML face-sheets under blast loading. a $\beta = 1$ and b $\beta = 0.5$

Fig. 5

Comparison of theoretical and FE calculation results for structural response time $\overline{T}$ versus impulse $\overline{I}$ of fully clamped FML double-layer sandwich plate under blast loading. a $\beta = 1$ and b $\beta = 0.5$

Fig. 6

FE calculation results for Mises stress distributions of clamped double-layer rectangular sandwich plate with FML face-sheets and metal foam cores under impulse loading $\overline{I} = 0.0017$. a $\beta = 1$ and b $\beta = 0.5$

In order to research the deformation process of FML double-layer sandwich plates under impulsive loading, the finite element model with $\beta = 1$ and $\overline{I} = 0.0031$ is taken as an example to study the deflection and velocity of the center point of the top face-sheet, interlayer sheet and bottom face-sheet versus time, as shown in Figures 7 and 8, where $\overline{t} = \frac{t}{L}\sqrt {\frac{{\sigma_{f} }}{{\rho_{f} }}}$ and $\overline{V} = V\sqrt {\frac{{\sigma_{f} }}{{\rho_{f} }}}$. It is seen that the difference in deflection between the top face-sheet and interlayer sheet between interlayer sheet and bottom face-sheet is different. This means that the top foam core and the bottom foam core are compressed to different degrees.

Fig. 7

FE calculation results for the central deflection of the top face-sheet, interlayer sheet and bottom face-sheet versus time curves of double-layer rectangular FML sandwich plate ($\beta = 1$) under impulse loading $\overline{I} = 0.0031$

Fig. 8

FE calculation results for the central velocity of the top face-sheet, interlayer sheet and bottom face-sheet versus time curves of double-layer rectangular FML plates ($\beta = 1$) under impulse loading $\overline{I} = 0.0031$

Figure 8 shows the velocities of the center point of the top face-sheet, interlayer sheet and bottom face-sheet versus time curves of the FML double-layer sandwich plate under blast loading with $\beta = 1$ and $\overline{I} = 0.0031$. As can be seen from Fig. 8, when the impulse loading is imposed on the top face-sheet, the velocity of the top face-sheet reduces rapidly at first, and the velocity of the interlayer sheet and the bottom face-sheet increase from zero. After $\overline{t} = 0.07$, the three sheets almost move at the same velocity.

Figure 9 shows the maximum central deflection $\overline{W}_{m}$ of the FML double-layer sandwich plates for different metal volume fraction f under blast loading, in which $\beta = 1$, $\overline{c} = 0.02$, $\overline{h} = 0.075$, $q = 2$, $\overline{\rho } = 0.1$, $\overline{\sigma } = 0.1$. As can be seen from Fig. 9, for the given impulse, with the increase of metal volume fraction, the maximum deflection decreases. That means the blast resistance is enhanced.

Fig. 9

The influence of metal volume fraction f on maximum central deflection $\overline{W}_{m}$ of the double-layer sandwich plate with FML face-sheets under blast loading

The maximum central deflection $\overline{W}_{m}$ for different metal-composite layer strength q under blast loading is shown in Fig. 10, in which $\beta = 1$, $\overline{c} = 0.02$, $\overline{h} = 0.075$, $f = 0.8$, $\overline{\rho } = 0.1$, $\overline{\sigma } = 0.1$. In particular, when $q = 1$, a FML double-layer sandwich plate can be treated as a metal plate. It is seen that as q increases, the maximum central deflection of the bottom face-sheet of the FML double-layer sandwich plate decreases and the blast resistance increases. This is because the strength of the top face-sheet, bottom face-sheet and interlayer sheet can be written as $\sigma_{f} = \sigma_{2} - f\left( {1 - q} \right)\sigma_{2}$. The strength of the FML panels increases, and the blast resistance increases.

Fig. 10

The influence of metal-composite layer strength ratio q on the maximum central deflection $\overline{W}_{m}$ of the double-layer sandwich plate with FML face-sheets under blast loading

Figure 11 shows the influence of metal foam density $\overline{\rho }$ on maximum central deflection $\overline{W}_{m}$ of the FML double-layer sandwich plate, in which $\beta = 1$, $\overline{c} = 0.02$, $\overline{h} = 0.075$, $f = 0.8$, $q = 2$, $\overline{\sigma } = 0.1$. As can be seen from Fig. 11 that the maximum deflection of FML double-layer sandwich plate decreases as the foam density increases. That is, the blast resistance of FML double-layer sandwich plate increases with the increase of the foam density. The reason is that when the foam density increases, the mass of the FML double-layer sandwich plate increases, the velocity and the maximum deflection of the bottom face-sheet decrease for the same impulse.

Fig. 11

The influence of the density of metal foam $\overline{\rho }$ on the maximum central deflection $\overline{W}_{m}$ for the double-layer sandwich plate with FML face-sheets under blast loading

Figure 12 shows the influence of foam strength $\overline{\sigma }$ on maximum central deflection $\overline{W}_{m}$ of the FML double-layer sandwich plate, in which $\beta = 1$, $\overline{c} = 0.02$, $h_{1} = 0.8{\text{mm}}$, $h_{2} = 0.4{\text{mm}}$, $\overline{h} = 0.075$, $f = 0.8$, $q = 2$, $\overline{\rho } = 0.1$. The results show that with the increase of the foam strength, the maximum deflection of FML double-layer sandwich plate at the center point of the bottom face-sheet becomes small for the given impulse. This may be because with the increase of the foam strength, the foam core can absorb more energy in the core compression stage, enhancing the explosion resistance.

Fig. 12

The influence of foam strength $\overline{\sigma }$ on the maximum central deflection $\overline{W}_{m}$ of the double-layer sandwich plate with FML face-sheets under blast loading

The difference of blast resistance between double-layer sandwich plate with metal and FML face-sheet is studied using the membrane mode solution. The sandwich plate are both set as square plates with the length of 2 m. The foam thickness is $h{ = 0}{\text{.2m}}$, the thickness of the metal face-sheet of the sandwich plate is 2 mm. In FML double-layer sandwich plate, there are two metal layers with thickness of 0.8 mm and one composite layer with thickness of 0.4 mm. The specific material properties are listed in Table 1, and the maximum central deflection $\overline{W}_{m}$ of bottom face-sheet versus impulse $\overline{I}$ curves for rectangular double-layer sandwich plates with FML face-sheets and metal face-sheets under impulse loading are compared in Fig. 13. It is shown that the mass of FML double-layer sandwich plate is only 92.44% of that of metal double-layer sandwich plate, while the maximum deflection for bottom face-sheet of FML double-layer sandwich plate is less than that of metal double-layer sandwich plate for the given impulse. That is, the FML double-layer sandwich plate has better blast resistance than metal double-layer sandwich plate with same mass.

Table 1 Material properties of metal double-layer sandwich plate and FML double-layer sandwich plate

Fig. 13

Analytical results for maximum central deflection $\overline{W}_{m}$ of bottom face-sheet versus impulse $\overline{I}$ for rectangular double-layer sandwich plate with FML face-sheets under impulse loading

6 Conclusions

The dynamic response of double-layer rectangular sandwich plate with FML face-sheets under blast loading is studied analytically and numerically in this paper. Introducing the material and geometrical parameters of composite layer in FML, the membrane mode solution and the so-called ‘bounds’ through circumscribing and inscribing squares of the exact yield locus for the dynamic response of double-layer rectangular FML double-layer plate under blast loading are obtained according to the modified rigid plastic model. It should be noted that the membrane mode solution doesn’t consider the coupling effect of axial force and bending. The analytical solution is verified by FE calculation. The results show that the blast resistance of FML double-layer sandwich plate increases with the increase of metal volume fraction, metal-composite layer strength, the density and the strength of metal foam. It is found that the FML double-layer sandwich plate possess better blast resistance compared with the metal double-layer sandwich plate.

Appendix A: The inscribing coefficient of inscribing yield criterion

The inscribing coefficient of compressed double-layer metal sandwich section is given in Ref. [30], and the inscribing coefficient of compressed sandwich section with FML face-sheets $\vartheta^{\prime}$ can be expressed as

$$\vartheta^{\prime} = \left\{ {\begin{array}{*{20}l} {\frac{{\sqrt {1 + 4k_{0} } - 1}}{{2k_{0} }},} \hfill & {J_{1} \ge 0} \hfill \\ {\frac{{\sqrt {k_{1}^{2} + 4k_{2} } + k_{1} }}{2},} \hfill & {J_{1} < 0{\text{ and }}J_{2} > 0} \hfill \\ {\frac{{\sqrt {k_{3}^{2} + 4k_{4} } - k_{3} }}{2},} \hfill & { \, J_{2} \le 0} \hfill \\ \end{array} } \right.$$

(A1)

where

$$k_{0} = \frac{{\left[ {2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]^{2} }}{A},$$

$$k_{1} = \frac{{4\overline{h}\left( {1 - \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }} - \varepsilon_{c2} } \right)\left( {1 - \varepsilon_{c2} } \right)\left[ {2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right] - \frac{3A}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}\left( {1 - \varepsilon_{c2} } \right)}}{{3\left[ {2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]^{2} \left( {1 - \varepsilon_{c2} } \right)^{2} }},$$

$$k_{2} = \frac{{9\left[ {C + \frac{{\left( {\frac{2}{3}\overline{h} + 1 - \varepsilon_{c2} } \right)^{2} }}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }} + \frac{{\varepsilon_{c2} - \varepsilon_{c1} }}{{2f\overline{\sigma }_{1} + 2\left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]\frac{{1 - \varepsilon_{c2} }}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }} - 4\overline{h}^{2} \left[ {1 - \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }} - \varepsilon_{c2} } \right]^{2} }}{{9\left[ {2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]^{2} \left( {1 - \varepsilon_{c2} } \right)^{2} }},$$

$$k_{3} = \frac{{2\left[ {2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]\left( {1 - \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }} - \varepsilon_{c2} } \right) + A}}{{\left[ {2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]^{2} }},$$

$$k_{4} = \frac{{2\overline{h} - \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }} + 2 - 2\varepsilon_{c2} }}{{2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}}} + \frac{{\frac{4}{3}\overline{h}\left( {\varepsilon_{c2} - \varepsilon_{c1} } \right) + \frac{{\varepsilon_{c2} - \varepsilon_{c1} }}{{2f\overline{\sigma }_{1} + 2\left( {1 - f} \right)\overline{\sigma }_{2} }}}}{{\left[ {2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}} \right]^{2} }},$$

$$J_{1} = \frac{{3\overline{h}}}{{2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}}} + \frac{{2\overline{h}^{2} }}{3A} - 1,$$

$$J_{2} = \frac{{3\overline{h} + \frac{3}{{2f\overline{\sigma }_{1} + 2\left( {1 - f} \right)\overline{\sigma }_{2} }}}}{{2\overline{h} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }}}} - \frac{{16\overline{h}^{2} - 6\overline{h}\left( {2 - \varepsilon_{c2} - \varepsilon_{c1} } \right) + \frac{{9\left( {\varepsilon_{c2} - \varepsilon_{c1} } \right)}}{{4f\overline{\sigma }_{1} + 4\left( {1 - f} \right)\overline{\sigma }_{2} }}}}{3A},$$

$$A = 4\overline{h}^{2} + \frac{1}{{f\overline{\sigma }_{1} + \left( {1 - f} \right)\overline{\sigma }_{2} }} + \frac{{8\overline{h}}}{3}\left[ {1 + \frac{1}{{2f\overline{\sigma }_{13} + 2\left( {1 - f} \right)\overline{\sigma }_{2} }}} \right] - \frac{1}{2}\left( {\varepsilon_{c2} + \varepsilon_{c1} } \right) - \frac{{4\overline{h}\left( {\varepsilon_{c2} + \varepsilon_{c1} } \right)}}{3},$$

$$C = \frac{{4\overline{h}}}{3}\left( {\frac{{8\overline{h}}}{3} + 2 - \varepsilon_{c2} - \varepsilon_{c1} } \right).$$