1 Introduction

In the cementing process of oil wells, cement or sometimes resin-based fluids are injected to permanently isolate a well zone from the reservoir fluids. Cement dates back from the ancient Rome [1], where volcanic sands with cementing properties appeared in many parts of the Mediterranean. Cement-like materials main characteristic is to harden with time. This process, also called hydration or curing, is irreversible, and characterized by an increase in apparent viscosity due to chemical reactions [2]. These reactions consume the water, turning the cement into a solid dry sheath. Despite still slightly porous, rigid cement most often manages to seal the well walls and avoid any flow exchange with the formation [3, 4].

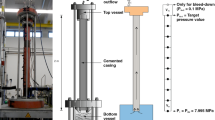
However, the fluid slurry injected must withhold the formation pressures along the well length throughout the curing process. The weight of fluids is transmitted downwards and generates an inner well pressure(hydrostatic pressure) that withholds the walls from collapsing. Pressure balance with the formation is achieved by adjusting fluids’ densities so that the well pressure is lower than the rock fracture gradient, but higher than formation pore pressure, as seen on Fig. 1. This is usually called operational envelope.

Fig. 1
figure 1

Fluids’ density adjusted to maintain pressure balance

Full size image

The main objective of cement, besides withholding the walls’ pressure, is isolating reservoir zones from the production well. Since curing is not instantaneous, in an unbalanced situation, cement viscosity should increase until it can prevent or at least minimize any fluid exchange between the well and the reservoir. Dellyes [5] presented rheology studies showing that fresh mixed cement slurries present shear thickening behavior at high shear rates. Tattersall [6] was one of the first to deeply analyse the rheology of a cement slurry. Using a coaxial cylinder viscometer, experimental data was gathered and the first flow curves of cement pastes were plotted. A shear thinning behavior was observed for the values tested. Later, Berg [7] reported that in fact, both behaviors are present, with shear thickening at high shear rates.

Although the tests performed by Tattersall [6] did not cover lower shear-rate ranges, the presented flow curves already indicated a point crossing the shear-stress axis different than zero. This is characteristic of yield stress fluids. The yield stress is the critical stress value beneath which the fluid behaves like a solid. Berg [7] and Min [8] showed the same Bingham [9] gel behavior on their respective studies. Tattersall rheometry results also presented hysteresis [6], indicating a structure breakdown at a finite time, which is a thixotropic characteristic. This was also observed by Berg, who was also able to identify reversible structure buildup [7]. Therefore, the early placed cement pastes curing at lower shear-rates are frequently modeled as thixotropic viscoplastic gels.

Field and experimental evidence reported that a cemented well inner pressure decreases a bit after placement, but before its complete cure. If this happens before viscosity buildup is complete, fluids from the reservoir might manage to flow into the well and ultimately to the surface. Actually this is considered to be the initial cause of some historical blowouts, where gas was able to flow through cement sheath layers. By this reason, many authors historically have studied the mechanisms responsible for this pressure drop during the hydration period [10,11,12,13,14].

The main mechanism is named cement shrinkage, and was first scientifically described by Mindess et al. [15]. It consists of a slight reduction of the mixture volume due to cure chemical reactions and moisture loss, which brings the cement congregates close together. On the oil industry, cement shrinkage is usually controlled with chemical additives that promote an abrupt increase of viscosity, adjusted to act moments before cement shrinkage occurs. Some empirical models were developed trying to predict how and when shrinkage happens.

If the well presents highly permeable zones along its length, it might also alter the well pressure drop. In that case, the annular well pressure might be enough to induce a filtration of the well fluid into the formation. This situation was initially observed and analysed in the early forties by Williamns et al. [16]. If just a part of the mass fraction of the well fluid filtrates into the formation, then it was named Loss Circulation.

Jones and Taylor [17] reviewed the rheometry techniques used to obtain several flow curves with different water-to-cement ratios. They also reviewed some mathematical models to predict the cement paste behavior for a range of water-to-cement ratios. Hansen [18] has evaluated experimentally the effects of the absence of water during cure, showing that poor water-to-cement ratio increases shrinkage, accelerates viscosity buildup and ultimately result into poor structural properties. This observations are in agreement with Berg [7] study on how solids concentration on cement results in slurries with higher yield stress.

Carbonate formations, widely present in the Brazilian pre-salt reservoirs, are known to be very heterogeneous [19] and susceptible to partial or total fluid exchanges with the well. In addition, carbonate formations usually present gas pockets. The misplace of the top of cement caused by fluid loss may unbalance the pressure profile and induce gas influxes. Therefore, an uncontrolled fluid loss during cementing in such environment may cause an early pressure drop, representing a serious risk to well integrity.

Several studies of pressure decay triggered by fluid loss phenomena have been done experimentally. Most advances made aimed the development of chemical additives that would prevent or minimize the fluid loss itself, as it can be seen on the recent work of Velayati et al. [20]. As an alternative, computational fluid dynamics is a considerably cheaper initial approach. It can be used to predict the pressure decay along the cementing process, or even indicate where losses might occur in a certain scenario. Therefore, the present article has the objective of presenting a simple yet cost-effective model that provides reasonably accurate predictions of pressure profiles in the presence of fluid loss zones.

Generally, due to the huge difference between the characteristic lengths of each dimension in a well, most literature models consider 1-D approximations to describe most flows along the well. However, when analyzing the fluid loss problem the radial and axial velocities are relevant, and both may vary with radius and length, i.e. \(u_{r} = u_{r}(r,z)\) and \(u_{z} = u_{z}(r,z)\).

Chenevert and Jin [10] elaborated a mathematical model to describe the time evolution of the downhole pressure by calculating a force balance in an annular element. It excludes inertia and considers that a volume reduction of the cement slurry causes a downward movement and consequently a shear force in the opposite direction. Their model also takes into account chemical shrinkage, fluid loss to the formation and gelation by using transient experimental data, but neglects compressibility. The elasticity is considered by employing a simple rheological model to describe the low-shear rate behavior. Later, the mathematical model of Chevernet and Jin [10] had been solved numerically via finite element method and the results agree quite well with field data reported by Cooke et al. [21]. Daccord [11] extended their model including mass conservation and compressibility of the slurry. A couple of years later, Prohaska [12] discussed this model in more details, emphasizing the importance of considering pressure effects on gel strength measurements.

More recently, Nishikawa and Wonjtawicz [14] developed a mathematical expression for predicting the downhole pressure as a function of time based on a dynamic approach. Their 2-D model approximates the annulus by a rectangular slot, neglects inertia and consider a slurry of constant compressibility. Additionally, they assume that chemical shrinkage does not contribute to volumetric change in early stages and that the rheology of the cement slurry is described by the Bingham equation, hence independent of time.

Rodrigues [22] reviewed thixotropic cement slurries characterization techniques applied in the literature. In order to characterize cement slurries, they applied a modified Herschel-Buckley model to fit rheometry measurements of cement slurries and its time-dependent behavior. Finally, Marchesini et al. [23] widely reviewed the past cement slurry curing models, and proposed a thixotropic constitutive model based on micro-structure construction and destruction parameters. He also presents his own rheometry analysis of some cement slurries and compare with the model proposed.

Regarding filtration modeling, Outmans [24] proposed distinct models to describe the mechanics of static and dynamic filtration. In the static condition, the filtrated only experiences velocities perpendicular to the plane of filtration. On the other hand, in a dynamic condition, a fluid is submitted to velocities parallel to the plane of filtration. Outmans also presented experimental evidence that the filtration under static conditions linearization leads to a boundary value problem mathematically analogous to the heat flow problem. However, this approach has not been used in the cementing fluid loss application.

In this work, the cement curing process in the presence of a fluid loss zone is investigated. The focus is on analysing the column pressure profile behavior immediately after placement.The investigation is performed through a numerical analysis using the finite element method. A 2-D multi-component mathematical model is proposed, focused on predicting the pressure profile during the early curing stages. Fluid loss is modeled as an outflow of just part of the slurry mass fraction though a permeable well wall. Different from the classical 1D models from the literature, the filtration modeled through the Outmans [24] static condition enables a better understanding of how the cement filter cake is formed. It shows how the cement slurry dehydrates close to outer walls, as fluid is lost to the formation.

2 Methodology

All cementing operations are divided in three main phases: mixing, placement and set. The focus of this work is the after placement stage, but immediately before chemical shrinkage effects take place. That assumption simplifies the equations so that the inner pipe is assumed static with respect to the formation.

2.1 Model hypothesis and equations

The well is defined using a global cylindrical frame of reference \(R Z \Theta\) on the top of the well, with Z axis pointing downwards. The well section evaluated, defined by the local frame of reference \(r z \theta\), is assumed axisymmetric, as showed by Fig. 2. Inner pipe eccentricities or wellbore enlargements are neglected, as well as any azimuthal velocities, in \(\theta\). Hence, the 3D well section geometry is simplified by a 2D axisymmetric domain \(\Omega\) and its boundaries \(\delta \Omega _i\), also presented in Fig. 2, where \(\vec {g}\) is the gravity acceleration; \(R_i\) and \(R_o\) are respectively the inner and outer annular radius; \({z_{min}}\) and \({z_{max}}\) are the top and bottom axial simulation limits.

Fig. 2
figure 2

Model geometry and 2D axisymmetric domain

Full size image

The overall problem is modeled as the annular flow of a non-Newtonian mixture, submitted to a filtrate loss zone. The simplified Navier-Stokes equations, with a modified SMD rheological model, are solved associated with the Outmans [24] static filtration hypothesis. Oatmans hypothesis describes the same filtration phenomena observed after cement placement at the fluid loss zone. The cement slurry is modeled as a mixture composed by two chemical species, hydrated cement (1) and water (2). The static filtration hypothesis assumes only one species(water) is filtered into the formation at the fluid loss zone, therefore this species is usually named filtrate.

Although this study analysis is focused after cement placement, it is still a transient problem. Dehydration and curing chemical reactions may considerably change the properties of the fluids, such as viscosity and density, as mentioned in the literature review. Temperature conditions may also influence those properties, but for the purpose of this study the well is considered isothermal. As this analysis is focused the early pressure drop impact of fluid loss, it is assumed that the transient thermal variations from displacement have achieved an equilibrium, and heat of hydration has yet not started in the initial curing moments.

The cement slurry is assumed a single-phase, isotropic and slightly compressible mixture composed by two chemical species. Since only one of those species filtrates into the formation, the local changes in the mass fractions of each species close to the walls cause local mixture density changes, according to Equation 1.

$$\begin{aligned} \rho \left( r,z,t \right) = C_1\rho _1(t) + C_2\rho _2 \end{aligned}$$
(1)

where r is the radial position; z is the axial position; t is the time; \(\rho _1\) and \(\rho _2\) are the densities of each chemical species; \(C_1\) and \(C_2\) are the concentrations of both chemical species and \(C_1 + C_2 = 1\).

Since two species are simulated and their concentration summation is one, only the mass fraction field of dissolved cement \({C_{1}}\) needs to be solved. Water concentration is simply given by \({C_2=1- C_1}\). Equation (2) shows the equation of mass transport for cement mass fraction \({C_{1}}\).

$$\begin{aligned} \left[ \frac{\partial \rho _1 C_1}{\partial t}\ + \rho _1 \nabla \cdot \left( C_1 \vec {u} \right) \right] = {\mathbb {D}}_{1,2}\nabla ^2 C_1 \end{aligned}$$
(2)

where t is time and \({\mathbb {D}}_{1,2}\) is the diffusivity of one specie into the other.

The problem simplifying hypothesis are summarized in Eq. 3.

$$\begin{aligned} {\left\{ \begin{array}{ll} i. \ \ \ \text {Isothermal well:} \ \frac{\partial {T}}{\partial {t}} \approx \frac{\partial {T}}{\partial {z}} \approx \frac{\partial {T}}{\partial {r}} \approx \frac{\partial {T}}{\partial {\theta }} \approx 0; \\ ii. \ \ \text {2-D Flow:} \ u_{\theta } \ll u_r, u_z \ \& \ \frac{\partial {u_z}}{\partial {\theta }} \approx \frac{\partial {u_r}}{\partial {\theta }} \approx 0 \\ iii. \ \text {Single phase with two complementary species:} \ C_1 + C_2 = 1; \\ \ \ \ \ \ \text {where 1-Dissolved Cement } \& \text { 2-Filtrate} \\ iv. \ \ \text {Isotropic Fluid}; \\ v. \ \ \ \text {Viscoplastic Fluid} + \text {Irreversible Set:} \ \eta = \eta (|{\dot{\gamma }}|,t); \\ vi. \ \ \text {Chemical shrinkage:} \ \rho _1 = \rho _1(t) \end{array}\right. } \end{aligned}$$
(3)

where T is the temperature; t is the time; \({\vec {u} = [u_r, u_z]}\) is the velocity field; \(C_{ijkl}\) is the simplified viscosity tensor for an isotropic fluid; \(\delta _{ij}\) is the Kronecker delta; \(\eta\) is the dynamic viscosity coefficient and \(\lambda\) is the second viscosity coefficient, both scalars.

Despite the mixture density \(\rho\) may change with time in the final instants, compressibility is neglected due to the low Mach numbers. Therefore, the flow is solved by the simplified mass and momentum equations, showed in their vector formulation respectively in Eqs. (4) and (5).

$$\begin{aligned}&\vec {u}\cdot \nabla \rho + \rho (\nabla \cdot \vec {u}) = 0 \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\partial \vec {u}}{\partial t} + \vec {u}\cdot \nabla \vec {u} = - \frac{1}{\rho }\nabla P + \frac{1}{\rho }\nabla \cdot \left( 2\eta \overline{\overline{D_u}}\right) + \vec {f_w} \end{aligned}$$
(5)

where \(\vec {u}\) is the mixture velocity field; \(\rho\) and \(\eta\) are the mixture density and dynamic viscosity coefficient, respectively; P is the pressure; \(\overline{\overline{D_u}}\) is the rate of deformation tensor and \(\vec {f_w}\) is the gravitational force by unit of volume.

The applied boundary condition for the inlet \(\delta \Omega _1\) is developed flow for velocity and mass fraction. In addition, the classical no-slip and no-penetration boundary conditions are assumed at the impermeable inner and walls \(\delta \Omega _3\) and \(\delta \Omega _4\). Finally, the Outmans [24] static filtration boundary condition is applied for the cement mass fraction, and imposed fluid loss average velocity at the permeable outlet \(\delta \Omega _5\), as referred in Fig. 2.

2.2 Rheological model

Consistently with the proposed scope, after placement cement is submitted only to lower shear rate ranges. The dissolved cement species is modeled as a viscoplastic fluid that sets after some characteristic time. Hence, its viscosity varies not only with the shear rate, but also with time.

The SMD model, presented by de Souza Mendes and Dutra [25], is commonly used to model the flow curve of a gel-like material where the viscosity is a function of the shear rate \({\dot{\gamma }}\). Therefore, the slurry viscosity \(\eta\) is modeled as showed in Eq. 6.

$$\begin{aligned} \eta ({\dot{\gamma }}) = \left[ 1-\exp {\left( \frac{-\eta _0 {\dot{\gamma }}}{\tau _y}\right) }\right] \left( \frac{\tau _y }{{\dot{\gamma }}} + K {\dot{\gamma }}^{n-1} + \eta _{\infty } \right) \end{aligned}$$
(6)

where \({\dot{\gamma }}\) is the shear rate, K is the consistency index, n the power-law index, \(\tau _{y}\) is the yield stress, and \(\eta _0\) and \(\eta _{\infty }\) are the Newtonian viscosity plateaus for low and high shear rates respectively.

Finally, using the same methodology presented by Rodrigues [26], the cure is modeled with a time dependent variation of the yield stress \(\tau _{y}\), and of the Newtonian viscosity plateau \(\eta _0\). This viscosity build-up models the effect observed when the cement starts to harden, and is given by Eq. 7.

$$\begin{aligned} {\left\{ \begin{array}{ll} \tau _y (t) = \tau _{y0} \exp {\left( \frac{t}{T_t}\right) }\\ \eta _0 (t) = \eta _0 \exp {\left( \frac{t}{T_t}\right) } \end{array}\right. } \end{aligned}$$
(7)

where \(\tau _{y0}\) and \(\eta _0\) are the initial yield stress and Newtonian viscosity plateau, respectively. \(T_t\) is the cement slurry transition time, and it is obtained from rheometry measurements of the viscosity build-up.

3 Numerical implementation

A classical finite element method apply continuous approximation spaces and use volumetric integrals of the weak formulation. Simplifying the integral notation with \(\langle a,b \rangle = \int _{\Omega } \left( a \cdot b \right) d\vec {x}\), this form of the conservation equations is shown in Eqs. 8, 9 and 10.

$$\begin{aligned}&\langle q \vec {u}, \nabla \rho \rangle + \langle \rho \left( \nabla \cdot \vec {u}\right) , q \rangle = 0 \end{aligned}$$
(8)
$$\begin{aligned}&\begin{aligned} \langle \frac{\vec {u}}{\Delta t} , \vec {v} \rangle - \langle \frac{\vec {u_0}}{\Delta t}, \vec {v} \rangle + \langle \vec {u}\cdot \nabla \vec {u} , \vec {v} \rangle =&\\ - \frac{1}{\rho }\langle \overline{\overline{T_P}} ,\overline{\overline{D_v}} \rangle + \langle \vec {g},\vec {v} \rangle&+ \frac{1}{\rho }{\oint \limits _{\delta \Omega _{1}}} - P_{in}\left( \vec {v} \cdot {\hat{n}} \right) ds \end{aligned} \end{aligned}$$
(9)
$$\begin{aligned}&\begin{aligned} \langle \frac{\rho _1 C_1}{\Delta t} , l \rangle - \langle \frac{\rho _{1_0} C_{1_0}}{\Delta t} , l \rangle + \langle \rho _1 \vec {u},\nabla C_1 l \rangle + \langle \rho _1 C_1\nabla \cdot \vec {u} , l \rangle =&\\ - {\mathbb {D}}_{1,2} \langle \nabla C_1 , \nabla l \rangle + {\mathbb {D}}_{1,2} {\oint \limits _{\delta \Omega }} \left( l \nabla C_1 \cdot {\hat{n}} \right) ds \end{aligned} \end{aligned}$$
(10)

where \(\rho\) is the mixture density and q is the finite element weight function correspondent to the pressure. \(\vec {u}\) and \(\vec {u_0}\) are the velocity vectors at current and previous time step respectively, and \(\vec {v}\) is the correspondent weight function. \(\overline{\overline{T_P}}\) and \(\overline{\overline{D_v}}\) are respectively the stress tensor and the weight function deformation tensor. \(\vec {g}\) is the gravity acceleration vector, \(P_{in}\) is the inlet pressure and \({\hat{n}}\) is the unity vector normal to the boundaries.

As mass flows into the formation through the permeable zone, the top of cement moves down. The model takes that into account, but without introducing the numerical problems of implementing a free surface boundary condition. As it can be seen in Fig. 2, the inlet boundary is at a depth \(z_{min}\) beneath the top of cement. Hence, the inlet boundary condition is a pressure condition which varies with time, based on the weight of the remaining column of cement above this point.

Regarding the mesh topology, an unstructured triangular mesh with local refinements was implemented. The chosen mesh elements are shown in Fig. 3, the classical Taylor-Hood elements set with linear approximations for pressure and quadratic approximations for velocity. In the same figure, the used mesh is represented sideways, with a detail zoom view of the local refinement close to the fluid loss zone outlet.

Fig. 3
figure 3

Taylor-Hood element set and mesh topology

Full size image

3.1 Validation and mesh test

Mesh tests were performed to obtain mesh independent solutions. The axial velocity profile is analysed at a fixed time step and column depth marked by the red dashed line in Fig. 4. The time step chosen corresponds to the maximum average annular velocity, and the expected profile is close to the Newtonian Poiseuille profile. The profiles are plotted for each tested mesh, and are shown in Fig. 5.

Fig. 4
figure 4

Meshes tested

Full size image

For mesh sizes higher than 5000 elements the results converge. As the simulation time does not increase drastically at the finer meshes, the chosen mesh was the finest one, with 8813 elements. On the sequence, the model results are qualitatively analyzed.

Fig. 5
figure 5

Velocity profiles for the meshes tested

Full size image

4 Results and discussion

The numerical solution of the governing equations was obtained using the finite element method. The set of rheological properties and model parameters used in this work simulations were obtained from the literature. Marchesini [23] rheological characterization curves of a gas-resistant slurry. The author presented flow curves of \(\tau\) increasing with the increasing shear rate \({\dot{\gamma }}\), despite of a minor shear banding region. In addition, the viscosity \(\eta\) was also presented decreasing with the increasing shear rate \({\dot{\gamma }}\). Finally, the thickening time was characterized by Marchesini at two shear rates: a high shear rate of 100s\(^{-1}\) and a low shear rate of 10s\(^{-1}\).

The rheological properties and model parameters were obtained fitting this experimental data with the proposed model. Hence, the extracted parameters used to simulate the reference case are: the initial yield stress \(\tau _{y0}= 19.79\) Pa; the consistency index \(K = 1.463\) Pa.s\(^n\); the power-law index \(n=0.54\); the low and high shear rates Newtonian viscosity plateaus \(\eta _0=4500\) Pa.s and \(\eta _{\infty }=0.295\) Pa.s; and the cement slurry transitioning time \(T_t=6000s\).

As defined in Fig. 2, the present work only analyzed scenarios where pure filtrate is lost through the high permeability zone. The axial length of this zone was arbitrarily set to be \(L_{FL}=10\)cm, which correspond \(0.25\%\) of the simulated well, and the fluid loss zone distance to the bottom was set to \(L_{B-FL}=40\) cm. This was intended to assure a certain pressure level at the loss zone, yet without directly suffer an influence from the top and bottom boundary conditions.

Fig. 6
figure 6

Fluid loss mass characteristic evolution with time and fitted flow rate

Full size image

The last input of the model is the fluid loss mass flow rate with time, which was obtained differentiating the drained filtrate mass evolution with respect to time. Therefore, a synthetic curve for the drained filtrate mass was defined approaching 100g of filtrate lost in around 12000s, as shown by solid blue line in Fig. 6. This characteristic asymptotic behavior for the drained filtrate mass, which comes from the static filtration theory, was first observed by Outmans [24] and it was widely referred in the literature.

Two different functions are used to fit the fluid loss mass flow rate curve: a linear ascending part, and a exponential decay, shown as the black dashed line in Fig. 6. The obtained curve expression was used to calculate the outlet velocity applied as boundary condition for the fluid loss region. Thus, the final parameters used to simulate the reference case are shown in Table 1.

Table 1 Reference Case parameters
Full size table

The cement column pressure drop characteristic behavior was observed and documented by several authors in the literature, such as Daccord [11], Velayati [20] and Khodadadi [27]. This profile clearly presents two separate slopes, due to gelation and shrinkage respectively, as illustrated in Fig. 7,

Fig. 7
figure 7

Characteristic literature pressure profile during cement cure

Full size image

The reference case was simulated for 12000s, equivalent to twice the slurry thickening time. The time-pressure profiles were predicted, and plotted in Fig. 8 for different well depths, marked at the domain schematics in the corresponding color of the graph. The curves match the behavior observed in the literature. Therefore, this case was used as reference, and compared in a sensitivity analysis performed with the model parameters.

Fig. 8
figure 8

Reference case pressure profiles for five different column depths during cement cure, in the presence of fluid loss

Full size image

Other aspects also indicate that the process qualitative behavior is indeed captured by the model. At the outlet, for example, only one chemical species is filtered into the rock formation. Therefore, it was expected that the dissolved cement mass fraction would increase with time at the fluid loss zone outlet, exactly as observed in the simulations as shown in Fig. 9.

Fig. 9
figure 9

Dissolved cement mass fraction field time evolution

Full size image

The initial cement mass fraction field was set with 75% of water. In Fig. 9, the big white arrows coming from the top and leaving by the fluid loss zone outlet, represent the average flow velocity direction. The area of concentrated cement(reddish strip) is the filter cake, and it forms by the accumulation of a dehydrated cement sheath in the fluid loss zone area, closer to the permeable left wall.

This accumulation of less hydrated cement, heavier than the surrounding fractions, generates a downward displacement of the formed cake due to its higher density. As a consequence, induced recirculation velocity profiles appear, indicated in Fig. 9 by the smaller white arrows beneath the and that also appear in the streamlines when analysing the velocity fields.

4.1 Fluid loss flow rate magnitude

The first parameter tested is the fluid loss flow rate magnitude. Despite the fluid loss velocity profile was maintained, a multiplication factor was applied, increasing the fluid loss flow rate magnitude. Figure 10 shows the time evolution of an dimensionless axial velocity profile at the specific depth of 2.5m, as represented in the small well schematic as a pink dashed line. This dimensionless velocity is obtained by dividing the axial velocity \(\vec {u}\) by the average fluid loss velocity \({\bar{u}}_{FL}\) inputted as a boundary condition at the outlet.

Fig. 10
figure 10

Difference in the radial velocity profiles at \(z=2.5\) m for different fluid loss flow rates

Full size image

The first velocity profiles correspond to the reference case. It can be noted that for higher flow rates, the velocity profile is slightly flatter and deviated to the left. For lower flow rates the fluid behaves as a very viscous Newtonian fluid, but as the flow rate increases, the viscoplastic behavior begins to affect the flow and flattens the profiles. Figures 11 and 12 show the pressure curves for flow rate multiplication factors of 10 and 20, respectively.

Fig. 11
figure 11

Simulated pressure for the fluid loss flow rate 10 times higher (solid line) in comparison with the reference case (dashed line)

Full size image
Fig. 12
figure 12

Simulated pressure for the fluid loss flow rate 20 times higher (plain line) in comparison with the reference case (dashed line)

Full size image

Notice that for these higher flow rates, the gelation slope is much more inclined due to the stronger fluid loss. In both figures, the dashed lines represent the reference case, and solid lines the respective parameter change.

4.2 Slurry thickening time

The second parameter evaluated is the slurry thickening time, which in the reference case is \(T_t = 6000s\). Figure 13 shows the pressure prediction for a transient time of 2000s, where some change in the shrinkage slope is observed. With the transient time of 1000s, the shrinkage slope anticipation is so abrupt that it starts to impact the gelation slope as well, as it can be seen in Fig. 14.

Fig. 13
figure 13

Pressure prediction for a slurry transient time of 2000s (solid line), in comparison with the reference case (dashed line)

Full size image
Fig. 14
figure 14

Pressure prediction for a slurry transient time of 1000s (solid line), in comparison with the reference case (dashed line)

Full size image

4.3 Rheological properties

Finally, the last parameters evaluated in the sensitivity analysis are the rheological properties. The shear stress curve is entirely shifted up and down, in order to map how these changes impact on the pressure predictions. Figure 15 shows the viscosity as a function of the shear rate for the reference case in red, and for both shifted cases on blue and cyan. Notice that the reference case average shear rate range is showed with a gray band in Fig. 15.

Fig. 15
figure 15

Shifted flow curves with in comparison with the reference case in red

Full size image

Figures 16 and 17 show the pressure prediction respectively for the flow curve shifted up and down.

Fig. 16
figure 16

Pressure prediction for the flow curve shifted-up in comparison with the reference case

Full size image
Fig. 17
figure 17

Pressure prediction for the flow curve shifted-down in comparison with the reference case

Full size image

The early pressure drop in Fig. 16 happens together with the flow rate ramp up passed as input at the outlet. A more viscous fluid, generates a higher pressure drop, than a low viscous one, and so, with a higher Newtonian viscosity plateau, the pressure drop is intensified.

On the other hand, the lower Newtonian viscosity plateau and lower yield stress of the shifted down curve, showed in Fig. 17, delays the viscosity buildup. This is equivalent to increase the transient time, which is known as a way to delay the pressure drop.

5 Final remarks

In this study, cement curing process on oil wells was analyzed in the presence of a fluid loss zone. A 2D model was proposed and implemented using the finite elements method. Qualitative adherence was observed in the model results. Quantities from computations were evaluated in a sensitivity analysis to observe variations in the pressure drop profiles.

Pressure profiles presented a decay with time in two different slopes, as expected. Concentration of cement field have presented intense dehydration close to the fluid loss zone. This was also expected and consistent with the literature description of a filter cake formation. Furthermore, for axisymmetric wells, the proposed model certainly enlightens the fluid loss impacts on the filter cake formation and how cement-to-water ratio may vary locally.

In the sensitivity analysis, the greatest changes in the pressure predictions were related to the fluid loss flow rate and to the slurry thickening time. For the simulated cases, viscosity stays almost all the time within the regularized Newtonian viscosity plateaus. Hence, higher values of fluid loss flow rate could be chosen for the reference case, to expose the rheological model to higher characteristic shear rates.

A natural continuation of this research passes by introducing additional features in the model, such as temperature variation. External temperature gradients could be directly introduced as boundary conditions, and its effects on the pressure could be evaluated. Computing the temperature field would also enable the evaluation of the heat of hydration on well pressure. Moreover, a 3D numerical model would enable the evaluation of pipe eccentricity and eroded wells influence in the fluid loss main flow, and consequently in the pressure drop.

Finally, the proposed model addresses the direct problem, where a fluid loss zone position is known or measured, and pressure drop can be predicted. The inverse problem could also be investigated, changing the boundary conditions at the outlet from velocity to pressure. This would allow the estimation of filtrate lost volumes for a known pressure profile.