1 Introduction

Cylindrical shell parts are widely used in aviation, aerospace, military, and other fields. Such parts are generally manufactured by deep drawing process. Due to the inadequacy of limiting drawing ratio (LDR), secondary deep drawing is often used to improve the LDR. This improvement is primarily based on the reduction of single-step deformation due to the increase in the drawing steps, which avoids the fracture caused by serious local wall thinning during the single-step forming process. Generally, according to whether the contact surface between punch and sheet metal changes, secondary deep drawing can be divided into positive secondary deep drawing and reverse deep drawing. Compared with the positive secondary deep drawing, the reverse deep drawing has the advantages of compact die structure, simple die positioning, and less bending deformation [1,2,3].

Reverse deep drawing is commonly used in traditional rigid die deep drawing. Although it has the above advantages, the die structure is complex, and the surface quality and forming accuracy of the formed parts cannot meet the harsh requirements in the aerospace field. In this study, the reverse deep drawing of cylindrical parts is implemented using granular medium. The rigid punch is used as the reverse deep drawing punch to avoid the wall thinning of the plate. The granular medium is used as the punch of positive deep drawing and the die of reverse deep drawing. The flexible die deep drawing of granular medium is combined with the reverse deep drawing to establish a new process. Due to the simultaneous realization of positive and reverse deep drawing in a set of die, the flow direction in the reverse deep drawing operation is opposite to that in the positive deep drawing, which is beneficial to offset the residual stress produced by positive deep drawing, thereby improving the forming conditions and increasing the forming limit of sheet metal. Granular medium does not produce scratches on the outer surface of the formed part, which is conducive to improving the surface quality of the part. Among the granular materials, solid granular medium has many unique properties. In the corresponding sheet metal forming process, the solid granular medium is used to replace the elastomer, liquid, and gas in the traditional rigid punch, die, or other flexible die forming processes. This process was proposed by Professor Zhao Changcai, Yanshan University [4, 5]. Further, Zhao Changcai et al. studied the pressure transmission performance and shear characteristics of granular medium under high pressure by using a self-designed experimental device. They also established a numerical simulation model of granular medium based on the discrete element method (DEM). Typical workpieces of various shapes were successfully trial-produced by using the deep drawing process of granular medium. Dong Guojiang [6, 7] developed the hot deep drawing process based on the cold forming process and successfully applied it to manufacture aluminum alloy sheets. In terms of theoretical analysis, based on the principle of plastic mechanics and bulk theory, Cao et al. [8, 9] studied the deformation law and stress state of granular medium sheet in the deep drawing process.

Since its first demonstration, several studies have been conducted on the granular medium forming process. Lang Lihui [10] and Li Pengliang [11] applied this process for the deep drawing of titanium alloy. The forming performance of granular medium under high temperature was studied, and cylindrical and box parts of titanium alloy were successfully trial-produced. Grüner et al. [12, 13] studied the basic mechanical properties of ceramic particles by experimental method and used them as a pressure transfer medium to form sheets and tubes. Furthermore, with the continuous increase in the application of high strength, difficult-to-deform, and low plasticity materials in the aerospace, automobile, and other fields, the solid granular medium forming process with high temperature resistance, strong pressure bearing capacity, and simple sealing is expected to receive considerable research attention in future. Accordingly, in this study, the reverse deep drawing process with solid granular medium is comprehensively examined through both numerical simulation and experiments. In the previous studies on reverse deep drawing with granular medium, due to the inaccurate selection of process parameters, the friction resistance and bending resistance between the sheet and the die were large, resulting in the problems of sheet flow and the low LDR. Finite element simulation is an effective approach to shorten the design cycle of stamping die, optimize the process, and improve the quality of stamping parts. The accuracy of parameters related to the material properties in the constitutive model directly affects the accuracy of finite element simulation. Therefore, to improve the forming quality and LDR of the sheet, it is crucial to establish a constitutive model that accurately reflects the deformation characteristics of the material in the reverse deep drawing process.

The sheet has obvious cyclic loading characteristics after bending, unloading, and reverse bending in the reverse deep drawing process [14]. In the existing studies, the influence of Bauschinger effect under reverse loading is usually ignored, and the cyclic loading characteristics are not considered, resulting in a large difference between the simulation and experimental results. Therefore, establishing an effective finite element model that includes the real deformation characteristics of the sheet, such as the directivity, strain strengthening effect, and Bauschinger effect, can improve the simulation accuracy and has important guiding significance for the study of granular medium reverse deep drawing process [15]. Recently, some hardening models considering cyclic loading have been proposed, such as the early stage linear kinematic hardening model proposed by Ziegler [16], the nonlinear kinematic hardening model proposed by Hodge [17], and the multi-surface hardening model proposed by Moroz [18]. Furthermore, Armstrong-Frederic (A-F) [19] nonlinear kinematic hardening model, Chaboche [20] superposition hardening model, and Ank [21] anisotropic nonlinear kinematic hardening model are widely used. The establishment of these models has laid a strong foundation for accurately describing the macroscopic deformation characteristics of sheet metal forming.

In this study, an anisotropic nonlinear kinematic hardening constitutive model is established based on the Hill48 yield criterion and A-F kinematic hardening model, and the reverse deep drawing process of granular medium is simulated. The simulation results are compared with those obtained using the isotropic hardening constitutive model based on Mises yield criterion. The granular medium reverse deep drawing test is established, and the simulation results of the two material models are compared with the experimental results. The accuracy and reliability of the two constitutive models are analyzed in terms of three aspects: wall thickness distribution and thinning, flange filling amount, and stress–strain history. This provides a high-precision finite element constitutive model for the subsequent optimization of process parameters and improving the ultimate drawing ratio of sheets. Overall, this study provides a reliable method for examining the deformation behavior of sheets under complex loading conditions, including unloading and reverse loading characteristics.

2 Description of constitutive model and acquisition of performance parameters

2.1 Isotropic hardening constitutive model based on Mises yield criterion

For isotropic materials, the yield function is independent of the choice of coordinate system, and the plastic deformation is only related to the second invariant J2 of the deviatoric tensor of stress. Therefore, J2 is used as the yield criterion. Consequently, Mises yield criterion can be expressed as follows: under certain deformation conditions, when the second invariant J2 of the deviatoric tensor of stress at a point in the stressed object reaches a certain value, this point begins to enter the plastic state, i.e.,

$${\left({\sigma }_{x}-{\sigma }_{y}\right)}^{2}+{\left({\sigma }_{y}-{\sigma }_{z}\right)}^{2}+{\left({\sigma }_{z}-{\sigma }_{x}\right)}^{2}+6\left({\tau }_{xy}^{2}+{\tau }_{yz}^{2}+{\tau }_{zx}^{2}\right)=2{\sigma }_{s}^{2}=6{K}^{2}$$
(1)

where σs and K are the yield point and shear yield strength of the material, respectively.

On the other hand, the equivalent stress \(\overline{\sigma }\) is

$$ \overline{\sigma } = \frac{1}{\sqrt 2 }\sqrt {\left( {\sigma_{x} - \sigma_{y} } \right)^{2} + \left( {\sigma_{y} - \sigma_{z} } \right)^{2} + \left( {\sigma_{z} - \sigma_{x} } \right)^{2} + 6\left( {\tau_{xy}^{2} + \tau_{yz}^{2} + \tau_{zx}^{2} } \right)} = \sigma_{s} $$
(2)

Therefore, Mises yield criterion can be expressed as follows: under certain deformation conditions, when the equivalent stress \(\overline{\sigma }\) at a point in the stressed object reaches a certain value, the point begins to enter the plastic state.

In Abaqus/Standard, the isotropic hardening constitutive model based on Mises yield criterion can be directly defined by the real stress–strain curve obtained using uniaxial tensile test.

2.2 Nonlinear kinematic hardening constitutive model based on Hill48 yield criterion

Most of the sheets used in deep drawing are anisotropic and have high material hardening rate, so Mises yield criterion and isotropic hardening model cannot truly reflect the plastic deformation behavior of sheet. Hill48 yield criterion considers the anisotropic characteristics of the material, and it is assumed that the contribution of stress to the plastic yield in each direction of the sheet is different, which can be used for describing the plastic behavior of the sheet forming process.

Assuming that the thickness anisotropy index r is constant during the plastic deformation process, if the sheet metal conforms to the flow rule of the total strain theory, then the r value can be obtained by measuring the strains in the width direction (εw) and thickness direction (εt) using a single tensile test. Specifically, the r value is expressed as follows:

$$r=\frac{{\varepsilon }_{w}}{{\varepsilon }_{t}}$$
(3)

The expressions for the ratio of six anisotropic yield stresses [18]: R11, R22, R33, R12, R13 and R23, can be derived by combining Hill48 anisotropic yield conditions. Since the material is in a plane stress state in the single-tension experiment, R13 and R23 are equal to 0.

$${R}_{11}=1$$
(4)
$${R}_{22}=\sqrt{\frac{{r}_{90}\left({r}_{0}+1\right)}{{r}_{0}\left({r}_{90}+1\right)}}$$
(5)
$${R}_{33}=\sqrt{\frac{{r}_{90}\left({r}_{0}+1\right)}{{r}_{0}+{r}_{90}}}$$
(6)
$${R}_{12}=\sqrt{\frac{3{r}_{90}\left({r}_{0}+1\right)}{\left(2{r}_{45}+1\right)\left({r}_{0}+{r}_{90}\right)}}$$
(7)

For the anisotropic behavior and Bauschinger effect exhibited by the material during plastic deformation, the kinematic hardening model gives a simple explanation that the yield surface of the material only moves as a rigid body and does not rotate in the stress space during deformation.

The yield surface function of kinematic hardening materials is generally expressed as follows:

$$\Phi =F\left({\sigma }_{ij}-{\alpha }_{ij}\right)-{\sigma }_{Y}=0$$
(8)

where \({\sigma }_{Y}\) is the initial yield stress and \({\alpha }_{ij}\) is the back stress.

The back stress represents the movement of the center of yield surface in the stress space, which plays a crucial role in the kinematic hardening model and yield surface evolution. Its value is related to the material hardening characteristics and deformation history. As shown in Fig. 1, the material is subjected to unidirectional elastic–plastic loading along the direction of \({\sigma }_{2}\), and the stress increases from \({\sigma }_{2}=0\) to \({\sigma }_{2}={\sigma }_{y}\). During the loading process, when the deformation state of the material changes from elastic deformation to plastic deformation, the center of the yield surface begins to move. When the stress in the \({\sigma }_{2}\) direction is loaded to the loading point 1, unloading and reverse loading are implemented to deform the material, and the material stress reaches the loading point 2 to produce reverse plastic yield. It is clear from Fig. 2 that the yield stress of the material under reverse loading is smaller than the initial yield stress \({\sigma }_{y}\).

Fig. 1
figure 1

Kinematic hardening (center movement of yield surface and corresponding uniaxial stress–strain curve)

Full size image
Fig. 2
figure 2

Uniaxial tensile test diagram of 304L stainless steel: a Test drawing machine diagram. b Uniaxial tensile specimen

Full size image

The A-F nonlinear kinematic hardening model has been extensively utilized to study the cyclic plastic behavior of materials. This model contains a linear hardening term and a dynamic restoration term. The evolution equation can be expressed as follows:

$$ d\alpha_{ij} = \frac{2}{3}Cd\varepsilon_{ij}^{p} - \gamma \alpha_{ij} d\overline{\varepsilon }^{p} $$
(9)

where \(C\) and \(\gamma \) are material parameters; \({\alpha }_{ij}\) is the back stress component; \(d{\varepsilon }_{ij}^{p}\) is the increment in the plastic strain; \(d\overline{\varepsilon }^{p}\) is the equivalent plastic strain increment, \(d\overline{\varepsilon }^{p} = \sqrt {\frac{{d\varepsilon_{ij}^{p} }}{{d\overline{\varepsilon }_{ij}^{p} }}}\).

When the material is subjected to uniaxial tensile loading, \(d\overline{\varepsilon }^{p} = d\varepsilon^{p}\). Therefore, it can be obtained that

$$d{\alpha }_{1}=\frac{2}{3}Cd{\varepsilon }_{1}^{p}-\gamma {\alpha }_{1}d{\varepsilon }_{1}^{p}$$
(10)

The above equation can be simplified as follows:

$$\frac{d{\alpha }_{1}}{\frac{2}{3}C-\gamma {\alpha }_{1}}=d{\varepsilon }_{1}^{p}$$
(11)

Integrating the above first-order differential equation, we get

$${\alpha }_{1}=\frac{2}{3}\frac{C}{\gamma }+\left({\alpha }_{1}^{0}-\frac{2}{3}\frac{C}{\gamma }\right){e}^{-\gamma \left({\varepsilon }_{1}^{p}-{\varepsilon }_{\mathrm{1,0}}^{p}\right)}$$
(12)

where \({\alpha }_{1}^{0}\) is the initial value of back stress, and \({\varepsilon }_{\mathrm{1,0}}^{p}\) is the initial value of plastic strain.

The initial conditions are \({\alpha }_{1}^{0}={\varepsilon }_{\mathrm{1,0}}^{p}=0\). Using these initial values, the back stress equation can be obtained as

$${\alpha }_{1}=\frac{2}{3}\frac{C}{\gamma }\left(1-{e}^{-\gamma {\varepsilon }_{1}^{p}}\right)$$
(13)

According to the above equation, the parameters \(C\) and \(\gamma \) can be determined by nonlinear fitting of the experimentally acquired plastic strain data and the real stress obtained from uniaxial tensile test of the sheet specimen. The six anisotropic parameters ( R11, R22, R33, R12, R13, R23) and kinematic hardening parameters (\(C\) and \(\gamma \)) were input into Abaqus material model library to simulate the reverse deep drawing process with granular medium based on the Hill48 yield criterion.

2.3 Material property testing

304L stainless steel plate was selected as the research object. 304L stainless steel is 18–8 austenitic stainless steel with good corrosion resistance and formability.

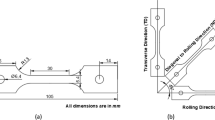
The numerical simulation parameters were obtained according to the China National Standard “Tensile testing method for metal materials at room temperature” (GB/T 228–2002). The uniaxial tensile test of the original sheet was conducted on the InspektTable-100 material universal testing machine. The standard size of the sheet specimen used in the unidirectional tensile test was 120 mm. Three groups of unidirectional tensile specimens were cut along the directions of 0°, 45°, and 90° with respect to the rolling direction. The strain rate during the tensile test was 0.0013 /sec.

To obtain the anisotropy coefficient, the axial strain and transverse strain during the deformation process of the specimen were recorded by an online strain measurement system based on digital image correlation (DIC). The testing machine and the DIC online strain measurement system are shown in Fig. 2a, and the size of the uniaxial tensile specimen is shown in Fig. 2b.

The engineering stress–strain curve of the large sample is obtained by the uniaxial tensile test, and the real stress–strain data are obtained according to the conversion formula, as shown in Fig. 3a. In the uniaxial tensile process of the specimen in three directions, the strains in the width and thickness directions are measured to obtain the r value, and the results are shown in Fig. 3b. According to Eq. (13), the initial yield point in the real stress–strain curve of 304L stainless steel plate is taken as the starting point of the back stress parameter fitting curve for obtaining the relevant parameters, as shown in Fig. 3c.

Fig. 3
figure 3

aTrue stress–strain curve of 304L plate. b Anisotropy coefficient of 304L plate. c Back stress parameter fitting curve

Full size image

The fitting equation is as follows:

$${\alpha }_{1}=a\left(1-{e}^{-b{\varepsilon }_{1}^{p}}\right)$$
(14)

The corresponding relationship between the parameters in the fitting Eq. (14) and the parameters in the back stress Eq. (13) is

$$a=\frac{2}{3}\frac{C}{\gamma }, b=\lambda $$

Substituting it into the back stress curve in Fig. 3c, it is obtained that a = 8.2, and b = 317. The final fitting parameters are obtained as follows:

$$C=\text{3885; }\gamma =317$$

The parameters of each material model are listed in Table 1 and Table 2.

Table 1 Simulation of material parameters required
Full size table
Table 2 Ratio of anisotropic yield stress of materials
Full size table

C is kinematic hardening modulus, γ is used to determine the rate of decrease of kinematic hardening modulus with the increase in plastic deformation.

3 Numerical simulation model for reverse deep drawing using granular medium

To compare the performance of anisotropic kinematic hardening and isotropic power hardening models in simulating the positive and negative composite deep drawing with granular medium, 304L stainless steel plates with a radius of 55 mm and thickness of 1 mm were selected for finite element simulation on Abaqus software.

Firstly, the friction coefficient between 304L stainless steel plate and die was examined using a friction and wear tester (produced by Center for Tribology (CETR), USA) with maximum allowable contact pressure of 30 MPa. Lubricants such as mineral oil, synthetic lubricating oil, grease, paraffin wax, and talcum powder were selected for the friction test. In the test, synthetic lubricating oil was selected as the binder in the blank holder area, where the lowest friction coefficient was 0.08 and the friction coefficient without lubrication was 0.18.

The friction coefficient between particle medium and plate and between particle medium and punch was measured to be 0.12 by shear test. The friction coefficient between punch and plate was set as 0.18; the friction coefficient between flange and plate was set as 0.08 (oil-based graphite lubrication). In this numerical model, all the components are defined as rigid bodies, except for plates and granular medium, which were considered as deformed bodies.

The plate was set to S4R. Further, hourglass control was selected, and five points were set in the thickness direction. The contact in the deep drawing process of granular media mainly includes two types: the contact surface between sheet and die, and the contact surface between granular and sheet and die. Both of these two contact types need to define normal contact attributes and tangential contact attributes in the definition process of numerical analysis. Because the deformation of the die and the thickness stress of the sheet are not large in deep drawing, the normal contact property of the sheet and the die is set to ‘HARD’ contact. The tangential contact property reflects the friction shear force between the contact surface of the plate and the die. In the modeling process, the penalty function is used to ensure that the two contact surfaces enter the sliding state smoothly from the bonding state.

C3D8R, hourglass control, and grid deformation were adopted in the solid particle medium unit. The Poisson’s ratio ν of this medium was selected as 0.45. The linear Drucker-Prager model was used to simulate the granular materials. In this study, GM particle medium included regular spherical particles with a size of 0.1–0.3 mm, and the friction angle was small. Therefore, the same definitions of tensile and compressive failure could be used to match the parameters of Drucker-Prager model and Mohr–Coulomb model. For the angle β between the plane of destruction of the granular medium and the plane of maximum principal stress and the Mohr–Coulomb internal friction angle θ, the following transformation relations between the linear Drucker-Prager model and the Mohr–Coulomb model are available:

$$\mathrm{tan}\beta =\frac{6\mathrm{sin}\theta }{3-\mathrm{sin}\theta }, X=\frac{3-\mathrm{sin}\theta }{3+\mathrm{sin}\theta }$$
(15)

where β is the angle between the damage plane of the granular material and the plane of maximum principal stress, as shown in Fig. 4a; θ is the Mohr–Coulomb internal friction angle of the granular material; and X is the ratio of triaxial tensile yield stress to triaxial compressive yield stress.

Fig. 4
figure 4

a The stress diagram. b Mohr envelope

Full size image

The point tangent to the Mohr circle and Mohr envelope indicates the plane orientation and the stress state on the plane when the damage is produced by the granular material, and it indicates the strength condition of the granular material. The angle between the Mohr envelope and the horizontal line is the internal friction angle θ of the granular medium, and the Mohr envelope is the shear strength of the granular material. The shear strength and the angle of internal friction of the granular medium can be found directly by graphical solution. Their values can also be found directly by the Mohr circle equation, as shown in Fig. 4(b). For the GM granular materials in this study, which are non-viscous particles, the internal friction angle of the materials can be found according to the Mohr–Coulomb strength yield criterion, which is as follows:

$$\tau =c-\sigma \mathrm{tan}\theta $$
(16)

where τ is the shear strength, and σ is the normal stress.

For non-viscous materials, c = 0. The shear strength of GM solid granules medium under different positive pressures was measured by the material shear performance test [22, 23], which was substituted into Eq. (16) to obtain the Mohr–Coulomb internal friction angle θ of 17.7°. It was then substituted into Eq. (15) to obtain the relevant parameter values, and the results are shown in Table 3. The dilation angle ψ of particles also has a significant influence on the sheet forming performance. Based on the experimental study of material shear performance, the dilation angle ψ of GM solid granules medium is obtained to be 17.5°.

Table 3 Simulation parameters for GM solid granules medium
Full size table

The finite element simulation model of reverse deep drawing using granular medium is shown in Fig. 5.The granule head is raised upward at a speed v1, and the upper and lower pressing edges are raised upward at a speed v2, which is less than v1. The granule head is used to compress the granular medium to implement positive deep drawing deformation of the sheet metal. The initial deep drawing ring is formed in the drawing groove. When the positive deep drawing reaches the depth H, the two speeds are consistent until the final forming process.

Fig. 5
figure 5

Finite element simulation model

Full size image

4 Experimental study on reverse deep drawing process of granular medium

A four-column numerical control hydraulic press with engineering tonnage of 500 tons was used in the test. The loading speed of the press was controlled to be 60 mm/min, and the force–displacement curve of the loading head was obtained. 304L stainless steel sheet metal with initial radius of 55 mm and initial thickness of 1 mm was selected as the test sheet metal. Non-metallic granules with SiO2 as the main component were selected as the pressure transmission medium [22, 23]. The granular size was φ 0.117–0.14 mm, and the Rockwell hardness was 48–55 HRC. The granules were smooth, round, and non-sticky. The maximum volume compression rate was approximately 12%. A schematic of the forming process is shown in Fig. 6a and b. In the reverse deep drawing process, according to the positional relationship between sheet metal and die, the sheet metal is divided into five deformation areas: flange area, drawing ring area, straight wall section, bottom fillet area, and bottom area, as shown in Fig. 6c. According to the constant volume condition and compressibility of granular medium, the filling amount of granular medium is determined to be 110 ml. A schematic of the reverse deep drawing using solid granular medium test die is shown in Fig. 6d.

Fig. 6
figure 6

a Diagram of Initial Installation State of Process Mold. b Process Diagram. c Sheet Metals Deforming. d Actual forming die. where: 1-upper edge pressing. 2-compression heads of solid granule medium. 3-reducing column. 4-solid granule medium. 5-sheet. 6-lower edge pressing. 7-punc. 8-feed cylinder. 9-adjustment gasket

Full size image

5 Comparison between test and simulation results

The simulation results of the isotropic hardening constitutive model based on Mises yield criterion and the kinematic hardening constitutive model based on Hill48 yield criterion were obtained by using the same process parameters. A comprehensive comparative analysis was conducted from three aspects: stress–strain curve, flange feeding amount, and wall thickness distribution and thinning. Further, the simulation results were compared with the experimental results to verify the accuracy and reliability of the two constitutive models.

5.1 Stress–strain curve of sheet metal flow direction in the deep drawing ring

The stable deformation state of the sheet in the deep drawing ring obtained by simulation is shown in Fig. 7. In the transition between the deep drawing ring area and the deep drawing ring area of the plate material, the nodes at section A that do not enter the deep drawing ring area are selected. The stress–strain curve of the upper surface and the lower bottom integral points along the instantaneous flow direction of the plate is extracted from the section A through the fillets of the drawbead and the movement to the point E, as shown in Fig. 8.

Fig. 7
figure 7

Node extraction position in deep drawing ring under steady state deformation

Full size image
Fig. 8
figure 8

Stress–strain history curves of isotropic hardening constitutive model based on Mises yield criterion and kinematic hardening constitutive model based on Hill48 yield criterion: a Upper integral point. b Lower integral points

Full size image

It can be seen in Fig. 8 that when the sheet metal flows from the flange area to the deep drawing ring area under the action of the front end tension, the bending moment caused by the die fillet leads to bending deformation. The bending sheet metal is stretched at the contact arc of the groove fillet under the action of the deep drawing ring and the straight wall of the die, and it continues to flow to the deep drawing ring area due to tension. The tangential stress of the sheet metal gradually increases due to the strain hardening and reaches the maximum value after entering the deep drawing ring area.

In Fig. 8, the stress of the kinematic hardening model under forward loading is not equal to the yield stress under reverse loading. The stress at the unloading point is greater than that at the yield point under reverse loading, which indicates the characteristics of Bauschinger effect and conforms to the kinematic hardening law. The stress–strain curve of the power hardening model is similar to that of the kinematic hardening model in the forward loading process. During the reverse loading process, the unloading point stress of the isotropic hardening constitutive model (based on Mises yield criterion) is much larger than that of the kinematic hardening constitutive model (based on Hill48 yield criterion).

5.2 Comparison of feeding amount in the flange area

The flange material gradually flows through the deep drawing ring area under the action of granular medium pressure and finally sticks to the straight wall section. A comparison between the simulation results of the two material models and the experimentally obtained flange shrinkage is shown in Fig. 9. At the same deep drawing height (the flange height from the bottom), the simulated flange shrinkage obtained by the kinematic hardening model is greater than that obtained by the isotropic hardening model. At the deep drawing height of 20 mm, the experimental flange shrinkage is 5.8 mm, while the corresponding value obtained by the kinematic hardening model is 6.41 mm, which indicates an error of 10.5% with respect to the experimental result. The shrinkage of the flange area obtained by the isotropic hardening model is 4.71 mm, and the error with respect to the experimental result is 18.8%.

Fig. 9
figure 9

Comparison of feeding amount in flange area

Full size image

5.3 Comparison of wall thickness distribution and thinning

The simulation results of positive and negative composite deep drawing using granular medium are based on two material constitutive models: isotropic hardening model based on Mises yield criterion and kinematic hardening constitutive model based on Hill48 yield criterion. The wall thinning data of each region of the sheet at drawing heights of 12.5 mm and 20.8 mm are extracted and compared with the experimental results, as shown in Fig. 10. Under the two material models, the maximum thinning point of wall thickness is at the transition point between the straight wall section and the punch fillet area. In the subsequent forming process, the convex die fillet area and the straight wall plate simulated by the isotropic hardening constitutive model are elongated, and the wall thickness is reduced during the forming process. The simulation results obtained by the nonlinear kinematic hardening constitutive model are consistent with the experimental results, and the maximum error is 3.2%.

Fig. 10
figure 10

Wall Thickness Distribution

Full size image

Based on the comprehensive comparison between simulation and experimental results, it is found that the reduction in wall thickness obtained by the kinematic hardening model is smaller, while the amount of feeding in the flange area is more. This is ascribed to the fact that the kinematic hardening model can reflect the characteristics of the Bauschinger effect. The nonlinear kinematic hardening constitutive model based on Hill48 yield criterion better reflects the cyclic loading characteristics in the process of positive and negative composite deep drawing using granular medium and effectively improves the simulation accuracy.

6 Conclusion

  1. (1)

    A kinematic hardening constitutive model based on Hill48 yield criterion was established considering the plate directivity, work hardening characteristics, and Bauschinger effect. From the perspective of stress–strain history relationship, the plate experienced continuous bending, unloading, reverse bending, and cyclic plastic deformation during the reverse deep drawing process.

  2. (2)

    The material parameters and anisotropic parameters of the kinematic hardening model were accurately determined. These parameters could be directly input into Abaqus simulation software, which eliminated the tedious secondary deep drawing process. The reliability and accuracy of the established anisotropic kinematic hardening model were verified through simulation and test of the reverse deep drawing process with granular medium.

  3. (3)

    The proposed model effectively simulated the cyclic loading deformation behavior of granular medium in the process of reverse deep drawing with enhanced accuracy. This provides a reliable method for the subsequent optimization of process parameters and offers insights into the cyclic loading deformation characteristics of reverse deep drawing process.