1 Introduction

Bearing is widely used in rotating machinery because of its unique advantages in the transmission process [1, 2]. The measurement and analysis of the dynamic response of the bearing-pedestal system are helpful to realize the monitoring and diagnosis of the system state signals [3, 4]. At the same time, the measurement and analysis of the system's dynamic response are helpful to avoid heavy economic losses and even casualties caused by sudden faults of rotating machinery [5]. Since the vibration signals are generally measured by sensors installed on the pedestal [6], the model considering the coupling between bearing and pedestal is more reasonable. The cylindrical roller bearing-pedestal system has a very important impact on the performance of an aeroengine. However, the working environment of aeroengine is complex. For example, fighters will repeatedly experience extreme gravity conditions such as weightlessness and overweight when performing tactical attack and tactical evasion. Therefore, the research on cylindrical roller bearing-pedestal system has high engineering application value.

Gupta [7, 8] deduced the motion equation of the bearing system and analyzed the traction slip relationship in cylindrical roller bearing. Leblanc et al. [9] established a plan dynamic model to analyze the bearing behavior. Han and Chu [10] presented a bearing three-dimensional nonlinear dynamic model and analyzed the response of the model under composite load. Wen et al. [11] and Han et al. [12] established a three degree of freedom dynamic model of the bearing cage, and analyzed the motion of the bearing cage under rotor unbalance force. Liu et al. [13] proposed a dynamic simulation method of locally defective bearing and studied the contact mechanical characteristics between ball and raceway. Jiang et al. [14] presented a dynamic model considering the three-dimensional geometric relationship of bearing defects and studied the influence of defect size on bearing contact form. Cao et al. [15] performed a dynamic model of a bearing-pedestal system and studied the influence of fit clearance on the vibration characteristics of the system. Shi et al. [16] studied the dynamic characteristics of the bearing outer ring and analyzed the sensitivity of temperature, speed, and load. Liu and Shao [17] proposed an improved bearing model and analyzed the influence of defect shape on bearing system vibration. Chen et al. [18] studied the characteristics of the bearing rotor system subjected to unbalanced force and analyzed the law of quasi-periodic motion of the system. Li et al. [19] derived the dynamic equations of the bearing body system and studied the sliding characteristics of the bearing body system. Wang et al. [20] proposed an improved nonlinear dynamic model of bearing to obtain the contact deformation between the bearing ball and raceway more accurately. Tu et al. [21] presented the dynamic model of cylindrical roller bearing considering slip and analyzed the influence of friction on the dynamic response of the bearing. Suryawanshi et al. [22] derived the dynamic model of rotor-bearing system considering fault angle, speed, and load and analyzed the influence of fault size on its vibration response. Chen et al. [23] established the kinematics and dynamics model of bearing rolling elements under whirl condition and analyzed the effects of different external loads, whirl radius, whirl frequency, and other factors on bearing slip. Pinedo-Sanchez et al. [24] proposed a new data analysis method to study the wear degree of each component of the rolling bearing system in the actual operation process. Zhang et al. [25] proposed a fractal dimension estimation method; used this method to study the fractal characteristics of rolling bearing vibration signals and used the fractal characteristics to diagnose rolling bearing faults. Yu and Pan [26] combined the intrinsic time scale decomposition with the graphic signal processing to extract composite fault signals from the aeroengine rolling bearing system.

From the mentioned references above, it indicates that many dynamic models of bearing body, vibration response of bearing rotor system, signal diagnosis are established and analyzed. However, there are few studies on the dynamic characteristics of cylindrical roller bearing-pedestal system considering sliding friction, Hertz contact, and time-varying load under different working conditions. The goal of this paper is to establish a dynamic model of a cylindrical roller bearing-pedestal system and use the model to analyze the effects of extreme gravity conditions, load, rotational speed, and mass on its dynamic behavior.

The remainder of this paper is organized as follows. In Sect. 2, the force of the cylindrical roller bearing-pedestal system is analyzed, and the dynamic model of the cylindrical roller bearing-pedestal system is proposed. In Sect. 3, through the rotor experimental bench with a cylindrical roller bearing-pedestal system, the simulation result of the dynamic model is verified by the experimental result. In Sect. 4, the dynamic characteristics of the system under extreme gravity conditions are analyzed, the sensitivity of the system to load and rotational speed is studied, and the influence of mass on the dynamic response of the system is discussed. Finally, the conclusions are drawn in Sect. 5.

2 Dynamic model of the system

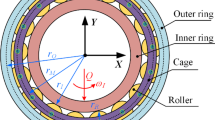
The simulation calculation of the dynamic model can simulate the state of the system in actual operation. To establish the dynamic model of the cylindrical roller bearing-pedestal system, the structure of the cylindrical roller bearing N205M is studied. The structure of the cylindrical roller bearing N205M is illustrated in Fig. 1.

Fig. 1
figure 1

Cylindrical roller bearing N205M

Full size image

As shown in Fig. 1, the cylindrical roller bearing N205M contains 13 rollers, and the included angle between two adjacent rollers and the origin O is 2π/13 rad. The positive directions of x and y are established through the Cartesian coordinate system. The included angle between the jth roller in the bearing structure and the positive direction of the x is defined as βj.

2.1 Force analysis of the dynamic model

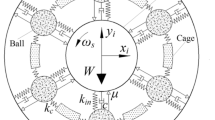
Figure 2 shows the dynamic model of the cylindrical roller bearing-pedestal system, which is composed of the equivalent dynamic model of the system and the force analysis model of the jth roller. The pressure in this paper is actually the extrusion force of the roller by the raceway or cage, which has the same properties as the friction force of the roller. According to Newton's third law, the pressure of the roller in this paper has the properties of acting force and reaction force. Therefore, the pressure in this paper is being handled as force.

Fig. 2
figure 2

Dynamic model of cylindrical roller bearing-pedestal system

Full size image

As shown in Fig. 2a, ri, rm, and ro are the radius of the inner race, the pitch radius, and the radius of the outer race. \(\dot{\varphi }_{{\text{c}}}\) and \(\dot{\varpi }_{j}\) are the speed of the cylindrical roller bearing cage and the speed of the cylindrical roller bearing roller. Fa, k, and c are the vertical load, the stiffness of the pedestal, and the damping coefficient of the pedestal. n is the speed of the shaft. ∆vij and ∆voj are the velocity difference between the inner and outer raceways and the bearing roller.

As shown in Fig. 2b, oj is the mass center of the jth roller, and mj is the mass of the jth roller. The roller in the cylindrical roller bearing N205M operates under the action of gravity, centrifugal force, frictions, and pressures. Among them, Fjm is the centrifugal force. Fji, Fjo, Fjfc, and Fjrc are the forces of friction on the bearing roller. Pji, Pjo, Pjfc, and Pjrc are the pressures on the bearing roller. \(\dot{\eta }_{j}\) is the rotation speed of the roller.

2.2 Derivation of system dynamic equations

Based on the established dynamic model of the cylindrical roller bearing-pedestal system, the system dynamic equations are derived. The dynamic equations comprehensively consider the factors such as sliding friction, Hertz contact, and time-varying load.

The dynamic equation of the roller rotation can be expressed as Eq. 1:

$$ m_{j} r_{{\text{r}}}^{2} \ddot{\eta }_{j} + F_{j}^{{{\text{fc}}}} r_{{\text{r}}} + F_{j}^{{{\text{rc}}}} r_{{\text{r}}} - F_{j}^{{\text{i}}} r_{{\text{r}}} - F_{j}^{{\text{o}}} r_{{\text{r}}} = 0 $$
(1)

where mj is the mass of the jth roller, rr is the radius of the roller, \(\ddot{\eta }_{j}\) is the acceleration of the bearing roller rotation, Fjfc is the friction between the front cage and the jth roller, Fjrc is the friction between the rear cage and the jth roller, Fji is the friction between the inner race and the jth roller, and Fjo is the friction between the outer race and the jth roller.

The dynamic equation of the roller revolution can be expressed as Eq. 2:

$$ m_{j} r_{{\text{m}}} \ddot{\varpi }_{j} - F_{j}^{{\text{i}}} + F_{j}^{{\text{o}}} + m_{j} g\cos \beta_{j} + P_{j}^{{{\text{fc}}}} - P_{j}^{{{\text{rc}}}} = 0 $$
(2)

where rm is the pitch radius, \(\ddot{\varpi }_{j}\) is the acceleration of the roller, g is the gravitational acceleration, and βj is the angle between the roller and the positive direction of x. Pjfc and Pjrc are the pressure of the front cage and the rear cage on the roller.

The dynamic equation of the roller along the bearing diameter can be expressed as Eq. 3:

$$ m_{j} \ddot{d}_{j} - P_{j}^{{\text{i}}} + P_{j}^{{\text{o}}} + m_{j} g\sin \beta_{j} + F_{j}^{{{\text{fc}}}} - F_{j}^{{{\text{rc}}}} - F_{j}^{{\text{m}}} = 0 $$
(3)

where \(\ddot{d}_{j}\) is the acceleration of the jth roller along the diameter direction, and Fjm is the centrifugal force. Pji and Pjo are the pressure of the inner race and the outer race on the jth roller.

The mass \(m_{j}\) can be expressed as Eq. 4:

$$ m_{j} = \rho {\uppi }r_{{\text{r}}}^{2} l $$
(4)

where ρ is the roller density, and l is the length of the roller.

The included angle βj can be calculated by Eq. 5

$$ \beta_{j} = \frac{2\pi }{{13}}\left( {j - 1} \right) + \dot{\varpi }_{j} t, \, j = 1, \, 2, \, . \, . \, . \, , \, 13. $$
(5)

where \(\dot{\varpi }_{j}\) is the speed of the bearing roller, and t is the running time.

The centrifugal force \(F_{j}^{{\text{m}}}\) can be calculated by Eq. 6:

$$ F_{j}^{{\text{m}}} = m_{j} r_{{\text{m}}} \dot{\varpi }_{j}^{2} $$
(6)

The friction \(F_{j}^{{{\text{fc}}}}\) can be calculated by Eq. 7:

$$ F_{j}^{{{\text{fc}}}} = \mu_{{\text{c}}} P_{j}^{{{\text{fc}}}} $$
(7)

where μc is the friction coefficient of the bearing cage.

The pressure \(P_{j}^{{{\text{fc}}}}\) can be calculated by Eq. 8:

$$ P_{j}^{{{\text{fc}}}} = k_{{\text{c}}} r_{{\text{m}}} \left( {\varpi_{j} - \varphi_{{\text{c}}} } \right)H\left( {\varpi_{j} - \varphi_{{\text{c}}} } \right) $$
(8)

where kc is the stiffness when the bearing cage and the bearing roller are pressed against each other, \(\varphi_{{\text{c}}}\) is the angular displacement of the bearing cage, and the Heaviside function \(H\left( {\varpi_{j} - \varphi_{{\text{c}}} } \right)\) can be calculated by Eq. 9

$$ H\left( {\varpi_{j} - \varphi_{{\text{c}}} } \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {\left( {\varpi_{j} - \varphi_{{\text{c}}} } \right) > 0,} \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {\left( {\varpi_{j} - \varphi_{{\text{c}}} } \right) \le 0.} \\ \end{array} } \\ \end{array} } \right. $$
(9)

The friction \(F_{j}^{{{\text{rc}}}}\) is given by Eq. 10:

$$ F_{j}^{{{\text{rc}}}} = \mu_{{\text{c}}} P_{j}^{{{\text{rc}}}} $$
(10)

The pressure \(P_{j}^{{{\text{rc}}}}\) is given by Eq. 11:

$$ P_{j}^{{{\text{rc}}}} = k_{{\text{c}}} r_{{\text{m}}} \left( {\varphi_{{\text{c}}} - \varpi_{j} } \right)H\left( {\varphi_{{\text{c}}} - \varpi_{j} } \right) $$
(11)

where the Heaviside function \(H\left( {\varphi_{{\text{c}}} - \varpi_{j} } \right)\) can be calculated by Eq. 12)

$$ H\left( {\varphi_{{\text{c}}} - \varpi_{j} } \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {\left( {\varphi_{{\text{c}}} - \varpi_{j} } \right) > 0,} \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {\left( {\varphi_{{\text{c}}} - \varpi_{j} } \right) \le 0.} \\ \end{array} } \\ \end{array} } \right. $$
(12)

The friction \(F_{j}^{{\text{i}}}\) can be expressed as Eq. 13

$$ F_{j}^{{\text{i}}} = - {\text{sign}}\left( {\Delta v_{j}^{{\text{i}}} } \right)\mu_{j}^{{\text{i}}} P_{j}^{{\text{i}}} $$
(13)

where \(\Delta v_{j}^{{\text{i}}}\) is the velocity difference between the bearing inner race and the bearing roller and \(\mu_{j}^{{\text{i}}}\) is the friction coefficient between the bearing inner race and the bearing roller.

The velocity difference \(\Delta v_{j}^{{\text{i}}}\) can be expressed as Eq. 14

$$ \Delta v_{j}^{{\text{i}}} = \frac{{2{\uppi }n}}{60}r_{{\text{i}}} - \dot{\eta }_{j} r_{{\text{r}}} - \dot{\varphi }_{{\text{c}}} r_{{\text{i}}} $$
(14)

where ri is the radius of the inner race.

The coefficient \(\mu_{j}^{{\text{i}}}\) can be calculated by Eq. 15

$$ \mu_{j}^{{\text{i}}} = \left\{ \begin{gathered} 0.04\left| {\Delta v_{j}^{{\text{i}}} } \right|\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\left| {\Delta v_{j}^{{\text{i}}} } \right| < 0.05,} \\ \end{array} } \\ \end{array} \\ 0.002\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } \\ \end{array} \begin{array}{*{20}c} {\left| {\Delta v_{j}^{{\text{i}}} } \right| \ge 0.05.} \\ \end{array} \\ \end{gathered} \right. $$
(15)

The pressure \(P_{j}^{{\text{i}}}\) can be expressed as Eq. 16

$$ P_{j}^{{\text{i}}} = k_{{\text{i}}} \left( {\Gamma_{j}^{{\text{i}}} } \right)^{10/9} H\left( {\Gamma_{j}^{{\text{i}}} } \right) $$
(16)

where ki is the contact stiffness when the inner ring and roller are pressed against each other, \(\Gamma_{j}^{{\text{i}}}\) is the displacement between the roller and inner race, and the Heaviside function \(H\left( {\Gamma_{j}^{{\text{i}}} } \right)\) can be calculated by Eq. 17:

\(H\left( {\Gamma_{j}^{{\text{i}}} } \right) = \left\{ {\begin{array}{*{20}c} {1\begin{array}{*{20}c} {} & {\Gamma_{j}^{{\text{i}}} > 0,} \\ \end{array} } \\ {0\begin{array}{*{20}c} {} & {\Gamma_{j}^{{\text{i}}} \le 0.} \\ \end{array} } \\ \end{array} } \right.\) 17.

The displacement \(\Gamma_{j}^{{\text{i}}}\) can be calculated by Eq. 18

$$ \Gamma_{j}^{{\text{i}}} = x_{{\text{i}}} \cos \beta_{j} + y_{{\text{i}}} \sin \beta_{j} - d_{j} $$
(18)

where xi, yi, and dj are the displacement of the inner raceway in the x direction, the displacement of the inner raceway in the y direction, and the displacement of the jth roller along the diameter direction.

The friction \(F_{j}^{{\text{o}}}\) can be calculated by Eq. 19

$$ F_{j}^{{\text{o}}} = - {\text{sign}}\left( {\Delta v_{j}^{{\text{o}}} } \right)\mu_{j}^{{\text{o}}} P_{j}^{{\text{o}}} $$
(19)

where \(\Delta v_{j}^{{\text{o}}}\) is the velocity difference between the bearing outer race and the bearing roller and \(\mu_{j}^{{\text{o}}}\) is the friction coefficient between the outer race and the jth roller.

The velocity difference \(\Delta v_{j}^{{\text{o}}}\) can be expressed as Eq. 20

$$ \Delta v_{j}^{{\text{o}}} = \dot{\varphi }_{{\text{c}}} r_{{\text{o}}} - \dot{\eta }_{j} r_{{\text{r}}} $$
(20)

where ro is the radius of the outer race.

The coefficient \(\mu_{j}^{{\text{o}}}\) is given by Eq. 21

$$ \mu_{j}^{{\text{o}}} = \left\{ \begin{gathered} 0.04\left| {\Delta v_{j}^{{\text{o}}} } \right|\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\left| {\Delta v_{j}^{{\text{o}}} } \right| < 0.05,} \\ \end{array} } \\ \end{array} \\ 0.002\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } \\ \end{array} \begin{array}{*{20}c} {\left| {\Delta v_{j}^{{\text{o}}} } \right| \ge 0.05.} \\ \end{array} \\ \end{gathered} \right. $$
(21)

The pressure \(P_{j}^{{\text{o}}}\) can be expressed as Eq. 22

$$ P_{j}^{{\text{o}}} = k_{{\text{o}}} \left( {\Gamma_{j}^{{\text{o}}} } \right)^{10/9} H\left( {\Gamma_{j}^{{\text{o}}} } \right) $$
(22)

where ko is the contact stiffness when the outer ring and roller are pressed against each other, \(\Gamma_{j}^{{\text{o}}}\) is the displacement between the roller and outer race, and the Heaviside function \(H\left( {\Gamma_{j}^{{\text{o}}} } \right)\) can be calculated by Eq. 23:

$$ H\left( {\Gamma_{j}^{{\text{o}}} } \right) = \left\{ {\begin{array}{*{20}c} {1\begin{array}{*{20}c} {} & {\Gamma_{j}^{{\text{o}}} > 0,} \\ \end{array} } \\ {0\begin{array}{*{20}c} {} & {\Gamma_{j}^{{\text{o}}} \le 0.} \\ \end{array} } \\ \end{array} } \right. $$
(23)

The displacement \(\Gamma_{j}^{{\text{o}}}\) is given by Eq. 24

$$ \Gamma_{j}^{{\text{o}}} = d_{j} $$
(24)

The dynamic equation of bearing inner ring can be expressed as Eq. 25

$$ \left\{ \begin{gathered} m_{{{\text{in}}}} \ddot{x}_{{\text{i}}} + \sum\limits_{j = 1}^{13} {P_{j}^{{\text{i}}} \cos \beta_{j} - } \sum\limits_{j = 1}^{13} {F_{j}^{{\text{i}}} \sin \beta_{j} } = 0 \hfill \\ m_{{{\text{in}}}} \ddot{y}_{{\text{i}}} + \sum\limits_{j = 1}^{13} {P_{j}^{{\text{i}}} \sin \beta_{j} } + \sum\limits_{j = 1}^{13} {F_{j}^{{\text{i}}} \cos \beta_{j} } + F = 0 \hfill \\ \end{gathered} \right. $$
(25)

where min is the mass of the shaft and inner ring, and F is the time-varying load of the cylindrical roller bearing-pedestal system.

The time-varying load F can be calculated by Eq. 26

$$ F = F_{a} \sin \left( {\frac{2\pi n}{{60}}t} \right) $$
(26)

where Fa is the vertical load.

The dynamic equation of the bearing cage can be expressed as Eq. 27

$$ I_{{\text{c}}} \ddot{\varphi }_{{\text{c}}} - \sum\limits_{j = 1}^{13} {P_{j}^{{{\text{fc}}}} r_{{\text{m}}} } + \sum\limits_{j = 1}^{13} {P_{j}^{{{\text{rc}}}} r_{{\text{m}}} } = 0 $$
(27)

where Ic is the inertia of the moment of the bearing cage.

The dynamic equation of bearing outer ring can be expressed as Eq. 28

$$ \left\{ \begin{gathered} m_{{{\text{out}}}} \ddot{x}_{{\text{o}}} - \sum\limits_{j = 1}^{13} {P_{j}^{{\text{o}}} cos\beta_{j} } + \sum\limits_{j = 1}^{13} {F_{j}^{{\text{o}}} sin\beta_{j} } + c\dot{x}_{{\text{o}}} + kx_{{\text{o}}} = 0 \hfill \\ m_{{{\text{out}}}} \ddot{y}_{{\text{o}}} - \sum\limits_{j = 1}^{13} {P_{j}^{{\text{o}}} \sin \beta_{j} } - \sum\limits_{j = 1}^{13} {F_{j}^{{\text{o}}} \cos \beta_{j} } + c\dot{y}_{{\text{o}}} + ky_{{\text{o}}} = 0 \hfill \\ \end{gathered} \right. $$
(28)

where mout is the mass of the outer ring and pedestal, k is the stiffness of the pedestal, and c is the damping coefficient of the pedestal.

The equation of the dynamic model of the cylindrical roller bearing-pedestal system is given by Eq. 29

$$ \left\{ \begin{gathered} \ddot{\eta }_{j} = \frac{1}{{m_{j} r_{{\text{r}}}^{2} }}\left[ { - F_{j}^{{{\text{fc}}}} r_{{\text{r}}} - F_{j}^{{{\text{rc}}}} r_{{\text{r}}} + F_{j}^{{\text{i}}} r_{{\text{r}}} + F_{j}^{{\text{o}}} r_{{\text{r}}} } \right] \hfill \\ \ddot{\varpi }_{j} = \frac{1}{{m_{j} r_{{\text{m}}} }}\left[ {F_{j}^{{\text{i}}} - F_{j}^{{\text{o}}} - m_{j} g\cos (\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} ) - P_{j}^{{{\text{fc}}}} + P_{j}^{{{\text{rc}}}} } \right] \hfill \\ \ddot{d}_{j} = \frac{1}{{m_{j} }}\left[ {P_{j}^{{\text{i}}} - P_{j}^{{\text{o}}} - m_{j} g\sin (\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} ) - F_{j}^{{{\text{fc}}}} + F_{j}^{{{\text{rc}}}} + F_{j}^{{\text{m}}} } \right] \hfill \\ \ddot{x}_{{\text{i}}} = \frac{1}{{m_{{{\text{in}}}} }}\left[ { - \sum\limits_{j = 1}^{13} {P_{j}^{{\text{i}}} cos(\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} )} + \sum\limits_{j = 1}^{13} {F_{j}^{{\text{i}}} sin(\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} )} } \right] \hfill \\ \ddot{y}_{{\text{i}}} = \frac{1}{{m_{{{\text{in}}}} }}\left[ { - \sum\limits_{j = 1}^{13} {P_{j}^{{\text{i}}} sin(\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} )} - \sum\limits_{j = 1}^{13} {F_{j}^{{\text{i}}} cos(\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} )} - F_{{\text{a}}} \sin (\frac{{2{\uppi }n}}{60}t)} \right] \hfill \\ \ddot{\varphi }_{{\text{c}}} = \frac{1}{{I_{{\text{c}}} }}\left[ {\sum\limits_{j = 1}^{13} {P_{j}^{{{\text{fc}}}} r_{{\text{m}}} } - \sum\limits_{j = 1}^{13} {P_{j}^{{{\text{rc}}}} r_{{\text{m}}} } } \right] \hfill \\ \ddot{x}_{{\text{o}}} = \frac{1}{{m_{{{\text{out}}}} }}\left[ {\sum\limits_{j = 1}^{13} {P_{j}^{{\text{o}}} cos(\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} )} - \sum\limits_{j = 1}^{13} {F_{j}^{{\text{o}}} sin(\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} )} - c\dot{x}_{{\text{o}}} - kx_{{\text{o}}} } \right] \hfill \\ \ddot{y}_{{\text{o}}} = \frac{1}{{m_{{{\text{out}}}} }}\left[ {\sum\limits_{j = 1}^{13} {P_{j}^{{\text{o}}} \sin (\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} )} + \sum\limits_{j = 1}^{13} {F_{j}^{{\text{o}}} \cos (\frac{{2{\uppi }}}{13}\left( {j - 1} \right) + \dot{\varpi }_{j} {\text{t}} )} - c\dot{y}_{{\text{o}}} - ky_{{\text{o}}} } \right] \hfill \\ \end{gathered} \right. $$
(29)

3 Experimental verification

The vibration signal of the cylindrical roller bearing-pedestal system is tested by the acceleration sensor. The experiment is carried out under the working condition of 3000 r/min and 20 N, the speed is adjusted by the control system, and the load is applied to the shaft through the loading device. Figure 3 shows the rotor experimental bench with the cylindrical roller bearing-pedestal system.

Fig. 3
figure 3

Rotor experimental bench with cylindrical roller bearing-pedestal system

Full size image

In Fig. 3, the acceleration sensors are arranged in the horizontal and vertical directions of the pedestal, respectively, and the data are collected through the vibration signal acquisition system. During the signal test, the sampling frequency of the test software is set to 20 kHz.

The Runge–Kutta algorithm is used to solve the dynamic equation of the cylindrical roller bearing-pedestal system shown in Eq. (29). In the process of solving, fourth-order derivation and fifth-order control accuracy are adopted. The structural parameters of the cylindrical roller bearing-pedestal system are listed in Table 1 [27,28,29].

Table 1 Structural parameters of cylindrical roller bearing-pedestal system [27,28,29]
Full size table

Under the same working conditions, the dynamic response of the system is obtained by numerical simulation. Then, the simulation results of the dynamic response under the same working conditions are compared with the measured data. The system dynamic response from the simulation is shown in Fig. 4, and the system dynamic response from the experiment is shown in Fig. 5.

Fig. 4
figure 4

System dynamic response from the simulation

Full size image
Fig. 5
figure 5

System dynamic response from the experiment

Full size image

The vibration signals in Figs. 4 and 5 are compared and analyzed. The simulation results show that the peak to peak value of the acceleration response in the x direction is 103.58 m·s−2 and the peak to peak value of the acceleration response in the y direction is 79.95 m·s−2. The measured results show that the peak to peak value of the acceleration response in the x direction is 123.21 m·s−2 and the peak to peak value of the acceleration response in the y direction is 72.42 m·s−2. The dynamic response of the cylindrical roller bearing-pedestal system in the x direction is slightly larger than that in the y direction, because the y direction is the direction of load application, which suppresses the vibration acceleration response to a certain extent. It can be seen that the measured results of the dynamic response are similar to the simulation results.

4 Dynamic characteristics analysis

4.1 Study on dynamic characteristics under extreme gravity conditions

The extreme gravity is defined as gravitational conditions above or below the earth's gravitational acceleration g. In the process of studying the dynamic characteristics of the system under extreme gravity, the rotational speed variation performed in the steady state situation is used for numerical simulation. The cylindrical roller bearing-pedestal system operates at 3000 r/min and 20 N load, and the dynamic responses of the cylindrical roller bearing-pedestal system under different gravity accelerations such as 0.2, 0.6, 3, and 5 g are obtained. The vibration acceleration of the cylindrical roller bearing-pedestal system under different gravity acceleration is illustrated in Fig. 6.

Fig. 6
figure 6

Vibration acceleration of the cylindrical roller bearing-pedestal system under different gravity accelerations

Full size image

As shown in Fig. 6, unlike the normal gravity state, the dynamic responses in the weightless state and the overweight state deteriorate to varying degrees. When the gravitational acceleration is g, the peak to peak (PTP) value, root mean square (RMS) value, rectified mean (RM) value and kurtosis (K) value of the system are the smallest. In the gravitational acceleration range of 0.2-5 g, the maximum deterioration degree of PTP value is 24.1%, the maximum deterioration degree of RMS value is 12.5%, the maximum deterioration degree of RM value is 12.0%, and the maximum deterioration degree of K value is 6.0%.

4.2 Sensitivity of the load and the rotational speed

Through the performance indexes such as the slip rate of the roller, slip rate of the cage, acceleration response, and roller displacement, the variation law of the dynamic characteristics of the cylindrical roller bearing-pedestal system with the change in the load and rotational speed is studied.

The slip rate of the roller in the cylindrical roller bearing-pedestal system can be expressed as Eq. 30

$$ P_{r} = \frac{{\dot{\eta } - \dot{\eta }_{j} }}{{\dot{\eta }}} \times 100\% $$
(30)

where \(\dot{\eta }\) is the rotation speed of the roller during pure rolling and \(\dot{\eta }_{j}\) is the rotation speed of the jth roller.

The rotation speed of the roller during pure rolling can be expressed as Eq. 31

$$ \dot{\eta } = \frac{{{\uppi }n}}{60} \times \frac{{r_{{\text{i}}} r_{{\text{o}}} }}{{r_{{\text{r}}} r_{{\text{m}}} }} $$
(31)

Figure 7 presents the slip rate of the roller under different loads and rotational speeds.

Fig. 7
figure 7

Slip rate of roller under different loads and rotational speeds

Full size image

It is noted from Fig. 7 that the slip rate of the roller is positively correlated with the rotational speed n. The change of n can easily cause a change in the slip rate of the roller. The slip rate of the roller at high speed is greater than that at low speed. However, with the change of load Fa, the slip rate of the roller changes little. Therefore, the slip rate of the roller is hardly affected by the Fa.

The slip rate of the cage in the bearing-pedestal system can be expressed as Eq. 32:

$$ P_{{\text{c}}} = \frac{{\dot{\varphi } - \dot{\varphi }_{{\text{c}}} }}{{\dot{\varphi }}} \times 100\% $$
(32)

where \(\dot{\varphi }\) is the revolution speed of the bearing cage during pure rolling and \(\dot{\varphi }_{{\text{c}}}\) is the revolution speed of the bearing cage.

The revolution speed of the bearing cage during pure rolling can be expressed as Eq. 33:

$$ \dot{\varphi } = \frac{{{\uppi }n}}{60} \times \frac{{r_{{\text{m}}} - r_{{\text{r}}} }}{{r_{{\text{m}}} }} $$
(33)

In Fig. 8, the slip rate of the cage is also positively correlated with the rotational speed n. The slip rate of the cage at high speed is bigger than that at low speed. At the same time, with the raise of Fa, the slip rate of the cage reduces slightly.

Fig. 8
figure 8

presents the slip rate of the cage under different loads and rotational speeds

Full size image

The acceleration response of the system under different loads and rotational speeds is illustrated in Fig. 9.

Fig. 9
figure 9

Acceleration response of the system under different loads and rotational speeds

Full size image

In Fig. 9, with the increase in rotational speed n and load Fa, the dynamic response of the system is significantly enhanced. Therefore, the rotational speed n and load Fa will have a great impact on the dynamic characteristics of the cylindrical roller bearing-pedestal system.

Figure 10 presents the displacement of the roller under different loads and rotational speeds. It is noted from Fig. 10 that the displacement of the roller increases significantly with the increase in the load Fa, indicating that the increase in load Fa is extremely easy to cause the increase of the displacement of the roller. However, with the increase of n, the displacement of the roller diminishes nonlinearly. The displacement of the roller is more affected by the load Fa than the rotational speed n.

Fig. 10
figure 10

Displacement of the roller under different loads and rotational speeds

Full size image

4.3 Law of dynamic response affected by mass

In addition to the extreme gravity conditions, load and rotational speed, the dynamic responses of the cylindrical roller bearing-pedestal system under different masses should be considered. The variation law of acceleration response of outer raceway in x direction with the mass mout change in bearing outer ring and pedestal is discussed. The accelerations of the system when mout is 5 kg, 10 kg, and 15 kg are obtained, respectively. Figure 11 shows the acceleration response of outer raceway in x direction.

Fig. 11
figure 11

Acceleration response of outer raceway in x direction

Full size image

The PTP and RMS values of the acceleration response of outer raceway in x direction are listed in Table 2.

Table 2 PTP and RMS values of the acceleration response of outer raceway in x direction
Full size table

Table 2 further indicates the details of Fig. 11. It is noted that the PTP and RMS values of acceleration of the cylindrical roller bearing-pedestal system are negatively correlated with the mass mout of the outer ring and pedestal. Among them, the PTP value of acceleration of the system decreased by 66.9% and the RMS value of acceleration of the system decreased by 66.7%. Therefore, properly adding the mass mout of the outer ring and pedestal in a certain range will help to suppress the vibration of the cylindrical roller bearing-pedestal system.

The variation law of acceleration response of inner raceway in x direction with the mass min change in shaft and inner ring is discussed. The accelerations of the system when min is 5 kg, 10 kg, and 15 kg are obtained, respectively. Figure 12 shows the acceleration response of inner raceway in x direction.

Fig. 12
figure 12

Acceleration response of inner raceway in x direction

Full size image

The PTP and RMS values of the acceleration response of inner raceway in x direction are listed in Table 3.

Table 3 PTP and RMS values of the acceleration response of inner raceway in x direction
Full size table

It is shown in Fig. 12 and Table 3 that the increase in the mass min of the shaft and inner ring can effectively suppress the vibration of the cylindrical roller bearing-pedestal system. Among them, the PTP value of acceleration response decreased by 64.1%, and the RMS value decreased by 63.1%.

5 Conclusions

A new dynamic model of the cylindrical roller bearing-pedestal system is conducted to analyze the system characteristics. The sliding friction, Hertz contact, and time-varying load are considered in this model. The limitations of the model are that it is only applicable to constant rotational speed system, isotropic system, and constant vertical load system. The dynamic characteristics of the system under extreme gravity conditions, the sensitivity of the load and rotational speed, and the law of dynamic response affected by mass are studied. The results of the paper are concluded as follows:

  1. 1.

    Compared with the normal gravity state, both the weightless state and overweight state will deteriorate the dynamic response of the system. In the range of 0.2-5 g, the maximum deterioration degree of PTP value is 24.1%, the maximum deterioration degree of RMS value is 12.5%, the maximum deterioration degree of RM value is 12.0%, and the maximum deterioration degree of K value is 6.0%.

  2. 2.

    In the cylindrical roller bearing-pedestal system, the slip rate of the bearing roller and cage is more sensitive to rotational speed than load. The slip rate is positively correlated with the rotational speed. The change inrotational speed can easily cause a change in the slip rate of the bearing roller and cage.

  3. 3.

    The rotational speed and load will have a great impact on the acceleration response of the cylindrical roller bearing-pedestal system. The displacement of the roller is more affected by load than rotational speed.

  4. 4.

    The vibration of the cylindrical roller bearing-pedestal system can be suppressed by appropriately increasing the mass mout and min.