1 Introduction

There are several applications in which helical grooves are required on a cylindrical surface. Examples include lubrication grooves for journal bearings, cooling grooves for molds, raceways for ball nuts, and internal and external threads. There are alternative processes to produce such grooves. One of them is helical milling. It is essential to choose a suitable cutting tool to produce helical grooves using the helical milling process. Different from an ordinary end mill, a ball-end mill can machine undercuts. Due to their shapes, these tools are also referred to as lollipop end mills [1]. This kind of tool is necessary for such an operation because the helical grooves require undercuts. Although the cross section of the tool is a circle, it does not produce a circular profile in the cross section of the workpiece due to the helical tool path in the helical milling process resulting in an overcut in the workpiece. In such a case, it becomes important to calculate the profile of the groove before the process. Virtual machining is the simulation of the machining processes and is used to prevent costly machining tests [2]. In this regard, analytical models remarkably simplify the simulation process [3].

Formulating a machined surface can be defined as the set of points on the surface and is required for NC simulation. The swept volume approach is usually used to derive the machined surfaces of a workpiece in NC simulation [4]. The swept volume of a tool can be considered as the unification of the instant tool volumes as the tool moves along the tool path. Derivation of the swept volume is the key because the machined surface of a workpiece is obtained by subtracting the swept volume of the tool from the volume of the workpiece [5]. Several methods were introduced in the early stages to derive the swept volume, such as envelope theory [6], sweep-envelope differential equation (SEDE) [7], Jacobian rank deficiency approach [8]. Some researchers focused on the swept volumes of specific cutting tools such as toroidal end mills [9, 10]. Mann and Bedii [11] introduced a generalized cross product imprint method for five-axis tool motion using the cutters that are the solids of revolution such as torus, cylinder, and sphere. Due to the restricted tool shapes, the cross-product imprint method gives the grazing curves more easily. Chiou and Lee [12] proposed a method based on the instantaneous swept profile of the cutter. They used seven parameters to model the generalized cutter geometry that consists of the upper cone, lower cone, and corner radius. Weinert et al. [13] introduced a solid modeling approach by using the boundary representation method to determine the swept volume of the tool. In this method, the swept volume was composed of the ingress, egress, and envelope surface constructed with NURBS. Gong and Wang [14] derived closed-form solutions for the envelope surfaces of the milling tools modeled by rotating the 2D Bezier curves and stated that the tool geometry is limited and self-intersections are not covered. Aras [5] introduced a method to determine the envelope surface of the cutting tool by decomposing the tool into characteristic and great circles derived from the two-parameter family of spheres. Lee and Nestler [15] used the Gauss map to derive the swept volume of the tool for simultaneous five-axis tool path and stated that the proposed method effectively derives the swept volume because there is no need to solve a group of partial differential equations. Rossignac and Kim [16] introduced a method to determine the boundary swept by a tube bounded by a one-parameter family of circles for the screw motion.

On the other hand, approximate techniques were proposed based on the tool discretization. Ferry and Yip-Hoi [17] used a solid modeler-based approach to derive the cutter-workpiece engagement by using the parallel portions of the removal volume that is the intersection of the workpiece and tool swept envelope. Boz et al. [18] used the dexel field method for the tool discretization to obtain the cutter-workpiece engagement required for cutting force calculations in machining. Inverse problems have also been investigated by using optimization techniques [19, 20]. In such cases, the optimum cutter geometry is determined to match the desired machined surface.

The cutting tool is usually modeled as a solid of revolution to obtain the machined part surface for the machining processes because this assumption simplifies the problem and gives a good approximation of the machined part surface due to the fact that the cutting speed is much higher than the feed rate in machining processes. When such an assumption is made, effects of many parameters such as the geometry of the cutting edge, number of cutting edges, feed rate, and spindle speed on the machined part surface are omitted. However, these parameters are only effective on the surface texture, not the surface profile as explained by the relationship between the cutting speed and feed rate. Based on the assumption, the problem is converted to the swept volume of a moving solid of revolution.

In this work, the swept volume approach was not used. Instead, the swept area of the cross section of the tool in the section plane was introduced. Since the cross section of the groove at any section that passes through the screw axis is identical in helical milling, the swept area approach can be used to derive the whole set of points on the machined surface. The work presented in this paper considers a well-defined tool path and tool, and therefore it was possible to derive an utterly analytical model. Thus, the model gives the exact profile of the groove produced by helical milling with a ball-end mill. The most important advantage of the model is that it does not require the solution of complex equations. The profile of the cross section of the groove can be derived by just entering the values for three parameters (pitch of the helix, the outer radius of the groove, and radius of the tool). According to the author’s knowledge, such a direct formulation of the cross-sectional profile of the groove in helical milling with a ball-end mill does not exist in the literature. The model can be applied to derive the cross section of both internal and external grooves produced by helical milling with a ball-end mill.

In the following sections, first, the analytical model was introduced. Then, the effects of the parameters on the groove profile were presented. In the section of CAD simulation, the form errors derived by a computer program were investigated and compared to those by the analytical model. In the section of experimental validation, two experiments were performed for specific cases to confirm the analytical model. Finally, the outcomes of the work were summarized in the section of conclusions.

2 Analytical modeling

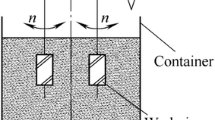
The helical milling process can be used to create an internal groove, a hole, or an external groove. External groove is created to the outer cylindrical surfaces. When the aim is to create an internal groove, an initial hole should be created before the process. Figure 1 illustrates the internal helical milling process with a ball-end mill that can machine undercuts. \({R}_{i}\) stands for the radius of the initial hole. The model considers a fixed reference plane that passes through the axis of the hole to observe the swept area of the tool in this section. The ball-end mill can be modeled as a sphere. The center of the sphere has been selected as the reference point for the ball-end mill, and cutter location (CL) has been used throughout the analysis. The general equation of a sphere is given in Eq. (1).

$${\left(x-{x}_{0}\right)}^{2}+{\left(y-{y}_{0}\right)}^{2}+{\left(z-{z}_{0}\right)}^{2}={r}^{2}$$
(1)

where \({x}_{0}\), \({y}_{0}\), and \({z}_{0}\) are center coordinates of the sphere, and \(r\) is the radius of the tool. The center coordinates can be expressed as the functions of the tool rotation angle in Eqs. (2–4). The first term in Eq. (3) is the reference point. Since a fixed plane is observed, \(z\)-axis coordinate of the sphere must be equal to zero every time.

Fig. 1
figure 1

The helical milling process with a ball-end mill

Full size image
$${x}_{0}=\left(R-r\right)\mathrm{cos}\varphi $$
(2)
$${y}_{0}=\frac{h}{2}-\frac{h\varphi }{2\pi }$$
(3)
$${z}_{0}=\left(R-r\right)\mathrm{sin}\varphi $$
(4)

where \(\varphi \) is the tool rotation angle with respect to the screw axis, \(R\) is the outer radius of the groove, \(h\) is the pitch of the helix. The equation of the cross section of the ball-end mill as a function of the tool rotational angle can be derived by substituting Eqs. (2–4) into Eq. (1) in Eq. (5). Equation (5) can be proved as follows. If the third term on the left side in Eq. (5) is taken to the right side, a circle equation is obtained with variable center coordinates given in Eqs. (2) and (3) and with variable radius as \({r}^{2}-{\left[\left(R-r\right)\mathrm{sin}\varphi \right]}^{2}\). This conforms to the investigated case. The tool profile can be expressed in the form of \(y=f\left(x,\varphi \right)\) in Eq. (6), which contains the upper and lower portions. Equation (6) with the positive coefficient of the first term can be used in the second quadrant of the x–y plane when deriving the cross-sectional profile of the groove because it gives the equation of the upper portion of the tool profile.

$${\left[x-\left(R-r\right)\mathrm{cos}\varphi \right]}^{2}+{\left[y-\frac{h}{2}+\frac{h\varphi }{2\pi }\right]}^{2}+{\left[0-\left(R-r\right)\mathrm{sin}\varphi \right]}^{2}={r}^{2}$$
(5)
$$y=\pm \sqrt{-{x}^{2}+2x\left(R-r\right)\mathrm{cos}\varphi +2Rr-{R}^{2}}-\frac{h\varphi }{2\pi }+\frac{h}{2}$$
(6)

As the tool rotation angle varies, a different circle occurs in the reference plane (x–y plane). It is also possible that there may not exist a circle in the reference plane for an interval of the tool rotation angle if \(R>2r\). The next step is the derivation of the equation of the curve that surrounds the circles. This procedure is called the swept area in this work. Figure 2 illustrates the formation of the swept area for the half-profile of the groove. In this figure, the instant half cross-sectional profiles of the tool in x–y plane are shown for some specific rotational angles of the tool. These profiles are the half circles since the cutting tool is modeled as a sphere. Only upper portions of the tool profiles are considered because the upper portion of the groove profile is investigated. In this graphical representation (Fig. 2), the outer boundary of the swept area is roughly visible. The equation of the cross-sectional profile of the groove can be derived using this approach. Equation (6) has two variables. For a specific value of \(x\), \(y\) reaches its highest value for a specific value of \(\varphi \). Fermat’s theorem was applied to Eq. (6) in Eq. (7) to find the highest value.

Fig. 2
figure 2

Formation of the swept area (\(R=20\) mm, \(r=9.95\) mm, and \(h=40\) mm)

Full size image
$$\frac{\partial y}{\partial \varphi }=\frac{\partial f\left(x,\varphi \right)}{\partial \varphi }=0$$
(7)

There are four solutions of Eq. (7). Equation (8) is derived by solving Eq. (7) for the second quadrant of \(x\)-\(y\) plane since this region is investigated. Equation (8) gives the tool rotation angle for the highest reachable point along \(y\)-axis for a specific value of \(x\).

$$\varphi ={\mathrm{cos}}^{-1}\left[\frac{1}{4{\pi }^{2}\left(R-r\right)x}\left(\sqrt{{x}^{2}\left[4{\pi }^{2}{h}^{2}+16{\pi }^{4}{\left(R-r\right)}^{2}\right]+{h}^{4}-8{\pi }^{2}Rr{h}^{2}+4{\pi }^{2}{h}^{2}{R}^{2}}-{h}^{2}\right)\right]$$
(8)

Substituting the right side of Eq. (8) into \(\varphi \) in Eq. (6), the equation of the upper portion of the cross-sectional profile of the groove is derived for the second quadrant of \(x\)-\(y\) plane as given in Eq. (9) for \({R}_{i}\le x\le R\), and \({R}_{i}\ge 2r-R\) when \(2r>R\). Then, the entire cross section of the groove can be derived by mirroring the upper portion along \(x\)-axis.

$$ \begin{aligned} & y = \sqrt { - x^{2} + \frac{1}{{2\pi^{2} }}\left( {\sqrt {x^{2} \left[ {4\pi^{2} h^{2} + 16\pi^{4} \left( {R - r} \right)^{2} } \right] + h^{4} - 8\pi^{2} Rrh^{2} + 4\pi^{2} h^{2} R^{2} } - h^{2} } \right) + 2Rr - R^{2} } \\ & \quad - \,\frac{h}{2\pi }\cos^{ - 1} \left[ {\frac{1}{{4\pi^{2} \left( {R - r} \right)x}}\left( {\sqrt {x^{2} \left[ {4\pi^{2} h^{2} + 16\pi^{4} \left( {R - r} \right)^{2} } \right] + h^{4} - 8\pi^{2} Rrh^{2} + 4\pi^{2} h^{2} R^{2} } - h^{2} } \right)} \right] + \frac{h}{2} \\ \end{aligned} $$
(9)

3 Influences of the parameters on the groove profile

The introduced model can be used for both internal and external helical milling processes. Therefore, the term “pseudo-groove” was used to indicate that the cross-sectional profile belongs to the unification of the internal and external grooves, although it is impossible to obtain them simultaneously in a complete helical milling process that is performed through the thickness of the workpiece. Figure 3 illustrates the cross-sectional profiles of the pseudo-grooves for some values of the tool radius (\(r\)) while the outer radius of the groove (\(R\)) is equal to 20 mm and the pitch of the helix (\(h\)) is 30 mm. Hidden line in the figures indicates the half great circle of the spherical tool. The left side of the pseudo-groove can be used when the internal groove is produced, and the right side can be used when the external groove is produced. The cross-sectional profile of the pseudo-groove can be compared to the great circle of the spherical tool to observe the deviation in the profile of the pseudo-groove. It reveals that the cross section is the prolate closed shape and is not symmetrical about the vertical axis that passes through the center of the great circle when \(R>2r\), and it is the open shape when \(R<2r\). However, it is symmetrical about the horizontal axis every time. It must be noted that a cross section will not occur for the external groove when \(R<2r\), since the right side of the pseudo-groove is the open shape. It is seen that the cross-sectional profile of the groove deviates significantly from the great circle of the spherical tool as the tool radius increases. It also turns out that the deviation is more severe for the right side of the pseudo-groove where the cross-sectional profile of the external groove is formed.

Fig. 3
figure 3

The pseudo-grooves for R = 20 mm and h = 30 mm. a r = 5 mm. b r = 8 mm. c r = 9.95 mm. d r = 10.05 mm. e r = 12 mm. f r = 15 mm

Full size image

The effect of the pitch of the helix on the cross-sectional profile is shown in Fig. 4. In these figures, the outer radius of the groove (\(R\)) was kept constant at 20 mm. Two different values of the tool radius (\(r\)) were used as 9 mm and 11 mm to obtain both closed shape and open shape cross-sectional profiles. Three levels of the pitch were selected as 20 mm, 30 mm, and 40 mm. As seen in the figures, the groove profile deviates from the ball-end mill’s great circle for both closed and open shape grooves as the pitch of the helix increases. Deviations of the groove profiles from the great circle of the tool are larger for the right sides of the curves.

Fig. 4
figure 4

The pseudo-grooves for R = 20 mm. a r = 9 mm. b r = 11 mm

Full size image

4 CAD simulation

An internal helical milling process was selected for the simulation. Solidworks 2016 was used to derive the cross-sectional profile of the groove. Simulation steps are shown in Fig. 5. The tool was considered as a sphere, and the tool path was depicted as a helix. The swept cut command was used to create the groove. Then, the solid was cut from the plane passing through the hole axis, and the cross section of the groove was derived. Five simulations were performed. The groove height in the cross section was used for comparison because the maximum error occurs in the groove height. The groove height is equal to two times the \(y\) value derived by substituting \({R}_{i}\) into \(x\) in Eq. (9). Simulation results belong to the groove heights selected randomly since many identical cross sections of the groove are available. During CAD simulation, it was observed that the groove height changes with respect to the selected cross section, although the variation is limited.

Fig. 5
figure 5

Simulation steps. a Creating the sphere and the helix. b After using swept cut command. c Derivation of the cross section of the groove after cutting the solid by the plane which passes through the hole axis. e Measurement of the groove height

Full size image

The groove heights derived by both analytical model and CAD simulation are shown in Table 1 with respect to various values of the radius of the tool (\(r\)), the radius of the hole (\({R}_{i}\)), the pitch of the groove (\(h\)), and the outer radius of the groove (\(R\)). According to the results, a deviation exists for every simulation as compared to the analytical model. The deviations are expected in the CAD simulation because it utilizes the splines for the curves and gives the approximate features. Peternell et al. [21] stated that a triangle mesh, NURBS, or a set of points are used to represent the boundary of the swept volume. In the case of a triangle mesh, one may conclude that a better approximation can be obtained by decreasing the mesh size. However, this also brings higher calculation costs.

Table 1 Comparison of simulation results with those of the analytical model in the aspect of groove height
Full size table

5 Experimental validation

Due to the existence of the tool’s shank, a complete groove profile cannot be created by an experiment in a helical milling process. One way to observe the one-half of the groove profile experimentally is to interrupt the helical milling process after the tool passes the cross section for the first time. Thus, the consecutive cuts are prevented from destroying the half groove profile formed by the lower portion of the tool. Since the tool is symmetrical, the groove profile is also symmetrical. Therefore, the experiment gives the complete cross-sectional profile of the groove. The experiment can also be performed by using a ball-nose-end mill (a ball-end mill without the undercut portion) because the lower portion of the tool creates the entire half cross section of the pseudo-groove. Based on this assumption, an experimental setup was prepared, as shown in Fig. 6. A 3-axis vertical CNC machine tool (Topper QVM610A + APC), a coated carbide ball-nose-end mill with a diameter of 18 mm (r = 9 mm) shown in Fig. 7, and mild steel as the workpiece material were used. The cutting tool has two cutting edges, and the helix angle is 30°. The tool has an overall length of 100 mm and a usable length of 45 mm. When it is mounted in the tool holder, the length to diameter ratio is 3. Two experiments were performed. In the first experiment, it was aimed to obtain a closed shape pseudo-groove. Therefore, the outer radius of the groove (\(R\)) was selected as 18.5 mm. The pitch of the helix (\(h\)) was 20 mm. In the second experiment, the values of the parameters were selected as \(r\) = 9 mm, \(R\) = 17.5 mm, and \(h\) = 20 mm for an open shape pseudo-groove. Initial holes required for the internal grooves were not produced before the experiments in order to observe the entire pseudo-grooves. Low spindle speed (1000 rpm) and feed rate (30 mm/min) were selected to ensure a fine surface finish.

Fig. 6
figure 6

Experimental setup

Full size image
Fig. 7
figure 7

Ball-nose-end mill

Full size image

During the cutting tests, the end mill cuts the material from both sides of the workpiece to create the groove. Therefore, one side of the end mill performs up milling, and the other performs down milling. The helix diameter of the tool path divides these regions. The end mill follows the counterclockwise downward path and rotates clockwise about its axis in the cutting tests. Therefore, the milling form is down milling for the outer surface and up milling for the inner surface. Though, the milling form is only effective on the surface texture.

The pictures of the machined parts are shown in Fig. 8a, b, and the cross-sectional profiles are shown in 8c and d. The cross-sectional profiles of the pseudo-grooves shown in Fig. 8e, f were obtained by using the analytical model for both cases. Data points were collected from the pictures of the created grooves with an interval of 0.5 mm along the horizontal axis and fitted to the curves obtained by the analytical model. A computer-aided design program (AutoCAD 2019) was used for this process after transferring and calibrating the pictures. Deviations of the experimental data points from the analytical curves along the vertical axis and corresponding R-squared values were calculated. According to the findings, the R-squared value is 0.9993 for the first experiment and 0.9987 for the second experiment. A slight deviation in the R-squared value is reasonable because of measurement error. As a result, it was revealed that the analytical model provided a good fit for the data points.

Fig. 8
figure 8

Pictures of the machined parts: a The first experiment. b The second experiment. Cross-sectional profiles of the grooves: c The first experiment. d The second experiment. Cross-sectional profiles of the grooves derived by the analytical model: e The first case. f The second case

Full size image

6 Conclusions

In this work, the cross-sectional profile of a groove machined by helical milling with a ball-end mill was derived by using the introduced analytical model. The model contains three parameters: the pitch of the helix, the outer radius of the groove, and the radius of the tool to determine the cross-sectional profile of the groove. A CAD simulation was performed to compare the profiles derived by the analytical model with those by the CAD simulations. The groove height was used for the comparison. It was revealed that a deviation occurs in the groove height for every simulation. Experimental work was also carried out for the validation of the analytical model. In conclusion, it was found that the model is very accurate and efficient in deriving the cross-sectional profile of a groove produced by the helical milling with a ball-end mill.

The model obtained in this work can also be applicable to helical grinding with a spherical grinding tool since helical milling and helical grinding processes are similar in terms of produced profiles. Apart from the application areas in manufacturing, the model can also be integrated into a CAD (computer-aided design) or NC simulation program. Since the most important part of the swept volume of a moving solid is the swept envelope apart from an ingress part and an egress part, the model can be used to obtain the cross-sectional profile of the swept envelope for the screw-sweep of a sphere. Then, the swept envelope can be generated by merging the cross-sectional profiles. Therefore, the main gain of this work is that it does not require a time-consuming routine to obtain the swept profile.