1 Introduction

In the recent years, many investigations have been conducted on the design of vehicles' active safety systems. Anti-lock brake systems (ABS), electronic stability control (ESC) by direct yaw-moment control (DYC) and active front steering (AFS) can be mentioned as the most important examples of these systems.

The vehicle motions in vertical, lateral, and longitudinal directions have interactions with each other, e.g., the braking action evidently affects vehicle’s pitch motion. In fact, there is no single system that can be effective over the entire range of vehicle performance including safety and comfort. To overcome the problem, an approach of integrated vehicle chassis control is proposed to improve steering, stability, and ride comfort of the vehicle.

Recently, several studies have been carried out to design the integrated control of ESC and AFS systems [1,2,3,4,5,6,7]. An integrated vehicle dynamics control has been established using AFS and ESC systems applying a nonlinear vehicle model with 7 degree-of-freedom (DOF) [1]. The upper layer controller adjusted the yaw rate to track a desired value utilizing fuzzy logic control.

Based on two control logics, a structure was designed for integrated control of two above-mentioned systems. The first logic supervised the control rules of each system, while the second one employed a multi-variable control strategy in frequency domain using the geometric location of the Characteristic Locus method [2]. A nonlinear vehicle model with 27-DOF was utilized in CarSim software for simulation. Optimal and sliding mode control (SMC) methods were applied to design the AFS and ESC controllers, respectively. A new method was proposed to coordinate the mentioned sub-systems [3]. A 9-DOF nonlinear vehicle model and the Dugoff tire model were used, and a new method was presented for adaptive optimal distribution of the braking and lateral tire forces.

An adaptive control algorithm was proposed for integrated control of the AFS and ESC subsystems using direct Lyapunov method. Variation of cornering stiffness was considered through adaptation laws to ensure robustness of the controller [4].

An integrated vehicle dynamics control based on a two-layer control strategy was presented for AFS and active rear braking systems to improve yaw stability. The upper layer was designed to integrate the control of AFS and active braking systems. The lower layer was considered to provide the desired yaw moment using active braking system [5]. The enhancement of lateral vehicle stability by coordination of AFS and DBS systems was studied. The SMC and model predictive control were applied [6, 7].

In each of these investigations, it can be observed that the vehicle stability and handling during maneuver have been enhanced through coordination of AFS and ESC systems. However, the severe braking action on straight roads on non-homogeneous surfaces, such as split-μ road, is another major challenge in relation to the vehicle stability. In this type of road, the friction coefficients are different for the left and right wheels. In this case, the vehicle becomes severely unstable because of generating asymmetric braking forces of the left and right tires. To overcome the yaw instability and minimize the stopping distance on such roads, the coordination of ABS and ESC systems can be a proper idea to prevent the yaw and lateral instabilities. However, this stability is achieved with the cost of increased stopping distance, which is not desired by the driver. In order to cope the problems of instability and increased stopping distance, another approach is proposed based on integrated control of the ABS, ESC, and AFS systems. In this method, by applying of a corrective steering angle to the front wheels, a considerable amount of the disturbance moment in yaw dynamic is attenuated by the AFS system. Thus, less power is needed for the ESC system [8, 9].

Song [10] investigated the integrated control of active rear steering and ESC systems. Various maneuvers were simulated on wet asphalt and snow-covered roads as well as severe braking action on straight and split-μ roads. The improvement of vehicle stability and controllability was concluded. It should be noted that the active rear steering system is usually not implemented in passenger cars. It is often used in commercial vehicles such as heavy and light trucks and trailers. Therefore, the results of this study cannot be much useful for engineers at automotive manufacturing companies.

Some important factors were not considered in designing the ABS in reference [8,9,10]. Since some state variables such as longitudinal vehicle velocity and tire slip ratio cannot be measured in a cost-efficient way, considerable errors can occur in the performance of the control system. As a result, a state estimator is required to guarantee the accuracy and robustness of control system. The second problem is some uncertainties such as road friction coefficient and the optimal tire slip ratio. The variations of braking force due to the changes in the tire-road friction coefficient are not negligible. Because the maximum braking force is highly dependent on the friction coefficient of road and the optimal tire slip ratio. Thus, for better ABS performance, the tire slip should be controlled in different road conditions.

Aalizadeh [11] designed a robust controller using adaptive neuro-fuzzy inference system (ANFIS) for AFS to overcome frictional uncertainties of tire forces.

The main task of the ABS is to generate the maximum braking force, which itself is highly dependent on the road-friction coefficient and the optimal tire slip ratio. In this case, its changes are not negligible. Therefore, wheel slip control should be designed to be able to adapt to different road conditions, so that it can accurately estimate the road-friction coefficient at any time.

Some investigations have been performed to estimate the coefficient of road friction and state variables in the ABS. In 2014, an ABS was proposed based on estimation of the road-friction coefficient and optimal tire slip. Sliding mode observer and extended Kalman filter were used to estimate the longitudinal vehicle velocity and the parameters of the Burckhardt tire model, respectively [12].

In another research, the friction coefficient of road was estimated for a vehicle equipped with just ESC, to improve the yaw and lateral stability using Pacejka tire model [13]. In this regard, the researcher presented an approach to estimate the tire-road friction coefficient by means of the distribution of braking forces [14]. Recently, the application of Kalman filter to estimate the variables of vehicle dynamics system has attracted a lot of attention [15, 16].

The main research contribution of this paper is improvement of stability for the vehicle braking on the split-μ road by estimating the road friction coefficient and optimal tire slip. In addition, the integrated control of ESC, ABS, and AFS systems is designed. The combination of all these cases has not been studied together. Therefore, the investigations of this work can be divided into the following three sections:

  • Integrated control of the ABS, ESC and AFS systems to enhance the lateral and yaw stability and minimize the stopping distance when braking on split-μ road.

  • Estimation of the state variables of system and the road friction coefficient using the UKF and algebraic equations of Dugoff tire model, respectively.

  • Estimation of the optimal tire slip ratio, utilizing the ANFIS.

Accordingly, in the second part of article, a nonlinear 7-DOF vehicle model, combined with the Dugoff tire model is explained. Then, the design of estimator using the UKF, the estimation method of road friction coefficient and determination of the optimal tire slip ratio using ANFIS are discussed in the third part. In the next section, the active braking and AFS systems are proposed through the SMC and fuzzy controllers, respectively. The performance of integrated control of ABS, ESC, and AFS systems are discussed with simulating the severe braking action on two split-μ and Mix-μ roads in the fifth part. Finally, the conclusions are listed in the sixth part.

2 Nonlinear vehicle dynamics model

In this section, a nonlinear vehicle model reflecting the actual vehicle characteristics is utilized to test the control schemes proposed in the study. The 7-DOF nonlinear vehicle model with front wheel steering includes longitudinal, lateral, yaw dynamics and four wheels rotational dynamics.

2.1 Full vehicle model with 7-DOF

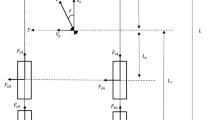
Figure 1 illustrates a 7-DOF vehicle dynamics model including the longitudinal, lateral and the yaw motions of the vehicle body and the rotation of four wheels. The subscripts \(i\) are 1, 2, 3, and 4 which are pertinent to the front-left, front-right, rear-left, and the rear-right wheels, respectively. The equations of the longitudinal, lateral and yaw motions are expressed as [13]:

$$ \begin{gathered} m\left( {\dot{v}_{x} - v_{y} \omega_{z} } \right) = \mathop \sum \limits_{i = 1}^{4} (F_{xwi} {\text{cos}}\delta_{i} - F_{ywi} {\text{sin}}\delta_{i} ) \hfill \\ \quad \quad \quad \quad \quad \quad = \mathop \sum \limits_{i = 1}^{4} F_{xi} \hfill \\ \end{gathered} $$
(1)
$$ \begin{gathered} m\left( {\dot{v}_{y} + v_{x} \omega_{z} } \right) = \mathop \sum \limits_{i = 1}^{4} (F_{xwi} {\text{sin}}\delta_{i} + F_{ywi} {\text{cos}}\delta_{i} ) \hfill \\ \quad \quad \quad = \mathop \sum \limits_{i = 1}^{4} F_{yi} \hfill \\ \end{gathered} $$
(2)
$$ \begin{aligned} & I_{z} \mathop {\omega_{z} }\limits = d\left( {F_{x1} + F_{x3} } \right) - d\left( {F_{x2} + F_{x4} } \right) \hfill \\ & \quad \quad \;\;+ a\left( {F_{y1} + F_{y2} } \right) - b\left( {F_{y3} + F_{y4} } \right) + M_{zc} \hfill \\ \end{aligned} $$
(3)

where \(M_{zc}\) is the corrective yaw moment created through the DYC method using the ESC system.

Fig. 1
figure 1

Schematic of the full vehicle model

Full size image

The motion of each wheel dynamics can be derived by:

$$ I_{\omega } \dot{\omega }_{i} = - R_{\omega } \left( {F_{xwi} - F_{zwi} f_{r} } \right) - T_{bi} $$
(4)

The terms \({F}_{xi}\) and \({F}_{yi}\) are the longitudinal and lateral tire-ground forces of the wheels in the ground frame (XY), respectively, with the specified wheel indicated by the subscript \(i\). \({F}_{xwi}\) and \({F}_{ywi}\) are the longitudinal and lateral forces of each tire in the tire frame (xy), respectively. The variable \({\delta }\) denotes the steering angle. In this study, only front wheels are steerable, so \({\delta }_{1 }={\delta }_{2 }={\delta }_{c }+{\delta }_{d}\) and \({\delta }_{3 }={\delta }_{4 }=0\). Also, \({\delta }_{c}\) is the corrective steering angle of front wheels applied by the AFS system. \({\delta }_{d}\) is also the driver steering angle. \({\omega }_{i}\) is the angular velocity of the wheel, \({F}_{zwi}\) is vertical load of the wheel, \({T}_{b}\) is the braking torque and \({f}_{r}\) is the rolling resistance coefficient of tire. The terms of \({v}_{x}\) and \({v}_{y}\) are the longitudinal and lateral velocities, \({\omega }_{z}\) is the yaw rate, \(m\) is the vehicle mass, \({I}_{z}\) and \({I}_{\omega }\) are the yaw moment of inertia and the wheel inertia moment, respectively. \({R}_{\omega }\) denotes the wheel radius. The parameters of \(a\) and \(b\) are the distance from front and rear axle to center of gravity (CG), \(d\) is the left/right half-track width. The sideslip angle of vehicle body is described as:

$$ \beta = \tan^{ - 1} (\frac{{v_{y} }}{{v_{x} }}) $$
(5)

2.2 Tire model

The nonlinear Dugoff tire model is used in this research, in which the tire longitudinal and lateral forces are considered as a function of the slip factor \({s}_{r}\) obtained by Eq. (6) in which, \(\mu \) is the road friction coefficient, \({\varepsilon }_{r}=0.015\) is the road adhesion reduction factor, \({C}_{\lambda }=50000\) and \({C}_{\alpha }=30000\) denote the longitudinal and cornering stiffness of the tire, respectively. The longitudinal and lateral forces of tire, \({F}_{xi}\) and \({F}_{yi}\), can be calculated from Eqs. (7) and (8), [4].

$$ sr_{i} = \left( {1 - \lambda_{i} } \right)\frac{{0.5\mu F_{zi} \left( {1 - \varepsilon_{r} v_{xwi} \sqrt {\lambda_{i }^{2} + {\text{tan}}^{2} \alpha_{i} } } \right)}}{{\sqrt {C_{\lambda }^{2} \lambda_{i }^{2} + C_{\alpha }^{2} {\text{tan}}^{2} \alpha_{i} } }} $$
(6)
$$ F_{xi} = \frac{{C_{\lambda } \lambda_{i} }}{{\left( {1 - \lambda_{i} } \right)}}f\left( {sr_{i} } \right) $$
(7)
$$ F_{yi} = \frac{{C_{\alpha } {\text{tan}}\alpha_{i} }}{{\left( {1 - \lambda_{i} } \right)}}f\left( {sr_{i} } \right) $$
(8)
$$ f\left( {sr_{i} } \right) = \left\{ {\begin{array}{*{20}c} {sr_{i} \left( {2 - sr_{i} } \right) sr_{i} < 1} \\ { 1 sr_{i} \ge 1 } \\ \end{array} } \right. $$
(9)

The wheel slip angle \(\left( {\alpha_{i} } \right)\) and the longitudinal wheel slip ratio (\(\lambda_{i} )\) are defined by Eqs. (10) and (11), respectively:

$$ \lambda_{i} = \frac{{R_{\omega } \omega_{i} - v_{xwi} }}{{\max \left( {R_{\omega } \omega_{i} , v_{x} } \right)}} $$
(10)
$$ \alpha_{i} = \delta_{i} - {\text{arctan}}\left( {\frac{{v_{ywi} }}{{v_{xwi} }}} \right) $$
(11)

3 Design of the estimator

The state variables are estimated using the UKF. Then, the road friction coefficient is estimated through the estimated variables and equations of the tire model. The estimation method of optimal slip ratio using ANFIS will be also presented.

3.1 Estimation of the vehicle state variables using the UKF

In this study, the state variables of the yaw rate, longitudinal and lateral velocities, as well as the slip ratio of the four wheels, are estimated using the UKF. However, it should be mentioned that due to their low expenses, the yaw velocity sensors are widely used in modern vehicles. Since a full observer has been employed in this research, this variable is also considered as to be estimated. It is noteworthy that the steering angle, longitudinal acceleration, and four-wheel rotational speeds are the measurable variables. The state variables are:

$$ x = \left[ {v_{x} , v_{y} , \omega_{z} , \lambda_{1} , \lambda_{2} , \lambda_{3} , \lambda_{4} , \mu_{r} , \mu_{l} } \right]^{T} $$
(12)

To estimate the state variables utilizing the UKF, it is necessary to create a discrete-time nonlinear state-space model based on the continuous-time model as follows:

$$ x_{k + 1} = f\left( {x_{k + 1} , u_{k} , t_{k} } \right) + w_{k} $$
(13)
$$ y_{k} = h\left( {x_{k} , t_{k} } \right) + v_{k} $$
(14)

where \(f\) is the vehicle system dynamics, \(x_{k}\) and \(t_{k}\) are the state and time at the sampling instant \(k\), \(u_{k}\) is the input to the system at the sampling instant \(k\), \(y_{k}\) is a set of noisy measurements determined by function of \(h\). \(w_{k}\) is the process noise, while \(v_{k}\) is the measurement noise. The added noises are assumed to be normally distributed Gaussian white noises with zero mean whose covariance matrices are \(Q\) and \(R\), respectively [17].

  1. a.

    The initial mean value of the system state variables, (\(\hat{x}_{0}^{ + }\)), and the initial covariance matrix of the estimation error \(e = x_{0} - \hat{x}_{0}^{ + } \), (\(P_{0}^{ + }\)), are given by equations of (15) and (16):

    $$ \hat{x}_{0}^{ + } = E\left( {x_{0} } \right) $$
    (15)
    $$ P_{0}^{ + } = E\left[ {\left( {x_{0} - \hat{x}_{0}^{ + } } \right)\left( {x_{0} - \hat{x}_{0}^{ + } } \right)^{T} } \right] $$
    (16)

    \(E\left( . \right)\), is mean value function.

  1. b.

    In the UKF, a series of sigma points are chosen based on a square root decomposition of the prior covariance. Then, these points are propagated through the true nonlinearity of the system.

  1. b.1

    Calculation of \(2n\) sigma points:

    First, \(2n\) sigma points are selected based on the mean and covariance of the random variable \(x\), where \(n\) is the number of state variables.

    $$ \hat{x}_{k - 1}^{\left( i \right)} = \hat{x}_{k - 1}^{ + } + \tilde{x}^{\left( i \right)} i = 1, \cdots , 2n $$
    (17)
    $$ \tilde{x}^{\left( i \right)} = \left( {\sqrt {n P_{k - 1}^{ + } } } \right)_{i}^{T} i = 1, \cdots , n $$
    (18)
    $$ \tilde{x}^{{\left( {n + i} \right)}} = - \left( {\sqrt {n P_{k - 1}^{ + } } } \right)_{i}^{T} i = 1, \cdots , n $$
    (19)
  2. b.2

    These sigma vectors are propagated through the nonlinear system function:

    $$ \hat{x}_{k}^{\left( i \right)} = f\left( {\hat{x}_{k - 1}^{\left( i \right)} , u_{k} , t_{k} } \right) $$
    (20)
  3. b.3

    Calculation of the mean and covariance for \(\hat{x}_{k}^{\left( i \right)}\) using mean and covariance of the posterior sigma points:

    $$ \hat{x}_{k}^{ - } = \frac{1}{2n}\mathop \sum \limits_{i = 1}^{2n} \hat{x}_{k}^{\left( i \right)} $$
    (21)
    $$ P_{k}^{ - } = \frac{1}{2n}\mathop \sum \limits_{i = 1}^{2n} (\hat{x}_{k}^{\left( i \right)} - \hat{x}_{k}^{ - } )(\hat{x}_{k}^{\left( i \right)} - \hat{x}_{k}^{ - } )^{T} + Q_{k - 1} $$
    (22)
  1. c.

    Measurement update:

  1. c.1

    Calculation of \(2n\) sigma points:

    First, \(2n\) sigma points are chosen as follows:

    $$ \hat{x}_{k}^{\left( i \right)} = \hat{x}_{k}^{ - } + \tilde{x}^{\left( i \right)} i = 1, \cdots , 2n $$
    (23)
    $$ \tilde{x}^{\left( i \right)} = \left( {\sqrt {n P_{k}^{ - } } } \right)_{i}^{T} i = 1, \cdots , n $$
    (24)
    $$ \tilde{x}^{{\left( {n + i} \right)}} = - \left( {\sqrt {n P_{k}^{ - } } } \right)_{i}^{T} i = 1, \cdots , n $$
    (25)
  2. c.2

    Nonlinear measurement equations are used to convert sigma points to \(\hat{y}_{k}^{\left( i \right)}\)

    $$ \hat{y}_{k}^{\left( i \right)} = h\left( {\hat{x}_{k}^{\left( i \right)} , t_{k} } \right) $$
    (26)
  3. c.3

    Calculation of the mean and covariance for \(\hat{y}_{k}^{\left( i \right)}\):

    $$ \hat{y}_{k} = \frac{1}{2n}\mathop \sum \limits_{i = 1}^{2n} \hat{y}_{k}^{\left( i \right)} $$
    (27)
    $$ P_{y} = \frac{1}{2n}\mathop \sum \limits_{i = 1}^{2n} (\hat{y}_{k}^{\left( i \right)} - \hat{y}_{k} )(\hat{y}_{k}^{\left( i \right)} - \hat{y}_{k} )^{T} + R_{k} $$
    (28)
  1. d.

    Covariance update:

    $$ P_{xy} = \frac{1}{2n}\mathop \sum \limits_{i = 1}^{2n} (\hat{x}_{k}^{\left( i \right)} - \hat{x}_{k}^{ - } )(\hat{y}_{k}^{\left( i \right)} - \hat{y}_{k} )^{T} $$
    (29)
    $$ K_{k} = P_{xy} P_{y}^{ - 1} $$
    (30)
    $$ \hat{x}_{k}^{ + } = \hat{x}_{k}^{ - } + K_{k} \left( {y_{k} - \hat{y}_{k} } \right) $$
    (31)
    $$ P_{k}^{ + } = P_{k}^{ - } - K_{k} P_{y} K_{k}^{T} $$
    (32)

3.2 Estimation of the road friction coefficient

The road conditions are determined by the \(SL\) quantity and according to Eq. (33) obtained by try and error. The parameters of \({\hat{\lambda }}_{3}\) and \({\hat{\lambda }}_{4}\) are the estimated values of longitudinal slip ratios corresponding to the rear-right and rear-left wheels using the UKF. Since the rear wheels are not steerable, calculating the forces of rear tires is less complicated in comparison with the front wheels. The reason is that in the front wheels, both longitudinal and lateral tire forces are generated due to the steerability of the wheels. Therefore, rear wheels are used to define the \(SL\) quantity.

$$ {\text{SL}} = \frac{{\hat{\lambda }_{4} }}{{\hat{\lambda }_{3} }} = \frac{{\mu_{r} }}{{\mu_{l} }} $$
(33)

For normal road conditions, the \(SL\) value is supposed to be 1, in which the friction coefficient of the left and right side is the same. Otherwise, the road will be of split-\(\mu \) type. For this situation, the friction coefficient of the right wheels is calculated by solving Eq. (34). It is obtained using the longitudinal dynamic equation of tire, longitudinal vehicle acceleration, and algebraic equations of Dugoff tire model, Eqs. (6–9).

$$ P_{1} \mu_{r}^{2} + P_{2} \mu_{r} + - ma_{x} = 0 $$
(34)

in which:

$$ P_{1} = \mathop \sum \limits_{i = 1}^{2} A_{2i - 1}^{2} B_{2i - 1} + \frac{1}{{SL^{2} }}\mathop \sum \limits_{i = 1}^{2} A_{2i}^{2} B_{2i} $$
(35)
$$ P_{2} = - 2\mathop \sum \limits_{i = 1}^{2} A_{2i - 1} B_{2i - 1} - \frac{2}{SL}\mathop \sum \limits_{i = 1}^{2} A_{2i} B_{2i} $$
(36)

After the calculation of \(\mu_{r}\), the friction coefficient of the left wheels (\(\mu_{l}\)) will be obtained using Eq. (33).

3.3 Estimation of the optimal tire slip ratio

In this section, the optimal tire slip ratio (\(\lambda_{m}\)) is estimated by ANFIS. In the slip \(\lambda_{m}\), the longitudinal tire force is its maximum value. Therefore, the braking force is maximized and the stopping distance is minimized. So, it seems that the estimation of value \(\lambda_{m}\) will lead to the improvement of ABS performance. Considering Eqs. (6) and (7) of Dugoff tire model, in longitudinal motion, the value \(\lambda_{m}\) is only dependent on the road friction coefficient, longitudinal tire velocity and vertical wheel load. Accordingly, an ANFIS is designed whose inputs are the three mentioned variables above. Its output is the optimal tire slip ratio. Three bell-shaped membership functions are chosen, which can be mathematically shown as follows in which, \(a\), \(b\), and c are three characteristics of membership functions modified during training.

$$ {\text{Bell}}\left( {x;a, b, c} \right) = \frac{1}{{1 + \left| {\frac{x - c}{a}} \right|^{2b} }} $$
(37)

The training and test data were obtained by several simulations based on equations of the Dugoff tire model for describing the tire-road friction force. Seven values of road friction coefficient from 0.3 to 0.9 with step of 0.1, eight values of longitudinal vehicle velocity from 5 to 40 m/s with step of 5 m/s and eight values of vertical wheel load from 1000 to 4500 N with step of 500 N have been used in the simulations. Therefore, a total of 7 × 8 × 8 = 448 input/output data will be generated, half of which have been selected for training data and the other half as test data.

Thus, a matrix with 448 rows and 4 columns is obtained. The first three columns are related to the inputs and the last column is related to the output. For both training and testing data, 224 sets have been selected. The hybrid algorithm is chosen for optimization process and the number of iterations is set to 40. The hybrid method is combination of least squares estimation and back propagation based on gradient descent algorithm. To evaluate the designed ANFIS, some types of analysis are carried out and the results can be seen in Figs. 2, 3, 4.

Fig. 2
figure 2

The variation of optimum slip ratio versus friction coefficient

Full size image
Fig. 3
figure 3

The variation of optimum slip ratio versus vertical wheel load

Full size image
Fig. 4
figure 4

The variation of optimum slip ratio versus vehicle speed

Full size image

The variation of optimum slip ratio versus the road friction coefficient, vertical wheel load and vehicle speed are plotted for both estimator and tire model in Figs. 2, 3, 4. The results of the ANFIS estimator and the tire model are compared. The simulation results show proper accuracy of estimation values with proposed ANFIS. It can be also found that the optimum slip ratio is dependent on the road friction coefficient, normal wheel load and the vehicle speed as shown in Figs. 2, 3, 4. In addition, the values of longitudinal velocity and vertical wheel load undergo considerable changes during braking. As a result, the estimation of optimal tire slip ratio is recommended to increase the accuracy of the ABS performance.

4 Design of the system controller

The design process of active braking and steering systems are presented in this section.

4.1 Design of the ESC system using DBS

In this part, a controller is designed to enhance the vehicle stability and force the vehicle to track a desired predefined yaw rate while keeping the vehicle sideslip angle as small as possible. Since the purpose of this research is to improve the vehicle stability in braking situation on straight split-\(\mu\) roads, the values of sideslip angle and yaw rate are assumed to be zero \((\omega_{d} = 0{\text{ and }}\beta_{d} = 0)\). Therefore, an ESP system through the DBS is proposed to keep the vehicle sideslip angle and yaw rate angle as small as possible.

The corrective yaw moment \(M_{zc}\) required to counteract the undesired yaw motion, is created by the DYC system through the DBS by assigning a proper slip ratio to each wheel. When the brake force is increased, the lateral force is reduced because of the inherent nonlinear tire characteristics. The different changes in the longitudinal and lateral tire forces will make a corrective yaw moment in different directions. The changes in the yaw moment will possess the same sign if the brake torque is applied to the outside front wheel for an over-steer correction and to the inside rear wheel for an under-steer correction.

The control system consists of two layers. The upper-layer controller determines the \(M_{zc}\) value using the SMC in order to track the desired yaw motion. Thereafter, the lower-layer controller computes the required longitudinal tyre force to create the \(M_{zc}\) and then according to the \(F_{x} - \lambda\) curve of nonlinear tire model, the desired slip ratio (\(\lambda_{d}\)) is obtained by interpolation method. Finally, the brake torque is generated through the SMC to maintain the slip ratio near the \(\lambda_{d}\) [13].

4.1.1 Upper-layer controller

In this section, the conventional SMC is applied to design the control system. The error function \(e_{y}\) for the yaw rate and side-slip angle integration includes the yaw rate error and the vehicle side-slip angle. It is assumed the desired values of yaw rate \(\left( {\omega_{zd} } \right)\) and vehicle side-slip angle \(\left( {\beta_{d} } \right)\) are zero. The error function and sliding surface \(s_{y}\) are defined by the following expression [13]:

$$ e_{y} = k_{y1} \left( {\omega_{z} - \omega_{zd} } \right) + \beta $$
(38)
$$ s_{y} = e_{y} + k_{y2} \mathop \int \limits_{0}^{t} e_{y} dt $$
(39)

where \(k_{y1}\) and \(k_{y2}\) are the strictly positive design scalars. By differentiating Eq. (39):

$$ \dot{s}_{y} = k_{y1} \dot{\omega }_{z} + \dot{\beta } + k_{y2} e_{y} $$
(40)

In Eq. (40), \(\dot{\omega }_{z}\) is substituted from Eq. (3).

$$ \dot{s}_{y} = k_{y1} \left( {\frac{{M_{z} + M_{zc} }}{{I_{z} }}} \right) + \dot{\beta } + k_{y2} e_{y} $$
(41)
$$ \begin{aligned} & M_{z} = d\left( {F_{x1} + F_{x3} } \right) - d\left( {F_{x2} + F_{x4} } \right) \hfill \\ & \quad\quad \;+ a\left( {F_{y1} + F_{y2} } \right) - b\left( {F_{y3} + F_{y4} } \right) \hfill \\ \end{aligned} $$
(42)

The time derivative of sideslip angle yields Eq. (43):

$$ \dot{\beta }\frac{1}{{1 + \tan ^{2} \left( \beta \right)}}\left( {\frac{{\dot{v}_{y} }}{{v_{x} }} - \frac{{\dot{v}_{x} }}{{v_{x} }}\tan \left( \beta \right)} \right) $$
(43)

For the sliding surface to asymptotically approach zero, its dynamics should be considered as follows:

$$ \dot{s}_{y} = - \eta_{y} {\text{sign}}\left( {s_{y} } \right) ; (\eta_{y} > 0) $$
(44)

Consequently:

$$ \frac{1}{2}\left( \frac{d}{dt} \right)s_{y}^{2} = \dot{s}_{y} s_{y} = - \eta_{y} {\text{sign}}\left( {s_{y} } \right)s_{y} < 0 $$
(45)

where sign(.) is the signum function and \(\eta_{y}\) is a positive constant. According to Eqs. (41–44), the corrective yaw moment \(M_{zc}\) is obtained. The \(M_{zc}\) expression is considered as control law:

$$ M_{zc} = - M_{z} + \hat{I}_{z} \left( {\frac{{ - \dot{\beta } - k_{y2} e_{y} - \eta_{y} {\text{sign}}\left( {s_{y} } \right) }}{{k_{y1} }}} \right) $$
(46)

where \(\eta_{y}\) is a strictly positive constant, \(\hat{I}_{z}\) is the estimated value of \(I_{z}\).

Now the stability of the proposed SMC system is proved. First, the function \(d\left( t \right)\) is defined as the disturbance moment in yaw vehicle dynamics. This is because of un-modeled dynamics and uncertainties in modeling the actual nonlinear dynamics of vehicle and tire.

$$ d\left( t \right) = \tilde{I}_{z} \dot{\omega }_{zd} - \frac{{\tilde{I}_{z} \dot{\beta }}}{{k_{y1} }} - \frac{{k_{y2} \tilde{I}_{z} e_{y} }}{{k_{y1} }} $$
(47)

where \(\tilde{I}_{z}\) is the difference between the estimated value \(\hat{I}_{z}\) and the actual value \(I_{z}\). So, \( \tilde{I}_{z} = \hat{I}_{z} - I_{z}\). The term \(d\left( t \right)\) is assumed to be bounded by the following equation:

$$ \left| {d\left( t \right)} \right| < \frac{{\hat{I}_{z} \eta_{y} }}{{ k_{y1} }} $$
(48)

As a result, the system uncertainties and disturbances are bounded. The candidate Lyapunov function is defined as:

$$ V = \frac{1}{2}I_{z} s_{y}^{2} $$
(49)

Using Eqs. (41) and (44) and expression \(s_{y} {\text{s}}i{\text{gn}}\left( {s_{y} } \right) = \left| {s_{y} } \right|\), the time derivative of the scalar \(V\) is calculated as:

$$ \dot{V} = s_{y} \left( {k_{y1} \tilde{I}_{z} \dot{\omega }_{zd} - \tilde{I}_{z} \dot{\beta } - k_{y2} \tilde{I}_{z} e_{y} } \right) - \hat{I}_{z} \left| {s_{y} } \right|\eta_{y} $$
(50)

Considering Eqs. (47) and (48), it can be written as:

$$ \begin{gathered} \dot{V} = k_{y1} s_{y} d\left( t \right) - \hat{I}_{z} \left| {s_{y} } \right|\eta_{y} \le k_{y1} \left| {s_{y} } \right|\left| {d\left( t \right)} \right| \hfill \\ - \hat{I}_{z} \left| {s_{y} } \right|\eta_{y} \le k_{y1} \left| {s_{y} } \right|\left( {\left| {d\left( t \right)} \right| - \frac{{\hat{I}_{z} \eta_{y} }}{{k_{y1} }}} \right) \hfill \\ \end{gathered} $$
(51)

It can be concluded from Eq. (48):

$$ \dot{V} < 0 $$
(52)

Since the function \(V\) is positive definite and \(V\) ̇is negative semi definite, therefore, it can be concluded according to the Barbalat’s Lemma that the designed control system is stable.

Chattering occurs in the control law because of the discontinuity term sign \((s_{y} )\). This chattering may increase highly control effort and excite un-modelled high-frequency dynamics as well. So, to mitigate this problem, the sign function is replaced by the saturation function \(sat (s_{y} /\phi )\) with a boundary layer thickness of \(\phi > 0\).

4.1.2 Lower-layer controller

After computing the \(M_{zc}\) in the upper-layer controller, the wheel, which is under braking, should be determined based on the control logic of the DBS in the lower-layer controller. Afterwards, the error function \(e_{b}\) and sliding surface \(s_{b}\) for the slip ratio are defined as follows:

$$ e_{b} = \lambda - \lambda_{d} $$
(53)
$$ s_{b} = e_{b} + k_{b} \mathop \int \limits_{0}^{t} e_{b} dt ; (k_{b} > 0) $$
(54)
$$ \dot{s}_{b} = - \eta_{b} sat\left( {s_{b} } \right) $$
(55)

Let us assume that \(k_{b}\) and \(\eta_{b}\) are the positive design parameters. By combining Eqs. (51–55), and (4), the controlled braking torque of each wheel, \(T_{bi}\), is obtained:

$$ \begin{gathered} T_{bi} = - R_{\omega } F_{xwi} - \frac{{I_{\omega } a_{xw} \omega_{i} }}{{v_{x} }} + \frac{{I_{\omega } v_{x} k_{b} e_{b} }}{{R_{\omega } }} \hfill \\ + \frac{{I_{\omega } v_{x} }}{{R_{\omega } }}\eta_{y} {\text{sat}}\left( {s_{b} } \right) \hfill \\ \end{gathered} $$
(56)

In Eq. (56), the longitudinal wheel acceleration \(a_{xw}\) and the angular velocity of the ith wheel \(\omega_{i}\) can be measured, while tire-road longitudinal force \(F_{xwi}\) and vehicle speed \(v_{x}\) are not directly measurable. Therefore, a state estimator should be applied to estimate these variables.

4.2 Design of the ABS

The design algorithm of the ABS system is similar to the DBS system to track the desired slip ratio. The only difference is that in the ABS, the desired slip ratio (\(\lambda_{d}\)) is the same as the optimum slip ratio (\(\lambda_{m}\).). Equations of (53) to (56) can be utilized to determine the control braking torque.

4.3 Design of the AFS

Since the AFS controls the lateral tire forces by changing the steering angle of front wheels, it is necessary to have a full recognition of the diagram of lateral tire force versus the lateral tire slip angle as well as its various regions. This diagram can be divided into three regions. The first, is a linear region, in which the vehicle handling is proportional to the steering angle. The second region is a nonlinear area, in which by increasing the slip angle, the tire force does not increase significantly. The third region is the saturation area, where the tire force does not change with the increase of tire slip angle and the vehicle handling is greatly reduced. Therefore, according to the slip angle of the vehicle, the amount of steering system usage can be determined.

Accordingly, a fuzzy controller is designed for the AFS system. The first input is the absolute value of tracking error for the vehicle side slip angle, and the second is the tracking error of yaw rate. Its output is the corrective steering angle of the front wheels (\(\delta_{c }\).).

As mentioned earlier, the desired values of yaw rate and the vehicle sideslip angle are set to be zero. Therefore, the inputs of the fuzzy controller are \(\left| \beta \right|\) and \(\omega_{z }\)., respectively.

As shown in Fig. 5, three membership functions and three linguistic variables of Lin, Nonlin and Sat are defined for vehicle sideslip angle, which are related to the linear, nonlinear and saturation regions of the lateral tire forces, respectively. Also, according to Fig. 6, five membership functions and linguistic variables of NB, NS, ZE, PS and PB are defined, which represent negative big, negative small, zero, positive small, positive, and positive big medium, respectively. In addition, as illustrated in Fig. 7, seven membership functions and linguistic variables are considered. The variables of NM and PM represent negative and positive medium, respectively. The centers and the parameters of membership functions are obtained by try and error. For example, the centers of membership functions of yaw rate input for linguistic variables of NS, ZE, and PS are −0.314, 0, and 0.22, respectively.

Fig. 5
figure 5

Membership functions for input variable of vehicle slip angle

Full size image
Fig. 6
figure 6

Membership functions for input variable of vehicle yaw rate

Full size image
Fig. 7
figure 7

Membership functions for output variable of corrective front steering angle

Full size image

A Mamdani method is employed in the fuzzy reasoning, whereas max–min inference method is chosen as aggregation operator. Defuzzification is performed using center-average method. The fuzzy rules are listed in Table 1.

Table 1 The fuzzy rule for the AFS system
Full size table

5 Simulation results and discussion

In order to evaluate the effectiveness and robustness of the designed estimator and controller, the 7-DOF vehicle dynamics model is considered for the simulation. First, the evaluation of the UKF to estimate the state variables is presented, and then, the estimation of tire-road friction coefficients is investigated under two different road conditions, mix-\(\mu\), and split- \(\mu\).

5.1 Evaluation of the UKF estimator

In this part, a double lane change maneuver is used to evaluate the accuracy of proposed UKF estimator. In this maneuver, the front wheel steering angle is set as a sinusoidal input with amplitude of \(4^{^\circ }\)(0.07 rad) and a frequency of 0.43 Hz as illustrated in Fig. 8. The vehicle runs at an initial velocity of 25 m/s on a dry road \(\left( {\mu = 0.9} \right)\). The sampling time in the simulations is set to be 2 ms. The vehicle parameters are given in Table 2. The simulation results are illustrated in Figs. 9, 10, 11.

Fig. 8
figure 8

Steering angle input of double lane change maneuver

Full size image
Table 2 Parameter values of the full vehicle model [13]
Full size table
Fig. 9
figure 9

Vehicle yaw rate response

Full size image
Fig. 10
figure 10

Side slip angle response

Full size image
Fig. 11
figure 11

Vehicle longitudinal velocity response

Full size image

The yaw rate of the vehicle with the UKF estimator (Estimated), and without estimator (Actual value) is illustrated in Fig. 9. The time response of side slip angle of the vehicle is depicted in Fig. 10, and Fig. 11 gives the longitudinal vehicle velocity. According to the simulation results, especially the analysis related to yaw rate and longitudinal vehicle speed (Figs. 9 and 11), it can be found that the estimated values using proposed UKF is perfectly precise and reliable without a noticeable error. The root mean square (RMS) value of estimation error for these signals is used to evaluate the UKF performance. The calculated RMS values of error for the yaw rate and longitudinal vehicle speed signals are 0.01 rad/s and 0.075 m/s, respectively. In Fig. 10, the estimation error is relatively considerable. This phenomenon is due to inadequate excitation in lateral direction. Because the maximum value of side slip angle is approximately one degree (0.0175 rad) which is a small amount compared with the other state variables.

5.2 Control system analysis on mix- μ road

The simulations are conducted under two different road friction conditions of mix- \(\mu\), and split- \(\mu\), to evaluate the effectiveness and robustness of the ABS system and the designed estimator. In both states, the initial vehicle speed is 25 m/s. In the simulation of mix- \(\mu\) road, the friction coefficients of the left and right wheels are equal at each moment. Although during driving, it may change similarly for all the wheels. In this case, it is assumed that the vehicle travels on two different surfaces of dry asphalt with \(\left( {\mu = 0.9} \right)\) and wet asphalt with \(\left( {\mu = 0.6} \right)\).

The performance of the ABS system is compared for the two states of with and without estimator of the road friction coefficient and the optimal longitudinal slip ratio (ABS with Est). In Fig. 12, the variation of road friction coefficient versus time is plotted, and the longitudinal vehicle velocity can be seen in Fig. 13. According to this figure, the stopping times are 4.43 s and 3.14 s for the only ABS system and system with estimator, respectively. This indicates that the ABS with estimator decreases the stopping time by about 29%.

Fig. 12
figure 12

Friction coefficient on the mix-μ road

Full size image
Fig. 13
figure 13

Longitudinal velocity of vehicle on the mix-μ road

Full size image

The vehicle trajectory until stopping is presented in Fig. 14. It is clear that the application of estimator for the road friction coefficient and the optimal tire slip ratio in the ABS, causes a reduction of 20% in the stopping distance. The actual and the estimated values of the road friction coefficients are depicted in Fig. 15. It is obvious that the estimated road friction coefficient quickly converges from an initial value to the real value.

Fig. 14
figure 14

Vehicle trajectory on the mix-μ road

Full size image
Fig. 15
figure 15

Road friction estimation results on the mix-μ road

Full size image

The braking torque, applied to the front-right wheel, is plotted in Fig. 16. As it can be seen, the maximum of braking torque is an acceptable value. In both the brake control systems without/with estimator, the initial value of road friction coefficient is assumed to be 0.6. Due to increase in this parameter, the braking torque generation capacity can be also increased, if the control system can estimate the actual value of road friction coefficient and use it to determine the braking torque. If the amount of friction coefficient used in the controller is significantly reduced from its actual value, the desired tire slip ratio will also decrease in relation to its optimal value, which in turn will reduce the active braking torque.

Fig. 16
figure 16

Braking torque of ABS for front-right wheel

Full size image

5.3 Control system analysis on split-μ road

In this analysis, the left wheels are on a wet road surface (\(\mu = 0.6\)) and the right ones are on a snow-covered paved road (\(\mu = 0.3\)). The initial vehicle speed is supposed to be 15 m/s. In this state, due to the generation of asymmetric braking forces on the sides of vehicle, yaw and lateral instabilities will appear. To solve this problem, integrated control of ABS, ESC, and AFS systems is proposed.

The coordination between ABS and ESC systems prevents yaw and lateral instabilities on such roads. Although this makes an increase of stopping distance undesired for the driver, to keep the stability of the vehicle and reduce the stopping distance, the integrated control of ABS, ESC and AFS systems is presented. In this approach, a braking force distribution algorithm should also be used. In this algorithm, the parameter \(\eta\) has been utilized defined as the ratio of the optimal tire slip of the rear-left wheel to that of the rear-right wheel:

$$ \eta = \frac{{\lambda_{m4} }}{{\lambda_{m3} }} $$
(57)

In Eq. (57), the parameter \(\lambda_{m}\) is found from the ANFIS system. The algorithms of integrated control for the ABS, ESC, and AFS systems are shown in Figs. 17 and 18.

Fig. 17
figure 17

Block diagram of the proposed vehicle dynamics control system with estimators

Full size image
Fig. 18
figure 18

Block diagram of the proposed vehicle dynamics control system with estimators

Full size image

The simulation results of the ABS alone, integrated control of ABS and ESC, and integrated control of ABS, ESC and AFS systems are illustrated in Figs. 19, 20, 21, 22, 23, 24, 25. In all three cases, the control system is combined with the estimators of the road friction coefficient and the optimum tire slip ratio. The responses of vehicle velocity and its trajectory are illustrated in Figs. 19 and 20, respectively.

Fig. 19
figure 19

Longitudinal velocity of vehicle on the split-μ road

Full size image
Fig. 20
figure 20

Vehicle trajectory on the split-μ road

Full size image
Fig. 21
figure 21

(A): Comparisons of yaw rate responses for different control strategies; (B): zoom in between 0.5 and 0.006 rad/s

Full size image
Fig. 22
figure 22

(A): Comparisons of sideslip angle for different control strategies; (B): zoom in between \(- 0.6^{^\circ }\) and \( 0.4^{^\circ }\)

Full size image
Fig. 23
figure 23

Braking torque of the wheels for integrated control of ABS, ESC and AFS systems on the split-μ road

Full size image
Fig. 24
figure 24

Road friction estimation results of left and right wheels on the split-μ road

Full size image
Fig. 25
figure 25

Corrective front steering angle for AFS system on the split-μ road

Full size image

The analysis results, including the stopping time and the maximum deviation of the vehicle from the straight line, can be seen in Table 3. As it can be observed, the stopping time and distance for the integrated control of ABS and ESC systems are 4.88 s and 37.87 m, respectively. These values have been decreased to 3.61 s and 22.35 m in the integrated control of ABS, ESC and AFS systems. It indicates a reduction of about 26% in the quantities.

Table 3 Stopping distance and maximum deviation from the straight line for different control strategies
Full size table

It should be noted that the stopping time for the ABS alone is 3 s, which is less compared with the other two systems. This lower stopping time cannot be considered as an advantage for ABS alone. Because according to Figs. 20, 21, 22, the values of lateral displacement, yaw rate and sideslip angle for ABS alone system are much higher.

It is noteworthy that the lateral displacement of the integrated control of ABS, ESC and AFS has increased from 0.14 to 0.24 m in comparison with integrated system without AFS. The values of yaw rate and lateral slip angle of the vehicle have also increased in the same way. The amounts of 0.24 m lateral displacement, 0.004 rad/s yaw rate, \(- 0.5^{^\circ }\) lateral slip angle are not significant values and will not be able to cause lateral and yaw instability. Therefore, these shortcomings can be negligible according to the high efficiency of integrated control of the three active systems in reducing the considerable amount of time and stopping distance.

The active braking torque of the wheels for integrated control of ABS, ESC and AFS systems can be seen in Fig. 23. The expressions of FR, FL, RR, RL are pertinent to the front-right, front-left, rear-right, and the rear-left wheels, respectively. As it can be observed, the maximum of braking torque is an acceptable value and there is no sudden variation or pulse on this diagram. It can be practical for the active braking system.

The actual and estimated values of the friction coefficient for the split-μ roads are shown in Fig. 24, in which the RW and LW represent the right and left wheels, respectively. According to this figure, the friction coefficient for both wheels converges from an initial value of 0.5 to its actual value with an acceptable rate.

However, there are some errors with a maximum value of 8%. This is because that in the estimation algorithm at any time, the values of a time step back from the active front steering angle are used. Since the steering angle of front wheels has a direct and indirect effect on the lateral and longitudinal tire forces, respectively, few errors have been observed in estimating the road friction coefficient. However, due to the challenging split- μ road and proper performance of longitudinal and lateral vehicle dynamics control, the small amount of error can be ignored. The active steering angle of front wheels is also illustrated in Fig. 25.

6 Conclusions

In this study, an integrated control system for longitudinal, lateral and yaw dynamics was introduced, using active braking and steering systems. The proposed active braking system based on SMC, includes two kinds of working modes. In severe braking conditions on two road types, straight roads, and the unstable cornering, the active braking system performs as an ABS and ESC, respectively. An integrated control of ABS, ESC, and AFS was designed to enhance the lateral and yaw vehicle stability on a straight split-\(\mu \) roads. The AFS was proposed based on fuzzy controller. The state variables of the system and road friction coefficients were estimated using the UKF and the algebraic equations of the Dugoff tire model, respectively. The ANFIS system was also used to estimate the optimal tire slip ratio, which has a significant influence on reducing the stopping time and distance. The severe braking action on straight road was analyzed in both mixed-\(\mu \) and split-\(\mu \) roads. The simulation results showed the better performance of the integrated control ABS, ESC and, AFS systems combined with the optimum tire slip estimator, in comparison with the integrated control of ABS, ESC and, ABS alone, in reducing time and distance of stopping by about 26%. This result was obtained in simulation of split-μ roads to improve the lateral and yaw vehicle stability.