Mesh stiffness model of a spur gear pair with surface roughness in mixed elastohydrodynamic lubrication

Abstract

The calculation of time-varying mesh stiffness for gear meshing in mixed EHL regime is of great importance to the accurate evaluation of tooth damage, contact fatigue life and wear performance of a gear transmission system. In this work, the mesh stiffness of a spur gear pair in mixed elastohydrodynamic line (EHL) contact is established in conjunction with a revised contact stiffness to include the effect of surface roughness and oil film. The revised contact stiffness of gear tooth surface in EHL contact is developed by combining the stiffness of both the rough gear tooth and liquid film based on the load-sharing concept, which is used to replace the Hertzian contact stiffness of ideal smooth cylinders in traditional gear mesh stiffness. To include the effect of tooth curvature on the asperity distribution at the gear tooth surface, the cylindrical contact coefficient is introduced and incorporated into the statistical micro-contact Greenwood and Williamson model (GW model) to derive the stiffness of rough curved gear tooth contact. The film thickness equation for mixed EHL line contact is employed together with the lubricant bulk modulus to predict the liquid film stiffness at different mesh positions. Effects of surface roughness, input torque, rotating speed and lubricant on the contact stiffness and EHL mesh stiffness are analyzed. Results show that the lubricant film stiffness is much higher than the solid part, especially at tip or root position. The fluctuation of mesh stiffness in single-to-double teeth contact is smaller than that calculated using Hertzian contact model, indicating a better transmission stationarity.

1 Introduction

Gear transmissions are widely used in numerous machinery and industrial applications, such as vehicles, ships and wind turbine. The gears generally operate in the line-contact mixed elastohydrodynamic lubrication (EHL) regime, in which the transmitted load is carried by both the asperities on the rough surface and the lubricant film between the mesh teeth [1,2,3]. The surface roughness, lubricant film and the mixed EHL regime of the gear teeth directly affect the time-varying mesh stiffness and thus play important role in tooth damage, contact fatigue life and wear performance of a gear transmission system [4,5,6,7].

The calculation of time-varying mesh stiffness in gear meshing process considering the lubricant film and mixed EHL regime is receiving increasing attention [8,9,10]. The modeling methods can be classified into two common methods as the Reynolds equation approach and the load-sharing approach. As for the Reynolds equation approach, full solution of the mixed EHL often includes solving the Reynolds equation, the film thickness equation and the elastic deformation equation with complicated iteration, to obtain the contact pressure, film thickness and the EHL mesh stiffness. For example, Zhou et al. [11] developed a normal and tangential oil film stiffness model of a spur gear through direct solving of the generalized Reynolds equation. However, the lubricant stiffness models were established in fully flooded lubrication regime and the effect of contact surface stiffness was not included. Ouyang et al. [12] proposed a tribo-dynamic model for high-speed spur gear based on the generalized one-dimensional Reynolds equation, in which the film thickness equation includes the tooth surface roughness. Shi et al. [13] studied the dynamic meshing and mixed-lubrication performance of the spur gear considering the three-dimensional machined surface roughness. These works concentrated on the lubrication and dynamic performances, while the mesh stiffness characteristics were not provided. Recently, Li et al. [14] derived the mesh stiffness of a spur gear pair in line-contact EHL. The stiffness was further employed in the coupled tribo-dynamic model to analyze the dynamic performance. However, effects of surface topography on the rigid body displacement and center oil film thickness were neglected.

Regarding the load-sharing approach, the statistical model of the rough surface is generally incorporated with the empirical film thickness equation to predict the mixed-lubrication performance. The statistical surface roughness parameters used to represent the surface profile, such as the standard deviation of the surface heights distribution and asperity distribution density, are included in the equations. It is convenient to analyze the effect of surface roughness on the performances and more applicable to practical engineering. Johnson et al. [15] pioneered the load-sharing concept that the total load is shared by the lubricant film and the interacting asperities. Gelinck and Schipper [16] applied the concept to the line-contact mixed-lubrication problem. Later, Lu et al. [17] experimentally verified the validation of the concept through the application to journal bearings. Dwyer-Joyce et al. [18] applied this approach to study the interfacial stiffness and film thickness for the point-contact between a sliding steel ball and a flat steel disk. Beheshti and Khonsari [19] applied this concept to investigate the wear performance in mixed EHL regime. However, the gear mesh stiffness was not concerned in these previous studies.

Although mesh stiffness models of spur gear operating in mixed EHL regime have been developed to predict dynamic performance, the current EHL models are established with the surface roughness and its effect on contact stiffness and oil film stiffness ignored. The purpose of this work is to develop an engineering approach that the influence of surface roughness and oil film on the time-varying mesh stiffness of a spur gear pair in mixed elastohydrodynamic lubrication can be considered using the load-sharing concept. Actually, this work is the further extension of our previous works on the normal contact stiffness of dry rough surface contact [20], rough line-contact mixed lubrication [21, 22] and rough line-contact EHL [23] to the application of gear mesh. In our previous work [23], the normal contact stiffness of two rough cylinders in line-contact EHL was studied. In this work, the contact stiffness of a meshing spur gear pair in rough line-contact EHL, which consists of the rough curved gear tooth surface contact stiffness and the lubricant film stiffness, is derived and used to replace the Hertzian contact stiffness of ideal smooth cylinders in traditional gear mesh stiffness expression. The rough contact of the gear tooth surface is characterized using the statistical asperity micro-contact Greenwood and Williamson model (GW model) [24]. The cylindrical contact coefficient is introduced to represent the effect of varying curvature radius on the distribution function of micro-asperities at the meshing interface. The corresponding contact stiffness expressions for solid asperity contact of curved gear tooth surface are derived. The empirical film thickness equation for mixed EHL line contact is employed together with the lubricant bulk modulus to predict the liquid film stiffness at different mesh positions along the line of action. The mesh stiffness is further obtained using the revised contact stiffness. Effects of surface roughness, input torque, rotating speed and lubricant viscosity on the mesh stiffness are analyzed. The developed model provides a new method to calculate the time-varying mesh stiffness of spur gear mesh in mixed EHL regime in respect of introducing surface roughness and lubricant property directly, which can be further used to predict the dynamic behavior of gear transmission system. In addition, the asperity load ratio obtained in the developed model can be also combined with the wear model to predict the wear performance of gears in practical EHL operation condition.

2 Gear mesh stiffness modelling methodology

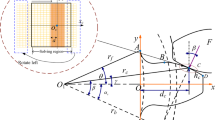
The lubricated contact of a spur gear pair with surface roughness is shown in Fig. 1. The actual contact of standard involute profiles between the gear and the pinion along the line of action (LOA) is represented by the contact of two cylinders at each mesh point. In a mesh cycle, the curvature radius of the cylinders, the transmitted force and entrainment speed vary as the mesh point travels along the LOA N₁N₂ from root to tip. At the mesh point K, two cylinders with radius R₁ and R₂, modulus of elasticity E₁ and E₂, Poisson’s ratio of v₁ and v₂, and shear modulus G₁ and G₂ are in contact under the normal load F, which is in the direction of the LOA and also normal to the two contacting teeth surface. The normal load F is supported by both solid-to-solid asperity contact and the fluid film, giving rise to an area of contact, deformation of the asperities and the compression of the fluid lubrication. The mean separation of the rough surfaces is h, which can be regarded as the lubricant film thickness. The gear and the pinion rotate with angular speed ω₁ and ω₂. The gear pair is in mixed elastohydrodynamic lubrication (EHL) line-contact regime, and the deformation of the asperities, the film thickness and the mesh stiffness between the meshing gear pair are dynamically varying due to the dynamic mesh motion process.

Fig. 1

Sketch diagram of a spur gear pair with surface roughness in mixed elastohydrodynamic lubrication

As the gear drive operates, the gear tooth and lubrication film experience elastic deformations. The total mesh deformation of a spur gear pair is composed of five parts as the tooth bending deformation, shear deformation, axial compression deformation, contact deformation and gear base deformation. Accordingly, the total mesh stiffness can be evaluated as [6, 25]

$$\frac{1}{k} = \left\{ {\begin{array}{*{20}c} {\frac{1}{{k_{b1} }} + \frac{1}{{k_{s1} }} + \frac{1}{{k_{a1} }} + \frac{1}{{k_{f1} }} + \frac{1}{{k_{b2} }} + \frac{1}{{k_{s2} }} + \frac{1}{{k_{a2} }} + \frac{1}{{k_{f2} }} + \frac{1}{{k_{h} }},\begin{array}{*{20}c} {} \\ \end{array} {\text{one tooth pair meshing}}} \\ {\frac{1}{{\lambda_{f1} k_{f1} }} + \frac{1}{{\lambda_{f2} k_{f2} }} + \sum\limits_{i = 1}^{2} {\left( {\frac{1}{{k_{b1,i} }} + \frac{1}{{k_{s1,i} }} + \frac{1}{{k_{a1,i} }} + \frac{1}{{k_{b2,i} }} + \frac{1}{{k_{s2,i} }} + \frac{1}{{k_{a2,i} }} + \frac{1}{{k_{h,i} }}} \right)} ,\begin{array}{*{20}c} {} \\ \end{array} {\text{double tooth pair meshing}}} \\ \end{array} } \right.$$

(1)

where k_b, k_s, k_a, k_fdenote the bending stiffness, shear stiffness, axial compressive stiffness and the stiffness due to the fillet foundation deflection, respectively, and k_h denotes the contact stiffness at the tooth surface. λ_f1 and λ_f2 are the correction coefficients of the fillet-foundation stiffness to compensate the repeated calculation of the stiffness of gear body for the double-tooth pair meshing [25]. Subscripts 1 and 2 denote the pinion and gear, respectively.

The first four parts of the stiffness for a pair of spur gears, namely the bending stiffness k_b, shear stiffness k_s, axial compressive stiffness k_a and base foundation stiffness k_f,can be calculated as follows [6, 26]:

$$\frac{1}{{k_{b} }} = \sum\limits_{i = 1}^{n} {\frac{{\cos^{2} \alpha_{1} (e_{i}^{3} + 3e_{i}^{2} d_{i} + 3e_{i} d_{i}^{2} )}}{{3{\text{EI}}_{i} }}}$$

(2)

$$\frac{1}{{k_{s} }} = \sum\limits_{i = 1}^{n} {\frac{{1.2e_{i} \cos^{2} \alpha_{1} }}{{{\text{GA}}_{i} }}}$$

(3)

$$\frac{1}{{k_{a} }} = \sum\limits_{i = 1}^{n} {\frac{{e_{i} \sin^{2} \alpha_{1} }}{{EA_{i} }}}$$

(4)

$$\frac{1}{{k_{f} }} = \frac{{\cos^{2} \alpha_{1} }}{EL}\left[ {L^{*} \left( {\frac{{U_{f} }}{{S_{f} }}} \right)^{2} } \right.{ + }\left. {P^{*} \left( 1 \right. + Q^{*} \tan^{2} \alpha_{1} } \right)\left. {{ + }M^{*} \left( {\frac{{U_{f} }}{{S_{f} }}} \right)} \right]$$

(5)

where α₁ is the pressure angle, E and G are the equivalent elastic modulus and shear modulus with ${1 \mathord{\left/ {\vphantom {1 E}} \right. \kern-\nulldelimiterspace} E} = {{(1 - v_{1}^{2} )} \mathord{\left/ {\vphantom {{(1 - v_{1}^{2} )} {E_{1} }}} \right. \kern-\nulldelimiterspace} {E_{1} }} + {{(1 - v_{2}^{2} )} \mathord{\left/ {\vphantom {{(1 - v_{2}^{2} )} {E_{2} }}} \right. \kern-\nulldelimiterspace} {E_{2} }}$ and ${1 \mathord{\left/ {\vphantom {1 G}} \right. \kern-\nulldelimiterspace} G} = {{(1 - v_{1}^{2} )} \mathord{\left/ {\vphantom {{(1 - v_{1}^{2} )} {G_{1} }}} \right. \kern-\nulldelimiterspace} {G_{1} }} + {{(1 - v_{2}^{2} )} \mathord{\left/ {\vphantom {{(1 - v_{2}^{2} )} {G_{2} }}} \right. \kern-\nulldelimiterspace} {G_{2} }}$, respectively, L is the tooth width, e_iis cross-sectional width of the micro-element, d_i is the distance from the load point to the micro-element, I_i and A_i are the equivalent cross-sectional modulus and equivalent cross-sectional area. The parameters of L*, M*, P*, Q*, U_f and S_f are constants [27]. The correction coefficients are determined using the fillet-foundation stiffness at the two rounded corners of the gear teeth as $\lambda_{f} = {{k_{fA} } \mathord{\left/ {\vphantom {{k_{fA} } {k_{fB} }}} \right. \kern-\nulldelimiterspace} {k_{fB} }}$, where k_fA and k_fB are the fillet-foundation stiffness of the point near the double tooth pair and the single tooth pair at the alternation of single and double tooth, respectively [25].

As for the contact stiffness k_h, the nonlinear Hertzian contact stiffness between ideal smooth cylinders is normally used and has the expression [25]

$$k_{h} = \frac{{E^{0.9} L^{0.8} F^{0.1} }}{1.275}$$

(6)

where F is normal load or the meshing force. Equation (6) shows that the nonlinear Hertzian contact stiffness is related to the tooth width, material parameters and meshing force. However, the gear meshing interface works in the mixed EHL regime and has a combination of rough surface contact and interaction with lubrication film, which is not an ideal smooth contact. Effects of the micro-geometry effects such as surface roughness and lubricant film on the dynamic meshing stiffness are not included in Eq. (6), and thus the model is unable to predict the mesh stiffness of a spur gear pair with surface roughness in mixed EHL regime for practical engineering applications.

In this work, a revised contact stiffness, k_c, of a meshing spur gear pair in rough line-contact EHL, which consists of the dry rough curved surface contact stiffness and the lubricant film stiffness, is derived and used to replace the Hertzian contact stiffness k_h of ideal smooth cylinders in the gear mesh stiffness expression of Eq. (1).

According to Johnson’s load-sharing concept, the total normal load for a gear tooth pair is supported by the interacting asperities and the lubricant film and expressed as [1, 18, 23]

$$F = \frac{F}{{\gamma_{1} }} + \frac{F}{{\gamma_{2} }}$$

(7)

where γ₁ and γ₂ are the scaling factors for the film and solid part, respectively, and follows the relationship

$$\frac{1}{{\gamma_{1} }} + \frac{1}{{\gamma_{2} }} = 1$$

(8)

The contact stiffness at the gear tooth interface, k_c, is contributed from the parallel action of the interacting asperities and the lubricant film and can be expressed as [18, 23]

$$k_{c} = k_{g} + k_{l}$$

(9)

where k_g is the stiffness of the contact asperities at gear tooth surfaces and k_l is the stiffness of the lubricant film, as shown in Fig. 2. The stiffness k_g is generated due to the contact deformation of interacting asperities on the tooth surface during gear meshing. Simultaneously, the fluid lubrication experiences compression and the film thickness will change, which also influences the stiffness of the lubricant film k_l. The combined contact stiffness k_c includes both parts when asperity contact and lubrication film interaction simultaneously exist, i.e., the surfaces are not completely separated by the lubricant film. However, for tooth surface in full elastohydrodynamic lubrication regime, the combined contact stiffness reduces to lubricant film stiffness due to the negligible asperity contact. In the following sections, the methods to obtain these two stiffnesses are presented.

Fig. 2

The combined contact stiffness model at the gear tooth surface

2.1 Contact stiffness of dry rough curved gear tooth surface

In this section, the stiffness of rough gear tooth contact is studied firstly. The surface topographies of gear tooth surface can be quite different at different working states, as the microscopic images shown in Fig. 3. Initially, the longitudinal roughness pattern to the circumferential rolling direction is clearly visible due to the grinding machining process [28]. With the evolution of loading cycles, the surface topography changes significantly. No obvious processing lines can be seen and the surface tends to be isotropic. Accordingly, the rough surface contact of the gear tooth pair can be characterized using the GW model, which is the basic statistical micro-contact model for rough surface contact based on the isotropic surface assumption [24].

Fig. 3

The microscopic images of gear teeth at different wear states ①: 1.5 × 10⁵ loading cycles, ②: 13.5 × 10⁵ loading cycles, ③: 43.5 × 10⁵ loading cycles, ④: 88.5 × 10⁵ loading cycles [28]

As shown in Fig. 1, the contact of standard involute profiles between the meshing gear pair at each mesh point can be represented by the contact of two cylinders with varying curvature radius in a mesh cycle. Considering the surface roughness, the two-cylinder-contact can be further equivalent to the contact between a cylinder with surface roughness and a rigid flat plane, as shown in Fig. 4. The equivalent radius of curvature of the cylinder is ${1 \mathord{\left/ {\vphantom {1 {R = {1 \mathord{\left/ {\vphantom {1 {R_{1} + {1 \mathord{\left/ {\vphantom {1 {R_{2} }}} \right. \kern-\nulldelimiterspace} {R_{2} }}}}} \right. \kern-\nulldelimiterspace} {R_{1} + {1 \mathord{\left/ {\vphantom {1 {R_{2} }}} \right. \kern-\nulldelimiterspace} {R_{2} }}}}}}} \right. \kern-\nulldelimiterspace} {R = {1 \mathord{\left/ {\vphantom {1 {R_{1} + {1 \mathord{\left/ {\vphantom {1 {R_{2} }}} \right. \kern-\nulldelimiterspace} {R_{2} }}}}} \right. \kern-\nulldelimiterspace} {R_{1} + {1 \mathord{\left/ {\vphantom {1 {R_{2} }}} \right. \kern-\nulldelimiterspace} {R_{2} }}}}}}$, and R₁ and R₂ are the radii of the two contacting cylinders at the mesh point. In the GW model, the topography of rough surface is described by asperities possessing spherical summits with identical radius of curvature and the height following a Gaussian distribution [24]. Recently, Xiao et al. [23] have derived the normal contact stiffness of the dry rough plane surface contact based on the statistical GW model. According to [23], the normal contact stiffness is expressed as

$$k_{g} \left( {h_{n} } \right) = 2n_{s} A_{n} E\sqrt {\beta \sigma } \int_{{h_{n} - d_{n} }}^{\infty } {\left( {z_{n} + d_{n} - h_{n} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \phi_{n} \left( {z_{n} } \right)dz_{n}$$

(10)

Fig. 4

The equivalent contact of a rough cylinder with a smooth surface for the two- cylinder-contact at each mesh point and the description of rough surface contact in the GW model

where n_s is the asperity distribution density, A_n is the nominal contact area, β is the asperity radius, and σ is the standard deviation of the surface heights distribution. The non-dimensional parameters are defined as

$$z_{n} = \frac{z}{\sigma },\begin{array}{*{20}c} {} \\ \end{array} h_{n} = \frac{h}{\sigma },\begin{array}{*{20}c} {} \\ \end{array} d_{n} = \frac{{d_{d} }}{\sigma },\begin{array}{*{20}c} {} \\ \end{array}, \phi_{n} \left( {z_{n} } \right) = \frac{1}{{\sqrt {2\pi } }}\left( {\frac{\sigma }{{\sigma_{s} }}} \right)\exp \left[ { - \frac{1}{2}\left( {\frac{\sigma }{{\sigma_{s} }}} \right)^{2} z_{n}^{2} } \right]$$

where z is the asperity height, h is the mean separation of the rough surface and the flat plane, d_d is the distance between the mean planes of summit heights and surface heights, σ_s is the standard deviation of asperity heights distribution, and $\phi_{n} \left( {z_{n} } \right)$ is the normalized probability density function of height distribution.

It is noted that the GW model only applies to the rough-plane contact, namely the curvature radius of the contact surface is infinite. However, for the rough contact of gear teeth, the surfaces are curved and the curvature radius is changing during the meshing process. The actual contact area of the curved surface is less than that of the plane surface, resulting in a smaller total number of asperities in contact. The cylindrical contact coefficient λ_c for the contact of two cylindrical surfaces, characterized by the ratio between actual contact area to the nominal contact area [29], is introduced to include the effect of curved surface on total number of asperities in contact and expressed as

$$\lambda_{c} = \left( {\frac{{S_{h} }}{{S_{t} }}} \right)^{r}$$

(11)

where S_h is the actual contact area, S_t is the nominal contact area of the two cylinders, and r is the integrated curvature with $r = {1 \mathord{\left/ {\vphantom {1 {R_{1} }}} \right. \kern-\nulldelimiterspace} {R_{1} }} + {1 \mathord{\left/ {\vphantom {1 {R_{2} }}} \right. \kern-\nulldelimiterspace} {R_{2} }}$. The actual contact area is obtained based on the Hertzian elastic contact given by [30]

$$S_{h} = 4L\sqrt {\frac{{FR_{1} R_{2} }}{{\pi E(R_{1} + R_{2} )}}}$$

(12)

The nominal contact area of the two cylinders is given by

$$S_{t} = 2\pi (R_{1} + R_{2} )L$$

(13)

Substituting Eqs. (12) and (13) into Eq. (11), the cylindrical contact coefficient λ_c is obtained as

$$\lambda_{c} = \left[ {\frac{{\sqrt {4FLR_{1} R_{2} {/}\pi E\left( {R_{1} + R_{2} } \right)} }}{{\pi (R_{1} + R_{2} )}}} \right]^{{\left( {\frac{1}{{R_{1} }} + \frac{1}{{R_{2} }}} \right)}}$$

(14)

where F is the normal load and L is the tooth width. It can be seen that λ_c is a function of the applied load, material and geometry of the two cylinders.

The total number of asperities deformed at curved meshing teeth surface is modified as

$$N_{c} = N\int\limits_{{h_{n} - d_{n} }}^{\infty } {\left[ {\lambda_{c} \phi_{n} \left( {z_{n} } \right)} \right]{\text{d}}z_{n} }$$

(15)

and the equivalent probability density function of height distribution for curved surface can be obtained as

$$\phi_{n}^{\prime } \left( {z_{n} } \right) = \frac{{\lambda_{c} }}{{\sqrt {2\pi } }}\left( {\frac{\sigma }{{\sigma_{s} }}} \right)\exp \left[ { - \frac{1}{2}\left( {\frac{\sigma }{{\sigma_{s} }}} \right)^{2} z_{n}^{2} } \right]$$

(16)

The contact stiffness of rough gear tooth surface is obtained by modifying the probability density function of height distribution in Eq. (10) using Eq. (16) and is rewritten as

$$k_{g} \left( {h_{n} } \right) = 2n_{s} A_{n} E\sqrt {\beta \sigma } \int_{{h_{n} - d_{n} }}^{\infty } {\left( {z_{n} + d_{n} - h_{n} } \right)^{\frac{1}{2}} } \phi_{n}^{\prime } \left( {z_{n} } \right){\text{d}}z_{n}$$

(17)

It can be seen that the contact stiffness of the dry rough curved gear tooth surface is function of the separation of rough surface h_n. The surface roughness σ_s, the asperity distribution density n_s and asperity radius β are also necessary to determine the stiffness. These three statistical parameters can be calculated using the spectral moments of the rough surface and expressed as [1, 20]

$$n_{s} = \frac{{m_{4} }}{{6\pi \sqrt 3 m_{2} }},\begin{array}{*{20}c} {} \\ \end{array} \beta = 0.375\sqrt {\frac{\pi }{{m_{4} }}} ,\begin{array}{*{20}c} {} \\ \end{array} \sigma_{s} = \sqrt {m_{0} }$$

(18)

where m₀, m₂, m₄ are the spectral moments of the rough surface and can be determined as [20]

$$m_{0} = E(z^{2} ) = \sigma_{s}^{2} ,\begin{array}{*{20}c} {} \\ \end{array} m_{2} = E\left[ {\left( {\frac{dz}{{dx}}} \right)^{2} } \right],\begin{array}{*{20}c} {} \\ \end{array} m_{4} = E\left[ {\left( {\frac{{d^{2} z}}{{dx^{2} }}} \right)^{2} } \right]$$

(19)

and z(x) is the height profile of the rough surface in direction x, which can be measured experimentally for practical gear tooth surface and E[] represents the statistical expectation. The relationship between σ and σ_s is ${\sigma \mathord{\left/ {\vphantom {\sigma {\sigma_{s} }}} \right. \kern-\nulldelimiterspace} {\sigma_{s} }} = {{n\beta \sigma } \mathord{\left/ {\vphantom {{n\beta \sigma } {\sqrt {(n\beta \sigma )^{2} - 3.71693 \times 10^{ - 4} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {(n\beta \sigma )^{2} - 3.71693 \times 10^{ - 4} } }}$[23].

2.2 Lubricant film stiffness

In this section, the lubrication film stiffness at different mesh positions of the gear tooth surface is studied. The ultrasound technique has been widely used to measure the film thickness and interfacial contact stiffness for rough surface contacts, by relating the reflection coefficient with contact stiffness using different acoustic models [18, 31,32,33,34]. According to the spring acoustic model, the lubricant film stiffness can be calculated using the lubricant bulk modulus and film thickness and expressed as

$$k_{l} = \frac{B}{{\sigma h_{n} }}A_{n}$$

(20)

where k_l is the lubricant film stiffness, B is the bulk modulus of the lubricant, σ is the standard deviation of surface heights distribution, and A_n is the nominal contact area. The bulk modulus of compressed lubricant is function of pressure and described as [18, 23]

$$B = \left\{ {1 - \frac{1}{{1 + B_{0}^{\prime } }}\log \left[ {1 + \frac{{p_{h} }}{{B_{00} \exp \left( { - \beta_{k} T_{t} } \right)}}\left( {1 + B_{0}^{\prime } } \right)} \right]} \right\}\left[ {B_{00} \exp \left( { - \beta_{k} T_{t} } \right) + p_{h} \left( {1 + B_{0}^{\prime } } \right)} \right]$$

(21)

where p_h is the mean pressure in lubricant, $B_{0}^{\prime }$ is the pressure change rate with $B_{0}^{\prime } \approx 1.1$[18], B₀₀ is the bulk modulus at ambient pressure and absolute zero temperature, and T_t is the temperature and β_k = 6.5 × 10^–3 K⁻¹[18]. The operating conditions of the gear pair are assumed to be steady-state and isothermal. Accordingly, the temperature is constant during the mesh process and the bulk modulus of the compressed lubricant will dynamically change due to the variation of mean pressure at the gear teeth. Equations (20) and (21) show that the lubricant film stiffness is dependent on the mean pressure in lubricant, lubricant property and film thickness.

Combining Eqs. (9), (17) and (20), the contact stiffness of gear tooth surface in mixed EHL line contact is obtained as

$$k_{c} \left( {h_{n} } \right) = 2n_{s} A_{n} E\sqrt {\beta \sigma } \int_{{h_{n} - d_{n} }}^{\infty } {\left( {z_{n} + d_{n} - h_{n} } \right)^{\frac{1}{2}} } \phi_{n}^{\prime } \left( {z_{n} } \right){\text{d}}z_{n} + \frac{B}{{\sigma h_{n} }}A_{n}$$

(22)

Equation (22) shows that it is necessary to determine the interface film thickness to calculate the combined contact stiffness.

The film thickness of the contact region at the mesh gear tooth can be assumed to be constant and equal to the central film thickness, as the film thickness profile shown in Fig. 5. In the contact region between the inlet and outlet, the lubricant film thickness is almost constant and closes to central film thickness except the local dropping near the outlet, although the film thickness exhibits significant variation outside the contact region [3, 9]. According to Gelinck and Schipper’s mixed EHL line-contact model, in which the load-sharing concept is applied to Moes’ equation for perfectly smooth line contact based on the assumption of Newtonian fluid, the dimensionless film thickness is given by [16]

$$\overline{h} = \left[ {\left( {\gamma_{1} } \right)^{s/2} \left( {H_{RI}^{7/3} + \left( {\gamma_{1} } \right)^{ - 14/15} H_{EI}^{7/3} } \right)^{3s/7} + \left( {\gamma_{1} } \right)^{ - s/2} \left( {H_{RP}^{ - 7/2} + H_{EP}^{ - 7/2} } \right)^{ - 2s/7} } \right]^{1/s} \left( {U\gamma_{1} } \right)^{1/2}$$

(23)

Fig. 5

Film thickness of the gear tooth interface. The contact occurs between the inlet region and outlet region

where

$$s = \frac{1}{5}\left( {7 + 8e^{{\left( {\frac{{ - 2\left( {\gamma_{1} } \right)^{ - 2/5} H_{EI} }}{{H_{RI} }}} \right)}} } \right)$$

$$\begin{aligned} H_{RI} =3M^{ - 1} ,\begin{array}{*{20}c} {} \\ \end{array} H_{EI} = 2.621M^{ - 1/5} ,\begin{array}{*{20}c} {} \\ \end{array} H_{RP} = 1.287Q^{2/3} ,\begin{array}{*{20}c} {} \\ \end{array} H_{EP} = 1.311M^{ - 1/8} Q^{3/4} \\ M=WU_{{}}^{ - 1/2} ,\begin{array}{*{20}c} {} \\ \end{array} W = \frac{F}{{{\text{ERL}}}},\begin{array}{*{20}c} {} \\ \end{array} U = \frac{{\eta_{0} u}}{ER},\begin{array}{*{20}c} {} \\ \end{array} Q = G_{c} U_{{}}^{1/4} \\ G_{c} = \alpha E,\begin{array}{*{20}c} {} \\ \end{array} H = \overline{h}U_{{}}^{ - 1/2} ,\begin{array}{*{20}c} {} \\ \end{array} \overline{h} = \frac{h}{R} \\ \end{aligned}$$

and G_c is the dimensionless material parameter, W is the dimensionless load, u is the relative interfacial motion at the contact region, η₀ is the inlet viscosity, and α is the pressure-viscosity coefficient.

In Eq. (23), the film thickness is also associated with the load scaling ratio. Equating the central contact pressure equations from the GW model and Gelinck and Schipper’s model [16], and applying the load-sharing concept, lead to another equation relating the film thickness and load scaling ratio as

$$p_{c} = \frac{2}{3}n_{g} \sigma_{sn}^{3/2} \overline{F}_{{}} F_{3/2} \left( {\frac{{\overline{h} - \overline{d}}}{{\sigma_{sn} }}} \right) = \left[ {1 + \left( {a_{1} n_{g}^{{a_{2} }} \sigma_{sn}^{{a_{3} }} W^{{a_{2} - a_{3} }} \gamma_{2}^{{a_{2} }} } \right)^{{a_{4} }} } \right]^{{1/a_{4} }} \frac{1}{{\gamma_{2} }}$$

(24)

where a₁ = 1.558, a₂ = 0.0337, a₃ =  − 0.442, a₄ =  − 1.70 and the non-dimensional parameters are defined as

$$n_{g} = n_{s} R\sqrt {\beta R} ,\begin{array}{*{20}c} {} \\ \end{array} \sigma_{sn} = \frac{{\sigma_{s} }}{R},\begin{array}{*{20}c} {} \\ \end{array} \overline{F} = \sqrt {\frac{4\pi LRE}{F}} ,\begin{array}{*{20}c} {} \\ \end{array} \overline{d} = \frac{{d_{d} }}{R}, ]; F_{3/2} \left( {\frac{{h - d_{d} }}{{\sigma_{s} }}} \right) = \frac{1}{{\sqrt {2\pi } }}\int_{{(h - d_{d} )/\sigma_{s} }}^{\infty } {\left( {z - \frac{{h - d_{d} }}{{\sigma_{s} }}} \right)}^{3/2} e^{{ - (1/2)s^{2} }} dz$$

The three unknown parameters of load scaling ratio and central film thickness γ₁, γ₂ and h can be determined by combining the three Eqs. (8), (23) and (24). The equivalent radius of curvature is varying along the LOA of a gear pair, as well as the corresponding relative motion velocity u and the film thickness. The film thickness and load scaling ratios are evaluated for each point along the LOA for the dynamic gear mesh motion. The scaling ratio γ₁ can be expressed in terms of γ₂ using Eq. (8) and substituted into Eq. (23). The obtained expression of film thickness h from Eq. (23) can be further substituted into Eq. (24) to generate an equation with γ₂ on both the left side and right side. This equation can be solved using the bisection scheme. The solution starts with assigning the interval for γ₂, and the initial value of γ₂ is assumed to be the midpoint of the interval. The product of left-hand side and right-hand side of Eq. (24) is used for the further divide of the interval. This algorithm is repeated until the difference between the maximum and minimum of the interval for γ₂ becomes smaller than 10^–5. Once the scaling ratio γ₂ is determined, the ratio γ₁ and the film thickness h can be determined. The combined contact stiffness can be obtained accordingly as well as the mesh stiffness. Figure 6 shows the flowchart for the calculation of the mesh stiffness.

Fig. 6

Flowchart for the calculation of the mesh stiffness of gear tooth in EHL contact

3 Results and discussion

3.1 Model validation

To validate the model, the film thickness predicted using the developed model is compared with Beheshti and Khonsari’s model [19] and Masjedi and Khonsari’s model [35], as shown in Fig. 7. Beheshti and Khonsari [19] developed a central film thickness equation, in which Pan and Hamrock’s central film thickness equation for smooth line contact is modified by including the effect of surface roughness. Masjedi and Khonsari [35] developed a central film thickness equation based on the simultaneous solution to the modified Reynolds equation and surface deformation with statistical elasto-plastic asperity micro-contact model. The parameters of standard involute spur gear used in calculation are listed in Table 1. The roughness parameters are listed in Table 2. The surface roughness values are chosen to be σ = 1.2, 2.4, 3.2 and 4.8 μm to represent medium to relative rough surfaces according to the precision grade of gear machining. The values for radius of asperity β and density of asperities n_s are from the parameters reported in published references with similar surface roughness values of σ = 1.58, 2.42, 3.09 and 4.81 μm [34, 36]. The other parameters used in calculations are B₀₀ = 9 GPa for oil lubricant at ambient pressure. The rotating speed is n = 600 r/in.

Fig. 7

Comparison of predicted film thickness with Beheshti and Khonsari [19], Masjedi and Khonsari [35] central film thickness equation for different surface roughness a σ = 1.2 μm b σ = 2.4 μm c σ = 3.2 μm d σ = 4.8 μm

Table 1 Parameters of standard involute spur gear used in calculation

Table 2 Parameters of surfaces with different roughness [34, 36]

It can be seen that the model predictions are in consistent with the results obtained using published film thickness equations. The film thickness is smaller in the single-tooth-pair contact region due to the higher transmitted normal load and becomes larger in the double-tooth-pair contact region as a result of decreased normal load. The model predictions show better agreement with reported film thickness equations near the pitch point of the gear tooth, namely the position with value zero in the abscissa axis of Fig. 7. The deviation increases as the position approaches to tip and root of the tooth, namely the position away from zero in the abscissa axis of Fig. 7. This is because the reported central film thickness equations were developed based on the rough-plane line contact and the variation of curvature radius at different mesh positions of the gear tooth were not considered. As the positions approach to tip and root, the variation of curvature radius increases and its effect on the contact of rough curved gear tooth surface becomes more significant. This leads to the increased difference between predicted film thicknesses. As the surface roughness increases, this effect becomes significant and the difference increases.

Furthermore, the predicted mesh stiffness values are compared with experimental measured results, as shown in Fig. 8. In contrast to the prevailing modeling of gear mesh stiffness, the experimental measurements are very limited, especially for gears operating in EHL condition. Raghuwanshi and Parey [37] measured the mesh stiffness of a pair of special manufactured external spur gears using digital image correlation (DIC) technique for both healthy and cracked gears. The mesh stiffness was calculated using the displacements of the tooth at contact point, which were extracted from the captured images from loading to full unloading. The parameters of the gears used in experiments are listed in Table 3. The surface roughness and lubrication were not provided; however, the gear pairs with smooth surfaces were established in their finite element model for validation. For comparison, three different sets of surface roughness values and lubricant viscosity are used for model predictions, which includes a nearly smooth surface with roughness σ = 0.08 μm and lubricant with very small viscosity η₀ = 0.023 Pa.s (Simulation 1 in Fig. 8), and two other simulations with increased surface roughness and viscosity as σ = 1.2 μm and η₀ = 0.023 Pa.s, and σ = 1.2 μm and η₀ = 0.095 Pa.s, respectively (Simulation 2 and Simulation 3 in Fig. 8). It can be seen that the model predictions are in good accordance with the experimental results for simulation 1. The differences between the results can be due to the different mesh conditions in experiment and model calculation, which increase with the surface roughness and the lubricant viscosity.

Fig. 8

Comparison of predicted mesh stiffness with experimental results. Simulation 1: σ = 0.08 μm, η₀ = 0.023 Pa s; Simulation 2: σ = 1.2 μm and η₀ = 0.023 Pa s; Simulation 3: σ = 1.2 μm and η₀ = 0.095 Pa s

Table 3 Parameters of gears used in experiments [37]

3.2 Effect of surface roughness, input torque, rotating speed and lubricant viscosity on contact stiffness

In this section, effects of surface roughness, input torque, rotating speed and lubricant viscosity on the contact stiffness of gear tooth mesh are studied. The parameters of standard involute spur gear and the roughness parameters listed in Tables 1 and 2 are used for calculations. Figure 9 shows the variation of transmitted load of the gear tooth pair along LOA. The load carried by each tooth varies along this line due to the periodic change of teeth number in contact. In the single-tooth-pair mesh region BC, the transmitted load equals the total load and decreases at the double-tooth-pair mesh regions AB and CD. The load decreases to about one-third of the total load at the approaching point A and recession point D.

Fig. 9

Variation of transmitted load along LOA

Figure 10 shows the variation of curvature radius along the LOA. The curvature radius of the driven gear increases, while that of the driving pinion decreases along the LOA. Figure 11 shows the cylindrical contact coefficient λ_c along the LOA for different input torques. The cylindrical contact coefficient λ_c increases firstly, then decreases and exhibits a peak value. The variation of contact coefficient λ_c along the LOA is in contrary to the difference of curvature radius between the gear and pinion. As the difference of the curvature radius decreases, the cylindrical contact coefficient λ_c increases. The peak value of λ_c occurs at the position where the difference of the curvature radius is minimum, indicating a maximum number of asperities in contact. The value of cylindrical contact coefficient λ_c increases with the input torque. It is also noted that the coefficient λ_c is smaller than unit, indicating that the total number of contacting asperities for rough curved surface is smaller than that of the rough plane surface.

Fig. 10

Variation of curvature radius along LOA

Fig. 11

Variation of cylindrical contact coefficient λ_c along the LOA for different input torques

Figure 12 shows the variation of predicted film thickness parameter along the LOA for different roughness values of σ = 1.2, 2.4, 3.2, 4.8 μm and different rotating speeds of n = 400r/min, 600 r/min, 800 r/min, 1000 r/min. The non-dimensional film thickness parameter defined as the film thickness divided by surface roughness, λ = h/σ_s, is utilized to represent the lubrication regime. Generally, mixed lubrication occurs with 1 < λ < 3 and λ > 3 for full elastohydrodynamic lubrication [1]. As shown in Fig. 12a, the film thickness parameter decreases as surface roughness increases at the same meshing position. For surfaces with larger roughness values, i.e., σ = 2.4, 3.2, 4.8 μm, the film thickness parameter is in the range of 1 < λ < 3. As for relatively smooth surface, i.e., σ = 1.2 μm, the film thickness parameter comes to λ > 3, indicating a full elastohydrodynamic lubrication. In this condition, the meshing gear tooth surfaces are fully separated by the lubricant film and the total normal load is completely carried by the fluid. The combined contact stiffness is composed of only the lubricant film stiffness. It can be also seen that the film thickness parameter exhibits a sudden decrease from double-to-single pair meshing and a sudden increase from single-to-double pair meshing, due to the change of transmitted load of the gear pair. The film thickness parameter is smaller in the region of single-tooth-pair contact due to the higher transmitted normal load and a decrease of film thickness. As shown in Fig. 12b, the film thickness parameter increases along with rotating speed as a result of the increased entrainment velocity and film thickness. It is noted that the operating condition is assumed to be isothermal. Actually, as the gear meshing operates, heat is generated and film temperature will rise, which will result in decrease in film thickness and film thickness parameter [38].

Fig. 12

The predicted film thickness parameter along the LOA for a different roughness values b different rotating speeds

Figure 13 shows the variation of lubricant bulk modulus along the LOA for different input torques. The bulk modulus in the single-tooth-pair meshing duration is larger than that of the double-tooth-pair meshing duration because of the increased mean pressure. As the input torque increases, the corresponding bulk modulus also increases.

Fig. 13

Variation of lubricant bulk modulus along the LOA for different input torques

Figure 14 shows the contact stiffness along the LOA for different roughness values. The contact stiffness of rough curved gear teeth surface, the lubrication film stiffness and the combined stiffness all exhibit sudden increase from double-to-single pair meshing and a sudden decrease from single-to-double pair meshing. The contact stiffness in single-tooth contact is higher than that in double-teeth contact due to the effect of a larger load. The lubricant film stiffness is larger than the solid part, and the ratio of lubricant to asperity stiffness is larger than unit, especially in the double-tooth-pair contact region, where the ratio is much higher than that in the single-tooth-pair contact region. The maximum stiffness ratio occurs at the position close to tip and root where the lubrication regime approaches to full elastohydrodynamic lubrication, as the film thickness parameter shown in Fig. 12. It can be also seen that both the solid stiffness and the lubricant film thickness decrease with surface roughness and also the combined contact stiffness. However, the ratio of lubricant to asperity stiffness increases with surface roughness, indicating a more pronounced change of lubricant film stiffness with roughness than that of the solid stiffness.

Fig. 14

Contact stiffness along the LOA for different roughness values a contact stiffness of dry rough curved gear teeth, b lubricant film stiffness, c combined contact stiffness, d ratio of lubricant to asperity stiffness

Figure 15 shows the stiffness along the LOA for different input torques. The contact stiffness of gear tooth, the lubrication film stiffness and the combined stiffness all increase with input torques, as a result of the increased deformation of asperities, while the decrease in film thickness. As the input torque increases, the ratio of lubricant to asperity stiffness decreases, indicating that the variation of solid asperity stiffness with torque is more significant than that of the liquid film stiffness. The similar increase in oil film stiffness with input torque is in consistence with that reported in [11, 14].

Fig. 15

Contact stiffness along the LOA for different input torques a contact stiffness of dry rough curved gear teeth, b lubricant film stiffness, c combined contact stiffness, d ratio of lubricant to asperity stiffness

Figure 16 shows the contact stiffness along the LOA for different rotating speeds. The contact stiffness of gear teeth, the lubrication film stiffness and the combined stiffness all decrease with increased rotating speeds. As the rotating speed increases, the entrainment velocity increases, leading to thicker film thickness and less asperity contact. The similar decrease in oil film stiffness with rotating speed is also reported in [11].

Fig. 16

Contact stiffness along the LOA for different rotating speeds a contact stiffness of dry rough curved gear teeth, b lubricant film stiffness, c combined contact stiffness, d ratio of lubricant to asperity stiffness

Figure 17 shows the stiffness along the LOA for different lubricant viscosities. The contact stiffness of gear tooth, the lubrication film stiffness and the combined stiffness all decrease with increased lubricant viscosities, due to the deterioration of lubricant flow and a larger film thickness.

Fig. 17

Contact stiffness along the LOA for different lubricant viscosities a contact stiffness of dry rough curved gear teeth, b lubricant film stiffness, c combined contact stiffness, d ratio of lubricant to asperity stiffness

3.3 Effect of surface roughness, input torque, rotating speed and lubricant viscosity on EHL mesh stiffness

The combined contact stiffness is further substituted into Eq. (1) to predict the mesh stiffness. Figure 18 shows the mesh stiffness of gear tooth in EHL regime for different roughness values, different input torques, different rotating speeds and different lubricant viscosities. The mesh stiffness at the double-teeth contact region is larger than that at the single-tooth contact. Comparing with the meshing stiffness predicted using the Hertzian contact model, the fluctuation of EHL mesh stiffness in single-to-double tooth contact becomes smaller, indicating a better transmission stationarity. The mesh stiffness of gear tooth in EHL regime decreases as the surface roughness or rotating speed or lubricant viscosity increases, due to the effect of decreased combined contact stiffness with increased surface roughness or rotating speed or lubricant viscosity, as that shown in Figs.14, 16 and 17. The increment of input torque substantially increases the EHL mesh stiffness.

Fig. 18

The mesh stiffness of gear tooth in EHL regime for a different roughness values, b different input torques, c different rotating speeds, d different lubricant viscosities

4 Conclusions

In this work, a revised contact stiffness model of a spur gear pair in mixed elastohydrodynamic line contact has been proposed based on load-sharing concept and further used to predict the mesh stiffness. The revised contact stiffness was determined from the stiffness of both the rough curved gear tooth surface and the lubricant film acting in parallel, which was used to replace the Hertzian contact stiffness of ideal smooth cylinders in traditional gear mesh stiffness expression. The cylindrical contact coefficient was incorporated into the GW statistical contact model to characterize the effect of tooth meshing curvature on the distribution function of micro-asperities at the meshing interface. The corresponding contact stiffness for curved rough gear tooth surface was derived. The lubrication film stiffness was evaluated for different mesh positions along the line of action. Effects of surface roughness, input torque, rotating speed and lubricant property on the combined contact stiffness and synthetic EHL mesh stiffness were analyzed. Results show that the lubricant film stiffness is much higher than the solid stiffness of rough gear tooth surface and dominates the total contact stiffness, especially at positions close to tip and root. The combined contact stiffness decreases with surface roughness and rotating speed, while increases with input torque and lubricant viscosity. The fluctuation of mesh stiffness in EHL regime in single-to-double teeth contact was smaller than that calculated using the Hertzian contact model. It is noted that the current study assumes the isothermal operating condition. Actually, as the gear meshing operates, heat is generated and film temperature will rise, which will result in reduction of lubricant viscosity and film thickness. Accordingly, the lubricant film stiffness will increase, as well as the combined contact stiffness. The mesh stiffness will consequently decrease. The predicted gear mesh stiffness in EHL regime can be further used to calculate the dynamic responses of the gear system. The asperity load ratio obtained in the developed model can be also combined with the wear model to predict the wear performance of gears in practical EHL operation condition.