Vibration and dynamic behavior of electrostatic size-dependent micro-plates

Abstract

The recent trend of using thin micro-plate structures in severe operational conditions caused the classical theory (CT) to be no longer suited in analyzing the dynamic characteristics of them. For this study, the modified version of the couple stress theory (MCST) is adopted. Then, using Hamilton’s principle and Kirchhoff plate theory, the dynamic form of the size-dependent equation of motion for micro-plates stimulated by electrostatic dynamic excitation is acquired. The mixed extended Kantorovich and differential transformation methods on partial differential equations are applied to obtain the mode shapes and natural frequencies. The mode shapes from the linear free vibration solution are used as the mode shapes of the assumed multi-mode displacement field. The displacement field is required to solve the dynamical equation of motion. The equations are subsequently solved by the fourth-order Runge–Kutta method. Some universal graphs are also presented using the MCST to predict the effects of the size effect, tensile and compressive residual stresses, and aspect ratio of micro-plate on the free vibration and dynamic behaviors of micro-plates around their static configuration. It is found that the non-dimensional natural frequency parameter varies linearly versus the other non-dimensional parameters of the micro-plate. Various interesting phenomena are observed from the current simulations of the dynamic response of micro-plates to both DC and AC excitation, as well as the boundary of the frequency behavior conversion. A comparison is drawn between the responses of the micro-plate based on the modified couple stress and CT taking the size dependency into account. To facilitate understanding of the physical phenomena observed in the results, a simple physical analog to the micro-plates is suggested. This physical analog, which describes the boundary of frequency behavior conversion, is the linear relationship between the non-dimensional parameters of the system. The study of this model can help to realize some of the complex responses of the micro-plates.

1 Introduction

In recent years, electrostatic micro-plates have largely attracted the attention of researchers, scientists, and engineers [1, 2]. It is well established that for providing an accurate and exact description of micro-material behaviors, they should be used with careful consideration of its pertinent microstructural features. Electrostatic actuators encompass a couple of conductive electrodes which one of them is movable and the other one is motionless. When any voltage is applied, the movable electrode is deflected toward a fixed one [3]. Compared to other microelectromechanical systems, micro-plates can play a more efficient role in such MEMS as micro-beams, micro-plates, and micro-resonators. Any exceed in electrostatic force can lead to occurring the pull-in instability and sudden adherence of the movable electrode to the motionless one [4, 5]. The literature suggests that the instability characteristics of microscales structures have been considered as the leading subject in some previous research attempts [6, 7].

Having reduced the dimensions to the submicron scale, the nanoscale phenomena appear, which should be considered in theoretical models [8]. One of the significant and essential phenomena in the nanoscale is the size dependency of microstructures [6]. Since the materials at the nanoscale are naturally discrete, the classical continuum theory is not regarded as a sufficiently beneficial one for considering the size-dependent behavior at nano-distances. In this respect, the classical continuum theory fails to present a precise and efficient solution [9]. The findings of experimental research works have shown considerable differences with those anticipated by the classical approach in the case of analyzing microstructure. For instance, concerning the crystalline materials, the results of experimental studies show that the behavior of these materials depends predominantly on the grain size.

The micro-plates and micro-beams have found to be extensively applied in nano-/micro-electrical mechanical systems (NEMS/MEMS). The size-dependent behavior of these microscale structures also has been indicated in many experiments [10]. This phenomenon was first realized in much plastic deformation in metals and polymers. As an instance, in a micro-torsion experiment of thin copper wires, Fleck et al. [11] found that the torsional hardness gets tripled when the diameter of the wire is reduced from 170 to 12 μm. In a similar work aimed at devising a bending test for thin nickel beams, Stolken and Evans [12] discovered that the reduction of beam’s thickness from 50 to 12.51 μm leads to a significant increase in plastic work hardening. This phenomenon has been recently discovered in the mechanical properties of polymers. Lam et al. [13] in the bending test of beams made of polymeric epoxy at microscale found that decreasing the beam’s thickness from 115 to 20 μm can increase the stiffness about 2.4 times. In the same token, McFarland et al. [14], in the bending test of polypropylene at microscale, reported that the obtained value for stiffness is four times larger than the value anticipated by the classical theory. As the findings of previous works suggest, size dependency is an intrinsic property of the microstructure to determine the mechanical properties of these materials accurately.

Furthermore, materials have a discrete nature which can be determined when they are focused on the atomic scale [15]. To deal with this issue, Francois and Eugene Cosserat [16] introduced a theory called the Cosserat continuum theory. They recognized three additional rotational degrees of freedom, which are independent of the displacement field. They also developed a mathematical model to analyze material with couple stresses [16]. With a 5-decade interval from the publishing of original work, the primary kinematic of Cosserat continuum theory was reworked by Gunther (1958) [17]. Introducing micro-inertia and referring it to the micro-polar theory, Gunther [18] carried out an extensive inquiry on the Cosserat theory. Such comprehensive studies on non-classical theory resulted in considering the size effect with the dimension of length in the formulation [19]. Mindlin [20] demonstrated that the stress concentration factor around the circular hole depends on the size of the hole. Couple stress theory, as a particular case of the micro-polar theory, was presented by Mindlin et al. [21]. Overgrowing progress in microstructure leads to introducing the nonlinear continuum theories because in a micro-/nanoscale, the classical elasticity loses its efficiency due to neglecting size effect, [22]. Couple stress [23,24,25], nonlocal elasticity [18], micro-polar elasticity [26], strain gradient elasticity [27,28,29,30], and surface elasticity [31] are excellent instances of the theories introduced and used to study microscale structure’s behaviors. The modified couple stress theory develops one material length scale parameter as an additional elastic constant to interpret the size dependency. In three separate studies, Papargyri-Beskou et al. [32, 33] and Lazopoulos [34] investigated the development of the micro-beam and micro-plate models based on the strain gradient elasticity theory. In this theory, three additional higher-order length scale parameters are introduced. Ke et al. [35] studied size dependency on the nonlinear free vibration of the single- and double-walled CNT using the theory of Eringen nonlocal elasticity. In another research work, Khosrozadeh et al. [36] taking a nonlinear interlayer van der Waals force into account investigated the free vibration of embedded double-walled CNT. In the same vein, the influence of the nonlocal component on the nonlinear vibration of multilayered graphene sheets was examined in [37]. Ramezani et al. [38] provided a short review of the micro-polar theory and explained the concept of energy pairs. In the subsequent work, they conducted an investigation on the micro-polar elastic beams and constitutive equations for micro-polar hyperelastic materials [39]. A new equilibrium relation to study the behavior of the couple stress theory was first introduced by Yang et al. [40]. They also proposed the MCST in which the two material length scale parameters were converted to only one. This simplification, as a useful advantage of MCST, makes it more preferable than the classical couple stress theory (CST), which has significant difficulty in terms of calculating its two length scale parameters. A large number of micro-beam and micro-plate models, including Timoshenko, Euler–Bernoulli, and Kirchhoff hypothesis, were introduced on the basis of MCST to identify the size effect in micro-/nanostructures. Some research studies were conducted based on the Kirchhoff micro-plate model in [41,42,43] on dynamic and static problems of micro-beam, using Timoshenko and Euler–Bernoulli models. Asghari et al. [44] studied static and vibration analyses of the size-dependent micro-beams constructed from functionally graded materials (FGM). In the same line of inquiry, based on the modified couple stress theory, Asghari [45] developed a geometric micro-plate model that possessed the features of the nonlinearity and size dependency. Ke et al. [46] employed the p-version of the Ritz method to study the effectiveness of the modified couple stress theory in the natural frequencies of micro-plates. They illustrated that the natural frequencies of the micro-plate increase largely when the value of micro-plate thickness reaches the value of the length scale parameter. Further, they [47] investigated the static bending, buckling, and free vibration of annular Mindlin micro-plates made of functionally graded materials based on the modified couple stress theory. The differential quadrature method (DQM) is used for solving governing equations, and it was indicated that if the ratio of the plate’s thickness to material length scale parameter becomes more significant than 10, the effect of the modified couple stress component could be avoided. Furthermore, in [48], based on the MCST, a non-classical rectangular Mindlin micro-plate is studied and static bending, buckling, and free vibration are analyzed. By the same hypothesis, another model in this regard was proposed in the framework of the MCST [49] and the influence of length scale parameter on static bending, buckling and free vibration performances of simply supported micro-plates is studied. Pursuing the same line of investigation, a size-dependent electromechanical model was developed by Tahani et al. [50] to analyze the free vibration and static pull-in instability of electrostatically pre-deformed micro-plates. The nonlinear dynamic behavior of micro-plates was studied by Farokhi and Ghayesh [51] using modified couple stress theory neglecting the effect of tensile and compressive residual stress and micro-plate aspect ratio. However, in their work geometrically imperfect micro-plates were considered which introduce initial curvature in the positive out-of-plane direction and the nonlinearity was considered in the theoretical model. Furthermore, numerical approaches including using approximate series expansions, and pseudo-arclength continuation technique, are applied to solve the governing equations.

Despite all these research attempts and proposed models, it seems that dynamic behavior in the framework of size-dependent micro-plates has been underestimated and received less attention. The present investigation adopted the modified couple stress theory to derive the governing equation of the micro-plates. Semi-analytic methods, such as EKM and DTM, are used to solve the governing equation. Results for free and forced vibration analysis of the micro-plate model are obtained using the appropriate methods to determine their size-dependent behavior. This study started with an elaboration on the basic concept of the modified couple stress theory. Next, the size-dependent Kirchhoff micro-plate model is discussed, and the governing equation will be presented. Then, semi-analytical methods such as DTM and EKM are presented and provided details of the solutions. In the fourth part, the vibration of micro-plates is obtained, and some tables and graphs are presented to verify the accuracy of this model. Finally, a parametric study with respect to the driving voltage amplitude indicating the significant effects of driving force on the dynamic behavior of the micro-plates is described.

2 Modified couple stress theory (MCST)

According to the MCST proposed by Yang et al. [40], both strain and curvature tensor are included in the strain energy density. As the assumptions of this theory suggest, the strain energy $\bar{U}$ in a deformed isotropic linear elastic material which has occupied region $\varOmega$ is given by:

$$ \bar{U} = \frac{1}{2}\int_{\varOmega } {\left( {\sigma_{ij} \varepsilon_{ij} + m_{ij} \chi_{ij} } \right)\;} {\text{d}}\varOmega $$

(1)

where $\sigma_{ij}$, $\varepsilon_{ij}$, $m_{ij}$, and $\chi_{ij}$ are the components of the Cauchy stress, strain tensor, deviatoric part of the couple stress tensor, and symmetric curvature tensors, respectively. These tensors can be inscribed as:

$$ \sigma_{ij} = \lambda \varepsilon_{ii} + 2\mu \varepsilon_{ij} , $$

(2)

$$ \varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right), $$

(3)

$$ m_{ij} = 2\mu l^{2} \;\chi_{ij} , $$

(4)

$$ \chi_{ij} = \frac{1}{2}\left( {\theta_{i,j} + \theta_{j,i} } \right) $$

(5)

where $u_{i}$ is the displacement vector, $\lambda$ and $\mu$ are Lame’s constants ($\mu = {\raise0.7ex\hbox{$E$} \!\mathord{\left/ {\vphantom {E {2\left( {1 + \upsilon } \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2\left( {1 + \upsilon } \right)}$}}$ is also known as shear modulus), l is a material length scale parameter, which can be estimated through special experimental tests [24, 25], and $\theta_{i}$ is the rotation vector described as:

$$ \theta_{i} = \frac{1}{2}e_{ijk} u_{k,j} $$

(6)

where $e_{ijk}$ is the permutation symbol. Apparently, in the modified couple stress theory, only one length scale parameter, i.e., l, included, in addition to two Lame’s constants in the constitutive equation [52].

3 The size-dependent micro-plate model

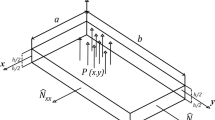
In Fig. 1, the schematic of a micro-plate with a length of a, a width of b in directions X and Y, respectively, and a thickness of h is presented which constructed from two conductive electrodes: one of them is movable, and the other one is fixed (ground). The initial distance between the non-actuated micro-plate and the fixed substrate is supposed to be g. Also, X, Y, and Z are the coordinates along the length, width, and thickness, respectively. Applying electrical force (voltage) between them leads to a movement of the movable electrode toward the fixed one. If the electrostatic force exceeds the elastic resistance of electrodes, it will lead to the pull-in instability and sudden adherence of the movable electrode to the fixed one [53, 54].

Fig. 1

The geometry of a rectangular micro-plate

In order to increase the efficiency of actuation and improve the sensitivity of detection, the distance between the capacitor plates is minimized and the area of the electrode is maximized. Under such conditions, the so-called squeeze-film damping is pronounced [55]. This phenomenon occurs as a result of the massive movement of the fluid underneath the micro-plate, which is resisted by the viscosity of the fluid. It should be noted that damping in microelectromechanical systems (MEMS) has a strong effect on their performance, design, and control. Damping influences the behavior of MEMS in various ways, depending on their design criteria and operating conditions [56]. Among all damping sources, viscous damping is the most significant source of energy loss in MEMS. In this study, in order to concentrate on other aspects of micro-plate design such as aspect ratio and residual stresses (because stress will inevitably be generated during the production process of micro-devices [57, 58]) and also study forced vibration and size dependency on the micro-plate performance, the damping effect is not considered.

According to the underlying hypothesis of the Kirchhoff thin micro-plate theory, the displacement field $\left( {U_{1} ,V_{1} ,W_{1} } \right)$ of an arbitrary point of the micro-plate can be illustrated as [59]:

$$ \begin{aligned} U_{1} \left( {X,Y,Z,t} \right) & = - Z\frac{\partial }{\partial X}W\left( {X,Y,t} \right) \\ V_{1} \left( {X,Y,Z,t} \right) & = - Z\frac{\partial }{\partial Y}W\left( {X,Y,t} \right) \\ W_{1} \left( {X,Y,Z,t} \right) & = W\left( {X,Y,t} \right) \\ \end{aligned} $$

(7)

where $\left( {U_{1} ,V_{1} ,W_{1} } \right)$ are the displacements along with the coordinate directions. From Eq. (7) it is clear that $\left( {U,V,W} \right)$ denote the displacements of a point which takes place on the mid-plane of the micro-plate along with the coordinate directions $\left( {X,Y,Z} \right)$. For micro-plates with negligible strains and displacement field, the nonzero strain components related to the displacement field reported in Eq. (7) can be written as [59]:

$$ \left\{ \begin{aligned} \varepsilon_{X} \hfill \\ \varepsilon_{Y} \hfill \\ \gamma_{XY} \hfill \\ \end{aligned} \right\} = - Z\left\{ \begin{aligned} \frac{{\partial^{2} W}}{{\partial X^{2} }} \hfill \\ \frac{{\partial^{2} W}}{{\partial Y^{2} }} \hfill \\ 2\frac{{\partial^{2} W}}{\partial X\partial Y} \hfill \\ \end{aligned} \right\} $$

(8)

In consideration of Eqs. (5, 6), the nonzero components of the rotation vector and the curvature tensor associated with the displacement field are obtained as follows:

$$ \theta_{X} = \frac{\partial W}{\partial Y},\;\;\theta_{Y} = - \;\frac{\partial W}{\partial X}, $$

(9)

$$ \left\{ \begin{aligned} \chi_{X} \hfill \\ \chi_{Y} \hfill \\ \chi_{XY} \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} \frac{{\partial^{2} W}}{\partial X\partial Y} \hfill \\ - \frac{{\partial^{2} W}}{\partial X\partial Y} \hfill \\ - \frac{1}{2}\left( {\frac{{\partial^{2} W}}{{\partial X^{2} }} - \frac{{\partial^{2} W}}{{\partial Y^{2} }}} \right) \hfill \\ \end{aligned} \right\} $$

(10)

The governing equation of motion and relating boundary conditions for the micro-plate is obtained using Hamilton’s principle. Hamilton’s principle can be declared as [60]:

$$ \int_{{t_{1} }}^{{t_{2} }} {\left( {\delta K - \delta \bar{U} + \delta W_{\text{ext}} } \right){\text{d}}t} = 0 $$

(11)

where $\delta K$, $\delta \bar{U}$, and $\delta W_{\text{ext}}$ represent virtual kinetic energy, virtual strain energy, and virtual work done by external forces, respectively. The virtual kinetic energy is:

$$ \begin{aligned} \delta K & = \int_{A} {\int_{ - h/2}^{h/2} {\rho \left( {\frac{\partial U}{\partial t}\delta \frac{\partial U}{\partial t} + \frac{\partial V}{\partial t}\delta \frac{\partial V}{\partial t} + \frac{\partial W}{\partial t}\delta \frac{\partial W}{\partial t}} \right){\text{d}}Z{\text{d}}A} } \\ & = \int_{A} {\left( {\rho h\frac{\partial W}{\partial t}\delta \frac{\partial W}{\partial t} + \rho \frac{{h^{3} }}{12}\left( {\frac{{\partial^{2} W}}{\partial X\partial t}\delta \frac{{\partial^{2} W}}{\partial X\partial t} + \frac{{\partial^{2} W}}{\partial Y\partial t}\delta \frac{{\partial^{2} W}}{\partial Y\partial t}} \right)} \right){\text{d}}A} \\ \end{aligned} $$

(12)

In Eq. (12) A is the mid-plane surface. In consideration of Eq. (1), the expression for virtual strain energy can be stated as:

$$ \begin{aligned} \delta \bar{U} & = \int_{A} {\int_{ - h/2}^{h/2} {\left( {\sigma_{ij} \delta \varepsilon_{ij} + m_{ij} \delta \chi_{ij} } \right)} } {\text{d}}Z{\text{d}}A \\ & = \int_{A} {\int_{ - h/2}^{h/2} {\left( {\sigma_{X} \delta \varepsilon_{X} + \sigma_{Y} \delta \varepsilon_{Y} + \sigma_{XY} \delta \gamma_{XY} + m_{X} \delta \chi_{X} + m_{Y} \delta \chi_{Y} + 2m_{XY} \delta \chi_{XY} } \right)} } {\text{d}}Z{\text{d}}A \\ & = \int_{A} {\left[ { - \varXi_{X} \delta \frac{{\partial^{2} W}}{{\partial X^{2} }} - 2\varXi_{XY} \delta \frac{{\partial^{2} w}}{\partial X\partial Y}} \right.} - \varXi_{Y} \delta \frac{{\partial^{2} W}}{{\partial Y^{2} }} + \varGamma_{X} \delta \frac{{\partial^{2} W}}{\partial X\partial Y} - \varGamma_{Y} \delta \frac{{\partial^{2} W}}{\partial X\partial Y} \\ & \quad \left. {\left. { + \varGamma_{XY} \left( {\delta \frac{{\partial^{2} W}}{{\partial Y^{2} }}} \right. - \delta \frac{{\partial^{2} W}}{{\partial X^{2} }}} \right)} \right]{\text{d}}A \\ \end{aligned} $$

(13)

in which the stress resultants $\varXi$ and $\varGamma$ are described as:

$$ \varXi_{i} = \int\limits_{ - h/2}^{h/2} {\sigma_{i} Z{\text{d}}Z} ,\;\left( {i = X,XY,Y} \right),\;\varGamma_{i} = \int\limits_{ - h/2}^{h/2} {m_{i} {\text{d}}Z} ,\;\left( {i = X,XY,Y} \right) $$

(14)

The virtual work done by distributed force and residual stress is obtained as:

$$ \begin{aligned} \delta W_{\text{ext}} & = \int\limits_{A} {f_{\text{external}} \delta W{\text{d}}A} \\ & = \int\limits_{X} {\int\limits_{Y} {\left\{ {\left( {\frac{{\varepsilon_{0} \varepsilon_{r} gV_{p} v_{e} \left( t \right) + \varepsilon_{0} \varepsilon_{r} V_{p}^{2} W}}{{g^{3} }}} \right)\delta W - \left( {\frac{{N_{X}^{r} \partial W}}{\partial X}\frac{\delta \,\partial W}{\partial X} + \frac{{N_{Y}^{r} \partial W}}{\partial Y}\frac{\delta \,\partial W}{\partial Y}} \right)} \right\}{\text{d}}X{\text{d}}Y} } \\ \end{aligned} $$

(15)

In Eq. (15), the external force per unit area of the micro-plates, $f_{\text{external}}$, is an electric load composed of a DC component ($V_{p}$) and an AC component $v_{e} \left( t \right)$. Also,$\varepsilon_{0}$ is the coefficient of the permittivity of the vacuum [3] and $\varepsilon_{r}$ is the coefficient of the relative permittivity of the fluid between two electrodes [23, 61]. Resultant axial residual forces per unit length $N_{x}^{r}$ and $\;N_{y}^{r} \;$ applied to the micro-plates [62] can be stated as:

$$ N_{X}^{r} = \sigma_{X}^{r} h,\;\;N_{Y}^{r} = \sigma_{Y}^{r} h $$

(16)

where $\sigma_{X}^{r}$ and $\sigma_{Y}^{r}$ show the axial residual stresses. Substituting Eqs. (12, 13, 15) into Eq. (11), integrating the outcomes by parts [60], as well as following some straightforward mathematical process, the equation of motion and boundary conditions are offered as follows [63]:

$$ \begin{aligned} & \frac{{\partial^{2} \varXi_{X} }}{{\partial X^{2} }} + 2\frac{{\partial^{2} \varXi_{XY} }}{\partial X\partial Y} + \frac{{\partial^{2} \varXi_{y} }}{{\partial y^{2} }} + N_{X}^{r} \frac{{\partial^{2} W}}{{\partial X^{2} }} + N_{y}^{r} \frac{{\partial^{2} W}}{{\partial Y^{2} }} + \frac{{\partial^{2} \varGamma_{XY} }}{{\partial X^{2} }} - \frac{{\partial^{2} \varGamma_{XY} }}{{\partial y^{2} }} \\ & \quad + \frac{{\partial^{2} \varGamma_{Y} }}{\partial X\partial Y} - \frac{{\partial^{2} \varGamma_{X} }}{\partial X\partial Y} = \,\,\rho h\frac{{\partial^{2} W}}{{\partial t^{2} }} - \frac{{\rho h^{3} }}{12}\left( {\frac{{\partial^{4} W}}{{\partial X^{2} \partial t^{2} }} + \frac{{\partial^{4} W}}{{\partial t^{2} \partial Y^{2} }}} \right), \\ \end{aligned} $$

(17)

$$ \begin{aligned} & \delta W:\frac{{\partial \varXi_{X} }}{\partial X}n_{X} + \frac{{\partial \varXi_{XY} }}{\partial Y}n_{X} + \frac{{\partial \varXi_{XY} }}{\partial X}n_{Y} + N_{X}^{r} \frac{\partial W}{\partial X}n_{X} + N_{Y}^{r} \frac{\partial W}{\partial Y}n_{Y} \\ & \quad + \frac{{\partial \varXi_{Y} }}{\partial Y}n_{Y} - \frac{1}{2}\frac{{\partial \varGamma_{X} }}{\partial Y}n_{X} - \frac{1}{2}\frac{{\partial \varGamma_{X} }}{\partial X}n_{Y} + \frac{{\partial \varGamma_{XY} }}{\partial X}n_{X} - \frac{{\partial \varGamma_{XY} }}{\partial Y}n_{Y} n_{Y} \\ & \quad + \frac{1}{2}\frac{{\partial \varGamma_{Y} }}{\partial Y}n_{X} + \frac{1}{2}\frac{{\partial \varGamma_{Y} }}{\partial X} + \frac{{\rho h^{3} }}{12}\frac{{\partial^{3} W}}{{\partial X\partial t^{2} }}n_{X} + \frac{{\rho h^{3} }}{12}\frac{\partial W}{{\partial Y\partial t^{2} }}n_{Y} = 0, \\ \end{aligned} $$

(18a)

$$ \delta \frac{\partial W}{\partial X}: - \varXi_{X} n_{X} - \varXi_{XY} n_{Y} + \frac{1}{2}\varGamma_{X} n_{Y} - \varGamma_{XY} n_{X} - \frac{1}{2}\varGamma_{Y} n_{Y} = 0, $$

(18b)

$$ \delta \frac{\partial W}{\partial Y}: - \varXi_{XY} n_{X} - \varXi_{Y} n_{Y} + \frac{1}{2}\varGamma_{X} n_{X} + \varGamma_{XY} n_{Y} - \frac{1}{2}\varGamma_{Y} n_{X} = 0 $$

(18c)

where $n_{i} \;\left( {i = X,Y} \right)$ are the components of a normal vector to the boundary of mid-plane. To write the equation of motion in terms of transverse displacement, i.e., W, stress and couple stress components can be described as:

$$ \left\{ \begin{aligned} \varXi_{x} \hfill \\ \varXi_{y} \hfill \\ \varXi_{xy} \hfill \\ \end{aligned} \right\} = \frac{{Eh^{3} }}{{12\left( {1 - \upsilon^{2} } \right)}}\left[ {\begin{array}{*{20}l} \begin{aligned} 1 \hfill \\ \upsilon \hfill \\ 0 \hfill \\ \end{aligned} & \begin{aligned} \;\;\;\upsilon \hfill \\ \;\;\;1 \hfill \\ \;\;\;0 \hfill \\ \end{aligned} & \begin{aligned} \;\;\;\;\;0 \hfill \\ \;\;\;\;\;0 \hfill \\ \left( {1 - \upsilon } \right)/2 \hfill \\ \end{aligned} \\ \end{array} } \right]\left\{ \begin{aligned} - \;\frac{{\partial^{2} W}}{{\partial X^{2} }} \\ - \;\frac{{\partial^{2} W}}{{\partial Y^{2} }} \\ - 2\;\frac{{\partial^{2} W}}{\partial X\partial Y} \\ \end{aligned} \right\}, $$

(19a)

$$ \left\{ \begin{aligned} \varGamma_{X} \hfill \\ \varGamma_{Y} \hfill \\ \varGamma_{XY} \hfill \\ \end{aligned} \right\} = \frac{{Ehl^{2} }}{1 + \upsilon }\left[ {\begin{array}{*{20}l} \begin{aligned} 1 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{aligned} & \begin{aligned} \;\;0 \hfill \\ \;\; - 1 \hfill \\ \;\;0 \hfill \\ \end{aligned} & \begin{aligned} \;\;\;0 \hfill \\ \;\;\;0 \hfill \\ - 1/2 \hfill \\ \end{aligned} \\ \end{array} } \right]\left\{ \begin{aligned} \frac{{\partial^{2} W}}{\partial X\partial Y} \\ \frac{{\partial^{2} W}}{\partial X\partial Y} \\ \frac{{\partial^{2} W}}{{\partial X^{2} }} - \frac{{\partial^{2} W}}{{\partial Y^{2} }} \\ \end{aligned} \right\} $$

(19b)

where $\upsilon$ is Poisson’s ratio and E is the elasticity modulus. By substituting Eqs. (19a, 19b) in Eq. (17) the governing equation of motion can be illustrated as:

$$ \begin{aligned} & \mu hl^{2} \nabla^{4} W + \frac{{Eh^{3} \nabla^{4} W}}{{12\left( {1 - \upsilon^{2} } \right)}} + \frac{{\rho h\partial^{2} W}}{{\partial t^{2} }} - \frac{{\rho h^{3} }}{12}\nabla^{2} \frac{{\partial^{2} W}}{{\partial t^{2} }} - \frac{{N_{X}^{r} \partial^{2} W}}{{\partial X^{2} }} - \frac{{N_{Y}^{r} \partial^{2} W}}{{\partial Y^{2} }} = \frac{{\varepsilon_{0} \varepsilon_{r} V_{p} v_{e} }}{{g^{2} }} \\ & \quad + \frac{{\varepsilon_{0} \varepsilon_{r} V_{p}^{2} W}}{{g^{3} }} \\ \end{aligned} $$

(20)

Equation (20) is the non-homogeneous form of the micro-plates. The operators $\nabla^{2}$ and $\nabla^{4}$ in 2D space can be presented as:

$$ \nabla^{2} = \left( {\frac{{\partial^{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} }}{{\partial Y^{2} }}} \right),\,\,\,\,\,\,\nabla^{4} = \nabla^{2} \nabla^{2} = \left( {\frac{{\partial^{4} }}{{\partial X^{4} }} + 2\frac{{\partial^{4} }}{{\partial X^{2} \partial y^{2} }} + \frac{{\partial^{4} }}{{\partial Y^{4} }}} \right) $$

(21)

In Eq. (20), $\rho$ is the density of micro-plates, h its thickness, t is the time,$V_{p}$ is a constant voltage applied, and $v_{e}$ is an alternating voltage. By ignoring the inhomogeneous terms in Eq. (20) which are relevant to the excitation, it is possible to get the eigenvalue problem. Because of the thinness of N/MEMS micro-plates, the rotary inertia term $\rho {\raise0.7ex\hbox{${h^{3} }$} \!\mathord{\left/ {\vphantom {{h^{3} } {12}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${12}$}}\nabla^{2} \frac{{\partial^{2} W}}{{\partial t^{2} }}$ is insignificant in comparison with the translatory inertia term $\rho h\frac{{\partial^{2} W}}{{\partial t^{2} }}$ and can be avoided [59, 64].

The following dimensionless parameters are presented for solving the equation:

$$ \begin{aligned} x & = \frac{X}{a}\,\,,\,\,y = \frac{Y}{b}\,\,\,\,,w = \frac{W}{g},\alpha = \frac{a}{b},\;\;\xi = 6\left( {1 - \upsilon } \right)\left( {\frac{l}{h}} \right)^{2} ,\;\tau = \frac{{12\left( {1 - \upsilon^{2} } \right)\varepsilon_{0} \varepsilon_{r} V_{p} v_{e} a^{4} }}{{Eh^{3} g^{3} }}, \\ N_{i = x,y} & = \frac{{12a^{2} \left( {1 - \upsilon^{2} } \right)N_{i}^{r} }}{{Eh^{3} }}\,\,\,\,,\hat{t} = \frac{t}{{a^{2} }}\sqrt {\frac{{Eh^{3} }}{{12\left( {1 - \upsilon^{2} } \right)\rho h}}} \,\,,\;\beta = \frac{{12\left( {1 - \upsilon^{2} } \right)\varepsilon_{0} \varepsilon_{r} V_{p}^{2} a^{4} }}{{Eh^{3} g^{3} }} \\ \end{aligned} $$

(22)

Upon substitution of the dimensionless parameters given in Eq. (22) into Eq. (20) and, moreover, multiplying both sides of Eq. (20) by $\frac{{a^{4} }}{g}\frac{{12\left( {1 - \upsilon^{2} } \right)}}{{Eh^{3} }}$, the following equation will be gained:

$$ \begin{aligned} & \frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} w}}{{\partial y^{4} }} + \xi \left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) - N_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad - N_{y} \alpha^{2} \frac{{\partial^{2} w}}{{\partial y^{2} }}\,\, + \frac{{\partial^{2} w}}{{\partial \hat{t}^{2} }} - \beta w - \tau = 0 \\ \end{aligned} $$

(23)

The dimensionless type of boundary conditions illustrated in Eqs. (18a–18c) for fully clamped micro-plate can also be submitted as:

$$ \left. {w\left( {x,y,t} \right)} \right|_{\;y = \;0\;,\;1} = \left. {\frac{\partial }{\partial y}w\left( {x,y,t} \right)} \right|_{\;y\; = \;0\;,\;1} = \left. {w\left( {x,y,t} \right)} \right|_{\;x = \;0\;,\;1} = \left. {\frac{\partial }{\partial x}w\left( {x,y,t} \right)} \right|_{\;x\; = \;0\;,\;1} = 0 $$

(24)

4 Solution procedure

In this section, a model for the free vibration behavior of micro-plates is developed and the associated eigenvalue problem by using mixed EKM and DTM is found. For this purpose, to find some natural frequencies and mode shapes, Eq. (23) is used by neglecting non-homogeneous term, i.e., $\left( \tau \right)$. To obtain natural frequencies and mode shapes, it is assumed that:

$$ w(x,y) = \varPhi_{mn} (x,y)\exp (i\omega t) $$

(25)

Finally, the results are presented as Eq. (26), where $\omega_{mn}$ represent the natural frequencies of the micro-plates.

$$ \begin{aligned} & \frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial y^{4} }} + \xi \left( {\frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial y^{4} }}} \right) \\ & \quad - N_{x} \frac{{\partial^{2} \varPhi_{mn} }}{{\partial x^{2} }} - N_{y} \alpha^{2} \frac{{\partial^{2} \varPhi_{mn} }}{{\partial y^{2} }} - \left( {\beta + \omega_{mn}^{2} } \right)\varPhi_{mn} = 0 \\ \end{aligned} $$

(26)

4.1 Extended Kantorovich method (EKM)

Taking the general procedure of the EKM [65] into account and using the Galerkin first-order approximation, the mode shape of micro-plates should be considered as a multiplication of single-term separable functions as presented below:

$$ \varPhi_{mn} \left( {x,y} \right) = f\left( x \right)q\left( y \right) $$

(27)

where $f\left( x \right)$ and $q\left( y \right)$ are unknown functions with respect to x and y to be ascertained. The dimensionless boundary conditions given in Eq. (24) can be expressed by consideration of separable functions as follows:

$$ f\left( 0 \right) = f\left( 1 \right) = \left. {\frac{{{\text{d}}f}}{{{\text{d}}x}}} \right|_{x = 0} = \left. {\frac{{{\text{d}}f}}{{{\text{d}}x}}} \right|_{x = 1} = 0\, $$

(28a)

$$ q\left( 0 \right) = q\left( 1 \right) = \left. {\frac{{{\text{d}}q}}{{{\text{d}}y}}} \right|_{y = 0} = \left. {\frac{{{\text{d}}q}}{{{\text{d}}y}}} \right|_{y = 1} = 0 $$

(28b)

In agreement with the general manner of the Galerkin method [60], the variational form of Eq. (26) can be expressed as:

$$ \begin{aligned} & \int_{0}^{1} {\int_{0}^{1} {\left\{ {\xi \left( {\frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial y^{4} }}} \right) + \frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{2} \partial y^{2} }}} \right.} } \\ & \quad \left. { + \alpha^{4} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial y^{4} }} - N_{x} \frac{{\partial^{2} \varPhi_{mn} }}{{\partial x^{2} }} - N_{y} \alpha^{2} \frac{{\partial^{2} \varPhi_{mn} }}{{\partial y^{2} }} - \left( {\beta + \omega_{mn}^{2} } \right)\varPhi_{mn} } \right\}\delta \varPhi_{mn} {\text{d}}x{\text{d}}y = 0 \\ \end{aligned} $$

(29)

Now, according to the variational calculus, in the first place, it is assumed that function $q\left( y \right)$ is an assigned known function ($\delta w = \delta f(x)q(y)$); therefore, substituting Eq. (27) into Eq. (26) it can be represented as:

$$ \begin{aligned} & \int_{0}^{1} {\left\{ {\int_{0}^{1} {\left\{ {\xi \left( {q\frac{{{\text{d}}^{4} f}}{{{\text{d}}x^{4} }} + 2\alpha^{2} \frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }}\frac{{{\text{d}}^{2} q}}{{{\text{d}}y^{2} }} + \alpha^{4} f\frac{{{\text{d}}^{4} q}}{{{\text{d}}y^{4} }}} \right) + q\frac{{{\text{d}}^{4} f}}{{{\text{d}}x^{4} }} + 2\alpha^{2} \frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }}\frac{{{\text{d}}^{2} q}}{{{\text{d}}y^{2} }}} \right.} } \right.} + \alpha^{4} f\frac{{{\text{d}}^{4} q}}{{{\text{d}}y^{4} }} \\ & \quad \left. {\left. { - N_{x} q\frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }} - N_{y} \alpha^{2} f\frac{{{\text{d}}^{2} q}}{{{\text{d}}y^{2} }} - \left( {\beta + \omega_{mn}^{2} } \right)fq} \right\}q{\text{d}}y} \right\}\delta f{\text{d}}x = 0 \\ \end{aligned} $$

(30)

Taking the fact that $\delta f$ has an arbitrary value through arranging the terms in Eq. (30), the following result is obtained:

$$ \begin{aligned} & \left( {2\alpha^{2} \int\limits_{0}^{1} {q\frac{{{\text{d}}^{2} q}}{{{\text{d}}y^{2} }}{\text{d}}q + 2\xi \alpha^{2} \int\limits_{0}^{1} {q\frac{{{\text{d}}^{2} q}}{{{\text{d}}y^{2} }}} {\text{d}}q - N_{x} \int\limits_{0}^{1} {q^{2} } {\text{d}}q} } \right)\frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }} + \left( {\int\limits_{0}^{1} {q^{2} {\text{d}}q + \xi \int\limits_{0}^{1} {q^{2} {\text{d}}q} } } \right)\frac{{{\text{d}}^{4} f}}{{{\text{d}}x^{4} }} \\ & \quad + \left( {\alpha^{4} \int\limits_{0}^{1} {q\frac{{{\text{d}}^{4} q}}{{{\text{d}}y^{4} }}} {\text{d}}q + \xi \alpha^{4} \int\limits_{0}^{1} {q\frac{{{\text{d}}^{4} q}}{{{\text{d}}y^{4} }}} {\text{d}}q - N_{y} \alpha^{2} \int\limits_{0}^{1} {q\frac{{{\text{d}}^{2} q}}{{{\text{d}}y^{2} }}} {\text{d}}q - \left( {\beta + \omega_{mn}^{2} } \right)\int\limits_{0}^{1} {q^{2} } {\text{d}}q} \right)f = 0 \\ \end{aligned} $$

(31)

Many integrals appearing in Eq. (31) can be written in a weakened form. Adopting this form of integrals not only can help to satisfy some of their boundary conditions, but it can reduce the number of integrations that are required to be calculated. Next, using the integration by parts, one can write:

$$ \frac{{{\text{d}}^{4} f}}{{{\text{d}}x^{4} }} + A\frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }} + \left( {B - \eta \omega_{mn}^{2} } \right)\;f = 0 $$

(32)

where

$$ \begin{aligned} \eta & = \frac{1}{1 + \xi },\quad A = \frac{{2\alpha^{2} \left( {1 + \xi } \right)\int_{0}^{1} {q\frac{{{\text{d}}^{2} q}}{{{\text{d}}y^{2} }}dq - N_{x} \int_{0}^{1} {q^{2} } {\text{d}}q} }}{{\left( {1 + \xi } \right)\int_{0}^{1} {q^{2} {\text{d}}q} }}, \\ B & = \frac{{\left( {1 + \xi } \right)\alpha^{4} \int_{0}^{1} {q\frac{{{\text{d}}^{4} q}}{{{\text{d}}y^{4} }}} {\text{d}}q - N_{y} \alpha^{2} \int_{0}^{1} {q\frac{{{\text{d}}^{2} q}}{{{\text{d}}y^{2} }}} {\text{d}}q - \beta \int_{0}^{1} {q^{2} } {\text{d}}q}}{{\left( {1 + \xi } \right)\int_{0}^{1} {q^{2} {\text{d}}q} }} \\ \end{aligned} $$

(33)

Equation (32) is a differential equation with constant coefficients, which can be solved efficiently via DTM.

4.2 Differential transformation method (DTM)

Zhou [66] proposed the differential transformation method for solving complicated differential equations. Although this method has been extracted from the Taylor series expansion, it is not addressed and considered the symbolic derivations. The DTM solution has been discussed in [67, 68] in detail, for various kinds of linear and nonlinear differential equations. The differential transform of the kth derivative of arbitrary function f(x) is stated as to $F(k) = \frac{1}{k!}\left( {\frac{{{\text{d}}^{k} f(x)}}{{{\text{d}}x^{k} }}} \right)_{{x = x_{0} }}$ where f(x) is the primary function and F(k) is the transformed function. The differential inverse transform of F(k) is represented as $f(x) = \sum\nolimits_{k = 0}^{\infty } {F(k)(x - x_{0} )^{k} } .$ Assuming an initial guess function, i.e. $q\left( y \right) = y^{2} \left( {y - 1} \right)^{2}$, and applying DTM, the solution for Eq. (32) takes the form:

$$ \begin{aligned} & \left( {k + 4} \right)\left( {k + 3} \right)\left( {k + 2} \right)\left( {k + 1} \right)F\left( {k + 4} \right) + A\left( {\left( {k + 2} \right)\left( {k + 1} \right)F\left( {k + 2} \right)} \right) \\ & \quad + \left( {B - \eta \omega_{mn}^{2} } \right)F\left( k \right) = 0 \\ \end{aligned} $$

(34)

Moreover, the differential transformations of boundary conditions are as the following:

$$ F\left( 0 \right) = F\left( 1 \right) = 0, $$

(35a)

$$ \sum\limits_{k = 0}^{n} {F\left( k \right)} = \sum\limits_{k = 0}^{n} {kF\left( k \right)} = 0 $$

(35b)

By solving Eqs. (34) and (35a), the deflection of the micro-plate is obtained:

$$ \begin{aligned} & f(x) = \sum\limits_{k = 0}^{n} {F(k)x^{k} } = rx^{2} + sx^{3} + \left( {\frac{ - 1}{12}Ar} \right)x^{4} + \left( {\frac{ - 1}{12}As} \right)x^{5} \\ & \quad + \,\left( {\frac{{\eta {\mkern 1mu} \omega_{mn}^{2} r}}{360} + \frac{{A^{2} r}}{360} - \frac{Br}{360}} \right)x^{6} + \left( {\frac{{\eta {\mkern 1mu} \omega_{mn}^{2} s}}{840} + \frac{{A^{2} s}}{840} - \frac{Bs}{840}} \right)x^{7} + \cdots \\ \end{aligned} $$

(36)

where $F(2) = r\,\,,\,\,F(3) = s.$ By imposing boundary conditions (35b) into Eq. (36) two algebraic equations will be obtained. To find nontrivial solutions, the determinant of the matrix coefficients must be set to zero to determine the natural frequencies. When the natural frequency ($\omega_{mn}^{{}}$) is achieved, by putting it in two algebraic equations, eigenvectors can be specified. For this purpose, after finding the value of natural frequencies, by normalizing the mode shapes (i.e., setting $r = 1$ or $s = 1$), the value of $s$ or r is obtained. In the process of EKM, if assumed, that function $f(x)$ is known, in this case, the unknown function q can be determined by the following equation [69]:

$$ \frac{{{\text{d}}^{4} q}}{{{\text{d}}y^{4} }} + A^{\prime}\frac{{{\text{d}}^{2} q}}{{{\text{d}}y^{2} }} + \left( {B^{\prime} - \chi^{\prime}\omega_{mn}^{2} } \right)\;q = 0 $$

(37)

where

$$ \begin{aligned} \chi^{\prime} & = \frac{1}{{\alpha^{4} \left( {\xi + 1} \right)}},\,\,\,\,A^{\prime} = \frac{{\left( {1 + \xi } \right)2\alpha^{2} \int_{0}^{1} {f\frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }}{\text{d}}f - N_{y} \alpha^{2} \int_{0}^{1} {f^{2} } {\text{d}}f} }}{{\left( {1 + \xi } \right)\alpha^{4} \int_{0}^{1} {f^{2} } {\text{d}}f}}, \\ B^{\prime} & = \frac{{\left( {1 + \xi } \right)\int_{0}^{1} {f\frac{{{\text{d}}^{4} f}}{{{\text{d}}x^{4} }}{\text{d}}f - N_{x} \int_{0}^{1} f \frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }}{\text{d}}f - \beta \int_{0}^{1} {f^{2} } {\text{d}}f} }}{{\left( {1 + \xi } \right)\alpha^{4} \int_{0}^{1} {f^{2} } {\text{d}}f}} \\ \end{aligned} $$

(38)

By solving differential Eq. (37), via DTM, the function q(y) is calculated. Next, by continuing the iterative process, one can utilize the solution of Eq. (32) (i.e. Eq. (36)) as a prescribed function and find the unknown function $q\left( y \right)$ using Eq. (37). The process should be continued until the convergence happens.

5 Results and discussions

To determine the number of iterations that must be done, a convergence analysis is carried out in Table 1 for a thin micro-plate with non-dimensional properties $N_{x} = N_{y} = 10\,\,,\beta = 10,\,\,\alpha = 1,\,\xi = 7.06$. From this table, it is evident that the convergence is so rapid and that it happens after the third iteration.

Table 1 Convergence analyses for the first non-dimensional natural frequency of a micro-plate with non-dimensional properties: $N_{x} = N_{y} = 10\,\,,\beta = 10,\,\,\alpha = 1,\,\xi = 7.06$

5.1 Validation

In order to verify the solution, a comparison is drawn between the natural frequencies predicted via the present study and those of the previously conducted investigations. The results of this comparison are demonstrated in Table 2. Indeed, these results are related to the natural frequencies as anticipated by the finite element method (FEM) and the virtual work principle [50]. It is noteworthy that the results are achieved using a three-pace iteration. The geometry and the constitutive material of the micro-plates are presented in Table 2. The observations of this section show that the suggested results are mainly in accordance with the finding of other research studies and the current approach is reliable to anticipate the vibration of micro-plates. For the sake of comparison study presented in Table 2, the reported dimensionless frequencies have been pre-multiplied by the coefficient of $\left( {2\sqrt 3 } \right)$ to make the same non-dimensional parameters as those considered in reference Askari and Arenas [70]. There are powerful theoretical and empirical bases for anticipating a free vibration analysis of plates. Many experimental studies have demonstrated free vibration in the analysis of plate. We have clarified this in Table 3 by reference to empirical research (Hazell and Mitchell 1986 [71]). Although a substantial body of research works have focused on the size-dependent free vibration of micro-plates up to now, it seems that the dynamic behavior of the rectangular micro-plates, subjected to a harmonic electrostatic excitation force, has not been received any attention. Accordingly, in the present study, for the first time, the forced vibration of a rectangular clamped micro-plates is considered.

Table 2 (a) Comparison of the non-dimensional natural frequencies with non-dimensional properties: $\beta = N_{x} = N_{y} = 0$. (b) Material properties and geometric of the micro-plate made of 110-direction silicon:$a = 100\,\upmu{\text{m}},h = 1\,\upmu{\text{m}},E = 169\,{\text{GPa,}}\rho = 2332\,{\text{kg/m}}^{3} ,l = 0.592\,\upmu{\text{m}}$

Table 3 Experimental and theoretical non-dimensional frequency parameter for the plate with non-dimensional properties $\xi = \beta = N_{x} = N_{y} = 0,\alpha = 1$

5.2 Analysis of free vibration behavior of micro-plates

To evaluate the results, initially assumed that $N_{x} = N_{y} = \beta = \tau = 0$. In this case, the vibration of the clamped micro-plate is involved in finding the non-dimensional natural frequency. This problem is solved by taking the different aspects of micro-plate into account and the results related to natural frequencies are provided. The findings of Milnea and Jones’s [72] study are entirely in line with the results, which are presented in Fig. 2. Also, in Fig. 3, functions $f(x)\,\,,q(y)\,\,{\text{and}}\,\,w(x,y) = \left. {f(x) \times q(y)} \right|_{{\left( {x,y} \right) = \left( {0.5,0.5} \right)}}$ are drawn. The results reported in the free vibration section have been obtained for clamped micro-plates with the following coefficients $(m,n) = (1,1),\upsilon = 0.3$, wherever these coefficients have not been specified.

Fig. 2

Clamped micro-plate non-dimensional natural frequency for the different aspects $\left( \alpha \right)$ of micro-plate

Fig. 3

Clamped micro-plate mode shape (m,n) = (4,2), $h/l = 63.40,\,\upsilon = 0.33,\,N_{x} = N_{y} = \tau = 0,\,\beta = 20,\,\alpha = 1/3$

Figure 4 shows the normalized fundamental natural frequency of micro-plate for different aspect ratios $\left( \alpha \right)$ relative to the natural frequency without voltage($\beta = N_{x} = N_{y} = 0$) in terms of the parameter, $\beta$ which is an increasing function of voltage DC. The following results are obtained from this figure.

Fig. 4

The fundamental natural frequency relative to the natural frequency without voltage according to the parameter $\beta$ in different aspect ratios $N_{x} = N_{y} = 0$

• In a specific aspect ratio, by increasing the DC voltage, the normalized fundamental natural frequency of micro-plate decreases and around pull-in voltage tends to the zero.

• In a specified $\beta$, the normalized natural frequency of micro-plate with the more significant aspect ratio is higher than that of with smaller aspect ratio.

• With increasing aspect ratio $\left( \alpha \right)$, pull-in voltage increases.

Figures 5, 6, 7, and 8 show the influence of the axial force on the non-dimensional fundamental natural frequency of clamped micro-plate for quantities of $\beta$ between 10 and 400, in relation to different aspect ratios.

Fig. 5

Effect of applied in-plane loads on the clamped micro-plate non-dimensional fundamental natural frequency at different values of $\beta ,N_{y} = 30,\alpha = 1$

Fig. 6

Effect of applied in-plane loads on the clamped micro-plate non-dimensional fundamental natural frequency at different values of $\beta ,N_{y} = 30,\alpha = 1.2$

Fig. 7

Effect of applied in-plane loads on the clamped micro-plate non-dimensional fundamental natural frequency at different values of $\beta ,N_{y} = 0,\alpha = 1$

Fig. 8

Effect of applied in-plane loads on the clamped micro-plate non-dimensional fundamental natural frequency at different values of $\beta ,N_{y} = 0,\alpha = 1.2$

In these figures, it can be observed that by increasing the parameter $N_{x}$, the micro-plate fundamental natural frequency increased, while by reducing $N_{x}$, the fundamental natural frequency of micro-plate gradually decreased to near unsustainable that is close to zero. Further, as these figures illustrate, in a specific aspect ratio $\left( \alpha \right)$ and $N_{x}$, increasing the DC voltage reduced the natural frequency of micro-plate substantially. Furthermore, increasing compressive axial force leads to the pull-in instability occurs at lower voltages. To evaluate the influence of the parameter $\left( \alpha \right)$ on the fundamental natural frequency of micro-plates, Figs. 9, 10, 11, and 12 are illustrated. These figures also suggest that increasing the tensile axial force result in a substantial increase in the natural frequency, and increasing compressive axial force leads to decreasing the natural frequency. Also, as it is observed, in the special value of $N_{y} \,{\text{and}}\,\beta$, increasing the micro-plate aspect ratio can increase the fundamental natural frequency of micro-plate. Furthermore, the figures suggested that increasing the micro-plate aspect ratio in each voltage causes higher resistance for the micro-plate, allowing the micro-plate to tolerate higher values of applied compressive traction before the pull-in instability occurs, i.e., larger values of natural frequencies.

Fig. 9

Effect of applied in-plane loads on the clamped micro-plate non-dimensional fundamental natural frequency at different values of $\alpha ,N_{x} = 20,\beta = 20$

Fig. 10

Effect of applied in-plane loads on the clamped micro-plate non-dimensional fundamental natural frequency at different values of $\alpha ,N_{x} = 20,\beta = 500$

Fig. 11

Effect of applied in-plane loads on the clamped micro-plate non-dimensional fundamental natural frequency at different values of $\alpha ,N_{x} = 0,\beta = 500$

Fig. 12

Effect of applied in-plane loads on the clamped micro-plate non-dimensional fundamental natural frequency at different values of $\alpha ,N_{x} = 0,\beta = 20$

The most important aspect of the present research from a practical point of view is considering the size dependency on the behavior of the microsensor/actuator under electrostatic loading. A complete analysis of the parameters can lead to a better understanding of the system behavior, which is very significant in the design. Besides, in Figs. 5, 6, 7, 8, 9, 10, 11, and 12, another linear relationship between the non-dimensional parameters of the micro-plate is found, which describes the boundary of frequency behavior conversion. Based on this important finding, some accurate and straightforward formulas are introduced for the prediction of natural frequencies of the micro-plates as well as the boundary of frequency behavior conversion in terms of geometric, voltage, and applied in-plane loads of the system. For instance, in Fig. 12 (case: modified couple stress theory $\left( {\alpha = 1.4} \right)$) by fitting linearly between the results of this graph exists a simple relation for the calculation of natural frequency in terms of applied in-plane load ($N_{y}$) as follows $\omega = 0.1295N_{y} + 91.64$. Also, in this case, the percentage difference in the amplitude vibration response, between the MCST ($\alpha = 1.4$) and the corresponding classical theory, is obtained about 45%. Therefore, accounting for the effect of couple stress components leads to the increase in the bending rigidity of the micro-plate and all of its natural frequencies.

Figures 13 and 14 show the variance of the ratio of ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ for a micro-plate under the effect of tensile and compressive axial forces versus the h/l parameter with different aspect ratios $\alpha$, respectively. These figures show that decreasing ${\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h l}}\right.\kern-0pt} \!\lower0.7ex\hbox{$l$}}$ results in increasing the ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ of the micro-plate. On the other hand, increasing the plate’s thickness, the results of the modified couple stress theory tend to those of classical theory and ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ tend to 1 (horizontal line), and the effect of the size dependency can be negligible. It is not surprising to find that both results from classic and modified couple stress theory are approximately equal. As it is obvious from these figures, the ratio ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ is dependent on the plate’s aspect ratio $\alpha$. Also, ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ is influenced more by the compressive axial residual forces than the tensile one. It is worth mentioning that a similar finding was offered by Tsiatas and Askari et al. [41].

Fig. 13

Variations of ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ versus the change of $h/l$ for micro-plates under tensile axial residual stress

Fig. 14

Variations of ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ versus the variation of $h/l$ for micro-plates under compressive axial residual stress

Given the fact that the effects of the axial forces on transverse mode shapes of the micro-plates are negligible [50, 55, 76], Eq. (26) can be rewritten by ignoring the effect of axial forces as follows:

$$ \left( {\frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial y^{4} }}} \right) - \lambda_{mn}^{{}} \varPhi_{mn} = 0 $$

(39)

where $\lambda_{mn}^{{}}$ are the eigenvalues corresponding to the eigenfunction $\varPhi_{mn}$. By comparing Eq. (39) and Eq. (26), it is clear that $\lambda_{mn}^{{}}$ will be as follows $\lambda_{mn}^{{}} = \frac{{\left( {\beta + \omega_{mn}^{2} } \right)}}{{\left( {1 + \xi } \right)}}$. As can be seen from Eq. (39), the size effect and electrostatic force parameters do not appear. Therefore, it is clear that the eigenvalue ($\lambda_{mn}^{{}}$) and the eigenfunction corresponding to this relation ($\varPhi_{mn}$) are independent of these two parameters and depend only on the micro-plate aspect ratio ($\alpha$). Therefore, it can be quickly concluded that the linear mode shapes of the system are entirely independent of the size effects and electrical field. With a similar argument mentioned in the above, it is clear that the electrostatic field does not affect the linear mode shapes of the system even when the micro-plate is under axial residual stresses. It should be noted that the values of axial residual stresses are usually not too large, and the dimension parameters corresponding to them adopt the values of about $N_{x} ,N_{y} \approx \pm 0.4$ ([50, 72]). In this paper, to investigate the effect of size dependency, it is assumed that the presented micro-plate is considered under significant axial residual stresses with dimensionless values $N_{x} ,N_{y} \approx \pm 40$. It is worth noting that these values are, therefore, large. Also, Zhao et al. [77], in addition to Tahani et al. [50] by using the finite element method, emphasized the negligible effect of the electrostatic field on the linear mode shape of the electromechanical systems even in micro-plates in conditions close to the instability. Providing mathematical proof for the independence of the natural frequency ratios calculated from the modified couple stress theory to their classical values seems essential, so that it can be written based on the assumed mode method as follows:

$$ {\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}} = \sqrt {\frac{{\int\limits_{A} {\left[ {\left( {\frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial y^{4} }}} \right)\left( {1 + \xi } \right) - N_{x} \frac{{\partial^{2} \varPhi_{mn} }}{{\partial x^{2} }} - N_{y} \alpha^{2} \frac{{\partial^{2} \varPhi_{mn} }}{{\partial y^{2} }}} \right]\varPhi_{mn} {\text{d}}A - \beta } }}{{\int\limits_{A} {\left[ {\left( {\frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} \varPhi_{mn} }}{{\partial y^{4} }}} \right) - N_{x} \frac{{\partial^{2} \varPhi_{mn} }}{{\partial x^{2} }} - N_{y} \alpha^{2} \frac{{\partial^{2} \varPhi_{mn} }}{{\partial y^{2} }}} \right]\varPhi_{mn} {\text{d}}A - \beta } }}} $$

(40)

According to Eq. (40) due to the application of pre-compressive stress, the relative decrease in the denominator versus its numerator is more than its relative increase due to the application of pre-tensioning stress. Thus, the effect of compressive stresses is more than the effect of their tensile values. Another important point is that increasing the electrostatic parameter reduces all the natural frequencies of the system both in classical theory and in the modified couple stress theory. Based on Eq. (40), it is clear that in the absence of axial residual stresses and electrostatic excitation, ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ is stated as Eq. (41), which is not only independent of the micro-plate aspect ratio coefficient and mode number of vibrations but also it does not depend on the boundary conditions of the micro-plate. That is to say, for each rectangular micro-plate, the ratio of ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ for each value of size effect ratio (${\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h l}}\right.\kern-0pt} \!\lower0.7ex\hbox{$l$}}$) is only a function of its Poisson coefficient.

$$ {\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}} = \sqrt {1 + \xi } = \sqrt {1 + 6(1 - \upsilon )\left( {\frac{l}{h}} \right)^{2} } $$

(41)

It is also easily proven for micro-plates without electrically driven and axial stresses that the dominant parameter which affects the ${\raise0.7ex\hbox{${\omega_{MCST} }$} \!\mathord{\left/ {\vphantom {{\omega_{MCST} } {\omega_{CT} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{CT} }$}}$ is $\upsilon$. Therefore, it is sufficient if we only study the effect of $\upsilon$ on the vibration characteristics.

5.3 Analysis of dynamic behavior of micro-plates in response to the electrostatic excitation by using the modal method

MEMS exhibit nonlinearities even when deformations are small. This is due to the nonlinearity of the electrostatic forces and the size of MEMS. Understanding the dynamic behavior of MEMS is very important for developing new MEMS devices and controlling their performance. The physical complexity in MEMS simulation arises from the multiple physical domains: electrical and mechanical, which are coupled by electrostatic forces giving rise to displacements. Additional complexities arise due to the implicit interdependence of electrostatic forces and deformations and the nonlinear dynamic behavior of MEMS. Several interesting physical nonlinear phenomena have been observed. Such phenomena are expected to persist and possibly interact in complicated ways in more complex MEMS structures. Understanding these phenomena and their underlying physics is important for designing and inventing new MEMS devices.

This section studies the dynamic behavior of micro-plates under electrostatic excitation by using the modal and the Galerkin method. Among various modes that have been used, it is found that the first one is the predominant mode on the dynamic behavior of micro-plates [78]. To determine the discretized form, by applying the Galerkin method, the solution $w$ in terms of the linear mode shapes is postulated as [79]:

$$ w\left( {x,y,t} \right) = \sum\limits_{m = 1}^{M} {\phi_{m} } \left( {x,y} \right)s_{m} \left( t \right) $$

(42)

where $M$ is a finite integer and $\phi_{m}$ is the generalized coordinate [79]. In the first step, it is assumed that the three primary modes involve in the dynamic response of the micro-plates. Having to substitute Eq. (42) into Eq. (23), multiplying the result with $\varPhi_{i}$, and integrating the outcome from 0 to 1, we obtain the following discretized form of the equations which describe the vibration response of the micro-plate in the matrix form:

$$ \left[ {\varPhi_{1} \,\,\,\varPhi_{2} \,\,\varPhi_{3} \,\,} \right]\left\{ \begin{aligned} \ddot{s}_{1} (t) \hfill \\ \ddot{s}_{2} (t) \hfill \\ \ddot{s}_{3} (t) \hfill \\ \end{aligned} \right\} + \left[ {g\left( {\varPhi_{1} } \right)\,\,\,g\left( {\varPhi_{2} } \right)\,\,g\left( {\varPhi_{3} } \right)\,\,} \right]\left\{ \begin{aligned} s_{1} (t) \hfill \\ s_{2} (t) \hfill \\ s_{3} (t) \hfill \\ \end{aligned} \right\} - \tau = 0 $$

(43)

where

$$ \begin{aligned} g\left( {\varPhi_{i} } \right) & = - N_{x} \frac{{\partial^{2} \varPhi_{i} }}{{\partial x^{2} }} - N_{y} \alpha^{2} \frac{{\partial^{2} \varPhi_{i} }}{{\partial y^{2} }} - \beta \varPhi_{i} + \frac{{\partial^{4} \varPhi_{i} }}{{\partial x^{4} }} + 2\alpha^{2} \frac{{\partial^{4} \varPhi_{i} }}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} \varPhi_{i} }}{{\partial y^{4} }} \\ & \quad + \xi \left( {\frac{{\partial^{4} \varPhi_{i} }}{{\partial x^{4} }} + \alpha^{2} \frac{{\partial^{4} \varPhi_{i} }}{{\partial x^{2} \partial y^{2} }} + \alpha^{4} \frac{{\partial^{4} \varPhi_{i} }}{{\partial y^{4} }}} \right) \\ \end{aligned} $$

(44)

According to the Galerkin method, it is assumed that the integration of Eq. (44) with weights $\varPhi_{i} \,\,,i = 1,2,3$ on micro-plate is equal to zero:

$$ \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left( {\left[ {\varPhi_{1} \,\,\,\varPhi_{2} \,\,\varPhi_{3} \,\,} \right]\left\{ \begin{aligned} \ddot{s}_{1} (t) \hfill \\ \ddot{s}_{2} (t) \hfill \\ \ddot{s}_{3} (t) \hfill \\ \end{aligned} \right\} + \left[ {g\left( {\varPhi_{1} } \right)\,\,g\left( {\varPhi_{2} } \right)\,g\left( {\varPhi_{3} } \right)\,} \right]\left\{ \begin{aligned} s_{1} (t) \hfill \\ s_{2} (t) \hfill \\ s_{3} (t) \hfill \\ \end{aligned} \right\} - \tau } \right)} } \varPhi_{i} {\text{d}}x{\text{d}}y = 0,\,i = 1,2,3 $$

(45)

After some simplification, the above equations can be reduced as matrix equations:

$$ \left[ M \right]\left\{ {\ddot{s}_{1} (t)} \right\} + \left[ N \right]\left\{ {s_{1} (t)} \right\} = \left[ T \right], $$

(46a)

$$ \begin{aligned} \left[ M \right] & = \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left[ {\begin{array}{*{20}l} {\varPhi_{1}^{2} } \hfill & {\varPhi_{1} \varPhi_{2} } \hfill & {\varPhi_{1} \varPhi_{3} } \hfill \\ {\varPhi_{2} \varPhi_{1} } \hfill & {\varPhi_{2}^{2} } \hfill & {\varPhi_{2} \varPhi_{3} } \hfill \\ {\varPhi_{3} \varPhi_{1} } \hfill & {\varPhi_{3} \varPhi_{2} } \hfill & {\varPhi_{3}^{2} } \hfill \\ \end{array} } \right]{\text{d}}x{\text{d}}y} } ,\,\,\left[ T \right] = \tau \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left\{ \begin{aligned} \varPhi_{1} \hfill \\ \varPhi_{2} \hfill \\ \varPhi_{3} \hfill \\ \end{aligned} \right\}{\text{d}}x{\text{d}}y} } ,\,\,\,\left\{ {s(t)} \right\} = \left\{ \begin{aligned} s_{1} (t) \hfill \\ s_{2} (t) \hfill \\ s_{3} (t) \hfill \\ \end{aligned} \right\}, \\ \left[ N \right] & = \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left[ {\begin{array}{*{20}l} {\varPhi_{1} g(\varPhi_{1} )} \hfill & {\varPhi_{1} g(\varPhi_{2} )} \hfill & {\varPhi_{1} g(\varPhi_{3} )} \hfill \\ {\varPhi_{2} g(\varPhi_{1} )} \hfill & {\varPhi_{2} g(\varPhi_{2} )} \hfill & {\varPhi_{2} g(\varPhi_{3} )} \hfill \\ {\varPhi_{3} g(\varPhi_{1} )} \hfill & {\varPhi_{3} g(\varPhi_{2} )} \hfill & {\varPhi_{3} g(\varPhi_{3} )} \hfill \\ \end{array} } \right]{\text{d}}x{\text{d}}y} } \\ \\ \end{aligned} $$

(46b)

Equation (46a) is a coupled linear differential system with constant coefficients, which include three equations with three unknowns. For solving these equations, the state-space method is used. To express these equations regarding state-space variables, the state variables are considered as:

$$ r_{1} \left( t \right) = s_{1} (t)\,\,,r_{2} \left( t \right) = s_{2} (t)\,\,\,,r_{3} \left( t \right) = s_{3} (t)\,\,,r_{4} \left( t \right) = \dot{s}_{1} (t)\,\,,r_{5} \left( t \right) = \dot{s}_{2} (t)\,\,\,,r_{6} \left( t \right) = \dot{s}_{3} (t) $$

(47)

Using Eqs. (47) and (46a), it can be rewritten as follows:

$$ \left\{ \begin{aligned} \dot{r}_{4} \left( t \right) \hfill \\ \dot{r}_{5} \left( t \right) \hfill \\ \dot{r}_{6} \left( t \right) \hfill \\ \end{aligned} \right\} = \left[ M \right]^{ - 1} \left( {\left[ T \right] - \left[ N \right]\left\{ \begin{aligned} r_{1} \left( t \right) \hfill \\ r_{2} \left( t \right) \hfill \\ r_{3} \left( t \right) \hfill \\ \end{aligned} \right\}} \right) $$

(48)

Also, according to Eq. (47), it can be written as

$$ \dot{r}_{1} \left( t \right) = r_{4} \left( t \right)\,\,,\dot{r}_{2} \left( t \right) = r_{5} \left( t \right)\,\,\,,\dot{r}_{3} \left( t \right) = r_{6} \left( t \right)\,\, $$

(49)

Simplification of Eqs. (48, 49) leads to Eq. (50):

$$ \left\{ \begin{aligned} \dot{r}_{1} \left( t \right) \hfill \\ \dot{r}_{2} \left( t \right) \hfill \\ \dot{r}_{3} \left( t \right) \hfill \\ \dot{r}_{4} \left( t \right) \hfill \\ \dot{r}_{5} \left( t \right) \hfill \\ \dot{r}_{6} \left( t \right) \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}l} {\left[ {\begin{array}{*{20}l} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]} & {\left[ {\begin{array}{*{20}l} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]} \\ {\left[ {\begin{array}{*{20}l} {} & {} & {} \\ {} & { - M^{ - 1} \times N} & {} \\ {} & {} & {} \\ \end{array} } \right]} & {\left[ {\begin{array}{*{20}l} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]} \\ \end{array} } \right]\left\{ \begin{aligned} r_{1} \left( t \right) \hfill \\ r_{2} \left( t \right) \hfill \\ r_{3} \left( t \right) \hfill \\ r_{4} \left( t \right) \hfill \\ r_{5} \left( t \right) \hfill \\ r_{6} \left( t \right) \hfill \\ \end{aligned} \right\} + \left\{ \begin{aligned} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ M^{ - 1} \times T \hfill \\ \end{aligned} \right\} $$

(50)

Equation (50) is the final form of the governing dynamical equations in the state space. The initial conditions for solving these equations are considered as:

$$ \dot{s}_{1} \left( 0 \right) = \dot{s}_{2} \left( 0 \right) = \dot{s}_{3} \left( 0 \right) = s_{1} \left( 0 \right) = s_{2} \left( 0 \right) = s_{3} \left( 0 \right) = 0 $$

(51)

Equation (47) with initial conditions, i.e., Eq. (48), can be easily solved by the fourth-order Runge–Kutta method (RK4). To measure the accuracy of the forced response analysis proposed in this research, the following results are validated with the information contained in the previously published article. Table 4 shows a comparison between the transverse displacement obtained by the current method and those obtained by [7] using the finite element method. As it is evident, there is a good agreement.

Table 4 Comparison of the transverse displacements of the micro-plate under uniformly distributed load with properties $a = b = 1000\,\upmu{\text{m}},\,h = 50\,\upmu{\text{m}},E = 70\;{\text{Gpa}},\rho = 2600\,{\text{kg/m}}^{3} ,\upsilon = 0.25$

Based on the linear plate analysis, the first natural frequency of the current micro-plate is found to be $\omega_{11} = 2.71 \times 10^{6} \,{\text{rad/sec}}$, which is the same as reported in the mentioned work [7]. Other frequencies of the current micro-plate are as follows;$\omega_{12} = \omega_{21} = 5.42 \times 10^{6} \,{\text{rad/sec}},\omega_{22} = 7.85 \times 10^{6} \,{\text{rad/sec}}$. The mode shapes corresponding to the micro-plate are also presented in Fig. 15.

Fig. 15

Mode shapes of the micro-plate:$a = b = 1000\,\upmu{\text{m}},\,h = 50\,\upmu{\text{m}},E = 70\,{\text{GPa}},\rho = 2600\,{\text{kg/m}}^{3} ,\upsilon = 0.25$

To show the capability of the solution method used in this work, again mentioned micro-plate is considered, but this time, the micro-plate is excited under the harmonic point force at ($X = 60 \times 10^{ - 6} \,{\text{m}},Y = 90 \times 10^{ - 6} \,{\text{m}}$) with the amplitude of $2 \times 10^{3}$ and the frequency equal to $10^{6}$. Figure 16 shows the transverse displacement of the mentioned micro-plate with the same properties as Fig. 15 under harmonic point excitation.

Fig. 16

Transverse displacement of the micro-plate under harmonic point excitation

To evaluate the dynamical response of micro-plate under electrostatic excitation, a micro-plate with non-dimensional properties as follows is considered: $\upsilon = 0.6\,,N_{x} = N_{y} = 0\,,\,\beta = 150,\,\,\tau = 100,\alpha = 1,h = 45.825l$. Figure 17 shows values $s_{i} (t),i = 1,2,3$ versus the time response when the micro-plate is under the sinusoidal excitation, i.e., $V = \tau \sin \left( {\varOmega t} \right),\varOmega = 50$. According to the order of the numbers in the second and third diagrams, it can be easily found out that the only dominant mode in the micro-plate dynamic behavior is only the first mode. This result also is observed in works by [57, 80].

Fig. 17

Time response to the sinusoidal excitation in the first three mode shapes $s_{1} \left( t \right),s_{2} \left( t \right),s_{3} \left( t \right)$

Figure 18 shows a half-section view of the micro-plate at different times by considering three primary modes in the Galerkin method. As seen by increasing time, the deflection of the micro-plate increased.

Fig. 18

Half of the micro-plate views at different times by considering three primary modes $V = \tau \sin \left( {\varOmega t} \right),\varOmega = 50$

Figures 19 and 20 show time response and phase plane plot related to electrostatic excitation obtained by considering the first mode shape.

Fig. 19

Time response to excitation in the first natural frequency $s_{1} \left( t \right)$

Fig. 20

Phase plane plot to excitation in the first natural frequency $s_{1} \left( t \right)$

$$ \begin{aligned} V & = \tau \sin \left( {\varOmega t} \right),\varOmega = 8. 6 3 4 ,\beta = 1000 \\ V & = \tau \sin \left( {\varOmega t} \right),\varOmega = 8. 6 3 4,\,\beta = 1000. \\ \end{aligned} $$

To verify the accuracy of the results in the current research, we first compare the results with the findings of Leissa [75]. As already mentioned, after the separation of variables, Eq. (23) is converted to the Eigenvalues equation. The eigenvalues equation by assuming fully clamped boundary conditions is solved, and the linear natural frequencies are obtained. For this purpose, the five fundamental frequencies are presented in Table 5. As seen, both results were in good agreement with each other.

Table 5 Comparison of the first four natural frequencies with non-dimensional properties $\xi = \beta = N_{x} = N_{y} = 0$

In Fig. 21 eight mode shapes of the micro-plate are presented. In this figure, the first category involves mode shapes (1,1), (1,2), (2,1), and (2,2), and the second category contains (3,3), (3,4), (4,1) and (4,4) mode shapes. A comparison between the frequencies of these two categories is presented in Table 6. As seen in Table 6, by increasing the width of the micro-plate (decreasing $\alpha$), values of natural frequencies related to these mode shapes decrease.

Fig. 21

The eight mode shapes (1,1), (1,2), (2,1), (2,2); (3,3), (3,4), (4,1), and (4,4) of clamped micro-plate: $\beta = 10,\alpha = 1/100,h/l = 63.40,\upsilon = 0.33$

Table 6 Comparison of the eight natural frequencies with non-dimensional properties $N_{x} = N_{y} = 0,\,\beta = 10,h/l = 63.40,\upsilon = 0.33$

5.3.1 Effects of the driving frequency

In another case, the micro-plate is examined, that its dimensions are taken to be $\beta = \tau = 20,\upsilon = 0.6\,,N_{x} = N_{y} = 0\,,\alpha = 1,h = 64.807l$. Based on the linear vibration of micro-plate analysis, the first natural frequency of the micro-plate is found to be $\omega (1,1) = \omega = 35.7362$. Figure 22a shows the dynamic response of the micro-plate driven by the voltage of $V = \tau \sin \left( {\varOmega t} \right),\varOmega = 20$. It is shown that a stable response is obtained. Figure 22b shows the phase plane plot related to electrostatic excitation. As seen in Fig. 22b, the system is stable; thus, the phase plane plot has a limit cycle.

Fig. 22

a Dynamic response of the micro-plate under harmonic driving voltage. b Phase plane plot to excitation in the first natural frequency

Figure 23a shows the dynamic response of the micro-plate driven by voltage of $V = \tau \sin \left( {\varOmega t} \right),\varOmega = \omega$. It can be concluded that as the micro-plate is stimulated by a harmonic force with the external frequency equal to the first natural frequency, the micro-plates have a stable dynamic response. Figure 23b shows the phase plane plot related to electrostatic excitation.

Fig. 23

a Dynamic reactions of the micro-plate under harmonic driving voltage. b Phase plane plot to excitation in the first natural frequency

Figure 24a shows the dynamic response of the micro-plate driven by the voltage of $V = \tau \sin \left( {\frac{\omega }{4}t} \right).$ It is scrutinized that a resonance condition occurs when a micro-plate oscillates under driving frequency which is equal to a quarter of its fundamental natural frequency. This tendency is similar to that perceived by Shi et al. [81] in a 1-D analysis of a micro-tweezer. Since the differential equation of the micro-plate is linear, the vibration amplitude of the system with the passing of time increased, and the phenomenon of resonance occurs. Put another way, due to lacking nonlinear terms in the governing equation, amplitude vibration is grown up and in a short time will be diverged. Figure 24b shows the phase plane plot related to electrostatic excitation.

Fig. 24

a Dynamic reactions of the micro-plate under harmonic driving voltage. b Phase plane plot to excitation in the first natural frequency

Figures 25a and 26a show the dynamic response of the micro-plate driven by the voltages of $V = \tau \sin \left( {0.95\frac{\omega }{4}t} \right)$ and $V = \tau \sin \left( {1.05\frac{\omega }{4}t} \right)$, respectively. It can be claimed that when the driving frequency is approximately equal to a quarter of the natural frequency of the micro-plate, in this condition, the dynamic response has a significant amplitude. This behavior is again matched with the declarations of Shi et al. [81] for 1-D analysis of a micro-tweezer. Figures 25b and 26b show the phase plane plot related to the mentioned electrostatic excitation.

Fig. 25

a Dynamic response of the micro-plate under harmonic driving voltage. b Phase plane plot to excitation in the first natural frequency

Fig. 26

a Dynamic response of the micro-plate under harmonic driving voltage. b Phase plane plot to excitation in the first natural frequency

Figure 27a presents the dynamic response of the micro-plate driven by the voltage of $V = \tau \sin \left( {3\frac{\omega }{4}t} \right)$. It is noteworthy that a stable response is acquired as the driving frequency is adequately clear of a quarter of the fundamental frequency of the micro-plate. Figure 27b shows the phase plane plot related to electrostatic excitation.

Fig. 27

a Dynamic response of the micro-plate under harmonic driving voltage. b Phase plane plot to excitation in the first natural frequency

6 Conclusions

The present work is mainly intended to examine the size-dependent dynamic analysis of clamped micro-plates. The attendance of the length scale in the MCST enables it to consider the size effect in microstructures. The mathematical image of the problem is reported using Kirchhoff micro-plate theory. MCST is used to study the influence of the size effect on the vibration and dynamical performance of the clamped micro-plates. The derived eigenvalue problem is solved semi-analytically by adopting the EKM and DTM. Accounting for the influence of the modified couple stress component results in increasing pull-in voltage and the stiffness of the micro-plates. The significant findings of this research can be summarized as follow:

• By increasing compressive load, bearing structures against electrical voltage will be reduced and led to the occurrence of pull-in instability at lower voltages. On the contrary, applying the tensile load lead to a delayed pull-in instability. These trends are due to the plate softening and stiffening behavior, respectively.

• By increasing the DC voltage, the fundamental natural frequency of the micro-plates decreases until it reaches zero in the vicinity of pull-in instability.

• Increasing the micro-plate’s aspect ratio $\left( \alpha \right)$, pull-in voltage and also the natural frequency of the micro-plates are increased. Moreover, the structure will tolerate higher compressive loads before the occurrence of the pull-in instability.

• Applying compressive/tensile loads reduces/increases the fundamental natural frequency of micro-plate.

• Considering the effect of the length scale parameter, increasing the stiffness of the structure results in increasing natural frequencies.

• The dependency of ${\raise0.7ex\hbox{${\omega_{\text{MCST}} }$} \!\mathord{\left/ {\vphantom {{\omega_{\text{MCST}} } {\omega_{\text{CT}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{\text{CT}} }$}}$ on the plate’s aspect ratio $\left( \alpha \right)$ is more considerable for micro-plate under compressive loads than tensile ones.

• In contrast with enhanced continuum theories such as modified couple stress theory, the classical theory, which neglects the size effects, is incapable of demonstrating size dependency.

• It is found that length scale parameter and electrostatic attraction do not have a sizeable effect on micro-plate mode shapes.

• The electrostatic attraction cannot create any changes in the micro-plates mode shapes.