1 Introduction

In the last two decades, a new class of materials known as FG-SMA has the material properties combining the advantages of functional gradient material and shape memory alloy material, which not only has the phase transformation property of SMA, but also has the material property varying gradually as the position changing of functional gradient material [1,2,3,4]. Moreover, there is no stress concentration when two materials are combined, which makes FG-SMA with a promising application prospect. Therefore, the nonlinear mechanical behavior analysis of FG-SMA material is of great significance [5,6,7].

According to the constituents and structure of the material, FG-SMA can be divided into two categories. One is mixing SMA with other materials and the volume fraction of SMA changing gradually, thus producing the FG-SMA; the other is produced by processing the SMA with special technics to change the inner microstructure of SMA, so as to create the FG-SMA with gradually varying properties. At present, due to the high production cost and complex manufacturing process, FG-SMA is mainly used in aerospace engineering and medical areas [8]. As a kind of FG-SMA medical guide wire, the tip portion of the guide wire must be sufficiently flexible to pass through the meandering blood vessels, so that the medical instruments can be introduced into a desired site: soft vessels in the brain, heart, liver, etc. What is more, FG-SMA has great potential to be used in information technology, new sensor technology and the emerging field of smart materials [9]. Due to its particular shape memory effect, pseudo-elasticity and without stress concentration, FG-SMA has been widely used in aerospace engineering and medical and other areas. All these particular characteristics go together with the martensite transformation and property gradients of FG-SMA. FG-SMA possesses the ability to transform spontaneously between the austenitic and martensitic variants under a variety of temperature or stress. Therefore, it is very important to study the phase transformation principle and property gradients of FG-SMA under the thermal and the mechanical loads.

The rapid development of SMA has laid a firm foundation for the study of FG-SMA. Asadi et al. [10] analytically investigated the exact solution for nonlinear thermal stability of geometrically imperfect hybrid laminated composite Timoshenko beams embedded with SMA fibers. Eshghinejad [11] studied the bending deformation of SMA beam based on complex constitutive model and the assumption of same properties between tension and compression. Asadi et al. [12] analytically calculated the natural frequencies of thermally buckled SMA-reinforced composite beams. Bajoria et al. [13] used a finite element method to analyze the bending deformation behavior of concrete beam using SMA. Asadi et al. [14,15,16,17] also studied the nonlinear vibration and thermal buckling of laminated beams with symmetric and asymmetric layup and armed by SMA wires. Damanpak et al. [18] controlled the shape of composite beams subjected to in-plane and transverse loadings using activated SMA actuators. Asadi et al. [19, 20] studied the effect of the orientation of the SMA fibers on the thermal buckling response of hybrid laminated composite plates and cylindrical shells.

Many researchers have further studied on FG-SMA and established multiple mechanical models in order to show the theory of phase transformation and the continuous change in property with position of FG-SMA. Tanaka and Liang [21, 22] established a new constitutive model with phenomenological theory, which presented a strong applicability for engineering. Some numerical simulation and experimental analysis of bending deformation of SMA wires were exhibited by Flor et al. [23]. They had a consideration about tension–compression asymmetry and used a numerical scheme to calculate the bending response. Nam et al. [24] used an experimental method to analyze the superelastic effect of FG-SMA. It is found that the FG-SMA showed the clear superelastic recovery. Liu et al. [25] studied the theoretical solution of pseudo-elastic response of FG-SMA cylinder, which found that the gradient of maximum transformation strain had a significant influence on the stress and martensite volume fraction distributions along the radial direction. Soltanieh et al. [26] presented a new algorithm about the spatial and time variations in martensite volume fraction along the wires. In recent years, the Brinson model is used for investigation of SMA behavior, and the geometrically nonlinear third-order shear deformation theory is used for modeling of sandwich plates. Asadi et al. [27, 28] researched the thermal buckling of FG-SMA sandwich plates. Their model was developed for both loading and unloading phases. Viet et al. [29] established a new analytical model for FG-SMA beam which is subjected to a concentrated tip load. The results showed that it was close to each case by a finite element method to analyze the bending deformation behavior of cantilever beam. Xue et al. [30,31,32,33] presented a phenomenological constitutive model and a finite element model to predict the mechanical behavior of FG-SMA based on the theory of thermodynamics. Finally, their results showed a reasonable agreement with the experimental results. Liu et al. [34, 35] studied the thermo-mechanical behaviors of FG-SMA composites, and it is found that the temperature change had a greater effect on the later phase transformation and showed a smaller effect on the initial phase transformation. Most of the existing studies, based on the assumption of the tension–compression symmetry, explored the superelastic effect and shape memory effect of FG-SMA beam. However, they ignored the different properties between tension and compression of FG-SMA materials and the influence of power exponent on mechanical behavior of FG-SMA beam, under the thermal and the mechanical loads.

The approach, based on the large deformation theory of beams, aims at solving the influence of power exponent on mechanical behavior of FG-SMA materials and the different properties between tension and compression of SMA materials. The tension–compression asymmetry coefficient \(\alpha\) [36] is used to amend original mechanical model. The volume fraction of shape memory alloy can be described by a power function along the thickness direction of the FG-SMA beam. Taking a basis of stress–strain relationship and a concern for critical phase transformation, a new simple model of mechanics is established. Considering the basic principles of composite materials, the split-step method is adopted to analyze the effect of \(\alpha\) and the power exponent on the FG-SMA beam under the thermal and the mechanical loads.

2 Nonlinear bending deformation of FG-SMA beam

2.1 The mechanical model of FG-SMA beam

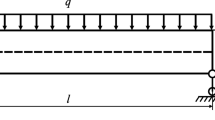
As can be seen in Fig. 1, the FG-SMA beam has a length \(l\) and a rectangular cross section of width \(b\) and height \(h\). In the process of bending deformation of FG-SMA beam, the distance of neutral axis to \(x\) axis is \(y_{n}\), under the bending moment \(M\). FG-SMA beam is composed of shape memory alloy and elastic material, and the volume fraction of shape memory alloy can be described by a power function \(f\left( y \right) = \left( {{y \mathord{\left/ {\vphantom {y h}} \right. \kern-0pt} h}} \right)^{n}\) along the thickness direction, where \(n\) is power exponent [30].

Fig. 1
figure 1

The mechanical model of FG-SMA beam

Full size image

2.2 The simplified constitutive model of stress–strain

In mixed phase, it is assumed that the Young’s moduli is constant, and the simplified constitutive model of stress–strain is obtained as shown in Fig. 2.

Fig. 2
figure 2

The simplified constitutive model of stress–strain

Full size image

In the above figure, \(\sigma_{ts} ,\sigma_{tf} ,\sigma_{cs}\) and \(\sigma_{cf}\) are the stresses at the beginning and end of phase transformation on the tension side and beginning and end of phase transformation on the compression side, respectively. \(\varepsilon_{ts} ,\varepsilon_{tf} ,\varepsilon_{cs}\) and \(\varepsilon_{cf}\) are the strains at the beginning and end of phase transformation on the tension side and beginning and end of phase transformation on the compression side, respectively. \(\varepsilon_{L}\) is the maximum residual strain.

According to the basic idea of continuum mechanics, FG-SMA beam meets the plane assumption in the process of bending deformation. The axial strain of FG-SMA beam can be expressed as Eq. (1)

$$\varepsilon = \frac{{y - y_{n} }}{\rho }.$$
(1)

The strain at the beginning of phase transformation on the tension side can be expressed as Eq. (2)

$$\varepsilon_{ts} = \frac{{\sigma_{ts} }}{{E_{A} }}.$$
(2)

The strain at the end of phase transformation on the tension side can be expressed as Eq. (3)

$$\varepsilon_{tf} = \varepsilon_{L} + \frac{{\sigma_{tf} }}{{E_{M} }}.$$
(3)

The stress of elastic material of FG-SMA beam can be expressed as Eq. (4)

$$\sigma_{A} = E_{0} \varepsilon .$$
(4)

The stress of SMA of the beam can be expressed as Eq. (5)

$$\sigma_{\text{SMA}} = E_{A} \varepsilon .$$
(5)

In the above equations, \(\rho\), \(E_{A}\), \(E_{M}\) and \(E_{0}\) are the radius of curvature, Young’s moduli in austenite, Young’s moduli in martensite and Young’s moduli in elastic material.

According to the principle of average stress in the mechanics of composite materials, the overall average stress can be expressed as Eq. (6)

$$\sigma \left( y \right) = \left[ {1 - f\left( y \right)} \right]\sigma_{A} + f\left( y \right)\sigma_{\text{SMA}} .$$
(6)

2.3 Tension–compression asymmetry coefficient

The stress and the strain of original mechanical model are amended by introducing \(\alpha\). Equation (7) defines the relationship between \(\alpha\) and the stress on tension side and compression side.

$$\alpha = \frac{{\sigma_{cs} - \sigma_{ts} }}{{\sigma_{cs} + \sigma_{ts} }} = \frac{{\sigma_{cf} - \sigma_{tf} }}{{\sigma_{cf} + \sigma_{tf} }}$$
(7)

2.4 Stress–strain relationship

With the increase in bending moment, FG-SMA beam undergoes a process from elastic deformation to phase transformation. The process of bending deformation of FG-SMA beam can be divided into two stages: initial stage and phase transformation stage.

2.4.1 Initial stage (\(\varepsilon_{t} \le \varepsilon_{ts}\))

In the initial stage, the maximum strain does not reach the strain at the beginning of phase transformation; the FG-SMA beam is total in austenite. The expression of stress distribution along the height of the cross section can be expressed as Eq. (8)

$$\sigma = \left[ {1 - f\left( y \right)} \right]\sigma_{A} + f\left( y \right)\sigma_{\text{SMA}} { 0} \le y \le h.$$
(8)

2.4.2 Phase transformation (\(\varepsilon_{t} \ge \varepsilon_{ts}\))

As can be seen in Fig. 3, when the maximum strain reaches the strain at the beginning of phase transformation, the phase transformation from austenite to martensite occurs and the neutral axis moves to the compression side. A, M and AM are the austenite, martensite and mixed phases, respectively. \(h_{i}\) is the distance of phase boundaries to \(x\) axis.

Fig. 3
figure 3

Beam cross section and microsegment bending deformation: a I stage of phase transformation, b II stage of phase transformation, c III stage of phase transformation and d IV stage of phase transformation

Full size image

It is shown in Fig. 3a, for \(\left| {\varepsilon_{c} } \right| \le \varepsilon_{cs}\) and \(\varepsilon_{ts} \le \varepsilon_{t} \le \varepsilon_{tf}\), it is the stage I of phase transformation. The phase transformation of the tension side surface material from austenite to martensite occurs. The phase boundary between mixed phase and austenite phase is BTA. The expression of stress distribution along the height of the cross section can be expressed as Eq. (9).

As can be seen in Fig. 3b, for \(\varepsilon_{cs} \le \left| {\varepsilon_{c} } \right| \le \varepsilon_{cf}\) and \(\varepsilon_{ts} \le \varepsilon_{t} \le \varepsilon_{tf}\), it is the stage II of phase transformation. The phase transformation of the compression side surface material occurs too. There is a new phase boundary (BCA) between mixed phase and austenite phase on the compression side. The expression of stress distribution along the height of the cross section can be expressed as Eq. (10).

In Fig. 3c, for \(\varepsilon_{cs} \le \left| {\varepsilon_{c} } \right| \le \varepsilon_{cf}\) and \(\varepsilon_{tf} \le \varepsilon_{t}\), it is the stage III of phase transformation. The surface material of tension side changes into martensite completely. There is a new phase boundary (BTM) between mixed phase and martensite phase on the tension side. The expression of stress distribution along the height of the cross section can be expressed as Eq. (11).

As shown in Fig. 3d, for \(\varepsilon_{cf} \le \left| {\varepsilon_{c} } \right|\) and \(\varepsilon_{tf} \le \varepsilon_{t}\), it is the stage IV of phase transformation. The surface material of compression side changes into martensite completely. There is a new phase boundary (BCM) between mixed phase and martensite phase on the compression side. The expression of stress distribution along the height of the cross section can be expressed as Eq. (12).

$$\sigma \left( y \right) = \left\{ {\begin{array}{*{20}l} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho },} \hfill & { 0\le y \le h_{1} } \hfill \\ {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } + f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right],} \hfill & {h_{1} \le y \le h} \hfill \\ \end{array} } \right.$$
(9)
$$\sigma \left( y \right) = \left\{ {\begin{array}{*{20}l} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } - f(y)\left[ {\sigma_{ts} \frac{1 + \alpha }{1 - \alpha } + E_{1} \left( {\frac{{y_{n} - y}}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}\frac{1 + \alpha }{1 - \alpha }} \right)} \right],} \hfill & {0 \le y \le h_{2} } \hfill \\ {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho },} \hfill & {h_{2} \le y \le h_{1} } \hfill \\ {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } + f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right],} \hfill & {h_{1} \le y \le h} \hfill \\ \end{array} } \right.$$
(10)
$$\sigma \left( y \right) = \left\{ {\begin{array}{*{20}l} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } - f(y)\left[ {\sigma_{ts} \frac{1 + \alpha }{1 - \alpha } + E_{1} \left( {\frac{{y_{n} - y}}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}\frac{1 + \alpha }{1 - \alpha }} \right)} \right],} \hfill & {0 \le y \le h_{2} } \hfill \\ {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho },} \hfill & {h_{2} \le y \le h_{1} } \hfill \\ {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } + f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right]} \hfill & {h_{1} \le y \le h_{3} } \hfill \\ {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } + f(y)\left[ {\sigma_{tf} + E_{M} \left( {\frac{{y - y_{n} }}{\rho } - \varepsilon_{L} - \frac{{\sigma_{tf} }}{{E_{M} }}} \right)} \right],} \hfill & {h_{3} \le y \le h} \hfill \\ \end{array} } \right.$$
(11)
$$\sigma \left( y \right) = \left\{ {\begin{array}{*{20}l} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } - f(y)\left\{ {\sigma_{tf} \frac{1 + \alpha }{1 - \alpha } + E_{M} \left[ {\frac{{y_{n} - y}}{\rho } - \left( {\varepsilon_{L} + \frac{{\sigma_{tf} }}{{E_{M} }}} \right)\frac{1 + \alpha }{1 - \alpha }} \right]} \right\},} \hfill & {0 \le y \le h_{4} } \hfill \\ {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } - f(y)\left[ {\sigma_{ts} \frac{1 + \alpha }{1 - \alpha } + E_{1} \left( {\frac{{y_{n} - y}}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}\frac{1 + \alpha }{1 - \alpha }} \right)} \right],} \hfill & {h_{4} \le y \le h_{2} } \hfill \\ {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho },} \hfill & {h_{2} \le y \le h_{1} } \hfill \\ {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } + f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right],} \hfill & {h_{1} \le y \le h_{3} } \hfill \\ {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho } + f(y)\left[ {\sigma_{tf} + E_{M} \left( {\frac{{y - y_{n} }}{\rho } - \varepsilon_{L} - \frac{{\sigma_{tf} }}{{E_{M} }}} \right)} \right], \, } \hfill & { \, h_{3} \le y \le h} \hfill \\ \end{array} } \right.$$
(12)

2.5 Balance equations

In the initial stage, the axial force balance equation and the bending moment balance equation can be found as Eqs. (13) and (14), respectively.

$$\int {\sigma \left( y \right){\text{d}}A} = \int_{0}^{h} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }b} {\text{d}}y = 0$$
(13)
$$\int {\sigma \left( y \right)y{\text{d}}A} = \int_{0}^{h} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }by} {\text{d}}y = M$$
(14)

In stage I of phase transformation, the axial force balance equation and the bending moment balance equation can be found as Eqs. (15) and (16), respectively.

In stage II of phase transformation, the axial force balance equation and the bending moment balance equation can be found as Eqs. (17) and (18), respectively.

In stage III of phase transformation, the axial force balance equation and the bending moment balance equation can be found as Eqs. (19) and (20), respectively.

In stage IV of phase transformation, the axial force balance equation and the bending moment balance equation can be found as Eqs. (21) and (22), respectively.

The neutral axis position, phase boundary position and curvature can be obtained by substituting the boundary conditions of different stages into the equilibrium equations.

$$\begin{aligned} \int {\sigma \left( y \right){\text{d}}A} &= \int_{0}^{{h_{1} }} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }} b{\text{d}}y \\ &\quad+ \int_{{h_{1} }}^{h} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b }\\&\quad {+ f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right]} b{\text{d}}y = 0 \end{aligned}$$
(15)
$$\begin{aligned} \int {\sigma \left( y \right)y{\text{d}}A} &= \int_{0}^{{h_{1} }} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }} by{\text{d}}y \\&\quad+ \int_{{h_{1} }}^{h} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by }\\&\quad{+ f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right]} by{\text{d}}y = M \end{aligned}$$
(16)
$$\begin{aligned} \int {\sigma \left( y \right){\text{d}}A} &= \int_{0}^{{h_{2} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b} \\&\quad{- f(y)\left[ {\sigma_{ts} \frac{1 + \alpha }{1 - \alpha } + E_{1} \left( {\frac{{y_{n} - y}}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}\frac{1 + \alpha }{1 - \alpha }} \right)} \right]} b{\text{d}}y \hfill \\& \quad + \int_{{h_{2} }}^{{h_{1} }} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }b{\text{d}}y} \\&\quad+ \int_{{h_{1} }}^{h} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b }\\&\quad{+ f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right]b{\text{d}}y} = 0 \hfill \\ \end{aligned}$$
(17)
$$\begin{aligned} \int {\sigma \left( y \right)y{\text{d}}A} &= \int_{0}^{{h_{2} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by }\\&\quad{- f(y)\left[ {\sigma_{ts} \frac{1 + \alpha }{1 - \alpha } + E_{1} \left( {\frac{{y_{n} - y}}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}\frac{1 + \alpha }{1 - \alpha }} \right)} \right]} by{\text{d}}y \hfill \\& \quad + \int_{{h_{2} }}^{{h_{1} }} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }by{\text{d}}y} \\ &\quad+ \int_{{h_{1} }}^{h} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by }\\&\quad{+ f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right]by{\text{d}}y} = M \hfill \\ \end{aligned}$$
(18)
$$\begin{aligned} \int {\sigma \left( y \right){\text{d}}A} = \int_{0}^{{h_{2} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b - f(y)\left[ {\sigma_{ts} \frac{1 + \alpha }{1 - \alpha } + E_{1} \left( {\frac{{y_{n} - y}}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}\frac{1 + \alpha }{1 - \alpha }} \right)} \right]} b{\text{d}}y \hfill \\ \quad + \int_{{h_{2} }}^{{h_{1} }} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }b{\text{d}}y} + \int_{{h_{1} }}^{{h_{3} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b + f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right]b{\text{d}}y} \hfill \\ \quad + \int_{{h_{3} }}^{h} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b + f(y)\left[ {\sigma_{tf} + E_{M} \left( {\frac{{y - y_{n} }}{\rho } - \varepsilon_{L} - \frac{{\sigma_{tf} }}{{E_{M} }}} \right)} \right]} b{\text{d}}y = 0 \hfill \\ \end{aligned}$$
(19)
$$\begin{aligned} \int {\sigma \left( y \right)y{\text{d}}A} = \int_{0}^{{h_{2} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by - f(y)\left[ {\sigma_{ts} \frac{1 + \alpha }{1 - \alpha } + E_{1} \left( {\frac{{y_{n} - y}}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}\frac{1 + \alpha }{1 - \alpha }} \right)} \right]} by{\text{d}}y \hfill \\ \quad + \int_{{h_{2} }}^{{h_{1} }} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }by{\text{d}}y} + \int_{{h_{1} }}^{{h_{3} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by + f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right]by{\text{d}}y} \hfill \\ \quad + \int_{{h_{3} }}^{h} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by + f(y)\left[ {\sigma_{tf} + E_{M} \left( {\frac{{y - y_{n} }}{\rho } - \varepsilon_{L} - \frac{{\sigma_{tf} }}{{E_{M} }}} \right)} \right]} by{\text{d}}y = M \hfill \\ \end{aligned}$$
(20)
$$\begin{aligned} \int {\sigma \left( y \right){\text{d}}A} = \int_{0}^{{h_{4} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b - f(y)\left\{ {\sigma_{tf} \frac{1 + \alpha }{1 - \alpha } + E_{M} \left[ {\frac{{y_{n} - y}}{\rho } - \left( {\varepsilon_{L} + \frac{{\sigma_{tf} }}{{E_{M} }}} \right)\frac{1 + \alpha }{1 - \alpha }} \right]} \right\}b} {\text{d}}y \hfill \\ \quad + \int_{{h_{4} }}^{{h_{2} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b - f(y)\left[ {\sigma_{ts} \frac{1 + \alpha }{1 - \alpha } + E_{1} \left( {\frac{{y_{n} - y}}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}\frac{1 + \alpha }{1 - \alpha }} \right)} \right]b} {\text{d}}y \hfill \\ \quad + \int_{{h_{2} }}^{{h_{1} }} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }b{\text{d}}y} + \int_{{h_{1} }}^{{h_{3} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b + f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right]b{\text{d}}y} \hfill \\ \quad + \int_{{h_{3} }}^{h} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }b + f(y)\left[ {\sigma_{tf} + E_{M} \left( {\frac{{y - y_{n} }}{\rho } - \varepsilon_{L} - \frac{{\sigma_{tf} }}{{E_{M} }}} \right)} \right]b} {\text{d}}y = 0 \hfill \\ \end{aligned}$$
(21)
$$\begin{aligned} \int {\sigma \left( y \right)y{\text{d}}A} \hfill \\ \quad = \int_{0}^{{h_{4} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by - f(y)\left\{ {\sigma_{tf} \frac{1 + \alpha }{1 - \alpha } + E_{M} \left[ {\frac{{y_{n} - y}}{\rho } - \left( {\varepsilon_{L} + \frac{{\sigma_{tf} }}{{E_{M} }}} \right)\frac{1 + \alpha }{1 - \alpha }} \right]} \right\}by} {\text{d}}y \hfill \\ \quad + \int_{{h_{4} }}^{{h_{2} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by - f(y)\left[ {\sigma_{ts} \frac{1 + \alpha }{1 - \alpha } + E_{1} \left( {\frac{{y_{n} - y}}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}\frac{1 + \alpha }{1 - \alpha }} \right)} \right]by} {\text{d}}y \hfill \\ \quad + \int_{{h_{2} }}^{{h_{1} }} {[E_{0} + f(y)(E_{A} - E_{0} )]\frac{{y - y_{n} }}{\rho }by{\text{d}}y} + \int_{{h_{1} }}^{{h_{3} }} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by + f(y)\left[ {\sigma_{ts} + E_{1} \left( {\frac{{y - y_{n} }}{\rho } - \frac{{\sigma_{ts} }}{{E_{A} }}} \right)} \right]by{\text{d}}y} \hfill \\ \quad + \int_{{h_{3} }}^{h} {[1 - f(y)]E_{0} \frac{{y - y_{n} }}{\rho }by + f(y)\left[ {\sigma_{tf} + E_{M} \left( {\frac{{y - y_{n} }}{\rho } - \varepsilon_{L} - \frac{{\sigma_{tf} }}{{E_{M} }}} \right)} \right]by} {\text{d}}y = M \hfill \\ \end{aligned}$$
(22)

2.6 Beam deflection

The nonlinear governing equations are derived by the expression of moment balance equations, which can be written as

$$\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = \left[ {1 + \left( {\frac{{{\text{d}}w}}{{{\text{d}}x}}} \right)^{2} } \right]^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \sqrt {\frac{{b\int_{{ - \varepsilon_{c} }}^{{\varepsilon_{t} }} {\sigma \varepsilon {\text{d}}\varepsilon } }}{M}} .$$
(23)

3 Model of critical stress

3.1 Theoretical analysis

The critical stresses that are used are dependent on temperature. This relationship is illustrated in the phase plot as shown in Fig. 4. Critical stresses of tension side can be simply found from the transformation lines. In this study, by substituting the critical stresses of tension side into Eq. (7), the compression side critical stresses are found.

Fig. 4
figure 4

Critical stresses for transformation or martensite twin conversion as functions of temperature

Full size image

The stresses at the beginning of martensite transformation can be expressed as

$$\sigma_{ms} = \left\{ {\begin{array}{*{20}l} {\sigma_{s}^{\text{cr}} { ,}} \hfill & {T \le M_{s} } \hfill \\ {\sigma_{s}^{\text{cr}} + C_{M} (T - M_{s} ) ,} \hfill & {T > M_{s} } \hfill \\ \end{array} } \right..$$
(24)

The stresses at the ending of martensite transformation can be expressed as

$$\sigma_{mf} = \left\{ {\begin{array}{*{20}l} {\sigma_{f}^{\text{cr}} ,} \hfill & {T \le M_{s} } \hfill \\ {\sigma_{f}^{\text{cr}} + C_{M} (T - M_{s} ),} \hfill & {T \le M_{s} } \hfill \\ \end{array} } \right..$$
(25)

The stresses at the beginning of austenite transformation can be expressed as

$$\sigma_{as} = C_{A} (T - A_{s} ) { }\quad T > A_{s} .$$
(26)

The stresses at the ending of austenite transformation can be expressed as

$$\sigma_{af} = C_{A} (T - A_{f} )\quad T > A_{f} .$$
(27)

where \(\sigma_{ms}\), \(\sigma_{mf}\), \(\sigma_{as}\) and \(\sigma_{af}\) are the stresses at the beginning and end of martensite transformation and beginning and end of austenite transformation, respectively. \(M_{s}\), \(M_{f}\), \(A_{s}\) and \(A_{f}\) are the temperature at the beginning and end of martensite transformation and beginning and end of austenite transformation, respectively. \(\sigma_{s}^{\text{cr}}\) is the beginning of critical stresses and \(\sigma_{f}^{\text{cr}}\) is the end of critical stresses. Both \(C_{A}\) and \(C_{M}\) are constants.

Material properties that are used to get the results are presented in Table 1 [21].

Table 1 Material properties for simulations
Full size table

4 Results and discussion

FG-SMA beam is composed of SMA and elastic material, and the volume fraction of SMA can be described by a power function along the thickness direction of FG-SMA beam. According to the theory of the mechanics of composites, the average stress is obtained by considering the stress of each component of the material. Liu et al. [25, 34, 35] and Xue et al. [30,31,32,33] had applied the conventional constitutive models of shape memory alloy to the functional gradient shape memory alloy and obtained some very good results. The validation study of the curvature of the FG-SMA beam is presented in Fig. 5. The size and material parameters of the beam are the same as Xue et al. [31]. When \(\alpha = 0.09375\), the curves clearly show that the theoretical results from this study are close to the results of Xue et al. So, the constitutive models which were proposed for conventional SMA materials can be used for FG-SMA.

Fig. 5
figure 5

The relationship between curvature and bending moment

Full size image

In this section, some numerical examples of the FG-SMA beam are given for explaining this theory clearly. The material properties are shown in Table 1. The FG-SMA beam has a length \(l = 400\;{\text{mm}}\) and a rectangular cross section of width \(b = 30\;{\text{mm}}\) and height \(h = 50\;{\text{mm}}\). The Young’s moduli of elastic material is \(E_{0} = 210\;{\text{GPa}}\).

4.1 Average stress

Figure 6 shows the properties of FG-SMA material, which possesses the excellent properties of both functionally graded material and shape memory alloy. The average stress in cross section subjected to different \(n\) at \(\alpha = 0.05\) and T = 60 °C is shown in Fig. 6a. The power exponent has a great influence on average stress in cross section subjected to bending moment. It can be found that the maximum tension stress is increasing and the maximum crushing stress is decreasing with increasing power exponent. The reducing ability of maximum tension stress of FG-SMA beam increases with the decreases in the power exponent. The average stress in cross section under different temperature at \(\alpha = 0.05\) and \(n = 1\) is shown in Fig. 6b. It can be learned that maximum tension stress and maximum crushing stress decrease with the increase in temperature. The reducing ability of maximum tension stress of FG-SMA beam increases with the decrease in temperature. The average stress in cross section subjected to different bending moments at \(\alpha { = }0.05\), T = 60 °C and \(n = 1\) is shown in Fig. 6c. By increasing the bending moment, the maximum tension stress and the maximum crushing stress increase. Researching the average stress in cross section of the FG-SMA beam and comparing to the SMA beam and elastic beam may be beneficial in engineering point of view, which is because FG-SMA can decrease the maximum stress usefully to prevent the destruction caused by oversize stress.

Fig. 6
figure 6

The average stress in cross section: a under different \(n\) at \(\alpha = 0.05\) and T = 60 °C, b under different \(T\) at \(\alpha = 0.05\) and \(n = 1\) and c under different bending moments at \(\alpha = 0.05\), T = 60 °C and \(n = 1\)

Full size image

4.2 Neutral axis

The influence of power exponent on neutral axis offset at \(\alpha = 0.05\) and T = 60 °C is shown in Fig. 7a. As can be seen, the neutral axis does not move in the initial stage, because the force was not enough to establish any transformation. When power exponent is changing, the initial position of the neutral axis is different. It can be found that the neutral axis offset and the rate of neutral axis moved to the tension side increase with the decrease in power exponent. The influence of temperature on neutral axis offset at \(\alpha = 0.05\) and \(n = 1\) is shown in Fig. 7b. By increasing the temperature, the rate of neutral axis moved to the tension side decreases at the same \(\alpha\) and \(n\). In the case of identical scaling description, an increase in temperature will hopefully make curve of neutral axis offset and bending moment move to right because the stress at the beginning of phase transformation increases with the increase in temperature. The influence of \(\alpha\) on neutral axis offset at \(n = 1\) and T = 60 °C is shown in Fig. 7c. The tension–compression asymmetry has a little effect on neutral axis offset. When \(\alpha\) changes, the curves of neutral axis offset and bending moment are almost the same. The characteristics of FG-SMA lead to the asymmetry of tension and compression sides, which reduce the influence of \(\alpha\) for neutral axis offset. While \(\alpha { = }0\), the neutral axis move to the compression side in phase transformation stage by an increment in bending moment. The reason is that the initial position of the neutral axis is not in the geometric center. The neutral axis offset is related to the martensitic phase fractions of surface material. When the phase change in tension side of surface material occurs, the neutral layer moves to the compression side until the surface material changes into martensite completely.

Fig. 7
figure 7

Neutral axis offset: a under different \(n\) at \(\alpha = 0.05\) and T = 60 °C, c under different \(T\) at \(\alpha = 0.05\) and \(n = 1\) and c under different \(\alpha\) at T = 60 °C and \(n = 1\)

Full size image

4.3 Curvature

The influence of \(n\) on curvature at T = 60 °C and \(\alpha { = }0.05\) is shown in Fig. 8a. The influence of temperature on curvature at \(\alpha { = }0.05\) and \(n = 1\) is shown in Fig. 8b. The influence of \(\alpha\) on curvature at T = 60 °C and \(n = 1\) is shown in Fig. 8c. In the initial stage, the relationship between curvature and bending moment is linear, but in the phase change stage, it is nonlinear. The slope of curvature-bending moment curve decreases with the increase in bending moment, which is because the Young’s moduli decreases after the mixing phase occurring. In the phase transformation stage, with the increase in \(n\), temperature and \(\alpha\), the bending moment increases in the case of given curvature. \(n\) and temperature have a great influence on curvature subjected to bending moment. But the \(\alpha\) has a little influence on curvature subjected to bending moment, which is because the characteristics of FG-SMA lead to the asymmetry of tension and compression sides. \(n\) also has a great influence on curvature subjected to bending moment in the initial stage. The reason is that the Young’s moduli increase with the increasing of \(n\) in the initial stage.

Fig. 8
figure 8

The relationship between curvature and bending moment: a under different \(n\) at \(\alpha = 0.05\) and T = 60 °C, b under different \(T\) at \(\alpha = 0.05\) and \(n = 1\) and c under different \(\alpha\) at T = 60 °C and \(n = 1\)

Full size image

4.4 Phase boundary

Figure 9 illustrates the influence of \(n\), temperature and \(\alpha\) on the movement of phase boundaries. The influence of \(n\) on movement of phase boundaries at \(\alpha = 0.05\) and T = 60 °C is shown in Fig. 9a. With the increase in \(n\), the displacement of the phase boundary on the compression side increases, the displacement of the phase boundary on the tension side decreases and the phase boundary on the tension and compression sides becomes more and more close to the geometric center of the cross section. The influence of temperature on the movement of phase boundaries at \(\alpha = 0.05\) and \(n = 1\) is shown in Fig. 9b. In this case, the curve slope of the relationship between phase boundary and bending moment decreases by increasing temperature. The temperature has a great influence on tension side and compression side. In the case of identical scaling description, an increase in temperature and an augmentation on power exponent will hopefully make curve of phase boundaries and bending moment move to right. The influence of \(\alpha\) on movement of phase boundaries at \(n = 1\) and T = 60 °C is shown in Fig. 9c. The phase boundary on either side of the cross section obviously presents asymmetry at \(\alpha = 0\) and \(\alpha \ne 0\), which is because the SMA is distributed as a power function along the thickness of the beam. The material is asymmetry about the geometric center, so the position of neutral axis is not in the geometric center. \(n\) and temperature have a great influence on tension side and compression side. \(\alpha\) has a great influence on the compression side, but it has a little influence on the tension side. It can be found that the curve of phase boundary movement-bending moment will move to right as the increase in \(n\) and temperature. It means that the phase transformation of FG-SMA beam becomes more and more difficult. As can be seen from Fig. 9a, the phase boundary of FG-SMA appears later than SMA under the same conditions. The property gradients make FG-SMA phase transformation more difficult. The movement rate of FG-SMA phase boundary is lower than SMA. The movement rate of FG-SMA phase boundary decreases with the increase in property gradients. It can be found from the comparison of Fig. 9a and b that the property gradients reduce the influence of phase transformation temperature on FG-SMA.

Fig. 9
figure 9

The movement of phase boundary: a under different \(n\) at \(\alpha = 0.05\) and T = 60 °C, b under different \(T\) at \(\alpha = 0.05\) and \(n = 1\) and c under different \(\alpha\) at T = 60 °C and \(n = 1\)

Full size image

4.5 Mid-span deflection

Figure 10 illustrates the influence of \(n\), temperature and \(\alpha\) on the mid-span deflection. The mid-span deflection subjected to different \(n\) at \(\alpha = 0.05\) and T = 60 °C is shown in Fig. 10a. The slope of middle span deflection-bending moment curve is different in the initial stage. It is illustrated that the slope and the mid-span deflection decreases by increasing \(n\). Under the case of constant value for temperature and \(\alpha\), the \(n\) has a lot of contributions to the value of bending moment when phase change takes place. With the increase in \(n\), the value of bending moment decreases. The mid-span deflection subjected to various temperatures at \(\alpha = 0.05\) and \(n = 1\) is shown in Fig. 10b. It can be seen that the mid-span deflection decreases by increasing temperature under the case of constant value for \(\alpha\) and \(n\). The temperature contributes obviously to the value of bending moment when phase change takes place. The mid-span deflection subjected to different \(\alpha\) at \(n = 1\) and T = 60 °C is shown in Fig. 10c. As can be seen, \(\alpha\) has a little influence on mid-span deflection subjected to bending moment. With the increase in \(\alpha\), the mid-span deflection slightly decreases under the case of constant value for temperature and \(n\).

Fig. 10
figure 10

The relationship between mid-span deflection and bending moment: a under different \(n\) at \(\alpha = 0.05\) and T = 60 °C, b under different \(T\) at \(\alpha { = }0.05\) and \(n = 1\) and c under different \(\alpha\) at T = 60 °C and \(n = 1\)

Full size image

4.6 Temperature and curvature

The influence of property gradients on the relationship between temperature and curvature is shown in Fig. 11. When the temperature is higher than 18.4 °C, the curvature decreased with the increase in temperature under the action of the same bending moment. When the temperature is lower than 18.4 °C, the change in temperature has a smaller influence on the curvature under the action of the same bending moment. The change in temperature affects the phase transformation of the FG-SMA. By increasing the temperature, the martensite transformation of FG-SMA becomes difficult. With the martensite transformation decreased, the elastic modulus of FG-SMA increased and the curvature decreased under the action of the same bending moment. It means that with the temperature decreased, the martensite transformation of FG-SMA becomes easy, which is in accordance with the characteristics of SMA. The property gradients affect the rate of curvature change with temperature. With the property gradients decreased, the faster the curvature change with temperature. With the property gradients decreased, the martensite transformation of FG-SMA decreased. In the same temperature range, the deformation of FG-SMA beam increased by decreasing the property gradients. The larger the property gradients, the smaller the effect of phase transformation temperature on the curvature of the FG-SMA beam.

Fig. 11
figure 11

The relationship between temperature and curvature

Full size image

5 Conclusion

In this paper, a new simple mechanics model is established to study the change in power exponent and the tension–compression asymmetry of FG-SMA under the thermal and the mechanical loads. The research focus on solving the influence of power exponent on mechanical behavior of FG-SMA and the different properties between tension and compression of FG-SMA, the \(\alpha\) is introduced to amend original mechanical model and the volume fraction of shape memory alloy can be described by a power function along the thickness direction of the FG-SMA beam. The characteristics of FG-SMA lead to the asymmetry of tension and compression sides, which reduce the influence of \(\alpha\) for bending deformation of FG-SMA beam. FG-SMA can decrease the maximum stress usefully to prevent the destruction caused by oversize stress. It illustrates that the phase transformation of FG-SMA beam becomes more and more difficult as the increase in temperature and power exponent. The model can simply and effectively analyze the change in power exponent and the tension–compression asymmetry of FG-SMA beam under the thermal and the mechanical loads. The study can provide a base for the design and in-depth investigation of FG-SMA material.