Optimal design of kinematic performance for a novel 2R1T parallel mechanism with pantograph units

Abstract

A new type of 2R1T 3-P_zP_xS parallel mechanism is presented in this paper to satisfy the needs of configuration innovation for multi-axis machining platform. The limb configuration with a planar pantograph unit and the 3-P_zP_xS mechanism configuration are proposed and optimized. The analytical solutions of the forward and inverse position for the mechanism are derived, which are convenient to subsequent motion planning and control. After obtaining the workspace of the mechanism by the boundary search algorithm, the influence of key scale parameters on the rotation capacity of the mechanism in the whole workspace is investigated, and the reasonable ranges of the scale parameters required for large rotation capacity of the mechanism are confirmed. Furthermore, based on the Jacobian matrix condition number, the global performance indices of the angular velocity and the angular acceleration of 3-P_zP_xS parallel mechanism are defined, and ultimately the optimal ranges of the scale parameters are determined according to these two performance indices. The above results lay a theoretical foundation for the further development of high-efficiency hybrid NC machining center.

1 Introduction

Parallel configuration equipment with the lower-mobility parallel mechanisms as the main mechanisms has been widely used in aviation, automobile, food and medicine industries. Among them, the 2R1T (R rotation; T translation) 3-DOF parallel mechanism is the most typical kind [1]. The 2R1T parallel mechanism can be directly used in machining process without the necessity for additional tool orientation-adjusting components, so the mass at the end of the mechanism is light and its dynamic characteristics are good [2]. The R_xR_yT_z (R_x, R_y and T_z: rotating around the x-axis, rotating around y-axis and translating along the z-axis, respectively) mechanism, most widely used as the core functional units, which can be integrated with the external serial axis of T_xT_y (translating along the x-axis, translating along the y-axis) to adjust the position of a workpiece, and then the 5-axis reconfigurable hybrid machining equipment can be built. In recent years, scholars at home and abroad have made a lot of academic achievements in configuration synthesis, kinematics analysis and performance optimization design for 2R1T parallel mechanisms.

The pantograph mechanism is a kind of mechanism which can change its space volume or shape according to a certain proportion [3]. Because of the advantages of high energy efficiency and convenient inertial force balance, a single pantograph mechanism as a modular unit is widely used in modular design of bionic, mobile, operating and extendable mechanisms via planar or spatial coupling [4]. Compared with the general parallel mechanism, the parallel mechanism with pantograph units has the advantages of simple and compact structure, simple solution for the forward and inverse positions, large workspace, large rotation capacity and kinematic decoupling [5].

Concerning the design and application research of pantograph mechanisms, Fang [6] proposed a new type of 4-DOF parallel robot mechanism with compact structure and large workspace by constructing the 6-DOF and 4-DOF rhombus kinematic limbs with large pantograph ratio. In order to develop a variety of multi-mode mobile mechanisms with the advantages of large deformation capacity, strong output, rapid response and flexible locomotion, Li [7,8,9] applied planar/spatial expandable mechanism as the extension ratio enlarging mechanism and hydraulic actuation as telescopic input. Briot [10] proposed a novel 4-DOF-decoupled parallel manipulator called the Pantopteron-4 which is made of three pantograph linkages, because of this architecture, having the same actuators for both robots, and the Pantopteron-4 displaces (theoretically) many times faster than the Isoglide-4 or the Quadrupteron. Based on pantograph mechanism, Huang et al. [11] proposed a new synthesis method for 1R1T remote center of motion (RCM) mechanism and obtained a variety of new configurations of minimally invasive surgical robot.

It is found that the application of planar/spatial pantograph units to 2R1T parallel mechanism is still rare. Some of the traditional 2R1T parallel mechanisms have the problems of complex structure, difficult position solving and poor rotational capacity. The purpose of this study is to design a unique parallel mechanism for the 5-axis high-efficiency hybrid NC machining center in order to overcome the drawbacks of traditional 2R1T parallel mechanisms. For this purpose, based on the pantograph linkage, a 2R1T parallel mechanism with planar pantograph units is proposed in this paper. The pantograph unit in the paper consists of single-degree-of-freedom rotation joints; thus, the stiffness and accuracy of the limb with a pantograph unit (compared to the limb with compound pairs) are more easily guaranteed in actual applications [12]. The limb with a planar pantograph unit can be easily analyzed and designed kinematically. This mechanism comprised of such limbs usually has such advantages as large workspace, large rotational capacity, compact and simple structure. The related results of this paper lay a necessary theoretical foundation for the study of 5-axis NC machine tool.

In Sect. 1, after completing the configuration design, the equivalent parallel mechanism 3-P_zP_xS is proposed. In Sects. 2 and 3, the analytical solutions for the forward and inverse position and Jacobian matrix of the mechanism are obtained. In Sect. 4, the parameter conditions resulting in positive kinematic singularities are confirmed. Furthermore, in Sect. 5, the influences of scale parameters on the rotation capacity of mechanism are confirmed. In Sect. 6, the optimal solutions of key scale parameters of mechanism are determined based on the global performance indices of angular velocity and angular acceleration. Finally, Sect. 7 provides a conclusion.

2 Configuration design and DOF analysis

In this section, four kinds of typical limb configurations with planar pantograph units are presented and selected. Afterward, the DOF of 3-P_zP_xS parallel mechanism is verified based on the screw theory.

2.1 Limb configurations with pantograph units

The DOF of a planar pantograph unit is usually 2T or 1R1T, and the DOF of a spatial pantograph unit is usually 3T or 2T1R [10]. In this paper, to realize 3DOFs of 2R1T parallel mechanism, a 2-DOF planar pantograph unit combined with a 3-DOF spherical joint is adopted to generate the limb configuration.

In this paper, four-limb configurations with planar pantograph units are presented. The specific schemes are shown in Table 1.

Table 1 Limb configurations with planar pantograph units

The ideal 2R1T parallel mechanisms are supposed to meet these requirements [13]: (1) simple structure, (2) large workspace, (3) kinematics decoupling, (4) high payload capability and (5) good motion/force transmission performance.

The characteristics of four-limb configurations in Table 1 are summarized as follows:

• Scheme I The active joint of the limb is the revolute joint located on the fixed platform. The workspace generated by the end of the limb is small and the actuated torque required is large.

• Scheme II There is floating prismatic joint [13] in the limb, so the stiffness and payload capacity of the limb is poor.

• Scheme III The guide path of the prismatic joint is located in the plane of the fixed platform, which is prone to produce interference among components.

• Scheme IV The prismatic joint on the fixed platform is the active joint, so the workspace generated by the end of the limb is large and the payload capacity is high; the guide path of the prismatic joint is perpendicular to the fixed frame, so it is less possible to result in interference.

The enclosed region enveloped by the green line is the limb workspace, as shown in Table 1. In the limb workspace, point S and point D have the same motion trajectory, and the point S can transfer the motion of point D to a position away from the active pairs in the limb plane, the trajectories of S and D are with different positions and same attitude. Hence, the end of limb can achieve a larger workspace with a relatively small input (γ or n) via the expansion of the pantograph unit (BCDE). The angle between the linkage AC and the ground shown in Table 1 is γ, and the active pairs are kinematic pairs A and B.

It can be seen from Table 1, from the perspective of each limb workspace, that the area of workspace of scheme I is mainly influenced by the linkage length l₃ and the rotation angle γ of linkage AC, the workspace of scheme II is mainly influenced by l₁ + l₂ and γ, and the scheme III and IV are mainly affected by l₃, the consolidation angle γ and the actuated distance of the prismatic joint n. When linkages in all schemes have the same lengths, respectively, and the γ values in all schemes are equal, it is found by numerical calculation that the workspace areas S_III and S_IV are larger than S_I and S_II. Moreover, in the machining application, the actuated prismatic joints are more common, so the schemes III and IV are more suitable. In the parallel mechanism presented in the paper, the three isomorphic limbs will be symmetrically arranged on the fixed platform in order to obtain better mechanical properties, and the moving platform of the parallel mechanism needs to obtain larger rotation capacity and workspace. In scheme III, the actuated directions of active prismatic joints in all the limbs are coplanar and easy to interfere with each other, and it is difficult to make the moving platform obtain large rotation capacity. In scheme IV, the actuated directions of active prismatic joints in all the limbs are perpendicular to the fixed platform plane, which can make the moving platform of the parallel mechanism obtain a larger rotation capacity. In this case, scheme IV is more suitable than scheme III obviously in this paper.

In summary, scheme IV has better comprehensive performance than the others, so it is chosen as the reasonable limb configuration in this paper to construct parallel mechanism.

2.2 Mechanism configuration

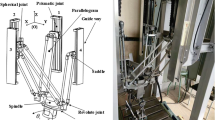
The proposed 2R1T parallel mechanism with pantograph units is shown in Fig. 1. It is composed of three identical limbs, a moving platform and a base. Any single limb i (i = 1, 2, 3, same as below) takes the prismatic joint as active joint, and its guide path is perpendicular to the base, the centroid of any prismatic joint is denoted as A_i. Any single limb i contains a closed-loop four-bar unit with four revolute joints, and each revolute axis is parallel to the base. In the limb i, the centroid of any revolute joint is denoted as B_i, C_i, D_i and E_i, respectively, and the centroid of the spherical joint of the moving platform is denoted as S_i.

Fig. 1

3-P_zP_xS parallel mechanism

A fixed coordinate system is established on the base: O_b-XYZ, the origin O_b is the centroid of the equilateral ΔM₁M₂M₃, the positive direction of z-axis is perpendicular upward to the base, the positive direction of x-axis is from O_b to M₁, and the positive direction of y-axis is determined by the right-hand rule. On the moving platform, the moving coordinate system is established as: O_a-xyz, the origin O_a is the centroid of equilateral S₁S₂S₃, the positive direction of x-axis is from O_a to S₁, the positive direction of z-axis is perpendicular upward to the moving platform, and the positive direction of the y-axis is determined by the right-hand rule. The angle between any two limb planes O_bO_aS_iM_i is 120°.

2.3 Mechanism of DOF analysis

The initial position of the moving platform is parallel to the base. As shown in Fig. 2, the coordinate system of the limb i is established: M_i-x_iy_iz_i, the positive direction of the x_i-axis is from O_b to M_i, the positive direction of the z_i-axis is perpendicular forward to the base, and the positive direction of the y_i-axis is determined by the right-hand rule. The axis of each revolute joint in the limb is set to be parallel to the y_i-axis of the limb coordinate system (i = 1, 2, 3, the same as below), and the three rotating axes of the spherical joint S_i are set to be parallel to the x_i- , y_i- and z_i-axis, respectively. In the limb coordinate system: M₁-x₁y₁z₁, the position vectors of the centroid of each joint of limb 1 are, respectively, expressed as

$$\begin{aligned} \begin{array}{*{20}c} {A_{1} = \left( {\begin{array}{*{20}c} {x_{A1} } & 0 & {z_{A1} } \\ \end{array} } \right)^{\text{T}} } & {B_{1} = \left( {\begin{array}{*{20}c} {x_{B1} } & 0 & {z_{B1} } \\ \end{array} } \right)^{\text{T}} } & {C_{1} = \left( {\begin{array}{*{20}c} {x_{C1} } & 0 & {z_{C1} } \\ \end{array} } \right)^{\text{T}} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {D_{1} = \left( {\begin{array}{*{20}c} {x_{D1} } & 0 & {z_{D1} } \\ \end{array} } \right)^{\text{T}} } & {E_{1} = \left( {\begin{array}{*{20}c} {x_{E1} } & 0 & {z_{E1} } \\ \end{array} } \right)^{\text{T}} } & {S_{1} = \left( {\begin{array}{*{20}c} {x_{S1} } & 0 & {z_{S1} } \\ \end{array} } \right)^{\text{T}} } \\ \end{array} \hfill \\ \end{aligned}$$

Fig. 2

Screw analysis of limb 1

Limb 1 is taken as an example to analyze the DOF of a limb. The motion screws corresponding to kinematic pairs in limb 1 can be expressed as:

$$\left\{ \begin{array}{l} \$_{11} = \left( {0\,0\,0;0\,0\,1} \right) \hfill \\ \$_{12} = \left( {0\,1\,0;z_{B1}\,0 \,- x_{B1} } \right) \hfill \\ \$_{13} = \left( {0\,1\,0\,;z_{C1}\,0 \,- x_{C1} } \right) \hfill \\ \$_{14} = \left( {0\,1\, 0;z_{D1}\,0 \,- x_{D1} } \right) \hfill \\ \$_{15} = \left( {0\,1\,0;z_{E1}\, 0\, - x_{E1} } \right) \hfill \\ \$_{16} = \left( {1\,0\,0;0\,z_{S1}\,0} \right) \hfill \\ \$_{17} = \left( {0\,1\,0;z_{S1}\,0\, - x_{S1} } \right) \hfill \\ \$_{18} = \left( {0\,0\,1;0\, - x_{S1}\, 0} \right) \hfill \\ \end{array} \right.$$

(1)

Based on the reciprocal screw principle of kinematic screws, the constraint screw of the limb 1 is obtained as follows:

$$\$_{11}^{r} = \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} ;\begin{array}{*{20}c} { - z_{S1} } & 0 & {x_{S1} } \\ \end{array} } \right)$$

(2)

where $\$_{11}^{r}$ is a constraint force line vector. It passes through the centroid of spherical joint S₁ and parallel to y₁-axis. Similarly, the constraint screws of the limbs 2 and 3 can be obtained. According to the symmetry of the parallel mechanism configuration in this paper, the moving platform is constrained by three constraint screws $\$_{11}^{r}$, $\$_{21}^{r}$ and $\$_{31}^{r}$ which pass through the centroids of the spherical joint S_i and parallel to the y_i-axis meanwhile do not intersect on the same plane, as shown in Fig. 3.

Fig. 3

Constraint screws of the moving platform

The three constraint screws are linearly independent; thus, the movement of the translation along the x- and y-axis and the rotation around the z-axis of the moving platform are restricted [14]. Therefore, this parallel mechanism in this paper has three DOFs: the moving platform rotating around the x-axis, the y-axis and translating along the z-axis.

Since the DOF of the planar pantograph unit in each limb is 2T [10], the pantograph units in Fig. 1 can be equivalent to two prismatic joints translating along z- and x- axis. Therefore, the mechanism shown in Fig. 1 can be equivalent to the 3-P_zP_xS parallel mechanism (P prismatic joint, S spherical joint) in Fig. 4, which is the reason of the mechanism was so named in this paper.

Fig. 4

3-P_zP_xS equivalent parallel mechanism

According to the constraint screws of the mechanism, it can be concluded that there is no common constraint screw in the parallel mechanism, that is, the number of common constraint is 0 and the rank of the mechanism is 6. In addition, there is neither redundant constraint nor passive degrees of freedom.

According to the modified Kutzbach–Grübler formula [13], the DOF of the parallel mechanism is calculated as follows:

$$M = d(n - g - 1) + \sum\limits_{i = 1}^{g} {f_{i} } + v - \xi = 6 \times (2 + 3 \times 2 - 3 \times 3 - 1) + 3 \times 5 = 3$$

(3)

In Eq. (3), M denotes the DOF of the mechanism; d the rank of the mechanism; n denotes the number of components including the fixed frame; g denotes the number of kinematic pairs; f_i denotes the DOF of kinematic pair i; v denotes the number of redundant constraints; and ξ denotes the passive degree of freedom in the mechanism.

The results of Eq. (3) confirm that 3-P_zP_xS parallel mechanism presented in this paper does have three DOFs.

3 Position analysis

Position analysis is to investigate the mathematical relationship between the input displacement of the driving joint and output displacement of the moving platform. The spatial attitude of the moving platform relative to the base is expressed by Z–Y–X Euler angle [15].

$$T = R_{z} \left( {\theta_{z} } \right)R_{y} \left( {\theta_{y} } \right)R_{x} \left( {\theta_{x} } \right) = \left[ {\begin{array}{*{20}c} {C\theta_{y} C\theta_{z} } & {C\theta_{z} S\theta_{x} S\theta_{y} - C\theta_{x} S\theta_{z} } & {S\theta_{x} S\theta_{z} + C\theta_{x} C\theta_{z} S\theta_{y} } \\ {C\theta_{y} S\theta_{z} } & {C\theta_{x} C\theta_{z} + S\theta_{x} S\theta_{y} S\theta_{z} } & {C\theta_{x} S\theta_{y} S\theta_{z} - S\theta_{x} C\theta_{z} } \\ { - S\theta_{y} } & {C\theta_{y} S\theta_{x} } & {C\theta_{x} C\theta_{y} } \\ \end{array} } \right]$$

(4)

In Eq. (4), θ_z, θ_y and θ_x are the Euler angles of the moving platform. C denotes cos and S denotes sin, the same as below.

(S_i)_a (i = 1, 2, 3, the same as below), i.e., the position vector of the centroids of the spherical joint S_i in the moving coordinate system O_a-xyz can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {(\varvec{S}_{1} )_{a} = (\begin{array}{*{20}c} r & 0 & 0 \\ \end{array} )^{\text{T}} } \hfill \\ {(\varvec{S}_{2} )_{a} = (\begin{array}{*{20}c} { - r/2} & { - \sqrt 3 r/2} & 0 \\ \end{array} )^{\text{T}} } \hfill \\ {(\varvec{S}_{3} )_{a} = (\begin{array}{*{20}c} { - r/2} & {\sqrt 3 r/2} & 0 \\ \end{array} )^{\text{T}} } \hfill \\ \end{array} } \right.$$

(5)

(S_i)_b, i.e., the position vector of S_i in the fixed coordinate system O_b-XYZ can be expressed as:

$$\left( {\varvec{S}_{i} } \right)_{b} = T\left( {\varvec{S}_{i} } \right)_{a} + \varvec{O}_{b} \varvec{O}_{a}$$

(6)

In Eq. (6), $\varvec{O}_{b} \varvec{O}_{a} = \left( {\begin{array}{*{20}c} x & y & z \\ \end{array} } \right)^{\text{T}}$

Considering the angle between any two limb planes of the three limbs is 120°, the centroids of the spherical joint S_i are constrained to move in the plane y = 0,$y = \sqrt 3 x$ and in the $y = - \sqrt 3 x$ plane, respectively, Eq. (6) can be expressed as:

$$\left\{ \begin{aligned} \left( {\varvec{S}_{1} } \right)_{b} = \left[ {\begin{array}{*{20}c} {\left( {S_{1} } \right)_{bx} } & {\left( {S_{1} } \right)_{by} } & {\left( {S_{1} } \right)_{bz} } \\ \end{array} } \right]^{\text{T}} \hfill \\ \left( {\varvec{S}_{2} } \right)_{b} = \left[ {\begin{array}{*{20}c} {\left( {S_{2} } \right)_{bx} } & {\left( {S_{2} } \right)_{by} } & {\left( {S_{2} } \right)_{bz} } \\ \end{array} } \right]^{\text{T}} \hfill \\ \left( {\varvec{S}_{3} } \right)_{b} = \left[ {\begin{array}{*{20}c} {\left( {S_{3} } \right)_{bx} } & {\left( {S_{3} } \right)_{by} } & {\left( {S_{3} } \right)_{bz} } \\ \end{array} } \right]^{\text{T}} \hfill \\ \end{aligned} \right.$$

(7)

The specific relationships among (S_i) _b are shown below:

$$\left\{ \begin{array}{l} \left( {S_{1} } \right)_{by} = 0 \hfill \\ \left( {S_{2} } \right)_{by} = \sqrt 3 \left( {S_{2} } \right)_{bx} \hfill \\ \left( {S_{3} } \right)_{by} = - \sqrt 3 \left( {S_{3} } \right)_{bx} \hfill \\ \end{array} \right.$$

(8)

Thus, the following constraints can be obtained as:

$$\left\{ \begin{array}{l} x = r\cos \theta_{z} \left( {\cos \theta_{y} - \cos \theta_{x} } \right)/2 - \sqrt 3 \sin \theta_{x} \sin \theta_{y} \sin \theta_{z} /6 \hfill \\ y = - r\cos \theta_{y} \sin \theta_{z} \hfill \\ \theta z = \arctan \left( {\sin \theta_{x} \sin \theta_{y} /(\cos \theta_{x} + \cos \theta_{y} )} \right) \hfill \\ \end{array} \right.$$

(9)

Therefore, θ_x, θ_y and z, i.e., the position and orientation of the moving platform, can be completely obtained, here z is an independent parameter.

3.1 Inverse position analysis

The inverse position analysis is to solve the input displacement of the driving joint (z₁, z₂, z₃) given θ_x, θ_y and z, i.e., the position and orientation of the moving platform. According to the relation between input and output displacement in the limbs, the position vector (S_i)_b of each limb in the fixed coordinate system O_b-XYZ can be derived as follows:

$$\left\{ \begin{array}{lll} \left( {S_{1} } \right)_{b} = \left( {\begin{array}{*{20}c} {R_{c} - \left( {2l_{1} + l_{2} } \right)C\alpha - l_{3} C\left( {\alpha + \beta 1} \right)} & 0 & {\left( {2l_{1} + l_{2} } \right)S\alpha + l_{3} S\left( {\alpha + \beta_{1} } \right) + z_{1} } \\ \end{array} } \right)^{\text{T}} \hfill \\ \left( {S_{2} } \right)_{b} = R_{Z} \left( {2\pi /3} \right)\left( {\begin{array}{*{20}c} {R_{c} - \left( {2l_{1} + l_{2} } \right)C\alpha - l_{3} C\left( {\alpha + \beta_{2} } \right)} & 0 & {\left( {2l_{1} + l_{2} } \right)S\alpha + l_{3} S\left( {\alpha + \beta_{2} } \right) + z_{2} } \\ \end{array} } \right)^{\text{T}} \hfill \\ \left( {S_{3} } \right)_{b} = R_{Z} \left( {4\pi /3} \right)\left( {\begin{array}{*{20}c} {R_{c} - \left( {2l_{1} + l_{2} } \right)C\alpha - l_{3} C\left( {\alpha + \beta_{3} } \right)} & 0 & {\left( {2l_{1} + l_{2} } \right)S\alpha + l_{3} S\left( {\alpha + \beta_{3} } \right) + z_{3} } \\ \end{array} } \right)^{\text{T}} \hfill \\ \end{array} \right.$$

(10)

Considering Eqs. (6) and (10), the analytical solution of the inverse position of 3-P_zP_xS parallel mechanism can be obtained as:

$$\left\{ \begin{array}{l} z_{1} = z - rS\theta_{y} - \left( {2l_{1} + l_{2} } \right)S\alpha - l_{3} S\left( {\alpha + \beta_{3} } \right) \hfill \\ z_{2} = z + rS\theta_{y} /2 - \sqrt 3 rC\theta_{y} S\theta_{x} /2 - \left( {2l_{1} + l_{2} } \right)S\alpha - l_{3} S\left( {\alpha + \beta_{1} } \right) \hfill \\ z_{3} = z + rS\theta_{y} /2 + \sqrt 3 rC\theta_{y} S\theta_{x} /2 - \left( {2l_{1} + l_{2} } \right)S\alpha - l_{3} S\left( {\alpha + \beta_{2} } \right) \hfill \\ \end{array} \right.$$

(11)

In Eq. (11)

$$\left\{ \begin{array}{l} \beta_{1} = \pm {\text{arc}}\;C\left( {\left( {x + rC\theta_{y} C\theta_{z} - R_{c} + \left( {2l_{1} + l_{2} } \right)C\alpha } \right)/l_{3} } \right) - \alpha \hfill \\ \beta_{2} = \pm {\text{arc}}\;C\left( {\left( {R_{c} - \sqrt 3 rC\theta_{y} S\theta_{z} - rC\theta_{x} C\theta_{z} - \sqrt 3 S\theta_{x} S\theta_{y} S\theta_{z} /3 - \left( {2l_{1} + l_{2} } \right)C\alpha } \right)/l_{3} } \right) - \alpha \hfill \\ \beta_{3} = \pm {\text{arc}}\;C\left( {\left( {R_{c} + \sqrt 3 rC\theta_{y} S\theta_{z} - rC\theta_{x} C\theta_{z} - \sqrt 3 S\theta_{x} S\theta_{y} S\theta_{z} /3 - \left( {2l_{1} + l_{2} } \right)C\alpha } \right)/l_{3} } \right) - \alpha \hfill \\ \end{array} \right.$$

(12)

3.2 Forward position analysis

The forward position analysis is to solve θ_x, θ_y and z, i.e., the output position and orientation of the moving platform given the actuated displacement, i.e., z₁, z₂ and z₃ of the mechanism.

Considering Eqs. (6) and (10), the analytical solution of the forward position of the 3-P_zP_xS parallel mechanism can be obtained as follows:

$$\left\{ \begin{array}{l} \theta_{x} = {\text{arc}}\;S\left( {\left[ {l_{3} \left( {S\left( {\alpha + \beta_{3} } \right) - S\left( {\alpha + \beta_{2} } \right)} \right) + z_{3} - z_{2} } \right]/3rC\theta_{y} } \right) \hfill \\ \theta_{y} = {\text{arc}}\;S\left( {\left[ {l_{3} \left( {S\left( {\alpha + \beta_{2} } \right) + S\left( {\alpha + \beta_{3} } \right) - 2S\left( {\alpha + \beta_{1} } \right)} \right) + \left( {z_{2} + z_{3} - 2z_{1} } \right)} \right]/3r} \right) \hfill \\ z = \left( {2l_{1} + l_{2} } \right)S\alpha + \left[ {l_{3} \left( {S\left( {\alpha + \beta_{1} } \right) + S\left( {\alpha + \beta_{2} } \right) + S\left( {\alpha + \beta_{3} } \right)} \right) + \left( {z_{1} + z_{2} + z_{3} } \right)} \right]/3 \hfill \\ \end{array} \right.$$

(13)

4 Velocity analysis

In the parallel mechanism, the mapping relation between the output velocity of the moving platform and the input velocity of the driving joint is embodied by the Jacobian matrix, which is powerful tool for kinematics analysis and design of parallel mechanisms [14]. The Jacobian matrix form can be derived by taking the derivative of two sides of Eq. (13) with respect to time

$${\mathbf{{\rm B}\dot{p}}} = {\mathbf{\rm A}}\dot{\varvec{\rho }}$$

(14)

In Eq. (14), B is the positive Jacobian matrix

$${\mathbf{B}} = \left( {\begin{array}{*{20}c} {\cos \theta_{x} } & 0 & 0 \\ 0 & {\cos \theta_{y} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right)$$

(15)

A is the inverse Jacobian matrix

$${\mathbf{A}} = \left( {\begin{array}{*{20}c} {\frac{ 2\sqrt 3vw}{{ 3\left( u \right)^{ 2} }}} & { - \frac{ 1}{u} - \frac{\sqrt 3vw}{{ 3\left( u \right)^{ 2} }}} & {\frac{ 1}{u} - \frac{\sqrt 3vw}{{ 3\left( u \right)^{ 2} }}} \\ { - \frac{ 2}{ 3r}} & {\frac{ 1}{ 3r}} & {\frac{ 1}{ 3r}} \\ {\frac{ 1}{ 3}} & {\frac{ 1}{ 3}} & {\frac{ 1}{ 3}} \\ \end{array} } \right)$$

(16)

$\dot{\rho }$ is the input velocity vector of the driving joint

$$\dot{\rho } = \left( {\begin{array}{*{20}c} {\dot{z}_{1} } & {\dot{z}_{2} } & {\dot{z}_{3} } \\ \end{array} } \right)^{\text{T}}$$

(17)

${\dot{\mathbf{p}}}$ is the output velocity vector of the moving platform

$${\dot{\mathbf{p}}} = \left( {\begin{array}{*{20}c} {\dot{\theta }_{x} } & {\dot{\theta }_{y} } & {\dot{z}} \\ \end{array} } \right)^{T}$$

(18)

Then the velocity Jacobian matrix of the mechanism can be expressed as:

$${\mathbf{G}} = {\mathbf{B}}^{{ - {\mathbf{1}}}} {\mathbf{A}}$$

(19)

In Eq. (16), u, v and w are, respectively, expressed as:

$$\begin{aligned} u & = \sqrt 3 r\cos \left( {\left[ {z_{2} + z_{3} - 2z_{1} - l_{3} \left( {2\sin \left( {\alpha + \beta_{1} } \right) - \sin \left( {\alpha + \beta_{2} } \right) - \sin \left( {\alpha + \beta_{3} } \right)} \right)} \right]/3r} \right) \\ v & = \sin \left( {\left[ {z_{2} + z_{3} - 2z_{1} - l_{3} \left( {2\sin \left( {\alpha + \beta_{1} } \right) - \sin \left( {\alpha + \beta_{2} } \right) - \sin \left( {\alpha + \beta_{3} } \right)} \right)} \right]/3r} \right) \\ w & = z_{2} - z_{3} + l_{3} \left( {\sin \left( {\alpha + \beta_{2} } \right) - \sin \left( {\alpha + \beta_{3} } \right)} \right) \\ \end{aligned}$$

5 Singularity analysis

Based on Jacobian matrixes, there are three types of kinematic singularities: inverse kinematic singularity, forward kinematics singularity and combined kinematic singularity [16].

5.1 Inverse kinematic singularity

The conditions for the occurrence of the inverse kinematic singularity are given as:

$$\det ({\mathbf{A}}) = 0\quad {\text{and}}\quad { \det }({\mathbf{B}}) \ne 0$$

(20)

det(A) can be obtained by substituting Eq. (13) into Eq. (16) as follows:

$$\det ({\mathbf{A}}) = \frac{2}{{3\sqrt 3 r^{2} \cos \left( {\sin \theta_{y} } \right)}}$$

(21)

Obviously, det(A) is impossible to be zero, so there is no inverse kinematic singularity in the parallel mechanism.

5.2 Forward kinematic singularity

The conditions for the occurrence of the forward kinematic singularity are given as:

$$\det ({\mathbf{A}}) \ne 0\quad {\text{and}}\quad \det ({\mathbf{B}}) = 0$$

(22)

In this paper, det(B) is obtained as follows:

$$\det ({\mathbf{B}}) = \cos \theta_{x} \cos \theta_{y}$$

When det(B) = 0, correspondingly, cosθ_x = 0 or cosθ_y = 0, that is, θ_x = ±π/2 or θ_y = ±π/2.

Figure 5 shows a singular configuration of the mechanism when θ_y = − π/2. At this time, the connection line S₂S₃ of the moving platform is parallel to the M₂M₃ on the base, and the moving platform is perpendicular to the base.

Fig. 5

Singularity analysis of the 3-P_zP_xS

5.3 Combined kinematic singularity

The conditions for the occurrence of combined kinematic singularity are given as:

$$\det ({\mathbf{A}}) = 0\quad {\text{and}}\quad \det ({\mathbf{B}}) = 0$$

(23)

Since det(A) is obviously not equal to zero, there is no combined kinematic singularity in the parallel mechanism.

6 Rotation capacity analysis

The analysis of rotational capacity is to evaluate the maximum range of rotation angles of the moving platform.

6.1 Workspace solving

In this paper, the scale parameters of 3-P_zP_xS parallel mechanism are specified as follows: the circumcircle radius of the base R_c = 210 mm, the circumcircle radius of moving platform r = 105 mm, linkage lengths of limb: A_iB_i = E_iS_i = l₁ = 65 mm, B_iC_i = D_iE_i = l₂ = 70 mm and B_iD_i = C_iE_i = l₃ = 55 mm. Given the travel ranges of joints: z_i ∈ [0.80 mm], β_i ∈ [π/4, 2π/3], i = 1, 2, 3. As shown in Fig. 6, the workspace of 3-P_zP_xS parallel mechanism can be obtained by the boundary search algorithm [14]. We can get the workspace according to the following ideas (Fig. 7):

Fig. 6

Workspace of the mechanism

Fig. 7

Workspace search process

6.2 Influence of scale parameters on rotation capacity

6.2.1 The influence of the ratio of the platform circumcircle radii

The ratio of r to R_c is defined as:

$$K = r/R_{c}$$

(24)

Owing to the symmetry of the mechanism configuration, it is easy to find that the variation trend of rotation angles θ_x and θ_y of the moving platform around x- and y-axis is similar, so this paper only studies the variation trend of θ_y.

Setting linkage lengths l₁, l₂ and l₃ as invariant value, the relationship between the displacement along z-axis of the centroid O_a of the moving platform and θ_y can be obtained as shown in Fig. 8a according to the workspace solving method in Sect. 5.1. The range of θ_y increases gradually with the decrease of K, indicating that the rotation capacity of the moving platform is enhanced. When K increases from 0.25 to 1.5, θ_y decreases gradually from ± 80° to about ± 10°, indicating that when K is small, especially when K is 0.25, the rotation capacity of the moving platform is high, which can meet the needs of clamping a workpiece only once and completing 5-axis machining better.

Fig. 8

Influence of scale parameters on θ_y

6.2.2 The influence of the linkage lengths

Given R_c = 210 mm, r = 105 mm. The influence of the length of each connecting linkage on θ_y is shown in Fig. 8b–d.

It can be observed from Fig. 8b, c that the increase of l₁ and l₂ has little effect on θ_y, and the displacement along z-axis of the centroid O_a of the moving platform increases with the increase in the length of the linkages, but the ranges of z does not change. From Fig. 8d, we can find that the ranges of θ_y and z increase with the increase of l₃.

7 Scale optimization based on kinematic performances

On the basis of workspace analysis, Gosselin proposed a class of global conditioning index [17] to evaluate such performances as dexterity, velocity and acceleration, etc. of mechanisms:

$$\eta_{J} = \frac{{\int\limits_{W} {\frac{1}{{K_{J} }}{\text{d}}W} }}{{\int\limits_{W} {{\text{d}}W} }}$$

(25)

In Eq. (25),$\eta_{J}$ is the global performance index of the mechanism; $K_{J} = \left\| {G_{J} } \right\| \cdot \left\| {G_{J}^{ + } } \right\|$ denotes the condition number (where ||·|| is the Frobenius norm of a matrix and “+” denotes the generalized inverse matrix of a matrix); J ∈ {G, H, or G + H}, G is Jacobian matrix and H is Hessian matrix [14]; W is the reachable workspace of the mechanism.

7.1 Global velocity performance indices of 3-P _z P _x S mechanism

The global angular velocity performance index $\eta_{{G_{\omega } }}$ and the global linear velocity performance index $\eta_{{G_{v} }}$ [18] in this paper is expressed, respectively, as:

$$\eta_{{G_{\omega } }} = \frac{{\int\limits_{W} {\frac{1}{{K_{{G_{\omega } }} }}{\text{d}}W} }}{{\int\limits_{W} {{\text{d}}W} }}\quad \eta_{{G_{v} }} = \frac{{\int\limits_{W} {\frac{1}{{K_{{G_{v} }} }}{\text{d}}W} }}{{\int\limits_{W} {{\text{d}}W} }}$$

(26)

In Eq. (26), G_ω is the angular velocity Jacobian matrix and G_v is the linear velocity Jacobian matrix.$K_{{G_{\omega } }} = \left\| {G_{\omega } } \right\| \cdot \left\| {G_{\omega }^{ + } } \right\|$ denotes the condition number of the angular velocity Jacobian matrix, and $K_{{G_{v} }} = \left\| {Gv} \right\| \cdot \left\| {Gv^{ + } } \right\|$ denotes the condition number of the linear velocity Jacobian matrix.

Considering Eqs. (14) and (19), it can be known as:

$${\dot{\mathbf{p}}} = \left[ G \right]\dot{\rho }$$

(27)

i.e.,

$$\left[ {\begin{array}{*{20}c} {\dot{\theta }_{x} } \\ {\dot{\theta }_{y} } \\ {\dot{z}} \\ \end{array} } \right] = G\left[ {\begin{array}{*{20}c} {\dot{z}_{1} } \\ {\dot{z}_{2} } \\ {\dot{z}_{3} } \\ \end{array} } \right]$$

Equation (27) can be divided into two equations as follows:

$$\left[ {\begin{array}{*{20}c} {\dot{\theta }_{x} } \\ {\dot{\theta }_{y} } \\ \end{array} } \right] = G_{\omega } \left[ {\begin{array}{*{20}c} {\dot{z}_{1} } \\ {\dot{z}_{2} } \\ {\dot{z}_{3} } \\ \end{array} } \right]\quad \dot{\varvec{z}} = G_{v} \left[ {\begin{array}{*{20}c} {\dot{z}_{1} } \\ {\dot{z}_{2} } \\ {\dot{z}_{3} } \\ \end{array} } \right]$$

(28)

Therefore, the Jacobian matrix G in this paper can be expressed as:

$$\varvec{G} = \left[ {\begin{array}{*{20}c} {\varvec{G}_{\omega } } \\ {\varvec{G}_{v} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {d_{ 1 1} } & {d_{ 1 2} } & {d_{ 1 3} } \\ {d_{ 2 1} } & {d_{ 2 2} } & {d_{ 2 3} } \\ {d_{ 3 1} } & {d_{ 3 2} } & {d_{ 3 3} } \\ \end{array} } \right]$$

(29)

G_ω and G_v of the mechanism can be expressed, respectively, as:

$$G_{\omega } = \left[ {\begin{array}{*{20}c} {d_{ 1 1} } & {d_{ 1 2} } & {d_{ 1 3} } \\ {d_{ 2 1} } & {d_{ 2 2} } & {d_{ 2 3} } \\ \end{array} } \right]\quad G_{v} = \left[ {\begin{array}{*{20}c} {d_{31} } & {d_{32} } & {d_{33} } \\ \end{array} } \right]$$

(30)

Substituting Eq. (13) into Eq. (29), all matrix elements can be obtained as follows:

$$\left\{ {\begin{array}{*{20}l} {d_{11} = - \frac{{2\sin \theta_{x} \sin \theta_{y} }}{{3r\cos \theta_{x} \cos \theta_{y} }}} \hfill \\ {d_{12} = \frac{{\sqrt 3 \cos \theta_{y} - \sin \theta_{x} \sin \theta_{y} }}{{3r\cos \theta_{x} \cos^{2} \theta_{y} }}} \hfill \\ {d_{13} = \frac{{\sqrt 3 \cos \theta_{y} + \sin \theta_{x} \sin \theta_{y} }}{{3r\cos \theta_{x} \cos^{2} \theta_{y} }}} \hfill \\ {d_{21} = - \frac{2}{{3r^{2} \cos^{2} \theta_{y} }}} \hfill \\ {d_{22} = \frac{1}{{3r^{2} \cos^{2} \theta_{y} }}} \hfill \\ {d_{23} = \frac{1}{{3r^{2} \cos^{2} \theta_{y} }}} \hfill \\ {d_{31} = \frac{1}{3}} \hfill \\ {d_{32} = \frac{1}{3}} \hfill \\ {d_{33} = \frac{1}{3}} \hfill \\ \end{array} } \right.$$

(31)

Obviously, G_v is a constant matrix, so $\eta_{{G_{v} }}$ is constant, and thus $\eta_{{G_{\omega } }}$ is investigated below only.

7.2 Global acceleration performance indices of 3-P _z P _x S mechanism

The global angular acceleration performance index $\eta_{{G_{\omega } + H_{\omega } }}$ and the global linear acceleration performance index $\eta_{{G_{v} + H_{v} }}$ [18] in this paper can be expressed, respectively, as:

$$\eta_{{G_{\omega } + H_{\omega } }} = \frac{{\int\limits_{W} {\frac{1}{{K_{{_{{G_{\omega } + H_{\omega } }} }} }}{\text{d}}W} }}{{\int\limits_{W} {{\text{d}}W} }}\quad \eta_{{G_{v} + H_{v} }} = \frac{{\int\limits_{W} {\frac{1}{{K_{{_{{G_{v} + H_{v} }} }} }}{\text{d}}W} }}{{\int\limits_{W} {{\text{d}}W} }}$$

(32)

In Eq. (32), H is Hessian matrix, it also can be categorized as the angular acceleration Hessian matrix H_ω and the linear acceleration Hessian matrix H_v.$K_{{G_{\omega } + H_{\omega } }} = b\left\| {G_{\omega } } \right\| \cdot \left\| {G_{\omega }^{ + } } \right\| + (a^{2} + 2a)\left\| {H_{\omega } } \right\| \cdot \left\| {H_{\omega }^{ + } } \right\|$ denotes the condition number of $\eta_{{G_{\omega } + H_{\varpi } }}$, and $K_{{G_{\text{v}} + H_{v} }} = b\left\| {G_{v} } \right\| \cdot \left\| {G_{v}^{ + } } \right\| + (a^{2} + 2a)\left\| {H_{v} } \right\| \cdot \left\| {H_{v}^{ + } } \right\|$ denotes the condition number of $\eta_{{G_{v} + H_{v} }}$. a is input velocity $\dot{\rho }$ error, and b is input acceleration $\ddot{\rho }$ error.

To take the derivative of two sides of Eq. (27) with respect to time, the following is given as:

$${\mathbf{\ddot{p}}} = \dot{\rho }^{T} \left[ H \right]\dot{\rho } + \left[ G \right]\ddot{\rho }$$

(33)

The elements in [H] are as follows:

$$H_{ij}^{k} = \frac{{\partial^{2} p_{k} }}{{\partial \rho_{i} \partial \rho_{j} }} = \left( {\begin{array}{*{20}c} {\frac{{\partial^{2} p_{1} }}{{\partial \rho_{i} \partial \rho_{j} }}} & {\frac{{\partial^{2} p_{2} }}{{\partial \rho_{i} \partial \rho_{j} }}} & {\frac{{\partial^{2} p_{3} }}{{\partial \rho_{i} \partial \rho_{j} }}} \\ \end{array} } \right)^{\text{T}}$$

(34)

In Eq. (34), k = 1, 2, 3, i = 1, 2, 3, j = 1, 2, 3, so the matrix [H] ∈ R^3×3×3.

Because G_v is a constant matrix, it is known that H_v is a zero matrix. Therefore, only $\eta_{{G_{\omega } + H_{\omega } }}$ is analyzed in follow sections.

Considering Eq. (34), H_ω of the mechanism can be obtained as follows:

$$H_{\omega } = \left[ {\begin{array}{*{20}c} {\varvec{g}_{1} } & {\varvec{g}_{2} } & {\varvec{g}_{3} } \\ {\varvec{g}_{4} } & {\varvec{g}_{5} } & {\varvec{g}_{6} } \\ \end{array} } \right]^{\text{T}}$$

(35)

In H_ω, each element g_i is $\varvec{g}_{i} = \left( {\begin{array}{*{20}c} {{\text{g}}_{i1} } & {{\text{g}}_{i2} } \\ \end{array} } \right)^{\text{T}}$, i = 1, 2, 3, 4, 5, 6.

All H_ω elements are as follows:

$$\left\{ {\begin{array}{*{20}l} {g_{11} = \frac{2}{{3r\left( {\sin^{2} \theta_{x} - 1} \right)}}} \hfill \\ {g_{12} = 0} \hfill \\ {g_{21} = - \frac{{\sin \theta_{y} - \sqrt 3 \cos \theta_{y} \sin \theta_{x} }}{{3r\cos^{2} \theta_{x} \cos^{2} \theta_{y} }}} \hfill \\ {g_{22} = \frac{{2\cos^{2} \theta_{y} \sin \theta_{x} - 4\sin \theta_{x} + \sqrt 3 \sin 2\theta_{y} }}{{6r\cos \theta_{x} \cos^{3} \theta_{y} }}} \hfill \\ {g_{31} = \frac{{\sin \theta_{y} + \sqrt 3 \cos \theta_{y} \sin \theta_{x} }}{{3r\cos^{2} \theta_{x} \cos^{2} \theta_{y} }}} \hfill \\ {g_{32} = \frac{{ - 2\cos^{2} \theta_{y} \sin \theta_{x} + 4\sin \theta_{x} + \sqrt 3 \sin 2\theta_{y} }}{{6r\cos \theta_{x} \cos^{3} \theta_{y} }}} \hfill \\ {g_{41} = 0} \hfill \\ {g_{42} = - \frac{{4\sin \theta_{y} }}{{3r^{2} \cos^{3} \theta_{y} }}} \hfill \\ {g_{51} = 0} \hfill \\ {g_{52} = \frac{{2\sin \theta_{y} }}{{3r^{2} \cos^{3} \theta_{y} }}} \hfill \\ {g_{61} = 0} \hfill \\ {g_{62} = \frac{{2\sin \theta_{y} }}{{3r^{2} \cos^{3} \theta_{y} }}} \hfill \\ \end{array} } \right.$$

(36)

7.3 Scale optimization based on global performance indices

According to the influence of scale parameters on the rotation capacity of the mechanism in Sect. 5.2, it can be known that l₃ has a more obvious effect on the range of θ_y compared with l₁ and l₂. Given that the other scale parameters are not variant, the range of r is 50–60 mm and the range of l₃ is 40–50 mm.

Owing to the absence of the analytical expression of $\eta_{{G_{\omega } }}$ and $\eta_{{G_{\omega } + H_{\omega } }}$, it is necessary to discretize Eqs. (26) and (32) as follows:

$$\eta_{{G_{\omega } }} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {\frac{1}{{KG_{\omega } }}} \right)_{i} } }}{n}$$

(37)

$$\eta_{{G_{\omega } + H_{\omega } }} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {\frac{1}{{K_{{G_{\omega } + H_{\omega } }} }}} \right)_{i} } }}{n}$$

(38)

Among Eqs. (37) and (38), i denotes the sequence number of a sampling point in the workspace and n denotes the total number of sampling points. Through Eqs. (37) and (38), $\eta_{{G_{\omega } }}$ and $\eta_{{G_{\omega } + H_{\omega } }}$ can be calculated, and the corresponding atlases are plotted in Figs. 9 and 10, respectively.

Fig. 9

$\eta_{{G_{\omega } }}$ atlas

Fig. 10

$\eta_{{G_{\omega } + H_{\omega } }}$ atlas

According to the statement [18] that the higher $\eta_{{G_{\omega } }}$ and $\eta_{{G_{\omega } + H_{\omega } }}$ are, the higher the dexterity and control accuracy of the mechanism are, it can be observed from Figs. 9 and 10 that the smaller r is, the greater $\eta_{{G_{\omega } }}$ and $\eta_{{G_{\omega } + H_{\omega } }}$ are. From Fig. 9, it can be seen that when r = 50–51 mm, l₃ = 40–42 mm, 44–46 mm and 48–50 mm, the angular velocity performance of the mechanism is better and the output error range of the angular velocity is smaller; from Fig. 10, it can be seen that when r = 50–52 mm, l₃ = 40–42 mm and 48–50 mm, the angular acceleration performance of the mechanism is better and the output error range of the angular acceleration is smaller.

Specifying R_c = 50 mm and l₃ = 40 mm, the obtained workspace of the mechanism by the boundary search algorithm [14] is shown in Fig. 11. Compared with the workspace in Fig. 7, the rotational capacity of the mechanism is improved significantly in Fig. 11: the extreme values of θ_x and θ_y are both increased between 70° and 80°.

Fig. 11

Optimized workspace of the 3-P_zP_xS mechanism

8 Conclusion

In order to satisfy the requirement of the configuration innovation of multi-axis hybrid machining equipments, a 2R1T parallel mechanism 3-P_zP_xS with planar pantograph units is proposed and researched in this paper. The corresponding achievements are as follows:

• 1. Several limb configurations with two-DOF planar pantograph units are proposed and selected according to workspace, payload capability and motion/force transmission performance. Hereby the equivalent 3-P_zP_xS parallel mechanisms are put forward.

• 2. The analytical solutions of the forward and inverse position for the mechanism are derived.

• 3. Based on the Jacobian matrix, the parameter conditions resulting in positive kinematic singularities are confirmed.

• 4. The reachable workspace of the mechanism is solved by the boundary search algorithm. Afterward, the influence of key scale parameters on the rotational capacity is investigated comprehensively, and the reasonable ranges of scale parameters with large rotational capacity are determined.

• 5. Based on the global performance indices of angular velocity and acceleration of 3-P_zP_xS parallel mechanism, the optimal ranges of the key scale parameters of the mechanism are obtained, and the rotational capacity of the mechanism is confirmed to be enhanced significantly after the parameter optimization.

The above results prove the rationality of the configuration design, the kinematics modeling and the solving of global angular velocity/acceleration performance indices proposed in this paper. The related results lay the necessary theoretical foundation for the further development of high-efficiency hybrid NC machining center.