Plate profile control during ultra-thin strip rolling utilizing work roll edge contact

Abstract

During ultra-thin strip cold rolling, a phenomenon of work roll edge contact always appears. Very serious work roll edge contact and an edge wave occur when the strip thickness decreases; however, it is difficult to eliminate these problems with traditional control methods. To accurately analyse the influence of the mechanism of work roll edge contact on the strip shape control for ultra-thin strips, a finite-length semi-infinite body model of the roll is established based on the boundary element method. Then, a new work roll edge contact model which is applied to the rolling process of a laboratory twenty-high mill was established. The results show that when very serious work roll edge contact and an edge wave occur, the strip shape defect cannot be eliminated by traversing the first intermediate roll. Therefore, the roll gap is adjusted by utilizing work roll edge contact to improve its profile.

1 Introduction

During cold rolling, a phenomenon of work roll edge contact always appears, which refers to the touch and flattening between the edges of work rolls. When work roll contact occurs, the transverse distribution of the rolling force, roll deflection, and strip profile contour will be affected [1,2,3,4].

In recent years, scholars have conducted theoretical and experimental studies about work roll edge contact. Considering the contact, Jiang [5, 6] established an influence function model of the 4-high mill. Afterwards, the model was used to analyse the influence of the contact phenomenon on contact pressure between rolls. The contact phenomenon was avoided by improving the work roll profile. Bai [7] and Dai [8] analysed the work roll edge contact phenomenon in rolling process of the six-high mill, which was controlled by applying the bending-up roll devices and traversing the backup roll. Based on the elastic cantilever beam and the influence function methods, Guan [9] studied the influences of the work roll contact on the cross-sectional shape of the strip and the contact pressure between rolls. Yang [10] proposed a new shape detection model based on the theoretical analysis, which consisted of wide channels in the middle of detection roll and narrow channels on both sides. Li [11] studied the relationship between work roll edge contact and edge drop in the silicon strip cold rolling, which provided theoretical guidance for the production of silicon strip.

From the above description, when a phenomenon of work roll edge contact appears in the rolling process, the phenomenon can be avoided by the traditional treatment methods which mainly include traversing the intermediate roll and applying the positive roll bending force. Nevertheless, hard ultra-thin strips are usually rolled by multi-roll mills; the work roll edge contact phenomenon in the rolling process is eliminated only by traversing the first intermediate roll. However, there is very serious work roll contact phenomenon and edge wave as the strip thickness decreases, which is difficult to be eliminated by traversing the first intermediate roll. In order to eliminate the edge waves, the roll gap will be adjusted by increasing the work roll edge contact, which is equivalent to applying a positive bending force to the work roll.

At present, the Foppl theory [12] and the semi-infinite body theory [13] are widely used to calculate the elastic flattening between rolls. In the semi-infinite body theory, the roll is assumed to be the infinite long, while the actual length of the roll is finite. In the Foppl theory, the roll elastic flattening is assumed to be a plane strain problem, ignoring the effect of axial strain. Therefore, the above models are inaccurate, especially near the end of the roll. In order to correct the error of the Foppl theory and the semi-infinite body theory, a finite-length semi-infinite body model of the roll is established based on the boundary element method. Also, the model is applied to the rolling process of twenty-high mill; the effect of the work roll contact on the adjustment of the plate profile is studied.

2 Theoretical analysis

2.1 Roll flattening model

To solve the flattening displacement between rolls, the roll is assumed to be a finite-length semi-infinite body model shown in Fig. 1a. And then, the displacement field under the action of $p_{i}$ is obtained based on the boundary integral equation method. Therefore, the boundary integral equation is established as Eq. (1).

$$ C_{ij} (P)u_{j} (P) + \int_{S} {t_{ij}^{ * } (P,Q)u_{j} (Q){\text{d}}S} = \int_{S} {u_{ij}^{ * } (P,Q)t_{j} (Q){\text{d}}S} $$

(1)

where S is the boundary; P is the source point; Q is the field point; $u_{j} (P)$ is the displacement in j direction; $t_{ij}^{*} (P,Q)$ is fundamental solution of elastic half space for the tractions; $u_{ij}^{*} (P,Q)$ is fundamental solution of elastic half space for displacements.

Fig. 1

Finite-length semi-infinite body: a initial model and b discrete model

When $P \in S_{1} ,S_{2}$, $t_{ij}^{*} (P,Q) = 0$; $P \in S_{2} ,S_{3}$, $t_{j} (Q) = 0$, therefore, Eq. (1) can be simplified to Eq. (2):

$$ u_{i} (P) + \int_{{S_{3} }} {t_{ij}^{ * } (P,Q)u_{j} (Q){\text{d}}S} = \int_{{S_{1} }} {u_{ij}^{ * } (P,Q)t_{j} (Q){\text{d}}S} $$

(2)

The model is discretized, and then, the displacement vector expressions $u_{3} (p_{i} )$ and $u_{1} (p_{i} )$ at the discrete point $p_{i}$ are shown in Eqs. (3) and (4). In the calculation of roll deformation, the $T_{j} (X_{2} )$ is an uniform distribution along the $X_{1}$ axis, and it is a quadratic distribution along the $X_{2}$ axis.

$$ \begin{aligned} \varvec{u}_{\varvec{3}} (P_{i} ) & = \sum\limits_{j = 1}^{n} {\int_{{S_{1} }} {\varvec{u}_{{\varvec{33}}}^{\varvec{*}} (P_{i} ,Q)\varvec{T}_{\varvec{j}} (X_{2} ){\text{d}}S} } {\kern 1pt} - \varvec{u}_{\varvec{1}} (P_{1} )\int_{{S_{3}^{l} }} {\varvec{t}_{{\varvec{31}}}^{\varvec{*}} (P_{i} ,Q)f^{\prime}(X_{2} ,X_{3} ){\text{d}}S} - \varvec{u}_{\varvec{1}} (P_{n} )\int_{{S_{3}^{r} }} {\varvec{t}_{{\varvec{31}}}^{\varvec{*}} (P_{i} ,Q)f^{\prime}(X_{2} ,X_{3} ){\text{d}}S} \\ & \quad - \varvec{u}_{\varvec{3}} (P_{1} )\int_{{S_{3}^{l} }} {\varvec{t}_{{\varvec{33}}}^{\varvec{*}} (P_{i} ,Q)f(X_{2} ,X_{3} ){\text{d}}S} - \varvec{u}_{\varvec{3}} (P_{n} )\int_{{S_{3}^{r} }} {\varvec{t}_{{\varvec{33}}}^{\varvec{*}} (P_{i} ,Q)f(X_{2} ,X_{3} ){\text{d}}S} \quad (i = 1, \ldots n) \\ \end{aligned} $$

(3)

$$ \begin{aligned} \varvec{u}_{\varvec{1}} (P_{i} ) & = \sum\limits_{j = 1}^{n} {\int_{{S_{1} }} {\varvec{u}_{{\varvec{13}}}^{\varvec{*}} (P_{i} ,Q)\varvec{T}_{\varvec{j}} (X_{2} ){\text{d}}S} } - \varvec{u}_{\varvec{1}} (P_{1} )\int_{{S_{3}^{l} }} {\varvec{t}_{{\varvec{11}}}^{\varvec{*}} (P_{i} ,Q)f^{\prime}(X_{2} ,X_{3} ){\text{d}}S} - \varvec{u}_{\varvec{1}} (P_{n} )\int_{{S_{3}^{r} }} {\varvec{t}_{{\varvec{11}}}^{\varvec{*}} (P_{i} ,Q)f^{\prime}(X_{2} ,X_{3} ){\text{d}}S} \\ & \quad - \varvec{u}_{\varvec{3}} (P_{1} )\int_{{S_{3}^{l} }} {\varvec{t}_{{\varvec{13}}}^{\varvec{*}} (P_{i} ,Q)f(X_{2} ,X_{3} ){\text{d}}S} - \varvec{u}_{\varvec{3}} (P_{n} )\int_{{S_{3}^{r} }} {\varvec{t}_{{\varvec{13}}}^{\varvec{*}} (P_{i} ,Q)f(X_{2} ,X_{3} ){\text{d}}S} \quad (i = 1,n) \\ \end{aligned} $$

(4)

$$ T_{j} (X_{2} ) = \frac{{3F_{j} }}{4b(j)}\left[ {1 - \left( {\frac{{X_{2} }}{b(j)}} \right)^{2} } \right] $$

(5)

where $F_{j}$ is the sum of the distribution forces on the j element, and $b(j)$ is half width of the j element.

In order to solve the boundary integral equation, the relationships of $u_{3}^{l} (Q)$ and $u_{3} (P_{1} )$; $u_{3}^{r} (Q)$ and $u_{3} (P_{n} )$; $u_{1}^{l} (Q)$ and $u_{1} (P_{1} )$; $u_{1}^{r} (Q)$ and $u_{1} (P_{n} )$ are established by finite element analysis and numerical fitting. Therefore, Eqs. (3) and (4) are simplified to Eqs. (6) and (7):

$$ u_{3} (P_{i} ) + K_{1i}^{l} \cdot u_{1} (P_{1} ) + K_{1i}^{r} \cdot u_{1} (P_{n} ) + K_{3i}^{l} \cdot u_{3} (P_{1} ) + K_{3i}^{r} \cdot u_{3} (P_{n} ) = \sum\limits_{j = 1}^{n} {\int_{{S_{1} }} {u_{33}^{ * } (P_{i} ,Q)T_{j} (X_{2} ){\text{d}}S} } {\kern 1pt} \quad (i = 1,2, \ldots n) $$

(6)

$$ u_{1} (P_{i} ) + K_{1i}^{l'} \cdot u_{1} (P_{1} ) + K_{1i}^{r'} \cdot u_{1} (P_{n} ) + K_{3i}^{l'} \cdot u_{3} (P_{1} ) + K_{3i}^{r'} \cdot u_{3} (P_{n} ) = \sum\limits_{j = 1}^{n} {\int_{{S_{1} }} {u_{13}^{ * } (P_{i} ,Q)T_{j} (X_{2} ){\text{d}}S} } \quad (i = 1,n) $$

(7)

where $K_{1i}^{l} = \int_{{S_{3}^{l} }} {t_{31}^{ * } (P_{i} ,Q)f^{\prime}(X_{2} ,X_{3} ){\text{d}}S}$; $K_{1i}^{r} = \int_{{S_{3}^{r} }} {t_{31}^{ * } (P_{i} ,Q)f^{\prime}(X_{2} ,X_{3} ){\text{d}}S}$; $K_{3i}^{l} = \int_{{S_{3}^{l} }} {t_{33}^{ * } (P_{i} ,Q)f(X_{2} ,X_{3} ){\text{d}}S}$; $K_{3i}^{r} = \int_{{S_{3}^{r} }} {t_{33}^{ * } (P_{i} ,Q)f(X_{2} ,X_{3} ){\text{d}}S}$; $K_{1i}^{l'} = \int_{{S_{3}^{l} }} {t_{11}^{ * } (P_{i} ,Q)f^{\prime}(X_{2} ,X_{3} ){\text{d}}S}$; $K_{1i}^{r'} = \int_{{S_{3}^{r} }} {t_{11}^{ * } (P_{i} ,Q)f^{\prime}(X_{2} ,X_{3} ){\text{d}}S}$; $K_{3i}^{l'} = \int_{{S_{3}^{l} }} {t_{13}^{ * } (P_{i} ,Q)f(X_{2} ,X_{3} ){\text{d}}S}$; $K_{3i}^{r'} = \int_{{S_{3}^{r} }} {t_{13}^{ * } (P_{i} ,Q)f(X_{2} ,X_{3} ){\text{d}}S}$.

For a certain example, the accuracy of the new model is verified by comparing the calculation results of the new model, the semi-infinite body model, and the Foppl model with the finite element simulation results [14].

2.2 Establishment of the work roll edge contact model for 20-high mill

The work roll contact phenomenon shown in Fig. 2 is very common, and there is a very serious edge drop and edge wave. After the appearance of the work roll contact, the force diagram of the work roll is shown in Fig. 3, where the work roll is subjected to the negative bending force generated by the backup roll and the positive bending force generated by the other work roll.

Fig. 2

Schematic of the work roll edge contact

Fig. 3

Force diagram of the work roll under work roll contact

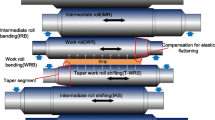
Then, based on this flattening model, a more accurate plate profile control model for the laboratory 20-high mill is established by coupling the roll flexural deflection model and the strip plastic deformation [15, 16]. The 20-high mill roll system arrangement and primary technological parameters are shown in Fig. 4 and in Table 1, respectively.

Fig. 4

20-High mill rolls system arrangement

Table 1 Primary technological parameters of the 20-high mill

Taking the A–B direction of the A-roll as a research object, the force balance equation, moment equilibrium equation, deflection equation, and displacement coordination function are established, respectively. The analysis of the A-roll in the other direction and the remaining rolls are similar to that of the A-roll in the A–B direction.

The force balance equation of A-roll along A–B direction can be shown as follows:

$$ q_{AB} ((1 + \sin (2\alpha_{1} - 90^{\circ} )) - P\sin \alpha_{1} = 0 $$

(8)

where $q_{AB}$ is pressure between A-roll and B-roll, $p$ is the rolling pressure, $\alpha_{1}$ is the angle centre connection line AB and horizontal line.

The moment equilibrium equation of A-roll along A–B direction can be shown as follows:

$$ \sum\limits_{i = 1}^{n} {q_{AB} (i)x(i)(1 + \sin (2\alpha_{1} - 90^{ \circ } )) - P(i)x(i)\sin \alpha_{1} } = 0 $$

(9)

where $x(i)$ is the position along roll axis.

Based on the influence function proposed by Shohet [17], the deflection equation of A-roll along A–B direction can be shown as follows:

$$ Y_{AB} (i) = \sum\limits_{j = 1}^{n} {G_{AL} (i,j)\left\{ {q_{AB} \left( j \right)\left[ {1 + \sin (2\alpha_{1} - 90)} \right] - p(j)\sin \alpha_{1} } \right\}} $$

(10)

where $G_{AL} (i,j)$ is A-roll bending influence coefficient.

The deformation compatibility equation of A-roll and B-roll can be shown as follows:

$$ Y_{A} (i) = Y_{B} (i) + \left[ {Z_{AB} ({\text{mid}}) - Z_{AB} (i)} \right] - \frac{{\Delta D_{AB} }}{2} + \beta_{AB} x(i) $$

(11)

where $Y_{A} (i)$ and $Y_{B} (i)$ are deflections of unit i on A-roll and B-roll along the A–B direction; $Z_{AB} ({\text{mid}})$ is roll flattening of roll centre along the A–B direction; $Z_{AB} (i)$ is roll flattening of unit i along the A–B direction; $\beta_{AB}$ is the rigid corner between A-roll and B-roll; $\Delta D_{AB}$ is the roll crown between A-roll and B-roll.

Considering with the work roll contact, the expression of the roll gap at the exit is as follows:

$$ h_{i} = \left\{ {\begin{array}{*{20}l} {h_{\text{mid}} - Y_{\text{w}}^{\text{u}} (i) - Y_{\text{w}}^{\text{d}} (i) + \frac{{\Delta D_{{{\text{w}}i}}^{\text{u}} }}{2} + \frac{{\Delta D_{{{\text{w}}i}}^{\text{d}} }}{2} - 2\left( {Z_{\text{ws}} ({\text{mid}}) - Z_{\text{ws}} (i)} \right)} \hfill \\ {\quad i = (2n - m)/2, \ldots ,(2n + m)/2} \hfill \\ {h_{\text{mid}} - Y_{\text{w}}^{\text{u}} (i) - Y_{\text{w}}^{\text{d}} (i) + \frac{{\Delta D_{{{\text{w}}i}}^{\text{u}} }}{2} + \frac{{\Delta D_{{{\text{w}}i}}^{\text{d}} }}{2} - 2\left( {Z_{\text{ws}} ({\text{mid}}) - Z_{\text{ww}} (i)} \right)} \hfill \\ {\quad i = 1, \ldots ,(2n - m - 2)/2\;\;{\text{and}}\;\;(2n + m + 2)/2, \ldots ,2n + 1} \hfill \\ \end{array} } \right. $$

(12)

where $h_{\text{mid}}$ is the value of the roll gap centre; $Y_{\text{w}}^{\text{u}} (i)$ is the up work roll deflection of i element; $Y_{\text{w}}^{\text{d}} (i)$ is the down work roll deflection of i element; $\Delta D_{{{\text{w}}i}}^{\text{u}}$ is up work roll crown of i element; $\Delta D_{{{\text{w}}i}}^{\text{d}}$ is the down work roll crown of i element; $Z_{\text{ws}} (i)$ is the roll flattening between the work roll and the strip of i element; $Z_{\text{ww}} (i)$ is the roll flattening between the up and down work rolls of i element.

The rolls gap value is adjusted when the initial value of the rolls gap is obtained in the theoretical model. The kiss between up and down rolls ends occurs if there is a negative rolls gap in a unit. In the model of the kiss between rolls ends, the contact force is increased in the unit to lift the roll gap when the negative roll gap occurs.

3 Theoretical results of the work roll edge contact

Based on the plate profile analytic model for 20-high mill, the adjustment effect of different control methods on the work roll edge contact and the ultra-thin strip shape is analysed when a very serious work roll edge contact phenomenon occurs. In the following example, the front and back tensions’ stress was 600 MPa and 500 MPa, respectively. The taper length and taper angle for the first intermediate roll are 50 mm and 0.002, respectively. The strip entry and exit thicknesses are 0.021 mm and 0.019 mm, respectively. The strip width is 68 mm. The effects of traversing the first intermediate roll and increasing the work roll edge contact on the plate profile are calculated.

3.1 Calculations of traversing the first intermediate roll

The calculations are shown in Fig. 5, where s represents the traverse displacement of the first intermediate roll. The results show that the contact pressure between the rolls gradually increases at the middle part of the work roll while decreases on the side of the strip. The rolling force shows the same rule. As the transverse displacement of the first intermediate roller increases, the strip edge drop phenomenon is obviously improved, but the distribution of the front tension indicates that there is still a wave defect at the edge of the strip. When s increases to 6 mm, although there are edge waves and centre waves on the surface of the strip, the phenomenon of work roll edge contact still exists. In summary, when a very serious work roll edge contact phenomenon exists, the effect of eliminating the edge waves by traversing the first intermediate roll is quite slight.

Fig. 5

Calculation results in different roll shifts including a contact pressure between the work roll and the first intermediate roll, b rolling pressure, c front tension, and d strip exit thickness

3.2 Calculations of utilizing the work roll edge contact

The above analysis shows that it is difficult to eliminate edge waves with the traditional control methods. From the force analysis of the work roll, it can be seen that the roll gap will be adjusted by utilizing the step roll as shown in Fig. 6 to improve the shape. In this paper, two kinds of step rolls are used for calculation. The boss height of the step rolls is 0.01 mm, and the boss lengths of step roll-1 and step roll-2 are 5 mm and 10 mm, respectively.

Fig. 6

Work roll contour underutilizing work roll edge contact

The calculations of utilizing the work roll edge contact are shown in Fig. 7. The results show that when the step roll in Fig. 6 is used, the contact pressure between rolls gradually decreases at the middle part of the work roll and increases on the side of the strip. However, the rolling pressure is significantly reduced near the edge of the strip and markedly increased at the edge of the step roll. The phenomenon of strip edge drop is obviously improved, and the distribution of the front tension indicates that the edge wave is eliminated. When using a step roll with a boss length of 10 mm and boss height of 0.01 mm, the edge drop is the least and the strip shape is the best. This is because the step roll increases the contact pressure between the work rolls, reducing the deflection of the work roll, thereby improving the work roll profile.

Fig. 7

Calculating results in different step work rolls including a contact pressure between the work roll and the first intermediate roll, b rolling pressure, c front tension, and d strip exit thickness

4 Experiment of the work roll edge contact

The trial rolling was carried out before the experiment. Firstly, the inkpad was applied to both ends of the up and down work rolls, and then, single-pass rolling was performed. It should be checked whether the up and down work rolls have inkpad after each pass. The phenomenon that the kiss between rolls ends is appeared during the rolling process when the inkpad appears at both ends of up and down work rolls. After the trial rolling, the phenomenon that the kiss between rolls ends was occurred when the front and back tension stress was 490 MPa and 425 MPa, respectively, the taper length of the first intermediate rolls was 60 mm and the taper angle was 0.002, the ultra-thin strip was rolled from 0.035 mm to 0.031 mm.

To verify the accuracy of the work roll contact model, the same process parameters as the theoretical calculation are used to carry out the ultra-thin strip rolling experiments. The effects of traversing the intermediate roll and utilizing the step roll on the plate profile are researched, respectively.

4.1 Experimental results of traversing the first intermediate roll

In view of the above theoretical analysis, the experimental results of traversing the first intermediate roll are shown in Fig. 8. When the traverse displacement of the first intermediate roll is zero, extremely serious waves appear on the surface of the ultra-thin strip. With the increase in displacement, the waves can be restrained to a certain degree. When the traverse displacement reaches 6 mm, the obvious centre waves appear on the surface, but there are still edge waves. It can be seen that the strip shape characteristics after rolling are consistent with the calculated front tension distributions. Therefore, in this case, it is very difficult to eliminate strip shape defects by traversing the first intermediate roll.

Fig. 8

Experimental results for a s = 0, b s = 3 mm, and c s = 6 mm

4.2 Experimental results of increasing the work roll edge contact

In view of the above theoretical analysis, the experimental results of increasing the work roll edge contact are shown in Fig. 9. The phenomenon of strip edge drop is obviously improved, and the distribution of the front tension indicates that the edge wave is eliminated. When using a step work roll, the edge waves are effectively suppressed, and the strip shape is the best until the boss length increases to 10 mm. It can be seen that the strip shape characteristics after rolling are consistent with the calculated front tension distributions. Therefore, when serious work roll edge contact and edge waves exist, the roll gap will be adjusted by utilizing work roll edge contact to achieve an improved shape.

Fig. 9

Experimental results for a flat roll, b step roll-1, and c step roll-2

In summary, the step roll shown in Fig. 6 can be directly used during ultra-thin strip cold rolling. The boss height is much smaller than the diameter of the work rolling; thus, when the strip thickness is relatively large, the work roll edge contact phenomenon will not occur. Nevertheless, when the strip thickness is relatively small, the step work roll can be used to increase the contact pressure to adjust the strip shape during the rolling process.

5 Conclusions

• 1. A finite-length semi-infinite body model of the roll is established based on the boundary integral equation method, which is applied to the rolling process of twenty-high mill, and an accurate work roll edge contact model is established. The calculations from the new model are consistent with the experimental results, verifying the accuracy of the model.

• 2. During ultra-thin strip cold rolling, a phenomenon of work roll edge contact always appears. There is a very serious work roll edge contact and an edge wave that occur as the strip thickness decreases, which is difficult to be eliminated with the traditional control methods. The effect of applying a positive bending force to the work roll can be achieved by improving the work roll edge contact.

• 3. Theoretical and experimental results show that when s increases to 6 mm, although there are edge waves and centre waves on the surface of the strip, there is a work roll edge contact phenomenon for the strip with entry thickness 0.021 mm and exit thickness 0.019 mm. When using a step roll with a boss length of 10 mm and boss height of 0.01 mm, the edge drop is the least and the strip shape is the best.