1 Introduction

Zirconia ceramics has obvious advantages in dental prosthodontics with the consideration of their excellent mechanical strength, outstanding wear resistance, superior esthetics, and so on [1,2,3]. However, when zirconia ceramics as a denture chews in the oral cavity, friction and wear is unavoidable [4, 5]. Liu et al. [6] investigated the friction and wear phenomenon between zirconia and natural enamel, and fatigue wear was found. Wang et al. conducted tribological tests of dental ceramics, and the results showed that the abrasive wear appeared [7]. There are two ways to reduce friction and wear which are the improvement in surface topography and lubricant. But the improvement in saliva in the oral cavity is difficult to put into practice. Thus, surface topography enhancement of zirconia ceramics is applied to the field of dental prosthodontics. Many investigations have indicated that surface topography feature is the key factor that affects friction and wear performance [8,9,10]. Li et al. [11] fabricated microdimple on copper surface by laser peen texturing (LPT), and it showed that friction coefficient with surface texture density of 13% could be decreased up to about 50% compared with that of untextured surface. Tang et al. [12] experimentally researched the relationship between surface texturing and friction and wear performance, and it had been known that friction could be reduced by 38%, while wear was decreased up to 72% when the dimple area fraction was 5%. Segu et al. [13] had created patterned microstructures by laser surface texturing technology, it presented friction coefficient with textured surface was lower than that with untextured surface, and dimple depth had an effect on friction coefficients reduction. From the above researches, it can be seen that there is a close link between surface topography and friction and wear performance. Therefore, it is necessary to fabricate suitable surface to improve friction and wear phenomenon.

Ultrasonic vibration-assisted grinding (UVAG) technology has been verified that it has outstanding advantages (long cutting life, low cutting force and so on) to fabricate hard and brittle materials [14,15,16,17,18]. For these advantages, in dental prosthodontics, UVAG technology is applied to fabricate ceramics restorations [19]. UVAG surface topography shows uniform and discontinuous grooves which have relationship with friction and wear performance [19]. Thus, in order to control friction and wear phenomenon of zirconia ceramics in dental prosthodontics, it is necessary to clarify the UVAG surface features. A series of researches have been conducted to clarify the UVAG surface quality and surface feature. Yan et al. [20] conducted two-dimensional ultrasonic-assisted grinding and diamond grinding experiments, surface roughness Ra was used to characterize surface quality, and it was 0.081 μm after UVAG, while it was 0.162 μm after DG. Guo et al. [21] introduced ultrasonic vibration-assisted grinding (UVAG) to machining microstructured surfaces and explained the relationship between cutting paraments and microstructured surface, the results showed that ultrasonic vibration could keep the edge sharpness of the microstructure, and there was no significant impact on microstructured surface roughness when spindle speed was from 1000 to 3000 rpm. However, quantitative relationships between geometric parameters on UVAG surface and grinding parameters have not been attained in these researches. While the quantitative relationships can be employed to design the surface topography in UVAG considering industrial demand, they provide a deep understanding of UVAG processing. Therefore, combined with friction and wear properties, five geometric parameters are proposed for UVAG surface in this paper. First of all, five geometric parameters are chosen to describe UVAG surface topography. The quantitative relationships between five geometric parameters and grinding parameters are proposed. Besides, UVAG verification tests are conducted on zirconia ceramics.

This study is made up of four sections. This section is introduction section. The quantitative relationships between five geometric parameters and grinding parameters are given in Sect. 2. UVAG verification tests are carried out to validate the quantitative relationships in Sect. 3. Conclusions are given in Sect. 4.

2 Surface topography model during UVAG

It has been proved that there are uniform and discontinuous grooves on the surface machined by UVAG [19]. In order to clearly illustrate these surface features, five geometric parameters are selected, which are width, depth, length of a single groove, spacing between two adjacent grooves in the feed direction on the UVAG surface and the number of grooves with the measured scale of 100 μm × 100 μm. The list of symbols in this work is given in Table 1.

Table 1 List of symbols
Full size table

2.1 Zirconia ceramics removal mechanism of a single grain during UVAG

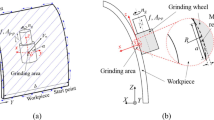
UVAG technology is the complex cutting process of the entire grains on the end of the tool, as shown in Fig. 1. Kinematics analysis of a single grain is selected to clarify kinematic relationships in UVAG. It is expressed as:

$$\left\{ {\begin{array}{*{20}l} {S_{x} = V_{\text{s}} t + r\;{ \cos }(\omega t)} \hfill \\ {S_{y} = r\;{ \sin }(\omega t)} \hfill \\ {S_{z} = A\;{ \sin }(2\pi ft)} \hfill \\ \end{array} } \right.$$
(1)

where f means ultrasonic vibration frequency, Hz; A is ultrasonic amplitude, μm; r denotes the rotational radius of a grain, mm; ω is angular velocity of a grain, rad/s; feed rate is Vs, mm/s; t is the cutting time of a grain, s.

Fig. 1
figure 1

Kinematic relationship in UVAG

Full size image

According to the crack system of a single grain of zirconia ceramics, it can be known that the width CL0 and depth Ch0 of the lateral crack can be presented by the following equation [22]:

$$C_{\text{L0}} = C_{2} \left( {{ \tan }\frac{\beta }{2}} \right)^{{\frac{ - 5}{12}}} \cdot \left[ {\frac{{E^{{\frac{3}{4}}} }}{{H_{\text{v}} K_{\text{IC}} \left( {1 - \upsilon^{2} } \right)^{{\frac{1}{2}}} }}} \right]^{{\frac{1}{2}}} \cdot F^{{\frac{5}{8}}}$$
(2)
$$C_{\text{h0}} = C_{2} \left( {{ \tan }\frac{\beta }{2}} \right)^{{ - \frac{1}{3}}} \cdot \frac{{E^{{\frac{1}{2}}} }}{{H_{\text{v}} }} \cdot F^{{\frac{1}{2}}}$$
(3)

where F is the force of a single grain, N; C2 = 0.226 [22]; υ denotes Poisson’s ratio of zirconia ceramics with β which is the apex angel of a single grain; KIC means fracture strength of zirconia ceramics, MPam1/2; E is the Young’s modulus, MPa; Hv is the hardness, MPa.

The total force of entire grains can be obtained as [23]:

$$\begin{aligned} F_{N} & = C_{0}^{{\frac{1}{8}}} \cdot C_{2}^{{ - \frac{15}{8}}} \cdot e^{{\frac{ - 1}{8}}} \cdot C_{\text{a}}^{{\frac{1}{12}}} \cdot K_{0} \cdot K_{1}^{{\frac{7}{8}}} \cdot \frac{{\left( {R_{2}^{2} - R_{1}^{2} } \right)^{{\frac{1}{8}}} }}{{\left( {R_{2} + R_{1} } \right)^{{\frac{7}{8}}} }} \cdot \left( {\frac{{D_{2} \cdot V_{\text{s}} }}{n}} \right)^{{\frac{7}{8}}} \\ & \quad \cdot \frac{{\left( {A + a_{\text{p}} } \right)^{{\frac{7}{8}}} }}{{A^{{\frac{1}{8}}} }} \cdot \frac{{H_{\text{v}}^{{\frac{21}{16}}} \cdot K_{\text{IC}}^{{\frac{1}{2}}} \cdot \left( {1 - \upsilon^{2} } \right)^{{\frac{1}{4}}} }}{{E^{{\frac{13}{16}}} \cdot \left( {{ \tan }\frac{\beta }{2}} \right)^{{\frac{13}{16}}} }} \\ \end{aligned}$$
(4)

where n is spindle speed, r/min; ap means cutting depth, mm; \(K_{0} = 2^{ - 33/16} \times 360^{7/8} \times \xi^{1/16} \times \pi^{ - 7/8} = 14.60\); \(K_{1} = 0.064n^{0.5738} \cdot V_{\text{s}}^{ - 0.8564} \cdot a_{\text{p}}^{ - 0.5313}\); \(C_{0} = [3 \times 0.88 \times 10^{ - 3} /(100 \times 2^{0.5} \rho )]^{2/3}\); D2 is the outer diameter of tool, mm; R2 is the outer radius, mm; R1 denotes the inner radius, mm; ρ means density of zirconia ceramics, g/cm3; Ca is the concentration of grains; e means the grain size, mm.

The effective grain number is expressed as:

$$N_{\text{all}} = C_{0} \frac{{C_{a}^{{\frac{2}{3}}} }}{{e^{2} }}\pi R_{2}^{2} .$$
(5)

Thus, the force of a single grain can be derived as:

$$\begin{aligned} F & = \frac{{F_{N} }}{{N_{\text{all}} }} = C_{0}^{{\frac{ - 7}{8}}} \cdot C_{2}^{{ - \frac{15}{8}}} \cdot e^{{\frac{15}{8}}} \cdot C_{a}^{{\frac{ - 7}{12}}} \cdot R_{2}^{ - 2} \cdot K_{0} \cdot \pi^{ - 1} \cdot K_{1}^{{\frac{7}{8}}} \cdot \frac{{\left( {R_{2}^{2} - R_{1}^{2} } \right)^{{\frac{1}{8}}} }}{{\left( {R_{2} + R_{1} } \right)^{{\frac{7}{8}}} }} \\ & \quad \cdot \left( {\frac{{D_{2} \cdot V_{\text{s}} }}{n}} \right)^{{\frac{7}{8}}} \cdot \frac{{\left( {A + a_{\text{p}} } \right)^{{\frac{7}{8}}} }}{{A^{{\frac{1}{8}}} }} \cdot \frac{{H_{v}^{{\frac{21}{16}}} \cdot K_{\text{IC}}^{{\frac{1}{2}}} \cdot \left( {1 - \upsilon^{2} } \right)^{{\frac{1}{4}}} }}{{E^{{\frac{13}{16}}} \cdot \left( {{ \tan }\frac{\beta }{2}} \right)^{{\frac{13}{16}}} }}. \\ \end{aligned}$$
(6)

Substituting Eq. 6 into Eqs. 2 and 3, CL0 and Ch0 can be calculated as:

$$C_{\text{L0}} = m \cdot n^{ - 0.2599} \cdot V_{\text{s}}^{0.07853} \cdot a_{\text{p}}^{ - 0.2906} \cdot \left( {A + a_{\text{p}} } \right)^{0.5469} \cdot A^{ - 0.07813}$$
(7)

where \(\begin{aligned} m & = 0.1087 \cdot C_{2}^{ - 0.1719} \cdot \left( {\tan \frac{\beta }{2}} \right)^{ - 0.5339} \cdot E^{ - 0.1328} \cdot H_{\text{v}}^{0.3203} \cdot K_{\text{IC}}^{ - 0.1875} \\ & \quad \cdot \left( {1 - \upsilon^{2} } \right)^{ - 0.09375} \cdot K_{0}^{0.625} \cdot C_{0}^{ - 0.5469} \cdot C_{a}^{ - 0.3646} \cdot e^{1.1719} \cdot R_{2}^{ - 1.25} \cdot D_{2}^{0.5469} \\ & \quad \cdot \left( {R_{2}^{2} - R_{1}^{2} } \right)^{0.07813} \cdot \left( {R_{2} + R_{1} } \right)^{ - 0.5469} \\ \end{aligned}\)

$$C_{\text{h0}} = m_{1} \cdot n^{ - 0.1865} \cdot V_{\text{s}}^{ - 0.06207} \cdot a_{\text{p}}^{ - 0.2324} \cdot \left( {A + a_{\text{p}} } \right)^{0.4375} \cdot A^{ - 0.0625}$$
(8)

where \(\begin{aligned} m_{1} & = 0.1664 \cdot C_{2}^{0.0625} \cdot \left( {\tan \frac{\beta }{2}} \right)^{ - 0.7396} \cdot E^{0.09375} \cdot H_{\text{v}}^{ - 0.3438} \cdot K_{0}^{0.5} \cdot C_{0}^{ - 0.4375} \\ & \quad \cdot C_{\text{a}}^{ - 0.2917} \cdot e^{0.9375} \cdot R_{2}^{ - 1} \cdot D_{2}^{0.4375} \cdot \left( {R_{2}^{2} - R_{1}^{2} } \right)^{0.0625} \cdot \left( {R_{2} + R_{1} } \right)^{ - 0.4375} . \\ \end{aligned}\)Since UVAG is an interrupted cutting process, the effective cutting time can be expressed as [23]:

$$t_{\text{valid}} = \, \frac{1}{\pi f} \cdot \left[ {\frac{\pi }{2} - { \arcsin }\left( {1 - \frac{\delta }{A}} \right)} \right]$$
(9)

where δ is the maximum cutting depth of a grain.

δ can be derived as [23]:

$$\delta^{2} = \frac{{720K_{1} \left( {A + a_{p} } \right) \cdot D_{2} \cdot V_{s} \cdot A \cdot e}}{{\left( {\frac{1}{2}\xi } \right)^{{\frac{1}{2}}} \cdot C_{2} \cdot C_{0} \cdot C_{a}^{{\frac{2}{3}}} \cdot \pi n \cdot \left( {R_{2} + R_{1} } \right)^{2} \cdot \left( {R_{2} - R_{1} } \right)}} \cdot \frac{{H_{v}^{{\frac{1}{2}}} }}{{E^{{\frac{1}{2}}} \cdot \left( {\tan \frac{\beta }{2}} \right)^{{\frac{1}{6}}} }}$$
(10)

where ξ = 1.85.

Therefore, the effective cutting length of one grain in a certain period can be derived as:

$$l_{0} = \frac{2\pi nr}{60} \cdot t_{\text{valid}}$$
(11)

where r is the rotational radius of the grain, mm.

Substituting Eqs. (9) and (10) into Eq. (11), the effective cutting length l0 can be obtained as:

$$l_{0} = \frac{2nr}{60} \cdot \frac{1}{f} \cdot \left[ {\frac{\pi }{2} - \arcsin \left( {1 - \frac{{720^{{\frac{1}{2}}} K_{1}^{{\frac{1}{2}}} \left( {A + a_{p} } \right)^{{\frac{1}{2}}} D_{2}^{{\frac{1}{2}}} V_{s}^{{\frac{1}{2}}} e^{{\frac{1}{2}}} }}{{(\frac{1}{2}\xi )^{{\frac{1}{4}}} C_{2}^{{\frac{1}{2}}} C_{0}^{{\frac{1}{2}}} C_{a}^{{\frac{1}{3}}} \pi^{{\frac{1}{2}}} n^{{\frac{1}{2}}} A^{{\frac{1}{2}}} \left( {R_{2} + R_{1} } \right)\left( {R_{2} - R_{1} } \right)^{{\frac{1}{2}}} }} \cdot \frac{{H_{v}^{{\frac{1}{4}}} }}{{E^{{\frac{1}{4}}} \left( {\tan \frac{\beta }{2}} \right)^{{\frac{1}{12}}} }}} \right)} \right]$$
(12)

Thus, according to the above analysis, it can be known the size of a groove (the width 2CL0, the depth Ch0 and the effective cutting length l0) which is formed by the crack system and the movement of one grain in a period, as shown in Fig. 2. Actually, interference is inevitable under the actual conditions. Therefore, interference phenomenon is analyzed by the following sections:

Fig. 2
figure 2

Schematic illustration of a groove in one period

Full size image

2.2 Analysis of actual width, depth and length of one groove on the surface based on overlapping

Assuming that the distribution of grains is uniform, the probability density function f (r) can be obtained as:

$$f(r) = \frac{1}{{R_{2} }}.$$
(13)

The distance of centerline between two successive grooves fabricated by two adjacent grains can be expressed as:

$$\Delta d = \left| {r_{x + 1} - r_{x} } \right|$$
(14)

where x means the xth groove.

Set \(r_{x} = d_{2}\), \(r_{x + 1} = d_{1} + d_{2}\), as shown in Fig. 3. d1 and d2 can be presented as:

$$d_{1} = r_{x + 1} - r_{x}$$
(15)
$$d_{2} = r_{x}$$
(16)
Fig. 3
figure 3

Schematic illustration of two successive grooves

Full size image

From Eqs. (14) and (15), it can be known that \(\Delta d = \left| {d_{1} } \right|\).

The probability density function of Δd can be expressed as:

$$P(\left| {d_{1} } \right| \le \Delta d) = P(d_{1} \le - \Delta d) + P(d_{1} \le - \Delta d).$$
(17)

The expected value of Δd can be calculated by a joint probability density function f(d1,d2) which can be presented as:

$$f\left( {d_{1} ,d_{2} } \right) = f(r_{1} (d_{1} ,d_{2} ),r_{2} (d_{1} ,d_{2} ))\left| J \right|$$
(18)

where J denotes the Jacobian determinant.

Therefore, from the above analysis, the expected value of Δd can be calculated by the following equations:

$$E(\Delta d) = \int_{0}^{d} {\Delta d \cdot f(\Delta d)} d(\Delta d) = \frac{1}{3}d$$
(19)

where d is 2CL0.

$$E(\Delta d) = \frac{1}{3}d = \frac{1}{3} \cdot 2C_{\text{L0}} = \frac{2}{3}C_{\text{L0}}$$
(20)

According to Eq. (20), the two successive overlapping grooves are described in Fig. 4. The overlapping of grooves in radial direction is caused by random distribution of grains in radial direction. The width dw1 of the overlapping groove can be derived as:

$$d_{\text{w1}} = C_{\text{L0}} + \frac{2}{3}C_{\text{L0}} + C_{\text{L0}} = \frac{8}{3}C_{\text{L0}} .$$
(21)
Fig. 4
figure 4

Two successive overlapping grooves

Full size image

During the actual UVAG process, the actual width dw, depth hd and length ld of one groove on the surface are affected by the overlapping of different grains which depends on grinding parameters (spindle speed n, feed rate Vs, cutting depth ap and power ratio k). It means that there are some differences between dw, hd, ld and dw1, Ch0, l0. In order to solve this problem, overlapping parameters k0 (\(k_{0} = c_{0} n^{{a_{10} }} V_{\text{s}}^{{a_{20} }} a_{\text{p}}^{{a_{30} }} k^{{a_{40} }}\)), k1 (\(k_{1} = c_{1} n^{{a_{11} }} V_{\text{s}}^{{a_{21} }} a_{\text{p}}^{{a_{31} }} k^{{a_{41} }}\)) and k2 (\(k_{2} = c_{2} n^{{a_{12} }} V_{\text{s}}^{{a_{22} }} a_{\text{p}}^{{a_{32} }} k^{{a_{42} }}\)) are introduced. Thus, the actual width dw, depth hd and length ld can be expressed as:

$$d_{\text{w}} = k_{0} \cdot d_{\text{w1}}$$
(22)
$$h_{\text{d}} = k_{1} C_{\text{h0}}$$
(23)
$$l_{\text{d}} = k_{2} \cdot l_{0} .$$
(24)

2.3 Analysis of spacing between two grooves on the surface

From Eq. (1), the kinematic equation of a single abrasive grain in the feed direction can be obtained as:

$$S(x) = V_{\text{s}} t + r\;{ \cos }(2\pi nt).$$
(25)

When time is t0, Eq. (25) can be derived as:

$$S(x_{0} ) = V_{\text{s}} t_{0} + r\;{ \cos }(2\pi nt_{0} ).$$
(26)

When time is t0 + T, Eq. (25) can be derived as:

$$S(x_{1} ) = V_{\text{s}} \left( {t_{0} + T} \right) + r\;{ \cos }(2\pi n\left( {t_{0} + T} \right))$$
(27)

where T is the rotating period of the tool, s,

$$T{ = }\frac{1}{n}.$$
(28)

Thus, the spacing Δd1 between two grooves fabricated by a single grain in unit period in the feed direction can be obtained as:

$$\Delta d_{1} = S(x_{1} ) - S(x_{0} ) = \frac{{V_{s} }}{n}.$$
(29)

During the actual UVAG process, the spacing df between two grooves on the surface is affected by the overlapping of different grains which depends on grinding parameters (spindle speed n, feed rate Vs, cutting depth ap and power ratio k). In order to solve this problem, an overlapping parameter k3 (\(k_{3} = c_{3} n^{{a_{13} }} V_{\text{s}}^{{a_{23} }} a_{\text{p}}^{{a_{33} }} k^{{a_{43} }}\)) is introduced. Therefore, the spacing df between two grooves on the surface can be presented as:

$$d_{\text{f}} = k_{3} \cdot \Delta d_{1} .$$
(30)

2.4 Analysis of number of grooves on the surface

During UVAG, there is an ultrasonic vibration. The vibration period T0 can be expressed as:

$$T_{0} = \frac{1}{f}$$
(31)

where f is ultrasonic vibration frequency, Hz.

Thus, the number N1 of grooves in one rotating period can be obtained as:

$$N_{1} { = }\frac{T}{{T_{0} }} = \frac{f}{n}$$
(32)

During the actual UVAG surface, it is difficult to count the number N1. The number N in unit area (100 μm × 100 μm) on the surface is used to replace N1. There are some differences between N1 and N because of the overlapping of different grains. The degree of overlapping depends on grinding parameters (spindle speed n, feed rate Vs, cutting depth ap and power ratio k). Therefore, an overlapping parameter k4 (\(k_{4} = c_{4} n^{{a_{14} }} V_{\text{s}}^{{a_{24} }} a_{\text{p}}^{{a_{34} }} k^{{a_{44} }}\)) is introduced. The number N can be expressed as:

$$N = k_{4} \cdot N_{1}$$
(33)

3 Experiments and results

3.1 Experimental details

UVAG experiments are conducted on a machine which is DMG Ultrasonic 20 linear, DMG, Germany. The frequency of ultrasonic vibration is 23,540 Hz in this study. The amplitude of ultrasonic vibration is replaced by power ratio. When power ratio varies from 0 to 100%, vibration amplitude changes from about 0 to 5 μm. 100% of power ratio equals to 34 W. The outer diameter of diamond tool (provided by Schott Diamantwerkzeuge GmbH in Germany) is 8 mm, while wall thickness is 0.6 mm. And grain size is D126. Zirconia ceramics (provided by Qinhuangdao Aidite High-Technical Ceramics, Co., Ltd) is used as workpieces. The mechanical properties are shown in Table 2. Synergy 915 is used as an external coolant.

Table 2 Mechanical properties of zirconia ceramics
Full size table

3.2 Obtaining k 0, k 1, k 2, k 3, k 4 and five surface feature parameters

Based on Eqs. (8), (12), (21), (22), (23), (24), (29), (30), (32) and (33), if the width dw, depth hd, length ld, spacing df and number N of surface are measured through experiments, the parameters k0, k1, k2, k3 and k4 can be obtained by the least square estimation (LSE) method. The experimental details for getting k0, k1, k2, k3 and k4 are given in Table 3. The five parameters (dw, hd, ld, df and N) are measured by laser microscope (KEYENCE, VK-X 100 series). In order to ensure the measurement accuracy of the width dw, depth hd, length ld, spacing df and number N on the machined surface, every parameter measurement is repeated five times. The five parameters are measured in the center of specimen in the feed direction. The average value will be considered as the final value of dw, hd, ld, df or N. When the number N is measured, the scale is 100 μm × 100 μm. UVAG surface topography is shown in Fig. 5. dw, ld, df and N are expressed in Fig. 5. hd is the depth of one groove. k0, k1, k2, k3 and k4 can be obtained as:

$$k_{0} = 0.2802n^{0.3203} V_{\text{s}}^{0.26347} \cdot a_{\text{p}}^{0.3601} \cdot k^{0.0830}$$
(34)
$$k_{1} = 0.9167n^{ - 0.1765} V_{\text{s}}^{ - 0.2403} a_{\text{p}}^{0.0594} k^{ - 0.9697}$$
(35)
$$k_{2} = 480.7286n^{ - 0.4739} V_{\text{s}}^{0.4675} a_{\text{p}}^{0.0711} k^{ - 0.0206}$$
(36)
$$k_{3} = 0.0123n^{1.2244} V_{\text{s}}^{0.6368} a_{\text{p}}^{0.0287} k^{0.4428}$$
(37)
$$k_{4} = 4.8540e^{ - 4} n^{1.0143} V_{\text{s}}^{ - 0.9483} a_{\text{p}}^{0.0030} k^{0.0461}$$
(38)
Table 3 Experimental details for getting k0, k1, k2, k3 and k4
Full size table
Fig. 5
figure 5

UVAG surface topography in group five

Full size image

Then, according to Eqs. (8), (12), (21), (22), (23), (24), (29), (30), (32), (33), (34), (35), (36), (37) and (38), five surface feature parameters (the width dw, depth hd, length ld, spacing df and number N) can be derived as:

$$d_{\text{w}} = 0.0198n^{0.0604} V_{\text{s}}^{0.3420} a_{\text{p}}^{0.3601} k^{0.0830}$$
(39)
$$h_{\text{d}} = 0.0033n^{ - 0.3630} V_{\text{s}}^{ - 0.3024} a_{\text{p}}^{ - 0.1730} k^{ - 0.9697}$$
(40)
$$\begin{aligned} l_{\text{d}} & = 0.002723n^{0.5261} V_{\text{s}}^{0.4675} a_{\text{p}}^{0.0711} k^{ - 0.0206} \\ & \quad \cdot \left[ {\frac{\pi }{2} - \arcsin \left( {1 - 1.1109n^{ - 0.2131} V_{\text{s}}^{0.0718} a_{\text{p}}^{ - 0.26565} } \right)} \right] \\ \end{aligned}$$
(41)
$$d_{\text{f}} = 0.0123n^{0.2244} V_{\text{s}}^{1.6368} a_{\text{p}}^{0.0287} k^{0.4428}$$
(42)
$$N = 4.8540e^{ - 4} n^{0.0143} V_{\text{s}}^{ - 0.9483} a_{\text{p}}^{0.0030} k^{0.0461} f$$
(43)

From Eqs. (39), (40), (41), (42) and (43), it can be seen that surface feature parameters are closely related to grinding parameters. dw and df show positive exponential correlation with all the grinding parameters (spindle speed, feed rate, cutting depth and power ratio). The relationship between hd and four grinding parameters is negative exponential. N, spindle speed, cutting depth and power ratio show positive exponential correlation, while it is negative exponential between N and feed rate. The relationship between ld and grinding parameters is complicated. There is not only exponential relation but also arcsine relation between ld and grinding parameters.

3.3 Comparison between theoretical values and experimental values

The verification experiments are carried out, as shown in Table 4. The experimental values of width dw, depth hd, length ld, spacing df and number N on the machined surface can be measured. According to Eqs. (39), (40), (41), (42) and (43), the theoretical values can be obtained. The comparison between theoretical values and experimental values is shown in Figs. 6, 7, 8, 9 and 10. It shows that the trends of theoretical values are consistent with those of experimental values.

Table 4 Verification experiments
Full size table
Fig. 6
figure 6

Width verification

Full size image
Fig. 7
figure 7

Depth verification

Full size image
Fig. 8
figure 8

Length verification

Full size image
Fig. 9
figure 9

Spacing verification

Full size image
Fig. 10
figure 10

Number verification

Full size image

4 Conclusions

A mathematic modeling of five geometric parameters (width dw, depth hd, length ld, spacing df and number N) for UVAG surface features of zirconia ceramics has been developed. The relationship between grinding parameters and five geometric parameters has been clarified theoretically. Finally, the experiments are conducted to verify the relationship. The conclusions are summarized as follows:

  1. 1.

    During the mathematic modeling, the overlapping of entire grains on the tool end face has been considered by calculating the expected value of center-to-center distance between two successive grooves and overlapping parameters. Grinding parameters have a close connection with the overlapping.

  2. 2.

    From the model, five geometric parameters (width dw, depth hd, length ld, spacing df and number N) of UVAG surface have been obtained. It shows that dw and df present exponential positive correlation with four grinding parameters, while hd has a negative exponential correlation with grinding parameters. ld has a complicated relationship with grinding parameters, and N is related to ultrasonic vibration frequency.

  3. 3.

    The theoretical values of mathematic modeling of five geometric parameters agree well with the experimental values. It provides a better understanding of characterizing surface topography of zirconia ceramics in UVAG.

In this work, it is innovative to put forward a mathematic model of geometric parameters for UVAG of zirconia ceramics. It can act as a reference for studying the surface topography of zirconia ceramics during UVAG.