Impedance boundary conditions for a time-domain finite-point method

Abstract

In this paper, we present the formulation of a time-domain impedance boundary model based on a finite-point approximation. Firstly, the scalar wave equation is numerically treated studying either the stability or the dispersion error in the case of a Cartesian regular mesh with standard clouds and weighted functions. Then, we develop the formulation of a locally reacting impedance boundary model suitable for the whole acoustic impedance range, and we carried out several numerical experiments to confirm the accuracy and the performance of the full model. Lastly, some conclusions and remarks of the method are discussed.

1 Introduction

Typically, engineers have the strong necessity to quantify the acoustic features of scenarios such as auditorium, concert halls or theaters. The strategy commonly used in these problems consists of computing the impulse response, which is defined as the response of the enclosure to the propagation of an unit impulse signal [1]. In computational simulations of the impulse response, there exist methods that are classified into two big groups: the geometrical methods, which are those methods based on optical approximations of the sound propagation and are used for predicting the impulse response of the high-frequency audible range, and the wave-based methods that describe the wave phenomena of the low-frequency range. These methods solve numerically the partial differential equation (PDE) that describes the sound propagation and the boundary conditions for characterizing the walls as for example, the impedance boundary model for modeling reflecting walls or Perfectly Matched Layers equations (PML) for porous absorbing material. In this context, there exist many scientific contributions that numerically compute the solution of these problems by using finite-difference time-domain algorithms (FDTD) [2, 3], digital waveguide methods (DWG) [4] or even pseudo-spectral time-domain methods (PSTD) [5, 6]. All these methods are characterized by their simplicity and compute velocity. Several contributions can be found in different problems such as source generation, the wave propagation or the implementation of boundary conditions, see, for instance, Refs. [7,8,9,10,11]. However, the problem is that they require regular Cartesian meshes for their implementation and most of the enclosures which room acoustics is interested have a complex geometry. These grids would lose plenty of the details of the boundaries considerably affecting the predictions and estimations of the acoustic parameters. In order to overcome this drawback, it is necessary to explore other possibilities with more flexible algorithms that can be stated on non-uniform meshes. For example, Ref. [12] presents an extension of the works done by Botledooren, Ref. [2], and formulates a room acoustics model based on finite volume method (FVM) in the time domain. Nevertheless, there is an important lack of references on this topic, and it seems reasonable to devote efforts to explore other approaches that also provide flexible algorithms with high performance demonstrated in different fields of computational mechanics. One of these techniques is meshfree methods, which have been successfully implemented in many fields of the engineering, but never in the context of room acoustic simulations and the calculation of impulse responses.

Meshfree or meshless methods are a group of numerical techniques that do not require a mesh or integration procedure for solving boundary value problem. The domain is discretized by a set of points also known as nodes. It is divided into local interpolation sub-domains, which are also called clouds; they consist of one central point, or star node, and several neighboring points chosen by means an appropriate rule, e.g., minimal distance criterion [13], eight-segment criterion [14], four-quadrant criterion [15] and others. A detailed view of the most important meshless methods and their relations is presented in [16]. Other helpful reviews on meshfree method can also be found in [17,18,19]. In this context, we present the formulation of a locally reacting impedance boundary model based on the wave equation by combining finite-difference techniques for the time derivative and meshless finite-point method (FPM) [20, 21] for the spatial derivatives. It should be mentioned that this work is a first approximation to build a room acoustic model based on FPM for realistic scenarios. Furthermore, some relevant features such as stability, dispersion error or the accuracy of the impedance walls are deeply analyzed and compared to the results of standard methods.

This paper is organized as follows: In Sect. 2, we introduce the formulation of the FPM for the wave equation, and a complete von Neumann analysis is developed with an homogeneous Cartesian mesh. Furthermore, the formulation of the impedance boundary conditions is presented, and some considerations of the boundary clouds are exposed. In Sect. 3, we present several numerical experiments showing the performance of the method. Finally, some important remarks are discussed in Sect. 4.

2 Time-domain impedance boundary model

In closed scenarios, it is assumed that the sound propagation occurs in a mechanical fluid, i.e., air, which is at completely rest before any sound source is introduced. Additionally, some intrinsic features, such as temperature or density, are also considered constant all along the enclosure. Therefore, under these conditions, it is reasonable to use the linear wave equation for describing the variations of the acoustic pressure, $u({\pmb {x}},t)$, as,

$$\begin{aligned} \frac{\partial ^2 u({\pmb {x}},t)}{\partial t^2}-c^2\varDelta u({\pmb {x}},t)=0, \end{aligned}$$

(1)

where the vector ${\pmb {x}}=(x,y)$ is referred to the position in the domain $\varOmega$ and the time is represented by variable t. Finally, note that $\varDelta$ is the Laplacian operator in two dimensions and c is the speed of sound which is assumed constant and isotropic.

The first step toward implementing a room acoustic model with a FPM consists of discretizing the time $t=n\delta _t$, where n is a positive integer and $\delta _t$ is the temporal sampling. Defining the time-discrete acoustic pressure as $u({\pmb {x}},t)=u^n({\pmb {x}})$ and approximating the second-order temporal derivative with a centered finite-difference operator of second order of accuracy, the semi-discrete wave equation is obtained, reading as follows,

$$\begin{aligned} u^{n+1}({\pmb {x}})= -u^{n-1}({\pmb {x}})+2 u^n({\pmb {x}})+(c\delta _t)^2 \varDelta u^n({\pmb {x}}). \end{aligned}$$

(2)

At this point, we are able to use a meshless finite-point method for approximating the spatial terms of the semi-discrete wave equation. In what follows, we present the general formulation of the method and the final discrete wave equation is derived.

2.1 The finite-point method (FPM)

In this section, we present briefly the basic formulation of the meshless FPM. This method was proposed by Oñate et al. [20, 21] to solve convective-transport and fluid-flow problems. In order to obtain the final system of discrete equations, the FPM approximates the local solution of a partial differential equation at each point of the discretized domain using a weighted least-squares technique and a point-collocation procedure. Because the approximation procedure used by this method is local, it is necessary to define a sub-domain $\varOmega _d$ for each point that contains the neighboring nodes, the cloud previously mentioned. An important aspect in the definition of clouds is that their superposition must produce the entire domain $\varOmega$.

With the discretized domain, let us define a function $u^n(\pmb {x})$, which is approximated by $\hat{u}^n(\pmb {x})$; $\hat{u}^n(\pmb {x})$ is only valid in the cloud $\varOmega _d$ associated with the star node $\pmb {x_d}$. The function $u^n(\pmb {x})$ is a linear combination of known functions $\pmb {p}(\pmb {x})$,

$$\begin{aligned} u^n(\pmb {x}) \cong \hat{u}^n(\pmb {x}) = \pmb {p}^T(\pmb {x}) \pmb {\alpha _d^n}, \quad \forall \pmb {x} \in \varOmega _d \end{aligned}$$

(3)

where $\pmb {p}(\pmb {x})$ is the vector that represents the basis of m linearly independent functions and $\pmb {\alpha _d}$ is a vector of constant parameters that are only valid in $\varOmega _d$. The elements of the interpolation basis may belong to any function family; nevertheless, in the FPM for simplicity the first m monomials polynomials are used.

Because Eq. (3) is valid for all $N_c$ points of the d-th sub-domain, the approximations $\hat{u}^n(\pmb {X})$ conform to a Vandermonde system that is given by the relation

$$\begin{aligned} \pmb {u^n}(\pmb {X^d}) \cong \pmb {\hat{u}^n}(\pmb {X^d}) = \pmb {P}^T(\pmb {X^d}) \cdot \pmb {\alpha _d^n}, \end{aligned}$$

(4)

where

$$\begin{aligned} \pmb {X^d}&= [{\pmb {x_{d,1}}}\ldots {\pmb {x_{d,N_c}}}]^T, \nonumber \\ \pmb {u^n}(\pmb {X^d})&= [u^n({\pmb {x_{d,1}}}) \ldots u^n({\pmb {x_{d,N_c}}})]^T, \nonumber \\ \pmb {\hat{u}^n}(\pmb {X^d})&= [\hat{u}^n({\pmb {x_{d,1}}}) \ldots \hat{u}^n({\pmb {x_{d,N_c}}})]^T, \nonumber \\ \pmb {\alpha _d^n}&= [\alpha _{d,1}^n \ldots \alpha _{d,N_c}^n]^T,\nonumber \\ \pmb {P}(\pmb {X^d})&= \left[ {\pmb {p}}({\pmb {x_{d,1}}})\ldots {\pmb {p}}({\pmb {x_{d,N_c}}}) \right] ^T. \end{aligned}$$

(5)

In general, the number of points $N_c$ that conform the cloud is greater than the number of functions m that define the basis; hence, the matrix $\pmb {P}(\pmb {X^d})$ is not usually rectangular. Thus, the interpolation property is lost, and the problem must be addressed with a numerical approximation. The coefficients of the vector $\pmb {\alpha _d^n}$ must be determined so that the weighted sums of the squared differences between the exact values $u^n(\pmb {x})$ and the approximated values $\hat{u}^n(\pmb {x})$ of each point are minimized according to

$$\begin{aligned} \min \left\{ \sum _{j=1}^{N_c} w({\pmb {x_{d,j}}}) \cdot \left( u^n({\pmb {x_{d,j}}}) - \hat{u}^n({\pmb {x_{d,j}}}) \right) ^2 \right\} , \end{aligned}$$

(6)

where $w({\pmb {x_{d,j}}})$ is a fixed weighting function that is defined in $\varOmega _d$ and evaluated for the node ${\pmb {x_{d,j}}}$, see refs. [20, 21]. The minimization process described by Eq. (6) leads to the expression for the vector $\pmb {\alpha _d^n}$

$$\begin{aligned} \pmb {\alpha _d^n} = \pmb {A}^{-1}(\pmb {X^d}) \pmb {B}(\pmb {X^d}) {\pmb {\lambda ^n}}(\pmb {X^d}), \end{aligned}$$

(7)

where ${\pmb {\lambda ^n}}(\pmb {X^d})$ represents the unknown parameters that are sought on the cloud. $\varOmega _d$ is defined as

$$\begin{aligned} \pmb {\lambda ^n}(\pmb {X^d}) = [\lambda ^n(x_{d,1}) \ldots \lambda ^n(x_{d,N_c})]^T. \end{aligned}$$

(8)

Additionally, the matrices $\pmb {A}(\pmb {X^d})$, $\pmb {B}(\pmb {X^d})$ and $\pmb {W(X^d)}$ are given as

$$\begin{aligned} \pmb {A}(\pmb {X^d}) = \pmb {P}(\pmb {X^d}) \pmb {W}(\pmb {X^d}) \pmb {P}^T(\pmb {X^d}), \quad \pmb {B}(\pmb {X^d}) = \pmb {P}^T(\pmb {X^d}) \pmb {W}(\pmb {X^d}), \end{aligned}$$

and $\pmb {W(X^d)}$ is an $N_c \times N_c$ diagonal matrix defined by

$$\begin{aligned} \pmb {W(X^d)} = \left[ {\text {diag}}\left( w({\pmb {x_{d,1}}}) \ldots w({\pmb {x_{d,N_c}}}) \right) \right] , \end{aligned}$$

(9)

where the weighting functions $w(\pmb {x_{d,j}})$ are derived to have unit values near the star node and zero values outside the $\varOmega _d$ sub-domains. Under the FPM, the common selection is the normalized weighting functions Gaussian, see refs. [20,21,22,23].

Fig. 1

Weighted least-squares procedure

Finally, replacing Eq. (8) in (3) leads to

$$\begin{aligned} \hat{u}^n(\pmb {x}) = \pmb {N}^T(\pmb {x}) \, {\pmb {\lambda ^n}}(\pmb {X^d}), \end{aligned}$$

(10)

where $\pmb {N}(\pmb {x})$ is the shape function matrix, which is defined as

$$\begin{aligned} \pmb {N}(\pmb {x}) = \pmb {p}^T(\pmb {x})\pmb {C}(\pmb {X^d}), \end{aligned}$$

(11)

where $\pmb {C}(\pmb {X^d}) = \pmb {A}^{-1}(\pmb {X^d})\pmb {B}(\pmb {X^d})$. Note that according to the least-square nature of the approximation, $u^n(\pmb {x}) \cong \hat{u}^n(\pmb {x}) \ne \lambda ^n(\pmb {x})$, see Fig. 1. In other words, the local values of the approximating function do not fit the nodal unknown values. Indeed, $\hat{u}^n(\pmb {x})$ is the true approximation, which we use to satisfy the differential equation and the boundary conditions. In this context, $\lambda (\pmb {x})$ are simply the unknown parameters that we aim to determine. According to these concepts and Eq. (9), it is possible to obtain

$$\begin{aligned} \hat{u}_x^n(\pmb {x}) = \pmb {N}_x^T(\pmb {x}) \, \pmb {\lambda ^n}(\pmb {X^d}) \quad {\text {and}} \quad \hat{u}_{xx}^n(\pmb {x}) = \pmb {N}_{xx}^T(\pmb {x})\, \pmb {\lambda ^n}(\pmb {X^d}), \end{aligned}$$

(12)

where $(\cdot )_x$ and $(\cdot )_{xx}$ denote the first and second space derivatives, respectively. Note that these derivatives are computed by taking the derivative of the basis functions $\pmb {p}(\pmb {x})$ in Eq. (3).

Finally, if the shape function matrix is evaluated at each star node (i.e., $\pmb {x}=(0,0)$ at each sub-domain) and Eqs. (11) and (12) are introduced into Eq. (2), we obtain the following implicit algebraic system that can be expressed as,

$$\begin{aligned} \pmb {N}^T(\pmb {0}) {\pmb {\lambda ^{n+1}}}(\pmb {X^d})&= -\pmb {N}^T(\pmb {0}){\pmb {\lambda ^{n-1}}}(\pmb {X^d})+2\pmb {N}^T(\pmb {0}){\pmb {\lambda ^{n}}}(\pmb {X^d})\nonumber \\&\quad +(c\delta _t)^2 (\pmb {N}^T_{\pmb {xx}}(\pmb {0})+\pmb {N}^T_{\pmb {yy}}(\pmb {0}) ){\pmb {\lambda ^n}}(\pmb {X^d}). \end{aligned}$$

(13)

Note that ${\pmb {\lambda ^{n+1}}}(\pmb {X^d})$ are the unknown quantities of the system at each sub-domain $\varOmega _d$. Observe that resulting system matrix would be sparse and its sparsity is related to the number of nodes that belong to the cloud.

2.2 Stability and dispersion error

In this section, we present the stability and dispersion analysis of the algorithm by using the classical von Neumann analysis. With this aim, we define an infinite Cartesian mesh with spatial samplings $\delta _x=\delta _y=\delta$. Moreover, for the implementation of $\pmb {N}(\pmb {0})$, $\pmb {N}_{xx}(\pmb {0})$ and $\pmb {N}_{yy}(\pmb {0})$. In order to focus on the phenomenon under study, the FPM parameters have fixed as $m=6$ for the polynomial basis function and $N_c=9$ for the number of points per clouds, that correspond to the central node and the first and second-order neighboring nodes. Finally, the weighting functions $w(\pmb {x_{d,j}})$ are defined equally in all the sub-domains $\varOmega _d$ fixing $q=1.1$ and $\beta =0.25$, since these coefficients are proved to give good results in previous works [24,25,26]; in any case, a detailed description of the effects of these coefficients on numerical approximation as well as guidelines for setting their values is presented in [22].

Under these assumptions, we are able to define the vector ${\pmb {\lambda ^{n}}}(\pmb {X^d})$ at each sub-domain $\varOmega _d$, in terms of local Cartesian discrete coordinates l, j as,

$$\begin{aligned} {\pmb {\lambda ^{n}}}(\pmb {X^d})=\{ \lambda ^n_{l,j}\}\quad l,j=\{-1, 0, 1\}. \end{aligned}$$

(14)

Note that the central node corresponds to the position $l=j=0$, whereas with other values of l and j, the first and second-order neighbor nodes are recovered. It is worth mentioning that for the analysis of linear systems, single-frequency plane-wave solutions may be assumed,

$$\begin{aligned} \lambda ^{n-1}_{l,j}&= e^{\iota (k_xl\delta +k_yj\delta )},\nonumber \\ \lambda ^{n}_{l,j}&= \mu e^{\iota (k_xl\delta +k_yj\delta )}, \nonumber \\ \lambda ^{n+1}_{l,j}&= \mu ^2 e^{\iota (k_xl\delta +k_yj\delta )}, \end{aligned}$$

(15)

where $k_x$ and $k_y$ are the wavenumber of the plane wave in the x and y directions, respectively, $\iota =\sqrt{-1}$ and $\mu$ represents the amplification factor at each time step. If Eqs. (14) and (15) are introduced into Eq. (13), we obtain the following amplification equation,

$$\begin{aligned} \mu ^2 + \mu \left( 2- \frac{4c^2\delta _t^2}{\delta ^2} \cdot \frac{h(k_x,k_y)}{f(k_x,k_y)} \right) +1 = 0 , \end{aligned}$$

(16)

where $-4h(k_x,k_y)/\delta ^2$ and $f(k_x,k_y)$ depend on the wavenumbers $k_x$ and $k_y$ taking the following explicit form,

$$\begin{aligned} h(k_x,k_y)&= \left[ (a_1+b_1) \cdot \bigg (\sin ^2\left( \frac{k_x\delta + k_y\delta }{2}\right) + \sin ^2\left( \frac{k_x\delta - k_y\delta }{2} \right) \bigg ) \right. \nonumber \\&\left. +\, (a_2+b_2)\cdot \sin ^2\left( \frac{k_y\delta }{2} \right) + (a_3+b_3) \cdot \sin ^2\left( \frac{k_x\delta }{2} \right) \right] ,\nonumber \\ \nonumber \\ f(k_x,k_y)&= 2 \cdot c_1 \bigg [ \cos (k_x\delta + k_y\delta ) + \cos (k_x\delta -k_y\delta ) \bigg ] +2\cdot c_2 \cdot \cos (k_y\delta )\nonumber \\&+ 2\cdot c_3 \cdot \cos (k_x\delta ) + c_4. \end{aligned}$$

(17)

Note that the parameters $a_i$, $b_i$ and $c_i$ are the first values of $\pmb {N}_{xx}(\pmb {0})$, $\pmb {N}_{yy}(\pmb {0})$ and $\pmb {N}(\pmb {0})$, respectively, at the sub-domain $\varOmega _d$, ordered from the left bottom to the right top neighbor node. As commonly known, the algorithm is considered stable whenever the solutions of the amplification equation, Eq. (16), are $|\mu |\le 1$. This factor depends on the Courant stability number, $S=c\delta _t/\delta$, and the ratio between $h(k_x,k_y)/f(k_x,k_y)$.

First, we study the behavior of $h(k_x,k_y)/f(k_x,k_y)$ evaluating at the whole range of wavenumbers, $0\le \{k_x,k_y\}\le 2\pi$. It is easy to observe that this ratio is always positive and its values are bounded in the range of [0, 2]. Considering the worst case of analysis, we find that the solutions of the amplification factor, Eq. (16), are bigger when the ratio between $h(k_x,k_y)/f(k_x,k_y)$ is maximum. Therefore, we can simplify Eq. (16) into

$$\begin{aligned} \mu ^2 + \mu \left( 2- 8S^2 \right) +1 = 0 . \end{aligned}$$

(18)

Finally, it can be straightforwardly observed that $|\mu |\le 1$ whenever $S\le 1/\sqrt{2}$. In fact, Eq. (18) is exactly the same expression than for the stability analysis of the leap-frog scheme, and in other dimensions, we can write the stability of the FPM as,

$$\begin{aligned} S=c\frac{\delta _t}{\delta }\le \frac{1}{\sqrt{D}}, \end{aligned}$$

(19)

where D represents the spatial dimension of the problem.

Similarly, the dispersion error is analyzed by defining the complete discrete plane wave,

$$\begin{aligned} \lambda ^{n}_{l,j}= e^{\iota (k_xl\delta +k_yj\delta -\omega _d n\delta _t)}, \end{aligned}$$

(20)

where $\omega _d$ is the angular frequency of the plane wave obtained in the numerical approximation, Eq. (13). Again, if we introduce Eqs. (14) and (20) into Eq. (13), the following dispersion relation for the FPM is obtained,

$$\begin{aligned} \sin ^2\left( \frac{\omega _d\delta _t}{2}\right) =S^2\frac{h(k_x,k_y)}{f(k_x,k_y)}. \end{aligned}$$

(21)

Note that Eq. (21) gives the relation between numerical frequency, $\omega _d$, for a given wavenumber vector when the FPM is used to approximate the wave equation. In fact, this frequency would be different than the analytical frequency $\omega$, and therefore, the numerical speed of sound, $c_{\mathrm{num}}$, would differ from the analytical velocity, c.

Fig. 2

(Left) the values of $c_{\mathrm{num}}/c$ versus the angle at three different frequencies. (Center) the values of $c_{\mathrm{num}}/c$ versus the frequency at three different angles. (Right) grayscaled color graph of the dispersion error for frequencies from 0 to 4000 Hz and orientations $0^{\circ }\le \theta \le 80^{\circ }$

In Fig. 2, we present different plots of Eq. (21) fixing both, the optimum Courant stability number and the temporal discretization $\delta _t=1/16{,}000$ s. First, in Fig. 2 (left), we present the values of $c_{\mathrm{num}}/c$ against the angle for three different frequencies, whereas in Fig. 2 (center), $c_{\mathrm{num}}/c$ is plotted versus the frequency at three different angles. Finally, a grayscale graph is depicted in Fig. 2 (right) where the x- and y-axis are the angle and the frequency, respectively, and color white represents values of $c_{\mathrm{num}}/c$ closer to one.

As expected, the numerical velocity strongly depends on the frequency and the angle. The best results are observed at $45^{\circ }$, where the dispersion error is null independently of the frequency tested, whereas the worst results are always located along the axis of the mesh. Moreover, the dispersion error is increased with the frequency, except at $45^{\circ }$, observing that, from 4000 Hz, the values of $c_{\mathrm{num}}/c$ would become high enough to be perceived by a listener. Finally, it is worth mentioning that either stability or dispersion results are very similar compared to the results of the leap-frog scheme. As reported in Refs. [2, 3], we observe the same stability criterion and a similar angular and frequency dependence of the dispersion error. Unfortunately, although the performance of the method is acceptable by the specialized literature, we expected to get a more isotropic algorithm since we are using clouds of eight neighbors. Note that this topic is further covered in Sect. 4.

2.3 Impedance boundary conditions

At this point, we have presented the formulation of a FPM for the discrete wave equation, and some features of the propagation algorithm, such as stability and dispersion error, have been discussed. However, to implement a complete room acoustics model, it is necessary to define proper boundary conditions capable of characterizing walls, ceilings and floors of any room acoustic scenario. Typically, in these type of applications, the impedance boundary model is used to characterize the behavior of a reflecting plane surface. This model relates, at the boundary, the acoustic pressure, $u(\pmb {x},t)$, and the particle velocity, $\pmb {v}(\pmb {x},t)$, at the normal direction of the surface, ${\hat {\mathbf{n}}}$, by a constant, Z, called the acoustic impedance, which is an intrinsic property of the wall and gives information about the reflection properties of the material. This model can be written only in terms of the acoustic pressure as,

$$\begin{aligned} \frac{\partial u(\pmb {x},t)}{\partial t}=-\frac{Z}{\rho }(\mathbf {\nabla }\cdot {\hat {\mathbf{n}}}) u(\pmb {x},t), \end{aligned}$$

(22)

where $\rho$ is a constant and represents the air density and $\mathbf {\nabla }$ is the Nabla operator projected to the outward normal direction of the impedance surface. As in Ref. [5], instead of directly discretizing Eq. (22), a temporal derivative is applied at both sides of the expression reading as

$$\begin{aligned} \frac{\partial ^2 u(\pmb {x},t)}{\partial t^2}=-\frac{Z}{\rho }(\mathbf {\nabla }\cdot {\hat {\mathbf{n}}}) \frac{\partial u(\pmb {x},t)}{\partial t}. \end{aligned}$$

(23)

Note that numerical approximations of Eq. (22) were always unstable for $Z>3\rho c$. On the other side, this expression, Eq. (23), allows us to create stable algorithms in the whole acoustic impedance range with high accuracies in the results. Therefore, and according to Ref. [5], for the first- and second-order temporal derivatives of Eq. (23), we use finite-difference operators of second-order accuracy, $\mathcal{{O}}(\delta _t)^2$. Hence, the resulting semi-discrete formulation of Eq. (23) reads as follows,

$$\begin{aligned} \left[ 1+\frac{Z\delta _t}{2\rho }(\mathbf {\nabla }\cdot {\hat {\mathbf{n}}})\right] u^{n+1}({\pmb {x}})= 2 u^n({\pmb {x}}) -\left( 1- \frac{Z\delta _t}{2\rho }(\mathbf {\nabla }\cdot {\hat {\mathbf{n}}})\right) u^{n-1}({\pmb {x}}). \end{aligned}$$

(24)

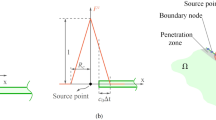
It is worth mentioning that, in general, the orientation of an impedance surface could be ${\hat {\mathbf{n}}}=(\cos \theta ,\sin \theta )$, where theta is the orientation with the x-axis. However, for simplicity, we expose the case when ${\hat {\mathbf{n}}}=(1,0)$, i.e., a surface oriented parallel to the y-axis. Other cases can be straightforwardly derived. Therefore, under these conditions and considering the tools given by FPM, more precisely Eqs. (10) and (12), we are able to discretize and approximate the spatial terms and their derivatives obtaining the following algebraic update equation,

$$\begin{aligned} \bigg (\pmb {N}^T(\pmb {0}) +\frac{Z\delta _t}{2\rho }\pmb {N}^T_x(\pmb {0})\bigg )\cdot {\pmb {\lambda ^{n+1}}}(\pmb {X^d})&= 2\pmb {N}^T(\pmb {0}){\pmb {\lambda ^{n}}}(\pmb {X^d})-\bigg (\pmb {N}^T(\pmb {0})\nonumber \\&-\frac{Z\delta _t}{2\rho }\pmb {N}^T_{\pmb {x}}(\pmb {0})\bigg ){\pmb {\lambda ^{n-1}}}(\pmb {X^d}). \end{aligned}$$

(25)

Observe that, as in Eq. (13), this expression depends on a vicinity of a node, $\pmb {X^d}$. The acoustic pressure and its spatial derivatives are transformed to local operators that control the contribution of the neighbor nodes of the cloud. Therefore, depending on the nature of the node (air or boundary node), we will use one of the two equations to assemble the system matrix. Moreover, it is important to mention that the election of the clouds of boundary nodes is restricted, because we cannot choose other boundary nodes at the cloud. In other words, in the cloud of a boundary node, only the star node should be a boundary node. Otherwise, simulations would be unstable.

Finally, it is worth mentioning that the locally reacting impedance boundary model is commonly used in this type of applications as a first approximation of a real wall because it is very simple and easy to implement, and we can get analytical expression of the model. For example, when a plane wave of amplitude 1 strikes with orientation $\theta$ on a surface with impedance Z, we can get the amplitude of the reflective wave, R as,

$$\begin{aligned} R=\frac{Z\cos \theta -\rho c}{Z\cos \theta +\rho c}. \end{aligned}$$

(26)

Note that, for this analysis, we assume Z to be a real positive number, which implies that Eq. (26) is independent of the frequency of the incident plane wave. Furthermore, we mention that since the range of the acoustic impedance, Z, goes from 0 to infinity, the reflection coefficient, R, is bounded into the range $[-1,1]$. It is important to remark the relevance of Eq. (26), because we will be able to compute the numerical error produced by the algorithm proposed through data obtained with computational simulations.

3 Numerical experiments

In this section, we present several numerical experiments capable of measuring the accuracy on different features of the time-domain finite-point algorithm. For all simulations, we create a 2-D square Cartesian lattice. Moreover, we fix the temporal discretization $\delta _t=1/16{,}000$ s and the optimal Courant stability number $S=1/\sqrt{2}$ is considered. We chose quadratic basis functions, $m=6$, and the clouds are composed by 9 nodes, including the star node.

On the other side, it is important to remark that, for the boundary nodes, we apply a different criterion for establishing the clouds than for an air node, which is defined in Eq. (14). As previously mentioned, we are constrained in the election of clouds at boundary nodes because, a part from the star node, we cannot include in the cloud another boundary node. Moreover, we are also restricted due to the location of the impedance boundary layers because they use to be at the edges of the domain. Therefore, the shape of clouds in boundary nodes differs than in air nodes. We should note that, for these experiments, we create the boundary clouds considering the constrains already exposed and also choosing the eight nodes closer to both, the normal direction of the wall and the distance of the star node. For simplicity, we fix the acoustic impedance $Z=0$ at the corners, to avoid the election of the clouds at these nodes.

3.1 Spectral analysis of room impulse response

First, we present a modal analysis of a two-dimensional room which computationally exhibits the numerical dispersion phenomenon previously studied. The idea consists of simulating the impulse response produced by a unit impulse signal in a totally reflecting room and analyzes the frequency spectrum of the signal. This spectrum shows the resonance frequencies of the enclosure. Note that the frequency modes can be analytically calculated and their values are compared to the numerical data. Under the conditions described before, we create a Cartesian mesh of $4\times 4$ m where we locate a punctual source in the middle of the square and a receiver at the position $1\times 1$ m. Furthermore, the unit impulse signal is approximated with a windowed sinc function of frequency 4000 Hz. Lastly, the impedance of the four boundary layers is fixed to $Z=10{,}000\rho c$, except the corners that we defined $Z=0$.

We let the system evolves during 1 s of time obtaining an infinite impulse response with no decay in the energy of the signal. In Fig. 3, we present the numerical results measured at the receiver. In the left, we plot the acoustic pressure against time, and we observe the direct sound between the source and the receiver and the first reflexions of the impulse response due to the totally reflecting boundary conditions. We should remark that although we present the results for 1 s of time, we tried with bigger times and no instabilities were observed. On the other side, we plot in Fig. 3 (right) the amplitude of the spectrum against the frequency showing the numerical modes associated with the signal. These modes are strongly related to the geometry of the enclosure and can be easily calculated. Note that the positions of these modes are represented in the plot with vertical gray lines.

Fig. 3

(Left) the first reflections at the receiver are depicted. (Right) the spectrum of the whole signal from 0 to 500 Hz is plotted. The vertical gray lines represent the modes analytically predicted

Observe that the numerical modes are almost coincident to the vertical gray lines. It is important to highlight that we only plot the range from 0 to 500 Hz because we need to ensure low dispersion errors. It means that, in this range, we get values of $c_{\mathrm{num}}/c$ close to 1, independently of the orientation, see Fig. 2. Therefore, the numerical modes simulated in this range should be equal to the analytical modes previously calculated. Finally, it is worth mentioning that some artifacts can be observed between predicted modes, whose amplitudes are two orders of magnitude smaller. We should remark that these artifacts are not analytically predicted and appear due to the definition of the numerical setup. In fact, these errors appear because the corners were implemented with $Z=0$, and conversely to the other walls, they reflect the whole energy of the incident wave but with inverted phase. However, with this experiment, we are able to measure the modes of the room with high accuracy and the artifacts are sufficiently low to be ignored.

3.2 Reflection analysis

The second numerical experiment is oriented to measure the accuracy of the locally reacting boundary conditions. The experiment attempts to recreate the conditions for obtaining the numerical reflection coefficient, $\hat{R}$. This measure will allow us to compare with the theoretical value of R, see Eq. (26), and get a measure of error for any orientation and a given frequency range. As reported in Ref. [27], we are able to measure the numerical reflection coefficient $\hat{R}$ with two different simulations. The main constrain of these experiments is that a huge lattices are demanded. For our experiments, we use meshes around $750\times 500$ nodes.

Fig. 4

The absolute error in decibels for different values of the normal reflection coefficient $R_n$ obtained with the numerical finite-point scheme. From up to down and left to right: a $R_n=1$, b $R_n=0.9$, c $R_n=0.8$, d $R_n=0.7$, e $R_n=0.6$, f $R_n=0.5$, g $R_n=0.4$, h $R_n=0.3$, i $R_n=0.2$, j $R_n=0.1$, k $R_n=0$, l $R_n=-0.1$, m $R_n=-0.2$, n $R_n=-0.3$, o $R_n=-0.4$, p $R_n=-0.5$, q $R_n=-0.6$, r $R_n=-0.7$, s $R_n=-0.8$, t $R_n=-0.9$ and u $R_n=-1$

Firstly, we simulate a unit impulse signal located very close to one wall and far from the others, and we locate receivers above the source and parallel to the wall. Note that each receiver corresponds to different orientations of impact. Unfortunately, not all the absorption observed at each receiver corresponds to the impact with an impedance wall. In two dimensions, also the propagation of the signal attenuates the field spreading the energy through the domain. Therefore, another simulation is carried out where a unit impulse signal is propagated in the free space and the attenuation due to the propagation is also numerically measured. With these informations, we are able to measure the reflection coefficient at different orientations and in the frequency range defined by the unit impulse signal.

The results of the numerical experiments are illustrated in Fig. 4. Each plot corresponds to the absolute error as a function of the angle of incidence, $\theta$, and the frequency. The error is plotted in a graded logarithmic scale where black corresponds to errors of a few negative dBs, whereas white corresponds to errors less than $-\,50$ dB. The label of each plot is the reflection factor for normal incidence, $R_n$ (i.e., R with $\theta =0^{\circ }$) which fixes the value of the impedance Z in the numerical simulation. Therefore for each value of $R_n$ (i.e., of Z), the numerical experiment is performed and the absolute error is computed for different angles given by the receiver locations for all frequencies less than 4000 Hz.

Independently of the impedance used, in general, we observe that the errors are low in the whole range of frequencies and angles. More specifically, the best results are in the region $R_n=[-1, -0.2]$, that corresponds to the impedance range $Z=[0,0.65\rho c]$, where we observe errors lower than $-40$ dBs in any angle and frequency. On the other side, the worst results are observed in the most absorbing regions, $R_n=[-0.1,0.4]$ (i.e., $Z=[0.7\rho c, 4\rho c]$) where the errors increase to $-\,25$ dBs at low orientations only for frequencies up to 2500 Hz. Finally, the rest of the range, $R_n=[0.5,1]$, which is equivalent to $Z>5\rho c$, the error decreases as increases the normal reflection coefficient, $R_n$, completely disappearing for $R_n=1$. The values of the error at this region are around $-35$ dBs, and the worst results never are lower than $-\,30$ dBs. Therefore, we conclude that the errors of the impedance boundary model, Eq. (25), are very low, and we get accurate results independently of the impedance chosen.

4 Conclusions and remarks

In this paper, we presented the formulation of an impedance boundary model based on a FPM. First, the semi-discrete wave equation has been approximated with standard meshless techniques. We also developed a deep analysis of the algorithm with an infinite Cartesian mesh, and some relevant features concerning the stability and dispersion error have been discussed. Moreover, we stated an impedance boundary model, which can be formulated in FPM, and it is stable for all the impedance ranges. Finally, several numerical experiments have been implemented, and different features of the algorithm have been analyzed.

In general, the results show an acceptable performance of the time-domain finite-point approximation. More concretely, we obtain analytical expressions of either the stability or the dispersion error observing high similarities compared to the results for the classical leap-frog scheme. First, by using a von Neumann analysis, we get the same stability condition $S\le 1/\sqrt{D}$, and then, from the dispersion error analysis, we observe a strong dependence on the angle of the numerical velocity at low frequencies, see Fig. 2. Unfortunately, although we define clouds of 8 nodes, which contains the first- and second-order neighbor nodes, the accuracy of the FPM is similar to a first-order algorithm. In fact, we expected a better performance and a more isotropic dispersion, since we are using more nodes. However, it seems that not only with more neighbor nodes the algorithm would improve the dispersion. Therefore, in order to obtain high-accurate and less-dispersive algorithms based on FPM, it is necessary to develop a criterion for establishing the definition of a mesh, the shape of the corresponding clouds and the weighting functions $w(\pmb {x_{d,j}})$.

On the other side, we also define a proper formulation of the impedance boundary model. This formulation allows us to build stable FPM algorithms, independently of the impedance of the walls used in the simulations. We present the results of the reflection coefficient, and we observe high accuracies in the whole angular-frequency range. Nevertheless, we should mention that we avoid to treat singularities such as corners (or corners and edges in three dimensions), because we focus on the formulation of the room acoustic model and the study of the main acoustic features of the finite-point algorithm. The study of a criterion for establishing clouds and weighting functions is not trivial at these type of nodes, and it requires a deep analysis in terms of the accuracy and stability of the algorithms. For example and to get an idea of the problem, we cannot define unequivocally the clouds at corners leading to several possibilities in the election of the neighbor nodes that considerably complicates the problem. As mentioned, the election of a proper mesh or cloud is necessary to be defined and analyzed under the formulation already exposed. Therefore, this work is a first attempt to build a room acoustic model based on a FPM, and it would be interesting to dedicate efforts in this direction to extend the analysis for non-homogeneous meshes and for different cloud configurations.