1 Introduction

Continuous casting is currently the most used technique in the world for the production of semi-finished steel and alloy goods. This process basically consists of the continuum solidification of alloys of steel, aluminum, or copper, resulting in a product with a shape of a billet, plate, or block [1, 2]. During the solidification process, in the cast machine, the ingot is subject in general to three cooling zones which are called: primary, secondary and tertiary regions. The primary region corresponds to the mold, which is water-cooled. This step is responsible for the formation of a thin metal shell, which must be able to prevent breakout due the ferrostatic pressure. At the secondary stage, the ingot is cooled by the water-cooled sprays. The final solidification step is at tertiary region, in which the ingot is cooled by radiation and natural convection. Since it was introduced in the industry, the continuous casting technique has been improved to prevent the formation of defects and hence reduce the costs and production time [1, 3]. Therefore, the operational steps must be carefully controlled to ensure stable, uninterrupted, and reproducible procedures [3]. Clearly, various complex physical elements are present in the operational process, such as transient effects (turbulence, argon injection, and superheat removal), periodic oscillations of the mold, ingot contraction at the mold region, contact with the rolls, casting speed, chemical composition, and the phase change [4,5,6,7,8,9].

However, the main physical phenomena source that affects the continuous casting is the heat transfer in all three regions. For instance, irregularities in the cooling process at the boundaries of the mold may induce an uneven solid ingot shell, which can produce breakpoints at the mold exit or crack formation [1, 5, 8, 10, 11]. These problems directly influence the quality and cost of production. Thus, the knowledge of the heat flow mechanism can provide important information to improve the industrial process [1, 10].

The volumetric shrinkage associated with the expansion caused by the metallostatic pressure during solidification can even cause irregularities in the solid shell formation. These factors can lead to grips and/or depressions of the ingot in the mold region. Wolf [12] performed solidification tests and developed a technique for estimating the potential tendency for depression and grip formation in continuous casting of the carbon steel alloys in mold region. The methodology involves the ferritic potential (FP), which indicates the solid fraction of ferrite according to the carbon equivalent concentration \(C_{\text{eq}} ({\text{wt}}\% )\).

Wolf also defined the following terms: steel type A with \(0.85 \le {\text{FP}} \le 1.05\), which exhibits tendency to form depression, and steel type B with \({\text{FP}} > 1.05\) or \({\text{FP}} < 0.85\), which has tendency to grip at the walls of the mold.

The knowledge of the heat flow mechanism can provide important information to improve the solidification process [1, 10]. In the literature, we can find numerous works with different approaches, which focus on the investigation of the heat transfer in continuous casting of steel. These methodologies can be divided into analytical [13, 14] and numerical–experimental [10, 15] procedures. It is worth noting that the numerical–experimental schemes have been received more attention. One of this application can be found in the work of Barcellos et al. [10], which apply a methodology that involves the solution of the Inverse Heat Conduction Problem (IHCP), in conjunction with the Finite Difference Method (FDM), to evaluate the heat transfer coefficient in the metal/mold interface. They also investigated the effect of the metal mold interface coefficient under different casting parameters, as casting speed, chemical composition, and geometry of the mold. Cheung et al. [15] also studied the interface coefficient at the mold. In this work, they introduced a technique that uses FDM and an artificial intelligence heuristic search method, which is able to choose the suitable heat transfer coefficient to optimize the cooling conditions and avoid defect formation in the billet production. Nevertheless, when it comes to investigation of heat transfer coefficient in continuous casting, most studies focus only at the mold region.

We propose an approach to evaluate the heat transfer coefficient for the whole continuous casting of steel process in terms of chemical composition, which is presented as a function of FP, casting temperature, and speed. These results can be used as background information in numerical experiments, which analyses ideal parameters during solidification process. The solution of the inverse heat conduction problem (IHCP) using a Finite Volume Method (FVM) and experimental temperature measurements data are able to make a complete physical description of the heat transfer coefficient behavior. More details about IHCP approach can be found in [10, 16,17,18,19,20,21].

The FVM is a conservative approach at the discrete-finite-volume level [22, 23]. It is also important to point out that the FVM has been applied to several areas, as for instance, in structural analyses [24,25,26], computational fluid dynamics [27] and fluid–structure iteration [28].

2 Physical model

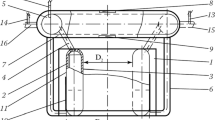
The main propose of this section is to define the procedure adopted to analyze the interfacial metal/mold heat transfer coefficient at the inner, outer and side face of the mold region. The domain and boundary condition is illustrated in the Fig. 1a. A unidimensional model was adopted, since this is a simplistic and a very effective way to evaluate these heat transfer coefficients.

Fig. 1
figure 1

Cross section of ingot mold. Schematic of the grid in vertical plane and the thermal resistances

Full size image

The unidimensional heat equation with a source term, q which is related to the phase change, might be expressed as:

$$\frac{\partial }{\partial t}(\rho cT) = \frac{\partial }{\partial x}\left( {k\frac{\partial T}{\partial x}} \right) + q,$$
(1)

where \(\rho\) (kg m−3) is the density, c (J kg−1 K−1) denotes the specific heat capacity, \(\kappa\) (W m−1 K−1) is the thermal conductivity, t (s) is the physical time, and T (K) stands for the temperature. The source term in Eq. (1) is given by:

$$\dot{q} = \rho L\left( {\frac{{\partial f_{s} }}{\partial T}\frac{\partial T}{\partial t}} \right),$$
(2)

where \(f_{\text{s}}\) is the solid fraction and L (J kg−1) is the latent heat. Substituting Eq. (2) into Eq. (1) and using the concept of apparent specific heat \((c^{{\prime }} ),\) \(c^{{\prime }} = c - L\left( {\frac{{\partial f_{\text{s}} }}{\partial T}} \right),\) we can rewrite Eq. (1) as:

$$\frac{\partial }{\partial t}(\rho c^{{\prime }} T) = \frac{\partial }{\partial x}\left( {\kappa \frac{\partial T}{\partial x}} \right).$$
(3)

The solid fraction, \(f_{\text{s}}\), depends on several factors such as alloy constituents as well as the diffusion during solidification. However, in this work, we assume the expression described in Garcia [29], which \(f_{\text{s}}\) depends only on the temperature, and it can be expressed by:

$$f_{\text{s}} = \left( {\frac{1}{{1 - k_{0} }}} \right)\left( {\frac{{T_{\text{L}} - T}}{{T_{\text{F}} - T}}} \right),$$
(4)

and

$$\frac{{\partial f_{\text{s}} }}{\partial T} = \left( {\frac{1}{{1 - K_{0} }}} \right)\left( {\frac{{T_{\text{L}} - T}}{{\left( {T_{\text{F}} - T} \right)^{2} }} - \frac{1}{{T_{\text{F}} - T}}} \right),$$
(5)

where \(K_{0}\) is the partition coefficient, where it was assumed to be constant and equal to 0.2 (carbon steel). \(T_{\text{F}}\) is the solvent melting temperature (iron), and \(T_{\text{L}}\) is the liquidus temperature, which is given by:

$$T_{\text{L}} ({^\circ }{\text{C}}) = 1537 - 88\% {\text{C}} - 8\% {\text{Si}} - 5\% {\text{Mn}} - 30\% {\text{P}} - 25\% {\text{S}} - 5\% {\text{Cu}} - 4\% {\text{Ni}} - 1.5\% {\text{Cr}} - 2\% {\text{Mo}} - 2\% {\text{V}} - 24\% {\text{As}} - 18\% {\text{Ti}}.$$
(6)

The steel composition and thermophysical properties used in this work are shown in Table 1. The material properties are defined in terms of the solid fraction, according to the following relationships:

$$\begin{aligned} c = f_{\text{s}} c_{\text{s}} + (1 - f_{\text{s}} )c_{\text{l}} , \hfill \\ \kappa = f_{\text{s}} k_{\text{s}} + (1 - f_{\text{s}} )\kappa_{\text{l}} , \hfill \\ \rho = f_{\text{s}} \rho_{\text{s}} + (1 - f_{\text{s}} )\rho_{\text{l}} , \hfill \\ \end{aligned}$$
(7)

where the subscripts s and l represent the properties of the solid and liquid phases, respectively.

Table 1 Thermophysical properties of metal and mold
Full size table

The convective effect present in the liquid pool is not considered in the current approach. Therefore, we replace the thermal liquid conductivity \((\kappa_{\text{l}} )\) by an effective thermal conductivity, \(\kappa_{\text{efe}}\), whose value is in the range of 5–10 times greater than the thermal coefficient of liquid material phase.

$$\kappa_{\text{efe}} = A\kappa_{\text{l}} ,$$
(8)

where 5 ≤ A ≤ 10. In this work, we adopted A = 7.

Using the finite volume method (FVM) in and explicit time integration, we obtain the following linear equation:

$$\frac{{\left. {\rho c^{{\prime }} T} \right|_{i}^{n + 1} - \left. {\rho c^{{\prime }} T} \right|_{i}^{n} }}{\Delta t}\Delta x = \left. {\left. {\frac{k}{\Delta x}} \right|_{ip1}^{{}} T_{i - 1}^{n} + \frac{k}{\Delta x}} \right|_{ip2}^{{}} T_{i + 1}^{n} - \left( {\left. {\frac{k}{\Delta x}} \right|_{ip1}^{{}} + \left. {\frac{k}{\Delta x}} \right|_{ip2}^{{}} } \right)T_{i}^{n} ,$$
(9)

where i denotes the control-volume and i − 1 and i + 1 denote its neighbors, n and n + 1 refers to the previous and current time-step, respectively, \(ip1\) and \(ip2\) correspond to the interfaces of control-volume i. It is convenient to reorganize Eq. (9) as:

$$T_{i}^{n + 1} = \left. {\left. {\frac{\Delta t}{{\rho_{i} c_{i}^{{\prime }} \Delta xA}}\frac{Ak}{\Delta x}} \right|_{ip1}^{{}} T_{i - 1}^{n} + \frac{\Delta t}{{\rho_{i} c_{i}^{{\prime }} \Delta xA}}\frac{Ak}{\Delta x}} \right|_{ip2}^{{}} T_{i + 1}^{n} - \frac{\Delta t}{{\rho_{i} c_{i}^{{\prime }} \Delta xA}}\left[ {\left( {\left. {\frac{Ak}{\Delta x}} \right|_{ip1}^{{}} + \left. {\frac{Ak}{\Delta x}} \right|_{ip2}^{{}} } \right) - 1} \right]T_{i}^{n} .$$
(10)

In the above equation, the thermal conductivity at each integration point might be expressed in terms of the inverse of the thermal resistance R (see Fig. 1), which leads to [10, 30]:

$$T_{i}^{n + 1} = \frac{\Delta t}{C}\left( {\frac{{T_{i - 1}^{n} }}{{R_{i - 1} + R_{i} }} + \frac{{T_{i + 1}^{n} }}{{R_{i + 1} + R_{i} }}} \right) - \frac{\Delta t}{C}\left[ {\left( {\frac{1}{{R_{i - 1} + R_{i} }} + \frac{1}{{R_{i + 1} + R_{i} }}} \right) - 1} \right]T_{i}^{n} ,$$
(11)

where C (J K−1) represents the accumulated energy [10] in a volume element i, R stands for thermal resistances evaluated at the control-volume i and its neighbors i − 1 and i + 1. The accumulated energy can be expressed as:

$$C = \rho_{i} c_{i}^{{\prime }} \Delta x,$$
(12)

and resistances is written by:

$$R_{i - 1} = \frac{{\Delta x_{i - 1} }}{{2\kappa_{i - 1} }},$$
(13a)
$$R_{i} = \frac{{\Delta x_{i} }}{{2\kappa_{i} }},$$
(13b)
$$R_{i + 1} = \frac{{\Delta x_{i + 1} }}{{2\kappa_{i + 1} }}.$$
(13c)

The numerical domain presents four boundary conditions (see Fig. 1), which must be carefully evaluated at following regions: interface mold/environment, interface metal/mold, and inside of the mold (at the center). For the control-volumes in contact with the walls of the mold (see Fig. 1), the thermal resistance is given by:

$$R_{\text{wall}} = \frac{1}{{h_{\text{m/m}} }},$$
(13d)

where \(h_{\text{m/m}}\) (W m−2 K−1) is the metal/mold heat transfer coefficient (Fig. 1). This coefficient represents the thermal resistance due to the gap or grip between the mold and metal. Further details about the physical model can be found in [10, 15, 30].

The approach to obtain the heat transfer coefficients at the metal/mold interfaces (inner, outer, and side faces) used in this work is similar to the one used by Barcellos et al. [10], which applied the FDM as the numerical approach. The boundary conditions were applied to the one-dimensional grid, as shown in Fig. 1. The temperatures of the water, \(T_{\text{wat}}\), the casting, \(T_{\text{cas}}\), and the heat transfer coefficient for the cooling water, \(h_{\text{wat}}\)\(\left( {h_{\text{wat}} = 24,528\;{\text{Wm}}^{ - 2} {\text{K}}^{ - 1} } \right)\) [31], were considered constant along all the length of the mold. The grid moves with the same speed of the continuous casting.

After the mold, the analyses of the heat transfer coefficients take place at the sprays section. This stage ensures the continued development of the solidified shell. In general, the secondary region is divided in three sub-zones according to the water flow rate. As the surface temperature of the ingot decreases, the flow rate and the number of sprays per zone also decrease, since the thermal resistance of the liquid steel heat transfer to the environment increases. Empirical formulations have been developed to relate the heat transfer coefficient at the spray region according to various parameters, such as type of nozzles, pressure and water flow rate, nozzle distance from the ingot, and the water temperature [32]. For the heat transfer coefficient at the spray region, we assumed that the heat transfer coefficient is dependent on the water flow rate, m, as proposed by Brimacombe et al. [33], which can be expressed by:

$$h_{\text{sprays}} = 0.366\;m^{n} ,$$
(14)

where n is a constant which must be adjusted with the aid of IHCP. The heat transfer coefficients for the secondary and tertiary regions are presented in the results’ section.

3 Numerical–experimental methodology

In the numerical experiments, we use a mesh with 1532 volumes, which was enough to ensure grid independently results. The time-step is chosen using the following expression:

$$\Delta t > \frac{\Delta x}{2\kappa }\rho c^{{\prime }} ,$$
(15)

which prevent instabilities in the explicit formulation employed.

For the experimental procedure, in the mold region, fifteen K Chromel–Alumel thermocouples, with diameter of 1.5 mm, were inserted at specific positions (see Fig. 2) in each three walls of the mold (inner, outer, and lateral). To reduce the possibility of deformation, the thermocouples were fixed in a 4 mm depth from the cold surface of the mold. To obtain the flux along the three faces, five thermocouples were positioned equally spaced on each face. The first three thermocouples were positioned closer to the meniscus, where larger heat transfer coefficients are expected. Figure 2a shows the lateral of the mold with the grooves where the thermocouples were inserted, and Fig. 2b shows the view of the top of a cross section of the mold.

Fig. 2
figure 2

Thermocouple distribution scheme. a Lateral of the mold, b cross-section of the mold

Full size image

With the purpose of evaluating the \(h_{\text{m/m}}\), a one-dimensional approach over a half ingot plus mold cross section was applied, as it is shown in Fig. 1. Water temperature was considered constant along all the length of the mold, and the casting temperature was measured by an immersion thermocouple tip before each process. The methodology for obtaining the heat transfer coefficient at each metal/mold interface consists of using the inverse solution of heat conduction equation (IHCP). The process starts by assuming a heat transfer coefficient between the ingot and mold interface equal to zero, and then the temperature field from the center of the ingot to the water is evaluated. Therefore, we compare the measured temperature with the calculated temperature. If the difference between the values does not satisfy the tolerance (± 1 °C), the coefficient \(h_{\text{m/m}}\) is updated by a \(\Delta h_{\text{m/m}}\) factor, which in our experiments was chosen as \(10^{ - 6} {\text{Wm}}^{ - 2} {\text{K}}^{ - 1}\). Thereby, when the algorithm finds one \(h_{\text{m/m}}\) which satisfies the tolerance, the procedure moves to the next thermocouple at the point \(\Delta tv_{\text{cas}}\), where \(v_{\text{cas}}\) is the casting speed, assuming the value previous calculated as the initial guess. The heat transfer coefficient does not change until the next thermocouple is found, when the previous process is repeated to evaluate a new heat transfer coefficient. It is worthwhile to mention that the tolerance temperature of the ± 1 °C was chosen after some numerical tests, which show that this is the minimal value which was able to make the process efficient without compromise the numerical results. A similar approach can be found in [1, 6, 10, 15].

A similar approach used in the mold region is used to evaluate the heat transfer coefficient to the secondary and tertiary regions, but now we measure the temperature of the surface of the ingot using an optical pyrometer. The numerical–experimental procedure for the sprays section, Eq. (14), is used to evaluate the exponent n, resulting in \(n = 0.56\) for the 1028D and 1034D steels and \(n = 0.63\) for the 1013D steel, similar results were found by Bolle and Moureau [32].

For the region of cooling by radiation/natural convection, the heat transfer coefficient is guessed using the value previous calculated at the end of the secondary region and its value is further adjusted with the temperature measured with the optical pyrometer (RAYTEK 23131). Once the heat transfer coefficient is calculated it does not change. This procedure was manually executed at fifteen defined points.

4 Results

The experimental data were obtained by monitoring 75 continuous casting of steel with the average duration of 45 min. At the primary cooling zone, the thermal measurements were monitored by a software and stored at each minute for posterior treatment. At the secondary and tertiary zones, the temperature measurements were taking manually with the use of the optical pyrometer (RAYTEK 23131). For this region, we chosen several fixed points in which fifteen measures were made; the surface temperature of the ingot was taken as the average of these measurements.

4.1 Analysis of the heat transfer coefficient in the mold region

The experimental data was obtained by monitoring 75 continuous steel casting processes with the average duration of 45 min. The chemical composition and the casting parameters process are shown in Table 2, where Tcas stands for the casting temperature.

Table 2 Chemical composition and casting parameters
Full size table

From the experimental data and the IHCP, the effects of chemical composition, represented by ferritic potential (FP) on the heat transfer coefficient \(h_{\text{m/m}}\), are shown in Fig. 3 for all the investigated surfaces of the mold. These results point out that the highest values of heat transfer coefficient are for those steels that have the high carbon concentration (Ceq), i.e., by increasing the ferritic potential, the coefficient decreases. Such behavior can also indicate the tendency of increasing the gap for type A, as well as gripping for type B steels, between the ingot and walls of the mold. The results show also, for both steels grades, that the greatest heat transfer values lie in the meniscus region and decreases along the mold length. Similar results can be found in [10, 34,35,36].

Fig. 3
figure 3

Effect of chemical composition on heat transfer coefficient: a side face, b inner face, c outer face. All the results have the same casting speed of 3.2 m/min

Full size image

The heat transfer coefficients at the three investigated surfaces (inner, outer, and lateral) for A and B steels are shown in Fig. 4.

Fig. 4
figure 4

Heat transfer coefficient at the three surfaces. a Steel type A, b steel type B

Full size image

In Figs. 3 and 4, it is possible to observe the heat transfer at the side face has the lowest value. We also observed the heat transfer coefficient profile at the outer face, for both A and B steel types, has the highest relative value except at the mold exit. This result can be explained by the higher contact between the ingot and the outer face of the mold due to action of the weight of the ingot combined with its bending. At the bottom of the mold, the ingot has suffered considerable contraction, hence increasing the gap between the ingot and mold with consequent increase of the thermal resistance.

The effect of casting speed on the heat transfer coefficient for steels A and B at the metal/mold interface for operating casting speed range (2.70–3.40 m/min) are shown in Figs. 5 and 6.

Fig. 5
figure 5

Casting speed influence on the heat transfer coefficient for steel type A—a side face, b inner face, c outer face

Full size image
Fig. 6
figure 6

Casting speed influence on the heat transfer coefficient for steel type B—a side face, b inner face, c outer face

Full size image

In Figs. 5 and 6, we can see that casting speed directly influences the heat flux for each type of steel. As the casting speed increases, the heat transfer coefficient becomes greater mostly next to the meniscus. According to de Barcellos et al. [10] and Chow et al. [37], such behavior is due to the three following main reasons: Firstly, high-speed results in a thinner solidified shell, which under action of the ferrostatic pressure deform easily, and therefore reduces the gap at each metal/mold interface. Secondly, the surface of the ingot will become hotter, which will increase the thermal gradient and hence the heat flow. Finally, with less thermal contraction the metal/mold interface will have a better contact.

The effect of casting temperature is shown in Fig. 7. From this figure, it is possible to observe that the effect of the casting temperature does not affect the heat transfer coefficient, and hence can be neglected. Similar conclusions can be found [10, 37].

Fig. 7
figure 7

Casting temperature influence on the heat transfer coefficient. a side face, b inner face, c outer face

Full size image

4.2 Analysis of the overall heat transfer coefficient

After obtaining the heat transfer coefficient, \(h_{\text{m/m}}\), for all parameters shown in Tables 1 and 2, we evaluated the overall heat transfer coefficient that takes into account all thermal resistances from the cooling water to the center of the ingot (see Fig. 1). The profile along with the length of the mold for the overall coefficient resembles to the \(h_{\text{m/m}}\) coefficient at each mold interface. This is an expected result since the \(h_{\text{m/m}}\) coefficient is responsible for the largest thermal resistance. Based on the results, we proposed a correlation for the overall heat transfer coefficient for each face that is given by:

$$h_{\text{overall}} = C_{0} + C_{1}^{{ez(t)\left( { - \frac{1}{{c_{2} }}} \right)}} ,$$
(16)

where \(z\left( t \right)\) \(\left( m \right)\) is the distance from the meniscus in the casting direction, and the constants \(C_{0}\), \(C_{1}\), and \(C_{2}\) are determined from the experimental data. The constants C0, C1, and C2 are shown in Table 3. Using the adjusted coefficients, we present the overall heat transfer coefficients in Fig. 8 for side (Fig. 8a) and inner (Fig. 8b) faces, for several continuous casting parameters.

Table 3 Constants of the overall heat transfer coefficient
Full size table
Fig. 8
figure 8

The overall heat transfer coefficient—a side face, b inner face

Full size image

The average and maximum relative error between the curves obtained from Eq. (15) and experimental results is about 4 and 7%, respectively.

4.3 Numerical–experimental analysis of the heat transfer coefficient in the sprays and radiation/natural convection zones

Based on the procedure described at the end of Sect. 3, we estimated the heat transfer coefficient for each zone of sprays and for radiation/natural convection (tertiary) zone for all carbon steels investigated. The flow rates and the heat transfer coefficients for the spay regions and the heat transfer coefficient for tertiary region for all steels analyzed are presented in Table 4.

Table 4 Water flow rates of and the convective heat transfer in the spays and radiation/natural convection zones
Full size table

5 Conclusions

In this work, the heat transfer behavior for a particular continuous casting process was studied using a numerical–experimental approach, IHCP, for all the three solidification stages (mold, secondary, and tertiary). This methodology provided satisfactory results since it could detect in the mold region the effect of the carbon content on the heat transfer coefficient for A and B steel types. Furthermore, the highest values of the heat transfer coefficient were observed at the outer face of the mold for all investigated parameters. Such a behavior was expected due to the bending of the mold and weight of the ingot that help to reduce the thermal resistance. Experimental measurements assist in the calibration of the numerical heat transfer coefficient in distinct solidification regions, such as mold, sprays, and radiation/natural convection. In the mold region, we analyzed the heat transfer at the side, inner, and outer face of the metal/mold interface. In the spray zones, we adopted the heat transfer coefficient as dependent of the flow rate of the water and the number of sprays per zone. Finally, in the radiation/natural convection stage, we verified a single coefficient for each interface. We also proposed a correlation to evaluate the global coefficient that takes into account all simulated parameters for the different steel types.