1 Introduction

Open channels are used in the mining, pulp and paper, as well as polymer processing and textile fiber industries (Develter and Duffy [12]; Fitton [13]; Fuentes et al. [15]; Kozicki and Tiu [24] and Sanders et al. [27]). Open channels are widely used in the mining industry where homogeneous non-Newtonian slurries have to be transported at moderately high concentrations around the plants and/or short distances because of the ease of operation in addition to the economical advantages. Due to the rapid increase in the slurries’ viscosities with concentration, the flow behaviour tends to be laminar and/or transitional rather than the usual turbulent conditions. Naturally, this transition is expected to be strongly influenced by the shape of the flow geometry and the rheological properties of the slurry.

In addition to this application, in the field of sediment laden flows where the flow is not homogeneous as in this work, many authors, e.g., see Baas et al. [2, 3] and Verhagen et al. [31] have done interesting work establishing different transition regimes as the concentration changes in a cross-sectional area. Materials tested included different concentrations of bentonite and kaolin suspensions. An array of ultrasound probes were used to measure the vertical velocity profiles. However, unfortunately, the corresponding rheological parameters were not measured independently but were rather derived from the measured suspended sediment concentrations. A Newtonian type transitional Reynolds number is used where the velocity is a depth averaged flow velocity and the effective viscosity was back calculated. They used a non-dimensional phase diagram to distinguish between the clay flow types such as leading waves only, mixing and erosion type or non- interacting type for the case of clay-laden density currents and soft substrates [31]. Furthermore, using the root mean square values of velocity, they also offered a phase diagram for the turbulent, transitional and laminar flows for bentonite and kaolin suspensions. However, the critical parameters relating to the transitions from one regime to another cannot be related to the true rheological parameters of their fluids thereby severely limiting the utility of their results [2, 3].

The effect of cross-sectional shape on the open channel flow of purely viscous non-Newtonian fluids design has not been fully investigated and is thus not yet entirely understood. The flow of homogeneous non-Newtonian fluids in open channels has received scant and sporadic attention by numerous authors such as Kozicki and Tiu [23], Wilson [32], Coussot [10, 11], Haldenwang [19], Haldenwang and Slatter [21], Haldenwang et al. [18, 22], Fitton [14], Burger et al. [4] and Slatter [28, 29]. Most of these analyses are based on the effectively one-dimensional models of the flow in an open channel and aided by empirical considerations.

Amongst the various open channel shapes, the semi-circular one is considered to be the most efficient. However, in practice, the most widely used one is the trapezoidal shaped since it offers more stable structural implementation. The rectangular and triangular shaped channels are special cases of the trapezoidal channel which also offer structural stability (Mott [26]).

The purpose in tailings slurries transportation is to achieve stable flow conditions throughout the conduit (pipe or open channel) and control or eliminate the conduit’s internal corrosion and/or erosion to extend the lifespan of the channel (Abulnaga [1]). Transitional flow is often characterized by its intrinsic unstable nature and may also be associated with a wavy motion leading to operational problems and overflows. Therefore, it is important to predict the end of laminar flow region and the onset of the transition region for a proper operation of such a facility.

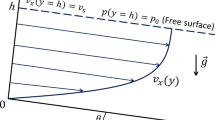
It is useful to recall here that the Froude and Reynolds numbers are used to determine the flow conditions in open channels as described in the literature in the context of water. These parameters which enable the characterisation of the different flow regimes together with the various open channel characteristics are summarized in Fig. 1.

Fig. 1
figure 1

Various channels shapes characteristics

Full size image

Over the years, the flow of water in open channels of various shapes has been studied extensively, e.g., see (Straub et al. [30]; Chow [9]). Straub et al. [30] presented a phenomenological analysis of the laminar flow of Newtonian fluids in flumes of various cross-sections using experimental data. They found that the laminar flow regime data can be described by a general relationship of the form f = K/Re where f is the usual Fanning friction factor, Re is the Newtonian Reynolds number and K is a purely numerical coefficient dependent on the channel shape. Burger et al. [4] conducted an extensive study on the laminar flow to delineate the shape effect for the flow of viscous non-Newtonian fluids in open channels. The K values obtained were 16.4 for the rectangular shape, 16.2 for the half-round shape, 17.4 for the trapezoidal shape and 14.6 for the triangular flume shape, all of which seem to be within ±10% of the widely used value of K = 16 for the laminar flow in a circular tube.

Burger et al. [4] found that the predicted results for smooth-walled, rectangular, triangular, and semi-circular shaped channels to be coincident with the experimental data when plotted as a friction factor f vs. the Reynolds number Re plot.

The friction factor is given by:

$$f = \frac{{ 2gR_{\text{h}} { \sin }\theta }}{{V^{ 2} }}$$
(1)

For purely viscous non-Newtonian fluids, Haldenwang et al. [18] introduced a Reynolds number (Re H) in rectangular channels as:

$$Re_{\text{H}} = \frac{{ 8\,\rho V^{ 2} }}{{\tau_{\text{y}} + k\,\left( {\frac{ 2V}{{R_{\text{h}} }}} \right)^{n} }}$$
(2)

In Eq. 2 k, τ y and n are the rheological parameters of the Herschel–Bulkley fluid model, R h the hydraulic radius, V the average fluid velocity and ρ the fluid density.

The fluids used by Haldenwang [20] consisted of solutions of Carboxymethyl cellulose (CMC) which was characterized as a shear-thinning fluid and suspensions of bentonite and kaolin clay characterized, respectively, as Bingham plastic and yield shear-thinning fluids. The Herschel–Bulkley model used to predict the flow of yield shear-thinning fluids was given by:

$$\tau = \tau_{\text{y}} + k \, \dot{\gamma }^{n} ,$$
(3)

with τ the average wall shear stress and \(\, \dot{\gamma }\) the shear rate. The Herschel–Bulkley model can be reduced to a shear-thinning model when the yield stress τ y = 0. When n = 1 and k becomes the plastic viscosity, the Herschel–Bulkley model is reduced to a Bingham plastic model. The yield shear-thinning model (3) can also be reverted to the Newtonian model when n = 1, k becomes the Newtonian viscosity and τ y = 0 (Chhabra and Richardson [8]).

Different investigators have developed various criteria to predict the laminar-turbulent transition region. This refers to the onset of transition from the laminar side of the flow. As it is such a complex region some efforts needs to be made to try and establish a workable protocol to predict this.

Limited information is available on transition, albeit it is neither as coherent nor as reliable as that for Newtonian fluids. For instance, Coussot [11] established a criterion for the onset of turbulence for the flow of Herschel–Bulkley model fluids to occur when the flow depth exceeds a critical value h given by:

$$h = \frac{ 1}{{\rho {\kern 1pt} \,g\,{ \sin }\theta }}\tau_{\text{y}} + k\,\left( {\frac{{ 404\,\left( {M + 1} \right)\,\rho \,\left( {g\,{ \sin }\theta } \right)^{ 2} }}{\text{kv}}} \right)^{{\left( {\frac{1}{ 2M + 1}} \right)}}$$
(4)

with

$$M = \frac{ 1}{n}$$

with n being the flow behaviour index and the flow velocity at transition being:

$$v = \left[ {\left( {\frac{M}{ 2M + 1}} \right)^{{\left( {\frac{M}{M - 1}} \right)}} - \left( {\frac{M}{ 2M + 1}} \right)^{{\left( {\frac{ 2M - 1}{M + 1}} \right)}} } \right]$$
(5)

Coussot’s [11] model is applicable to channels of rectangular and trapezoidal shapes.

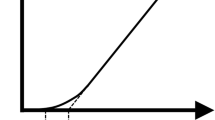
Subsequently, Haldenwang [19] proposed a model for the prediction of the onset of transition in rectangular flumes. He used a semi-log plot of Reynolds number vs. Froude number and showed that for each channel inclination, i.e., the value of θ, the shape of the curve seemed to be similar. The onset of transition was deemed to occur at a point where the slope of Fr–Re curve changed. A typical transition locus from 1° to 5° slope is shown in Fig. 2. The critical Re for the onset of transition is thus given as:

Fig. 2
figure 2

Onset of transition locus for 5% kaolin slurry in a 300 mm triangular flume

Full size image
$${Re}_{\text{c}} = 853.1 \left({\mu{\big/} {\mu_{\text{w}}}} |\dot{\gamma } = 100\;{\text{s}}^{{-1}} \right)^{-0.21} Fr + 12630 \left({\mu{\big/} {\mu_{\text{w}}}} |\dot{\gamma } = 1 0 0\;{\text{s}}^{{-1}} \right)^{-0.75}$$
(6)

with µ being the apparent viscosity at different shear rates, µ w the viscosity of water and Fr the Froude number. The onset of “fully turbulent regime” was deemed to be the point at which the Froude number is maximum (Haldenwang [19]). The “full turbulence” locus is shown in Fig. 3.

Fig. 3
figure 3

Onset of “full turbulence” 5% kaolin slurry in a 300 mm triangular flume

Full size image

The critical Reynolds number at the onset of the fully turbulent flow is expressed as:

$$Re_{\text{c}}\left( {\text{turb}} \right) = 3812 \left( {\mu {\big/}{\mu_{\text{w}} }|\dot{\gamma } = 500\,{\text{s}}^{{- 1}} } \right)^{-0.52} Fr + 9626 \left( {\mu {\big/}{\mu_{\text{w}} }|\dot{\gamma } = 500\,{\text{s}}^{{-1}} } \right)^{-0.65}$$
(7)

The main advantage of Eqs. (6) and (7) lies in their simplicity and the fact that the only required fluid property is the apparent viscosity at shear rates of 100 and 500 s−1 thereby obviating the need of fitting the data to a rheological model. When plotting apparent viscosity versus shear rate of different fluids used in this work it seems that for a shear rate of 100 s−1, the apparent viscosities are very similar, and therefore, one could expect the shear stresses to be very similar. Examining the experimental data it seems as though the onset of transition occurs at about 100 s−1. A similar approach was followed for the onset of full turbulence. (Haldenwang [19], Haldenwang et al. [22]).

Recently, Fitton [14] has also developed a criterion used to determine the laminar-turbulent point of transition in open channels. He made use of the Colebrook–White friction factor for turbulent flow, as well as the Darcy friction factor for laminar flow to determine the transition point which was deemed to be simply the intersection of these two friction factor plots as shown in Fig. 4. The Darcy friction factor f D is four times the Fanning friction factor f and is given by:

Fig. 4
figure 4

Prediction of transition. 7.2% kaolin in water slurry flowing in 150 mm rectangular channel

Full size image
$$f_{D} = \frac{64}{Re}$$
(8)

The Colebrook–White friction factor for turbulent flow in open channels is given by:

$$\frac{1}{{\sqrt{4f}}} = -2{\text{log}}\left({\frac{\varepsilon }{{14.84R_{\text{h}}}} + \frac{2.51}{{{Re}\sqrt {4f} }}} \right)$$
(9)

Using Coussot’s [10] sheet flow criterion where the flow depth to the channel width h/B is less than 0.1, in 2013 Slatter [28, 29] proposed a new model for sheet flow. He used only the data points which met the sheet flow (thin film) criteria from the Haldenwang [19] database. The Reynolds number he proposed for sheet flow is as follows:

$$Re_{4} = \frac{{ 8\rho V^{ 2} }}{{k^{\prime}_{*} \frac{ 3V}{{R_{\text{h}} }}^{{n^{\prime}_{*} }} }} ,$$
(10)

where \(k^{\prime}_{*}\) is the apparent sheet flow fluid consistency and \(n^{\prime}_{*}\) the apparent flow behaviour index.

Transition was established using the normalised adherence function (NAF) which was defined by the wall shear stress ratio and is given by:

$$\uptau_{{ 0 {\text{ Ratio}}}} = \frac{{\uptau_{{ 0 {\text{ Actual}}}} }}{{\uptau_{{ 0 {\text{ Laminar}}}} }}$$
(11)

For the onset of transition from laminar flow Slatter, [28] proposed a Reynolds number Re 4 of 700 and its evaluation is shown in Fig. 5 where the wall shear stress is plotted against the bulk shear rate for a 3.8% CMC solution.

Fig. 5
figure 5

Slatter’s transition model for 3.8% CMC solution

Full size image

Slatter [29] established another criterion of transition which is independent of the channel characteristic dimension as:

$$V_{\text{c}} = 2 6\sqrt {\frac{{\tau_{\text{y}} }}{\rho }}$$
(12)

Equation (12) is very similar to that presented by Govier and Aziz [17] for pipe flow except for the numerical constant of 19 instead of 26.

The Blasius friction factor for turbulent flow is given by:

$$f = 0.079 {Re}^{0.25}$$
(13)

Burger et al. [6] modified the Blasius equation for pipe flow and established new coefficients for specific open channel shapes which are given in Table 1. This equation was used in this work for turbulent flow predictions.

Table 1 Modified Blasius c and d values for different shape channels [7]
Full size table

In an attempt to consolidate the entire flow regime, following the approach of Garcia et al. [16], Burger [7] established a composite power law relationship in channels of rectangular, triangular, semi-circular and trapezoidal shapes. His model can accommodate open channel data in the laminar, transition and turbulent flow regimes and is expressed as:

$$f = F_{2} + \frac{{\left( {F_{1} - F_{2} } \right)}}{{\left( { 1+ \left( {\frac{Re}{t}} \right)^{e} } \right)^{j} }}$$
(14)

where F 1 and F 2 are the power law relationships given, respectively, by:

$$F_{\text{1}} = a\,{Re}^{b}$$
(15)

and

$$F_{\text{2}} = c\,Re^{d} ,$$
(16)

where a, b, c and d are fitting parameters for the composite power law relationship whereas e and j are the composite power law exponents.

The coefficients of the composite power law relationships are summarized in Table 2.

Table 2 Parameters in composite power law correlation for each shape based on Re H [7]
Full size table

This model cannot, however, accurately predict the onset of transition of full turbulence as is the objective of this work but enables one to determine friction factor values for any Reynolds number.

From the literature available on transitional flow in open channels, it can be seen that there are no conclusive guidelines on the prediction of transition. Thus, the aim of this work was to investigate the effect of the channel cross-sectional shape on transitional flow of non-Newtonian fluids by critically evaluating the different models currently available in the literature and provide a predictive model of transitional flow in smooth rectangular, triangular, trapezoidal and semi-circular shaped channels.

The organization for the remainder of the paper will be as follows:

  • The experimental procedure and test fluids used will be briefly described.

  • Existing transition models will be compared.

  • New models for three shapes namely trapezoidal, triangular and semi-circular as a well as a combined model incorporating all four shapes will be proposed. Only the combined model will be described in detail

  • The new models for the individual shapes will then be compared with the combined models as well as the existing models found in the literature

2 Experimental procedure and test fluids used

The databases used for the derivation of models in this work come from two doctoral projects, one by Haldenwang [19] and the other by Burger [7]. The work was conducted at the Flow Process and Rheology Centre of the Cape Peninsula University of Technology. Both databases have been published: For rectangular channels by Haldenwang and Slatter [21] and for rectangular, trapezoidal, half-round and triangular shapes by Burger et al. [4].

The work was conducted in a 10 m by 300 mm wide tilting channel which could be partitioned to become 150 mm wide. In addition, the other shapes could be inserted in the rectangular channel. Slopes of 1–5° degrees were achieved by tilting the open channel with a hydraulic ram.

The flume is fitted with an in-line tube viscometer which has three tubes with diameters 13, 18 and 80 mm. Each pipe was fitted with an electromagnetic flow meter and the pressure drops in the pipes were measured with high and low differential pressure transducers. The in-line measurement of the rheology of the fluids ensured that reliable rheology was used for the channel flow experiments.

The flow depth in the channel was measured with digital depth gauges at two positions 5 and 6 m from the entrance of the channel where the flow was steady and entrance and exit effects were minimal. All the instruments were electronically linked to a PC via a data logger.

The maximum flow rate achieved was 45 l s−1 from a Warman 4 × 3 centrifugal slurry pump. For lower flow rates, a 100 mm progressive cavity positive displacement pump was used.

The velocity in the channel was calculated from the flow meter data and flow cross-sectional area which was determined from the flow depth measurement. For each slope, flow rates were varied to achieve the widest range so that where possible flow from laminar to turbulent could be measured.

The fluids used were different concentrations of kaolin, characterized as a yield pseudoplastic suspension, bentonite as a Bingham plastic suspension, and carboxymethyl cellulose (CMC) as a power-law solution.

A more detailed description of the test work can be found in Haldenwang [19], Haldenwang and Slatter [21], Burger et al. [5] and Burger [7].

3 Model evaluation—existing models

The models proposed by Haldenwang [19], Coussot [11], Fitton [14] and Slatter [28, 29] were evaluated for power law, Bingham plastic and yield shear-thinning fluids at the onset of transition to determine the best model for rectangular flumes.

The log standard error (LSE) in this study was based on the difference between the observed critical velocity and the calculated critical velocity using different critical Reynolds numbers. The smaller the LSE value, the more accurate the model is.

The log standard error (Lazarus and Nielson [25]) is defined as:

$${\text{LSE}} = \frac{{\sqrt {\sum {\left( {{ \log }\left( {V_{\text{obs}} } \right) - { \log }\left( {V_{\text{calc}} } \right)} \right)^{ 2} } } }}{{N - 1}}$$
(17)

Figure 6a illustrates the data points for the Haldenwang’s [19, 21], Fitton’s [14] and Slatter’s [28, 29] models applicable to power law fluids which fall within the 20% margins but one cannot determine the best model from mere observation. On the histogram in Fig. 6b, the frequency depicted on the y-axis is the number of critical velocity values. The % deviation on the x-axis shows the deviation range these critical velocity values lie in. When one considers the histogram only, it is not easy to determine the best predictive model. Thus, more evidence was produced by calculating the LSE of the critical velocity deviation. The LSE values for different models were presented in Table 3 which indicates that Haldenwang’s [19, 22] model gives the best prediction. This is also indicated in Table 3 where 52% of data points which lie in the ±20% deviation region are predicted by the Haldenwang’s model for rectangular channels.

Fig. 6
figure 6

a Comparison between Haldenwang, Fitton and Slatter models for transition for power law fluids. b Frequency vs.  % deviation of transition data points corresponding to a. c Comparison between Fitton and Haldenwang models for transition for Bingham plastic fluids. d Frequency vs. % deviation of transition data points corresponding to c. e Comparison between Coussot, Fitton, Haldenwang and Slatter models for transition for yield shear-thinning fluids. f Frequency vs. % deviation of transition data points corresponding to (e)

Full size image
Table 3 Statistical analysis for power law models
Full size table

Fitton [14] and Haldenwang [19, 22] models were used to predict transition velocities for Bingham plastic fluids. It is shown in Fig. 6c, d that Haldenwang’s model gives a better prediction in comparison with Fitton’s model with 54% of data falling within the 20% deviation margins as indicated in Table 4.

Table 4 Statistical analysis for Bingham plastic models
Full size table

Coussot [11], Fitton [14], Haldenwang [19, 22] and Slatter [28, 29] models were used to predict transition velocities for yield shear-thinning fluids. Haldenwang’s predictions of transition velocity work best for yield shear-thinning fluids compared to the Slatter, Fitton and Coussot predictions as indicated in Table 5. The performance of the models used was illustrated in Fig. 6e, f.

Table 5 Statistical analysis for yield shear-thinning models
Full size table

Haldenwang’s [19, 22] model is the only model available in the literature which could be used to predict the end of transitional flow. Thus, no comparison could be made.

4 Adaptation of Haldenwang’s model to other shapes

The same method developed by Haldenwang [19] to obtain the critical transition Reynolds numbers for a rectangular channel was used to develop transition models for triangular, semi-circular and trapezoidal shaped flumes. In addition a combined model, which incorporates the rectangular, triangular, semi-circular and trapezoidal flume data, was developed. The procedure to develop the combined model which includes data for all four shapes is shown in the next section. The rectangular data was published by Haldenwang and Slatter [21] and the data for the other shapes by Burger et al. [5].

The first step is to obtain the critical Reynolds numbers which was used for the combined model to obtain the slope (q) and the y-intercept (p) values for the linear equation representing the transition locus shown in Fig. 2. These were plotted against the apparent viscosities at a shear rate of 100 s−1 for the onset of transition, and a shear rate of 500 s−1 for the end of transition. A shear rate of 100 s−1 was chosen since at that value the apparent viscosity was similar for various fluids in the region of the onset of transitional flow and a similar observation was noted at a shear rate of 500 s−1 for the onset of turbulent flow (Haldenwang [19] and Haldenwang et al. [22]). Figure 7 shows the slope (q) against the apparent viscosity and the y-intercept (p) vs. the apparent viscosity is illustrated in Fig. 8 for the onset of transition.

Fig. 7
figure 7

Onset of transition locus—relationship of m-values with apparent viscosity at a shear rate of 100 s−1 for all fluids in all flumes used

Full size image
Fig. 8
figure 8

Onset of transition locus—relationship of y-intercept values with apparent viscosity at a shear rate of 100 s−1 for all fluids in all flumes used

Full size image

Figures 7 and 8 show the two power law relationships used to obtain the critical Reynolds number at the onset of transition for all flumes data used.

From the relationships shown in Figs. 7 and 8, a critical Reynolds number for predicting the onset of transitional flow in various channels shapes was established using the Froude number as the dependent variable, the power law equation in Fig. 7 as the slope and the power law equation in Fig. 8 as the intercept of Eq. (18). The same procedure was used for the equations developed for the other shapes.

Admittedly the rather large scatter and relatively low R 2 value seen in Figs. 7, 8, 9 and 10 are discomforting, but in assessing this figure it should be borne in mind that data for different materials and different shapes are being included here. Also, the value of R 2 in non-linear regression is only indicative and has no sound theoretical meaning for the degree of fit. Transitions are always ill defined and occur over a range of conditions, akin to that in the case of flow of Newtonian fluids in pipes where the so-called transition zone exists in the range 2000 < Re < 4000 or so. The results seen in Figs. 7, 8, 9 and 10 should be interpreted in this spirit.

Fig. 9
figure 9

Onset of ‘Full turbulence’ locus—relationship of slope values with apparent viscosity at a shear rate of 500 s−1 for all fluids in all flumes used

Full size image
Fig. 10
figure 10

Onset of ‘Full turbulence’ locus—relationship of y-intercept values with apparent viscosity at a shear rate of 500 s−1 for all fluids in all flumes used

Full size image

The critical Reynolds number at the onset of transitional flow is expressed as:

$${Re}_{\text{c}} = 141 \, \left( {\mu |\dot{\gamma } = 100\;{\text{s}}^{{-1}} } \right)^{-0.28} Fr + 67 \, \left( {\mu |\dot{\gamma } = 100\;{\text{s}}^{{-1}} } \right)^{-0.71}$$
(18)

The constant 141 has a unit of Pa s0.28 and the constant 67, a unit of Pa s0.71.

If the viscosity of the non-Newtonian fluid at the shear rate of 100 s−1 is divided by the viscosity of water (10−3 Pa s) Eq. 18 can be expressed as:

$${Re}_{\text{c}}\,{\text{}} = 975 \left({\mu {\big/}{\mu_{\text{w}} |\dot{\gamma}}} = 100\,{\text{s}}^{-1}\right)^{-0.28} Fr + 9038 \left({\mu {\big/}{\mu_{\text{w}} |\dot{\gamma}}} = 100\,{\text{s}}^{-1}\right)^{-0.71}$$
(19)

The two relationships obtained for the upper critical Reynolds number are shown in Figs. 9 and 10.

The critical Reynolds number at the end of transitional flow is expressed as:

$$Re_{\text{c(turb)}} = 154(\mu \left| {\dot{\gamma } = 500\;{\text{s}}^{{ - 1}} } \right.)^{{-0.44}} Fr + 100(\mu \left| {\dot{\gamma } = 500} \right.\;{\text{s}}^{{-1}} )$$
(20)

The constant 154 has a unit of Pa s0.44 and the constant 100, a unit of Pa s0.65.

Eq. (20) is then written as follows:

$${Re}_{{{\text{c}}\,\left( {\text{turb}} \right)}}\, {\text{ }} = 3218 \left( {\mu {\bigg/}{\mu_{\text{w}} }}|\dot{\gamma } = 500\,{\text{s}}^{-1}\right)^{-0.44} Fr + 8913 \left( {\mu {\bigg/}{\mu_{\text{w}} }}|\dot{\gamma } = 500\,{\text{s}}^{-1}\right)^{-0.65}$$
(21)

The combined models [Eqs. (18) and (20)] for transition were evaluated for 6% kaolin slurry flowing in a 150 mm rectangular channel as illustrated in Fig. 11.

Fig. 11
figure 11

Evaluation of the combined transition models

Full size image

The combined model can be used to predict the transition in the four channel shapes studied here.

Transitional flow models (Eqs. (22)–(27)] in triangular, semi-circular and trapezoidal channel shapes were developed following the Haldenwang’s [19] approach which was described for the establishment of the combined model. The power–law relationships obtained for the triangular, semi-circular and trapezoidal channel shapes are similar to Figs. 7 and 8. However, the predictive models obtained at the onset of transition in open channels of triangular, semi-circular and trapezoidal shapes are given from Eqs. (22) to (24), respectively.

$${Re}_{\text{c}} {\text{Triangular}} = 1695 \, \left( {\mu {\big/}{\mu_{\text{w}} }} |\dot{\gamma } = 100\,{\text{s}}^{-1} \right)^{-0.36} Fr + 3388 \, \left( {\mu {\big/}{\mu_{\text{w}} |\dot{\gamma}}} = 100\,{\text{s}}^{-1} \right)^{-0.51}$$
(22)
$${Re}_{\text{c}} {\text{ Semi-circular}} = 733 \, \left( {\mu {\big/}{\mu_{\text{w}}}} |\dot{\gamma} = 100\;{\text{s}}^{-1} \right)^{-0.28} Fr + 14033 \, \left( {\mu {\big/}{\mu_{\text{w}}}} |\dot{\gamma} = 100\;{\text{s}}^{-1} \right)^{-0.9}$$
(23)
$${Re}_{\text{c}} {\text{Trapezoidal}} = 1068 \left( {\mu {\big/}{\mu_{\text{w}}}}|\dot{\gamma} = 100\,{\text{s}}^{-1}\right)^{-0.34} Fr + 2545 \left( {\mu {\big/}{\mu_{\text{w}}}}|\dot{\gamma} = 100\,{\text{s}}^{-1}\right)^{-0.36}$$
(24)

The ends of transition in triangular, semi-circular and trapezoidal open channels are given from Eq. (25) to (27), respectively.

$${Re}_{\text{c}} {\text{Triangular}} = 5595 \, \left( {\mu {\big/}{\mu_{\text{w}}}} |\dot{\gamma } = 500\,{\text{s}}^{-1} \right)^{-0.4} Fr + 7027 \, \left({\mu {\big/}{\mu_{\text{w}} }}|\dot{\gamma } = 500 {\text{s}}^{-1} \right)^{-0.62}$$
(25)
$${Re}_{\text{c}} {\text{ Semi-circular}} = 3423 \, \left( {\mu {\big/}{\mu_{\text{w}}}} |\dot{\gamma} = 500\;{\text{s}}^{-1} \right)^{-0.49} Fr + 17386 \, \left({\mu {\big/}{\mu_{\text{w}}}} |\dot{\gamma } = 500\;{\text{s}}^{-1} \right)^{-0.85}$$
(26)
$${Re}_{\text{c}} {\text{Trapezoidal}} = 3582 \left( {\mu {\big/}{\mu_{\text{w}}}} |\dot{\gamma} = 500\;{\text{s}}^{-1} \right)^{-0.45} Fr + 2460 \left( {\mu {\big/}{\mu_{\text{w}}}} |\dot{\gamma} = 500\;{\text{s}}^{-1} \right)^{-0.85}$$
(27)

5 Comparison of new models with those found in the literature

The adapted models were evaluated in their respective channel shapes with the combined model as well as the models found in the literature by taking into account the shape applicability.

5.1 Rectangular shape

The critical Reynolds number developed by Haldenwang [19, 22] for a rectangular flume is compared against Coussot’s [11] model, Fitton’s [14] model and the combined model. The combined model was developed using data for all four different flume shapes. From Fig. 12a, it is not easy to determine the best prediction. The LSE values presented in Table 6 indicate that the combined model with the lowest LSE value gives the best prediction of transitional flow followed by Haldenwang’s model. Coussot’s predictive model gives the worst prediction with a greater standard deviation of 0.62 as presented in Table 6. However, one can observe the spread of the critical velocity values predicted by various models in Fig. 12b. From Fig. 12b, it is seen that Coussot’s prediction is negatively skewed. The rectangular and combined models are positively skewed. The Fitton model then gives a poor prediction with a wide distribution of data over the ±20% deviation range.

Fig. 12
figure 12

a Onset of transition in a rectangular flume. b Frequency vs. % deviation of transition data points corresponding to (a)

Full size image
Table 6 Statistical analysis for the onset of transition in a rectangular flume
Full size table

5.2 Triangular shape

The adapted critical Reynolds number for triangular flumes is compared against the combined model and the Fitton’s model. From Fig. 13a, it can be seen that all models give a good prediction of transitional flow with the best ones being the triangular and the combined models as presented in Table 7 and Fig. 13b show the data distribution on a % deviation basis. It is shown that the triangular model is skewed to the right with a narrow distribution of data whereas Fitton’s model gives a wide distribution of data.

Fig. 13
figure 13

a Onset of transition in a triangular flume. b Frequency vs. % deviation of transition data points corresponding to (a)

Full size image
Table 7 Statistical analysis for the onset of transition in a triangular flume
Full size table

5.3 Semi-circular shape

The adapted critical Reynolds number for semi-circular flumes is compared against the combined model and Fitton’s model. It is shown in Fig. 14b that the combined and Fitton models are then positively skewed. From Fig. 14a and Table 8, it can be seen that the semi-circular model gives the best prediction since it gives the lowest LSE value and 67% of data points falling within the 20% margins which is higher than the combined and Fitton’s models. Fitton’s model gives the worst prediction of transitional flow with 41% data points falling within the ±20% deviation range as presented in Table 8.

Fig. 14
figure 14

a Onset of transition in a semi-circular flume. b Frequency vs. % deviation of transition data points corresponding to (a)

Full size image
Table 8 Statistical analysis for the onset of transition in a semi-circular flume
Full size table

5.4 Trapezoidal shape

The adapted critical Reynolds number applicable to trapezoidal channels is compared against the combined, Fitton’s and Coussot’s models. From Fig. 15a, it can be seen that all models give a good prediction of transitional flow except for Coussot’s prediction as presented in Table 9. It is then also seen in Table 9 that the proposed critical Reynolds number for trapezoidal flumes gives the best prediction of the laminar-turbulent transition as it gives the lowest LSE and standard deviation values as well as a higher percentage of the data points falling within the 20% margins.

Fig. 15
figure 15

a Onset of transition in a trapezoidal flume. b Frequency vs. % deviation of transition data points corresponding to (a)

Full size image
Table 9 Statistical analysis for the onset of transition in a trapezoidal flume
Full size table

While the results are widely distributed or in some cases there is a bias, but most of the points are within ±20% band which is comparable to the accuracy of the models and therefore, this behaviour is probably statistically not significant.

After comparison of various models, an overall performance is summarised in Table 10.

Table 10 Overall performance of transitional flow models used for different flume shapes
Full size table

The numbers in Table 10 indicate the ranking from the best model (i.e., 1) to the worst (i.e., 6). Thus, from Table 10 it can be seen that the combined model can be used to predict transition in the rectangular, triangular, semi-circular and trapezoidal channels. The adapted models can be applied to their specific flume shapes. The combined and adapted models for different shapes are also applicable to power-law, Bingham plastic and yield shear-thinning fluids.

Table 11 gives a summary of models to be used in the four channels shapes considered in this work.

Table 11 Summary of models to be used
Full size table

6 Conclusions

The prediction of transitional flow of non-Newtonian fluids in open channels was investigated. A score was developed for the overall performance of transitional flow models used for different flume shapes using statistical analysis. This numeric (score) criterion revealed that the models of Coussot and that of Slatter received low scores while the Fitton’s model gave an average performance over the entire range of flume shapes. By combining all the transition data for the four shapes of the open channels studied herein, a new correlation “combined model” was developed for the prediction of the onset of transition and onset of full turbulence which can adequately accommodate the four different channel shapes for all fluids tested. The benefit of having one model to predict the onset of transition for various open channel shapes outweighs the marginal improvement in predictions obtained with the adapted semi-circular, triangular and trapezoidal models which are only valid for those shapes.

In conclusion, it can be said that after a detailed comparison of experimental data with model velocities was conducted for power law, Bingham plastic and yield shear-thinning fluids, it was found that the composite model adequately predicted transition for all shapes tested in this work with an acceptable level of reliability.

The model can be used by engineers to predict transition of non-Newtonian fluids in open channels of at least the shapes that were tested in this work. This is important as open channels are either designed for laminar flow or turbulence as the transition zone is unstable.

As far as can be ascertained, it is the first time that a systematic study has been carried out on the effect of open channel shape on the transitional flow of different types of non-Newtonian fluids.