1 Introduction

The natural convection heat transfer in an enclosure with isothermal side walls has been investigated in many previous studies. The natural convection in a cavity is important due to its applications in cooling of electronic packages, solar technology, crystal growth in liquids, glass melting, isolation in buildings, and safety aspects of gas cooled reactors. In many of these applications, the performance of the system and the quality of the final product are influenced by the temperature distribution and heat transfer rates in the system. For example, in a casting process, the fragmentation of crystals is a direct function of the temperature treatment [1]. The presence of a magnetic field could result in formation of textures along an easy-magnetization axis in a casting process of a metallic melt for producing of a textured material [2].

In a cavity filled with a fluid, the presence of the temperature difference induces a buoyancy force which results in fluid motion. This phenomenon is known as “natural convection”. When the cavity is filled with an electrically conducting liquid and subject to a magnetic field, the moving fluid experiences the Lorentz force and its effect is to resist the fluid motion [3]. This effect, consequently, alters the heat transfer rate and the temperature distribution in the cavity. Thus, the magnetic field in magnetohydrodynamic flows (MHD) may be utilized as a controlling agent for the flow and temperature distributions in the cavity in order to increase the quality of some products. For instance, the action at a distance of a magnetic field on the metals processing industry include the control of liquid metals in continuous casting process and electro-magnetically supported melts [4]. Another important application of liquid metals is in nuclear engineering applications. The metal coolants are much denser than the conventional liquids such as water which has been utilized in power plants. The metal liquids can remove heat more rapidly, and hence, they can provide much higher power density compared to water. Moreover, the cooling with water requires a high pressurized system to raise the boiling point of the water. The higher the pressure is, the higher the safety maintenance issues are. In contrast, the liquid metals can be utilized at very high temperatures in a low pressurized system. Another important advantage of liquid metals is its radiation shielding properties that makes them attractive in nuclear applications. As the liquid metals are highly electrically conducting, they can be pumped using an electromagnetic field [5].

In recent years, the effect of magnetic field has been examined on the convective heat transfer of MHD flows in molten electrically-conducting liquids. Sathiyamoorthy and Chamkha [6, 7] have studied the effect of a magnetic field on the natural convection heat transfer of molten gallium for various magnetic field inclination angles and uniformly or linearly heated adjacent walls. Gontijo and Cunha [8] have experimentally investigated the heat transfer rate and the thermo-magnetic convection inside a cavity with an aspect ratio near unity. They reported that by using a very dilute suspension of a magnetic composite with a particle volume fraction of 0.5%, the average temperature of the fluid inside a cavity decreases up to 10% and the Nusselt number increases about 10% by applying a moderate magnetic field. Maatki et al. [9] have investigated the convection heat transfer of a binary mixture in a three-dimensional cavity in the presence of a magnetic field.

Selimefendigil et al. [10] have analyzed the effect of magnetic field on the natural convection of ferrofluids in a differentially-heated cavity in which the hot wall is subjected to partial heating while the rest of the wall is insulated. The authors have examined the effect of a magnetic dipole on the natural convective heat transfer in the cavity. Sheikholeslami et al. [11] have considered the enclosure space between two tubes where the inner tube is elliptic shape. The authors have studied the MHD natural convection heat transfer of CuO nanofluids in the enclosure. They found an increase of heat transfer enhancement by the increase of the magnetic field. Jena et al. [12] have studied the effect of the magnetic field on the natural convective heat transfer of molten gallium in a three-dimensional cavity heated from below. Malvandi et al. [13] have studied the effect of magnetic field on the convection heat transfer of a magnetic nanofluid inside a vertical channel. They concluded that the presence of a magnetic field reduces the thermal advantages of nanofluids. Adesanya et al. [14] have analyzed the free convective flow of an MHD fluid through a channel with time periodic boundary condition by considering the effects of Joule dissipation. Chamkha et al. [15] have investigated the entropy generation in a differentially-heated cavity filled with a CuO-water nanofluid by considering the effect of a magnetic field. The authors reported that the magnetic field can suppress the entropy generation rate.

Mojumder et al. [16] have studied the effect of magnetic field on the natural convection and entropy generation of a magnetic nanofluid in a half-moon shaped cavity with semi-circular bottom heater considering various values of the magnetic parameter and different inclination angles of cavity and the position effect of the heaters. Selimefendigil et al. [17] have addressed the effect of magnetic field strength and angle on the convective heat transfer of CuO nanofluids in a lid-driven cavity. They found that the angle of the magnetic field shows a significant effect of on the convective heat transfer rate and that the presence of a magnetic field reduces the convective heat transfer in the cavity. Rashidi et al. [18] have investigated the effect of a magnetic field on the mixed heat transfer in a channel with a sinusoidal wall filled with Al2O3 nanofluid. They reported an enhancement of heat transfer in the presence of the magnetic field. In all of the mentioned studies, the effect of the presence of a magnetic field on the flow and heat transfer in a cavity has been studied for fluids in liquid phase without any phase change.

There are some experimental and numerical studies regarding solid–liquid phase-change involving natural convection effects. Gau and Viskanta [19] have performed experimental test for measuring the melting interface of solidification of a pure metal (Gallium). Following the study of Gau and Viskanta [19], Brent et al. [20] have reported a numerical solution for melting of Gallium in a rectangular differentially-heated cavity using a fixed grid approach known as the enthalpy-porosity technique. They compared the obtained numerical results with the experimental results of Gau and Viskanta [19] and found comparatively a good agreement. Bertrand et al. [21] have performed a benchmark numerical study for melting simulation of solid in a rectangular cavity by considering the natural convection effects. Various numerical methods in different laboratories were utilized to simulate the melting process of Tin and Octadecane.

Fan and Khodadadi [22] have reported an excellent review of the heat transfer studies regarding to simulation and experiments of phase-change material. Very recently, Kumar et al. [23] have experimentally analyzed melting of a cuboid lead subject to a constant heat flux boundary condition. A neutron radiography method was employed to visualize the melting interface. Then, an image processing technique was utilized to extract the molten interface radiography images. It is worth noticing that the lead provides shielding effects and is important in the design of transportation packages for nuclear material. Kumar et al. [24] have also experimentally studied the effect of boundary heat flux conditions on the melting behavior of a cuboid lead using an infra-red thermography technique. The results indicate that the buoyancy effects are very important in the melting of lead for Rayleigh number of order 107.

Ranjbar et al. [25] and Kashani et al. [26] have studied solidification of a nano-enhanced phase-change material (NEPCM) in a wavy cavity. Tiari et al. [27] have examined the effect of the presence of a fin (heat-pipe type) on the phase-change behavior of a high melting temperature phase-change material. Tiari et al. [28] have also studied the melting behavior of potassium nitrate as phase-change material in a cavity supported with heat-pipe type fins.

The present study aims to theoretically address the influence of a uniform magnetic field on the phase-change behavior of an electrically-conducting material involving natural convection effects.

2 Geometric and mathematical models

2.1 Formulation of the problem

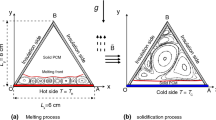
Consider a cavity with the width L x and height L y . A schematic view of the physical model is represented in Fig. 1. This figure shows a two-dimensional square cavity filled with an electrically-conducting frozen substance such as gallium or an electrolyte with a fusion temperature T f. The right and left walls of the cavity are at the isothermal temperatures T c and T h where T h > T f > T c. The bottom and top walls are insulated. As depicted in Fig. 1, in the melting process, three states in the cavity can be assumed, a fully solid state, the mushy state and the fully liquid state. The mushy region state is a two-phase region that is a mixture of the solid and liquid phases. In the mushy region, the volume fractions of the liquid and the solid are functions of the temperature which will be discussed in details later. It is assumed that the cavity is initially filled with a solid substance at the fusion temperature T f. A uniform magnetic field with magnitude B 0 is applied normal to the vertical walls as shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of physical model

Full size image

2.2 Governing equations

All of the enclosure walls are considered to be impermeable and the no-slip velocity boundary conditions is employed. The top and bottom walls are considered well insulated and the side walls are isothermal. All of the enclosure walls are assumed perfectly electrically-conducting. Moreover, the Boussinesq approximation is adopted. The temperature differences are assumed to be small, and hence, the thermophysical properties in each phase are assumed to be constant, and the Boussinesq approximation is applicable for considering the density changes in liquid phase. However, the thermo-physical changes due to phase change are taken into account as the density, heat capacity and thermal conductivity for the solid and liquid phases of a substance could be different. It is also assumed that Joule heating effects as well as the viscous dissipation effects and radiation effects are negligible. The induced magnetic field due to the induced current in the cavity is neglected as the magnetic Reynolds number (Re m) is small Indeed, the magnetic Reynolds number (Re m = uL/(μ 0 σ)) shows the ratio of the induction of a magnetic field by the motion of the fluid to the magnetic diffusion where u is the velocity scale, L is the flow length scale, μ 0 is the permeability of free space, and σ is the electrical conductivity of the liquid. Here, it is assumed that the induced magnetic field, produced by the motion of the electrically-conducting fluid, is negligible compared to the applied magnetic field B 0. Considering the above assumptions, the conservation equations for mass, momentum, temperature and electric transfer are written as:

Continuity

$$\nabla \cdot {\mathbf{u}} = 0$$
(1)

Momentum

$$\frac{{\partial {\mathbf{u}}}}{\partial t} + ({\mathbf{u}}\cdot\nabla ){\mathbf{u}} = - \frac{1}{\rho }\nabla P + v\nabla^{2} {\mathbf{u}} + \frac{{\mathbf{J}}}{\rho } \times {\mathbf{B}} + \beta {\mathbf{g}}(T - T_{\text{f}} ) + S(T){\mathbf{u}}$$
(2)

Energy

$$\frac{\partial T}{\partial t} + ({\mathbf{u}}).\nabla T = \alpha \nabla^{2} T - \frac{L}{{C_{p} }}\frac{\partial \varphi (T)}{\partial t}$$
(3)

Electric transfer

$${\mathbf{J}} = \sigma ( - \nabla \phi + {\mathbf{u}} \times {\mathbf{B}})$$
(4a)
$$\nabla^{2} \phi = {\mathbf{B}}\cdot\omega ,\quad \omega = \nabla \times {\mathbf{u}},$$
(4b)

where u, B, ω, ϕ and J are the velocity, the magnetic field, the vorticity and the voltage field (the electric potential), and the current density, respectively. The variables P, T, and ϕ denote the pressure, the temperature, and the volume fraction of the liquid phase, respectively. Here, t is time and g is the vector of gravitational acceleration constant. In addition, α is the thermal diffusivity, L is the latent heat of fusion, C P is the heat capacity at constant pressure, ρ is the density, β is the thermal expansion coefficient, ν is the kinematic viscosity, and σ is the electric conductivity. In Eq. (2), the term S(T)·u indicates a source term for forcing the fluid velocity to zero in solid phase which will be discussed in more details later. The subscripts of s and l denote the solid and liquid phases, respectively.

Sreenivasan et al. [29] discussed the effect of magnetic field on the flow motion and concluded that for the case of 2D steady flow in the cases in which the magnetic field lies in the plane of the fluid motion and concluded that the term B·ω is zero; hence, the governing equations of Eq. (4a, 4b) reduces to \(\nabla^{2} \phi = 0\). Taking into account that the enclosure walls are perfectly electrically-conducting, they could provide a very low resistance guide path for the induced current. Indeed, perfectly conducting walls provide a resistance-free path from the induced current which indicates that the electric field vanishes everywhere in the cavity, i.e. \(\nabla \phi = 0\). Therefore, it can be concluded that the electric field can be neglected inside the enclosure [6].

Invoking these conditions, the team of J × B in the momentum equation reduces to σ B 2 [7]. Thus, the governing equations for mass, momentum and thermal energy represented here in dimensional Cartesian coordinates x, y as follows:

Continuity

$$\frac{\partial u}{\partial x} + \frac{\partial \nu }{\partial y} = 0$$
(5)

Momentum in x-direction

$$\rho \left( {\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = - \frac{\partial p}{\partial x} + \mu \left( {\frac{{\partial^{2} u}}{{\partial x^{{^{2} }} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + S(T)\,u$$
(6)

Momentum in y-direction

$$\rho \left( {\frac{\partial v}{\partial t} + u\frac{\partial \nu }{\partial x} + v\frac{\partial \nu }{\partial y}} \right) = - \frac{\partial p}{\partial y} + \mu \left( {\frac{{\partial^{2} \nu }}{{\partial x^{{^{2} }} }} + \frac{{\partial^{2} \nu }}{{\partial y^{{^{2} }} }}} \right) + \rho g\beta (T - T_{\text{f}} ) - (\sigma B_{0}^{2} ){\kern 1pt} \nu + S(T){\kern 1pt} \nu$$
(7)

Energy

$$\frac{\partial T}{\partial t} + u\frac{{\partial {\rm T}}}{\partial x} + v\frac{{\partial {\rm T}}}{\partial y} = \alpha \left( {\frac{{\partial^{2} {\rm T}}}{{\partial x^{{^{2} }} }} + \frac{{\partial^{2} {\rm T}}}{{\partial y^{{^{2} }} }}} \right) + \frac{L}{{c_{\text{p}} }}\frac{\partial \varphi \left( T \right)}{\partial t},$$
(8)

where α = α l φ + α s(1 − φ) and B 0 is the magnitude of the uniform magnetic field. Here, φ is the melt fraction which is evaluated using the temperature as:

$$\varphi (T) = \left\{ {\begin{array}{*{20}c} 0 & {T < T_{\text{f}} } \\ {\frac{{T - T_{\text{f}} }}{\Delta T}} & {T_{\text{f}} < T < T_{\text{f}} + \frac{\Delta T}{2},} \\ 1 & {T > T_{\text{f}} + \Delta T} \\ \end{array} } \right.$$
(9)

where ΔT is the mushy-zone temperature range. The source term of S(T) in the momentum equation is introduced as a continues equation for phase transient using the Carman–Koseny equation as [30, 31]:

$$S(T) = - A_{\text{mesh}} \frac{{(1 - \varphi (T))^{2} }}{{\varphi (T)^{3} + \varepsilon }},$$
(10)

where ε is a small number constant to prevent division by zero. In this study, the value of ε = 10−3 is used as reported in similar studies in the open literature.

Based on the problem description, the boundary conditions are written as:

$${\text{Heated wall}}{\kern 1pt} \quad x = 0, \, y = y:u = 0, \, v = 0, \, T = T_{\text{h}}$$
(K)
$${\text{Cooled wall}}{\kern 1pt} \quad x = L_{x} , \, y = y:u = 0, \, v = 0,\;T = T_{\text{c}}$$
(11b)
$${\text{Top wall}}\quad {\kern 1pt} x = x, \, y = \, L_{y} :u = 0, \, v = 0,\frac{\partial T}{\partial y} = 0$$
(11c)
$${\text{Bottom wall}}{\kern 1pt} \quad {\kern 1pt} x = x, \, y = 0:u = 0, \, v = 0,\frac{\partial T}{\partial y} = 0,$$
(11d)

where L x and L y are the width and height of the enclosure, respectively. In addition, a reference pressure point with the relative pressure of zero is adopted at the top left corner of the enclosure. It is appropriate to express Eqs. (5)–(8) into the non-dimensional forms using dimensionless variables as following:

$$X = \frac{x}{{L_{y} }},\quad Y = \frac{y}{{L_{y} }},\quad U = \frac{{uL_{y} }}{{\alpha_{\text{l}} }},\quad V = \frac{{vL_{y} }}{{\alpha_{\text{l}} }},\quad \theta = \frac{{T - T_{\text{f}} }}{{T_{\text{h}} - T_{\text{f}} }}$$
(12a)
$$F_{0} = \frac{{t\alpha_{l} }}{{L_{y}^{2} }},\quad S\left( T \right) = \frac{{S\left( T \right)L_{y}^{2} }}{{\rho \alpha_{\text{l}} }},\quad P = \frac{{pL_{y}^{2} }}{{\rho \alpha_{\text{l}}^{2} }},\quad \gamma = \frac{\alpha }{{\alpha_{\text{l}} }},\quad R_{k} = \frac{{k_{\text{s}} }}{{k_{\text{f}} }},\quad {\text{AR}} = \frac{{L_{y} }}{{L_{x} }}$$
(12b)

The relevant dimensionless parameters are then:

$${\text{Ra}} = \frac{{\rho^{2} c_{\text{l}} g\beta L_{y}^{3} (T_{\text{h}} - T_{\text{f}} )}}{{\mu k_{\text{l}} }},\quad {\text{Ste}} = \frac{{c_{\text{l}} (T_{\text{h}} - T_{\text{f}} )}}{L},\quad \Pr = \frac{{c_{\text{l}} \mu }}{{k_{\text{l}} }},\quad {\text{Ha}} = B_{0} L_{y} \sqrt {\frac{\sigma }{\rho \upsilon }} ,$$
(13)

where Ra is the Rayleigh number, Ste is the Stefan number, Pr is the Prandtl number and Ha is the Hartmann number. Substituting Eqs. (12a, 12b) and (13) into Eqs. (5)–(8), the corresponding non-dimensional form of the governing Eqs. (14)–(17) is obtained as:

Continuity:

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$
(14)

Momentum in x-direction:

$$\frac{\partial U}{{\partial F_{0} }} + U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial p}{\partial X} + \Pr \left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) + S(\theta )\,U$$
(15)

Momentum in y-direction:

$$\frac{\partial V}{{\partial F_{0} }} + U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial p}{\partial Y} + \Pr \left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) + {\text{Ra}}{\kern 1pt} \Pr \theta - ({\text{Ha}})^{2} \Pr \cdot V + S(\theta )\,V$$
(16)

Energy:

$$\frac{\partial \theta }{{\partial F_{0} }} + u\frac{\partial \theta }{\partial X} + \nu \frac{\partial \theta }{\partial Y} = \gamma \left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right) - \frac{1}{\text{Ste}}\frac{\partial \varphi \left( \theta \right)}{{\partial F_{0} }},$$
(17)

where

$$\gamma = \varphi \left( \theta \right) + \frac{{\alpha_{\text{s}} }}{{\alpha_{\text{l}} }}(1 - \varphi (\theta ))$$
(18)

In this way, in liquid zone \((\theta > 0,\varphi = 1)\), \(\gamma = 1\), and in the solid zone \((\theta < 0,\varphi = 0)\), \(\gamma = \frac{{\alpha_{\text{s}} }}{{\alpha_{\text{l}} }}\).

Upon using the variables introduced in Eq. (12a, 12b), the non-dimensional boundary conditions are:

$${\text{Heated wall}}\quad X = 0: \, U = 0, \, V = 0, \, \theta_{\text{h}} = 1$$
(19a)
$${\text{Cooled wall}}\quad X = 1: \, U = 0, \, V = 0,\theta_{\text{c}} = \frac{{T_{\text{c}} - T_{\text{f}} }}{{T_{\text{h}} - T_{\text{f}} }}$$
(19b)
$${\text{Top wall}}\quad Y = {\text{AR}}:U = 0, \, V = 0,\frac{\partial \theta }{\partial Y} = 0$$
(19c)
$${\text{Bottom wall}}\quad Y = 0:U = 0, \, V = 0,\,\;\frac{\partial \theta }{\partial Y} = 0,$$
(19d)

where assuming the cold wall temperature T c at the fusion temperature of T f (i.e. T c = T f) gives θ c = 0.

The melt volume fraction as a function of θ is written as:

$$\varphi (\theta ) = \left\{ {\begin{array}{*{20}c} 0 & {\theta < 0} \\ {\frac{\theta }{\Delta \theta }} & {0 < \theta < \Delta \theta } \\ 1 & {\theta > \Delta \theta } \\ \end{array} } \right.,$$
(20)

where \(\Delta \theta = \frac{\Delta T}{{T_{\text{h}} - T_{\text{f}} }}\).

3 Numerical method

To analyze the present problem, the obtained set of Eqs. (14)–(19a, 19b, 19c, 19d) along with the boundary conditions Eqs. (19a, 19b, 19c, 19d) have been calculated using the powerful method that is called the finite element [32, 33]. The continuity equation, Eq. (14), is employed as a constraint to satisfy the mass conservation. Hence, the constraint for continuity equation is introduced as a penalty parameter (χ) in the momentum equations as described by Reddy [33]. Therefore, the pressure is written as:

$$P = - \chi \left( {\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y}} \right)$$
(21)

Using Eq. (21), the momentum equations are reduced as:

$$\frac{\partial U}{\partial Fo} + U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial }{\partial X}\left( {\chi \left( {\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y}} \right)} \right) + \Pr \left( {\frac{\partial U}{\partial X} + \frac{\partial U}{\partial Y}} \right) + S(\theta )\,U$$
(22)
$$\begin{aligned} \frac{\partial V}{\partial Fo} + U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial }{\partial Y}\left( {\chi \left( {\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y}} \right)} \right) + \Pr \left( {\frac{\partial V}{\partial X} + \frac{\partial V}{\partial Y}} \right) \hfill \\ + {\text{Ra}}{\kern 1pt} { \Pr }\theta - ({\text{Ha}})^{2} \Pr \cdot V + S(\theta )\,V \hfill \\ \end{aligned}$$
(23)

Thus, in the above equations the continuity Eq. (8) is satisfied for very large values of the penalty parameter (χ = 107) [33]. Now, the velocities (U and V) as well as the temperature are expanded invoking a basis set \(\left\{ {\zeta_{k} } \right\}_{k = 1}^{N}\) as,

$$U \approx \sum\nolimits_{k = 1}^{N} {U_{k} \zeta (X,Y),\quad \;V \approx } \sum\nolimits_{k = 1}^{N} {V_{k} \zeta (X,Y),} \;\quad \theta \approx \sum\nolimits_{k = 1}^{N} {\theta_{k} \zeta (X,Y)}$$
(24)

for −0.5 < X<+ 0.5 and 0 < Y<1. It should be noted that the basic functions for U and V velocities and the temperature are the same, and thus, the total number of nodes variables is N. Invoking the Galerkin finite element method, the non-linear residual for the governing equations of momentum Eqs. (22) and (23) as well as the energy equation Eq. (17) at nodes of internal domain Ω are derived as,

$$\begin{aligned} R_{\text{i}}^{1} &= \sum\limits_{k = 1}^{N} {U_{k} \int_{\varOmega } {\frac{{\partial \xi_{K} }}{{\partial F_{0} }}{\text{d}}X{\text{d}}Y} } + \sum\limits_{k = 1}^{N} {U_{{_{k} }} } \int_{\varOmega } {\left[ {\left( {\sum\limits_{k = 1}^{N} {U_{k} \zeta_{k} } } \right)\frac{{\partial \zeta_{k} }}{\partial X}\zeta_{k} {\text{d}}X{\text{d}}Y} \right.} \hfill \\ &\quad \left. { + \left( {\sum\limits_{k = 1}^{N} {V_{k} \zeta_{k} } } \right)\frac{{\partial \zeta_{k} }}{\partial Y}\zeta_{k} {\text{d}}X{\text{d}}Y} \right]\zeta_{\text{i}} {\text{d}}X{\text{d}}Y \hfill \\ & \quad + \sum\limits_{k = 1}^{N} {U_{k} } \int_{\varOmega } {\frac{{\partial \xi_{i} }}{\partial X}\left[ {\left( \chi \right)\frac{{\partial \xi_{K} }}{\partial X}{\text{d}}X{\text{d}}Y} \right]} + \sum\limits_{k = 1}^{N} {V_{k} } \int_{\varOmega } {\frac{{\partial \xi_{i} }}{\partial X}\left[ {\left( \chi \right)\frac{{\partial \xi_{K} }}{\partial Y}{\text{d}}X{\text{d}}Y} \right]} \hfill \\ &\quad + \Pr \sum\limits_{k = 1}^{N} {U_{k} } \int_{\varOmega } {\left[ {\frac{{\partial \xi_{i} }}{\partial X}\frac{{\partial \xi_{K} }}{\partial X} + \frac{{\partial \xi_{i} }}{\partial Y}\frac{{\partial \xi_{K} }}{\partial Y}} \right]{\text{d}}X{\text{d}}Y + S(\theta )\sum\limits_{k = 1}^{N} {\int_{\varOmega } {\left( {\sum\limits_{k = 1}^{N} {\left( {U_{k} \zeta_{k} } \right)\zeta_{i} } } \right){\text{d}}X{\text{d}}Y} } } \hfill \\ \end{aligned}$$
(25)
$$\begin{aligned} R_{\text{i}}^{2} &= \sum\limits_{k = 1}^{N} {V_{k} \int_{\varOmega } {\frac{{\partial \xi_{K} }}{{\partial F_{0} }}{\text{d}}X{\text{d}}Y} } + \sum\limits_{k = 1}^{N} {V_{{_{k} }} } \int_{\varOmega } {\left[ {\left( {\sum\limits_{k = 1}^{N} {U_{k} \zeta_{k} } } \right)\frac{{\partial \zeta_{k} }}{\partial X}} \right.} \left. { + \left( {\sum\limits_{k = 1}^{N} {V_{k} \zeta_{k} } } \right)\frac{{\partial \zeta_{k} }}{\partial Y}} \right]\zeta_{\text{i}} {\text{d}}X{\text{d}}Y \hfill \\ & \quad + \sum\limits_{k = 1}^{N} {U_{k} } \int_{\varOmega } {\frac{{\partial \xi_{\text{i}} }}{\partial Y}\left[ {\left( \chi \right)\frac{{\partial \xi_{K} }}{\partial X}{\text{d}}X{\text{d}}Y} \right]} + \sum\limits_{k = 1}^{N} {V_{k} } \int_{\varOmega } {\frac{{\partial \xi_{\text{i}} }}{\partial Y}\left[ {\left( \chi \right)\frac{{\partial \xi_{K} }}{\partial Y}{\text{d}}X{\text{d}}Y} \right]} \hfill \\ & \quad + \Pr \sum\limits_{k = 1}^{N} {V_{k} } \int_{\varOmega } {\left[ {\frac{{\partial \xi_{i} }}{\partial X}\frac{{\partial \xi_{K} }}{\partial X} + \frac{{\partial \xi_{i} }}{\partial Y}\frac{{\partial \xi_{K} }}{\partial Y}} \right]{\text{d}}X{\text{d}}Y} + {\text{Ra}}\Pr \int_{\varOmega } {\left( {\sum\limits_{k = 1}^{N} {\theta_{k} \zeta_{k} } } \right)\zeta_{\text{i}} {\text{d}}X{\text{d}}Y} \hfill \\ & \quad + ({\text{Ha}})^{2} \Pr \sum\limits_{k = 1}^{N} {\int_{\varOmega } {\left( {\sum\limits_{k = 1}^{N} {V_{k} \zeta_{k} } } \right)\zeta_{\text{i}} {\text{d}}X{\text{d}}Y} } + S(\theta )\sum\limits_{k = 1}^{N} {\int_{\varOmega } {\left( {\sum\limits_{k = 1}^{N} {\left( {V_{k} \zeta_{k} } \right)\zeta_{\text{i}} } } \right){\text{d}}X{\text{d}}Y} } \hfill \\ \end{aligned}$$
(26)
$$\begin{aligned} R_{\text{i}}^{3} &= \sum\limits_{k = 1}^{N} {\theta_{k} \int_{\varOmega } {\frac{{\partial \xi_{K} }}{{\partial F_{0} }}\zeta_{\text{i}} {\text{d}}X{\text{d}}Y} } + \sum\limits_{k = 1}^{N} {\theta_{{_{k} }} } \int_{\varOmega } {\left[ {\left( {\sum\limits_{k = 1}^{N} {U_{k} \zeta_{k} } } \right)\frac{{\partial \zeta_{k} }}{\partial X}} \right.} \left. { + \left( {\sum\limits_{k = 1}^{N} {V_{k} \zeta_{k} } } \right)\frac{{\partial \zeta_{k} }}{\partial Y}} \right]\zeta_{\text{i}} {\text{d}}X{\text{d}}Y \hfill \\ & \quad + \gamma \sum\limits_{k = 1}^{N} {\theta_{k} } \int_{\varOmega } {\left[ {\frac{{\partial \xi_{\text{i}} }}{\partial X}\frac{{\partial \xi_{K} }}{\partial X} + } \right.} \left. {\frac{{\partial \xi_{\text{i}} }}{\partial Y}\frac{{\partial \xi_{K} }}{\partial Y}} \right]{\text{d}}X{\text{d}}Y + \frac{1}{\text{Ste}}\sum\limits_{k = 1}^{N} {\varphi_{k} \left( \theta \right)} \int_{\varOmega } {\frac{{\partial \xi_{K} }}{{\partial F_{0} }}\zeta_{\text{i}} {\text{d}}X{\text{d}}Y} , \hfill \\ \end{aligned}$$
(27)

where the linear basis functions are adopted. The three-point Gaussian quadrature is also utilized to evaluate the integrals terms in the Eqs. (25)–(26). Considering the momentum equations, the terms incorporating the penalty parameter (χ) are computed using the two-point Gaussian quadrature employing the reduced integration penalty formulation [33]. The non-linear residual equations, Eqs. (25)–(27), are solved by the Newton–Raphson method to compute the coefficients of the expansions (i.e. U k , V k and θ k ) in Eq. (24). The detailed solution procedure could be found in [32, 34]. Additionally, uniform meshes in both the X and Y directions are adopted in which the discretized equations are implemented. Therefore, the utilized elements are quadrilateral elements. Considering the quadrilateral elements, \(\zeta\) can be linearly approximated as c 1 + c 2 X + c 3 Y + c 4 XY where c 1–c 4 are coefficients which can be obtained using the grid points. For each of the initial velocity and initial temperature, a value of zero is selected as initial guesses. The iteration process commenced until the residuals for the momentum residual equation, i.e. j = 1 and 2, and the heat equation, i.e. j = 3, satisfy \(\sum {(R_{\text{i}}^{j} )} \le 10^{ - 7}\). A backward differentiation formula (BDF) of variable order (between 1 and 2) associated with free time steps is utilized [35]. The results of the present code have been successfully validated against the numerical and experimental results of phase-change heat transfer in a cavity filled with phase-change materials [21, 23] and against the works conducted by Sathiyamoorthy and Chamkha [6, 7] who have examined the natural convection flow under a magnetic field in a square cavity filled with an electrically-conducting fluid.

3.1 Grid check

In order to check the grid independency of the solution, the calculations were repeated for several grid sizes in the case of A mush = 1×105, ∆T = 0.05 K, Pr = 0.0216, Ra = 1×105, Ste = 0.039, γ = 1. Table 1 indicates the required time for simulation of about 90% of melting for various grid sizes. The liquid fraction for different grid sizes is also depicted in Fig. 2. The results of Fig. 2 indicate that the grid size of 150 × 150 can provide acceptable accuracy. Hence, the results of the present study are carried out using the grid size 150 × 150.

Table 1 The required time for grid size independency
Full size table
Fig. 2
figure 2

The melting interface for various grid sizes

Full size image

3.2 Validation of the results

To check the precision of the solution, several investigations have been performed. As the first case, the experimental results of Gau and Viskanta [19] and the numerical results available in literature for a rectangular cavity with aspect ratio (height/width) of 0.714 are adopted and compared with the results of the current study. In the experiment of Gau and Viskanta [19], the left wall is hot while the top and bottom walls are insulated.

Gau and Viskanta [19] have evaluated the melting interface using the pour-out method and the probing method. The evaluated melting interface for this problem is also numerically addressed by Kashani et al. [26], Tiari et al. [27], Khodadadi and Hosseinzadeh [36], Berant et al. [20], Joulin et al. [37], Viswanta and Jaluria [38] and Desai and Vafai [39]. The summary of the available numerical results are plotted in Fig. 3a, b. As seen, the results of the present study are in reasonable agreement with the available experimental and numerical results. In the case of F 0 = 3.48, the results are somehow different from the experiment but in agreement with the numerical results. The previous authors have concluded that the difference between the numerical and experimental results in this case could be due to the method of evaluating the melting interface in the experiment of Gau and Viskanta [19]. The authors have measured the melting interface mechanically using a manual mechanical probe. For high values of F 0 the solid–liquid interface of melting could be unstable, and hence, distinguishing the precise shape of interface is hard.

Fig. 3
figure 3

A comparison between the experimental and numerical results available in literature and the present results when γ = 1 and neglecting the magnetic effects a, b uniformly heated left and cooled right and the bottom and top walls are insulated, Ra = 6×105 Pr = 0.0216

Full size image

As another validation, the benchmark study of Bertrand et al. [21] is adopted in a case in which Ra = 1 × 107, Pr = 50, Ha = 0 and γ = 1. A literature review shows that many researchers have compared their numerical results with the benchmark results reported by Bertrand et al. [21]. Figure 4 shows the melting interface evaluated in the previous studies and those reported by Bertrand et al. [21]. The results of the current study have also been plotted in Fig. 4 as a comparison. This figure shows that the present numerical results are in very close agreement with the experimental results.

Fig. 4
figure 4

A comparison between the melting interface reported by Bertrand et al. [21] and the current results (τ = F 0 × Ste)

Full size image

Also, as another comparison, the results of the present study are compared with the experimental results reported by Kumar et al. [23] for melting of lead. Kumar et al. [23] have examined the melting of lead contained in a stainless steel cuboid. In the study of Kumar et al. [23], there was a heater mounted at one of the vertical side walls of the cavity which provided a constant heat flux, while the other walls were insulated. The authors have carried out the photography of solid–liquid interface movement during melting of lead using neutron radiography. The non-dimensional parameters of the experiment set-up of Kumar et al. [23] are shown in Table 2. Initially, heater is put on and temperature will increase on both sides. In the experiment of Kumar et al. [23], when melting commenced, the temperature at the right hand side wall (the heater side) was higher than that of the left hand side wall. Therefore, a linear temperature distribution was the initial condition for the commencing of the melting process. As Kumar et al. [23] have performed the experiment for the case of constant heat flux, the Rayleigh number and Stefan number are needed to be calculated on the basis of the constant heat flux as: Ste* = C p q″cond L x /(kL) and Rayleigh number based on constant heat flux is given by Ra* = gβq″cond L 4 y /(kαν).

Table 2 Input provided for one case in simulation Kumar et al. [23]
Full size table

Here, the results of the present study are compared with the experimental results reported by Kumar et al. [23] (Fig. 5).

Fig. 5
figure 5

A comparison between the results of benchmark study of Kumar et al. [23] and the current results at different non-dimensional time steps of F 0 = 0.37, F 0 = 0.73, F 0 = 1.10 and F 0 = 2.2

Full size image

As seen, the results of the present study are in very good agreement with the experimental results reported by Kumar et al. [23].

For the case of magnetohydrodynamic flows, Sathiyamoorthy and Chamkha [7] have studied the effect of the presence of magnetic effects on natural convection of electrically-conducting liquids. The top and left walls of the cavity in the study of Sathiyamoorthy and Chamkha [7] are considered to be isothermal at the hot temperature of T h. The top and right walls are also considered to be isothermal at the cold temperature of T c. Here, As a comparison, the current results are compared with the results of Sathiyamoorthy and Chamkha [7] by assuming that the cavity is filled with a molten metal and the same boundary conditions as described in [7]. Figure 6 shows a comparison between the streamlines and isotherms reported by Sathiyamoorthy and Chamkha [7] and the results of the current study when Ra = 105, Pr = 0.054 and two Hartmann numbers of Ha = 50 and Ha = 100. Figure 6 indicates good agreement between the both studies.

Fig. 6
figure 6

Isotherms and streamlines with reference to Sathiyamoorthy and Chamkha [7] and the results of present study

Full size image

As yet another comparison for the magnetic field effect, the results of the current research are compared with the finding of Al-Mudhaf and Chamkha [40]. Al-Mudhaf and Chamkha [40] have studied numerically the natural convective flow of electrically-conducting gallium and germanium liquid metals in an inclined rectangular enclosure in the presence of a uniform magnetic field due to a transverse temperature gradient. The results of the comparison between these two studies have been summarized in Table 3 when Ra = 105, Pr = 0.025, S = 45° (where S is the enclosure inclination angle).

Table 3 The average Nusselt number, \(\overline{{\rm Nu}}\) reported by Al-Mudhaf and Chamkha [40] and the present research
Full size table

4 Results and discussion

Now, as a case study, consider a cavity with the size of L x  = 6.35 cm, L y  = 6.35 cm filled with gallium. The temperature at the hot wall is T h = 38 °C and at the cold wall is T c = 28.3 °C. The thermophysical properties of gallium are represented in Table 4. In this case, the corresponding non-dimensional parameters are: Pr = 0.0216, Ste = 0.039, Ra = 6×105 and γ = 1. These non-dimensional parameters are considered as the default non-dimensional parameters in this study and the calculations are performed for these set of non-dimensional parameters otherwise they will be stated.

Table 4 Thermophysical of pure gallium
Full size table

Figure 7 shows the streamlines and isotherms of the melting process at the beginning of the melting process, i.e. τ = F 0 × Ste = 0.015, for various values of the magnetic field strength when Ra = 6×105. At the background of the streamlines figures, the contours of the volume fraction of the liquid phase (φ) are plotted. As seen, the liquid phase is commenced in the vicinity of the hot wall. A large region near the cold wall is remained frozen yet. A fast variation of the volume fraction from unity (only liquid) to zero (only solid) occurs at the interface, controlled by Eq. (21) as a function of temperature. These figures demonstrate that the increase of the Hartmann number slightly affects the melting process. It is clear that the magnetic field effect tends to reduce the velocity of the fluid as it is always against the motion of the fluid. At the beginning of the melting process, there is a narrow region filled with molten trapped between two solid walls (the heater and the melting interface). Therefore, the fluid motion is slow, and the variation of the magnetic field could not induce a significant effect on the motion and melting process. Figure 8 depicts the shape of the interface at the non-dimensional time step of τ = 0.015 for various values of the Hartmann number. This figure is in agreement with the results of Fig. 7 and indicates that the presence of the magnetic field is not important at the beginning stages of the melting process.

Fig. 7
figure 7

Isotherms and streamlines for τ = F 0 × Ste = 0.015 when a Ha = 0, b Ha = 30, c Ha = 50, d Ha = 70, e Ha = 100

Full size image
Fig. 8
figure 8

The melting interface for various Hartmann numbers at τ = 0.015

Full size image

Figure 9 shows the streamlines and isotherms of the melting process at time step of τ = 0.04 for various values of Ha. This figure indicates that after elapsing of a while, the melting interface is pushed forward into the frozen area. When the magnetic field is weak (i.e. Fig. 9a, b), there are three circulation cells in the molten region. These circulation flows take the heat from the hot wall and try to distribute it on the frozen interface. Hence, regarding the three circulation flow streams, three caved regions on the interface can be seen. As the magnetic field gets strong, the circulation cells break down into a large circulation cell. In this case, the caved regions disappeared and obviously the molten rate is decreased. A comparison between the shapes of the solid–liquid interfaces is depicted in Fig. 10. This figure demonstrates that the increase of the Hartmann number results in a smoother interface shape, but it decreases the molten volume fraction.

Fig. 9
figure 9

Isotherms and streamlines for τ = F 0 × Ste = 0.04 when a Ha = 0, b Ha = 30, c Ha = 50, d Ha = 70, e Ha = 100

Full size image
Fig. 10
figure 10

The melting interface for various Hartmann numbers at τ = 0.04

Full size image

Figure 11 demonstrates the effect of the Hartmann number on the streamlines and isotherms in the cavity at the non-dimensional time of τ = 0.08. This time for the melting of gallium as described at the beginning of this section is equivalent to 10 min from the beginning of the melting process. Figure 11a is in agreement with Fig. 9a and confirms the presence of three circular flows in the absence of the magnetic field effect. Figure 11b depicts that the presence of a weak magnetic field reduces the circulation patterns into just two. The further increase of the magnetic field effect results in large circulation patterns and prevents the formation of local circulation patterns.

Fig. 11
figure 11

Isotherms and streamlines for τ = F 0 × Ste = 0.08 when a Ha = 0, b Ha = 30, c Ha = 50, d Ha = 70, e Ha = 100

Full size image

This figure indicates that the effect of the magnetic field is more obvious in the top side of the cavity rather than the bottom side. Indeed, the molten liquid absorbs the heat by conduction from the hot plate, and then it moves upward due to the buoyancy forces. Therefore, the top of cavity in the molten region is filled with a hot molten. Then, the hot molten interacts with the cold interface and moves downward. As a result, there is a large caved area filled with molten near the top of the cavity. As the hot molten at the top moves downward and interacts with the cold frozen interface, it loses heat and gets colder and colder. Therefore, when the molten reaches the bottom of the cavity, it has lost a considerable amount of heat, and hence, the molten region at the bottom of the cavity is a narrow area. Figure 12 summarizes the obtained solid–liquid interface at the non-dimensional time of τ = 0.08 for various values of the magnetic field parameter (Ha). As seen in Fig. 12, the position of the interface at the bottom of the cavity is not a monotonic function of Ha. As the Hartmann number increases, the interface moves towards the hot plate, until the Hartmann number is around Ha = 70 and then it moves back toward the cold wall.

Fig. 12
figure 12

The melting interface for various Hartmann numbers at τ = 0.08

Full size image

As mentioned, at the bottom part of the cavity, the change in the position of the interface is not a monotonic function of the magnetic field strength (Ha). Indeed, the position and the shape of the interface are functions of the convective and diffusive heat transfer mechanisms. When the Hartmann number is small, the increase of Ha mostly affects the fluid velocity at the regions where the fluid velocity is high. In this region, which is about the middle height of the cavity next to the melting interface, the shape of the mushy region and the melting interface is under the significant influence of the variation of the magnetic field. Consequently, the shape of the interface at the upper regions of the cavity gives directions to the fluid flow moving from the upper to the lower side along the melting interface. Hence, the shape of the interface near the bottom of the cavity is under the influence of the fluid flow. As a result, and as seen for the low values of the Hartmann number, (Ha = 0–50), the position of the melting interface next to the bottom part of the cavity almost follows the expected flow patterns monastically. However, as the Hartmann number gets very strong, it almost suppresses the natural convection flows and significantly decreases the melting volume fraction. In this case, the overall position of the melting interface is seized to advance and the interface shape also gets flattened. Therefore, in this case, a different trend of behavior for the change in the location of the melting interface at the bottom part of the cavity can be seen. As a summary, it can be said that the shape and the position of the melting interface at the bottom part of the cavity are functions of the shape of the interface at the upper region of the cavity as well as the overall position of the melting interface. The change in the Hartmann number has the tendency to change the shape of the interface at the upper region as well as the overall position of the melting interface (the melting volume fraction), and hence, based on the magnitude of the Hartmann number, two different trends of change in the position of the melting interface at the bottom part of the cavity can be expected.

Figure 13 illustrates the streamlines and isotherms contours inside the cavity in the non-dimensional time of τ = 0.15 for various values of the Hartmann number. In this case, most regions of the cavity are filled with the liquid phase and the fluid can freely move inside the cavity. A jet of hot fluid is present near the hot wall which drives the hot liquid upward. There is also a downward jet of cold liquid at the interface side. The hot liquid is almost present along the top wall while the cold liquid exists along the bottom wall. There is a stratified region at the core of the cavity in which the heat transfer occurs in the vertical direction from top to bottom. Near the bottom of the cavity, there is a local slow circulation regime which results in a very low temperature gradient at the bottom of the cavity near the solid–liquid interface region (the mushy region). At this region where the temperature gradient is low and almost linear, the thickness of the mushy region is also increased (as seen in the volume fraction contours in the background of the streamline contours). Figure 14 surmises the melting interfaces for various values of the Hartmann number when τ = 0.15. This figure shows that the trend of the motion of the interface at the bottom of the cavity follows the trend of behavior observed in Fig. 12. For low values of the Hartmann number, e.g. Ha = 30 and 50, the melting interface is closer to the cold wall compared to that of Ha = 0. In contrast, the melting interface for high values of the Hartmann number, e.g. Ha = 70 and 100, is not as close to the cold wall as that of Ha = 0. This is because of the fact that the presence of the magnetic field induces a magnetic force that tends to suppress the natural convection velocity in the cavity. The decrease of velocity reduces the strength of the advective heat transfer mechanism in the cavity. Thus, the more increase of the magnetic field (the raise of Ha) the more the suppression of melting.

Fig. 13
figure 13

Isotherms and streamlines for τ = F 0 × Ste = 0.15 when a Ha = 0, b Ha = 30, c Ha = 50, d Ha = 70, e Ha = 100

Full size image
Fig. 14
figure 14

The melting interface for various Hartmann numbers at τ = 0.15

Full size image

It is also interesting that for the cases of Ha = 0, 30 and 50, the temperature gradients next to the hot wall and the melting front (melting interface) are strong and the isotherms are close together. The temperature distribution in the core of the cavity is almost horizontal. This trend of behavior is similar to the temperature distribution for a regular cavity with a high Rayleigh number [41]. However, as the Hartmann number increases (Ha = 70 and 100), the gradients of temperature next to the hot wall and the melting front decrease and the temperature distribution forms almost a vertical shape. This temperature distribution could be of interest in some of the engineering applications or in a metallurgical process where a uniform temperature distribution is demanded.

Figure 15 shows the overall volume fraction of the molten phase, i.e. the liquid phase, as a function of the non-dimensional time (τ) for Hartmann numbers in the range Ha = 0–100. As observed in Fig. 9, at the early stages of the melting process, the conduction heat transfer is the dominant effect in the cavity, and hence, the effect of the presence of the magnetic field is negligible. As the fraction of the liquid phase increases and the molten region gets wider, the natural convective flows get stronger, which boosts the effect of the magnetic field. As mentioned, the magnetic field tends to decrease the velocity of the molten as it always acts against the motion direction of the fluid. The decrease of the molten motion results in the decrease of the convective heat transfer in the cavity. As the Hartmann number increases, the effect of the magnetic field increases. Therefore, as seen in Fig. 15, the increase of Ha results in decreases in the molten volume fraction.

Fig. 15
figure 15

Effect of magnetic induction on liquid fraction for various Hartmann numbers

Full size image

5 Conclusion

The impact of magnetic induction on the melting process of a metallic electrically-conducting phase-change material (PCM) in an enclosure was investigated. There was a temperature difference between the side walls of the cavity and the bottom and top walls were well insulated. An enthalpy-porosity approach was utilized to model the phase-change process. The effect of buoyancy forces were taken into account using the Boussinesq model. The results of the present study were compared with different numerical and experimental results available in the literature and were found in good agreement. The results were reported in the form of the melting volume fraction and contours to study the effect of the magnetic field (Hartmann number) on phase-change heat transfer and melting behavior of an electrically-conducting PCM in the cavity. The results showed that the increase of the Hartmann number would decrease the rate of phase-change process. The presence of a uniform magnetic field was found to play an effective role in the melting front and controlled velocity of flow. Of course, it is important to notice that even in the case of a strong applied magnetic field, i.e. Ha = 100, the melt front area in the upper parts of the enclosure was still in a convex shape, and hence, the melting front was not perfectly uniform.

Since in the present study, the angle of the magnetic field was assumed to be constant in the horizontal direction, the magnetic controlling parameter was solely the Hartmann number. The results demonstrated that the increase of the intensity of the applied magnetic field (increase of Hartmann number) could suppress the flow velocity, but it could not well control the temperature distribution and the melting front shape. However, the change in the inclination angle of the magnetic field may induce more significant controlling mechanism on the flow, heat transfer and the melting front which can be studied in future researches.