1 Introduction

Reflection and transmission as well as attenuation of sound from the interface of two different media have had challenging phenomena for acousticians during the last decades. Acousticians have used different assumptions and methods to analyze the variation of sound at the boundary of the two media. Snell’s law and Fresnel reflection and transmission coefficients are basic relations in this area of study which consider the impedance differences of the two media. However, different factors which are present at the sea surface region can cause difficulties in the path towards accurate solution of sound transmission through the surface boundary. Factors such as presence of waves, bubble clouds and wind speed are some of the important ones [1]. Knowing the effects of each factor and its origin are the complication of sound transmission simulations. The wide range of subjects in this area, e.g., underwater communication channels [2–8], evaluation of sonar performance [9–11], marine life [12–14], oceanography [15–17] among others, has led to numerous researches which have concentrated on these influential phenomena on the sound. Doppler effects [18–21], attenuation and absorption [22–25], bubble population [26–29], and sound transmission [12, 30–33] as well as the environmental conditions such as wave propagation in shallow water [2, 34–36], surface waves [37–40], and bottom effects [41–43] can be considered as interesting subjects among vast number of the published works. The current study focuses on the effects of impedance, sea surface roughness (due to the presence of wind-generated waves) and subsurface bubbles on the attenuation, scattering, and transmission of sound through the sea surface.

Earliest studies in examining the sound at the interface of two media have mostly focused on the impedance differences [44]. The most recent studies in this area have been conducted by Godin [44–47] through studying the transmitted and reflected acoustic power fluxes from the air–water interface and presenting the anomalous transparency of water–air interface. Also the enhanced sound transmission (EST) model for low frequency underwater point source is introduced and experimentally verified by Calvo et al. [48, 49]. Also, many theoretical [50–60] and experimental [61–67] studies have studied sound transmission through the water–air interface by focusing on the acoustic field in water due to the existence of airborne noise sources such as helicopters propeller-driven aircraft and supersonic transport.

Regarding the scattering of sea surface, perturbation method makes it possible to estimate the rough sea surface scattering loss and has been used by Marsh [68], Bass [69] and Brekhovskikh and Lysanov [70] among others to develop different methods for modeling the free surface scattering loss. Another approach in this area which is based on the classical physics methods was proposed by pioneers like Rayleigh, Helmholtz, Kirchhoff and Born [71]. To provide experimental data in this regard, Chapman and Harris [72], among others [73–75], conducted extensive measurements of surface scattering strength using omni-directional hydrophones and by applying explosive sources for low frequencies in spectral region from 400 to 6400 Hz. Also, the sea surface backscattering strength at low frequencies (70–1000 Hz) have been presented by Ogden and Erskine [76, 77] through critical sea tests (CST), covering a variety of wind speeds from 3.0 to 17.5 m/s as well as mean grazing angles from 5° to 30°.

On the other hand, many researchers have focused on the field of subsurface bubble clouds and theories regarding sound propagation in liquids containing bubbles [27, 71, 78–82]. Medwin [71] studied the depth dependence of bubbly layer effects on the attenuation of incident sound and concluded that this layer is a non-ignorable factor in sound propagation. Prosperetti [81] suggested the natural sound-producing mechanisms at frequencies between 20 and 500 Hz due to wave–turbulence interactions and oscillating bubble clouds. Fialkowski and Gauss’s [82] investigations resulted in the importance of bubbles role in surface scattering strength with decreasing grazing angle and increasing frequency and wind speed in the ocean. Verestchagina and Fedotovsky’s conclusion [83–85], presented and validated their theory which is a mathematical version of resonance dispersion model (RDM) in gas–liquid media and used it to show that bubbles’ dynamic density should be taken into account for sound propagation in bubbly water at low frequency range (below 200 Hz). According to their theory, it is conceivable to obtain resonance dependent phase velocity, dynamic density, and sound damping factor in the bubbly water medium.

As deduced from the literature, in addition to the classical impedance contrast of air and water, both surface roughness and subsurface bubble clouds have crucial roles in the sound transmission, scattering and attenuation in sea surface. Accordingly, the main focus of the present manuscript is to simultaneously implement theses parameters in the HKF model to better simulate the acoustic behavior of sea surface and to model the compound influence of theses parameters. In the next section, the reformed Helmholtz-Kirchhoff-Fresnel (HKF) method is presented in which the subsurface bubble population is included in the classic HKF method. Afterward, the algorithm of the computer program SSVASL (sea surface virtual acoustic simulator lab) is presented, validated and used to show the effect of different parameters on the sound propagation at sea surface environment.

2 The reformed Helmholtz-Kirchhoff-Fresnel method

As stated before, the main concern of the present study is to simulate the compound effects of sea surface roughness, subsurface bubbles and impedance differences in the transmission, scattering and attenuation of sound at sea surface. First, the basic governing equations should be presented. The basic equations of the scattered and transmitted fields at sea surface due to an incident continuous wave of frequency ω = kc from a point source [71] can be written as

$$U\left( Q \right) = \frac{{\mathcal{R}}}{4\pi }\mathop \int \limits_{S} \frac{\partial }{\partial x} \left(U_{\text{S}} \frac{{e^{ - ikR} }}{R}\right){\text{d}}S$$
(1)
$$U^{'} \left( {Q^{'} } \right) = \frac{{\mathcal{T}}}{4\pi }\mathop \int \limits_{S} \left[ {U_{\text{s}} \frac{\partial }{\partial n}\left( {\frac{{e^{{ - ik^{'} R^{'} }} }}{{R^{'} }}} \right) - \frac{{e^{{ - ik^{'} R^{'} }} }}{{R^{'} }}\frac{{\partial U_{\text{s}} }}{\partial n}} \right]_{S} {\text{d}}S.$$
(2)

Theses equations are derived by considering constant or slow varying reflection (\({\mathcal{R}}\)) and transmission (\({\mathcal{T}}\)) coefficients over the surface element (Fig. 1). In these equations, U(Q) and U′(Q′) are scattered and transmitted fields, respectively, k ′ is equal to ω/c′, and c′ is the sound speed in the second medium. Q is the sound source and Q′ is the imaginary source in the second medium and s and n are interface elements and normal vector to the interface element, respectively (Fig. 2). Also, coefficients \({\mathcal{R}}\) and \({\mathcal{T}}\) are coefficients of an infinite plane wave at an infinite plane interface and U s is the field at the interface position in the absence of scattering surface and reflected field. Detailed derivation of these solutions is presented by Medwin and Clay [71].

Fig. 1
figure 1

Geometry of sound scattering and transmission through air–water interface. ρ and c are medium’s density and sound speed, respectively. ds and n are interface elements and normal vector to the interface element, respectively. Q is sound source and Q′ is the imaginary source in the second medium

Full size image
Fig. 2
figure 2

Geometry for the facet scattering calculation. The element area dS is elevated –ξ above the x ′ y′ plane

Full size image

To find the acoustic pressure field, the HKF integral is used as follows:

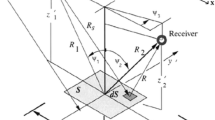
$$\begin{aligned} P\left( f \right) \approx \frac{{iP_{0} R_{0} {\mathcal{R}}_{12} k\left( {\cos \psi_{1} + \cos \psi_{2} } \right)e^{{ - ik\left( {R_{1} + R_{2} } \right)}} }}{{4\pi R_{1} R_{2} }} \hfill \\ \;\;\;\;\;\;\;\;\mathop \int \limits_{{ - x_{1} }}^{{x_{1} }} {\text{d}}x^{'} \mathop \int \limits_{{ - y_{1} }}^{{y_{1} }} D\exp \left\{ { - i\left[ {\frac{{x'^{2} }}{{x_{f}^{2} }} + \frac{{y'^{2} }}{{y_{f}^{2} }} + kx\left( {\sin \psi_{1} - \sin \psi_{2} \cos \psi_{3} } \right) - ky^{'} \sin \psi_{2} \sin \psi_{3} + k\xi \left( {\cos \psi_{1} + \cos \psi_{2} } \right)} \right]} \right\}{\text{d}}y' \hfill \\ \end{aligned}$$
(3)

The applied parameters in Eq. 3 are shown in Fig. 2. The acoustic point source is defined as

$$p_{\text{inc}} = \frac{{D_{t} P_{0} R_{0} \exp [i(\omega t - kR_{\text{s}} )]}}{{R_{\text{s}} }}$$
(4)

where p inc is the arrival pressure to the sea surface region, R s is the range from the source to the surface element dS (Fig. 3), P 0 is the source pressure at range R 0 = 1m, D t is the Gaussian transmission function, W g and L g are the half-beam width to D t  = e −1. By applying Eq. 4 and assuming a three phase medium (water–bubbly water–air), the general expression for the mean-squared scattered pressure field can be derived in the following form:

$$\langle pp^{*} \rangle = p_{0}^{2} R_{0}^{2} \frac{{{\mathcal{R}}_{13}^{2} K^{2} G^{2} (\theta )Ae^{i\omega \tau } }}{{8\pi^{2} R_{1}^{2} R_{2}^{2} }}\mathop \int \nolimits \mathop \int \limits_{\infty }^{\infty } \begin{array}{*{20}c} {G W e^{{2i\left( {\alpha \xi + \beta \eta } \right)}} } \\ \end{array} d\xi d\eta$$
(5)

where A = πXY is the insonified area. As observed in Eq. 3, the original HKF integral incorporates only the free surface roughness. However, in Eq. 5, \({\mathcal{R}}_{13}\) represents the reflection coefficient for three phase media through which subsurface bubble population is considered as the third medium between the air and the water. The procedure for obtaining proper quantity of \({\mathcal{R}}_{13}\) based on the properties of bubbly water medium are discussed later.

Fig. 3
figure 3

Scattering geometry. Differential area dS is at the position x, y and has height ξ with respect to the mean surface

Full size image

As a simplified presentation, Eq. 5 can be written in the simpler form of

$$\langle pp^{*} \rangle = p_{0}^{2} R_{0}^{2} \frac{A}{{R_{1}^{2} R_{2}^{2} }}S$$
(6)

where S is the scattering coefficient for three phases of air, water, bubbly water media at the sea surface and is defined as follows:

$$S = \frac{{{\mathcal{R}}_{13}^{2} K^{2} G^{2} (\theta )Ae^{i\omega \tau } }}{{8\pi^{2} }}\mathop \int \nolimits \mathop \int \limits_{\infty }^{\infty } \begin{array}{*{20}c} {G W e^{{2i\left( {\alpha \xi + \beta \eta } \right)}} } \\ \end{array} {\text{d}}\xi {\text{d}}\eta$$
(7)

To obtain the scattering strength level in decibels, S is commonly used to be 10 times the logarithm of surface scattering coefficient, \(s = 10 \log_{10} S\).

After deriving the main equations of the sound propagation at the free surface, the transmission, scattering, and attenuation of sound are discussed by incorporating the effect of bubbly water layer into the equations.

By applying the subsurface bubble population effects to the transmission change (TC) relation presented by Medwin and Hagy relation [60], the following relation is derived for transmission change:

$$\begin{aligned} {\text{TC}} &= 10\log \frac{{\left\langle {p_{2} p_{2}^{*} } \right\rangle }}{{p_{{1s}}^{2} }} = 10\log \left[e^{ - R} \left( {1 + \frac{{Dc_{2} \cos \theta_{1} }}{{Hc_{1} \cos \theta_{2} }}} \right)^{ - 2} \right. \hfill \\ &\quad\times (2\cos \theta_{1} \cos \theta_{2} )^{2} \hfill \\ &\quad \left. + \mathop \sum \limits_{i} \frac{{\pi A_{i} {\mathcal{T}}_{i}^{2} L^{2} \cos^{2} \theta_{2mi} F_{i}^{2} S(R_{i} , K_{xy} L)}}{{\lambda_{2}^{2} r_{2i}^{2} (\cos \theta_{1} /\cos \theta_{1i} )^{2} }}\right] \hfill \\ \end{aligned}$$
(8)

where c 1 and c 2 are sound speeds in the first and the second medium, respectively. Also, θ 1, θ 2, D and H, are the incident and refracted angles and the receiver and source positions, respectively (Fig. 4). Other variables are defiend in Table 1.

Fig. 4
figure 4

Geometry of transmission into second medium from a localized point source in the air. A is the insonified area. H and D are the source height, and receiver depth (with respect to the air–water interface, A), respectively

Full size image
Table 1 Definition of variables in Eq. 8
Full size table

Subscript i in Eq. 8 represents the rough surface elements. In fact, in order to determine the values of TC in this method, it is necessary to dicretisize the rough interface of the air–water. Afterward, by determining the variables shown in Table 1 for each of the surface elements, it is conceivable to obtain the values of TC.

As mentioned earlier, the bubbly water layer should also be incorporated in the attenuation. To this end, the approach of Tolstoy [86] presented in Eq. 9 has been used as the basis.

$$\frac{{p_{\text{B}} }}{{p_{\text{D}} }} = \varepsilon (2\pi x)^{0.5} k_{1}^{1.5} e^{{ - x\alpha_{\text{Tol}} }}$$
(9)

where α Tol is the sound damping coefficient, ɛ is a constant which can be calculated explicitly for any shape of the roughness elements [86], x is the propagation range, k 1 is the wave number in the first medium, p B is the boundary pressure, and p D represents the arrival pressure. Tolstoy [86] developed an approach for determining α Tol based on the roughness of the interface and impedance contrast between two media. By using this value of α Tol and Eq. 9, Tolstoy [86] obtained the boundary and arrival pressure ratio (\(\frac{{p_{\text{B}} }}{{p_{\text{D}} }}\)) which has good agreement with the experimental data.

To incorporate the attenuation of the bubbly water layer, the following equation is presented.

$$\alpha_{\text{tot}} = \frac{{\alpha_{{{\text{w}} - {\text{bw}}}} \times \alpha_{{{\text{bw}} - {\text{a}}}} }}{{\alpha_{{{\text{w}} - {\text{bw}}}} + \alpha_{{{\text{bw}} - {\text{a}}}} }}$$
(10)

where α w−bw and α bw−a are the damping coefficients at the water–bubbly water and air–bubbly water interfaces, respectively, defined as in the following equations.

$$\alpha_{{{\text{w}} - {\text{bw}}}} = \ln \left( {\frac{{p_{{{\text{D}}1}} \times (\varepsilon (2\pi x_{1} )^{0.5} k_{1}^{1.5} )}}{{p_{{{\text{B}}1}} }}} \right)^{{\frac{1}{{x_{1} }}}}$$
(11)
$$\alpha_{{{\text{bw}} - {\text{a}}}} = \ln \left( {\frac{{p_{{{\text{D}}2}} \times (\varepsilon (2\pi x_{2} )^{0.5} k_{2}^{1.5} )}}{{p_{\text{B2}} }}} \right)^{{\frac{1}{{x_{2} }}}}$$
(12)

where x 1 and x 2 are the propagation ranges in the first and the second media, respectively; while k 1 and k 2 are sound wavenumbers in the first and the second media (Fig. 5).

Fig. 5
figure 5

Sound attenuation at the sea surface. P B1 and P B2 are boundary pressures at the water–bubbly water and air–bubbly water interfaces, respectively

Full size image

3 Acoustic coefficients bubbles

Effects of the subsurface bubble clouds can be considered as three physical mechanisms [40] including refraction, forward and backward scattering as well as absorption which were studied in the last sections. In this section, two different approaches are adopted for modeling the subsurface bubbles: dispersive and non-dispersive behavior of bubbles. As mentioned earlier, based on the RDM approach, at frequency range below 200 Hz, the dynamic behavior of the bubbly medium should be considered. Since in the current study, frequency range below 1000 Hz is considered, it is divided into two portions: one below 200 Hz in which RDM is implemented and the other between 200 and 1000 Hz according to void fraction of the bubbly medium. However, for the purpose of comparison, scattering, transmission, and attenuation of the sound at the sea surface region are provided in some cases due to void fraction of the bubbly medium at frequency range below 200 Hz. Without considering the bubbles dispersion effects, sound speed in bubbly water and density of this medium can be determined through the following relations [71]

$$C_{\text{bw}} = C_{\text{w}} \left\{ {1 - \left[ {\frac{{(Y^{2} - 1)}}{{(Y^{2} - 1)^{2} + \delta^{2} }}} \right]\left[ {\frac{{3\phi Y^{2} }}{{2a^{2} K_{\text{R}}^{ 2} }}} \right]} \right\}$$
(13)
$$\rho_{\text{bw}} = \left( {1 - \phi } \right)\rho_{\text{w}} + \phi \rho_{\text{a}}$$
(14)

where C w and C bw are sound speeds in water and bubbly water, respectively, ρ bw, ρ w, and ρ a are densities of bubbly water, water, and air. K R = ω R/C w and ω R are the values of the wavenumber and angular frequency at resonance, respectively. Y is equal to ω R/ω, ϕ is the void fraction of the bubbly water medium, δ is the total damping obtained by sum of thermal, viscosity, and reradiation damping coefficients in the bubbly medium [71] and a is the dominant bubble radius. Through Eqs. 13 and 14, the impedance of bubbly water medium can be determined. However, if the resonance dispersion of sound in bubbly water medium is considered, according to RDM, the dynamic density and phase velocity of the sound need to be applied. In such a circumstance, the dynamic density of the bubbly water medium and the phase velocity of the sound are obtained by Eqs. 15 and 18, respectively.

$$\rho_{\text{bw}}^{*} = \rho_{\text{w}} \left( {\left( {\frac{{\rho^{*} }}{{\rho_{\text{w}} }}} \right)_{0} + \frac{\phi }{{\gamma_{0} }}\left(\frac{A'}{a}\right)^{2} \frac{{(2\omega /\omega_{2} )^{2} }}{{1 - (2\omega /\omega_{2} )^{2} }}} \right)$$
(15)
$$\left( {\frac{{\rho^{*} }}{{\rho_{\text{w}} }}} \right)_{0} = (1 - \phi )/(1 + 2\phi );\;\gamma_{0} = \frac{1 + 2\phi }{2(1 - \phi )}$$
(16)
$$\beta^{*} = \frac{1 - \phi }{{\rho_{\text{w}} C_{\text{w}}^{2} }} + \frac{\phi }{{\rho_{\text{a}} C_{\text{a}}^{ 2} }}$$
(17)
$$C_{\text{bw}}^{*} = \frac{1}{{\sqrt {\beta^{*} \rho_{\text{bw}}^{*} } }}$$
(18)

Here, ρ *bw is the dynamic density of bubbly water and C *bw is the sound phase velocity; γ 0 is the added mass parameter for spherical bubbles. A′ is the amplitude of medium oscillations and ω 2 is the natural frequency of the spheroid oscillations of the bubbles [87].

Once the impedances are determined for both dispersive and non-dispersive conditions, it is necessary to determine the reflection and transmission coefficients in Eqs. 1 and 2, respectively. In Eqs. 7 and 8, \({\mathcal{R}}_{13}\) and \({\mathcal{T}}_{i}\) (in this case, \({\mathcal{T}}_{13}\)) are the reflection and transmission coefficients at the rough bubbly air–water interface, respectively. These coefficients, for a three phase media with the middle thin layer, can be expressed as follows [71]:

$$\begin{aligned} {\mathcal{R}}_{13} = \frac{{{\mathcal{R}}_{12} + {\mathcal{R}}_{23} \exp ( - i2\phi_{2} )}}{{1 + {\mathcal{R}}_{12} {\mathcal{R}}_{23} \exp ( - i2\phi_{2} )}} \hfill \\ {\mathcal{T}}_{i} = {\mathcal{T}}_{13} = \frac{{{\mathcal{T}}_{12} {\mathcal{T}}_{23} \exp ( - i\phi_{2} )}}{{1 + {\mathcal{R}}_{12} {\mathcal{R}}_{23} \exp ( - i2\phi_{2} )}} \hfill \\ \end{aligned}$$
(19)

where ϕ 2 is expressed as

$$\phi_{2} = k_{\text{bw}} z\cos \theta_{2}$$
(20)

Here, k bw = 2πf/C bw is the wavenumber in the middle medium of bubbly water; C bw is the sound speed in bubbly water medium in non-dispersive condition. θ 2 is the refraction angle in the middle medium, while \({\mathcal{R}}_{12}\) and \({\mathcal{R}}_{23}\) are the reflection coefficients. \({\mathcal{T}}_{12}\) and \({\mathcal{T}}_{23}\) are the transmission coefficients (Fig. 6) and z is the bubbly water mean depth (Fig. 6).

Fig. 6
figure 6

Reflection and transmission at the three phase sea surface media

Full size image

It is worth mentioning that the water–bubbly water interface is an imaginary interface considered for modeling the sea surface region (Fig. 6). Previous investigators such as Kuo in Marsh-Kuo perturbation theory [1], have considered the same imaginary interface between the water and bubbly water media.

4 SSVASL algorithm and verification

In the last sections, scattering, transmission, and attenuation of the sound at the three phase sea surface region, based on the reformed HKF model, were discussed. It was also mentioned that impedance differences, surface roughness, and subsurface bubble clouds can have compound effects on each of the mentioned phenomena. In the reformed HKF method, influences of all three stated factors are considered. Therefore, it becomes possible to obtain more realistic results. The sea surface virtual acoustic simulator lab (SSVASL) is developed based on the proposed reformed HKF method. Considering the sound attenuation, this simulator based on the defined environmental and source conditions, is capable of determining the refracted as well as scattered acoustic pressure fields from the sea surface. Also, in this approach, it is viable to determine parameters such as transmission change (TC), surface scattering strength s, and damping coefficient α at the sea surface. Figure 7 represents the SSVASL algorithm by which SSVASL determines the sound-related parameters at sea surface region.

Fig. 7
figure 7

SSVASL algorithm based on reformed HKF method for the acoustical system at the sea surface

Full size image

As seen in Fig. 7, based on the defined input data by the user, SSVASL calculates the transmission, scattering, and attenuation of the sound based on the calculated acoustic pressure fields. When the wind-generated subsurface bubble population is determined, physical properties of the bubbly water medium such as its impedance based on either RDM or non-dispersive condition (according to sound frequency) are computed. Therefore, the thin layer of the bubble clouds is identified and along with water and air media, forms three phase region of the sea surface. Surface correlation length L, and sea surface characteristic function \({\mathcal{W}}\) are the other two required variables which are related to the sea surface condition. In the transmission phenomenon, based on Eq. 8, it is imperative to discretize the sea surface to determine the variables shown Table 1, for each of the surface elements. Subsequently, by considering all the element-related terms of Eq. 8, it is conceivable to determine the value of TC at the sea surface. In addition, through determining the boundary pressure P B at the interfaces, the damping coefficient at the sea surface can be determined. In Fig. 7, indexes j and i represent various receiver locations and sea surface elements, respectively. In fact, for each receiver grid j in the media, the scattering strength s, the damping coefficient α (function of the distance and sea surface physical variables), and the transmission change are determined. The general procedure for obtaining these parameters is shown in the flowchart of Fig. 7 in more details. In the following section, comparison of the obtained results by SSVASL against the well-known experimental data and theoretical approaches is provided.

To verify the developed code, sound scattering, and transmission from the rough bubbly air–water interface is modeled and compared against experimental and other theoretical results.

4.1 Validation of sound scattering from rough bubbly air–water interface

Ogden and Erskine (O/E) [76, 77], through CST results determined three different regimes for sound scattering from the sea surface. In the first regime in which wind speed range is less than about 7 m/s, the results are generally consistent with the scattering from the rough surface. In the second regime which is valid at wind speeds about 10 m/s and frequencies about 500 Hz, results are generally consistent with the scattering from the subsurface bubble cloud. They also determined a transition zone as the third regime between the other two regimes in which compound effects of the rough surface and the subsurface bubble population should be considered. McDonald et al. [88] concluded that accurate results can be achieved by applying perturbation theory in the first regime, at the second regime, and Chapman-Harris (CH) empirical relation and combination of these two methods in the transition region. Since the reformed HKF method considers both surface roughness and subsurface bubble population mechanisms, it becomes possible to study the scattering strength results in different regimes.

The CST-7 experiments were conducted in different environmental and source conditions. Here, three different runs from CST-7 runs are adopted which are shown in Table 2. Each run reports the scattering strength results at various frequencies (below 1000 Hz) and grazing angles (below 30°). From each run, two frequencies in RDM spectral frequency range, and three frequencies in non-dispersive region (according to subsurface bubble population behavior) are considered to examine the subsurface bubble population effects on the arriving sound to the sea surface.

Table 2 Summary of selected CST-7 runs
Full size table

Figure 8 shows the scattering strength results based on 11C run conditions at frequencies 78 and 154 Hz. According to Ogden and Erskine’s conclusion, at these frequencies and 11C’s wind speed (13 m/s), the first regime is dominant. Consequently, the surface roughness mechanism determines the scattering strength. In Fig. 8a, b, the scattering strengths based on the reformed HKF method are illustrated in both dispersive and non-dispersive conditions as well as CH and perturbation theory. Chapman-Harris results are depicted at the minimum and maximum of the considered frequency range by Ogden and Erskine. As pointed out earlier, in the first regime, perturbation theory is more accurate. It is observed that the trends of scattering strength results based on the reformed HKF method and CST-7 are more consistent with the perturbation theory’s trend. Since in this regime, subsurface bubble population is not dominant, it seems that consideration of whether dispersion or non-dispersion models affect the final scattering strength results is important.

Fig. 8
figure 8

Scattering strength in RDM spectral frequency range, based on 11C run conditions at frequency: a 78 Hz, b 154 Hz

Full size image

Figure 9 shows the scattering strength results based on 16B run conditions at frequencies 82 and 158 Hz. In the 16B run, wind speed is more than that of 11C run, which results in the dominance of the first regime at frequency 82 Hz and the transition regime at frequency 158 Hz. In fact, since wind speed 17.5 m/s is the maximum considered wind speed by O/E, and RDM dominance range is below frequency 200 Hz, in RDM’s spectral frequency range at any wind speed, either the first regime or the third regime (transition regime) is dominant. In other words, there is no case in RDM’s frequency range in which the second regime becomes dominant. In Fig. 9a, the scattering strength results are shown and since the first regime is dominant here, the reformed HKF results as well as CTS-7 results are more consistent with the perturbation results. On the other hand, in Fig. 9b, the transition regime is dominant which shifts the scattering strength results towards that of Chapman-Harris curve. However, the scattering strength results in both dispersive and non-dispersive states do not display considerable differences.

Fig. 9
figure 9

Scattering strength in RDM spectral frequency range, based on 16B run conditions at frequency: a 82 Hz, b 158 Hz

Full size image

The scattering strengths results based on 26B run conditions at frequencies 74 and 150 Hz are depicted in Fig. 10. Here, wind speed is much less than the other two cases. The first regime’s dominance implies that surface roughness mechanism plays a more important role in the scattering strength results. In both plots of Fig. 10a, b, like Fig. 8, the values of scattering strength are closer to the perturbation theory results. Furthermore, considering the effects of bubbles resonance dispersion does not dramatically change the scattering strength results compared to the non-dispersive state. This seems reasonable, since the surface roughness is the dominant mechanism in the first regime.

Fig. 10
figure 10

Scattering strength in RDM spectral frequency range, based on 28B run conditions at frequency: a 74 Hz, b 150 Hz

Full size image

Figure 11 shows the scattering strength results based on 11C run condition in frequency range 200–1000 Hz in which non-dispersive behavior of the subsurface bubble population is considered. As mentioned earlier, in this range, the void fraction beneath the sea surface as a result of subsurface bubble presence is the reason that passing sound experiences a much smoother variation in its impedance. In Fig. 11, according to the considered frequencies and wind speed in 11C run, the second and third regimes are expected to be dominant. In Fig. 11a, the third regime is dominant and hence, the results of reformed HKF and CST-7 are between perturbation theory and Chapman-Harris results. In Fig. 11b, c, according to their frequencies, the second regime and consequently the subsurface bubble population are dominant. As pointed out earlier, based on the Ogden and Erskine’s conclusion [76], the Chapman-Harris empirical relations is more accurate than the perturbation theory in this case.

Fig. 11
figure 11

Scattering strength in non-dispersive frequency range, based on 11C run conditions at frequency: a 218 Hz, b 510 Hz, c 950 Hz

Full size image

Figure 12 shows the scattering strength results based on 16B run conditions in which wind speed is higher than that of 11C run. In fact, in Fig. 12, only the second regime is dominant in all frequencies between 200 and 1000 Hz and at wind speed 17.5 m/s. Therefore, it is anticipated that results of the reformed HKF and CST-7 scattering strengths be more consistent with Chapman-Harris results.

Fig. 12
figure 12

Scattering strength in non-dispersive frequency range, based on 16B run conditions at frequency: a 222 Hz, b 518 Hz, c 962 Hz

Full size image

In Fig. 13, the results of scattering strengths are obtained based on 26B run conditions in which wind speed is 5 m/s. At this wind speed, the first regime is dominant; hence, the results of scattering strengths are more consistent with that of perturbation theory.

Fig. 13
figure 13

Scattering strength in non-dispersive frequency range, based on 26B run conditions at frequency: a 218 Hz, b 502 Hz, c 962 Hz

Full size image

Figure 14 depicts three parametric analyses of the scattering strength vs. various frequencies, wind speeds and grazing angles. In addition, in all of these studies, source location depth and pressure in range of 1 m to the source are 20 m and 1 Pascal, respectively. In Fig. 14, Chapman-Harris empirical relation at wind speed 3 and 17.5 m/s as well as perturbation theory are applied to show each regime’s region. Figure 14a represents the scattering strengths as a function of grazing angle at frequency 200 Hz and various wind speeds. Here, the first and the third regimes are involved in variation of the surface scattering strengths. It can be seen that almost all of the reformed HKF results are located between the plots of Chapman-Harris (3 m/s) and perturbation theory. Figure 14b represents the scattering result at frequency 500 Hz in which all three regions are possibly involved. Despite the results of reformed HKF in Fig. 14a, here all optimized HKF curves (except 2.5 m/s curve) are located between CH 17.5 m/s and perturbation theory curves. This shows the effect of frequency increase at the same conditions. In fact, it is seen that increase in frequency shifts up all the scattering strength curves. Figure 14c shows the scattering strength results at the same conditions as Fig. 13b, c, but at higher frequency. Here, compared to Fig. 13a, b, similar effects of frequency increase on the scattering strengths can be concluded. However, at constant frequencies, increase in grazing angle and wind speed generally results in the increase of scattering strength values.

Fig. 14
figure 14

Scattering strength of the optimized HKF method as a function of wind speed and grazing angle in 3 different frequencies compared with Chapman-Harris and perturbation method results: a 200 Hz, b 500 Hz, c 1000 Hz

Full size image

4.2 Validation of transmission through rough bubbly air–water interface

In the previous section, effects of different variables on sound scattering strength at the sea surface for a submerged point source were studied. In this section, sound transmission through the rough bubbly air–water interface is targeted. As mentioned earlier, the impedance difference, rough surface, and subsurface bubble population are crucial variables which should be considered for studying the sound characteristic at the sea surface. Also, as discussed, all of these variables are involved in the reformed HKF formulation. For the scattering cases, a submerged point source according to CST-7 run conditions is chosen. For the transmission phenomenon, since authors have not come across any similar reported results for the submerged point source, considering the same input variables of SSVASL, they selected FELIPEX experimental results in which transmission of an airborne point source through the real sea surface is studied [67]. These experiments have reported all the required initial data for the reformed HKF method which makes it possible to compare the final results. Medwin et al. [67] compared the results of original HKF with experimental cases of FELIPEX. However, they did not consider the subsurface bubble population effects which led to an underestimation of transmission change (TC) values. Since in the current study, the effects of subsurface bubble population on the incident sound are included, both scattering and transmission of the sound can be studied at the rough bubbly air–water interface. In this section, considering the resonance dispersion of subsurface bubbles as well as non-dispersive condition, transmission change (TC) for a localized point source in the air is studied based on the reformed HKF.

As mentioned in Sect. 3, to obtain TC values based on Eq. 13, the rough surface should be discretized. Afterward, variables shown in Table 1 should be determined for each of the surface elements. Since in this study, wind-generated waves are aimed at, wind speed over the sea surface is applied to determine the surface correlation length L where it is needed [89]. However, for the purpose of verification, surface correlation length is initialized according to FLIPEX tests. Medwin and Hagy [67] only considered the influences of surface geometric roughness on the sound transmission and neglected the subsurface bubble clouds effects. As mentioned earlier, since the subsurface bubble population effects are involved in the current study, it is conceivable to examine different roles of this thin layer at low frequencies. Therefore, in the frequency ranges below 200 Hz and also between 200 and 1000 Hz, the resonance dispersion and non-dispersive effects are studied, respectively. For all verification cases, the surface correlation length L, surface elements mean width ∆L, and rms height h rms, are considered to be 1.5, 7.5 m, and 13 cm, respectively, according to FELIPEX. Also based on FELIPEX, air and water densities are considered to be, respectively, 330 and 1020 kg/m3 and sound speed in air and water are assumed to be 330 and 1470 m/s, respectively. As far as the impedance of thin bubbly water medium is concerned, dispersive and non-dispersive behavior of the bubbles are considered according to the frequency.

Figure 15 shows the experimental data of FLIPEX as well as the results of the current study at frequency range below 200 Hz. In Fig. 15a, the localized airborne source is at a height 180 m with respect to the sea surface. Since surface acoustic roughness parameter R is a function of variables including incident and refraction angles, the rms wave height, and frequency, it is necessary to determine a proper range for R in which RDM is adequate. In this case, incident and refraction angles are zero (normal incidence), and as mentioned earlier, the rms wave height is considered to be 0.13 cm. Hence, by considering the maximum frequency range of RDM, the maximum value of surface acoustic roughness is determined as R = 0.15. Through the same procedure, it is conceivable to determine the valid range for R in the case of Fig. 15b. In Fig. 14b, sound source is offset 75 m from the position of receivers. In fact, refraction angle (θ 2) is 40° and 85° for the receivers localized at position 90 and 6 m, respectively.

Fig. 15
figure 15

Transmission Change in RDM spectral frequency range as a function of surface acoustical roughness R, for a point source 180 m above the sea surface. Correlation length and rms wave height are, respectively, considered as 1.5 and 0.13 m at: a normal incidence, b source is offset 75 m from the position of receivers

Full size image

Figure 16 shows the TC results for non-dispersive and normal incidence case in frequency range between 200 and 1000 Hz for a localized airborne point source at height H = 180 m. Also, in order to check the effects of the receiver position, it is localized at two different locations D = 6 m and D = 90 m. As evident in Fig. 16, by increasing the receiver’s depth, the general value of TC diminishes. Also, it is clear that through considering the effects of subsurface bubble cloud as well as the surface geometric roughness role in Eq. 13, the underestimation of the original HKF method is resolved. In cases of Fig. 16, it is the frequency increase that causes an increase in the surface acoustic roughness R at constant rms wave heights as well as constant incident and refraction angles. Therefore, a decrease in TC as a result of an increase in R indicates the effect of frequency increase on the decrease of TC. This general reduction is true for both of the considered receivers’ depth.

Fig. 16
figure 16

Transmission Change as a function of surface acoustical roughness at two different D/H ratios of 0.067 and 0.5. Surface correlation length and rms wave height are considered to be 1.5 and 0.13 m, respectively

Full size image

In Fig. 17, Transmission Change in normal incidence at various wind speeds 5, 10, 15 m/s and for two different D/H ratios of 0.065 and 0.5 are studied to examine the subsurface bubble population effects on dispersive condition. In fact, in Fig. 17, the frequency range is considered below 200 Hz. Therefore, the resonance dispersion effect of the subsurface bubbles is dominant. In addition, the increase of surface acoustic roughness R is due to the frequency variation, while the wind speed and D/H ratio for each curve are considered constant. Based on the offered results in Fig. 17, it can be seen that as wind speed increases which implies increase of subsurface bubbles population as well as surface rms height, TC decreases at a constant D/H ratio. Also, as D/H ratio increases at the same wind speeds and frequency range, again TC decreases. Likewise, at constant wind speeds and D/H ratios, as the acoustical roughness R increases due to variation of frequency within the considered spectral region below 200 HZ, TC decreases.

Fig. 17
figure 17

TC variation at the normal incidence and frequency range 50–1000 Hz at three wind speeds 5, 10, and 15 m/s, and D/H ratios of 0.067 and 0.5

Full size image

Figure 18 represents transmission change at frequencies 200 Hz, 500 Hz, and 1000 Hz. Here, frequencies are considered in non-dispersive spectral region. Similar to Fig. 17, two different D/H ratios of 0.067 and 0.5 are considered. However, varying the wind speeds in range of 2–15 m/s at constant frequencies is the reason that surface acoustic roughness R varies. Here, TC results are studied at constant frequencies and D/H ratios, while wind speed varies. As mentioned earlier, in non-dispersive state, an increase in wind speed results in an increase in the void volume beneath the sea surface as well as increase of rms wave height. Here, at constant frequencies and D/H ratios, TC values generally decrease, while wind speed increases. Also, frequency increase from 100 to 500 Hz or 1000 Hz shifts the TC values towards lower quantities. Since the frequency and wind speed through their corresponding terms in Eq. 12, indirectly affect the surface acoustical roughness R, and due to the fact that wind speed determines the subsurface bubble population, one may conclude based on TC values in Figs. 17 and 18 that in the normal incidence, increase in both frequency and wind speed causes a reduction in TC values and vice versa.

Fig. 18
figure 18

TC variation at the normal incidence and at wind speeds between 2 and 12 m/s at three frequencies 100, 500, and 1000 Hz, and D/H ratios of 0.067 and 0.5

Full size image

4.3 Validation of the attenuation at the rough bubbly air–water interface

In the previous sections, scattering and transmission of the sound at the sea surface region were discussed. The dispersive and non-dispersive effects of the subsurface bubble population were examined at different wind speeds, frequencies, and grazing angles. In this section, sound attenuation at the rough bubbly sea surface is investigated. As mentioned earlier, three phase media of water, bubbly water, and air is considered at the sea surface. Consequently, as the incident sound enters the sea surface region, it is attenuated at the water–bubbly water interface and bubbly water–air interface. Also, the bubbly water itself causes the attenuation of the propagation sound.

To study the sound attenuation at the sea surface, two different cases are considered for each of the dispersive and non-dispersive conditions. In the first case, sound attenuation at the water–bubbly water interface is computed for both dispersive and non-dispersive states. In the second case, attenuation of the sound at the bubbly water–air interface is discussed. For each case, results of the SSVASL code is verified by Tolstoy’s approach outlined in Sect. 2. It will be shown that SSVASL results are in a good agreement with Tolstoy’s approach. However, since Tolstoy’s approach is not capable of determining the sound attenuation in the three phase media, and the authors have not come across any similar work with the same input of SSVASL for determining the sound attenuation in a three phase media (with similar characteristics of the sea surface), verification of SSVASL in each of the mentioned cases will be considered as the general accuracy of SSVASL. Therefore, Eq. 15 is considered for obtaining the total damping coefficient of the sound at the sea surface.

Figure 19 shows the results of damping coefficients as a function of frequency at water–bubbly water interface at three different void fractions in both dispersive and non-dispersive states. In fact, the damping coefficients in the frequency range below 200 Hz is presented to show the manner in which dispersive behavior of subsurface bubble population is different from that of non-dispersive situation. As evidenced in Fig. 19, it is seen that as void fraction ϕ increases, the damping coefficients in both dispersive and non-dispersive conditions increase. However, dispersive behavior of the subsurface bubbles at frequency range below 200 Hz increases the damping coefficients noticeably in each case. Furthermore, the trends of damping coefficients as frequency increases in both dispersive and non-dispersive conditions are the same. In Fig. 19, the results of reformed HKF show good agreement with Tolstoy’s approach which is initialized based on the same conditions.

Fig. 19
figure 19

Damping coefficients at water–––bubbly water interface at frequency range below 200 Hz and at void fraction: a ϕ = 0.08, b ϕ = 0.12, c ϕ = 0.15

Full size image

Figure 20 depicts damping coefficients at air–bubbly water interface in three various void fractions. Dispersive and non-dispersive states as well as two different rms wave heights of the sea surface are considered to calculate the damping coefficients based on the reformed HKF method and Tolstoy’s approach. As evidenced in Fig. 20a, as void fraction and frequency increase, the damping coefficients in both approaches increase. Furthermore, similar to the cases in Fig. 19, the damping coefficients are greater in dispersive state. In Fig. 20b which is for a higher rms wave height compared to Fig. 20a, the damping coefficients are larger. However, in the plots of Fig. 20a, b, the trend of damping coefficients in dispersive and non-dispersive states are the same as frequency increases. In addition, like water–bubbly water case, the dispersive behavior of bubbles in this case also plays an important role and causes an increase in the damping coefficients compared to the non-dispersive state. Verestchagina and Fedotovsky [83] reported the same results when the resonance dispersion behavior of bubbles is dominant.

Fig. 20
figure 20

Damping coefficients according to Tolstoy’s approach and the reformed HKF at air–bubbly water interface; at frequency range below 200 Hz, as well as three different void fractions and rms wave heights: a h rms = 0.75 m, b h rms = 1.5 m

Full size image

Figure 21 displays the results of the damping coefficient for the water–bubbly water interface at frequency range 200–1000 Hz and three different void fractions based on both the reformed HKF method and Tolstoy’s approach. Here, non-dispersive condition is considered. As evident in Fig. 21, an increase in void fraction and frequency results would yield an increase in the damping coefficients. Considering the non-dispersive condition, Fig. 22 shows the results of damping coefficient at air–bubbly water interface at two different rms wave heights as well as three different void fractions. Here, an increase in both frequency and void fraction causes an increase in damping coefficients. Also, Fig. 22b compared to Fig. 22a which is computed in lower wave height, has greater damping coefficients. As illustrated in the flowchart of Fig. 7, the SSVASL code determines the damping coefficients based on the pressures at the interfaces. Therefore, the pressure over the air–bubbly water interface is hereby applied as the boundary pressure, and the pressure over the water–bubbly water interface as the arrival pressure.

Fig. 21
figure 21

Damping coefficients according to Tolstoy’s approach and the reformed HKF method at water–bubbly water interface at frequency range 200–1000 Hz and three void fractions based on the reformed HKF method and Tolstoy’s approach

Full size image
Fig. 22
figure 22

Damping coefficients according to Tolstoy’s approach and the reformed HKF method at air–bubbly water interface; at frequency range 200–1000 Hz as well as three different void fractions and rms wave heights: a h rms = 0.75 m, b h rms = 1.5 m

Full size image

Figures 23 and 24 represent the total damping coefficients at three phase sea surface region at two frequency ranges below 200 and 200–1000 Hz. In Fig. 23, at frequency range below 200 Hz, both dispersive and non-dispersive effects of the bubbles are considered. On the other hand, in Fig. 24, non-dispersive state is considered. Both Figs. 23 and 24 represent the total damping coefficients at the sea surface, considering three void fractions of ϕ = 0.08, 0.12, and 0.14, and two different rms wave heights of h rms = 0.75 and 1.5 m. As evident in Figs. 23 and 24, as the rms wave height, frequency, and void fraction increase, the total damping coefficient of the sound at the sea surface generally increases.

Fig. 23
figure 23

Total damping coefficients based on the reformed HKF method at three phase sea surface region; at frequency range below 200 Hz as well as three different void fractions and rms wave heights: a h rms = 0.75 m, b h rms = 1.5 m

Full size image
Fig. 24
figure 24

Total damping coefficients based on the reformed HKF method at three phase sea surface region; at frequency range 200–1000 Hz as well as three different void fractions and rms wave heights: a h rms = 0.75 m, b h rms = 1.5 m

Full size image

5 Conclusions

In underwater acoustics, sea surface plays a significant role in most of the important topics such as communication channels, sonar performance, marine life, oceanography and seismic investigations among others. In most mathematical models, the sea surface effects on the sound propagation at the sea surface, the bubbly water layer bellow the air–water surface is neglected, despite its important effect on the sound propagation. The current study focuses on incorporating the effect of the subsurface bubble layer in the HKF equations and investigates the compound effect of the impedance differences, surface roughness, and subsurface bubble population on sound propagation near the free surface. Since subsurface bubble population has different behaviors in various frequency ranges, in the frequency range below 200 Hz, the resonance dispersion model (RDM) is adopted and in the frequency range between 200 and 1000 Hz, the void fraction of bubbly water medium is considered.

After the derivation of the new equations and presentation of the equations of the reformed HKF, this method has been implemented in a computer code (SSVASL) and verified against experimental data.

Because of the complexity of the sound propagation near the sea surface, any newly presented model should be carefully verified. Therefore, the transmission, scattering, and attenuation modeled by the new equation set have been verified separately and extensively against FLIPEX experimental tests, critical sea tests (CST) and Tolstoy’s theory.

As a main conclusion, it has been illustrated that the presented reformed HKF provides more accurate results than the existing methods, due to the fact that the bubble population influence is taken into consideration in virtually all aspects of the sound propagation at the sea surface.