1 Introduction

Polyurethane foams are using as interior components of automobiles such as seats, headrests, armrests, roof liners, dashboards and instrument panels. Also, it is using as an applicable material for seats in aerospace applications. Polyurethane formulations cover wide ranges of stiffness, hardness, and density. The aim of this work is to study the vibrational behavior of polyurethane foam. Many studies have invested mechanical characteristics of this material, which exists in different types of stiffness. These studies try using system identification methods to estimate nonlinear stiffness, damping and viscoelastic parameters regarding this material. Flexible polyurethane foam is a complex material, which behavior and composition are under investigation, because it is used significantly in engineered systems [1–3]. The automotive industry is a great user of research on foam behavior due to its widespread use in automotive interiors and seats [4].

Flexible polyurethane foam shows nonlinear and viscoelastic behaviors. For generic polyurethane foam, the force is generally a nonlinear function of the strain. The stress–train relationship is highly nonlinear and depends on the strain rate, as seen from the stres–strain curve of foam obtained from a uniaxial cyclic compression test [5].

The foam has hysteretic behavior and the curve has a nonlinear shape. Corresponding to a different compression mechanism, almost three distinct compression regions can be identified [2, 6]. In the first region, the struts bend elastically under the load while static stiffness remains almost constant. In the second region, the struts bend and in the third region the material effectively becomes softer [4]. Foam materials are further complicated by differences between the static and dynamic stiffness [7].

There is a widely used technique, similar to the quasi-static testing method to obtain the approximate linear dynamic stiffness and energy loss properties. This method is as follows: the foam is compressed very slowly to the desired strain level, and is then taken through a small amplitude cyclic displacement about that compression level. The resultant force–displacement measurements yield a near-elliptical loop. It is now assumed that in this small amplitude cycling, the foam is behaving as a linear material, equivalently representable as a linear spring and dashpot. Then the effective modulus of elasticity \(E\), and loss factor \(\eta\) can be estimated [3]. The linear viscous damping and stiffness coefficients, \(c\) and \(k\) respectively, can also be obtained from this measurement [8].

Increasing amplitudes of harmonic excitation causes the force–displacement curves deviate from their elliptical shape. For very large amplitudes, the hysteresis loop changes from its near-elliptical shape (dashed line) and has assumed a highly distorted form (solid line). Therefore, the force in the material will be a nonlinear function of displacement. It is seen that the pseudo-major axis may be approximated by an oddly symmetric function about the static compression level [4].

One important dynamic behavior of foam is viscoelasticity. Viscoelastic material have significantly different linear elasticity response [9] and they show characteristics of a vibrational damper [10, 11]. Under constant compressive strain the force in the foam decreases by passing time (relaxation) [12]. In addition, over time the strain increases (creeps) if the foam is loaded with a given mass [13]. Also subjected to dynamic excitations, viscoelasticity will affect the behavior of foam and it shows additional dynamic creep beyond its static equilibrium [1, 2]. The dynamic viscoelastic behavior causes that when relaxation test data is used to identify foam viscoelastic parameters, the resulting parameters do not necessarily yield accurate predictions of the dynamic response behavior.

The dependencies of the foam behavior on different parameters, and presenting different characteristics under different circumstances, have been the motivation of this study. In this study, the issues associated to solve an integro-differential equation have been resolved by multiple time scales method (MTSM). An integro-differential equation could not be solved by regular methods. In this research, an approximation of such an equation has been practiced by MTSM for the first time and the damped frequency of system is studied. The foam behavior under free and forced vibrations is considered. The forced vibration is divided into primary resonances, hard excitations, sub-harmonic and super harmonic. The response of system has been investigated and effects of different viscoelastic parameters on the behavior of the foam is discussed.

2 System identification

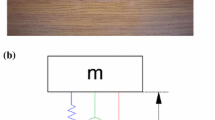
A schematic of the foam and its representation as a mass-spring-damper system is shown in Fig. 1. The physical system consists of a foam block with a mass on top constrained to have uni-directional motion in vertical axis. The mass on the foam produces compression in the foam. This setup can be represented as a mass-spring-damper system, where the spring element really represents the nonlinear viscoelastic spring, and the damper element accounts for additional damping in the foam not modeled by the viscoelastic element, and the friction at the vertical posts [5].

Fig. 1
figure 1

Single degree-of-freedom foam block schematic model [5]

Full size image

The system model incorporates constitutive model of flexible polyurethane foam. In this study, it is assumed that the foam has nonlinear elastic and linear viscoelastic properties. Thus, the restoring force in the material is assumed to possess the following form [4]:

$$F\left( t \right) = c\dot{z} + \sum\nolimits_{j = 1}^{M} {k_{j} x^{j} } - k\int\limits_{0}^{t} {\varGamma \left( {t - \tau } \right)z\left( \tau \right)d\tau } .$$
(1)

A model of this form can account for displacement-based stiffness nonlinearities, and by selecting the appropriate form of the relaxation kernel, it can also be used to model the elements of the foam’s time-dependent dynamic behavior. Equation of motion for the presented system in Fig. 1 is shown to be [14, 15]:

$$M\textit{\"{x}} + c\dot{x} + \sum\nolimits_{j = 1}^{M} {k_{j} x^{j} } + k\int_{ - \infty }^{t} {\sum\nolimits_{i = 1}^{N} {a_{i} e^{{ - \alpha_{i} \left( {t - \tau } \right)}} x} \left( \tau \right)d\tau } = F\left( t \right).$$
(2)

The lower limit on the integral term has been changed to \(- \infty\) , essentially forcing the equation of motion to represent steady state dynamic behavior, where transient effects due to startup have decayed. Thus, approximating the dynamic stiffness by a polynomial of the form [4] would be a good starting point in the modeling process for the nonlinear elastic properties of the foam:

$$F_{\text{k}} = k_{1} x + k_{3} x^{3} + k_{5} x^{5}$$
(3)

where \(F_{\text{k}}\) is the elastic force in the material and \(x\) is the uniaxial compression in the material around a static compression level.

Considering an approximate expression for the two term expansion (\(N = 2\)) of the integral in Eq. (2), finally the governing equation for SDOF polyurethane foam would be:

$$M\textit{\"{x}} + c\dot{x} + k_{1} x + k_{3} x^{3} + k_{5} x^{5} - k\int_{ - \infty }^{t} {\sum\nolimits_{i = 1}^{2} {a_{i} e^{{ - \alpha_{i} \left( {t - \tau } \right)}} x} \left( \tau \right)d\tau } = F\left( t \right).$$
(4)

3 Multiple time scales method

Multiple scale method is a perturbation approach that converts time into different time scales. In this method, different time scales is introduced and the time derivatives will be expanded. In MTSM the single time variable is replaced by an infinite sequence of independent time scales [16–20].

The solvability conditions, which guarantee the elimination of secular terms in the fast variable, impose consistency constraints on the structure of the approximate solution. Specifically, mutual consistency of solvability conditions regarding to different orders must be ensured.

A weakly nonlinear harmonic oscillator with periodic forcing is analyzed in [21] and [22]. In [21] it is pointed out that, different choices of the free amplitudes, lead to conflicting results. In [22], the effect of multiple resonances on the dynamics of a suspended cable is studied. It is found that choices of the free amplitudes that do not take into account the dependence of the latter on the slow time scale, do not lead to a Hamiltonian structure of the reconstituted equation for the amplitude of the zero-order term. Such difficulties are resolved if one uses “free” amplitudes, which guarantee that solvability conditions, which pertain to different orders are mutually consistent.

The following non-dimensional parameters can be used for transforming Eq. (4) into a dimensionless ones:

$$\omega_{n} = \sqrt {\frac{{k_{1} }}{M}} ,\;\zeta = \frac{c}{{2\sqrt {k_{1} M} }},\,\,\frac{c}{M} = 2\zeta \omega_{n} ,\;\frac{{k_{3} }}{M} = \gamma_{1}^{2} ,\;\frac{{k_{5} }}{M} = \gamma_{2}^{2} ,\;\frac{{a_{1} }}{M} = \lambda_{1} ,\;\frac{{a_{2} }}{m} = \lambda_{2} ,\;\frac{F\left( t \right)}{M} = E(t).$$

So, Eq. (4) becomes:

$$\textit{\"{x}} + 2\zeta \omega_{n} \dot{x} + \omega_{n}^{2} x + \gamma_{1}^{2} x^{3} + \gamma_{2}^{2} x^{5} - \omega_{n}^{2} \int_{ - \infty }^{t} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t - \tau } \right)}} x\left( \tau \right)d\tau } = } E(t).$$
(5)

Let’s consider all nonlinear terms and damping force are measured by \(\varepsilon\) with respect to linear restoring force i.e.:

$$\textit{\"{x}} + \omega_{n}^{2} x + \varepsilon \left( {2\zeta \omega_{n} \dot{x} + \gamma_{1}^{2} x^{3} + \gamma_{2}^{2} x^{5} - \omega_{n}^{2} \int_{ - \infty }^{t} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t - \tau } \right)}} x\left( \tau \right)d\tau } } } \right) = E(t).$$
(6)

Here, \(\varepsilon\) is considered to be perturbation parameter. In MTSM the perturbation parameter is usually a small parameter which represents a physical property.

Expanding \(x\) in two terms by considering different scales lead to:

$$x\left( t \right) = x_{0} \left( t \right) + \varepsilon x_{1} \left( t \right).$$
(7)

And time scales as:

$$\left\{ \begin{aligned} t_{0} = t \hfill \\ t_{1} = \varepsilon t \hfill \\ \end{aligned} \right. \to t = t_{0} + \varepsilon t_{1} ,$$
(8)
$$\frac{d}{dt} = \frac{d}{{dt_{0} }} + \varepsilon \frac{d}{{dt_{1} }} = \left( {D_{0} + \varepsilon D_{1} } \right),\,\,D_{0} = \frac{d}{{dt_{0} }},\,D_{1} = \frac{d}{{dt_{1} }}$$
(9)
$$\frac{{d^{2} }}{{dt^{2} }} = \left( {D_{0}^{2} + 2\varepsilon D_{0} D_{1} } \right).$$
(10)

The approximate expression for the two term expansion (\(N = 2\)) of the integral in Eq. (6), using Eqs. (7) and (8), it would be:

$$\varepsilon \int_{ - \infty }^{t} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t - \tau } \right)}} x\left( \tau \right)d\tau } } \approx \varepsilon \int_{ - \infty }^{{t_{0} + \varepsilon t_{1} }} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t_{0} + \varepsilon t_{1} - \tau_{0} - \varepsilon \tau_{1} } \right)}} \left( {x_{0} \left( \tau \right) + \varepsilon x_{1} \left( \tau \right)} \right)\left( {d\tau_{0} + \varepsilon d\tau_{1} } \right)} } .$$

Considering two term expansion of \(\varepsilon\) in MTS method, expression above is simplified as:

$$\approx \varepsilon \int_{ - \infty }^{{t_{0} + \varepsilon t_{1} }} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t_{0} - \tau_{0} } \right)}} x_{0} \left( \tau \right)d\tau_{0} } } \approx \varepsilon \int_{ - \infty }^{{t_{0} }} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t_{0} - \tau_{0} } \right)}} x_{0} \left( \tau \right)d\tau_{0} } } .$$
(11)

4 Free vibrations

For free vibrations, the system exposed to an initial displacement. It means that the term \(E\left( t \right)\) in Eq. (6) will be neglected. Using expression (11) as an approximation for the integral term in Eq. (6) accompanied by Eqs. (7–10) lead to:

$$\left( {D_{0}^{2} + 2\varepsilon D_{0} D_{1} } \right)\left( {x_{0} + \varepsilon x_{1} } \right)\,\, + \omega_{n}^{2} \left( {x_{0} + \varepsilon x_{1} } \right) + \varepsilon \left[ \begin{aligned} & 2\zeta \omega_{n} \left( {D_{0} + \varepsilon D_{1} } \right)\left( {x_{0} + \varepsilon x_{1} } \right) + \,\gamma_{1}^{2} \left( {x_{0} + \varepsilon x_{1} } \right)^{3} \hfill \\& + \gamma_{2}^{2} \left( {x_{0} + \varepsilon x_{1} } \right)^{5} - \omega_{n}^{2} \int_{ - \infty }^{{t_{0} }} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t_{0} - \tau_{0} } \right)}} x_{0} \left( \tau \right)d\tau_{0} } } \hfill \\ \end{aligned} \right] = 0.$$
(12)

Equaling the same coefficients of \(\varepsilon^{0}\) and \(\varepsilon^{1}\) to zero, it is obtained that:

$$O( {\varepsilon^{0} } ):\,\,D_{0}^{2} x_{0} + \omega_{n}^{2} x_{0} = 0$$
(13)
$$O\left( {\varepsilon^{1} } \right):\,\,D_{0}^{2} x_{1} + \omega_{n}^{2} x_{1} = - 2D_{0} D_{1} x_{0} - 2\zeta \omega_{n} D_{0} x_{0} - \gamma_{1}^{2} x_{0}^{3} - \gamma_{2}^{2} x_{0}^{5} + \omega_{n}^{2} \int_{ - \infty }^{{t_{0} }} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t_{0} - \tau_{0} } \right)}} x_{0} \left( \tau \right)d\tau_{0} } } .$$
(14)

A general solution to Eq. (13) is:

$$x_{0} = A\left( {t_{1} } \right)e^{{i\omega_{n} t_{0} }} + \bar{A}\left( {t_{1} } \right)e^{{ - i\omega_{n} t_{0} }}$$
(15)

where \(A\) is a complex function of \(t_{1}\) and \(\bar{A}\) is the complex conjugate of \(A\). Equation (13) should be substituted in Eq. (14). To prevent non-periodic solution, the secular term, (the coefficients of \(e^{{ \pm i\omega_{n} t_{0} }}\)) must be eliminated [15]. Hence, to eliminate the secular term:

$$2iA'\omega_{n} + 3\gamma_{1}^{2} A^{2} \bar{A} + 10\gamma_{2}^{2} A^{3} \bar{A}^{2} + 2i\zeta \omega_{n}^{2} A + i\psi_{0} \omega_{n}^{3} A - \psi_{1} \omega_{n}^{2} A = 0$$
(16)

where:

$$\psi_{0} = \left( {\frac{{\lambda_{1} }}{{\alpha_{1}^{2} + \omega_{n}^{2} }} + \frac{{\lambda_{2} }}{{\alpha_{2}^{2} + \omega_{n}^{2} }}} \right),\;\psi_{1} = \left( {\frac{{\lambda_{1} \alpha_{1} }}{{\alpha_{1}^{2} + \omega_{n}^{2} }} + \frac{{\lambda_{2} \alpha_{2} }}{{\alpha_{2}^{2} + \omega_{n}^{2} }}} \right)$$
(17)

and prime denotes derivative with respect to \(t_{1}\). Equation (16) is in agreement with one-term harmonic balance solution to the same system given in [23]. It is convenient to write \(A\) in a polar form as:

$$A\left( {t_{1} } \right) = \frac{1}{2}b\left( {t_{1} } \right)e^{{i\beta \left( {t_{1} } \right)}}$$
(18)

hence:

$$A' = \frac{dA}{{dt_{1} }} = \frac{1}{2}\left( {b' + i\beta '} \right)e^{i\beta }$$
(19)

substituting Eqs. (18) and (19) in Eq. (16) and separating real and imaginary parts:

$$b' = - \frac{1}{2}\omega_{n} b\left( {\omega_{n} \psi_{0} + 2\zeta } \right)$$
(20)
$$\beta ' = \frac{1}{{16\omega_{n} }}\left( {5\gamma_{2}^{2} b^{4} + 6\gamma_{1}^{2} b^{2} - 8\omega_{n}^{2} \psi_{1} } \right)$$
(21)

considering initial conditions, the solution to (20) and (21) is obtained by letting \(\beta_{0} = 0\) as:

$$b\left( {t_{1} } \right) = b_{0} e^{{ - \,\,\,\frac{1}{2}\omega_{n} \left( {\omega_{n} \psi_{0} + 2\zeta } \right)t_{1} }}$$
(22)
$$\beta \left( {t_{1} } \right) = \frac{{b_{0}^{2} - b\left( {t_{1} } \right)^{2} }}{{32\omega_{n}^{2} \left( {\omega_{n} \psi_{0} + 2\zeta } \right)}}\left( {5\gamma_{2}^{2} \left( {b_{0}^{2} + b\left( {t_{1} } \right)^{2} } \right) + 12\gamma_{1}^{2} } \right) - \frac{1}{2}\omega_{n} \psi_{1} t_{1} .$$
(23)

Thus, one term approximate solution for free vibration of the system using MTSM would be:

$$x_{0} = Ae^{{i\omega_{n} t_{0} }} + \bar{A}\left( {t_{1} } \right)e^{{ - i\omega_{n} t_{0} }} = \frac{1}{2}be^{{i\left( {\omega_{n} t_{0} + \beta } \right)}} + \frac{1}{2}be^{{ - i\left( {\omega_{n} t_{0} + \beta } \right)}} = b\cos \left( {\omega_{n} t_{0} + \beta } \right).$$
(24)

According to Eq. (23), it is clear that the frequency is a function of amplitude of vibration. As \(t \to + \infty\), considering Eq. (22), the amplitude of frequency decays and so \(b \to 0\).

5 Forced vibrations

When an external excitation is applied to the system, forced vibration behavior of the system is demonstrated. It is considered that an external excitation is applied to the system:

$$E\left( t \right) = F\cos \left( {\varOmega t} \right).$$
(25)

Primary resonances, non-resonant excitations, super-harmonic excitations and sub-harmonic behavior are investigated and the response of system in each case is obtained.

5.1 Primary resonances

When linear frequency of the system \(\omega_{n}\) and frequency of excitation \(\varOmega\) are close together (\(\varOmega \approx \omega_{n}\)) primary resonances occurs. Detuning parameter \(\sigma\) is defined to show this nearness:

$$\varOmega = \omega_{n} + \varepsilon \sigma .$$
(26)

If applied excitation and nonlinear terms have the same order, a uniformly valid approximate solution will be obtained. Hence, considering \(F = \varepsilon f\) in Eq. (25), using two term expansions MTSM in Eq. (7) and substituting Eqs. (26) and (27) into Eq. (25) and equating two first orders of \(\varepsilon\):

$$O( {\varepsilon^{0} } ):\,\,D_{0}^{2} x_{0} + \omega_{n}^{2} x_{0} = 0$$
(27)
$$O\left( {\varepsilon^{1} } \right):\,\,D_{0}^{2} x_{1} + \omega_{n}^{2} x_{1} + 2D_{0} D_{1} x_{0} + 2\zeta \omega_{n} D_{0} x_{0} + \gamma_{1}^{2} x_{0}^{3} + \gamma_{2}^{2} x_{0}^{5} - \omega_{n}^{2} \int_{ - \infty }^{{t_{0} }} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t_{0} - \tau_{0} } \right)}} x_{0} \left( \tau \right)d\tau_{0} } } = f\cos \left( {\varOmega t_{0} } \right).$$
(28)

Equation (28) demonstrates that non-linear terms and excitation are in the same term. Equation (27) has a solution like Eq. (15). The solution of Eq. (27) is substituted into Eq. (28). To avoid non uniform solution, the secular term should be removed as:

$$2i\omega_{n} A' + 2i\zeta \omega_{n}^{2} A + 3\gamma_{1}^{2} A^{2} \bar{A} + 10\gamma_{2}^{2} A^{3} \bar{A}^{2} + i\psi_{0} \omega_{n}^{3} A - \psi_{1} \omega_{n}^{2} A - \frac{1}{2}fe^{{i\sigma t_{1} }} = 0.$$
(29)

\(A\left( {t_{1} } \right)\) is considered in polar form. Real parts and imaginary parts from obtained expression are separated to obtain:

$$b'\left( {t_{1} } \right) = - \frac{1}{{2\omega_{n} }}\left( {\psi_{0} \omega_{n}^{3} b + 2\zeta \omega_{n}^{2} b + f\sin \left( { - \sigma t_{1} + \beta } \right)} \right)$$
(30)
$$\beta '\left( {t_{1} } \right) = \frac{1}{{16b\omega_{n} }}\left( {6\gamma_{1}^{2} b^{3} + 5\gamma_{2}^{2} b^{5} - 8\omega_{n}^{2} \psi_{1} b - 8f\cos \left( { - \sigma t_{1} + \beta } \right)} \right).$$
(31)

Term \(t_{1}\) can be removed by turning Eqs. (30) and (31) into an autonomous form [5] letting \(\sigma t_{1} - \beta \left( {t_{1} } \right) = \theta\):

$$b'\left( {t_{1} } \right) = - \frac{1}{{2\omega_{n} }}\left( {\psi_{0} \omega_{n}^{3} b + 2\zeta \omega_{n}^{2} b - f\sin \left( \theta \right)} \right)$$
(32)
$$\theta ' = \sigma - \frac{1}{{16\omega_{n} b}}\left( {6\gamma_{1}^{2} b^{3} + 5\gamma_{2}^{2} b^{5} - 8\omega_{n}^{2} \psi_{1} b - 8f\cos \left( \theta \right)} \right).$$
(33)

The steady-state motion is the point where time derivatives are equal to zero [5]. Hence, considering \(\beta '\left( {t_{1} } \right) = 0\) and \(\theta '\left( {t_{1} } \right) = 0\) will conduct the system to its steady motion. Using Eqs. (32) and (33), the frequency–response of system during primary resonances is obtained as:

$$\sigma = \frac{1}{{\omega_{n} }}\left( {\frac{3}{8}\gamma_{1}^{2} b^{2} + \frac{5}{16}\gamma_{2}^{2} b^{4} + \frac{1}{2}\omega_{n}^{2} \psi_{1} \pm \frac{1}{2}\sqrt {\left( {\frac{f}{b}} \right)^{2} - 4\left( {\zeta \omega_{n}^{2} - \frac{1}{2}\omega_{n}^{3} \psi_{0} } \right)^{2} } } \right).$$
(34)

5.2 Stability of steady-state motion

The stability of state–state motion has been considered using the nature of singular points. To this aim one can consider:

$$\left\{ \begin{aligned} b = b_{0} + b_{1} \hfill \\ \theta = \theta_{0} + \theta_{1} \hfill \\ \end{aligned} \right..$$
(35)

Substituting Eq. (35) into Eq. (32) and (33), expanding the expression for small \(b_{1}\) and \(\theta_{1}\), keeping the linear terms in \(b_{1}\) and \(\theta_{1}\), noting that \(b_{0}\) and \(\theta_{0}\) satisfy steady-state motion, it is obtained that:

$$\begin{aligned} b_{1}^{'} = - \left[ {\frac{1}{2}\psi_{0} \omega_{n}^{2} + \zeta } \right]b_{1} + \left[ {\frac{{f\cos \left( {\theta_{0} } \right)}}{{2\omega_{n} }}} \right]\theta_{1} . \hfill \\ \theta_{1}^{'} = \left[ { - \frac{f}{{2\omega_{n} b_{0}^{2} }} - \frac{{2\gamma_{1}^{2} b_{0} }}{{\omega_{n} }} - \frac{{5\gamma_{2}^{2} b_{0}^{3} }}{{4\omega_{n} }}} \right]b_{1} + \left[ { - \frac{{f\sin \left( {\theta_{0} } \right)}}{{2\omega_{n} b_{0} }}} \right]\theta_{1} \hfill \\ \end{aligned}$$
(36)

Hence, the stability of steady-state motion can be investigated by considering the eigenvalues of the coefficient matrix on the right hand side of Eq. (36). Considering the steady-state motion of Eqs. (32) and (33) and Eq. (36) the eigenvalue equation can be obtained as:

$$\left| {\begin{array}{*{20}c} { - \left[ {\frac{1}{2}\psi_{0} \omega_{n}^{2} + \zeta } \right] - \lambda } & {\left[ {\frac{{3\gamma_{1}^{2} b_{0}^{3} }}{{8\omega_{n} }} + \frac{{5\gamma_{2}^{2} b_{0}^{5} }}{{16\omega_{n} }} - \frac{1}{2}\omega_{n} \psi_{1} b_{0} - b_{0} \sigma } \right]} \\ {\left[ { - \frac{f}{{2\omega_{n} b_{0}^{2} }} - \frac{{2\gamma_{1}^{2} b_{0} }}{{\omega_{n} }} - \frac{{5\gamma_{2}^{2} b_{0}^{3} }}{{4\omega_{n} }}} \right]} & { - \left[ {\frac{1}{2}\psi_{0} \omega_{n}^{2} + \zeta } \right] - \lambda } \\ \end{array} } \right| = 0.$$
(37)

Expanding (37) yields:

$$\lambda^{2} + 2\lambda \left[ {\frac{1}{2}\psi_{0} \omega_{n}^{2} + \zeta } \right] + \left[ {\frac{1}{2}\psi_{0} \omega_{n}^{2} + \zeta } \right]^{2} + \left[ {\frac{{3\gamma_{1}^{2} b_{0}^{3} }}{{8\omega_{n} }} + \frac{{5\gamma_{2}^{2} b_{0}^{5} }}{{16\omega_{n} }} - \frac{1}{2}\omega_{n} \psi_{1} b_{0} - b_{0} \sigma } \right]\left[ {\frac{f}{{2\omega_{n} b_{0}^{2} }} + \frac{{2\gamma_{1}^{2} b_{0} }}{{\omega_{n} }} + \frac{{5\gamma_{2}^{2} b_{0}^{3} }}{{4\omega_{n} }}} \right] = 0.$$
(38)

Thus the steady-state motion is unstable when:

$$\varGamma = \left[ {\frac{1}{2}\psi_{0} \omega_{n}^{2} + \zeta } \right]^{2} + \left[ {\frac{{3\gamma_{1}^{2} b_{0}^{3} }}{{8\omega_{n} }} + \frac{{5\gamma_{2}^{2} b_{0}^{5} }}{{16\omega_{n} }} - \frac{1}{2}\omega_{n} \psi_{1} b_{0} - b_{0} \sigma } \right]\left[ {\frac{f}{{2\omega_{n} b_{0}^{2} }} + \frac{{2\gamma_{1}^{2} b_{0} }}{{\omega_{n} }} + \frac{{5\gamma_{2}^{2} b_{0}^{3} }}{{4\omega_{n} }}} \right] < 0.$$
(39)

5.3 Non-resonant hard excitation

When \(\varOmega\) is away from \(\omega_{n}\), frequency of excitations does not cause any resonances in system and its effects is highlighted due to high amplitudes. \(F\) in this case is from order one. Following the same procedure as primary resonances and considering the same orders of \(\varepsilon\) one can get:

$$O( {\varepsilon^{0} } ):\,\,D_{0}^{2} x_{0} + \omega_{n}^{2} x_{0} = F\cos \left( {\varOmega t_{0} } \right)$$
(40)
$$O\left( {\varepsilon^{1} } \right):\,\,D_{0}^{2} x_{1} + \omega_{n}^{2} x_{1} + 2D_{0} D_{1} x_{0} + 2\zeta \omega_{n} D_{0} x_{0} + \gamma_{1}^{2} x_{0}^{3} + \gamma_{2}^{2} x_{0}^{5} - \omega_{n}^{2} \int_{ - \infty }^{{t_{0} }} {\sum\nolimits_{i = 1}^{2} {\lambda_{i} e^{{ - \alpha_{i} \left( {t_{0} - \tau_{0} } \right)}} x_{0} \left( \tau \right)d\tau_{0} } } = 0.$$
(41)

The solution to Eq. (35) is:

$$x_{0} = A\left( {t_{1} } \right)e^{{i\omega_{n} t_{0} }} + \bar{A}\left( {t_{1} } \right)e^{{ - i\omega_{n} t_{0} }} + Be^{{i\varOmega t_{0} }} + Be^{{ - i\varOmega t_{0} }}$$
(42)

where \(B = {F \mathord{\left/ {\vphantom {F {2\left( {\omega_{n}^{2} - \varOmega^{2} } \right)}}} \right. \kern-0pt} {2\left( {\omega_{n}^{2} - \varOmega^{2} } \right)}}\). Substituting Eq. (37) in Eq. (36) and because of \(\varOmega\) is away from \(\omega_{0}\), the secular term is:

$$\begin{aligned} 2i\omega_{n} A' + 2i\zeta \omega_{n}^{2} A + 6\gamma_{1}^{2} B^{2} A + 30\gamma_{2}^{2} B^{4} A + 60\gamma_{2}^{2} B^{2} \bar{A}A^{2} + 10\gamma_{2}^{2} \bar{A}^{2} A^{3} + \hfill \\ 3\gamma_{1}^{2} \bar{A}A^{2} + i\omega_{n}^{3} \varOmega^{2} \psi_{2} A - \omega_{n}^{2} \varOmega^{2} \psi_{3} A + i\omega_{n}^{3} \psi_{4} A - \omega_{n}^{2} \psi_{5} A = 0 \hfill \\ \end{aligned}$$
(43)

where:

$$\begin{aligned} \psi_{2} = \left( {\frac{{\lambda_{1} }}{{\left( {\alpha_{1}^{2} + \omega_{n}^{2} } \right)\left( {\alpha_{1}^{2} + \varOmega^{2} } \right)}} + \frac{{\lambda_{2} }}{{\left( {\alpha_{2}^{2} + \omega_{n}^{2} } \right)\left( {\alpha_{2}^{2} + \varOmega^{2} } \right)}}} \right),\;\psi_{3} = \left( {\frac{{\lambda_{1} \alpha_{1} }}{{\left( {\alpha_{1}^{2} + \omega_{n}^{2} } \right)\left( {\alpha_{1}^{2} + \varOmega^{2} } \right)}} + \frac{{\lambda_{2} \alpha_{2} }}{{\left( {\alpha_{2}^{2} + \omega_{n}^{2} } \right)\left( {\alpha_{2}^{2} + \varOmega^{2} } \right)}}} \right) \hfill \\ \psi_{4} = \left( {\frac{{\lambda_{1} \alpha_{1}^{2} }}{{\left( {\alpha_{1}^{2} + \omega_{n}^{2} } \right)\left( {\alpha_{1}^{2} + \varOmega^{2} } \right)}} + \frac{{\lambda_{2} \alpha_{2}^{2} }}{{\left( {\alpha_{2}^{2} + \omega_{n}^{2} } \right)\left( {\alpha_{2}^{2} + \varOmega^{2} } \right)}}} \right),\;\psi_{5} = \left( {\frac{{\lambda_{1} \alpha_{1}^{3} }}{{\left( {\alpha_{1}^{2} + \omega_{n}^{2} } \right)\left( {\alpha_{1}^{2} + \varOmega^{2} } \right)}} + \frac{{\lambda_{2} \alpha_{2}^{3} }}{{\left( {\alpha_{2}^{2} + \omega_{n}^{2} } \right)\left( {\alpha_{2}^{2} + \varOmega^{2} } \right)}}} \right) \hfill \\ \end{aligned}$$
(44)

\(A\left( {t_{1} } \right)\) is considered in polar form in Eq. (38). Solving the derived equations from obtained expression in real and imaginary parts lead to:

$$b\left( {t_{1} } \right) = b_{0} e^{{ - \frac{1}{2}\omega_{n} \left( {2\zeta + \omega_{n} \psi_{4} + \omega_{n} \varOmega^{2} \psi_{2} } \right)t_{1} }}$$
(45)
$$\beta \left( {t_{1} } \right) = \frac{1}{{16\omega_{n} }}\left( \begin{aligned} \left( {240B^{4} \gamma_{2}^{2} t_{1} + 48B^{2} \gamma_{1}^{2} t_{1} - 8\varOmega^{2} \omega_{n}^{2} \psi_{3} t_{1} - 8\omega_{n}^{2} \psi_{5} t_{1} } \right) + \hfill \\ \frac{{b_{0}^{2} - b^{2} }}{{\omega_{n} \left( {\varOmega^{2} \omega_{n} \psi_{2} + \omega_{n} \psi_{4} + 2\zeta } \right)}}\left( {120B^{2} \gamma_{2}^{2} + \frac{{5\gamma_{2}^{2} }}{2}\left( {b_{0}^{2} + b^{2} } \right) + 6\gamma_{1}^{2} } \right) \hfill \\ \end{aligned} \right).$$
(46)

5.4 Super-harmonic resonance

In Eq. (26) when \(\varOmega\) is near to \({1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}\omega_{n}\) one can get:

$$3\varOmega = \omega_{n} + \varepsilon \sigma$$
(47.)

Using Eq. (42) in Eqs. (35) and (36) the secular term will be:

$$\begin{aligned} 2i\omega_{n} A' + 2i\omega_{n}^{2} \zeta A + 60\gamma_{2}^{2} B^{2} \bar{A}A^{2} + 30\gamma_{2}^{2} B^{4} A + 10\gamma_{2}^{2} \bar{A}^{2} A^{3} + 5\gamma_{2}^{2} B^{5} e^{{i\sigma t_{1} }} + \gamma_{1}^{2} B^{3} e^{{i\sigma t_{1} }} + 3\gamma_{1}^{2} \bar{A}A^{2} + \hfill \\ 6B^{2} \gamma_{1}^{2} A + 20\gamma_{2}^{2} B^{3} \bar{A}Ae^{{i\sigma t_{1} }} + i\omega_{n}^{3} \varOmega^{2} \psi_{2} A - \omega_{n}^{2} \varOmega^{2} \psi_{3} A + i\omega_{n}^{3} \psi_{4} A - \omega_{n}^{2} \psi_{5} A + 10\gamma_{2}^{2} B^{3} e^{{ - i\sigma t_{1} }} A^{2} = 0 \hfill \\ \end{aligned}$$
(48)

Substituting Eq. (18) in Eq. (43), letting \(\sigma t_{1} - \beta = \theta\) and grouping real and imaginary terms lead to:

$$\omega_{n} b^{\prime} + \omega_{n}^{2} \zeta b + \frac{1}{2}\omega_{n}^{3} \varOmega^{2} \psi_{2} b + \frac{1}{2}\omega_{n}^{3} \psi_{4} b + \left( {\frac{5}{2}B^{3} \gamma_{2}^{2} b^{2} + 5B^{5} \gamma_{2}^{2} + B^{3} \gamma_{1}^{2} } \right)\sin \left( {\sigma t_{1} - \beta } \right) = 0$$
(49)
$$\begin{aligned} - \omega_{n} b\beta^{\prime} + 15\gamma_{2}^{2} B^{4} b + \frac{15}{2}\gamma_{2}^{2} B^{2} b^{3} + \frac{5}{16}\gamma_{2}^{2} b^{5} + 3\gamma_{1}^{2} B^{2} b + \frac{3}{8}\gamma_{1}^{2} b^{3} - \frac{1}{2}\psi_{3} \varOmega^{2} \omega_{n}^{2} b \hfill \\ \,\,\,\,\,\, - \frac{1}{2}\psi_{5} \omega_{n}^{2} b + \left( {5B^{5} \gamma_{2}^{2} + \frac{15}{2}B^{3} \gamma_{2}^{2} + B^{3} \gamma_{1}^{2} } \right)\cos \left( {\sigma t_{1} - \beta } \right) = 0 \hfill \\ \end{aligned}$$
(50)

Considering the system in steady-state condition will be resulted to:

$$\begin{aligned} \sigma = \frac{1}{{4\omega_{n} }}\left( {240B^{4} \gamma_{2}^{2} + 120B^{2} \gamma_{2}^{2} b^{2} + 5\gamma_{2}^{2} b^{4} - 8\varOmega \omega_{n}^{2} \psi_{3} + 48B^{2} \gamma_{1}^{2} + 6b^{2} \gamma_{1}^{2} - 8\omega_{n}^{2} \psi_{5} } \right) \hfill \\ \,\,\,\,\,\,\,\,\, \pm 2\frac{{\left( {10B^{2} \gamma_{2}^{2} + 15\gamma_{2}^{2} b^{2} + 2\gamma_{1}^{2} } \right)}}{{\omega_{n} }} \times \sqrt {\left( {\frac{{B^{3} }}{b}} \right)^{2} - \left( {\frac{{\omega_{n}^{2} \left( {\omega_{n} \varOmega^{2} \psi_{2} + \omega_{n} \psi_{4} + 2\zeta } \right)}}{{10B^{2} \gamma_{2}^{2} + 5\gamma_{2}^{2} b^{2} + 2\gamma_{1}^{2} }}} \right)^{2} } \hfill \\ \end{aligned}$$
(51)

5.5 Sub-harmonic resonance

When frequency of external excitation \(\varOmega\) is near to \(3\omega_{n}\), sub-harmonic resonances appears. Hence, it is considered that:

$$\varOmega = 3\omega_{n} + \varepsilon \sigma$$
(52)

Letting Eq. (47) in Eqs. (35) and (36) and extracting secular terms yield:

$$\begin{aligned} 2i\omega_{n} A^{\prime} + 2i\zeta \omega_{n}^{2} A + 30\gamma_{2}^{2} B^{4} A + 10\gamma_{2}^{2} \bar{A}^{2} A^{3} + 3\gamma_{1}^{2} \bar{A}A^{2} + 6\gamma_{1}^{2} B^{2} A + 60\gamma_{2}^{2} B^{2} \bar{A}A^{2} + i\omega_{n}^{3} \varOmega^{2} \psi_{2} A \hfill \\ - \omega_{n}^{2} \psi_{3} \varOmega^{2} A + i\omega_{n}^{3} \psi_{4} A - \omega_{n}^{2} \psi_{5} A + \left( {3\gamma_{1}^{2} B\bar{A}^{2} + 30\gamma_{2}^{2} B^{3} \bar{A}^{2} + 20\gamma_{2}^{2} B\bar{A}^{3} A} \right)e^{{i\sigma t_{1} }} + 5\gamma_{2}^{2} BA^{4} e^{{ - i\sigma t_{1} }} \hfill \\ \end{aligned}$$
(53)

Considering \(A\left( {t_{1} } \right)\) in polar form Eq. (48) in an autonomous system using \(\theta = \sigma t_{1} - 3\beta\), by grouping real and imaginary terms:

$$\omega_{n} b^{\prime} + \zeta \omega_{n}^{2} b + \frac{1}{2}\left( {\varOmega^{2} \psi_{2} + \psi_{4} } \right)\omega_{n}^{3} b + \left( {\frac{15}{2}B^{3} \gamma_{2}^{2} + \frac{15}{16}B\gamma_{2}^{2} b^{2} + \frac{3}{4}B\gamma_{1}^{2} } \right)b^{2} \sin \left( {\sigma t_{1} - 3\beta } \right) = 0$$
(54)
$$\frac{1}{16}\left( \begin{aligned} - 16\omega_{n} \beta^{\prime} + 240B^{4} \gamma_{2}^{2} + 120\gamma_{2}^{2} B^{2} b^{2} + 5\gamma_{2}^{2} b^{4} + 48B^{2} \gamma_{1}^{2} + 6\gamma_{1}^{2} b^{2} \hfill \\ - 8\omega_{n}^{2} \left( {\varOmega^{2} \psi_{3} + \psi_{5} } \right) + \left( {120B^{3} \gamma_{2}^{2} b + 25B\gamma_{2}^{2} b^{3} + 12\gamma_{1}^{2} Bb} \right)\cos \left( {\sigma t_{1} - 3\beta } \right) \hfill \\ \end{aligned} \right)b = 0$$
(55)

Letting \(b^{\prime} = 0\) and \(\theta^{\prime} = 0\) is equal to steady-state motion of the system in this case as:

$$\begin{aligned} \sigma = \frac{1}{{16\omega_{n} }}\left( {720\gamma_{2}^{2} B^{4} + 360\gamma_{2}^{2} B^{2} b^{2} - 24\omega_{n}^{2} \varOmega^{2} \psi_{3} + 15\gamma_{2}^{2} b^{4} + 144\gamma_{1}^{2} B^{2} + 18\gamma_{1}^{2} b^{2} - 24\omega_{n}^{2} \psi_{5} } \right) \hfill \\ \,\,\,\,\,\,\,\, \pm \frac{{\left( {120B^{2} \gamma_{2}^{2} + 25\gamma_{2}^{2} b^{2} + 12\gamma_{1}^{2} } \right)}}{{16\omega_{n} }} \times \sqrt {\left( {3Bb} \right)^{2} - \left( {\frac{{8\omega_{n}^{2} \left( {\omega_{n} \varOmega^{2} \psi_{2} + \omega_{n} \psi_{4} + 2\zeta } \right)}}{{40B^{2} \gamma_{2}^{2} + 5\gamma_{2}^{2} b^{2} + 4\gamma_{1}^{2} }}} \right)^{2} } \hfill \\ \end{aligned}$$
(56)

6 Results and discussion

The default value of different parameters is taken from [1]. These default values are as: \(M = 2.3^{kg}\) \(C = 13^{{{{Ns} \mathord{\left/ {\vphantom {{Ns} m}} \right. \kern-0pt} m}}}\), \(k_{1} = 1840^{{{N \mathord{\left/ {\vphantom {N m}} \right. \kern-0pt} m}}}\), \(k_{3} = - 7e6^{{{N \mathord{\left/ {\vphantom {N {m^{3} }}} \right. \kern-0pt} {m^{3} }}}}\), \(k_{5} = 2e10^{{{N \mathord{\left/ {\vphantom {N {m^{5} }}} \right. \kern-0pt} {m^{5} }}}}\), \(a_{1} = - 0.44 + 0.1i^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0pt} s}}}\), \(a_{2} = - 0.44 - 0.1i^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0pt} s}}}\), \(\alpha_{1} = 3 + 0.22i^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0pt} s}}}\), \(\alpha_{2} = 3 - 0.22i^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0pt} s}}}\) And \(\varepsilon = 0.1\) is considered for all cases.

The focus of the presented study is on the effects of viscoelastic parameters on the vibrational responses of the foam block system. To this aim the effects of viscoelastic parameters i.e. \(a_{1}\), \(a_{2}\), \(\alpha_{1}\) and \(\alpha_{2}\) will be discussed.

Viscoelastic parameters lend themselves to \(\psi_{0}\) and \(\psi_{1}\) during free vibrations. Figure 2 shows the effects of different values of \(\psi_{0}\) on the amplitude and phase of the system. It is clear that the system includes a viscous type of damping, which makes it non-conservative and the amplitude of oscillations decays with time. Equation (22) also shows this behavior. The higher values of \(\psi_{0}\) forces the system to be damped rapidly. And negative values of \(\psi_{0}\) postpone the damping procedure. As derived in Eqs. (22) and (23) the amplitude of the system decays with time and the phase of the system take a linear shape. The slope of this line is dependent to \(\psi_{1}\) and a decrease in \(\psi_{0}\) would decrease phase of the system.

Fig. 2
figure 2

Effects of \(\psi_{0}\) on: (Left) \(b\) and (Right) \(\beta\); for default value of other parameters

Full size image

Amplitude of the system (Eq. 22), does not change by variation in \(\psi_{1}\); however, phase of the system changes significantly as \(\psi_{1}\) is changing. This behavior is illustrated in Fig. 3.

Fig. 3
figure 3

Effects of \(\psi_{1}\) on \(\beta\); for \(\varepsilon = 0.1\) and default value of other parameters

Full size image

In the presence of an external force, as mentioned in Sect. 5, when \(\varOmega\) and \(\omega_{n}\) are near together, primary resonances occurs. Frequency–response equation is derived as Eq. (34). To compare the obtained results with previous studies [23], the effects of external excitation amplitude on the frequency–response is presented in Fig. 4. Results from this figure are in total accordance with previous studies [4, 23]. \(b_{0}\) in this figure represents the initial displacement according to Eq. (45) and \(Mg\) preserves as external weight on the foam according for Fig. 1.

Fig. 4
figure 4

Effects of excitation amplitude on frequency–response due to primary resonances

Full size image

As it is clear in Fig. 4, the resonances of the system occurs about 4.5 Hz. When the amplitude of external excitation is low (\(0.05Mg\)) the effects of nonlinearity is negligible and the response almost resembles the linear viscoelastic system. A resonance occurs near the linear natural frequency (\(\omega_{0}\)) of 4.5 Hz. The orders of magnitude of higher harmonics contribution are smaller than that of the fundamental frequency. Cubic stiffness overcomes the nonlinear behavior by increasing input amplitude to about \(0.1Mg\), and the amplitude shows softening. Hardening behavior is obvious at higher values of input amplitudes \(1Mg\), where the fifth order nonlinearity is dominant. It should be noted that at higher input levels, the higher harmonics also reveal more contribution to the solution \(x\left( t \right)\). Further increase in input amplitudes, the resonant frequency tend to be increased. As the input amplitude is increased, the softening spring behavior at the beginning is replaced by a hardening behavior.

Considering the defined parameters, the stability condition for primary resonances according to Eq. (39), is shown in Fig. 5.

Fig. 5
figure 5

The stability condition of the system considering the defined parameters

Full size image

Effects of viscoelastic parameters (\(\psi_{0}\) and \(\psi_{1}\)) in this case is shown in Figs. 6 and 7. According to Fig. 6, changes in \(\psi_{0}\) do not affect the resonance frequency of system. However, for the values of \(\psi_{0}\) equal to \(\pm 0.05\) the system does not show any resonance behavior. In other words, these values damp the vibration of the system in a way that the system does reflect any resonance about resonance frequency. As \(\psi_{0}\) increases the resonance of system appears. The system shows softening behavior for \(\psi_{0} = - 0.01\) to \(\psi_{0} = 0.001\) and for \(\psi_{0} = 0.01\) the hardening behavior of system in obvious.

Fig. 6
figure 6

Effects of \(\psi_{0}\) on primary resonances of the system

Full size image
Fig. 7
figure 7

Effects of \(\psi_{1}\) on primary resonances of the system

Full size image

The interesting point is that, unlike \(\psi_{0}\) which affect the behavior of the system, \(\psi_{1}\) changes the resonance frequency of the foam system. This is illustrated in Fig. 7.

According to Fig. 7, the system behaves in the same way as \(\psi_{1}\) increases or decreases and it shifts along frequency axis. However, the frequency resonance increases as the \(\psi_{1}\) is increasing.

For Non-resonant hard excitations, sub-harmonic and super-harmonic response of the system, the viscoelastic parameters lend themselves to \(\psi_{2}\), \(\psi_{3}\), \(\psi_{4}\) and \(\psi_{5}\). According to Eqs. (45) and (46) where the response of the system to non-resonant hard excitations is obtained, the amplitude of the system in this case in affected by \(\psi_{2}\) and \(\psi_{4}\) only. The decaying nature of amplitude of the system is obvious. Hence, as \(\psi_{2}\) and/or \(\psi_{4}\) increases (while the other terms i.e. \(\omega_{n}\) and \(\varOmega^{2}\) are always positive) damping of the system will be strengthened and amplitude is decreased as these parameters are increased. For phase of system according to Eq. (46), is concluded that an increase in \(\psi_{2}\) and/or \(\psi_{4}\) lead to a decrease in system phase. However, the phase of system is affected by \(\psi_{2}\) and \(\psi_{3}\) and \(\psi_{4}\) and \(\psi_{5}\). Equation (46) shows that \(\psi_{3}\) and \(\psi_{5}\) are multiplied by a negative sign while the other parameters are always positive. Hence, it is concluded that increasing these parameters will decrease phase of the system. On the other side, \(\psi_{2}\) and \(\psi_{4}\) are in denominator of the expression and an increase in these parameters leas to a decrease in system phase. Finally, it should be stated that phase of system will be decreased as \(\psi_{2}\), \(\psi_{3}\), \(\psi_{4}\) and \(\psi_{5}\) is increased. These behaviors are illustrated in Figs. 8 and 9.

Fig. 8
figure 8

Effects of \(\psi_{2}\) and/or \(\psi_{4}\) on amplitude of system due non-resonant hard excitation

Full size image
Fig. 9
figure 9

Effects of \(\psi_{2}\), \(\psi_{3}\), \(\psi_{4}\) and \(\psi_{5}\) on system phase due non-resonant hard excitation

Full size image

The super-harmonic response of order three arises at higher input amplitudes. A small peak can be seen in the amplitude of the first and third harmonics of the response near an excitation frequency of 1.5 Hz which is close to one-third the frequency of the system resonance. According to Eq. (56) which representing frequency response of system in super-harmonic case, it is clear that the response is affected by \(\psi_{2}\), \(\psi_{3}\), \(\psi_{4}\) and \(\psi_{5}\). Effects of \(\psi_{2}\) and \(\psi_{4}\) are almost the same as they are in one term with positive coefficients. Also, both \(\psi_{3}\) and \(\psi_{5}\) affects the system in almost a same way. The effects of \(\psi_{2}\) on frequency response of system is presented in Fig. 10.

Fig. 10
figure 10

Effects of \(\psi_{2}\) on frequency response of system in super-harmonic state and for \(F = 0.15Mg\)

Full size image

It is clear that, the system has a resonance frequency about \(1.5Hz\) in this case and for values of \(\psi_{2}\) less than -0.01 and greater than 0.01 this resonance behavior is vanished. For values of \(\psi_{2}\) between -0.01 and 0.01 as \(\psi_{2}\) increases the peak of amplitude increases and then decreases.

Also changes in \(\psi_{3}\) leads to changes in resonance frequency of system. An increase in \(\psi_{3}\) lead to a decrease in resonance frequency and vice versa. The system behaves in the same manner but it shifts in frequency axis forward and backward due to changes in \(\psi_{3}\). Figure 11 shows this behavior.

Fig. 11
figure 11

Effects of \(\psi_{3}\) on frequency response of system in super-harmonic state and for \(F = 0.15Mg\)

Full size image

Finally, the behavior of system in steady state in sub-harmonic case in obtained in Eq. (56) when an excitation frequency is close to three times the resonance frequency of the system. Just like before, the system in this case is affected by viscoelastic parameters: \(\psi_{2}\), \(\psi_{3}\), \(\psi_{4}\) and \(\psi_{5}\). Again in this case, \(\psi_{2}\) and \(\psi_{4}\) act in the same way and \(\psi_{3}\) and \(\psi_{5}\) have the same effects. The behavior of system is shown in Figs. 12 and 13.

Fig. 12
figure 12

Effects of \(\psi_{2}\) on frequency response of system in sub-harmonic case and for \(F = 0.25Mg\)

Full size image
Fig. 13
figure 13

Effects of \(\psi_{3}\) on frequency response of system in sub-harmonic state and for \(F = 0.25Mg\)

Full size image

7 Conclusions

Using multiple time scales method, both free and forced vibration of polyurethane foam has been practiced in this study. Dynamics of system is considered as a single degree of freedom, linear viscoelastic oscillator with a polynomial stiffness. The nonlinearity in the model comprised of stiffness nonlinearities of orders three and five. The model for viscoelastic contribution of the foam was assumed to be linear and the relaxation kernel was assumed to consist of two terms. The governing equation is an integro-differential equation and an approximation of solution to such equation has been presented by MTSM.

Approximate periodic solutions were developed based on the multiple time scales approach. The multiple time scales equations were utilized for the formulation of system response. The resulting equations were found to be nonlinear functions of parameters. Free and forced vibration of the system were investigated. The forced vibration behavior of system was considered through primary resonances, non-resonant hard excitation, sub-harmonic and super harmonic. Analysis of the steady-state response of a nonlinear model for the foam-mass system to harmonic input was also presented.

Using simulations with realistic values of system parameters, it was confirmed that the approximations based on the two-term approximation were accurate compared to previously presented studies. The results agree qualitatively with previously published results obtained through different experimental techniques and analytical approaches. The effects of viscoelastic factors on the system response were also discussed. Future works would be dealing with experimental studies and semi-analytical methods for solving polyurethane foam equations.