Longitudinal stability and control augmentation with robustness and handling qualities requirements using the two degree of freedom controller

Abstract

This paper presents a practical design of longitudinal stability and control augmentation system (SCAS) using a two degree of freedom (TDOF) controller. It is based on the linear quadratic regulator (LQR) technique in the frequency domain, via spectral factorization. The controller exhibits robustness to plant uncertainties, related with variation due to different operation conditions, and incorporates various aircraft handling qualities (HQ) requirements to comply with certification authority’s requests. The project results in an unique set of fixed gain TDOF controller for a plant dynamics which changes with a $V_{\text {CAS}}\times x_{\text {cg}}$ envelope. The project is done aiming at the industrial implementation of TDOF controller in fly-by-wire aircrafts.

1 Introduction

The traditional design of flight control laws typically uses nonlinear techniques to make the aircraft insensitive to changes in flight conditions and aircraft configuration (e.g., mass, center of gravity ($x_{\text {cg}}$), airspeed, altitude, flap position, etc.). The inability to take into account these changes in the design can result in stability degradation over the flight envelope. A dynamic mode that is stable and adequately damped in one flight condition may become either lightly damped or even unstable in another one. In commercial aircraft, such as stability degradation, can cause some discomfort to passengers and, even worst, reduce the pilot capability to handling the aircraft. Therefore, improving stability is an additional target to flight control laws.

Feedback control also provides benefits in terms of aircraft weight reduction, aerodynamic efficiency and optimization of fuel consumption. Such benefits are shown in [1], with the use of fly-by-wire control laws of a new transport aircraft. Such control laws are known in aeronautics as stability augmentation systems (SAS), if they affect damping and natural frequencies to improve the aircraft transient response, or, as control augmentation systems (CAS), if the purpose is to give the pilot more precise control, for instance the sideslip $\beta$ limiter [2].

To improve the aircraft stability, different control strategies, such as gain scheduling, are widely used in the industry [3]. The main idea of this methodology is to design a set of linear controllers for specific operating points over the flight envelope. Gain interpolation is then used between the points to ensure the operation along the entire aircraft envelope. Some of the algorithms used to generate the gain scheduling correspond to linear quadratic regulator (LQR) and eigenstructure assignment among others [2]. Theoretical works applied to the aircraft control are presented in [4, 5] and [6]; therefore, only some of them presents the gains schedule process.

The most important publications are [7] where the comparison of classical LQR is presented (solution of Riccati equation) with Optimal Cooperative control of Ch-47 helicopter; [8] show the results of LQR technique applied to the lateral control of the Boeing 767, later [9] applied the technique on a flexible civil aircraft. Recently, [10] presented the use of advanced flight controls research and development applied to business jet aircraft. [11] propose a methodology to assess the robust stability and robust performance of Automatic Flight Control Systems (AFCS) using gain scheduling and optimization and [12] add the quantum particle swarm optimization (QPSO) to improve the LQR. However, all the mentioned works use the LQR in the time domain employing a considerable number of linear models to guarantee a specific performance and robustness in the overall flight envelope; this process generates several gain scheduling tables.

To improve these methodologies, the $H_{\infty }$ strategy was applied by [13], trying to reduce the number of points in the gain schedule process, use an unique structure instead of several gain tables and to increase the operating domain with a lower set of gains. With the same purpose and aiming its industrial implementation, this paper presents an alternative project, the two degree of freedom (TDOF) controller proposed by [14] to design stability and control augmentation systems.

Some advantages of TDOF controller are its pragmatical design, once it depends only on two parameters (a third one can be added to corrects the steady state error); in comparison with the LQR controllers mentioned above, its project is done in the frequency domain instead of time domain. The feedback gains affects the stability of the system and the pre-filter the response characteristics. The controller exhibits robustness to plant uncertainties and if the sensitivity and complementary sensitivity functions are considered [15], the controller achieves disturbances rejection and noise attenuation [16]. Additionally, the controller has a unique structure (e.g., does not contain tables). The strategy in the frequency domain (solution of Diophantine equation) has been successfully implemented only for the trajectory control problem in a SCARA¹ robot [17].

This paper presents as novelty an alternative practical project in the development of control laws for fly-by-wire aircrafts, adding handling qualities requirements to comply with certification authority’s request. The TDOF controller application is made on a business jet aircraft; also it is possible to design it for commercial and cargo aircrafts.

In Sect. 2, the mathematical model is described. Handling qualities criteria are presented in Sect. 3. The main characteristics of the TDOF controller and its algorithm are described in Sect. 4. The design of controller and linear simulations is presented in Sect. 5. The baseline aircraft handling qualities analysis and results are presented in Sect. 6. The results of nonlinear simulations for regulation and tracking maneuvers are presented in Sect. 7. Finally, the conclusions are presented.

2 Mathematical modeling

The motion of an aircraft as a rigid body can be described by a set of nonlinear simultaneous differential equations. These equations, representing the translational and rotational motion of the aircraft, can be formulated as state variable (SV) equations expressed as:

$$\begin{aligned} \dot{x}(t)&= {} f[x(t),u(t)] \end{aligned}$$

(1)

$$\begin{aligned} y(t)&= {} h[x(t),u(t)] \end{aligned}$$

(2)

where x(t) is the internal state vector, $\dot{x}$ is the derivative of x(t) with respect to time, u(t) is the control vector [in this paper, the control vector is given only by elevator deflection $\delta _{e}(t)$] and y(t) is the measured outputs.

The origin of the body axis system $(x_{b},y_{b},y_{b})$ illustrated in the Fig. 1 ² is the aircraft center of gravity $x_{\text {cg}}$. The $x_{b}$ axis is directed toward the nose of the aircraft, the $y_{b}$ axis toward the right wing, and the $z_{b}$ axis toward the bottom of the aircraft. Additionally, Fig. 1 shows the angular velocities roll, pitch and yaw rate (p, q, r). The attitude angles $(\phi , \theta , \psi )$, angle of attack $\alpha$ and sideslip angle $\beta$ are also illustrated; details can be consulted in [2] and [18]. The nonlinear model of the generic business jet aircraft assembled in Matlab/Simulink presented in [19] is considered in this paper.

Fig. 1

Coordinate systems and main aircraft variables

A common practice in flight controls, when designing and analyzing control systems, is to linearize the aircraft equations around an operating point (trim point). Therefore, nonlinear equations of the aircraft (1)–(2) are linearized for different operating points of its envelope, usually parameterizing by airspeed and altitude.

The longitudinal axis linear models of aircraft, obtained at different operation points to design and analyze the TDOF controller, are represented by standard linear state equation given by

$$\begin{aligned} \dot{x}(t)&= {} A x(t) + B \delta _{e}(t) \nonumber \\ y(t)&= {} C x(t) \end{aligned}$$

(3)

where $A \in \mathcal {R}^{4 \times 4}$ is the state matrix, $B \in \mathcal {R}^{4 \times 1}$ is the input matrix, $C \in \mathcal {R}^{1 \times 4}$ is the output matrix and $x=[V_{\text {TAS}} ~\alpha ~ q ~ \theta ]^{\text{T}}$ is the state variable. In this paper, the main interest is the relationship from elevator deflection $\delta _{e}(t)$ to pitch rate q(t), which transfer function is defined as:

$$\begin{aligned} G(s)=\dfrac{q(s)}{\delta _{e}(s)} \end{aligned}$$

(4)

2.1 Actuator and sensors models

The actuator and sensors models are introduced in the analysis model, only to verify the closed-loop stability and to evaluate the handling qualities.

The actuator model corresponds to a second-order filter. Table 1 presents the adopted values of natural frequency and damping for the actuator.

Table 1 Elevator actuator parameters

The sensors dynamics were modelled considering the delays presented in Table 2.

Table 2 Transport delay of sensors

The transfer function of time delay is irrational (it has not s-polynomial in the numerator and denominator). For this reason, it is necessary to use an approximation in the form of rational transfer function. The approximation used corresponds to 4th order Padé approximation.

2.2 Mass, airspeed and center of gravity configurations

The robustness specifications for the aircraft longitudinal dynamics were analyzed considering the flight envelope configurations for mass m, calibrated airspeed $V_{\text {CAS}}$ and center of gravity along the body x axis $x_{\text {cg}}$. Table 3 shows the set of nine models extracted form aircraft envelope, considering three airspeed conditions and an arrangement of five $x_{\text {cg}}$ mass configurations. The main target of the proposed design is to get a unique fixed gain TDOF controller to cover all conditions of Table 3.

Table 3 Linear models generated for $V_{\text{CAS}} \times x_{\text{cg}}$ envelope

3 Handling qualities

Three handling qualities (HQ) criteria are used in the design. As suggested in references [13] and [6], the use of the HQ criteria is made in the design verification phase to evaluate good response to a pilot input. From [20], the response of the pilot is evaluated according to the following criteria:

• Level 1 satisfactory: Flying qualities clearly adequate for the mission Flight Phase. Desired performance is achievable with minimal pilot compensation.

• Level 2 acceptable: Flying qualities adequate to accomplish the mission Flight Phase, but some increase in pilot workload or degradation in mission effectiveness, or both.

• Level 3 controllable: Flying qualities such that the aircraft can be controlled in the context of the mission Flight Phase, even though pilot workload is excessive or mission effectiveness is inadequate, or both.

3.1 Modal criteria

This criterion is related essentially with the damping ratios of aircraft modes: the short period and the phugoid [2].

The slow oscillating mode, known in aviation terms, as phugoid is generally under-damped. It mainly affects the pitch attitude and the true velocity. To reach the flying qualities required for level 1 of a typical HQ criterion such as the Cooper Harper, the phugoid damping ratio shall be greater than 0.04 [20].

A rapid oscillating mode (short period) mostly affects the transient responses in the baseline aircraft angle of attack $\alpha$, pitch rate q and load factor Nz. To meet the flying qualities required for level 1, then the short period damping ratio shall be greater than 0.4 [20].

3.2 Bandwidth criterion

The criterion establishes that a measure of the handling qualities of an aircraft is based on its stability margin when commanded by pilot in a closed loop compensatory pitch attitude tracking task. The maximum frequency that such closed loop tracking can be accomplished without disturbing stability is referred to as bandwidth [21].

The control bandwidth of aircraft is critically important to good handling and the flight control system easily modifies it. The control bandwidth is further complicated by the fact that it varies with the inputs–outputs variables involved. Namely, control and handling difficulties may arise when the bandwidth of an input–output relationship is lower than it should be. For this reason, all input–output bandwidth properties should be consistent and chosen to lead to good aircraft handling and adequate stability margins. Two measures for that are the pitch attitude and the flight path angle bandwidth criterion (attitude bandwidth versus flight path bandwidth indicate consonance between attitude and flight path response) [22].

From frequency response, the pitch attitude bandwidth is defined as the lower of the pitch attitude gain bandwidth, $\omega _\mathrm{{BW}_\mathrm{{gain}}}$, and the pitch attitude phase bandwidth, $\omega _\mathrm{{BW}_\mathrm{{phase}}}$. Otherwise, the gain bandwidth, $\omega _\mathrm{{BW}_\mathrm{{gain}}}$, is defined by the frequency at which the gain margin is 6 dB; in other words, it is the frequency correspondent to the gain 6 dB higher than the gain when the phase is −180° . The phase gain bandwidth, $\omega _\mathrm{{BW}_\mathrm{{phase}}}$, is defined by the frequency at which the phase margin is 45°, or this is the frequency at which the phase first passes −135° (is 45° higher than −180°) [23].

3.3 Phase delay criterion

In [23], it is established that the roll-off in phase due to a time delay $\tau$ is a linear function of frequency. It is observed that, at frequencies around and higher than the bandwidth frequency, the curve of the Bode phase response of a high-order function is reasonably well matched by the equivalent phase delay. Consequently, the phase delay based on the baseline aircraft attitude response may be defined by following equation:

$$\begin{aligned} \tau _{p} = \frac{\Delta \phi _{2\omega _{180}}}{2\omega _{180}} \frac{\pi }{180} \end{aligned}$$

(5)

where $2\omega _{180}$ is twice the neutral stability frequency, i.e., the frequency at −180° phase, and $\Delta \phi _{2\omega _{180}}$ is the phase at that frequency.

Table 4 summarizes the handling quality boundaries being considered in the design procedure.

Table 4 Handling qualities requirements

4 Two degree of freedom controller

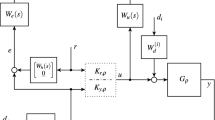
The design of the TDOF, the dominant dynamics is the aircraft. Therefore, the actuator and sensor transfer functions are not considered in the controller design. The structure of the TDOF controller is presented in Fig. 2.

Fig. 2

TDOF controller structure

The baseline aircraft longitudinal axis to be controlled is represented by the minimal, strictly proper rational transfer function given by Eq. (4):

$$\begin{aligned} G(s) = \frac{c(s)}{a(s)}=\frac{q(s)}{\delta _{e}(s)} \end{aligned}$$

(6)

where polynomials a(s) and c(s) are co-prime, with degrees n and m $(m<n)$. The inputs d(s) and $\eta (s)$ correspond to aircraft disturbance and sensor noise signal. The polynomials h(s), k(s) and $\hat{q}(s)$ of degrees $n-1$ are the controller functions.

The closed-loop transfer function from r(s) to q(s), without aircraft disturbance d(t) and sensor noise signal $\eta (t)$ is

$$\begin{aligned} \frac{q(s)}{r(s)}=\frac{\kappa c(s) \hat{q}(s)}{a(s)k(s)+c(s)h(s)}=\frac{\kappa c(s) \hat{q}(s)}{\delta (s)} \end{aligned}$$

(7)

where $\kappa \in \mathcal {R}$ and $\delta (s)$ represents the closed-loop polynomial.

The controller guarantees a good output regulation, by positioning per design the roots of $\delta (s)$ far enough into the left half s plane. However, the design could increase the system bandwidth sufficiently to produce the baseline aircraft control effort $\delta _{e}(t)$ saturation; in our case, the elevator commands cannot exceed the physical design limits. Complementarily, one way of obtaining a desirable output regulation, without requiring an excessive control effort signal, is to design the aircraft longitudinal axis controller by minimizing the LQR performance index, which is

$$\begin{aligned} J_{\text {LQR}}= \int ^{\infty }_{0} \left\{ \rho ( r(t)-q(t))^2 + \delta _{e}(t)^{2} \right\}{\text{d}}t \end{aligned}$$

(8)

The excessive output excursions and the control effort required to prevent such excursions can be obtained by minimizing the Eq. (8). The adjustable weighting factor $\rho \in \mathcal {R}^{+}$ can be used to obtain appropriate trade-offs between these two conflicting goals. The time solution of (8) corresponds to matrix gains calculated by the Riccati equation and the equivalent solution in the frequency domain is known as spectral factorization [14].

4.1 Spectral factorization

Since the polynomials a(s) and c(s) have real coefficients, it follows that both:

$$\begin{aligned} a(j \omega )a(-j\omega )&= {} |a(j \omega )|^{2} \ge 0 \nonumber \\ c(j \omega )c(-j\omega )&= {} |c(j \omega )|^{2} \ge 0 ~\forall ~ \text{ real } \omega \end{aligned}$$

(9)

Therefore, it is possible to define:

$$\begin{aligned} \Delta (s) = a(s) a(-s)+\rho c(s)c(-s) \end{aligned}$$

(10)

where $\Delta (s)$ is an even polynomial given by:

$$\begin{aligned} \Delta (s) = (-1)^{n} s^{2n}+ \Delta _{2n-2} s^{2n-2}+ \dots + \Delta _{2} s^{2}+\Delta _{0} \end{aligned}$$

(11)

The 2n roots of $\Delta (s)$ are obtained with $\rho$ varying from 0 to $\infty$ and represent a special root locus which is termed as root-square locus, i.e., if $\lambda _{j}$ is a root of $\Delta (s)$, then $-\lambda _{j}$ is also a root of $\Delta (s)$. Consequently, $\Delta (s)$ can be expressed by a spectral factorization as:

$$\begin{aligned} \Delta (s) = [\Delta (s)]^{+}[\Delta (s)]^{-}=\delta ^{F^{*}}(s)\delta ^{F^{*}}(-s) \end{aligned}$$

(12)

where n stable roots of $[\Delta (s)]^{+}$ allow to obtain $\delta ^{F^{*}}(s)$.

By duality, spectral factorization also can be used to obtain the n stable roots of $\delta ^{H^{*}}(s)$, which is defined as the left half-plane spectral factor of

$$\begin{aligned} \bar{\Delta }(s)&= {} a(s) a(-s)+ \sigma c(s) c(-s) \nonumber \\&= {} [\bar{\Delta }(s)]^{+}[\bar{\Delta }(s)]^{-} \nonumber \\&= {} \delta ^{H^{*}}(s)\delta ^{H^{*}}(-s) \end{aligned}$$

(13)

where each choice of $\sigma \in \mathcal {R}^{+}$ in Eq. (13) implies a corresponding $\delta ^{H^{*}}(s)$; consequently, the pre-filter $\hat{q}(s)$ is calculated as function of n stable roots of $\delta ^{H^{*}}(s)$. Then, for

$$\begin{aligned} k(s) = s^{n-1}+k_{n-2} s^{n-2}+ \dots + k_{1}s+k_{0} \end{aligned}$$

(14)

and

$$\begin{aligned} h(s) = h_{n-1}s^{n-1}+ \dots + h_{1}s+h_{0} \end{aligned}$$

(15)

it is possible to solve the Diophantine equation.

$$\begin{aligned} a(s) k(s)+c(s)h(s)= \delta ^{F^{*}}(s) \hat{q} (s) \end{aligned}$$

(16)

Equation (16) can be written as:

$$\begin{aligned} \mathcal {S} \mathcal {V} = \bar{\delta } \end{aligned}$$

(17)

where

$$\begin{aligned} \mathcal {S}= & {} \left( \begin{array}{cccccccc} a_{0} &{} 0 &{} \dots &{} 0 &{} c_{0} &{} 0 &{} \dots &{} 0 \\ a_{1} &{} a_{0} &{} \dots &{} 0 &{} c_{1} &{} c_{0} &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ a_{n-1} &{} a_{n-2} &{} \dots &{} a_{0} &{} c_{n-1} &{} c_{n-2} &{} \dots &{} c_{0} \\ 1 &{} a_{n-1} &{} \dots &{} a_{1} &{} 0 &{} c_{n-1} &{} \dots &{} c_{1} \\ 0 &{} 1 &{} \dots &{} a_{2} &{} 0 &{} 0 &{} \dots &{} c_{2} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \dots &{} 1 &{} 0 &{} 0 &{} \dots &{} 0 \end{array} \right) \nonumber \\ \mathcal {V}= & {} \left( \begin{array}{cccccccc} k_{0}&k_{1}&\dots&k_{n-1}&h_{0}&h_{1}&\dots&h_{n-1} \end{array} \right) ^{T} \nonumber \\ \bar{\delta }= & {} \left( \begin{array}{cc} \left( \delta ^{F^{*}}(s) \hat{q} (s) \right) _{0} \\ \left( \delta ^{F^{*}}(s) \hat{q} (s) \right) _{1} \\ \vdots \\ \left( \delta ^{F^{*}}(s) \hat{q} (s)\right) _{2n-2} \\ \left( \delta ^{F^{*}}(s) \hat{q} (s)\right) _{2n-1} \end{array}\right) \nonumber \end{aligned}$$

From Eq. (17), the real coefficients of gains h(s) and k(s) are obtained.

5 Design of TDOF controller

The linear model used to design the TDOF controller corresponds to aircraft take-off condition at (altitude = 2000 ft, $V_{\text{CAS}}=93$ knots, $x_{\text {cg}} = 0.47$ and mass = 11,500 Kg). The matrices A, B and C obtained at this condition for longitudinal axis are given by

$$\begin{aligned} A= & {} \left( \begin{array}{cccc} -0.0533 &{} 5.3316 &{} -0.0770 &{} -9.8060 \\ -0.0083 &{} -0.6399 &{} 0.9736 &{} 0.0000 \\ 0.0033 &{} -0.4201 &{} -0.5483 &{} 0 \\ 0 &{} 0 &{} 1.0000 &{} 0 \end{array} \right) \nonumber \\ B= & {} \left( \begin{array}{cccc} 0.0193&-0.0545&-1.2061&0 \end{array} \right) ^\mathrm{{T}} \nonumber \\ C= & {} \left( \begin{array}{cccc} 0&0&1&0 \end{array} \right) \end{aligned}$$

(18)

According Eq. (3), the transfer function $\dfrac{q(s)}{\delta _{e}(s)}$ is given by:

$$\begin{aligned} \dfrac{-1.206 s^{3} - 0.8132 s^{2} - 0.09385 s + 2.828e^{-018}}{s^{4} + 1.242 s^{3} + 0.8675 s^{2} + 0.08011 s + 0.05443} \end{aligned}$$

(19)

where the eigenvalues and damping are presented in Table 5.

Table 5 Eigenvalues of design linear model

To verify the accuracy of the linear model design, the response of aircraft to $\delta _{e}$ doublet was compared with nonlinear response at the same condition. Figure 3 illustrates the open loop response of both models, where it is possible to verify that the linear model is representative of aircraft dynamics at the selected operation condition and suitable to the design purpose; also it is possible to confirm that the long period dynamics is unstable.

Fig. 3

Linear and nonlinear response to $\delta _{e}$ doublet

5.1 Design results

Figure 4 allows verifying the root-square locus from Eq. (10) considering three values of weighting factor $\rho$.

Fig. 4

A Root-Square locus plot for $\Delta (s)$

Figure 5 allows verifying the root-square locus from Eq. (13) considering three values of weighting factor $\sigma$.

Fig. 5

A Root-Square locus plot for $\bar{\Delta }(s)$

To comply with the requirements given in the Table 4, the values of root-square locus for weighting factors $\rho = 5$ and $\sigma = 2$ are selected. They are detailed in Table 6.

Table 6 The values of root-square locus

The weighting factor $\rho$ makes possible fulfilling with the closed loop stability requirements (fast pole location without actuator saturation) through the calculation of $\Delta (s)$ to obtain the polynomial $\delta ^{F^{*}}(s)$ as:

$$\begin{aligned} \delta ^{F^{*}}(s) = s^{4} + 3.4606 s^{3} + 2.4481s^{2} + 0.4717s + 0.0544 \end{aligned}$$

(20)

at the same time, the weighting factor $\sigma$ helps to fulfilling with handling qualities requirements (values greater than 2 do not meet the requested) through the calculation of $\bar{\Delta }(s)$ to obtain the polynomial $\delta ^{H^{*}}(s)$ as:

$$\begin{aligned} \delta ^{H^{*}}(s) = s^{4} + 2.5077 s^{3} + 1.7859s^{2} + 0.3522s + 0.0543 \end{aligned}$$

(21)

Considering Eq. (21), the pre-filter $\hat{q}(s)$ is calculated as:

$$\begin{aligned} \hat{q}(s) = (s + 0.9381) (s+1.3718) (s+real(0.0989 - 0.1803j) \end{aligned}$$

(22)

Finally, using the Diophantine Eq. (17), the 3rd order polynomials h(s) and k(s) presented in Table 7 are obtained.

Table 7 TDOF controller gains

Figure 6 illustrates the simulation results obtained, for all nine model conditions, using a pulse input signal, the gains of Table 7 and a selected $\kappa = -1$. In these results, it is evident from the steady-state error.

Fig. 6

Pulse input response $\kappa =-1$

Figure 7 illustrates again, the simulation results obtained using a pulse input signal, the gains of Table 7 and a selected $\kappa = -2.99$.

Fig. 7

Pulse input response $\kappa = -2.99$

Results presented in the Figs. 6 and 7 allow to verify that the $\kappa$ gain was tuned considering the mean value in steady state of all model configurations. Therefore, gains were selected based on the frequency, damping and steady-state error around zero.

6 Handling qualities analysis

The closed loop poles of all linear model conditions of Table 3 are represented by the filled squares illustrated in Fig. 8. From this, results can be verified that requested short period damping requirements are reached, in this case greater or equal than 0.7.

Fig. 8

Close loop poles

Figure 9 illustrates the Nichols plots for linear models, where the horizontal and vertical axis of rhomboid represents the phase and gain margin boundaries, respectively. From these, results can be verified that the requirements for gain and phase margin requested in Table 4 are satisfied, that is the phase margin is greater than 45° and gain margin is greater than 10 dB.

Fig. 9

Magnitude versus phase for elevator

Figure 10 illustrates the gain versus frequency response of elevator. This result shows that the crossover frequency for all cases is around 2 radians per second, which is considered appropriate for this design.

Fig. 10

Gain versus frequency for elevator

Figure 11 shows the results for $\gamma$ bandwidth versus $\theta$ bandwidth, where the filled points represent each analyzed case. The limits presented in this figure were obtained from [13] and [21] and they are applicable for a business jet aircraft.

Fig. 11

$\gamma -{\text{bandwidth}}$ versus $\theta -{\text{bandwidth}}$

The results accomplish the requirements for the bandwidth criteria presented in Table 4, because $\theta$-bandwidth is greater than 2 radians by second and the $\gamma$-bandwidth is greater than 0.6 radians by second.

Figure 12 shows the results for phase delay criteria versus $\theta$-bandwidth.

Fig. 12

Phase delay versus $\theta$-bandwidth

The results accomplish the requirements for the criterion presented in Table 4, because $\theta$-bandwidth is greater than 2 radians by second and the phase delay $\tau _{p}$ is lower than 0.09 seconds.

7 Nonlinear simulation results

This section presents the results of nonlinear simulations; two cases are considered, the first one is regulation with and without TDOF controller and the second is tracking to compare with gain schedule technique (with interpolated tables).

7.1 Regulation

Figure 13 shows the longitudinal input of nonlinear simulation until 20 s.

Fig. 13

Longitudinal stick input

The nonlinear simulation results for the aircraft in cruise condition, at altitude = 5000 ft, $V_{\text {CAS}}$ = 142 knots, $x_{\text {cg}}$ = 0.32 and mass = 13,500 Kg, are illustrated in Fig. 14.

Fig. 14

Nonlinear simulation results

From the results, it can be observed and verified that the augmented aircraft response (with TDOF controller) when compared with the non-augmented aircraft (without TDOF controller) does not present oscillations, therefore as waited achieves a significantly better response.

7.2 Tracking

Figure 15 shows the longitudinal input of nonlinear simulation until 20 s. The positive input is given between 3 and 6.5 s; the input has been set equal to 0 between 6 and 20 s.

Fig. 15

Longitudinal stick input

The nonlinear simulation results for the aircraft in take-off condition, at altitude = 2000 ft, $V_{\text {CAS}}$ = 80 knots, $x_{\text {cg}}$ = 0.30 and weight = 14,000 Kg, are illustrated in Fig. 16.

Fig. 16

Comparison results TDOF Vs. Gain Scheduling

From the results, it can be seen that the aircraft with TDOF controller presents a faster response to reach 12.5° of $\theta$ when compared with the gain schedule controller (interpolated gain tables are illustrated in the Fig. 17).

Fig. 17

Gain scheduling breakpoints

8 Conclusions

This paper presents the project of Stability and Control Augmentation System with two TDOF controller. To design the controller, LQR technique in the frequency domain, via spectral factorization, is used and handling qualities requirements are included in the design criteria.

The design uses a linear model. The weighting factors $\rho$ and $\sigma$ were selected using the root-square locus. The gain $\kappa$ was tuned considering zero steady error for a pulse input response. The handling qualities analysis was performed to guarantee compliance with certification authority’s requests.

The robustness to uncertainties was verified considering the controller at models with different configuration of mass, center of gravity and airspeed. Also, simulation with nonlinear model was performed showing the performance of TDOF controller in regulation and tracking maneuvers.

The design of TDOF controller was demonstrated to be a straightforward approach. Moreover, it represents an practical alternative solution to gain schedule technique. In this case, it is possible to use a unique fixed structure instead of interpolated tables. From the point view of certification, it can be asserted that verification process would be simplified using this project.