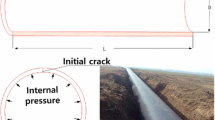
Abstract
Detonation-driven fracture problems in tube under dynamic load have received plenty of attention because of various ranges of applications, such as oil and gas pipeline systems, new rocket engine such as pulse detonation engine, and pressurized aircraft fuselages. This paper reports the crack growth modeling in a thin aluminum tube under gaseous detonation load. Because of three-dimensional fracture dynamics with gas dynamics coupled phenomena, analytical modeling is complicated. Thus, a finite element method was applied. The finite element modeling and simulation of the tube under detonation moving load were performed using commercial code Abaqus. This simulation leads to obtain structural response of the tube to detonation load. The simulations were compared with experimental and analytical results from the literature for elasto-dynamic response of cylindrical shells with finite length under internal detonation loading. Cohesive element with traction–separation law was used for crack growth modeling along with crack tip opening displacement value obtained from experimental–numerical analysis from previous research. The final section of the paper is dedicated to investigating differences and comparisons between the numerical crack propagation simulations and experimental results reported in the literature. It has been demonstrated that using cohesive elements with some modifications can improve the numerical accuracy. The obtained results are more similar to the experimental results than numerical results available in literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nowadays, cylindrical tubes are used in various applications, such as oil/gas/water transportation systems, aviation industries, power generation, and in a variation form of internal moving load it can be addressed in the blood vessel system. In these cylindrical structures, cracks are most likely to occur along the axial direction, and they can produce serious fault in the serviceability of the structures. By referring to the literature on fracture mechanics problems dealing with tubes, we can see that most of them deal with either quasi-static or fatigue loading [1]. Detonation-driven tube fracture is distinguished from quasi-statically loaded tube fracture for two main reasons. First, the flexural waves caused by traveling loads can result in oscillatory strains whose amplitudes are dependent on the speed of the traveling load and can be several times higher than those predicted by static formulas. Second, dynamical fracture parameters can be quite different from equivalent static forms [2]. Loading simulation is the first part of studying detonation-driven fracture in tube which we can find several studies concerning the structural response of tubes to shock or detonation loading [e.g., 3–9]. However, these studies did not involve a fracture mechanics approach because they did not consider pre-flaws and cracks.
Cirak et al. [10] performed large-scale fluid–structure interaction simulation of viscoplastic deformation and fracturing of the experimental aluminum tube of Chao and Shepherd [2]. Their results showed some inconsistencies with the experiments, particularly with respect to the crack growth magnitude, speed (2–3 times higher than experimental), and premature cracking of the flap edges [11]. Mirzaei and Karimi carried out finite element (FE) simulations of detonation-driven fracture of a thin aluminum tube using the crack tip opening angle (CTOA) [12] and compared the results with the experimental work of Chao and Shepherd [1]. Mirzaei [13] analyzes an accidental explosion of gas cylinder containing hydrogen. Then, Mirzaei et al. [14] carried out FE simulation of this accident. They reported that the self-similar growth of the initial axial crack in the main body of the cylinder was a fatigue-type incremental growth governed by the structural waves.
A method for the prediction of dynamic crack propagation in shells with explicit FE methods was developed by Song and Belytschko [15]. Detonation-driven dynamic fracture of thin-walled shells was modeled using FE simulation by Gato and Gato and Shie [16, 17], and Gato [18] simulated the same problem using meshfree method. Mirzaei et al. [19] presented an analysis and simulation of the catastrophic failure of a compressed natural gas fuel tank. These are recent studies in this area.
The contribution of the current study is to provide numerical simulations for detonation-driven fracture of a thin aluminum tube and compare the results with the experimental results of [1]. The modeling of this study was carried out using the capabilities of the commercial code Abaqus. In the previous investigations, fracture energy parameter was computed by static plain strain fracture toughness while detonation load is a phenomenon that requires dynamic parameters. For this purpose, a dynamic CTOA value seems better approximation of crack growth under internal gaseous detonation. For this purpose, the simulation was performed based on dynamic CTOA obtained by Mirzaei and Karimi [12]. This paper is organized as follows: Sect. 2 gives a description of gaseous detonation load, its characteristics and results of tube response to internal moving load; the crack growth simulation using cohesive elements, crack retardation and arresting and crack branching are discussed in Sect. 3, and in Sect. 4 final remarks and a conclusion are presented.
2 Moving load simulation
Leading shock and a reaction zone are elements of a gaseous detonation wave. The gaseous detonation shock provides the thermodynamic conditions for the reaction zone, and the reaction zone releases energy to support the shock wave. Detonation propagation diagram in a tube with a closed end is shown in Fig. 1.
Detonation propagation in tube with a closed end [8]
The pressure history for this type of loading can be represented by an exponential approximation to the Taylor–Zeldovich model as follows [20]:
In the above equation, P 1 is the initial pressure of the gas mixture, P 2 is the peak pressure, P 3 is the final pressure, T is the exponential decay factor, V cj is the Chapman–Jouguet (CJ) velocity, P atm is the atmospheric pressure, x is the distance variable, t is the time variable, and H is the step function.
Structural response of tube to detonation loading was carried out with the Abaqus/explicit code [21]. To calculate the structural response to an internal moving pressure load, an elasto-dynamic calculation was carried out. For the tube 2 as shown in Fig. 2, the half-model consisted of 31,500 eight-node brick elements. The element distribution in the radial, longitudinal, and circumferential directions is 3, 350, and 30, respectively. Boundary conditions of the problem can be treated as simple-support which once used in Sect. 2 [9]. The material and geometrical properties of the aluminum 6061-T6 tube are given in Table 1.
Tube assembly schematic for detonation experiment [18]
The FE simulation and modeling of the moving load with the required profile are carried out with Abaqus using a VDLOAD user-writing subroutine. The VDLOAD subroutine parameters include CJ speed, initial pressure, maximum pressure, final pressure and exponential decay factor with the values of 2365 m/s, 0.0 MPa, 2.6 MPa, 0.5 MPa, and 0.15 ms, respectively. Figure 3 shows the comparison between the experimental [1], analytical [9], and numerical hoop strain history results for a point at distance 0.2822 m from the entrance of the tube.
The result of the FE simulation and the analytic solution are obtained for a duration which includes the initial detonation loading and the subsequent reflections of the flexural waves at the flanges. If one detonation with speed V travels tube with length L in t second(s), simulation time was considered about 3t. In general, there is a good agreement between these results up to 4.24 ms which corresponds to the traveling of one detonation load duration.
3 Crack propagation modeling
Figure 4 shows the geometry of the model and the FE mesh. Instead of modeling an axially oriented notch, shaped as a semi elliptical surface crack which was used by [1], a through thickness crack offered by [22] with the length of 8.115 mm was used in this study. The original semi-elliptical surface crack was 35.2 mm long and 0.64 mm deep within a 0.89-mm wall thickness, which can cause severe problems with regard to the shape and aspect ratios of the elements.
The following subsections present detailed analyses of the crack growth in thin-walled tube.
3.1 Cohesive element methodology for crack propagation simulation
It is necessary to consider more than one parameter for simulation of problems dealing with ductile crack growth, because a single-parameter treatment of cracked structures may not converge to accurate results. Thus, we need to use either two-parameter fracture mechanics model, or referring to other solutions based on damage mechanics models [22, 23]. In this regard, cohesive zone (CZ) modeling has been used in this research which is based on the concept that the crack tip stresses cannot be infinite. Thus, the damage law is represented by the so-called Traction–separation (T–S) law (Fig. 5) which is an energy criterion. This law represents the constitutive behavior of the cohesive elements. This element has three parameters: the cohesive energy G c, the cohesive strength σ c and the critical separation δ c in which the last two parameters are independent, and the cohesive energy can be extracted from them. The cohesive strength and the critical separation can be determined with either experimental tests or previous numerically established results. In the current work, a 3D CZ model has been developed to simulate crack propagation under detonation load. The CZ method has already been implemented in Abaqus commercial code to simulate crack initiation and propagation.
In general, the cohesive elements have two surfaces which connect the faces of two adjacent solid elements with generally initial zero thickness (see Fig. 6). When the energy release rate reaches the critical value G c , the crack starts to propagate. As said before, constitutive equation is used to relate the traction to the relative displacement at the cohesive surfaces.
The cohesive strength is selected as: \(\sigma_{\text{c}} = 2\sigma_{\text{ys}}\) using the procedure outlined by Li and Siegmund [24] and Cirak et al. [10], where \(\sigma_{\text{ys}}\) is the yield strength of the bulk material. The value of G c is obtained from dynamic critical CTOA as reported in [12]. Modeling approaches based on macroscopic levels of deformation, such as the CTOA, appear to provide a viable growth criterion for thin materials. The critical CTOA is calculated from the critical crack tip opening displacement (CTOD) by:
where x is the distance from crack front, wherein CTOA and CTOD are calculated. Mirzaei and Karimi [25] carried out a WARP3D simulation for determination of critical CTOA. The distance parameter L c is 0.763 mm [x in Eq. (2)]. The critical CTOA obtained from this simulation is 4.61°. Thus, using
The computed value of the critical cohesive fracture energy based on critical CTOA is 16,953 j/m2.
To have accurate results of crack modeling using the CZ model, a minimum number of elements are required to simulate properly the variations within the CZ [26]. Hillerborg et al. [27] proposed a model to estimate the CZ length which is
where E is the Young’s modulus of the material. Therefore, eight elements over the CZ length are used in this model to be able to fully resolve the variations within this zone.
3.2 FE simulation results and discussion
3.2.1 Simulation with fixed cohesive fracture energy
In this section, different models with initial crack rather than those presented in Sect. 2 are created. Simulation is carried out with detonation loading parameters according to Table 2. The detonation load will propagate along tube until it reaches end of the tube. Boundary conditions of the problem can be treated as simple-support as Sect. 2. A through-thickness crack with 8.115 mm length is considered in the middle of the tube. This model contained 95,040 eight-node brick element and the simulation time is set to fully cover the traveling load as well as two reflections. The cohesive elements are inserted between solid elements along crack path and in circumferential direction to capture crack curving and branching. The material and geometrical properties of the tube are given in Table 1.
The value of the critical cohesive fracture energy was considered to be equal to 16,953 j/m2. Results of this simulation are depicted in Fig. 7 which f and b refer to forward and backward crack tips, respectively.
The simulations presented in Fig. 7 seem to be expressive of a number of actual propagation characteristics including flap bulging. It can be seen that propagation of crack front tip is more than the back tip. This phenomenon is due to the pressure difference between two sides of the crack so that they experienced higher pressure at most time of load traveling. This phenomenon, however, is not true at two different time(s). First time is when the detonation wave just arrived to the crack tip (at 0.127 ms) where the pressure distribution inside the tube is similar to Fig. 8. As can be seen, back tip has higher pressure while the crack growth is not started yet. In this case, once crack start to growth, the back tip will have lower pressure than the front tip. The second time occurs when the detonation load travels tube completely and pressure within the tube has reached its final value, P 3. After this, both crack tips will have approximately same growth rate because they are experiencing same level of pressure.
On the other hand, there is one major inconsistency between the FE simulation results of Fig. 7 and the actual crack growth features which is the crack speed of simulation is two times the actual average crack speed during the self-similar growth. The reason is that this simulation was done without considering the retardation effects of cyclic crack growth [14]. This problem has been solved in the following section.
Figure 9 shows crack growth with constant critical cohesive fracture energy. Both growth value and growth speed (slope of the graph) of the crack front tip are higher than the back tip. Crack growth speed for front tip is 576.9 m/s and for back tip is 481.33 m/s, both of which are two times higher than experimentally reported in [1].
3.2.2 Retardation effects simulation of cyclic crack growth
Based on results reported in [14], a cycle-by-cycle FE simulation of crack closure seems the best choice that could lead simulation results to be similar to the experimental. Therefore, the modeling of fatigue crack closure characteristics should be considered. To precise FE modeling of fatigue crack closure phenomenon, it is necessary to define contact between the elements and use of small scale element size leading to high computational cost. It seems that the best way to simulate fatigue crack closure is applying the critical work of traction–separation at every stage for forward and backward sides to achieve similar rate of crack growth to the actual one. The ranges of the critical cohesive fracture energy that provided the best agreement between the simulations and the actual growth increments were 16,593–53,900 and 16,953–59,852 j/m2 for the backward and forward directions, respectively, which handled with Abaqus using a VUSDFLD user-written subroutine. The Abaqus calls this subroutine at all integration points of elements which have material properties defined using the field variables. Stresses and strains are calculated at each incremental load step, which in the case of explicit analysis is automatically calculated by Abaqus, and evaluated by the failure criteria to determine the occurrence of crack propagation and failure and the mode of failure. Figure 10 shows snapshots of crack growth simulation results with retardation at different time intervals.
In practice, the incorporation of closure affects the overall crack speed, thus the crack experiences a relatively higher number of cycles to propagate to a certain length.
Figure 11 shows forward and backward crack growth with retardation. Average crack growth speed in front tip and back tip is 254.9 and 174.29 m/s, respectively. It is noteworthy that the rate of crack growth with retardation is the same as those experimentally reported in [1].
3.2.3 Crack branching simulation
One of the important aspects of detonation-driven fracture is the cyclic bulging of the crack flaps [1]. This phenomenon is caused due to the vibrational motion state of points over the crack surfaces. Detonation load produces transverse waves which remained even after detonation disappearance. These transverse waves produce radial and vibrational motion everywhere that result in vibrational strain in circumferential direction and extends bulged area. As a result of bulged area extension, large tensile stresses can progress in this region in the longitudinal direction of the tube. Since cracks usually have a tendency to propagate perpendicular to the maximum value of principal stress directions, the initial self-similar crack propagation changes into a circumferential crack propagation by curving around the bulged region. Due to symmetry, if the energy release rate of the crack is high enough to support two crack fronts, then the occurrence of branching at this point is also possible.
Crack grows too fast in the circumferential direction after branching, but this growth is not cyclic. It is important to note that the initial self-similar growth which was in the pure mode I—opening fracture mode—in the beginning, turning to a mixture of modes I and III at this time. During the crack growth in the initial self-similar surface, the mode III—tearing or out-of-plane fracture mode—effect is negligible and mode I absolutely dominant. After crack curving and branching, shear component of cohesive elements of the front crack tip began to increase rapidly, which demonstrates that the increasing effect of mode III is a rapid, although mode I is dominant. Appearance of mode III crack growth is due to bulged area tendency to bend after crack curving and branching. This willingness to bend the finite element model in order to leave enough of the environment is shown. Figure 12 shows the FE simulation of the flap bulging, tendency to bending, and the resultant crack branching.
4 Conclusion remarks
In this paper, a three-dimensional FE simulation of crack propagation in thin-walled cylinder using cohesive element methodology was presented. The key motivation for this study was the modeling of the detonation response of an aluminum tube. FE simulation results show that every detonation load would cause a spectrum of displacement and thus strain and stress fluctuations in the tube wall. These strains and stresses can be further gradually amplified by the interference between the forward traveling waves and the waves reflected due to flanges. The following conclusion remarks were drawn from the present investigation:
-
1.
Due to the dynamic effects of the high speed load, the resultant displacement fields are oscillatory. Thus, a pattern of circumferential and vibrational strains is produced. These strains are observed even after disappearance of detonation load.
-
2.
Permanent bulging of the fracture surfaces is detectable in FE simulations. This phenomenon is due to changes of the fracture surface point location in the presence of bending waves. The bulged area has increased as a result of crack length increase. Thus, it is produced tensile stress in the axial direction.
-
3.
Cohesive zone model for crack growth analysis is accurate, distinguishing from other methods, and suitable for the simulation of complex phenomena such as detonation-driven fracture because of its unique capabilities such as the ability to simulate crack growth in a direction other than the self-similar plane. However, this method has its own high sensitivity to the cohesive elements parameters which must be chosen very carefully because it may converge to inaccurate results with not well-sited parameters. Also, cohesive element implemented in Abaqus has some limitations for use. For example, tube model needs many cohesive elements with very small geometry to capture a good crack curving angle. On the other side, high number of cohesive elements may lead to increase in computational time.
-
4.
Realistic prediction of the crack growth for cylindrical tubes subjected to internal moving load such as detonation requires the consideration of special method like retardation and closure effects that help simulation to be more similar to actual crack growth. Cyclic crack growth during the self-similar propagation of the mode I and cyclic bulging of the crack flaps are two important phenomena as reported in previous work, and simulated in this investigation. Crack closure phenomenon in every stage of the self-similar fatigue growth has a significant effect on crack growth rate.
-
5.
Experimental reports on detonation fracture and failure are very limited because it’s a high cost test and may lead to explosion, if the equipments are not well installed. In those limited cases, the crack growth rate has more attention than the nature and characteristics of cracks. Therefore, further experimental studies and coupled-solid–fluid analysis are needed in this regard. Good understanding about the nature of fluid–structure interaction phenomena such as shock and detonation is an appropriate way in to get closer simulation results to the experimental one.
Abbreviations
- CJ:
-
Chapman–Jouguet
- CTOA:
-
Crack tip opening angle
- CTOD:
-
Crack tip opening distance
- CZ:
-
Cohesive zone
- FE:
-
Finite element
- T–S:
-
Traction–separation
References
Chao TW (2004) Gaseous detonation-driven fracture of tubes, Dissertation, California Institute of Technology
Chao TW, Shepherd JE (2005) Fracture response of externally flawed aluminum cylindrical shells under internal gaseous detonation loading. Int J Frac 134(2):59–90. doi:10.1007/s10704-005-5462-x
Tang S (1965) Dynamic response of a tube under moving pressure. Proc Am Soc Civil Eng 5:97–122
Reismann H (1965) Response of a pre-stressed cylindrical shell to moving pressure load. In: Ostrach S, Scalon RH (eds) Eighth Midwest Mechanics Conference, pp 349–363
de Malherbe MC, Wing RD, Laderman AJ, Oppenheim AK (1966) Response of a cylindrical shell to internal blast loading. J Mech Eng Sci 8:91–98. doi:10.1243/JMES_JOUR_1966_008_012_02
Simkins TE (1987) Resonance of flexural waves in gun tubes. Technical Report ARCCBTR-87008, US Army Armament Research
Thomas GO (2002) The response of pipes and supports to internal pressure loads generated by gaseous detonations. J Press Vessel Technol 124:66–73. doi:10.1115/1.1427342
Beltman WM, Burcsu EN, Shepherd JE, Zuhal L (1999) The structural response of cylindrical shells to internal shock loading. J Press Vessel Technol 121:315–322. doi:10.1115/1.2883709
Mirzaei M, Mazaheri K, Biglari H (2005) Analytical modeling of the elastic structural response of tubes to internal detonation loading. Int J Press Vessel Pip 82(12):883–895. doi:10.1016/j.ijpvp.2005.07.008
Cirak F, Deiterding R, Mauch SP (2006) Large-scale fluid–structure interaction simulation of viscoplastic and fracturing thin-shells subjected to shocks and detonations. Comput & Struct 85:1049–1065. doi:10.1016/j.compstruc.2006.11.014
Deiterding R, Cirak F, Meiron D (2006) Computational results for the fracturing tube validation experiment. ASCI/ASAP Research review Caltech. http://www.cacr.caltech.edu/asc/wiki/pub/FracturingTube/WebHome/DetFracSim.ppt
Mirzaei M, Karimi R (2006) Crack growth analysis for a cylindrical shell under dynamic loading. In: Proceedings of ASME PVP 2006/11th international conference on pressure vessel technology, ICPVT-11, July 23–27, Vancouver, BC, Canada. doi:10.1115/PVP2006-ICPVT-11-94041
Mirzaei M (2008) Failure analysis of an exploded gas cylinder. Eng Fail Anal 15(7):820–834. doi:10.1016/j.engfailanal.2007.11.005
Mirzaei M, Harandi A, Karimi R (2009) Finite element analysis of deformation and fracture of an exploded gas cylinder. Eng Fail Anal 16(5):1607–1615. doi:10.1016/j.engfailanal.2008.10.018
Song JH, Belytschko T (2009) Dynamic fracture of shells subjected to impulsive loads. J App Mech 76(5). doi: 10.1115/1.3129711
Gato C (2010) Detonation-driven fracture in thin shell structures: numerical studies. App Math Mod 34:3741–3753. doi:10.1016/j.apm.2010.02.011
Gato C, Shie Y (2010) Detonation-driven fracture in thin shell structures: numerical studies. Combust Explos Shock Waves 46:103–110. doi:10.1007/s10573-010-0017-5
Gato C (2010) Meshfree analysis of dynamic fracture in thin-walled structures. Thin-Walled Struct 48:215–222. doi:10.1016/j.tws.2009.10.011
Mirzaei M, Malekan M, Sheibani E (2013) Failure analysis and finite element simulation of deformation and fracture of an exploded CNG fuel tank. Eng Fail Anal 30:91–98. doi:10.1016/j.engfailanal.2013.01.015
Beltman W.M, Shepherd J.E (1998) The structural response of tubes to detonation and shock loading, Parts I and II, Technical Report FM98-3, California Institute of Technology
ABAQUS User’s manual V6.10-1, Dassault Systems 2004–2010
Anderson TL (1995) Fracture mechanics, fundamentals and applications. CRC Press, Boca Raton
Cornec A, Scheider I, Schwalbe KH (2003) On the practical application of the cohesive model. Eng Fract Mech 70:1963–1987. doi:10.1016/S0013-7944(03)00134-6
Li W, Siegmund T (2002) An analysis of crack growth in thin-sheet metal via a cohesive zone model. Eng Fract Mech 69:2073–2093. doi:10.1016/S0013-7944(02)00013-9
Mirzaei M (2010) Finite element analysis of deformation and fracture of cylindrical tubes under internal moving pressures. In: Moratal D (ed) Finite element analysis. Sciyo, Croatia. doi:10.5772/58224
Falk ML, Needleman A, Rice JR (2001) A critical evaluation of cohesive zone models of dynamic fracture. J Phys IV Proc 543–550. doi:10.1051/jp4%3A2001506
Hillerborg A, Modeer M, Petersson PE (1976) Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem Concr Res 6:773–782
Acknowledgments
I thank Prof. Mirzaei for his comprehensive and valuable guidance as my supervisor during M.Sc. period. The author also gratefully acknowledge the important support of the Computational Fracture Mechanics laboratory of Tarbiat Modares University, Tehran-Iran.
Author information
Authors and Affiliations
Corresponding author
Additional information
Technical Editor: Lavinia Maria Sanabio Alves Borges.
Rights and permissions
About this article
Cite this article
Malekan, M. Finite element simulation of gaseous detonation-driven fracture in thin aluminum tube using cohesive element. J Braz. Soc. Mech. Sci. Eng. 38, 989–997 (2016). https://doi.org/10.1007/s40430-014-0270-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40430-014-0270-8