1 Introduction

Assessment the effects of site conditions on its seismic response is important to perform precise and realistic analysis of structures that are built on or around the site. These effects are generally divided into two categories: effects of local deposits and those of topography. In this regard, the effect of topographic irregularities on ground motions is of great importance. Recent studies have indicated that topographic irregularities (e.g., mountain ridges or valley notches) have caused significant changes to strong ground motions during earthquakes. Investigations on many earthquakes occurred in the past also indicated the effect of surface topographic changes on ground response. The September 19, 1985 Michoacan earthquake (Ms = 8.1) only resulted in moderate damages around the epicenter (near the Pacific coast of Mexico). However, it caused extensive damages to a site located as far as 350 km away from Mexico City (Kramer 1996). Another example of the effects of topography was seen in records taken by a seismograph installed on the piers of the Pacoima dam in southern California. The seismograph recorded horizontal peak accelerations as high as 1.25 g in both directions during the 1971 San Fernando earthquake (ML = 6.4). These values recorded by this seismograph were significantly larger than those expected for an earthquake of such magnitude (Kramer 1996). Other evidences of topographic effects are also available in Alaska 1964 (Idriss 1968), Canal Beagle Chile 1985 (Celebi 1991), Northridge 1994 (Bouchon and Barker 1996), and Athens 1999 (Gazetas et al. 2002). The significance of local site effects is shown by the fact that earthquake causes vast damages to some certain regions and only slight damages to others.

Seismic ground response problems can be performed by one-dimensional analysis in some simple cases such as parallel soil layers, horizontal bedrock and etc. (e.g., Groholski et al. 2016; Kaklamanos et al. 2015). In other cases such as irregular topography, buried structures, inclined soil layers or bedrock, two- or even three-dimensional analyses are required to evaluate the effects of these conditions on seismic site response (e.g., Chen et al. 2015; Soltani and bagheripour 2017, 2018; Raptakis et al. 2005; Sadeghi-Farshbaf et al. 2019). Based on the domain of analyses, these methods can be done using time- or frequency-domain approaches. In time-domain studies, the equation of motion is solved using step by step integration in small time intervals to evaluate nonlinear behavior of the soil layers during earthquakes (e.g., Alielahi et al. 2013; Liang et al. 2017). In frequency-domain methods the equation of motion is transferred to frequency domain and the nonlinear behavior of the soil is estimated using equivalent linear properties (e.g., Deng and Ostadan 2008; Soltani and Bagheripour 2020). Considering the importance of analyzing ground response problems during earthquakes, many researchers have tried to develop or optimize these methods (e.g., Gribovszki and Vaccari 2004; Javdanian and Pradhan 2019; Suhadolc et al. 2004; Dhanya et al. 2017; Biswas et al. 2018; Bazrafshan Moghaddam and Bagheripour 2011).

In this study the ground response of different sites is evaluated during an earthquake using two-dimensional analysis in Plaxis software. To focus on seismic response of irregular topographies, free field condition, single valley and double valleys are considered and the interaction of two adjacent valleys are investigated.

2 The numerical method

There are several methods to simulate ground response problems (e.g., Finite Element Method (FEM), Finite Difference Method (FDM), and Boundary Element Method (BEM)). Meanwhile, the FEM is one of the most popular and widely used methods due to its capabilities. Nevertheless, accurate simulation of boundary conditions is of great importance for this concept which is discussed in the following sections. In order to understand the principles and formulations associated with FEM, readers are referred to (Desai and Kundu 2001).

Based on FEM formulation, the domain of the analysis under dynamic load can be simulated using equation of motion which can be written as follows (Kramer 1996):

$$ M\ddot{u} + C\dot{u} + Ku = f $$
(1)

In Eq. (1), M, C and K are mass, damping, and stiffness matrices, respectively. Also \( u \) is introduced to evaluate the displacement of each node in the domain and then, \( \dot{u} \) and \( \ddot{u} \) are velocity and acceleration of the nodes, respectively. Finally f shows the force vector which applied to the model.

Generally to evaluate the mass matrix, consistent or lumped mass matrices could be used. In the consistent mass matrix, the same interpolation function is adopted to develop it. On the other hand, in the lumped one, which is a diagonal matrix, a simpler interpolation function is used. In general and regarding the accuracy of these two types of mass matrices, one can say, the lumped matrix provides more accurate results and the process of the analysis is shorter. Therefore, the lumped matrix is generally superior to the consistent type in calculations (Yoshida 2015). In Plaxis software the mass matrix considered as a lumped matrix.

Time integration schemes can be categorized into explicit and implicit approaches. Despite some limitations, explicit scheme is relatively simple to formulate. Implicit schemes is rather complicated, however, the process of calculation is more trustworthy and accurate. Among implicit schemes, Newmark method is often adopted which is used in Plaxis software (Bringkgreve and Vermeer 1998).

In this study in order to solve the equation of motion in time-domain, displacement and velocity in time \( t + \Delta t \) can be derived as follows using Newmark method (Bringkgreve and Vermeer 1998):

$$ u^{t + \Delta t} = u^{t} + \dot{u}^{t} \Delta t + ((1/2 - a)\ddot{u}^{t} + a\ddot{u}^{t + \Delta t} )\Delta t^{2} $$
(2-a)
$$ \dot{u}^{t + \Delta t} = \dot{u}^{t} + ((1 - b)\ddot{u}^{t} + b\ddot{u}^{t + \Delta t} )\Delta t $$
(2-b)
$$ u^{t + \Delta t} = u^{t} + \Delta u $$
(2-c)

In the above equations, \( \Delta t \) is time step and coefficients a and b determine the accuracy of the numerical time integration. The applicable range for a and b to ensure a stable solution is as follows:

$$ b \ge 0.5 $$
(3-a)
$$ a \ge {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}(0.5 + b)^{2} $$
(3-b)

However, common value as a = 0.3025 and b = 0.60 are adopted here (Bringkgreve and Vermeer 1998).

Equation (2) can also be rewritten as:

$$ \ddot{u}^{t + \Delta t} = \lambda_{0} \Delta u - \lambda_{2} \dot{u}^{t} - \lambda_{3} \ddot{u}^{t} $$
(4-a)
$$ \dot{u}^{t + \Delta t} = \dot{u}^{t} + \lambda_{6} \ddot{u}^{t} + \lambda_{7} \ddot{u}^{t + \Delta t} ,\;{\text{or}} $$
(4-b)
$$ \ddot{u}^{t + \Delta t} = \lambda_{0} \Delta u - \lambda_{2} \dot{u}^{t} - \lambda_{3} \ddot{u}^{t} $$
(5-a)
$$ \dot{u}^{t + \Delta t} = \lambda_{1} \Delta u - \lambda_{4} \dot{u}^{t} - \lambda_{5} \ddot{u}^{t} $$
(5-b)

in which the coefficients λ0 to λ7 were introduced in the time step and in a and b integration coefficients.

Using the implicit scheme, Eq. (1) at \( t + \Delta t \) is written generally as follows:

$$ M\ddot{u}^{t + \Delta t} + C\dot{u}^{t + \Delta t} + Ku^{t + \Delta t} = f^{t + \Delta t} $$
(6)

Using Eqs. (4) to (6) and further mathematical operations and then simplification, one can obtain:

$$ (\lambda_{0} M + \lambda_{1} C + K)\Delta u = f_{ext}^{t + \Delta t} + M(\lambda_{2} \dot{u}^{t} + \lambda_{3} \ddot{u}^{t} ) + C(\lambda_{4} \dot{u}^{t} + \lambda_{5} \ddot{u}^{t} ) - f_{\text{int}}^{t} $$
(7)

According to Eq. (7), Δu can be obtained and added to earlier displacement (ut) to evaluate the ground response during an earthquake.

2.1 Viscous boundaries

In ground response analyses, accurate simulation of boundary conditions and radial attenuation of wave energy is of particular importance. Application of boundaries with any constrain may lead to so called “trap box” effect for seismic waves in the model and hence to fictitious results. For dynamic analysis, however, boundaries have to be placed far enough and farther than to be the boundaries in static analysis. Further, introduction of boundaries at far distance virtually means large mesh required in FE model with excessive elements which entails also extra calculation time and core memory. As the size of the divisions decreases, the influence of boundary conditions becomes a prime concern. Using large elements in simulated model, filter high-frequency components of the response because of short wave length of these components. Based on the previous investigations, the maximum size of each element should be less than 1/10th to 1/8th of the wave length related to the highest frequency content of the incident load (Bringkgreve and Vermeer 1998).

When viscous boundaries are applied, equivalent dampers are used instead of commonly used boundary constraints. Such equivalent dampers absorb stresses induced to the boundary. It further means that such dampers act when stress waves are travelling outward the domain. Components of absorbed normal and shear stress are defined as follows when an equivalent dampers is introduced in x direction.

$$ \sigma_{n} = \, {-}c_{1} \rho v_{p} \dot{u}_{x} $$
(8-a)
$$ \tau = \, {-}c_{2} \rho v_{s} \dot{u}_{y} $$
(8-b)

In the above equations, \( \rho \) is the density of materials, vp and vs are respectively the velocity of the compressional and shear waves, while c1 and c2 are relaxation coefficients that are applied to the model to enhance the performance of the viscous boundaries. The interesting point is that if incident compressional waves reach the model’s vertical boundaries, c1 and c2 coefficients are reduced to unity (c1 =  c2 = 1). However, in presence of shear waves, the damping effect of viscous boundaries would not be adequate if coefficients c1 and c2 are neglected. In fact, the effect of these boundaries is increased directly with the increase in c2 value. Recent studies have shown that application of c1 = 1 and c2 = 0.25 would optimize the absorbing effect of these boundaries (Bringkgreve and Vermeer 1998). Fundamental formulation of these viscous boundaries is based on the procedure described in (Lysmer and Kuhlemeyer 1969).

3 Problem definition

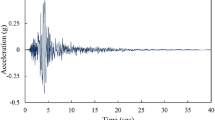
Although less attention has been paid to evaluate the seismic response of empty valleys compared with other irregularities, they have a significant effect on changing the nature of seismic waves. These types of valleys have importance in theoretical studies and engineering applications since may have large numbers of inhabitants due to various life resources. In addition some of the important structures like dams, bridges and briefly many infrastructures have been built in these types of valleys. To evaluate the amplification of topography and soil layer, a two-dimensional model is considered using Plaxis which is one of the most powerful and applicable software to simulate infinite or semi-infinite soil and rock medium. Soil layer is assumed overlain rigid bedrock and seismic excitation adopted is an acceleration time history of Tabas earthquake (1978) which is induced to the bottom of the model (Fig. 1, Table 1). Response is investigated at the ground level at three points for the effect of soil layer and topographic irregularities on amplification or attenuation of seismic waves.

Fig. 1
figure 1

a Acceleration time history; and b Fourier amplitude of Tabas earthquake (1978)

Full size image
Table 1 The earthquake used in this study
Full size table

In this study, the bottom boundary of the considered domain is fixed in two directions to model the rigid bedrock. Also, lateral boundaries are limited in the vertical and held open in the horizontal directions to simulate a semi-infinite environment.

The accuracy of the model has shown in (Soltani and Bagheripour 2017) using the results obtained from the current method with those of FE-IFE (Finite-Infinite Element) method including non-dimensional diagrams for horizontal and vertical displacement amplitude, through the valley span and its surrounding area. Comparison of the results of two methods confirms the proper performance of the coupled FEM and viscous boundaries in simulating infinite and semi-infinite environments.

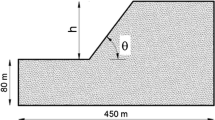
In this study a valley environment is adopted as shown in Fig. 2. Each valley considered symmetric whose maximum depth is h and adopted to constant value as 100 m. L and l are half of the top and bottom span of the valley and adopted to fixed values as 100 m and 50 m, respectively. Also d refers to center to the center distances of the valleys (Fig. 2b) and considered 125 m and 275 m for different cases of double valleys. In this study, more than 10,000 elements applied using mentioned criteria and convergence study. The size of domain of the analysis was also 650 × 200 m.

Fig. 2
figure 2

Configuration of adopted a single valley; and b double valleys

Full size image

It should be noted that, in each specific site, the appropriate size of the mesh domain should be determined based on observing the free filed condition of the nodes near the vertical boundaries. In other words, the criteria of appropriate mesh domain is achieving the similar behavior of the nodes near the vertical boundaries compared with the nodes in actual free field semi-infinite media.

To evaluate the effect of topography in its surrounding area, three points are selected, point A is at the bottom and center of the valley and points B and C are at 100 m and 200 m off the valley center, respectively (Fig. 2a and b). The characteristics of the soil layer are assumed as Table 2.

Table 2 Characteristics of the soil layer considered in this study
Full size table

4 Results and discussion

In order to evaluate the effect of adjacent valleys, the results on the ground surface are shown by the acceleration time history as well as acceleration response spectrum and Fourier amplitude spectrum of different points. Table 3, summarized the results of different parameters in considered points. Comparing the results of all cases showed that, in the case of topography the seismic response is amplified significantly. For example, comparison the peak value of spectral acceleration in different points reveals that, with the addition of single irregularity to the model, the response values are greatly amplified. In fact, the irregular topography change the nature of the seismic waves passing through the soil layer. Furthermore, the amplification increases with the addition of the second valley when the interaction effect between irregular topographies becomes apparent. As the valleys moved away from each other, the interaction effect is decreased. It is noteworthy that, at point C, due to its distance from the irregularities, the results obtained are less effective than the interaction between topographies.

Table 3 Comparison of results of different cases at points A, B and C
Full size table

At point A and according to Fig. 3a–c the response at the ground level is completely different for considered cases. In the case of free field condition and single valley, the response has a PGA (Peak Ground Acceleration) of 0.01 g and 0.24 g, respectively. Therefore, there has been considerable amplification in the case of a single valley compared with free field condition. This amplification is related to repeated interference of the waves in the environment due to the irregularity. In the case of double valleys with d = 125 m and d = 275 m, and considering the interaction effect of valleys, the values of PGAs are reaches to 0.77 g and 0.57 g, respectively. Comparison the results in Fig. 3a–c showed that the interactions effect decrease as the two valleys move away and the results approach the single valley state.

Fig. 3
figure 3

Comparison of (a) acceleration time histories; b Fourier amplitude spectra; and c acceleration response spectra (for 5% damping) at point A

Full size image

Figure 3c shows the values of acceleration response spectra obtained from four cases at point A. As can be inferred from this figure, the acceleration response spectra of valleys are amplified compare with free field condition. Also the difference between the cases of single valley and double valleys is attributed to the extent of amplification resulting from interaction of irregular topographies, something that is ignored in one-dimensional analyses. It is also clear that as the valley moves away the interaction effect of double valleys decreases. This reduction can continue until the interaction effect gradually disappear and the results of double valleys with far distance are very close with those of single valley.

At point B, as could be observed in Fig. 4a–c, by moving away from the center of the valley, the response approaches the single valley case and the interaction between valleys decrease. The trend of the results shows that as the valleys move further apart, the response of double valleys become closer to those of single valley. This can be deduced by comparing Figs. 3, 4, and 5.

Fig. 4
figure 4

Comparison of (a) acceleration time histories; b Fourier amplitude spectra; and c acceleration response spectra (for 5% damping) at point B

Full size image
Fig. 5
figure 5

Comparison of (a) acceleration time histories; b Fourier amplitude spectra; and c acceleration response spectra (for 5% damping) at point C

Full size image

In this study, investigations showed that point C is, in fact, an upper limit at which the interaction effect of double valleys is almost vanished (Fig. 5 and Table 3). Complementary investigations also revealed in larger distances (relative to valley center), the same phenomenon is observed. It should be noted that by changing the geometry of the valleys and the frequency content of the incident wave, this distance could be changed. Therefore, dimension of the mesh domain in numerical studies depends on both geometric characteristics and seismic zone of the interested site. To obtain an optimized model size and to reach free field condition, the valley dimension should not be regarded as unique parameter, rather, these dimensions should be normalized with respect to bedrock depth.

Based on the obtained results presented in Figs. 3c, 4c, and 5c, it is revealed that, the maximum amplification has occurred in the low-period content (less than 1 s). It is noteworthy, due to the fact that the use of maximum displacement values, which associated with high-period components, cannot provide the precise analysis, therefore, the acceleration components were used to present the results. On the other hand, in order to study the frequency content of the incident waves to the bedrock and the waves received at the ground surface, the Fourier amplitude spectrum and acceleration response spectrum were shown.

5 Conclusion

In this study a practical model was presented to evaluate the effect of wave scatter in topographical irregularities as well as free field condition. The ground response was evaluated using a realistic model based on FEM coupled with viscous boundaries. The solution was based on fully non-linear soil behavior in time-domain. The time history of Tabas earthquake, (1978), was adopted as an incident wave which was induced to bedrock. The results was obtained at soil surface at three points to evaluate the effect of single valley as well as interaction of double valleys on seismic response of a site. The free field condition was also modelled to comparison.

The results showed that the response of the valley was significantly increased compared with free field condition. Also in the study of the interaction between adjacent valleys, the results showed that as the valleys move away from each other, the interaction effect would be drastically reduced, so, the interaction effect would be almost negligible at sufficient distances. Moving away from the center of the valley, the amplification of the topography decreases, as observed at point A with the highest and at point C with the lowest amplification. Variations of amplification and attenuation were seen inside the valley and around it which is related to surface waves and their interference with incident and reflected waves in two-dimensional model. The variations could have a significant effect on the seismic response of structures constructed in and around the valley. It should be noted that variation on ground response due to topographical effects is an important parameter to select the site location or design of important structures especially those with linear behavior. This study highlights the fact that, when evaluating the response of topographic irregularity, surrounding area must be considered in addition to local topography.