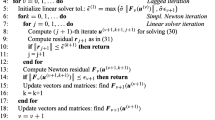Direct versus iterative methods for forward-backward diffusion equations. Numerical comparisons

Abstract

By far, the standard implementation of finite difference schemes for forward–backward partial differential equations consists in employing an iterative method. This paper collects a series of numerical results which demonstrate that a direct implementation can reduce the computing time. An effective way of choosing the seed for the iterative method naturally arises.

1 Introduction

This work has been motivated by reference [11], which proposes a couple of finite difference schemes for solving certain problem of interest to the nuclear engineering community. To specify, the problem is the one defined on $Q = [-1,1]\times [Z_{\mathrm{ini}},Z_{\mathrm{fin}}]$ by the Fokker-Planck equation

$$\begin{aligned} \mu \displaystyle \frac{\partial \psi }{\partial z} + \alpha \psi - \sigma \frac{\partial }{\partial \mu }\left[ D(\mu ) \displaystyle \frac{\partial \psi }{\partial \mu }\right] = W\ \text{ for }\ (\mu ,z) \in Q, \end{aligned}$$

(1)

being $D(\mu ) = 1 - \mu ^2$, and the incoming flux conditions

$$\begin{aligned} \psi (\mu ,Z_{\mathrm{ini}})= & {} f(\mu )\ \text{ for }\ \mu \in (0,1], \end{aligned}$$

(2)

$$\begin{aligned} \psi (\mu ,Z_{\mathrm{fin}})= & {} g(\mu )\ \text{ for }\ \mu \in [-1,0), \end{aligned}$$

(3)

where $\alpha$, $\sigma$ and W are known functions of $(\mu ,z)$ with $\alpha \ge 0$ and $\sigma > 0$, and f and g are known functions of $\mu$.

The following paragraph, excerpted from [11], is intended for those readers interested in theoretical considerations:

“The fact that the $\mu = 0$ extreme is open in conditions (2) and (3) as well as the absence of boundary conditions at $|\mu | = 1$ can be explained by physical considerations [...] From the mathematical viewpoint, there are also analytical reasons that support the well-posedness of Problem (1)–(3) in many particular cases; the interested reader might like to consult references [2, 3, 5, 6, 10, 12], and [13]. In particular, the absence of boundary conditions at $|\mu | = 1$ is related to the degeneracy of the inner diffusion coefficient $1 - \mu ^2$ at $|\mu | = 1$.”

Again in [11] it is explained that the schemes defined therein admit of two different implementations, one of them which is of iterative type and another one which is not, and which we shall refer to as direct. The precise meaning that both concepts, iterative and direct, have in the present context will be clarified in subsequent paragraphs. Then, the direct implementation is chosen, and no comparison with the other approach in terms of computing time is made.

From a general perspective, this equation belongs to the category of the forward-backward or two-way partial differential equations (PDEs). It is remarkable the fact that, before [11], the existing literature on the numerical resolution of this kind of problems by means of finite difference methods has given prominence to propose and analyze iterative algorithms (see [7, 8, 14,15,16]). One can legitimately wonder if this preference was somehow linked to the limited processor’s speed and vector performance which was available some years or decades ago, or perhaps to the degree of complexity of the data functions, to the specific finite difference scheme employed for the discretization, or to the choice of the linear solver. So, it is natural to investigate whether, as a general statement, the iterative approach results in a faster method. The major contribution of this paper is to provide a body of numerical evidence that supports the idea that in fact the direct method is frequently superior, and that, as a consequence, it must not be disregarded when solving the type of problems which are herein treated.

With the aim of illustrating the matter in question, let us consider the simple forward-backward heat equation

$$\begin{aligned} x\displaystyle \frac{\partial u}{\partial t} - \displaystyle \frac{\partial ^2 u}{\partial x^2} = f(x,t),\quad (x,t)\in [-1,1]\times [T_{\mathrm{ini}},T_{\mathrm{fin}}]. \end{aligned}$$

(4)

The PDE (4) is parabolic when $x > 0$ and backward parabolic when $x < 0$. Consequently, leaving apart the necessity of imposing some type of boundary conditions at $|x| = 1$, it demands to split the spatial domain $[-1,1]$ into two parts, (0, 1] and $[-1,0)$, in order to impose an initial condition on (0, 1] and a final condition on $[-1,0)$ (see [16]). From a numerical “finite differences” standpoint, it is clear that this problem cannot be solved with a marching method by means of one single sweep, as it is the case for the heat equation $\frac{\partial u}{\partial t} - \frac{\partial ^2 u}{\partial x^2} = f(x,t)$; indeed, for the equation (4) it is not possible to advance starting at time $t = T_{\mathrm{ini}}$ because the initial condition only holds on (0, 1], and it is not possible either to go back starting at time $t = T_{\mathrm{fin}}$ because the final condition only holds on $[-1,0)$. As said above, the standard treatment is of iterative type, and consists in:

• 1. Providing a seed, that is to say, a guess of the solution on the interface $\{0\}\times [T_{\mathrm{ini}},T_{\mathrm{fin}}]$,

• 2. Solving on $[0,1]\times [T_{\mathrm{ini}},T_{\mathrm{fin}}]$, advancing in time,

• 3. Solving on $[-1,0]\times [T_{\mathrm{ini}},T_{\mathrm{fin}}]$, going back in time,

• 4. Updating the value on the interface, and

• 5. Iterating steps 2, 3 and 4 until convergence is achieved.

It is not being claimed that all kind of forward-backward PDEs can be solved in this way. In fact, there are more complex examples that must viewed from some other perspective (see [1]), but the problem (1)–(3) admits of a similar treatment.

As an alternative to the method above, one has what it is called in this paper the direct approach, consisting in solving the problem simultaneously on the whole time-space domain, treating time t as another spatial variable, as if one were solving, in the elliptic manner, the Dirichlet problem for the Poisson equation in two dimensions.

The principle of the iterative approach is that it is much faster to march in time than to solve on the whole time-space domain by means of the direct approach. In other words, it is much faster to solve N linear square systems of order I than one single linear square system of order $I\times N$. However, since in this case marching in time implies performing iterations, the following question arises: is it possible that the number of iterations caused the iterative method to be slower than the direct method? This is a point of interest that, to our knowledge, has not been explored yet.

This paper focuses on showing that the direct approach is clearly advantageous over the iterative approach when solving the problem (1)–(3) by means of a certain finite difference scheme. The scope of this assertion goes beyond the example studied; we have conducted other numerical experiments which confirm that the direct method must also be seriously considered for solving other forward-backward PDEs by means of other finite difference schemes. To the authors’ knowledge, there is no reference apart from [11] where the direct method, as it is being understood here, be used.

The paper is organized as follows: Sect. 2 establishes some basic hypotheses and notations. Sections 3 and 4 include, respectively, descriptions of the direct and iterative algorithms. Section 5 collects the numerical results and their analysis. Some further explanations are given in Sect. 6, and finally Sect. 7 contains the conclusions.

2 Prefatory comments

It is clear that in Problem (1)–(3) z is the time-like variable and $\mu$ is the space-like one. Then, Eqs. (2) and (3) can be interpreted, respectively, as an initial and a final condition.

In respect of hypotheses on the data functions, we shall assume that

$$\begin{aligned}&\alpha ,\ \sigma \ \text{ and }\ W\ \text{ are } \text{ continuous } \text{ on }\ Q,\ \alpha \ge 0,\ \sigma > 0, \end{aligned}$$

(5)

$$\begin{aligned}&f\ \text{ is } \text{ continuous } \text{ on }\ [0,1],\ g\ \text{ is } \text{ continuous } \text{ on }\ [-1,0]. \end{aligned}$$

(6)

Recall that $Q = [-1,1]\times [Z_{\mathrm{ini}},Z_{\mathrm{fin}}]$.

Let $\{(\mu _i,z_n):\ i\in \{1,\dots ,I\},\ n\in \{1,\dots ,N\}\}$ be a mesh of Q obtained as the Cartesian product of two uniform meshes of $[-1,1]$ and $[Z_{\mathrm{ini}},Z_{\mathrm{fin}}]$, and think of using a finite difference scheme over this mesh. Let $h = \frac{2}{I-1}$ be the distance between $\mu$-nodes and let $k = \frac{{Z_{\mathrm{fin}}}- {Z_{\mathrm{ini}}}}{N-1}$ be the distance between z-nodes.

Among all possible finite difference schemes, we choose the odd scheme described in [11], which is the best option out of the two schemes studied therein. Consequently, I (the number of $\mu$-nodes) is assumed to be odd, and $\mu _{i^\star } = 0$ if $i^\star = \frac{I+1}{2}$.

The following notations will be also employed: $\overline{D}_{i} = D(\mu _i)$, $\overline{D}_{i\pm \frac{1}{2}} = D(\mu _i\pm \frac{h}{2})$; $\overline{\alpha }_{i}^{n} = \alpha (\mu _i,z_n)$, $\overline{\sigma }_{i}^{n} = \sigma (\mu _i,z_n)$, $\overline{W}_{i}^{n} = W(\mu _i,z_n)$; $\overline{f}_{i} = f(\mu _i)$, $\overline{g}_{i} = g(\mu _i)$; $\psi _i^n \approx \psi (\mu _i,z_n)$, understanding that $\psi$ is the exact solution of Problem (1)–(3).

3 Description of the direct algorithm

As said in Sect. 2, the finite difference scheme we choose is the so-called odd scheme of [11], which exhibits order 2 with respect to each of the two variables when the exact solution is regular on the compact set Q. It reads as follows (from Eqs. (7) to (12)):

• For $(i,n) \in \{1\}\times \{1,\dots ,N-1\}$,

  $$\begin{aligned}&\left( -\frac{\mu _1}{k} + \frac{\overline{\alpha }_{1}^{n}}{2} + \frac{\overline{\sigma }_{1}^{n} \overline{D}_{2}}{2 h^2} \right) \psi _1^n + \left( -\frac{\overline{\sigma }_{1}^{n} \overline{D}_{3}}{8 h^2} \right) \psi _2^n \nonumber \\&\quad + \left( -\frac{\overline{\sigma }_{1}^{n} \overline{D}_{2}}{2 h^2} \right) \psi _3^n + \left( \frac{\overline{\sigma }_{1}^{n} \overline{D}_{3}}{8 h^2} \right) \psi _4^n \nonumber \\&\quad + \left( \frac{\mu _1}{k} + \frac{\overline{\alpha }_{1}^{n+1}}{2} + \frac{\overline{\sigma }_{1}^{n+1} \overline{D}_{2}}{2 h^2} \right) \psi _1^{n+1} \nonumber \\&\quad + \left( -\frac{\overline{\sigma }_{1}^{n+1} \overline{D}_{3}}{8 h^2} \right) \psi _2^{n+1} + \left( -\frac{\overline{\sigma }_{1}^{n+1} \overline{D}_{2}}{2 h^2} \right) \psi _3^{n+1} \nonumber \\&\quad + \left( \frac{\overline{\sigma }_{1}^{n+1} \overline{D}_{3}}{8 h^2} \right) \psi _4^{n+1} = \frac{\overline{W}_{1}^{n} + \overline{W}_{1}^{n+1}}{2}. \end{aligned}$$

  (7)

• For $(i,n) \in \left( \{2,\dots ,i^\star - 1\}\cup \{i^\star + 1,\dots ,I-1\}\right) \times \{1,\dots ,N-1\}$,

  $$\begin{aligned}&\left( -\frac{\overline{\sigma }_{i}^{n} \overline{D}_{i-\frac{1}{2}}}{2 h^2} \right) \psi _{i-1}^n \nonumber \\&\quad + \left( -\frac{\mu _i}{k} + \frac{\overline{\alpha }_{i}^{n}}{2} + \frac{\overline{\sigma }_{i}^{n} \left( \overline{D}_{i-\frac{1}{2}} + \overline{D}_{i+\frac{1}{2}}\right) }{2 h^2} \right) \psi _i^n \nonumber \\&\quad + \left( -\frac{\overline{\sigma }_{i}^{n} \overline{D}_{i+\frac{1}{2}}}{2 h^2} \right) \psi _{i+1}^n + \left( -\frac{\overline{\sigma }_{i}^{n+1} \overline{D}_{i-\frac{1}{2}}}{2 h^2} \right) \psi _{i-1}^{n+1} \nonumber \\&\quad + \left( \frac{\mu _i}{k} + \frac{\overline{\alpha }_{i}^{n+1}}{2} + \frac{\overline{\sigma }_{i}^{n+1} \left( \overline{D}_{i-\frac{1}{2}} + \overline{D}_{i+\frac{1}{2}}\right) }{2 h^2} \right) \psi _i^{n+1} \nonumber \\&\quad + \left( -\frac{\overline{\sigma }_{i}^{n+1} \overline{D}_{i+\frac{1}{2}}}{2 h^2} \right) \psi _{i+1}^{n+1} = \frac{\overline{W}_{i}^{n} + \overline{W}_{i}^{n+1}}{2}. \end{aligned}$$

  (8)

• For $(i,n) \in \{i^\star \}\times \{2,\dots ,N-1\}$,

  $$\begin{aligned}&\left( -\frac{\overline{\sigma }_{i^\star }^{n}}{h^2} \right) \psi _{i^\star -1}^n + \left( \overline{\alpha }_{i^\star }^{n} + \frac{2\overline{\sigma }_{i^\star }^{n}}{h^2} \right) \psi _{i^\star }^n + \left( -\frac{\overline{\sigma }_{i^\star }^{n}}{h^2} \right) \psi _{i^\star +1}^n \nonumber \\&\quad = \overline{W}_{i^\star }^{n}. \end{aligned}$$

  (9)

• For $(i,n) \in \{I\}\times \{1,\dots ,N-1\}$,

  $$\begin{aligned}&\left( \frac{\overline{\sigma }_{I}^{n} \overline{D}_{I-2}}{8 h^2} \right) \psi _{I-3}^n + \left( - \frac{\overline{\sigma }_{I}^{n} \overline{D}_{I-1}}{2 h^2} \right) \psi _{I-2}^n \nonumber \\&\quad + \left( - \frac{\overline{\sigma }_{I}^{n} \overline{D}_{I-2}}{8 h^2} \right) \psi _{I-1}^n + \left( -\frac{\mu _I}{k} + \frac{\overline{\alpha }_{I}^{n}}{2} + \frac{\overline{\sigma }_{I}^{n} \overline{D}_{I-1}}{2 h^2} \right) \psi _I^n \nonumber \\&\quad + \left( \frac{\overline{\sigma }_{I}^{n+1} \overline{D}_{I-2}}{8 h^2} \right) \psi _{I-3}^{n+1} + \left( - \frac{\overline{\sigma }_{I}^{n+1} \overline{D}_{I-1}}{2 h^2} \right) \psi _{I-2}^{n+1} \nonumber \\&\quad + \left( -\frac{\overline{\sigma }_{I}^{n+1} \overline{D}_{I-2}}{8 h^2} \right) \psi _{I-1}^{n+1} \nonumber \\&\quad + \left( \frac{\mu _I}{k} + \frac{\overline{\alpha }_{I}^{n+1}}{2} + \frac{\overline{\sigma }_{I}^{n+1} \overline{D}_{I-1}}{2 h^2} \right) \psi _I^{n+1} = \frac{\overline{W}_{I}^{n} + \overline{W}_{I}^{n+1}}{2}. \end{aligned}$$

  (10)

• For $(i,n) \in \{i^\star ,\dots ,I\}\times \{1\}$,

  $$\begin{aligned} \psi _i^1 = \overline{f}_{i}. \end{aligned}$$

  (11)

• For $(i,n) \in \{1,\dots ,i^\star \}\times \{N\}$,

  $$\begin{aligned} \psi _i^N = \overline{g}_{i}. \end{aligned}$$

  (12)

The direct algorithm, which is well defined whenever $I\ge 5$, I odd, and $N\ge 3$, consists in solving the previous linear system of $I\times N$ equations for the $I\times N$ unkowns $\psi _i^n$.

We would like to mention that, at the time the paper [11] was written, we were not aware of the beautiful work [7] by Joel N. Franklin and Eugene R. Rodemich, where the main ideas leading to the odd scheme were already stated (specifically, within the Sect. 6.2 on the balanced difference method). Let these lines serve as a tribute to them.

It must be noticed that the idea of “direct method” which concerns us is different from the one used in [7]. The direct method proposed in [7], when adapted to our problem, would imply to solve $2(N-1)$ linear systems of order $I-1$ (which in terms of computing time amounts to perform $N-1$ iterations with the iterative method) plus one final linear system of order $N-2$. As it will be seen, performing $N-1$ iterations is not enough to be faster than the direct method as it is being understood in this paper.

4 Description of the iterative algorithm

Consider the following subsets of Q: $Q_- = [-1,0)\times [Z_{\mathrm{ini}},Z_{\mathrm{fin}}]$, $Q_+ = (0,1]\times [Z_{\mathrm{ini}},Z_{\mathrm{fin}}]$, and $Q_0 = \{0\}\times [Z_{\mathrm{ini}},Z_{\mathrm{fin}}]$ (see Fig. 1).

Fig. 1

Domain $Q = Q_- \cup Q_0 \cup Q_+$, with indication of the incoming flux boundary conditions. The dotted vertical line represents the subset $Q_0$

The aim of the iterative algorithm is to compute the solution of the same linear system (7)–(12), with the caveat of taking $I \ge 7$, observing that it is possible to use a marching strategy in the variable z by working separately on each of the subdomains $Q_+$ and $Q_-$. Clearly, one must advance when solving on $Q_+$ and must go back when solving on $Q_-$ (see Fig. 1).

In order to start this procedure, an initial guess of the solution on the points of the mesh belonging to $Q_0$ is required. The set of these values is updated after performing one forward march on $Q_+$ and one backward march on $Q_-$ until convergence is achieved or a given number of iterations has been carried out.

In application to particular cases of our problem, and also to other forward–backward PDEs, proofs of convergence for iterative algorithms based on the same guidelines can be found (see [7, 8, 15] and [16]).

Fig. 2

The points where the seed is required have been boxed

The detailed description reads as follows (every time we say “on $Q_0$” we actually mean “on the relative interior of $Q_0$”, that is, on $\{0\}\times (Z_{\mathrm{ini}},Z_{\mathrm{fin}})$):

• STEP 0. The seed:

  Provide the algorithm with an initial guess of the values of the solution on $Q_0$:

  $$\begin{aligned} \left( \psi _{i^\star }^n\right) ^{[0]}\ \text{ for }\ n \in \{2,\dots ,N-1\}. \end{aligned}$$

  (13)

  This set of values is usually called the seed of the iterative algorithm. Fig. 2 shows the points of the mesh where the seed is given.

  A good choice of the seed, which amounts to say choosing values close to the exact solution of the discrete problem, will make the iterative process converge in fewer iterations. Maybe the simplest reasonable possibility lies in the idea of joining the pairs $(Z_{\mathrm{ini}},f(0))$ and $(Z_{\mathrm{fin}},g(0))$ by means of a straight line:

  $$\begin{aligned} \left( \psi _{i^\star }^n\right) ^{[0]} = f(0) + [g(0) - f(0)] \frac{(n-1)}{(N-1)}\ \text{ for }\ n \in \{2,\dots ,N-1\}. \end{aligned}$$

  (14)

  However, a better seed can be obtained as follows: firstly, solve the problem with the direct method using a coarse grid (in order to spend only a negligible amount of time), and then take the restriction to $Q_0$ of this numerical solution as the basis to calculate the seed in Eq. (13) by means of linear interpolation. Neither spline interpolation nor piecewise cubic Hermite interpolation, the other two possibilities offered by our Matlab$^{{\textregistered }}$ version, has outperformed the linear one in any of our numerical experiments.

• STEP 1. Computation of values on ${\varvec{Q}}_+$ at iteration ${\varvec{q}} + \mathbf{1}$:

  For a fixed number $q\in {\mathbb {N}}\cup \{0\}$, assume that

  $$\begin{aligned} \left( \psi _{i^\star }^n\right) ^{[q]}\ \text{ for }\ n \in \{2,\dots ,N-1\} \end{aligned}$$

  (15)

  are known, and obtain all values on $Q_+$ at iteration $q + 1$, i. e.,

  $$\begin{aligned} \left( \psi _i^n\right) ^{[q + 1]}\ \text{ for }\ (i,n) \in \{i^\star + 1,\dots ,I\}\times \{1,\dots ,N\}, \end{aligned}$$

  (16)

  by solving Eq. (8, for $i\in \{i^\star + 1,\dots ,I-1\}$), (10), and (11), with the aid of the boundary values (15).

  This is done by means of a one-step forward marching procedure starting from the known values at $z = Z_{\mathrm{ini}}$ given by Eq. (11).

• STEP 2. Computation of values on ${\varvec{Q}}_-$ at iteration ${\varvec{q}} + \mathbf{1}$:

  Obtain all values on $Q_-$ at the same iteration $q + 1$, i.e.,

  $$\begin{aligned} \left( \psi _i^n\right) ^{[q + 1]}\ \text{ for }\ (i,n) \in \{1,\dots ,i^\star - 1\}\times \{1,\dots ,N\}, \end{aligned}$$

  (17)

  by solving Eqs. (7), (8, for $i\in \{2,\dots ,i^\star - 1\}$), and (12), with the aid of the same boundary values (15).

  This is done by means of a one-step backward marching procedure starting from the known values at $z = Z_{\mathrm{fin}}$ given by Eq. (12).

• STEP 3. Update (computation of values on ${\varvec{Q}}_\mathbf{0}$ at iteration ${\varvec{q}} + \mathbf{1}$):

  Update of the values on $Q_0$ can be done by using Eq. (9). That is to say, the updated values

  $$\begin{aligned} \left( \psi _{i^\star }^n\right) ^{[q + 1]}\ \text{ for }\ n \in \{2,\dots ,N-1\} \end{aligned}$$

  (18)

  can follow from

  $$\begin{aligned}&\left( -\frac{\overline{\sigma }_{i^\star }^{n}}{h^2} \right) \left( \psi _{i^\star -1}^n\right) ^{[q + 1]} + \left( \overline{\alpha }_{i^\star }^{n} + \frac{2\overline{\sigma }_{i^\star }^{n}}{h^2} \right) \left( \psi _{i^\star }^n\right) ^{[q + 1]} \nonumber \\&\quad + \left( -\frac{\overline{\sigma }_{i^\star }^{n}}{h^2} \right) \left( \psi _{i^\star +1}^n\right) ^{[q + 1]} = \overline{W}_{i^\star }^{n}. \end{aligned}$$

  (19)

  However, it is possible to accelerate convergence by over-relaxing the update, in the way we explain now: firstly, one computes

  $$\begin{aligned} \left( {\tilde{\psi }}_{i^\star }^n\right) ^{[q + 1]}\ \text{ for }\ n \in \{2,\dots ,N-1\} \end{aligned}$$

  (20)

  from

  $$\begin{aligned}&\left( -\frac{\overline{\sigma }_{i^\star }^{n}}{h^2} \right) \left( \psi _{i^\star -1}^n\right) ^{[q + 1]} + \left( \overline{\alpha }_{i^\star }^{n} + \frac{2\overline{\sigma }_{i^\star }^{n}}{h^2} \right) \left( {\tilde{\psi }}_{i^\star }^n\right) ^{[q + 1]} \nonumber \\&\quad + \left( -\frac{\overline{\sigma }_{i^\star }^{n}}{h^2} \right) \left( \psi _{i^\star +1}^n\right) ^{[q + 1]} = \overline{W}_{i^\star }^{n}, \end{aligned}$$

  (21)

  and, finally, the updated values are computed from

  $$\begin{aligned} \left( \psi _{i^\star }^n\right) ^{[q + 1]} = \omega \left( {\tilde{\psi }}_{i^\star }^n\right) ^{[q + 1]} + (1 - \omega ) \left( \psi _{i^\star }^n\right) ^{[q]} \end{aligned}$$

  (22)

  for $n \in \{2,\dots ,N-1\}$, where $\omega \in {\mathbb {R}}$ is a given relaxation parameter.

  Notice that $\omega = 1$ means that no relaxation is being deployed. The value of $\omega$ cannot be 0, otherwise no update is taking place, but being different from 0 is not guarantee of convergence. Among those values of $\omega$ offering convergence, the optimal one should be employed, but as of today the issue of finding a closed expression for this optimum (or for an estimation of it) has not been investigated; accordingly, the values of $\omega$ used in Sect. 5 when reporting the numerical results have been found by performing several trials, looking for values that reduce the number of iterations in a significant way with respect to the case $\omega = 1$.

  The idea of relaxing the update in forward-backward diffusion problems has already been used in [15] and [16].

• STEP 4. Checking convergence:

  Let us define the vectors ${\mathbf {u}}^{[q]}, {\mathbf {u}}^{[q + 1]} \in {\mathbb {R}}^{N-2}$ as follows:

  $$\begin{aligned} u^{[q]}_j = \left( \psi _{i^\star }^{j+1}\right) ^{[q]},\quad u^{[q + 1]}_j = \left( \psi _{i^\star }^{j+1}\right) ^{[q + 1]} \end{aligned}$$

  (23)

  for $j \in \{1,\dots ,N-2\}$.

  Given a small real number $\varepsilon > 0$, we say that the algorithm has converged with $\varepsilon$-tolerance if

  $$\begin{aligned} \frac{\Vert {\mathbf {u}}^{[q + 1]} - {\mathbf {u}}^{[q]}\Vert }{1 + \Vert {\mathbf {u}}^{[q + 1]}\Vert } \le \varepsilon , \end{aligned}$$

  (24)

  where $\Vert \cdot \Vert$ stands for the Euclidean norm in ${\mathbb {R}}^{N-2}$. The quotient in Eq. (24) will be referred to as the residual.

  In the event that condition (24) is not satisfied, one sets $q = q + 1$ and goes back to STEP 1. If on the contrary condition (24) holds, then the process finishes and the last computed values are taken as the ultimate numerical solution:

  $$\begin{aligned} \psi _i^n = \left( \psi _i^n\right) ^{[q+ 1]}\ \text{ for }\ (i,n) \in \{1,\dots ,I\}\times \{1,\dots ,N\}. \end{aligned}$$

  (25)

  Notice that both the solution (25) and the number of iterations needed for getting it depend on the seed, on the relaxation parameter $\omega$, on the tolerance parameter $\varepsilon$, and on the norm used in the stopping criterium (24).

In what follows, an iteration will be the process which consists in performing steps 1, 2, 3, and 4.

5 Numerical results

In this section, $Z_{\mathrm{ini}}= 0$, $Z_{\mathrm{fin}}= 1$, and $E_{\mathrm{abs}}(Q) = \max _Q |\psi _{\mathrm{grid}} - \psi |$, where $\psi _{\mathrm{grid}}$ is representing the approximate solution and the maximum is taken over the set of all nodes. Computations have been performed by running Matlab$^{{\textregistered }}$, R2015a, on a personal computer with an $\hbox {Intel}^{{\textregistered }}$ Core™ i7-4790 @ 3.60 GHz processor.

Matlab$^{{\textregistered }}$ automatically chooses, via the single character “$\backslash$”, direct methods for solving the linear systems involved: LAPACK for the linear systems of the iterative method, and UMFPACK for the only linear system of the direct method. More information about these routines can be found in the reference [4].

All matrices involved in the resolution process are sparse and banded. In the case of the direct method, our code vectorizes the definition of the matrix in order to avoid loops, and, as it is natural, the ordering of the equations and unknowns is chosen so as to produce small bandwidth. We remark that the matrices needed in the iterative algorithm are much easier to deal with, and do not require any special treatment.

The computing times within the tables are given in seconds, and are counting

• For the iterative method: the time needed for reaching convergence, or, in non-convergent experiments, until a maximum of 2000 iterations have been carried out.

• For the direct method: the time spent in defining the matrix plus the time devoted to solving the linear system.

When the seed for the iterative method is said to be computed with the (11, 10)-direct method, what is meant is that one uses the direct method with $I = 11$, $N = 10$ to solve the full problem, and then computes the seed, from the restriction of this solution to $Q_0$, by means of linear interpolation.

Lastly, the suffixes “IT” and “D” in the tables stand, respectively, for “iterative” and “direct”.

5.1 Test 1

This is a test taken from [11]. One chooses

$$\begin{aligned} \alpha (\mu ,z)= & {} |\sin (12 \mu z)|, \end{aligned}$$

(26)

$$\begin{aligned} \sigma (\mu ,z)= & {} 1 + \sin (12 \mu z) \cos (12 \mu z),\end{aligned}$$

(27)

$$\begin{aligned} \psi (\mu ,z)= & {} \ln (2 + \mu ^2 + z^3), \end{aligned}$$

(28)

and W, f and g are computed so that $\psi$ be the exact solution.

5.1.1 Results obtained with the iterative method

Let us analyze some numerical results obtained with the iterative method. Results collected in Tables 1 and 2 show the influence that the choice of the seed has got in the number of iterations needed for convergence, while Table 3 shows that the number of iterations grows if no relaxation is done.

The meaning of “no convergence” in these three Tables 1, 2 and 3 is that convergence has not been reached yet, but the algorithm behaves in a convergent way; in other words, convergence is expected if more iterations are allowed. By way of example, we report in the last row of Table 2 the value of the residual after 2000 iterations.

Table 1 Numerical results for test 1 by means of the iterative method with seed given by Eq. (14), $\omega = 2$, and $\varepsilon = 10^{-8}$

Table 2 Numerical results for test 1 by means of the iterative method with seed given by the (11, 10)-direct method, $\omega = 2$, and $\varepsilon = 10^{-8}$

Table 3 Numerical results for test 1 by means of the iterative method with seed given by the (11, 10)-direct method, $\omega = 1$ (no relaxation), and $\varepsilon = 10^{-8}$

In each one of the Tables 1, 2 and 3, a constant value of the relaxation parameter $\omega$ has been used, but it is quite clear that results can be improved by choosing different values of $\omega$ for different meshes. With this spirit, Table 4 sets forth the number of iterations needed for convergence as a function of $\omega$ for three different meshes; this is the kind of analysis we have done for choosing the quasi-optimal relaxation parameters in Table 5, which is reporting the quasi-best results that one can expect to achieve with the iterative method.

Table 4 Number of iterations needed for convergence versus $\omega$ for test 1. The seed is given by the (11, 10)-direct method, and $\varepsilon = 10^{-8}$. “Divergence” is meaning blowing up of the numerical solution

Notice that, although convergence has been reached, the result on the last row of Table 5 is not satisfactory, because the order 2 of the method is not being respected; in other words, a smaller value of $\varepsilon$ must be used when solving with the (1001, 901)-mesh, which in turn means that more than 519 iterations are really needed to get the correct numerical solution.

Table 5 Numerical results for test 1 by means of the iterative method with seed given by the (11, 10)-direct method, and $\varepsilon = 10^{-8}$. The value of $\varepsilon$ is not small enough to keep accuracy in the last row (cf. Table 6)

In convergent cases, the iterative algorithm behaves like a globally convergent method. To give an instance, if we solve with $(I,N) = (101,91)$, $\omega = 5$, $\varepsilon = 10^{-8}$, and use the seed given by

$$\begin{aligned} \left( \psi _{i^\star }^n\right) ^{[0]} = -10^6\ \text{ for }\ n \in \{2,\dots ,N-1\}, \end{aligned}$$

(29)

then convergence is achieved in 368 iterations (cf. Table 5). Observe that this seed is a long way away from the exact solution, the values of which on $Q_0$ are between $\ln 2$ and $\ln 3$.

5.1.2 Results obtained with the direct method

Table 6 is showing the results obtained with the direct method for several meshes. An expression like ${ t \ =\ t_1\ +\ t_2}$ means that $t_1$ seconds were needed to define the matrix and $t_2$ seconds were needed to solve the linear system. By selecting the three rows (11, 10), (101, 91), (1001, 901) (or (33, 29), (321, 281), (3201, 2801)), the order 2 of the method can be seen by eye.

Table 6 Numerical results for test 1 with the direct method

When the computing times in Table 6 are compared with those in Table 5, the superiority of the direct method is apparent for meshes not finer than $(I,N) = (1001,901)$, which by the way is fine enough to produce a very small error equal to $5.85 \times 10^{-7}$.

Since the linear systems which are solved when using the iterative algorithm are square of order $\frac{I + 1}{2}$ while the system solved when using the direct method is square of order $I \times N$, it is clear that the superiority of the direct method cannot be maintained as the mesh is refined ad infinitum, but the point is that the range of meshes for which the direct method is faster contains the meshes that are typically used.

Let us comment now on the meshes finer than $(I,N) = (1001,901)$. We have checked that one iteration takes 8.55 seconds if $(I,N) = (3201,2801)$, and hence even for this fine mesh the iterative algorithm should converge in no more than $\frac{1023.9}{8.55} \approx 119$ iterations to be faster than the direct method; this is very optimistic: indeed, the residual (with seed given by the (11, 10)-direct method and $\omega = 12$) after 119 iterations is equal to $1.32 \times 10^{-5}$, far away from the tolerance, which must be less than $10^{-8}$ to take profit of this fine mesh. This reasoning proves that the direct method is the fastest at least for all meshes in Table 6.

5.2 Test 2

This is a test taken from [9] which was also used in [11]. One chooses

$$\begin{aligned}&\alpha (\mu ,z) = 0.02,\quad \sigma (\mu ,z) = 0.01,\quad W(\mu ,z) = 0, \end{aligned}$$

(30)

$$\begin{aligned}&f(\mu ) = 1,\quad g(\mu ) = 2. \end{aligned}$$

(31)

In this case, the exact solution is not explicitly known. The numerical results seem to indicate that it is continuous and that, despite the $\mathrm{C}^\infty$ regularity of the data, has got singularities in its partial derivatives of first order at $(\mu ,z) \in \{(0,0), (0,1)\}$. This lack of regularity prevents the scheme from having order 2 when applied to this problem. Plots and numerical results can be found in [9] and [11].

Even when, regardless the data functions, the matrices’ patterns are the same for the same mesh, the reader will observe some differences in the computing times between this test and the previous one. To explain this phenomenon, simply notice that LU factorization does pivoting based not only on the pattern but on the values as well. So changing the values can easily change the pivot order, which in turn can affect the time (and also the amount of memory) taken.¹

5.2.1 Results obtained with the iterative method

Tables 7 and 8 are analogous to Tables 4 and 5, and must be interpreted alike.

Table 7 Number of iterations needed for convergence versus $\omega$ for test 2. The seed is given by the (11, 10)-direct method, and $\varepsilon = 10^{-8}$. “Divergence” is meaning blowing up of the numerical solution

Table 8 Numerical results for test 2 by means of the iterative method with seed given by the (11, 10)-direct method, and $\varepsilon = 10^{-8}$

5.2.2 Results obtained with the direct method

Once more, results in Tables 8 and 9 show that the direct method outperforms the iterative one. For this test, one iteration with $(I,N) = (3201,2801)$ takes about 2.90 s, and arguments already used prove that the direct method is faster for this mesh, and hence for all meshes in Table 9.

Table 9 Numerical results for test 2 with the direct method

6 Some additional comments

It has already been explained in Sect. 5.1.2 that asymptotically, which in this case is meaning “as the mesh is being more and more refined”, the iterative algorithm will always win from a certain fineness onwards. However, from a practical perspective, the question that one must answer is whether the meshes which are going to be used are among those which make the direct method be the fastest or not. In relation to this standpoint, our experiments indicate that the direct method is the one that must be used for a wide range of meshes.

We detail in the following points several arguments that play in favour of the direct method in the framework we are:

• 1. The number of iterations needed for convergence depends strongly on the value of the relaxation parameter $\omega$, but the optimum value of this parameter is not known in advance and, moreover, can be different for different meshes.

• 2. When one refines the mesh, one should obtain a better, more accurate, solution. In order to compute the solution with the expected accuracy, the tolerance parameter $\varepsilon$ might have to be reduced, what would increase the number of iterations. On the other hand, the direct method does not suffer from this inconvenience.

• 3. Loops cannot be avoided when coding the iterative algorithm: one external loop in iterations, one internal loop for solving on $Q_+$, and one internal loop for solving on $Q_-$. On the contrary, loops are not needed to code the direct method, except for the ones that might be demanded by the linear solver.

It has been said before that the direct method can be also the best option when solving other forward-backward problems by means of finite difference schemes, but nothing about concrete examples has been written yet. In the next lines, we are going to comment on the problem studied by Franklin and Rodemich in [7] and on the problem considered by Vanaja and Kellogg in [16] when $a = a(x)$, which by the way contains as a particular case the forward–backward heat equation (4). Both problems share the following property: if no relaxation is performed, i. e., if the iterative method is applied with $\omega = 1$, then the direct method is the fastest one by a large margin for meshes of typical fineness. When one does relaxation, it is worth mentioning separately the behaviour of the algorithms. The tolerance parameter for the iterative algorithm will still be $\varepsilon = 10^{-8}$.

Franklin and Rodemich’s problem. If this problem is discretized with the balanced scheme, the direct method is faster even if a quasi-optimal relaxation parameter $\omega$ is employed for performing the update in the iterative method, no matter if the seed is computed by means of Eq. (14) or via the (11, 10)-direct method. The only way for the iterative method to calculate the solution in times that are comparable to those of the direct one is that the seed be computed with the $(I_{\mathrm{seed}},N_{\mathrm{seed}})$- method, being $(I_{\mathrm{seed}},N_{\mathrm{seed}})$ the size of a mesh finer than (11, 10). A couple of examples are as follows:

• If $I = 1001$ and $N = 901$, the direct method uses 12.59 s. The time used by the iterative method can be reduced to 8.81 s by taking $(\omega ,I_{\mathrm{seed}},N_{\mathrm{seed}}) = (1.5,301,300)$, what leads to 179 iterations.

• If $I = 1601$ and $N = 701$, the direct method uses 14 s. The time used by the iterative method can be reduced to 13 s by taking $(\omega ,I_{\mathrm{seed}},N_{\mathrm{seed}}) = (1.5,501,500)$, what leads to 233 iterations.

The point is that the optimal values $\omega ,I_{\mathrm{seed}},N_{\mathrm{seed}}$ leading to the minimum computing time are not known in advance, and that there is the possibility that the iterative method diverge for certain values of $\omega$. The quasi-optimal choice in the examples above has been found after performing several trials with our code. Moreover, the number of iterations and hence the computing time are very sensitive to variations of these parameters. Notice that, in any case, the direct method would have to be coded in order to compute the seed.

Vanaja and Kellogg’s problem with ${{a}} = {{a(x)}}$. If this problem is discretized with the implicit Euler scheme, we find for the first time in this paper a situation where the iterative method can be faster than the direct one when the seed is computed by means of Eq. (14), hence without the help of the direct method. We report now two examples obtained when $a(x) = x$ and $f \equiv 1$ (a and f are those of reference [16]). Nonetheless, the iterative method is soon slower than the direct one, or even divergent, if the values of $\omega$ below are altered:

• If $I = 321$ and $N = 281$, the direct method uses 0.52 s. The time used by the iterative method can be reduced to 0.40 s by taking $\omega = 20$, what leads to 34 iterations.

• If $I = 1001$ and $N = 901$, the direct method uses 7.26 s. The time used by the iterative method can be reduced to 2.70 s by taking $\omega = 105.5$, what leads to 70 iterations.

Again, the point is that the optimal value of $\omega$ is not known in advance. We can add that in this case it varies considerably ($\omega = 20$, $\omega = 105.5$) when one changes the mesh.

7 Conclusions

Our numerical experiments show that the direct method is faster, in some cases much faster, than the iterative method when one solves the problem (1)–(3) with the odd-scheme from reference [11]. This fact makes one suspect that the same could happen when solving other forward-backward PDEs by means of other finite difference schemes. Experiments carried out for Franklin and Rodemich’s and Vanaja and Kellogg’s problems demonstrate that this is indeed the case.

Since the saving in computing time can be really important, the recommended strategy for solving the problems above or others which behave alike is to use the direct approach, keeping in mind that we are always thinking of meshes of typical fineness.

The importance of iterative methods would be greater if future research allows knowing in advance the optimal value of $\omega$ (also of $I_{\mathrm{seed}}$ and $N_{\mathrm{seed}}$) for a given mesh.

The examples we are thinking of share the property of being one-dimensional in the space-like variable. Specific new numerical tests should be conducted in order to explore this question in multidimensional problems.