Neighborhood-related q-rung orthopair fuzzy covering-based rough set models and their applications for multi-attribute decision making

Abstract

In the current intelligent era, with the increasing complexity and diversification of productive practices, it is usually necessary to get a balanced consideration of many aspects of the decision-making problem. One of the most important and popular methods to solve decision problems is multi-attribute decision making (MADM). Traditional MADM problems in q-rung orthopair fuzzy (q-ROF) environment aggregate evaluation information by means of aggregation operators. However, aggregation operators are improper to effectively solve some complicated problems. To settle this problem, we come up with a new method based on neighborhood-related q-ROF covering-based rough set (NRq-ROFCRS) models for MADM problem in this paper. To define these models, several q-ROF logical operators are firstly defined. Next the concepts of q-ROF neighborhood systems of an object, q-ROF minimal and maximal description of an object and q-ROF covering are defined. On this basis, four t-norm-based q-ROF neighborhood operators (Tq-ROFNOs) and four overlap function-based q-ROF neighborhood operators (Oq-ROFNOs) are proposed. For a finite q-ROF covering, combining four Tq-ROFNOs and six q-ROF coverings results in 24 Tq-ROFNOs and only sixteen groups of Tq-ROFNOs are obtained. We also combine four Oq-ROFNOs and six q-ROF coverings and prove that only seventeen groups of Oq-ROFNOs are obtained. Then partial order relations among 16 groups of Tq-ROFNOs and 17 groups of Oq-ROFNOs are discussed, respectively. Moreover, four types of NRq-ROFCRS models are defined based on q-ROF neighborhood operators and the groups and partial order relations of neighborhood-related q-ROF approximate operators are discussed. Finally, a novel method for MADM problems by integrating NRq-ROFCRS models with TOPSIS method is put forward and the effectiveness and the reasonableness of our method are verified by experiments.

1 Introduction

In the current intelligent era, problems in productive practices become more uncertain and complicated. Traditional methods are no longer suitable for solving these uncertain and complicated issues. In this paper, we establish some NRq-ROFCRS models to deal with MADM problems. In this section, some research progress about fuzzy covering-based rough set (FCRS), q-ROF set (q-ROFS) and MADM is reviewed.

1.1 A brief review of FCRS

Rough set, which is used to handle incomplete, imprecise, vague and uncertain data, was put forward by Pawlak (1982). In Pawlak’s rough set model, equivalence relation is an essential concept to set up the lower and upper approximation of the subset A of the universe to approximately characterize A. However, in practical application, the equivalence relation is difficult to be satisfied for many problems. Therefore, the application of rough set theory is limited in practice. To remove this limitation, many attempts have been made by scholars to replace equivalence relations with some more general mathematical concepts.

As the extension of rough set, we observe that the covering-based rough set (CRS) model (Zakowski 1983) is one of the most general models. The two approximate operators used to define the CRS model in Zakowski (1983) do not satisfy duality. In Pomykala (1987), Pomykala constructed two dual approximation operators. Bonikowski et al. (1998) used minimum description to give another CRS model in the non-dual case and Tsang et al. (2008) investigated this CRS model. Some another kinds of CRS models were introduced in Zhu (2007, 2009); Zhu and Wang (2007).

To further develop the CRS model, some scholars combined the CRS model with the fuzzy rough set (FRS) model to study the FCRS model after the FRS model proposed (Dubois and Prade 1990). Then a lot of these hybrid models have been proposed. For example, a fuzzy covering was constructed by applying a fuzzy relation in Deng et al. (2007). Another type of fuzzy coverings was constructed by applying promoted fuzzy rough operators in Li et al. (2008). Two new CFRS models were proposed by means of fuzzy $\beta$-neighborhoods in Ma (2016). Later, Yang and Hu (2017) proposed three kinds of fuzzy $\beta$-coverings by means of FRSs. Inspired by the idea of fuzzy neighborhoods on fuzzy coverings proposed in D’eer et al. (2017), Yang et al. introduced some neighborhood-related FCRS models by means of overlap function-based fuzzy neighborhood operators in Qi et al. (2023). To solve complicated problems, Zhan and Sun (2020) introduced three classes of intuitional fuzzy covering-based rough set (IFCRS) by means of intuitional fuzzy-neighborhoods and intuitional fuzzy complementary neighborhood. Then generalized IF covering-based models were proposed by Zhang et al. (2019). Pythagorean fuzzy covering-based rough set (PFCRS) models and q-ROF covering-based rough set (q-ROFCRS) models were proposed by means of q-ROF $\beta$-neighborhoods and q-ROF complementary $\beta$-neighborhoods in Garg and Atef (2022); Zhang (2016). In this paper, we integrate q-ROF with CRS and propose q-ROFCRS models based on q-ROFNOs which are defined in this paper inspired by the ideas in D’eer et al. (2017) and Qi et al. (2023).

1.2 A brief review of q-ROF set

To deal with inaccurare and incomplete information, fuzzy set theory was proposed by Zadeh (1965). However, when dealing with the problem with hesitant information, the fuzzy theory is usually invalid. To solve this problem, Atanassov put forward intuitional fuzzy set (IFS) (Atanassov 2016) in 1986. In IFS, the sum of the membership degree (MD) and the non-membership degree (NMD) can not be lager than 1. Comparing with the traditional fuzzy set, IFS is more flexible and practical in handling ambiguous and uncertain information because it considers information of membership, non-membership and hesitancy. Since then, the research on IFS theory has attracted great attention from scholars in many fields, such as machine learning (Laxmi et al. 2021), medical diagnosis (Son and Thong 2015), pattern recognition (Vlachos and Sergiadis 2007), decision-making (Xu 2007) and so on.

However, IFS has some restrictions to deal with some complicated problems in practical application. For example, when an expert adopt his opinion in terms of 0.8 and 0.3 as MD and NMD, it is obviously beyond the range of IF. In order to solve these problems, Yager put forward Pythagorean fuzzy rough set (PFS) (Yager 2016), which has been presented by Atanassov (1989) (reprinted in Atanassov (2016)) earlier and referred to as intuitionistic fuzzy set of second type, which satisfies the condition that the sum of squares of the MD and the NMD can not be lager than 1. Since then many valuable researches (Yager 2016; Zhang 2016) related to PFS have been proposed by scholars.

Recently, as the extension of IFS and PFS (Intuitionistic Fuzzy Set of Second Type), q-ROF set (q-ROFS) was proposed by Yager in Yager (2017) which satisfied the condition that the sum of qth power of the MD and the NMD of q-ROFS can not be lager than 1 (see Fig. 1). Compared with PFS, q-ROFS provides decision-makers with more information expression space and stronger information modeling ability by capturing two truth values in the range [0, 1], one of which gauges the truth value of the clause “x belongs to set” and the other gauges the truth value of the clause “x does not belong to set” (Alcantud 2023). And q-ROFS is more flexible when dealing with uncertain information by adjusting the parametic family q. Hence, q-ROFS has attracted a lot of attention and has been widely used to handle complicated decision-making problems, such as Peng et al. (2018), Liu et al. (2018), Hussain et al. (2019) and Garg and Atef (2022). To enrich the theory and application of q-ROFS, we generalize t-norm, t-conorm, overlap function, fuzzy implication, fuzzy covering and FCRS to q-ROFS theory in this paper.

Fig. 1

Comparison of spaces of IFS, PFS and q-ROFS

1.3 A brief review of MADM

In the current intelligent era, with the increasing complexity and diversification of productive practices, it is usually necessary to get a balanced consideration of many aspects of the decision-making problem. MADM is a process for making decisions over the feasible alternatives which are characterized by multiple (usually conflicting) attributes. MADM has become an important tool in decision-making analysis and a lot of investigations about MADM have been proposed by scholars.

Nowadays, many effective methods were proposed to deal with MADM problems, such as the TODIM method (Llamazares 2018), the aggregation operator method (Xu and Da 2003) and the TOPSIS method (Hwang and Yoon 1981; Zhang et al. 2021; Qi et al. 2023). So far, TOPSIS method which was proposed by Hwang and Yoon (1981) has become a practical and effective method to solve decision-making problems. The main idea is to sort alternatives by the distance between them and the positve ideal solution and the negative ideal solution. The optimal alternative is closest to the positve ideal solution and farthest from the negative ideal solution. In the current intelligent era, the information becomes more complicated and diverse, and the limitations of traditional TOPSIS methods become impossible to ignore. Therefore, scholars have tried to extend the traditional TOPSIS method to more complicated fuzzy environments. For example, IF-TOPSIS methodology for MADM problem was put forward by Zhan and Sun (2020). PF-TOPSIS method for the multiple criteria decision making was put forward by Zhang and Xu (2014). q-ROF TOPSIS was put forward to select suppliers for speech recognition products by Liu and Wang (2018). In our paper, we enrich the TOPSIS method in q-ROF environment and propose a novel method to deal with MADM problem by means of NRq-ROFCRS models.

1.4 Motivations and main works

q-ROF aggregation operators are usually used in most cases for decision problems in q-ROF environment. Most of the aggregation operators used to investigate decision-making problems have low resolution in distinguishing the optimal alternative and counter-intuitive phenomena in real life. This may make it invalid or improper for decision makers to choose the optimal alternative for the problem with independent or conflicting criteria. Therefore, we are eager to find a new way to deal with these problems in q-ROF environment.

The combination of fuzzy rough set in complex environments and TOPSIS method may be a promising topic for complicated decision-making problems. Some relevant research has been carried out on this topic. For example, a new method based on generalized IFCRS models and TOPSIS method is proposed for MADM problem (Zhang et al. 2019). Methods based on PFCRS models with TOPSIS method or q-ROFCRS models with TOPSIS method for MADM problem are proposed in Garg and Atef (2022), where PFCRS models are defined on PF $\beta$-covering approximation space by means of PF $\beta$-neighborhoods, PF complementary $\beta$-neighborhoods and q-ROFCRS models are defined on q-ROF $\beta$-covering approximation space by means of q-ROF $\beta$-neighborhoods, q-ROF complementary $\beta$-neighborhoods. From the above discussion, the major motivations of our paper as follows:

• 1. In Zhang et al. (2019), Xu et al. proposed four kinds of IF neighborhoods based on IF t-norm and its residual implication. As a significant extension of IFS, q-ROFS is more flexible for handling uncertain information. It is natural to extend the IF neighborhoods based on t-norm and its implication to q-ROF environment. In addition, Yang et al. defined the overlap function-based fuzzy neighborhoods based on overlap function and its implication in Qi et al. (2023). Extending the overlap function-based fuzzy neighborhoods to the q-ROF environment is also a meaningful task.

• 2. The existing q-ROFCRS models (Zhang et al. 2019; Hussain et al. 2019) are defined on q-ROF $\beta$-covering neighborhoods by disjunctive and conjunctive operations. Inspired by these ideas, integrating other q-ROF logical operators and q-ROF neighborhood operators based on q-ROF coverings to define q-ROFCRS models is an excellent idea.

• 3. For the majority of TOPSIS methods in the q-ROF environment, they aggregate evaluation information by means of aggregation operators (Peng et al. 2018; Liu et al. 2018; Hussain et al. 2019). However, the great majority of q-ROF aggregation operators have low resolution in distinguishing the optimal alternative and counterintuitive phenomena in real life, which makes TOPSIS methods invalid. Therefore, it may be invalid or improper for decision makers to choose the optimal alternative for the problem with independent or conflicting criteria by the majority of existing q-ROF aggregation operators. q-ROF t-norm and q-ROF overlap function defined in this paper are two new kinds of binary aggregate functions which can deal with these problems. It is a natural idea to construct some q-ROF rough set models based on q-ROF t-norm and q-ROF overlap function to establish a new TOPSIS method.

Based on the above motivations, we propose some neighhorhood-related q-ROF covering-based rough set models and a novel method for MADM problem. The main innovations of our paper are as follows:

• 1. To explore the covering approximation space in q-ROF environment, we propose concepts of q-ROF t-norm, q-ROF t-conorm, q-ROF overlap function, q-ROF implication, q-ROF covering and q-ROF neighborhood systems of an object, q-ROF minimal and maximal description of an object and q-ROF covering, which enrich the q-ROFS theory.

• 2. Fuzzy neighborhood operators are extended to the q-ROF environment and four Tq-ROFNOs and Oq-ROFNOs are proposed. In light of four Tq-ROFNOs and six q-ROF covering, one original coverings and fiver derived ones, 24 Tq-ROFNOs are proposed. Similarly, 24 Oq-ROFNOs are proposed. Moreover, the equalities and partial order relationships of Tq-ROFNOs and Oq-ROFNOs are presented, respectively.

• 3. In light of 24 Tq-ROFNOs and 24 Oq-ROFNOs, four types of NRq-ROFCRS models which can be seen as extensions of IFCRS (Zhang et al. 2019) are presented. In addition, the properties, groups and partial order relationships of these NRq-ROFCRS models are also presented.

• 4. We propose a novel method for MADM problem by integrating q-ROFCRS models with TOPSIS method. And an illustrate example of assessment of new faculty position is analyzed to show the effectiveness and rationality of our method.

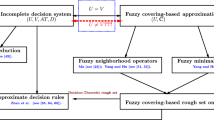
The layout of this paper is presented as follows. Some basic concepts that shall be used in the sequel are reviewed in Sect. 2. Some fuzzy logical operators on q-ROFS, such as q-ROF t-norm, q-ROF overlap function and their residual implications, are defined in Sect. 3. In Sect. 4, q-ROF neighborhood systems, four kinds of q-ROFNOs based on q-ROF t-norms and four kinds of q-ROFNOs based on q-ROF overlap functions are defined. Moreover, properties of q-ROFNOs are discussed and eight q-ROF coverings derived from the original q-ROF covering are defined. Groups of q-ROFNOs on finite fuzzy coverings and their lattice relationships are discussed in Sect. 5. In Sect. 6, some NRq-ROFCRS models are defined and properties and relations of q-ROF approximation operators are illustrated. In Sect. 7, we put forward a novel approach to solve MADM problem under q-ROF setting by means of TOPSIS method and NRq-ROFCRS models. The effectiveness and reasonableness of our proposed method are illustrated in Sect. 8. We make some conclusions and outline the future research in Sect. 9. In the end, the proofs of propositions and lemmas of this paper are presented in Sect. 10.

2 Preliminaries

Some fundamental concepts that shall be used in the sequel are reviewed in this section. Throughout this paper we assume that U is a nonempty finite universe.

2.1 q-ROFS

q-ROFS (Yager 2017) can deal with the problem with hesitant, and uncertain information in reality and has higher flexibility and allows experts to express their preferences in a wider range by adjusting parameter q. Note that 1-rung orthopair fuzzy set is Atanassov’s intuitionistic fuzzy set and 2-rung orthopair fuzzy set is intuitionistic fuzzy set of second type (Atanassov 1989, 2016) which is popularized as PFS. In this part, we recall the basic definition and some operations of q-ROFS.

Definition 1

Yager (2017) Let U be a nonempty finite universe, a q-ROFS Q on U is difined as:

$$\begin{aligned} Q=\{<\varepsilon ,\mu (\varepsilon ),\nu (\varepsilon )> \mid \varepsilon \in U\} \end{aligned}$$

where $\mu (\varepsilon )$ is the membership degree and $\nu (\varepsilon )$ is the non-membership degree of $\varepsilon$ to the set Q, and $0 \le \mu (\varepsilon ) \le 1$,$0 \le \nu (\varepsilon ) \le 1$, $0 \le (\mu (\varepsilon ))^q + (\nu (\varepsilon ))^q \le 1$, q is a positive integer. A q-ROF number (q-ROFN) is usually expressed as $Q = (\mu (\varepsilon ), \nu (\varepsilon ))$. $\mathscr {F}_q(U)$ denotes the collection of q-ROF sets.

Definition 2

Yager (2017) Let $Q_1 = (\mu _1(\varepsilon ), \nu _1(\varepsilon ))$ and $Q_2 = (\mu _2(\varepsilon ), \nu _2(\varepsilon ))$ be two q-ROFNs. Then the following operations are defined.

• 1. $Q_1 \bigcup Q_2 = (\max \{\mu _1(\varepsilon ), \mu _2(\varepsilon ) \}, \min \{\nu _1(\varepsilon ), \nu _2(\varepsilon ) \})$;

• 2. $Q_1 \bigcap Q_2 = (\min \{\mu _1(\varepsilon ), \mu _2(\varepsilon ) \}, \max \{\nu _1(\varepsilon ), \nu _2(\varepsilon ) \})$;

• 3. $Q_1^c = (\nu _1(\varepsilon ), \mu _2(\varepsilon ))$;

• 4. $Q_1\subseteq Q_2$ if $\mu _1(\varepsilon ) \le \mu _2(\varepsilon )$ and $\nu _1(\varepsilon ) \ge \nu _2(\varepsilon )$;

• 5. $Q_1 = Q_2$ if $Q_1\subseteq Q_2$ and $Q_2\subseteq Q_1$;

2.2 Triangular norm, triangular conorm and residual implications derived from triangular norm

Triangular norm (t-norm) and triangular conorm (t-conorm) are operations which generalize the logical conjunction and logical disjunction to fuzzy logic. Fuzzy implications belong to main logical operations in fuzzy logic. In this subsection, we firstly review the concepts of t-norm, t-conorm and fuzzy implication. Then we recall a particular kind of fuzzy implication: residual implications derived from t-norm ($I_{T}$-implication). At last, the definition of residual fuzzy difference operator derived from t-conorm ($D_{S}$-difference) is reviewed.

Definition 3

Klement et al. (2013) A t-norm $T: [0,1]^2\rightarrow [0,1]$ is a binary operation, if T is commutative, associative, increasing, and satisfies $T(1,\varepsilon ) = \varepsilon$ for $\varepsilon \in [0,1]$.

Definition 4

Klement et al. (2013) A t-conorm $S: [0,1]^2\rightarrow [0,1]$ is a binary operation, if S is commutative, associative, increasing, and satisfies $S(0,\varepsilon ) = \varepsilon$ for $\varepsilon \in [0,1]$.

Definition 5

Klement et al. (2013) A fuzzy implication $I: [0,1]^2\rightarrow [0,1]$ is a binary operation, if I satisfies the following three axioms for $\varepsilon ,\eta ,\theta \in [0,1]^2$,

• 1. $I(\varepsilon ,\theta ) \le I(\eta ,\theta )$ whenever $\varepsilon \ge \eta$;

• 2. $I(\varepsilon ,\eta ) \le I(\varepsilon ,\theta )$ whenever $\eta \le \theta$;

• 3. $I(0,0) = I(0,1) = I(1,1) = 1, I(1,0) = 0$.

Definition 6

Alsina et al. (2006) Let T be a left-continuous t-norm on $[0,1]^2$. A binary operation $I_{T}: [0,1]^2\rightarrow [0,1]$ given by

$$\begin{aligned} I_{T}(\varepsilon ,\eta ) = \sup \{z \in [0,1]\mid T(\varepsilon ,z)\le \eta \}, \end{aligned}$$

is usually called a residual implication derived from t-norm ($I_{T}$ implication).

Definition 7

Zheng and Wang (2005) Let S be a right-continuous t-conorm on $[0,1]^2$. A binary operation $D: [0,1]^2\rightarrow [0,1]$ given by

$$\begin{aligned} D(\varepsilon ,\eta ) = \inf \{z \in [0,1] \mid S(z,\eta )\ge \varepsilon \} \end{aligned}$$

is called a residual fuzzy difference operator derived from t-conorm ($D_{S}$-difference).

2.3 Overlap function, grouping function and residual implication derived from overlap function

Overlap function and grouping function are special kinds of aggregation oprators which associative law is non-necessary. In this subsection, the concepts of overlap function, grouping function and residual implication derived from overlap function ($I_{O}$-implication) are reviewed.

Definition 8

Bustince et al. (2010) An overlap function $O: [0,1]^2\rightarrow [0,1]$ is a binary function, if O satisfies the following five conditions for $\varepsilon ,\eta ,\theta \in [0,1]$,

• 1. commutativity: $O(\varepsilon ,\eta ) = O(\eta ,\varepsilon )$;

• 2. boundary condition: $O(\varepsilon ,\eta ) = 0 \Leftrightarrow \varepsilon \eta = 0$;

• 3. boundary condition: $O(\varepsilon ,y) = 1 \Leftrightarrow \varepsilon \eta = 1$;

• 4. monotonicity: $O(\varepsilon ,\eta ) \le O(\varepsilon ,\theta )$ whenever $\eta \le \theta$;

• 5. continuity: O is simultaneously continuous with respect to two variables.

An overlap function O which satisfies $O(1,\varepsilon ) \le \varepsilon$ for $\varepsilon \in [0,1]$ is called 1-section deflation and an overlap function O which satisfies $O(1,\varepsilon ) \ge \varepsilon$ for $\varepsilon \in [0,1]$ is called 1-section inflation.

Based on above definition, an overlap function O satisfies the associativity whenever O is exchangeable, i.e., $O(\varepsilon ,O(\eta ,\theta )) = O(\eta ,O(\varepsilon ,\theta ))$ for $\varepsilon , \eta ,\theta \in [0,1]$.

Definition 9

Bustince et al. (2012) A grouping function $G: [0,1]^2\rightarrow [0,1]$ is a binary function, if G satisfies the following five conditions for $\varepsilon ,\eta ,\theta \in [0,1]$,

• 1. commutativity: $G(\varepsilon ,\eta ) = G(\eta ,\varepsilon )$;

• 2. boundary condition: $G(\varepsilon ,\eta ) = 0 \Leftrightarrow \varepsilon = \eta = 0$;

• 3. boundary condition: $G(\varepsilon ,\eta ) = 1 \Leftrightarrow \varepsilon = 1$ or $\eta = 1$;

• 4. monotonicity: $G(\varepsilon ,\eta ) \le G(\varepsilon ,\theta )$ whenever $\eta \le \theta$;

• 5. continuity: G is simultaneously continuous with respect to two variables.

A grouping function G which satisfies $G(0,\varepsilon ) \le \varepsilon$ for $\varepsilon \in [0,1]$ is called 0-section deflation and a grouping function G which satisfies $G(0,\varepsilon ) \ge \varepsilon$ for $\varepsilon \in [0,1]$ is called 0-section inflation.

Based on the above definition, a grouping function G satisfies the associativity whenever G is exchangeable, i.e., $G(\varepsilon ,G(\eta ,\theta )) = G(\eta ,G(\varepsilon ,\theta ))$ for all $\varepsilon , \eta ,\theta \in [0,1]$.

Definition 10

Dimuro and Bedregal (2015) Let $O: [0,1]^2\rightarrow [0,1]$ be an overlap function. The bivariate function $I_O: [0,1]^2\rightarrow [0,1]$ defined by

$$\begin{aligned} I_{O}(\varepsilon ,\eta ) = \max \{z \in [0,1] \mid O(\varepsilon ,z) \le \eta \}, \end{aligned}$$

is the residual implication derived from overlap function ($I_{O}$ implication).

3 Some fuzzy logical operators on q-ROF

Theoretical research on t-norm, t-conorm, overlap function and implication have been extended to IFS (Wen et al. 2021; Cornelis et al. 2004, 2002) in recent years. To enrich the thoery and application of q-ROF, we give the concepts of q-ROF t-norm, q-ROF t-conorm, q-ROF overlap function and two kinds of residual q-ROF implications which derived from q-ROF t-norm and q-ROF overlap function for the first time in this section. Before given these definitions, we firstly give the definition of L that we should be used in the sequel.

Definition 11

Cornelis et al. (2004) Denote $L = \{(\varepsilon _1,\varepsilon _2) \in [0,1]^2 \mid \varepsilon _1^q + \varepsilon _2^q\le 1\}$, where q is a positive integer. Then for $(\varepsilon _1, \varepsilon _2), (\eta _1, \eta _2)\in L$, the relation $\preceq _L$ on L is defined as follows:

$$\begin{aligned} (\varepsilon _1, \varepsilon _2) \preceq _L (\eta _1, \eta _2) \Leftrightarrow \varepsilon _1 \le \eta _1, \varepsilon _2 \ge \eta _2. \end{aligned}$$

It is easy to prove that the relation $\preceq _L$ is a partial ordering and the pair $(L, \preceq _L)$ is a complete lattice with smallest element $0_L = (0,1)$ and greatest element $1_L = (1, 0)$. The operators $\wedge _L$ and $\vee _L$ on $(L, \preceq _L)$ are defined by

$$\begin{aligned} \begin{aligned} (\varepsilon _1, \varepsilon _2) \wedge _L (\eta _1, \eta _2) = (\min (\varepsilon _1, \eta _1),\max (\varepsilon _2,\eta _2)),\\ (\varepsilon _1, \varepsilon _2) \vee _L (\eta _1, \eta _2) = (\max (\varepsilon _1, \eta _1),\min (\varepsilon _2,\eta _2)), \end{aligned} \end{aligned}$$

(1)

for $(\varepsilon _1, \varepsilon _2), (\eta _1, \eta _2)\in L$. And other relations on L are defined as follows:

$$\begin{aligned} \begin{aligned} (\varepsilon _1, \varepsilon _2)\succeq _L (\eta _1, \eta _2) \Leftrightarrow \varepsilon _1 \ge \eta _1, \varepsilon _2 \le \eta _2,\\ (\varepsilon _1, \varepsilon _2)\succ _L (\eta _1, \eta _2) \Leftrightarrow \varepsilon _1> \eta _1, \varepsilon _2< \eta _2,\\ (\varepsilon _1, \varepsilon _2)\prec _L (\eta _1, \eta _2) \Leftrightarrow \varepsilon _1 < \eta _1, \varepsilon _2 > \eta _2, \\ (\varepsilon _1, \varepsilon _2) = (\eta _1, \eta _2) \Leftrightarrow \varepsilon _1 = \eta _1, \varepsilon _2 = \eta _2, \end{aligned} \end{aligned}$$

for $(\varepsilon _1, \varepsilon _2), (\eta _1, \eta _2)\in L$.

In fact, L is a collection of q-ROFNs. Next, the extensions of t-norm and t-conorm in q-ROF environment are given as follows.

Definition 12

A q-ROF t-norm $\mathscr {T}: L \times L\rightarrow L$ is a binary operation, if $\mathscr {T}$ satisfies the following four axioms for $\varepsilon , \eta , \theta \in L$,

• (T1) commutativity: $\mathscr {T}(\varepsilon , \eta ) = \mathscr {T}(\eta , \varepsilon )$;

• (T2) associativity: $\mathscr {T}(\varepsilon , \mathscr {T}(\eta ,\theta )) = \mathscr {T}(\mathscr {T}(\varepsilon , \eta ), \theta )$;

• (T3) monotonicity: $\mathscr {T}(\varepsilon , \eta ) \preceq _L \mathscr {T}(\varepsilon , \theta )$ whenever $\eta \preceq _L \theta$;

• (T4) boundary condition: $\mathscr {T}(\varepsilon , 1_L) = \varepsilon$.

Definition 13

A q-ROF t-conorm $\mathscr {S}: L \times L\rightarrow L$ is a binary operation, if $\mathscr {S}$ satisfies (T1)-(T3) and $\mathscr {S}(0_L,\varepsilon ) = \varepsilon$ for $\varepsilon \in L$.

Then we illustrate the construction method of q-ROF t-norm by means of t-norm T in Definition 3 and t-conorm S in Definition 4.

Proposition 1

Let T be a t-norm on [0, 1] and S be a t-conorm on [0, 1] which satisfy $T(\rho ,\delta ) \le 1 - S(1-\rho , 1-\delta )$ for $\rho , \delta \in [0,1]$. For $\varepsilon = (\varepsilon _1,\varepsilon _2) \in L, \eta = (\eta _1,\eta _2) \in L$, the mappings $\mathscr {T}: L\times L\rightarrow L$ and $\mathscr {S}: L\times L\rightarrow L$ defined by

$$\begin{aligned} \mathscr {T}(\varepsilon , \eta ) = \bigg (\root q \of {T(\varepsilon ^q_1, \eta ^q_1)}, \root q \of {S(\varepsilon ^q_2, \eta ^q_2)}\bigg ), \end{aligned}$$

$$\begin{aligned} \mathscr {S}(\varepsilon , \eta ) = \bigg (\root q \of {S(\varepsilon ^q_1, \eta ^q_1)}, \root q \of {T(\varepsilon ^q_2, \eta ^q_2)}\bigg ), \end{aligned}$$

are q-ROF t-norm and q-ROF t-conorm, respectively, where q is a positive integer.

Example 1

Consider the following mappings on L, for $\varepsilon = (\varepsilon _1,\varepsilon _2), \eta = (\eta _1,\eta _2)\in L$,

• 1. $\mathscr {T}_M(\varepsilon ,\eta ) = (\min \{\varepsilon _1,\eta _1\}, \max \{\varepsilon _2,\eta _2\})$;

• 2. $\mathscr {T}_P(\varepsilon ,\eta ) = \bigg (\varepsilon _1 \eta _1, \root q \of {\varepsilon ^q_2+\eta ^q_2-\varepsilon ^q_2\eta ^q_2}\bigg )$;

• 3. $\mathscr {T}_L(\varepsilon ,\eta ) = \left( \max \left\{ \root q \of {\varepsilon ^q_1+\eta ^q_1-1}, 0\right\} ,\min \left\{ \root q \of {\varepsilon ^q_2+\eta ^q_2}, 1\right\} \right)$.

It is easily verified that above functions are q-ROF t-norm.

From the perspective of application, additive generators can be used to simplify the choice of appropriate q-ROF t-norms for a given problem because we only need to consider functions with single variable rather than two variables, reducing computational complexity in this way. In Klement et al. (2013), there exist several additional generators of t-norm and t-conorm defined on [0, 1]. Next, in order to construct q-ROF t-norm by means of one-place functions, we introduce the definition of additive generator pair and multiplicative generator pair of q-ROF t-norm as follows.

Definition 14

Let T be a t-norm on [0, 1] which has some additive generator $t: [0,1]\rightarrow [0,\infty ]$ and S be a t-conorm on [0, 1] which has some additive generator $s: [0,1]\rightarrow [0,\infty ]$ and $T(\rho ,\delta ) \le 1 - S(1-\rho ,1-\delta )$ for $\rho , \delta \in [0,1]$. Then, for $\varepsilon ,\eta \in L$, the function $\mathscr {T}:L\times L\rightarrow L$ given by

$$\begin{aligned} \mathscr {T}(\varepsilon ,\eta ) = (t^{-1/q}(t(\varepsilon _1^q)+t(\eta _1^q)), s^{-1/q}(s(\varepsilon _2^q)+s(\eta _2^q))) \end{aligned}$$

is a q-ROF t-norm. (t, s) is called an additive generator pair of q-ROF t-norm $\mathscr {T}$.

Definition 15

If $t: [0,1]\rightarrow [0,\infty ]$ and $s: [0,1]\rightarrow [0,\infty ]$ are additive generators of t-norm T and t-conorm S which satisfy $T(\rho ,\delta ) \le 1 - S(1-\rho ,1-\delta )$ for $\rho , \delta \in [0,1]$. Then if we define the strictly increasing function $\gamma : [0,1]\rightarrow [0,1]$ by

$$\begin{aligned} \gamma (\rho )=e^{-t(\rho )} \end{aligned}$$

and the strictly decreasing function $\xi : [0,1]\rightarrow [0,1]$ by

$$\begin{aligned} \xi (\rho )=e^{-s(\rho )}. \end{aligned}$$

Then, for $\varepsilon , \eta \in [0,1]$, the function $\mathscr {T}:L\times L\rightarrow L$ given by

$$\begin{aligned} {\mathscr {T}}(\varepsilon ,\eta ) = (\gamma ^{-1/q}(\gamma (\varepsilon _1^q){\cdot {\gamma }}(\eta _1^q)), \xi ^{-1/q}(\xi (\varepsilon _2^q)\cdot \xi (\eta _2^q))) \end{aligned}$$

is a q-ROF t-norm. $(\gamma , \xi )$ is called a multiplicative generator pair of q-ROF t-norm $\mathscr {T}$.

Moreover, we illustrate the extension of the implication in q-ROF environment as follows.

Definition 16

An binary function $\mathscr {I}: L \times L\rightarrow L$ is called a q-ROF implication, if $\mathscr {I}$ satisfies the following axioms,

• 1. $\mathscr {I}(\varepsilon ,\theta ) \succeq _L \mathscr {I}(\eta ,\theta )$ whenver $\varepsilon \le \eta$;

• 2. $\mathscr {I}(\varepsilon ,\eta ) \preceq _L \mathscr {I}(\varepsilon ,\theta )$ whenver $\eta \le \theta$;

• 3. $\mathscr {I}(0_L,0_L) = \mathscr {I}(0_L,1_L) = \mathscr {I}(1_L,1_L) = 1_L, \mathscr {I}(1_L,0_L) = 0_L$.

In addition, we illustrate the definition of q-ROF residual implication (q-ROF $R_T$-implication) and its construction method by means of residual implication $I_T$ and residual fuzzy difference operator $D_S$.

Definition 17

Let $\mathscr {T}$ be a continuous q-ROF t-norm on $L\times L$. A binary operation $\mathscr {I}_{T}: L \times L\rightarrow L$ given by

$$\begin{aligned} \mathscr {I}_{T}(\varepsilon ,\eta ) = \sup \{z \in {L} \mid \mathscr {T}(\varepsilon ,z)\preceq _L \eta \} \end{aligned}$$

is called a q-ROF $R_T$-implication derived from q-ROF t-norm $\mathscr {T}$.

Proposition 2

Let T be a continuous t-norm on $[0,1]^2$, S be a continuous t-conorm on $[0,1]^2$, $I_{T}$ be a residual implication $[0,1]^2$ derived from T and $D_{S}$ be a residual fuzzy difference operator on $[0,1]^2$ derived from S. Then the function $\mathscr {I}_{T}:L\times L\rightarrow L$ given by

$$\begin{aligned} \mathscr {I}_{T}(\varepsilon ,\eta ) = \bigg (\min \bigg \{\root q \of {I_{T}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg \},\root q \of {D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg ) \end{aligned}$$

is a q-ROF $R_T$-implication.

Example 2

Consider the following q-ROF $R_T$-implications on $L\times L$:

• 1. When $T_M(\rho , \delta ) = \min \{\rho , \delta \}$, ${S_M(\rho , \delta )} = \max \{\rho , \delta \}$ for $\rho ,\delta \in [0,1]$, the residual implication $I_{T}$ and the residual fuzzy difference operator $D_{S}$ are

  $$\begin{aligned} \begin{aligned} I_{T}(\rho , \delta ) = \left\{ \begin{array}{ll} 1, &{} \rho \le \delta ,\\ \delta , &{} \rho> \delta , \end{array} \right. \end{aligned} \quad \begin{aligned} D_{S}(\delta , \rho ) = \left\{ \begin{array}{ll} 0, &{} \delta \le \rho ,\\ \delta , &{} \delta > \rho . \end{array} \right. \end{aligned} \end{aligned}$$

  Then, for $\varepsilon = (\varepsilon _1,\varepsilon _2), \eta = (\eta _1,\eta _2) \in L$,

  $$\begin{aligned} \begin{aligned} \mathscr {I}_{T}(\varepsilon , \eta ) = \left\{ \begin{array}{ll} (1,0), &{} \varepsilon _1 \le \eta _1, \varepsilon _2 \ge \eta _2\\ \bigg (\root q \of {1-\eta ^q_2},\eta _2\bigg ), &{} \varepsilon _1 \le \eta _1, \varepsilon _2< \eta _2,\\ (\eta _1,0) &{} \varepsilon _1> \eta _1, \varepsilon _2 \ge \eta _2,\\ (\eta _1,\eta _2) &{} \varepsilon _1 > \eta _1, \varepsilon _2 < \eta _2. \end{array} \right. \end{aligned} \end{aligned}$$

• 2. When $T_P(\rho , \delta ) = \rho \delta$, ${S_P(\rho , \delta )}= \rho + \delta - \rho \delta$ for $\rho ,\delta \in [0,1]$, the residual implication $I_{T}$ and the residual fuzzy difference operator $D_{S}$ are

  $$\begin{aligned} \begin{aligned} I_{T}(\rho , \delta ) = \left\{ \begin{array}{ll} 1, &{} \rho \le \delta ,\\ \frac{\delta }{\rho }, &{} \rho> \delta , \end{array} \right. \end{aligned} \quad \begin{aligned} D_{S}(\delta , \rho ) = \left\{ \begin{array}{ll} 0, &{} \delta \le \rho ,\\ \dfrac{\delta - \rho }{1 - \rho }, &{} \delta > \rho . \end{array} \right. \end{aligned} \end{aligned}$$

  Then, for $\varepsilon = (\varepsilon _1,\varepsilon _2), \eta = (\eta _1,\eta _2) \in L$,

  $$\begin{aligned} \begin{aligned} \mathscr {I}_{T}(\varepsilon , \eta ) = \left\{ \begin{array}{ll} (1,0), &{} \varepsilon _1 \le \eta _1, \varepsilon _2 \ge \eta _2\\ \bigg (\root q \of {\frac{1 - \eta ^q_2}{1-\varepsilon ^q_2}},\root q \of {\frac{\eta ^q_2 - \varepsilon ^q_2}{1-\varepsilon ^q_2}}\bigg ), &{} \varepsilon _1 \le \eta _1, \varepsilon _2< \eta _2,\\ \bigg (\frac{\eta _1}{\varepsilon _1},0\bigg ) &{} \varepsilon _1> \eta _1, \varepsilon _2 \ge \eta _2,\\ \bigg (\min \bigg \{\root q \of {\frac{1 - \eta ^q_2}{1-\varepsilon ^q_2}},\frac{\eta _1}{\varepsilon _1}\bigg \},\root q \of {\frac{\eta ^q_2 - \varepsilon ^q_2}{1-\varepsilon ^q_2}}\bigg ) &{} \varepsilon _1 > \eta _1, \varepsilon _2 < \eta _2. \end{array} \right. \end{aligned} \end{aligned}$$

• 3. When $T_L(\rho , \delta ) = \max \{\rho + \delta - 1, 0\}$, ${S_L(\rho , \delta )} = \min \{\rho + \delta , 0\}$ for $\rho ,\delta \in [0,1]$, the residual implication $I_{T}(\rho , \delta ) = \min \{1 - \rho +\delta , 1\}$ and the residual fuzzy difference operator $D_{S}(\delta , \rho ) = {\max \{\delta - \rho ,0\}}$. Then, for $\varepsilon = (\varepsilon _1,\varepsilon _2), \eta = (\eta _1,\eta _2) \in L$,

  $$\begin{aligned} \begin{aligned} \mathscr {I}_{T}(\varepsilon , \eta ) = \left\{ \begin{array}{ll} \bigg (\min \bigg \{1, \root q \of {1+\eta ^q_1-\varepsilon ^q_1}, \root q \of {1-\eta ^q_2+\varepsilon ^q_2}\bigg \},\root q \of {\eta ^q_2-\varepsilon ^q_2}\bigg ), &{} \varepsilon _2 \le \eta _2\\ \bigg (\min \bigg \{1, \root q \of {1+\eta ^q_1-\varepsilon ^q_1}, \root q \of {1-\eta ^q_2+\varepsilon ^q_2}\bigg \},0\bigg ), &{} \varepsilon _2 > \eta _2,\\ \end{array} \right. \end{aligned} \end{aligned}$$

Then, we also give the extension of overlap function in q-ROF environment as follows.

Definition 18

A q-ROF overlap function $\mathscr {O}: L \times L\rightarrow L$ is a binary function, if $\mathscr {O}$ satisfies the following five conditions for $\varepsilon ,\eta ,\theta \in L$,

• (O1) commutativity: $\mathscr {O}(\varepsilon ,\eta ) = \mathscr {O}(\eta ,\varepsilon )$;

• (O2) boundary condition: $\mathscr {O}(\varepsilon ,\eta ) = 0_L$ if and only if $\varepsilon \eta = 0_L$;

• (O3) boundary condition: $\mathscr {O}(\varepsilon ,\eta ) = 1_L$ if and only if $\varepsilon \eta = 1_L$;

• (O4) monotonicity: $\mathscr {O}(\varepsilon ,\eta ) \preceq _L \mathscr {O}(\varepsilon ,\theta )$, whenever $\eta \preceq _L \theta$;

• (O5) continuity: $\mathscr {O}$ is simultaneously continuous with respect to two variables.

The 1-section deflation of a q-ROF overlap function $\mathscr {O}$ is

• (O6) $\mathscr {O}(1_L,\varepsilon ) \preceq _L \varepsilon$ for $\varepsilon \in L$;

and the 1-section inflation of a q-ROF overlap function $\mathscr {O}$ is

• (O7) $\mathscr {O}(1_L,\varepsilon ) \succeq _L \varepsilon$ for $\varepsilon \in L$.

Based on above definition, a q-ROF overlap function $\mathscr {O}$ satisfies the associativity whenever $\mathscr {O}$ is exchangeable, i.e.,

• (O8) $\mathscr {O}(\varepsilon ,\mathscr {O}(\eta ,\theta )) = \mathscr {O}(\eta ,\mathscr {O}(\varepsilon ,\theta ))$ for $\varepsilon , \eta ,\theta \in L$.

In addition, we illustrate the construction method of q-ROF overlap function by means of overlap function O and grouping function G.

Proposition 3

Let O be an overlap function on [0, 1] and G be a grouping function on [0, 1] with $O(\rho ,\delta ) \le 1-G(1-\rho ^q, 1-\delta ^q)$ for $\rho ,\delta \in [0,1]$. For $\varepsilon = (\varepsilon _1,\varepsilon _2), \eta = (\eta _1,\eta _2) \in L$, the function $\mathscr {O}:L\times L\rightarrow L$ defined by

$$\begin{aligned} \mathscr {O}(\varepsilon ,\eta ) = \bigg (\root q \of {O(\varepsilon ^q_1,\eta ^q_1)}, \root q \of {G(\varepsilon ^q_2,\eta ^q_2)}\bigg ), \end{aligned}$$

is a q-ROF overlap function.

The following q-ROF overlap functions which shall be used in the sequel are induced by overlap function O and grouping function G.

Example 3

For $\varepsilon = (\varepsilon _1, \varepsilon _2), \eta = (\eta _1, \eta _2) \in L$, consider the following q-ROF overlap function with different conditions.

• 1. The q-ROF overlap function $\mathscr {O}_2^V$ satisfies (O6):

  $$\begin{aligned} \begin{aligned} \mathscr {O}_2^V(\varepsilon , \eta ) = \left\{ \begin{array}{ll} (\root q \of {O_1},\root q \of {G_1}), &{} \varepsilon ^q_1,\eta ^q_1\in (0.5,1],\varepsilon ^q_2,\eta ^q_2 \in [0,0.5);\\ (\root q \of {O_1}, \max \{\varepsilon _2,\eta _2\}), &{} \varepsilon ^q_1,\eta ^q_1\in (0.5,1], \varepsilon ^q_2 \in [0.5,1] \text {~or~} \eta ^q_2 \in [0.5,1];\\ (\min \{\varepsilon _1,\eta _1\}), \root q \of {G_1}), &{} \varepsilon ^q_2,\eta ^q_2 \in [0,0.5), \varepsilon ^q_1\in [0,0.5] \text {~or~} \eta ^q_1 \in [0,0.5];\\ (\min \{\varepsilon _1,\eta _1\}), \max \{\varepsilon _2,\eta _2\}), &{} otherwise, \end{array} \right. \end{aligned} \end{aligned}$$

  where $O_1 = \frac{1+(2\varepsilon _1^q-1)^2(2\eta _1^q-1)^2}{2}$, $G_1 = \frac{1-(1-2\varepsilon _2^q)^2(1-2\eta _2^q)^2}{2}$.

• 2. The q-ROF overlap function $\mathscr {O}_{m\frac{1}{2}}$ satisfies (O7):

  $$\begin{aligned} \mathscr {O}_{m\frac{1}{2}}(\varepsilon , \eta ) = \bigg (\min \bigg \{\sqrt{\varepsilon _1},\sqrt{\eta _1}\},~\root q \of {1-\min \{\sqrt{1-\varepsilon ^q_2},\sqrt{1-\eta ^q_2}\bigg \}}\bigg ). \end{aligned}$$

• 3. The q-ROF overlap function $\mathscr {O}^V_{mM}$ satisfies (O6) and (O7):

  $$\begin{aligned} \begin{aligned} \mathscr {O}^V_{mM}(\varepsilon , \eta ) = \left\{ \begin{array}{ll} (\root q \of {O_2},\root q \of {G_2}), &{} \varepsilon ^q_1,\eta ^q_1\in (0.5,1],\varepsilon ^q_2,\eta ^q_2 \in [0,0.5);\\ (\root q \of {O_2}, \max \{\varepsilon _2,\eta _2\}), &{} \varepsilon ^q_1,\eta ^q_1\in (0.5,1], \varepsilon ^q_2 \in [0.5,1] \text {~or~} \eta ^q_2 \in [0.5,1];\\ (\min \{\varepsilon _1,\eta _1\}), \root q \of {G_2}), &{} \varepsilon ^q_2,\eta ^q_2 \in [0,0.5), \varepsilon ^q_1\in [0,0.5] \text {~or~} \eta ^q_1 \in [0,0.5];\\ (\min \{\varepsilon _1,\eta _1\}), \max \{\varepsilon _2,\eta _2\}), &{} otherwise, \end{array} \right. \end{aligned} \end{aligned}$$

  where $O_2 = \frac{1+\min \{2\varepsilon ^q_1-1,2\eta ^q_1-1\}\max \{(2\varepsilon _1^q-1)^2,(2\eta _1^q-1)^2\}}{2},~G_2 =\frac{1}{2}- \frac{\min \{1-2\varepsilon ^q_2,1-2\eta ^q_2\}\max \{(1-2\varepsilon _2^q)^2,(1-2\eta _2^q)^2\}}{2}$.

Analogously, from the viewpoint of application, additive generators make it simple to choose the appropriate q-ROF overlap function for a given problem because we only need to consider functions with single variable rather than two variables, reducing computational complexity in this way. In Dimuro et al. (2016) and Dimuro et al. (2014), there exist several additional generators of overlap function and grouping function defined on [0, 1]. Next, in order to construct q-ROF overlap function by means of one-place functions, we introduce the definition of additive generator pair of q-ROF overlap as follows.

Definition 19

Let O be an overlap function on [0, 1] which has some additive generator pair $(\gamma , \vartheta )$, where $\gamma : [0,1]\rightarrow [0,\infty ]$, $\vartheta :[0,\infty ]\rightarrow [0,1]$ and G a grouping function on [0, 1] which has some additive generator pair $(\varrho ,\tau )$, where $\varrho : [0,1]\rightarrow [0,\infty ]$, $\tau :[0,\infty ]\rightarrow [0,1]$ and $O(\lambda ,\delta ) \le 1 - G(1-\lambda ,1-\delta )$ for $\lambda , \delta \in [0,1]$. Then, for $\varepsilon ,\eta \in L$, the function $\mathscr {O}:L\times L\rightarrow L$ given by

$$\begin{aligned} \mathscr {O}(\varepsilon ,\eta ) = (\vartheta ^{1/q}(\gamma (\varepsilon _1^q)+\gamma (\eta _1^q)), \tau ^{1/q}(\varrho (\varepsilon _2^q)+\varrho (\eta _2^q))), \end{aligned}$$

is a q-ROF overlap function. The quadruple $(\gamma , \vartheta , \varrho ,\tau )$ is called an additive generator pair of q-ROF overlap function $\mathscr {O}$.

In Qiao and Hu (2018), Qiao and Hu introduce the concepts of multiplicative generator pair for overlap function and grouping function. We introduce the concept of a multiplicative generator pair of q-ROF overlap function by means of their concepts.

Definition 20

If (g, h) is a multiplicative generator pair of the overlap function O on [0, 1], where $g,h: [0,1]\rightarrow [0,1]$ and $(\varphi ,\psi )$ is a multiplicative generator pair of the grouping function G on [0, 1], where $\varphi ,\psi : [0,1]\rightarrow [0,1]$, and $O(\lambda ,\delta ) \le 1 - G(1-\lambda ,1-\delta )$ for $\lambda , \delta \in [0,1]$. Then, for $\varepsilon , \eta \in L$, the function $\mathscr {O}:L\times L\rightarrow L$ given by

$$\begin{aligned} {\mathscr {O}}(\varepsilon ,\eta ) = (g^{1/q}(h(\varepsilon _1^q)\cdot h(\eta _1^q)), \varphi ^{1/q}(\psi (\varepsilon _2^q){\cdot {\psi }}(\eta _2^q))), \end{aligned}$$

is a q-ROF overlap function. The quadruple $(g, h, \varphi ,\psi )$ is called a multiplicative generator pair of q-ROF overlap function $\mathscr {O}$.

Moreover, we also give the definition of q-ROF residual implication (q-ROF $R_O$-implication) derived from q-ROF overlap function as follows.

Definition 21

Let $\mathscr {O}$ be a q-ROF overlap function on $L\times L$. A binary operation $\mathscr {I}_{O}$ on $L\times L$ given by

$$\begin{aligned} \mathscr {I}_{O}(\varepsilon ,\eta ) = \max \{z \in [0,1]\mid \mathscr {O}(\varepsilon ,z)\preceq _L \eta \}, \end{aligned}$$

is called a q-ROF $R_O$-implication derived from q-ROF overlap function.

In the end, we introduce the concept of residual fuzzy difference operator derived from grouping function G and put forward the method of constructing q-ROF $R_O$-implication with it.

Definition 22

Let G be a grouping function on $[0,1]^2$. A binary operation $\mathscr {D}: [0,1]^2 \rightarrow [0,1]$ given by

$$\begin{aligned} \mathscr {D}(\varepsilon ,\eta ) = \min \{z \in [0,1]\mid G(z,\eta )\ge \varepsilon \} \end{aligned}$$

is called a residual fuzzy difference operator derived from grouping function G.

Proposition 4

Let O be an overlap function on $[0,1]^2$ and G be a grouping function on $[0,1]^2$, $I_{O}$ be a residual implication on $[0,1]^2$ derived from O and $\mathscr {D}$ be a residual fuzzy difference operator on $[0,1]^2$ derived from G. Then the q-ROF $R_O$-implication can be defined by

$$\begin{aligned} \mathscr {I}_{O}(\varepsilon ,\eta ) = \bigg (\min \bigg \{\root q \of {I_{O}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg \},\root q \of {\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg ). \end{aligned}$$

Example 4

In this Example, we compute the q-ROF $R_O$-implications on L derived from the q-ROF overlap functions in Example 3. For $\varepsilon = (\varepsilon _1,\varepsilon _2), \eta = (\eta _1,\eta _2) \in L$ and $\rho , \delta \in [0,1].$

• 1. It is easily verified that $\mathscr {O}_2^V$ is derived from $O_2^V$ and $G_2^V$ which are defined by

  $$\begin{aligned} \begin{aligned} O_2^V(\rho , \delta ) = \left\{ \begin{array}{ll} \frac{1+(2\rho -1)^2(2\delta -1)^2}{2}, &{} \rho , \delta \in (0.5, 1],\\ \min \{\rho , \delta \}, &{} otherwise, \end{array} \right. \end{aligned} \end{aligned}$$
  $$\begin{aligned} \begin{aligned} G_2^V(\rho ,b) = \left\{ \begin{array}{ll} \frac{1- (1-2\rho )^2(1-2\delta )^2}{2}, &{} \rho , \delta \in [0,0.5),\\ \max \{\rho , \delta \}, &{} otherwise. \end{array} \right. \end{aligned} \end{aligned}$$

  The residual implication $I_{O_2^V}$ and the residual fuzzy difference operator $\mathscr {D}_{G_2^V}$ are

  $$\begin{aligned} \begin{aligned} I_{O_2^V}(\rho , \delta ) = \left\{ \begin{array}{ll} \min \bigg \{1, \frac{\sqrt{2\delta -1}}{2(2\rho -1)}+ \frac{1}{2}\bigg \}, &{} \rho \in (0.5,1], \delta \in [0.5,1],\\ \delta , &{} \delta \in [0,0.5),\rho > \delta ,\\ 1 , &{} \rho \in [0,0.5],\rho \le \delta , \end{array} \right. \end{aligned} \end{aligned}$$
  $$\begin{aligned} \begin{aligned} \mathscr {D}_{G_2^V}(\delta , \rho ) = \left\{ \begin{array}{ll} \max \bigg \{0, \frac{1}{2}-\frac{\sqrt{1- 2\delta }}{2(1-2\rho )}\bigg \}, &{} \rho \in [0.0.5), \delta \in [0.0.5],\\ \delta , &{} \delta \in (0.5,1],\rho < \delta ,\\ 0 , &{} \rho \in [0.5,1],\rho \ge \delta . \end{array} \right. \end{aligned} \end{aligned}$$

  Then

  $$\begin{aligned} \begin{aligned} \mathscr {I}_{O_2^V}(\varepsilon , \eta ) = \left\{ \begin{array}{ll} \bigg (\min \bigg \{\root q \of {I_1},\root q \of {1-D_1}\bigg \},\root q \of {D_1}\bigg ), &{} \varepsilon ^q_1\in (0.5,1], \eta ^q_1\in [0.5,1],\varepsilon ^q_2 \in [0,0.5), \eta ^q_2\in [0.0.5],\\ \bigg (\min \bigg \{\root q \of {I_1},\root q \of {1-\eta _2^q}\bigg \},\eta _2\bigg ), &{} \varepsilon ^q_1\in (0.5,1], \eta ^q_1\in [0.5,1],\eta ^q_2 \in (0.5,1],\varepsilon _2< \eta _2\\ (\root q \of {I_1},0), &{} \varepsilon ^q_1\in (0.5,1], \eta ^q_1\in [0.5,1],\varepsilon ^q_2 \in [0.5,1],\varepsilon _2 \ge \eta _2,\\ \bigg (\min \bigg \{\eta _1,\root q \of {1-D_1}\bigg \},\root q \of {D_1}\bigg ), &{} \eta ^q_1 \in [0,0.5),\varepsilon _1> \eta _1, \varepsilon ^q_2 \in [0,0.5), \eta ^q_2\in [0,0.5],\\ \bigg (\min \bigg \{\eta _1,\root q \of {1-\eta _2^q}\bigg \},\eta _2\bigg ), &{} \eta ^q_1 \in [0,0.5),\varepsilon _1> \eta _1, \eta ^q_2 \in (0.5,1],\varepsilon _2< \eta _2,\\ (\eta _1, 0), &{}\eta ^q_1 \in [0,0.5),\varepsilon _1 > \eta _1,\varepsilon ^q_2 \in [0.5,1],\varepsilon _2 \ge \eta _2,\\ \bigg (\min \bigg \{1,\root q \of {1-D_1}\bigg \},\root q \of {D_1}\bigg ), &{} \varepsilon ^q_1 \in [0,0.5],\varepsilon _1 \le \eta _1, \varepsilon ^q_2 \in [0,0.5), \eta ^q_2\in [0,0.5],\\ \bigg (\min \bigg \{1,\root q \of {1-\eta _2^q}\bigg \},\eta _2\bigg ), &{} \varepsilon ^q_1 \in [0,0.5],\varepsilon _1 \le \eta _1, \eta ^q_2 \in (0.5,1],\varepsilon _2 < \eta _2,\\ (1, 0), &{} \varepsilon ^q_1 \in [0,0.5],\varepsilon _1 \le \eta _1, \varepsilon ^q_2 \in [0.5,1],\varepsilon _2 \ge \eta _2,\\ \end{array} \right. \end{aligned} \end{aligned}$$

  where $I_1 = \min \bigg \{1, \frac{\sqrt{2\eta _1^q -1}}{2(2\varepsilon _1^q-1)}+ \frac{1}{2}\bigg \},~D_1 = \max \bigg \{0, \frac{1}{2}-\frac{\sqrt{1- 2\eta _2^q}}{2(1-2\varepsilon _2^q)}\bigg \}$.

• 2. It is easily verified that $\mathscr {O}_{m\frac{1}{2}}$ is derived from $O_{m\frac{1}{2}}$ and $G_{m\frac{1}{2}}$ which are defined by

  $$\begin{aligned} O_{m\frac{1}{2}}(\rho ,\delta ) = \min \bigg \{\sqrt{\rho },\sqrt{\delta }\bigg \},~G_{m\frac{1}{2}}(\rho ,\delta )=1-\min \bigg \{\sqrt{1-\rho },\sqrt{1-\delta }\bigg \}. \end{aligned}$$

  The residual implication $I_{O_{m\frac{1}{2}}}$ and the residual fuzzy difference operator $\mathscr {D}_{G_{m\frac{1}{2}}}$ are

  $$\begin{aligned} \begin{aligned} I_{O_{m\frac{1}{2}}}(\rho , \delta ) = \left\{ \begin{array}{ll} 1, &{} \sqrt{\rho } \le \delta ,\\ \delta ^2, &{} \sqrt{\rho } > \delta ,\\ \end{array} \right. \end{aligned} \end{aligned}$$
  $$\begin{aligned} \begin{aligned} \mathscr {D}_{G_{m\frac{1}{2}}}(\delta , \rho ) = \left\{ \begin{array}{ll} 1-(1-\delta )^2, &{} \rho < 1-(1-\delta )^2,\\ 0, &{} \rho \ge 1-(1-\delta )^2.\\ \end{array} \right. \end{aligned} \end{aligned}$$

  Then

  $$\begin{aligned} \begin{aligned} \mathscr {I}_{O_{m\frac{1}{2}}}(\varepsilon , \eta ) = \left\{ \begin{array}{ll} (\min \{1,\root q \of {1-D}\},\root q \of {D}), &{} \sqrt{\varepsilon _1} \le \eta _1, \varepsilon ^q_2< 1-(1-\eta ^q_2)^2,\\ (1,0), &{} \sqrt{\varepsilon _1} \le \eta _1, \varepsilon ^q_2 \ge 1-(1-\eta ^q_2)^2,\\ (\min \{\eta _1^2,\root q \of {1-D}\},\root q \of {D}), &{} \sqrt{\varepsilon _1}> \eta _1, \varepsilon ^q_2 < 1-(1-\eta ^q_2)^2,\\ (\eta _1^2,0), &{} \sqrt{\varepsilon _1} > \eta _1, \varepsilon ^q_2 \ge 1-(1-\eta ^q_2)^2. \end{array} \right. \end{aligned} \end{aligned}$$

  where $D = 1-(1-\eta _2^q)^2$.

• 3. It is easily verified that $\mathscr {O}^V_{mM}$ is derived from $O^V_{mM}$ and $G^V_{mM}$ which are defined by

  $$\begin{aligned} \begin{aligned} O^V_{mM}(\rho , \delta ) = \left\{ \begin{array}{ll} \frac{1+\min \{2\rho -1,2\delta -1\}\max \{(2\rho -1)^2,(2\delta -1)^2\}}{2}, &{} \rho , \delta \in (0.5, 1],\\ \min \{\rho , \delta \}, &{} otherwise, \end{array} \right. \end{aligned} \end{aligned}$$
  $$\begin{aligned} \begin{aligned} G^V_{mM}(\rho , \delta ) = \left\{ \begin{array}{ll} \frac{1-\min \{1-2\rho ,1-2\delta \}\max \{(1-2\rho )^2,(1-2\delta )^2\}}{2}, &{} \rho , \delta \in [0,0.5),\\ \max \{\rho , \delta \}, &{} otherwise. \end{array} \right. \end{aligned} \end{aligned}$$

  The residual implication $I_{O_2^V}$ and the residual fuzzy difference operator $\mathscr {D}_{G_2^V}$ are

  $$\begin{aligned} \begin{aligned} I_{O^V_{mM}}(\rho , \delta ) = \left\{ \begin{array}{ll} \min \{1,\max \{\frac{\sqrt{2\delta -1}}{2\sqrt{2\rho -1}},\frac{2\delta -1}{2(2\rho -1)^2}\}+\frac{1}{2}\}, &{} \rho \in (0.5,1], \delta \in [0.5,1],\\ \delta , &{} \delta \in [0,0.5),\rho > \delta ,\\ 1 , &{} \rho \in [0,0.5],\rho \le \delta , \end{array} \right. \end{aligned} \end{aligned}$$
  $$\begin{aligned} \begin{aligned} \mathscr {D}_{G^V_{mM}}(\delta , \rho ) = \left\{ \begin{array}{ll} \max \{0, \min \{\frac{1}{2}-\frac{\sqrt{1- 2\delta }}{2\sqrt{1-2\rho }},\frac{1}{2}-\frac{1-2\delta }{2(1-2\rho )^2} \}\}, &{} \rho \in [0.0.5), \delta \in [0.0.5],\\ \delta , &{} \delta \in (0.5,1],\rho < \delta ,\\ 0 , &{} \rho \in [0.5,1],\rho \ge \delta . \end{array} \right. \end{aligned} \end{aligned}$$

  Then

  $$\begin{aligned} \begin{aligned} \mathscr {I}_{O_2^V}(\varepsilon , \eta ) = \left\{ \begin{array}{ll} (\min \{\root q \of {I_2},\root q \of {1-D_2}\},\root q \of {D_2}), &{} \varepsilon ^q_1\in (0.5,1], \eta ^q_1\in [0.5,1],\varepsilon ^q_2 \in [0,0.5), \eta ^q_2\in [0,0.5],\\ (\min \{\root q \of {I_2},\root q \of {1-\eta _2^q}\},\eta _2), &{} \varepsilon ^q_1\in (0.5,1], \eta ^q_1\in [0.5,1],\eta ^q_2 \in (0.5,1],\varepsilon _2< \eta _2\\ (\root q \of {I_2},0), &{} \varepsilon _1\in (0.5,1], \eta _1\in [0.5,1],\varepsilon _2 \in [0.5,1],\varepsilon _2 \ge \eta _2,\\ (\min \{\eta _1,\root q \of {1-D_2}\},\root q \of {D_2}), &{} \eta ^q_1 \in [0,0.5),\varepsilon _1> \eta _1, \varepsilon ^q_2 \in [0.0.5), \eta ^q_2\in [0,0.5],\\ (\min \{\eta _1,\root q \of {1-\eta _2^q}\},\eta _2), &{} \eta ^q_1 \in [0,0.5),\varepsilon _1> \eta _1, \eta ^q_2 \in (0.5,1],\varepsilon _2< \eta _2,\\ (\eta _1, 0), &{}\eta ^q_1 \in [0,0.5),\varepsilon _1 > \eta _1,\varepsilon ^q_2 \in [0.5,1],\varepsilon _2 \ge \eta _2,\\ (\min \{1,\root q \of {1-D_2}\},\root q \of {D_2}), &{} \varepsilon ^q_1 \in [0,0.5],\varepsilon _1 \le \eta _1, \varepsilon ^q_2 \in [0,0.5), \eta ^q_2\in [0,0.5],\\ (\min \{1,\root q \of {1-\eta _2^q}\},\eta _2), &{} \varepsilon ^q_1 \in [0,0.5],\varepsilon _1 \le \eta _1, \eta ^q_2 \in (0.5,1],\varepsilon _2 < \eta _2,\\ (1, 0), &{} \varepsilon ^q_1 \in [0,0.5],\varepsilon _1 \le \eta _1, \varepsilon ^q_2 \in [0.5,1],\varepsilon _2 \ge \eta _2,\\ \end{array} \right. \end{aligned} \end{aligned}$$

  where $I_2 = \min \{1,\max \{\frac{\sqrt{2\eta _1^q-1}}{2\sqrt{2\varepsilon _1^q-1}},\frac{2\eta _1^q-1}{2(2\varepsilon _1^q-1)^2}\}+\frac{1}{2}\},~D_2 = \max \{0, \min \{\frac{1}{2}-\frac{\sqrt{1- 2\eta _2^q}}{2\sqrt{1-2\varepsilon _2^q}},\frac{1}{2}-\frac{1-2\eta _2^q}{2(1-2\varepsilon _2^q)^2}\}\}$.

4 q-ROF neighborhood opeartors based on a q-ROF covering

The concepts of q-ROF fuzzy covering, q-ROFNOs are proposed and the extensions of fuzzy neighborhood systems, four fuzzy neighborhood operators in q-ROF theory are discussed firstly in this section. Then the properties of four q-ROFNOs are put forward. Finally, given a q-ROF covering $\mathcal {C}$, we introduced q-ROF extensions of the derived coverings derived coverings $\mathcal {C}_1$, $\mathcal {C}_2$, $\mathcal {C}_3$, $\mathcal {C}_4$, $\mathcal {C}_{\cup }$, $\mathcal {C}_{\cap }$, $\hat{\mathcal {C}}_3$ and $\hat{\mathcal {C}}_4$.

4.1 q-ROF neighborhood system

In the following, the extension of fuzzy covering in q-ROF theory is illustrated.

Definition 23

Let U be a universe, ${\mathbb {I}}$ be an index set and $\mathscr {F}_q(U)$ denote the collection of q-ROF subsets on U. $\mathcal {C} = \{\Gamma _i \in \mathscr {F}_q(U) \mid \Gamma _i\ne \emptyset , i \in {\mathbb {I}}\}$ is called a q-ROF covering on U, if for each $\varepsilon \in U$, there exists a $i_\varepsilon \in {\mathbb {I}}$ which satisfies $\Gamma _{i_\varepsilon }(\varepsilon ) = 1_L$. When ${\mathbb {I}}$ is referred to as a finite set, $\mathcal {C}$ is defined as a finite q-ROF covering; otherwise, $\mathcal {C}$ is an infinite q-ROF covering.

Next, we extend the concept of fuzzy neighhood system in q-ROF theory and put forward the definition of q-ROF neighborhood system of $\varepsilon \in U$ as follows.

Definition 24

Let U be a universe and $\mathcal {C}$ be a q-ROF covering on U. A collection

$$\begin{aligned} \mathscr {C}(\mathcal {C}, \varepsilon ) = \{\Gamma \in \mathcal {C}\mid \Gamma (\varepsilon )\succ _L 0\} \end{aligned}$$

is called the q-ROF neighborhood system of $\varepsilon \in U$.

By definition of q-ROF covering, $\mathscr {C}(\mathcal {C}, \varepsilon ) \ne \emptyset$ for all $\varepsilon \in U$, since there always exists a q-ROFS $\Gamma \in \mathcal {C}$ satisfying $\Gamma (\varepsilon ) = 1_L$. Note that if $\mathcal {C}$ is a fuzzy covering, $\mathscr {C}(\mathcal {C}, \varepsilon )$ degenerates into a fuzzy neighborhood system in D’eer et al. (2017). Next, we discuss the extension of fuzzy minimal and maximal description of $\varepsilon \in U$ in q-ROF theory.

Definition 25

Let $\mathcal {C}$ be a q-ROF covering on U. A collection

$$\begin{aligned} \widetilde{md}(\mathcal {C}, \varepsilon ) = \{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )\mid (\forall K \in \mathscr {C}(\mathcal {C}, \varepsilon ))(K(\varepsilon ) = \Gamma (\varepsilon ), K \subset \Gamma \Rightarrow K = \Gamma )\} \end{aligned}$$

is called the q-ROF minimal description of $\varepsilon \in U$. A collection

$$\begin{aligned} \widetilde{MD}(\mathcal {C}, \varepsilon ) = \{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )\mid (\forall K \in \mathscr {C}(\mathcal {C}, \varepsilon ))(K(\varepsilon ) = \Gamma (\varepsilon ), K \supset \Gamma \Rightarrow K = \Gamma )\} \end{aligned}$$

is called the q-ROF maximal description of $\varepsilon \in U$.

Note that $\widetilde{md}(\mathcal {C}, \varepsilon ) \subseteq \mathscr {C}(\mathcal {C}, \varepsilon )$, $\widetilde{MD}(\mathcal {C}, \varepsilon ) \subseteq \mathscr {C}(\mathcal {C}, \varepsilon )$ and $\mathscr {C}(\mathcal {C}, \varepsilon )$, $\widetilde{md}(\mathcal {C}, \varepsilon )$, $\widetilde{MD}(\mathcal {C}, \varepsilon )$ are still collections of q-ROF sets on U. Further, if $\mathcal {C}$ is a fuzzy covering, $\widetilde{md}(\mathcal {C}, \varepsilon ), \widetilde{MD}(\mathcal {C}, \varepsilon )$ degenerate into the fuzzy minimal and maximal description of $\varepsilon$ defined in D’eer et al. (2017), respectively. Analogously to the property of the fuzzy minimal and maximal description of $\varepsilon$, if $\widetilde{MD}(\mathcal {C}, \varepsilon )$ ($\widetilde{md}(\mathcal {C}, \varepsilon )$) is closed under supremum (resp. infimum), $\widetilde{MD}(\mathcal {C},\varepsilon )$ (resp. $\widetilde{md}(\mathcal {C},\varepsilon )$) has following property:

Proposition 5

Assume that any ascending (resp. descending) chain of the q-ROF covering $\mathcal {C}$ on U is closed under supremum (resp. infimum), i.e., for any set $\{\Gamma _i \in \mathcal {C}\mid i \in {\mathbb {I}}\}$ with $\Gamma _i \subseteq \Gamma _{i+1}$ (resp. $\Gamma _i \supseteq \Gamma _{i+1}$), then

$$\begin{aligned} \sup \limits _{i \in {\mathbb {I}}} \Gamma _i = \mathop \cup \limits _{i \in {\mathbb {I}}} \Gamma _i \in \mathcal {C}~~(resp. \inf \limits _{i \in {\mathbb {I}}} \Gamma _i = \mathop \cap \limits _{i \in {\mathbb {I}}} \Gamma _i) \in \mathcal {C}. \end{aligned}$$

Let $\Gamma \in \mathscr {C}(\mathcal {C},\varepsilon )$, then there exist $\Gamma _1 \in \widetilde{MD}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma _1(\varepsilon ) = \Gamma (\varepsilon )$ and $\Gamma \subseteq \Gamma _1$ (resp. $\Gamma _2 \in \widetilde{md}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma _2(\varepsilon ) = \Gamma (\varepsilon )$ and $\Gamma \supseteq \Gamma _2$).

Obviously, Proposition 5 always holds when the q-ROF covering $\mathcal {C}$ is finite. The following example illustrates that condition on $\mathcal {C}$ is necessary in Proposition 5.

Example 5

Let $U = (\varepsilon ,\eta )$ and the q-ROF covering $\mathcal {C} = \{\Gamma _n \mid n\in {\mathbb {N}}{\setminus }\{0\}\} \cup \{\Gamma ^* = \{(\varepsilon ,0.8,0.3), (\eta ,1,0)\}\}$, where $\Gamma _n = \{(\varepsilon ,1,0), (\eta ,\dfrac{1}{n},1-\frac{1}{n})\}$. Note that $\Gamma ^* \in \widetilde{md}(\mathcal {C}, \varepsilon )$ and $\Gamma _{n+1} \subseteq \Gamma _n$, $\Gamma _n \notin \widetilde{md}(\mathcal {C}, \varepsilon )$. Therefore, there is no fuzzy set $\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )$ such that $\Gamma (\varepsilon ) = (1,0)$.

4.2 q-ROFNOs

The concept of q-ROFNOs as the extension of fuzzy neighborhood operator in q-ROF theory is defined as follows.

Definition 26

Let U be an universe and $\mathscr {F}_q(U)$ be the collection of q-ROF subsets on U. A mapping $N: U\longrightarrow \mathscr {F}_q(U)$ is called a q-ROFNO.

From Definition 26, it is obvious that the q-ROFNO maps every element $\varepsilon \in U$ to a q-ROFS $N(\varepsilon )$. Note that the q-ROF binary relation is a mapping $R: L \times L \longrightarrow L$. By taking $N(\varepsilon )(\eta ) = R(\varepsilon ,\eta )$ for $\varepsilon ,\eta \in U$, the q-ROFNO N on U is equivalent to the q-ROF binary relation R on U. Analogously to the q-ROF fuzzy binary relation, the reflexivity, symmetry and $\mathscr {T}$-transitivity of the q-ROFNO N are defined as follows.

Definition 27

Let U be a universe and N be a q-ROFNO on U. Then

• 1. N is reflexive $\Leftrightarrow$ $N(\varepsilon )(\varepsilon ) = 1$ for $\varepsilon \in U$;

• 2. N is symmetric $\Leftrightarrow$ $N(\varepsilon )(\eta ) = N(\eta )(\varepsilon )$ for $\varepsilon ,\eta \in U$;

• 3. N is $\mathscr {T}$-transitive $\Leftrightarrow$ $\mathscr {T}(N(\varepsilon )(\eta ),N(\eta )(\theta ))\le N(\varepsilon )(\theta )$ for $\varepsilon ,\eta ,\theta \in U$, where $\mathscr {T}$ is a q-ROF t-norm.

4.2.1 The first kind of q-ROFNOs

Based on concepts of q-ROF t-norm and q-ROF overlap function given in Sect. 3, the extensions of q-ROFNOs on q-ROF covering are introduced by means of q-ROF minimal and maximal desciption of $\varepsilon \in U$. We can now introduce two extensions of the first kind of fuzzy neighborhood operators in D’eer et al. (2017) and Qi et al. (2023) under q-ROF theory.

Definition 28

Let $\mathcal {C}$ be a q-ROF covering on U and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication. Then the q-ROFNO $N_1^\mathcal {C}$ of $\varepsilon \in U$ defined by

$$\begin{aligned} N_1^\mathcal {C}(\varepsilon ): U\rightarrow L:v\mapsto \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )), \end{aligned}$$

is the first kind of t-norm-based q-ROFNO (Tq-ROFNO).

Note that if $\mathcal {C}$ is a fuzzy covering on U, $N_1^\mathcal {C}$ degenerates into the first type of fuzzy neighborhood operator defined in D’eer et al. (2017).

Definition 29

Let $\mathcal {C}$ be a q-ROF covering on U and $\mathscr {I}_{O}$ be a q-ROF $R_O$-implication. Then the q-ROFNO ${\mathbb {N}}_1^\mathcal {C}$ of $\varepsilon \in U$ defined by

$$\begin{aligned} {\mathbb {N}}_1^\mathcal {C}(\varepsilon ): U\rightarrow L:\eta \mapsto \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{O}(\Gamma (\varepsilon ),\Gamma (\eta )), \end{aligned}$$

is the first kind of overlap function-based q-ROFNO (Oq-ROFNO).

Note that if $\mathscr {I}_{O}$ is defined by the q-ROF overlap function $\mathscr {O}$ which satisfies (O8), the ${\mathbb {N}}_1^\mathcal {C}$ is a kind of $N_1^\mathcal {C}$. And other equivalent definitions of $N_1^\mathcal {C}$ and ${\mathbb {N}}_1^\mathcal {C}$ by means of $\mathscr {C}(\mathcal {C}, \varepsilon )$ and $\widetilde{md}(\mathcal {C}, x)$ can be introduced as follows.

Proposition 6

Let $\mathcal {C}$ be a finite q-ROF covering on U and $\mathscr {I}_{T}$ be a $R_T$-implication. Then it holds that

$$\begin{aligned} \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \inf \limits _{\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) \end{aligned}$$

for $\varepsilon ,\eta \in U$.

Proposition 7

Let $\mathcal {C}$ be a finite q-ROF fuzzy covering on U and $\mathscr {I}_{O}$ be a $R_O$-implication. Then it holds that

$$\begin{aligned} \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{O}(\Gamma (\varepsilon ),\Gamma (\eta )) = \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {I}_{O}(\Gamma (\varepsilon ),\Gamma (\eta )) = \inf \limits _{\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {I}_{O}(\Gamma (\varepsilon ),\Gamma (\eta )) \end{aligned}$$

for $\varepsilon ,\eta \in U$.

4.2.2 The second kind of q-ROFNOs

Analogously, two extensions of the second kind of fuzzy neighborhood operators in D’eer et al. (2017) and Qi et al. (2023) under q-ROF theory are defined as follows.

Definition 30

Let $\mathcal {C}$ be a q-ROF covering on U and $\mathscr {T}$ be a q-ROF t-norm. Then the q-ROFNO $N_2^\mathcal {C}$ of $\varepsilon \in U$ defined by

$$\begin{aligned} N_2^\mathcal {C}(\varepsilon ): U\rightarrow L:y\mapsto \sup \limits _{\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )), \end{aligned}$$

is the second kind of Tq-ROFNO.

Note that if $\mathcal {C}$ is a fuzzy covering on U, $N_2^\mathcal {C}$ degenerates into the sencond kind of fuzzy neighborhood operator defined in D’eer et al. (2017).

Definition 31

Let $\mathcal {C}$ be a q-ROF covering on U and $\mathscr {O}$ be a q-ROF overlap function. Then the q-ROFNO ${\mathbb {N}}_2^\mathcal {C}$ of $\varepsilon \in U$ defined by

$$\begin{aligned} {\mathbb {N}}_2^\mathcal {C}(\varepsilon ): U \rightarrow L:y\mapsto \sup \limits _{\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {O}(\Gamma (\varepsilon ),\Gamma (\eta )), \end{aligned}$$

is the second kind of Oq-ROFNO.

Note that if the q-ROF overlap function $\mathscr {O}$ satisfies (O8), ${\mathbb {N}}_2^\mathcal {C}$ is a sort of $N_2^\mathcal {C}$.

4.2.3 The third kind of q-ROFNOs

Two extensions of the third kind of fuzzy neighborhood operators in D’eer et al. (2017) and Qi et al. (2023) under q-ROF theory can also be defined as follows.

Definition 32

Let $\mathcal {C}$ be a q-ROF covering on U and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication. Then the q-ROFNO $N_3^\mathcal {C}$ of $\varepsilon \in U$ defined by

$$\begin{aligned} N_3^\mathcal {C}(\varepsilon ): U\rightarrow L:y\mapsto \inf \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )), \end{aligned}$$

is the third kind of Tq-ROFNO.

Note that if $\mathcal {C}$ is a fuzzy covering on U, $N_3^\mathcal {C}$ degenerates into the third kind of fuzzy neighborhood operator defined in D’eer et al. (2017).

Definition 33

Let $\mathcal {C}$ be a q-ROF covering on U and $\mathscr {I}_{O}$ be a q-ROF $R_O$-implication. Then the q-ROFNO ${\mathbb {N}}_3^\mathcal {C}$ of $\varepsilon \in U$ defined by

$$\begin{aligned} {\mathbb {N}}_3^\mathcal {C}(\varepsilon ): U\rightarrow L:y\mapsto \inf \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )} \mathscr {I}_{O}(\Gamma (\varepsilon ),\Gamma (\eta )), \end{aligned}$$

is the third kind of Oq-ROFNO.

Note that if $\mathscr {I}_{O}$ is defined by the q-ROF overlap function $\mathscr {O}$ which satisfies (O8), ${\mathbb {N}}_3^\mathcal {C}$ is a kind of $N_3^\mathcal {C}$.

4.2.4 The fourth kind of q-ROFNOs

At last, we introduce two extensions of the fourth kind of fuzzy neighborhood operators in D’eer et al. (2017) and Qi et al. (2023) under q-ROF theory.

Definition 34

Let $\mathcal {C}$ be a q-ROF covering on U and $\mathscr {T}$ be a q-ROF t-norm. Then the q-ROFNO $N_4^\mathcal {C}$ of $\varepsilon \in U$ defined by

$$\begin{aligned} N_4^\mathcal {C}(\varepsilon ): U\rightarrow L:\eta \mapsto \sup \limits _{\Gamma \in \mathcal {C}} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )), \end{aligned}$$

is the fourth kind of Tq-ROFNO.

Note that if $\mathcal {C}$ is a fuzzy covering on U, $N_4^\mathcal {C}$ degenerates into the fourth kind of fuzzy neighborhood operator defined in D’eer et al. (2017).

Definition 35

Let $\mathcal {C}$ be a q-ROF covering on U and $\mathscr {O}$ be a q-ROF overlap function. Then the q-ROFNO ${\mathbb {N}}_4^\mathcal {C}$ of $\varepsilon \in U$ defined by

$$\begin{aligned} {\mathbb {N}}_4^\mathcal {C}(\varepsilon ): U\rightarrow L:\eta \mapsto \sup \limits _{\Gamma \in \mathcal {C}} \mathscr {O}(\Gamma (\varepsilon ),\Gamma (\eta )), \end{aligned}$$

is the fourth kind of Oq-ROFNO.

Note that if the q-ROF overlap function $\mathscr {O}$ satisfies (O8), ${\mathbb {N}}_4^\mathcal {C}$ is a sort of $N_4^\mathcal {C}$. And other equivalent definitions of $N_4^\mathcal {C}$ and ${\mathbb {N}}_4^\mathcal {C}$ by means of $\mathscr {C}(\mathcal {C}, \varepsilon )$ and $\widetilde{MD}(\mathcal {C}, x)$ can be introduced as follows.

Proposition 8

Let $\mathcal {C}$ be a finite q-ROF covering on U and $\mathscr {T}$ be a q-ROF t-norm. Then it holds that

$$\begin{aligned} \sup \limits _{\Gamma \in \mathcal {C}} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \sup \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \sup \limits _{\Gamma \in \widetilde{MD}(\mathcal {C}, x)} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \end{aligned}$$

for $\varepsilon ,\eta \in U$.

Proposition 9

Let $\mathcal {C}$ be a finite q-ROF covering on U and $\mathscr {O}$ be a q-ROF overlap function. Then for all $\varepsilon ,\eta \in U$, it holds that

$$\begin{aligned} \sup \limits _{\Gamma \in \mathcal {C}} \mathscr {O}(\Gamma (\varepsilon ),\Gamma (\eta )) = \sup \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {O}(\Gamma (\varepsilon ),\Gamma (\eta )) = \sup \limits _{\Gamma \in \widetilde{MD}(\mathcal {C}, x)} \mathscr {O}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned}$$

4.3 Properties of q-ROFNOs

In D’eer et al. (2017) and Qi et al. (2023), the reflexivity, symmetry and transitivity of four kinds of fuzzy neighborhood operators discussed respectively. In this subsection, we illustrate that whether or under what conditions these properties of q-ROFNOs can be maintained. Firstly, we consider the reflexivity of q-ROFNOs.

Proposition 10

Let $\mathcal {C}$ be a finite q-ROF covering on U, $\mathscr {T}$ be a q-ROF t-norm and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication. Then $N_1^\mathcal {C}, N_3^\mathcal {C}$ and $N_4^\mathcal {C}$ are reflexive. Moreover, if $\mathcal {C}$ is finite, $N_2^\mathcal {C}$ is reflexive.

Proposition 11

Let $\mathcal {C}$ be a finite q-ROF covering on U, $\mathscr {O}$ be a q-ROF overlap function satisfied (O6) and $\mathscr {I}_{O}$ be a q-ROF R-implication. Then ${\mathbb {N}}_1^\mathcal {C}, {\mathbb {N}}_3^\mathcal {C}$ and ${\mathbb {N}}_4^\mathcal {C}$ are reflexive. Moreover, if $\mathcal {C}$ is finite, ${\mathbb {N}}_2^\mathcal {C}$ is reflexive.

The condition $\mathscr {O}$ which satisfies (O6) is necessary in the above proposition. An example is given to illustrate this fact.

Example 6

Let $U = \{\varepsilon ,\eta \}$ and $\mathcal {C} = \{\Gamma _1, \Gamma _2\}$ be a q-ROF covering with $\Gamma _1 = \{\left\langle \varepsilon , 1, 0 \right\rangle , \left\langle \eta , 0.81, 0.25 \right\rangle \},~ \Gamma _2 = \{\left\langle \varepsilon , 0.64, 0.36 \right\rangle , \left\langle \eta , 1, 0 \right\rangle \}$. The q-ROF overlap function $\mathscr {O}_{m\frac{1}{2}}$ which satisfies ($\mathscr {O}7$) and $\mathscr {I}_{O_{m\frac{1}{2}}}$ in Example 4 are used to define operators ${\mathbb {N}}_1^\mathcal {C}$ and ${\mathbb {N}}_3^\mathcal {C}$. Then ${\mathbb {N}}_1^\mathcal {C}(\varepsilon )(\varepsilon ) = {\mathbb {N}}_3^\mathcal {C}(\varepsilon )(\varepsilon ) = (0.1296,0).$ Hence, ${\mathbb {N}}_1^\mathcal {C}$ and ${\mathbb {N}}_3^\mathcal {C}$ are not reflexive.

Secondly, we conclude that only the fourth kind of q-ROFNOs $N_4^\mathcal {C}$ and ${\mathbb {N}}_4^\mathcal {C}$ are symmetric.

Proposition 12

Let $\mathcal {C}$ be a finite q-ROF covering on U and $\mathscr {T}$ be a q-ROF t-norm which is used to define $N_4^\mathcal {C}$. Then, $N_4^\mathcal {C}$ is symmetric, i.e. $N_4^\mathcal {C}(\varepsilon )(\eta ) = N_4^\mathcal {C}(\eta )(\varepsilon )$ for $\varepsilon ,\eta \in U$.

Proposition 13

Let $\mathcal {C}$ be a finite q-ROF covering on U and $\mathscr {O}$ be a q-ROF overlap function which is used to define ${\mathbb {N}}_4^\mathcal {C}$. Then, ${\mathbb {N}}_4^\mathcal {C}$ is symmetric, i.e. ${\mathbb {N}}_4^\mathcal {C}(\varepsilon )(\eta ) = {\mathbb {N}}_4^\mathcal {C}(\eta )(\varepsilon )$ for $\varepsilon ,\eta \in U$.

Finally, we discuss the transitivity of q-ROFNOs. Before that, we put forward the definiton of $\mathscr {O}$-transitivity.

Definition 36

Let ${\mathbb {N}}$ be a q-ROF neithborhood operator on U and $\mathscr {O}$ be a q-ROF overlap function. If for $\varepsilon ,\eta ,\theta \in U$, ${\mathbb {N}}$ satisfies $\mathscr {O}({\mathbb {N}}(\varepsilon )(\eta ),{\mathbb {N}}(\eta )(\theta ))\preceq _L {\mathbb {N}}(\varepsilon )(\theta )$, then ${\mathbb {N}}$ is $\mathscr {O}$-transitive.

Proposition 14

Let $\mathscr {T}$ be a continuous q-ROF t-norm and $\mathscr {I}_T$ be a q-ROF $R_T$-implication on $L\times L$. Then for $\varepsilon ,\eta ,\theta \in L$, we have $\mathscr {T}(\mathscr {I}(\varepsilon ,\eta ),\mathscr {I}(\eta ,\theta )) \preceq _L \mathscr {I}(\varepsilon ,\theta )$.

Proposition 15

Let $\mathcal {C}$ be a finite q-ROF covering on U, $\mathscr {T}$ be a continuous q-ROF t-norn and $I_{T}$ be a q-ROF $R_T$-implication which is used to define $N_1^\mathcal {C}$ and $N_3^\mathcal {C}$. Then $N_1^\mathcal {C}$ and $N_3^\mathcal {C}$ are $\mathscr {T}$-transitive, i.e.,

$$\begin{aligned}{} & {} \mathscr {T}(N_1^\mathcal {C}(\varepsilon )(\eta ),N_1^\mathcal {C}(\eta )(\theta )) \preceq _L N_1^\mathcal {C}(\varepsilon )(\theta ), \\{} & {} \quad \mathscr {T}(N_3^\mathcal {C}(\varepsilon )(\eta ),N_3^\mathcal {C}(\eta )(\theta )) \preceq _L N_3^\mathcal {C}(\varepsilon )(\theta ), \end{aligned}$$

for $\varepsilon ,\eta \in U$.

According to the above proposition, $N_1^\mathcal {C}$ and $N_3^\mathcal {C}$ are T-transitive. But the following example illustrate that ${\mathbb {N}}_1^\mathcal {C}$ and ${\mathbb {N}}_3^\mathcal {C}$ may be not O-transitive.

Example 7

Let $U = \{\varepsilon ,~\eta ,~\theta \}$ and $\mathcal {C} = \{\Gamma _1,~\Gamma _2\}$ be a q-ROF covering with $\Gamma _1 = \{\left\langle \varepsilon ,~ 1,~ 0 \right\rangle , \left\langle \eta ,~ 1,~0 \right\rangle ,\left\langle \theta ,~ 1, ~0 \right\rangle \}$, $\Gamma _2 = \{\left\langle \varepsilon , ~0.64, ~0.49 \right\rangle , \left\langle \eta , ~0.75, ~0.36 \right\rangle ,\left\langle \theta ,~ 0.49,~ 0.64 \right\rangle \}$ and $q = 3$. The q-ROF overlap function $\mathscr {O}_D = (x_1^2y_1^2$, $\root q \of {1-(1-x_2^q)^2(1-y_2^q)^2})$ which satisfies (O6) and

$$\begin{aligned} \begin{aligned} \mathscr {I}_D = \left\{ \begin{array}{ll} \bigg (\min \bigg \{1,\root q \of {1-D_x}\},\root q \of {D_x}\bigg ), &{} x_1^2 \le y_1, y^q_2> 1-(1-x^q_2)^2,\\ (1,0), &{} x_1^2 \le y_1, y^q_2 \le 1-(1-x^q_2)^2,\\ \bigg (\min \bigg \{\frac{\sqrt{y_1}}{x_1},\root q \of {1-D_x}\bigg \},\root q \of {D_x}\bigg ) &{} x_1^2> y_1, y^q_2> 1-(1-x^q_2)^2,\\ \bigg (\frac{\sqrt{y_1}}{x_1},0\bigg ) &{} x_1^2 > y_1, y^q_2 \le 1-(1-x^q_2)^2, \end{array} \right. \end{aligned} \end{aligned}$$

is used to define q-ROF operators ${\mathbb {N}}_1^\mathcal {C}$ and ${\mathbb {N}}_3^\mathcal {C}$, where $x=(x_1,x_2),~y=(y_1,y_2) \in L$, $D_x = 1-\frac{\sqrt{1-y_2^q}}{1-x_2^q}$. Then we have that

$$\begin{aligned} {\mathbb {N}}_1^\mathcal {C}(\eta )(\varepsilon )= & {} {\mathbb {N}}_3^\mathcal {C}(\varepsilon ,\eta ) = (1, 0), \\ {\mathbb {N}}_1^\mathcal {C}(\varepsilon )(\theta )= & {} {\mathbb {N}}_3^\mathcal {C}(\varepsilon ,\theta ) = (1, 0), \\ {\mathbb {N}}_1^\mathcal {C}(\eta )(\theta )= & {} {\mathbb {N}}_3^\mathcal {C}(\eta ,\theta ) = (0.9333, 0.4626). \end{aligned}$$

Thus, $\mathscr {O}_D({\mathbb {N}}_1^\mathcal {C}(\eta )(\varepsilon ), {\mathbb {N}}_1^\mathcal {C}(\varepsilon )(\theta )) \succ _L {\mathbb {N}}_1^\mathcal {C}(\eta )(\theta )$ and $\mathscr {O}_D({\mathbb {N}}_3^\mathcal {C}(\eta )(\varepsilon ), {\mathbb {N}}_3^\mathcal {C}(\varepsilon )(\theta )) \succ _L {\mathbb {N}}_3^\mathcal {C}(\eta )(\theta )$. Therefore, operators ${\mathbb {N}}_1^\mathcal {C}$ and ${\mathbb {N}}_3^\mathcal {C}$ is not $\mathscr {O}$-transitive.

4.4 q-ROF coverings derived from a q-ROF covering

We put forward the definitions of the q-ROF coverings $\mathcal {C}_1,\mathcal {C}_2,\mathcal {C}_3,$ $\mathcal {C}_4,\hat{\mathcal {C}}_3,\hat{\mathcal {C}}_4,\mathcal {C}_{\cup }$ and $\mathcal {C}_{\cap }$ derived from the given q-ROF covering $\mathcal {C}$ in this subsection.

Definition 37

Let $\mathcal {C}$ be a q-ROF covering on U. Then define the following collections of q-ROF sets:

• 1. $\mathcal {C}_1 = \cup \{\widetilde{md}(\mathcal {C},\varepsilon )\mid \varepsilon \in U\}$;

• 2. $\mathcal {C}_2 = \cup \{\widetilde{MD}(\mathcal {C},\varepsilon )\mid \varepsilon \in U\}$;

• 3. $\mathcal {C}_{\cup } = \mathcal {C}{\setminus } \{\Gamma \in \mathcal {C}\mid \exists \mathcal {C}^{\prime }\subseteq \mathcal {C}{\setminus } \{\Gamma \}, \Gamma = \bigcup \mathcal {C}^{\prime } \}$;

• 4. $\mathcal {C}_{\cap } = \mathcal {C}{\setminus } \{\Gamma \in \mathcal {C}\mid \exists \mathcal {C}^{\prime }\subseteq \mathcal {C}{\setminus } \{\Gamma \}, \Gamma = \bigcap \mathcal {C}^{\prime } \}$.

From the above definition, we can conclude that $\mathcal {C}_1,\mathcal {C}_2,\mathcal {C}_{\cup },\mathcal {C}_{\cap }$ are all non-empty q-ROF subsets of the original q-ROF covering $\mathcal {C}$. The following two propositions statement that $\mathcal {C}_1,\mathcal {C}_2,\mathcal {C}_{\cup }$ are also finite q-ROF subcoverings of $\mathcal {C}$ if the original q-ROF covering $\mathcal {C}$ is finite and $\mathcal {C}_{\cap }$ is a q-ROF subcoverings of $\mathcal {C}$ if $\mathcal {C}$ is infinite.

Proposition 16

Let $\mathcal {C}$ be a finite q-ROF covering. Then $\mathcal {C}_1,\mathcal {C}_2,\mathcal {C}_{\cup }$ are finite q-ROF subcoverings of $\mathcal {C}$.

The condition of finiteness for $\mathcal {C}$ in Proposition 16 is necessary. The necessity of condition for $\mathcal {C}_1$ and $\mathcal {C}_2$ is illustrated by Proposition 5. In the following example, we illustrate the necessity of condition for $\mathcal {C}_{\cup }$.

Example 8

Let $U = \{\varepsilon \}$ and $\mathcal {C} = \{\Gamma _n = \{\left\langle \varepsilon , 1-\frac{1}{n}, \frac{1}{n} \right\rangle \mid n\in {\mathbb {N}}{\setminus }\{0\}\} \bigcup \{\Gamma ^* = \{\left\langle \varepsilon , 1, 0 \right\rangle \}\}$. It is obvious that $\sup \{\Gamma _n \mid n\in {\mathbb {N}}{\setminus }\{0\}\} = \Gamma ^*$. Thus, $\Gamma ^* \notin \mathcal {C}_{\cup }$. Therefore, $\mathcal {C}_{\cup }$ is not a q-ROF covering.

Proposition 17

Let $\mathcal {C}$ be a q-ROF covering on U. Then $\mathcal {C}_{\cap }$ is a q-ROF subcoverings of $\mathcal {C}$.

Furthermore, if $\mathcal {C}$ be a finite q-ROF covering, we obtain that $\mathcal {C}_2$ is a q-ROF subcovering of $\mathcal {C}_{\cap }$ and $\mathcal {C}_1 = \mathcal {C}_{\cup }$.

Proposition 18

Let $\mathcal {C}$ be a finite q-ROF covering. Then $\mathcal {C}_2$ is a q-ROF subcoverings of $\mathcal {C}_{\cap }$.

Note that in the above proposition, the finiteness condition of the q-ROF covering is also necessary for $\mathcal {C}$. The following example illustrates that $\mathcal {C}_2$ is not necessarily a subcovering of $\mathcal {C}_{\cap }$ if $\mathcal {C}$ is infinite.

Example 9

Let $U = \{\varepsilon \}$ and $\mathcal {C} = \{\Gamma _n = \{\left\langle \varepsilon , \frac{1}{3} + \frac{1}{n}, \frac{1}{2n} \right\rangle \mid n\in {\mathbb {N}}{\setminus }\{0\}\} \cup \{\Gamma ^* = \{\left\langle x, \frac{1}{3}, 0 \right\rangle \}\}$. It is obvious that $\inf \{\Gamma _n \mid n\in {\mathbb {N}}{\setminus }\{0\}\} = \Gamma ^*$. Thus, $\Gamma ^* \notin \mathcal {C}_{\cap }$, but $\Gamma ^* \in \mathcal {C}_2$. Therefore, $\mathcal {C}_2$ is not a subcovering of $\mathcal {C}_{\cap }$.

Proposition 19

Let $\mathcal {C}$ be a finite q-ROF covering on U. Then $\mathcal {C}_1 = \mathcal {C}_{\cup }$.

Inspired by the definition $\mathcal {C}_3,\mathcal {C}_4$ in D’eer et al. (2017) and $\mathscr {C}_3,\mathscr {C}_4$ in Qi et al. (2023), the concepts of four new q-ROF coverings by q-ROF neiborhood operators $N_1^\mathcal {C},N_4^\mathcal {C}$ and ${\mathbb {N}}_1^\mathcal {C},{\mathbb {N}}_4^\mathcal {C}$ are defined as follows.

Definition 38

Let $\mathcal {C}$ be a q-ROF covering on U. Then define the following collections of q-ROF sets:

• 1. $\mathcal {C}_3 = \{N_1^\mathcal {C}(\varepsilon ) \mid \varepsilon \in U\}$;

• 2. $\mathcal {C}_4 = \{N_4^\mathcal {C}(\varepsilon )\mid \varepsilon \in U\}$;

• 3. $\hat{\mathcal {C}}_3 = \{{\mathbb {N}}_1^\mathcal {C}(\varepsilon )\mid \varepsilon \in U\}$;

• 4. $\hat{\mathcal {C}}_4 = \{{\mathbb {N}}_4^\mathcal {C}(\varepsilon )\mid \varepsilon \in U\}$.

Additionally, we can prove that $\mathcal {C}_3,\mathcal {C}_4,\hat{\mathcal {C}}_3,\hat{\mathcal {C}}_4$ are also q-ROF coverings.

Proposition 20

Let $\mathcal {C}$ be a q-ROF covering on U, $\mathscr {T}$ be a q-ROF t-norm to construct $\mathcal {C}_4$ and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implicaton to construct $\mathcal {C}_3$. Then $\mathcal {C}_3$ and $\mathcal {C}_4$ are q-ROF coverings.

Proposition 21

Let $\mathcal {C}$ be a q-ROF covering on U, $\mathscr {O}$ be a q-ROF overlap function to construct $\hat{\mathcal {C}}_4$ and $\mathscr {I}_{O}$ be a q-ROF $R_O$- implicaton to construct $\hat{\mathcal {C}}_3$. If $\mathscr {O}$ satisfies (O6), then $\hat{\mathcal {C}}_3$ and $\hat{\mathcal {C}}_4$ are q-ROF coverings.

The above two propositions can be proved from the fact that $N_1^\mathcal {C}, N_4^\mathcal {C}, {\mathbb {N}}_1^\mathcal {C}$ and ${\mathbb {N}}_4^\mathcal {C}$ are all reflexive.

5 The groups of q-ROFNOs on a finite q-ROF covering and their lattice relationships

In this section, we disscuss relations between Tq-ROFNOs based on a q-ROF covering $\mathcal {C}$ and relations between Oq-ROFNOs based on a q-ROF covering $\mathcal {C}$, respectively. We assume that the q-ROF covering $\mathcal {C}$ is finite, we can disregard $\mathcal {C}_{\cup }$ since $\mathcal {C}_1 = \mathcal {C}_{\cup }$. Note that two q-ROFNOs are different or incomparable when two fuzzy neighborhood operators are different or incomparable in classical fuzzy environment. Therefore, we only need to study whether the equalities and partial order relations of q-ROFNOs are also maintained.

Relations between q-ROF neighborhood system based on different q-ROF coverings are firstly considered.

Proposition 22

Let $\mathcal {C}$ be a finite q-ROF covering. Then for $\varepsilon \in U$, it holds that

• 1. $\widetilde{md}(\mathcal {C}_1,\varepsilon ) = \widetilde{md}(\mathcal {C},\varepsilon )$;

• 2. $\widetilde{MD}(\mathcal {C}_2,\varepsilon ) = \widetilde{MD}(\mathcal {C},\varepsilon )$;

• 3. $\widetilde{MD}(\mathcal {C}_{\cap },\varepsilon ) = \widetilde{MD}(\mathcal {C},\varepsilon )$.

Proposition 23

Let $\mathcal {C}$ be a finite q-ROF covering. Then it holds that $\widetilde{md}(\mathcal {C}_{\cap },\varepsilon ) \bigcap \mathcal {C}_2 \subseteq \widetilde{md}(\mathcal {C}_2,\varepsilon )$ for $\varepsilon \in U$.

5.1 Equalities among q-ROFNOs on finite q-ROF coverings

In this subsection, the equalities of q-ROFNOs based on different q-ROF coverings are discussed when the orignal covering $\mathcal {C}$ is finite.

Firstly, we consider the equivalences of Tq-ROFNOs $N_1^{\mathcal {C}}, N_1^{\mathcal {C}_1}, N_1^{\mathcal {C}_3}$ and $N_1^{\mathcal {C}_{\cap }}$.

Proposition 24

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication and q-ROFNOs $N_1^{\mathcal {C}}, N_1^{\mathcal {C}_1}, N_1^{\mathcal {C}_3}$ and $N_1^{\mathcal {C}_{\cap }}$ are defined by $\mathscr {I}_{T}$. Then

• 1. $N_1^{\mathcal {C}} = N_1^{\mathcal {C}_1}$;

• 2. $N_1^{\mathcal {C}} = N_1^{\mathcal {C}_3}$ if $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication of a continuous q-ROF t-norm;

• 3. $N_1^{\mathcal {C}} = N_1^{\mathcal {C}_{\cap }}$.

In light of the above proposition, t-norm-based q-ROFNOs $N_1^{\mathcal {C}}, N_1^{\mathcal {C}_1}, N_1^{\mathcal {C}_3}$ and $N_1^{\mathcal {C}_{\cap }}$ are still equal in q-ROF setting. When the q-ROF overlap function satisfies (O8) which used to difine these q-ROFNOs, it degenerates into a t-norm and ${\mathbb {N}}_1^{\mathcal {C}}, {\mathbb {N}}_1^{\mathcal {C}_1}, {\mathbb {N}}_1^{\mathcal {C}_3}, {\mathbb {N}}_1^{\mathcal {C}_{\cap }}$ are still equal on the basis of the above proposition. A natural question is whether q-ROFNOs ${\mathbb {N}}_1^{\mathcal {C}}, {\mathbb {N}}_1^{\mathcal {C}_1}, {\mathbb {N}}_1^{\mathcal {C}_3}, {\mathbb {N}}_1^{\mathcal {C}_{\cap }}$ are still equivalent when the q-ROF overlap function satisfies (O6). The following proposition gives a positive answer to this question.

Proposition 25

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {I}_{O}$ be a q-ROF $R_O$-implication and ${\mathbb {N}}_1^{\mathcal {C}}, {\mathbb {N}}_1^{\mathcal {C}_1}$ and ${\mathbb {N}}_1^{\mathcal {C}_{\cap }}$ are defined by $\mathscr {I}_{O}$. Then

• 1. ${\mathbb {N}}_1^{\mathcal {C}} = {\mathbb {N}}_1^{\mathcal {C}_1}$;

• 2. ${\mathbb {N}}_1^{\mathcal {C}} = {\mathbb {N}}_1^{\mathcal {C}_{\cap }}$.

In light of the above proposition, we show that equivalences of overlap function-based q-ROFNOs ${\mathbb {N}}_1^{\mathcal {C}}, {\mathbb {N}}_1^{\mathcal {C}_1}, {\mathbb {N}}_1^{\mathcal {C}_{\cap }}$ are still maintained. In fact, ${\mathbb {N}}_1^{\mathcal {C}_3}$ is different with others since the q-ROF overlap function satisfying (O6) is not $\mathscr {O}$-transitive. Next, we study the equivalence of q-ROFNOs $N_2^{\mathcal {C}}$ and $N_2^{\mathcal {C}_1}$.

Proposition 26

Let $\mathcal {C}$ be a finite q-ROF covering and Tq-ROFNOs $N_2^{\mathcal {C}}, N_2^{\mathcal {C}_1}$ be defined by q-ROF t-norms $\mathscr {T}$, then $N_2^{\mathcal {C}} = N_2^{\mathcal {C}_1}$.

Moreover, we study the equivalence of q-ROFNOs ${\mathbb {N}}_2^{\mathcal {C}}$ and ${\mathbb {N}}_2^{\mathcal {C}_1}$. When the q-ROF overlap function used to define ${\mathbb {N}}_2^{\mathcal {C}}, {\mathbb {N}}_2^{\mathcal {C}_1}$ satisfies (O8), it is a t-norm, and ${\mathbb {N}}_2^{\mathcal {C}}, {\mathbb {N}}_2^{\mathcal {C}_1}$ degenerate into $N_2^{\mathcal {C}}$ and $N_2^{\mathcal {C}_1}$. Therefore, they are still equal. The following proposition study the equivalence of ${\mathbb {N}}_2^{\mathcal {C}}$ and ${\mathbb {N}}_2^{\mathcal {C}_1}$ when the q-ROF overlap function used to define ${\mathbb {N}}_2^{\mathcal {C}}$ and ${\mathbb {N}}_2^{\mathcal {C}_1}$ satisfies (O6).

Proposition 27

Let $\mathcal {C}$ be a finite q-ROF covering and ${\mathbb {N}}_2^{\mathcal {C}}, {\mathbb {N}}_2^{\mathcal {C}_1}$ be defined by a q-ROF overlap function $\mathscr {O}$ satisfying (O6), then ${\mathbb {N}}_2^{\mathcal {C}} = {\mathbb {N}}_2^{\mathcal {C}_1}$.

Then, we consider the equivalences of q-ROFNOs $N_3^{\mathcal {C}}, N_3^{\mathcal {C}_2}, N_3^{\mathcal {C}_{\cap }}$ and the equivalences of ${\mathbb {N}}_3^{\mathcal {C}}, {\mathbb {N}}_3^{\mathcal {C}_2}, {\mathbb {N}}_3^{\mathcal {C}_{\cap }}$ when the q-ROF overlap function which is used to define them satisfies (O6).

Proposition 28

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication derived from q-ROF t-norm and q-ROFNOs $N_3^{\mathcal {C}}, N_3^{\mathcal {C}_2}, N_3^{\mathcal {C}_{\cap }}$ be defined by $\mathscr {I}_{T}$, then

• 1. $N_3^{\mathcal {C}} = N_3^{\mathcal {C}_2}$;

• 2. $N_3^{\mathcal {C}} = N_3^{\mathcal {C}_{\cap }}$.

Proposition 29

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {I}_{O}$ be a q-ROF $R_O$-implication derived from the q-ROF overlap function $\mathscr {O}$ satisfying (O6) and ${\mathbb {N}}_3^{\mathcal {C}}, {\mathbb {N}}_3^{\mathcal {C}_2}, {\mathbb {N}}_3^{\mathcal {C}_{\cap }}$ be defined by $\mathscr {I}_{O}$, then

• 1. ${\mathbb {N}}_3^{\mathcal {C}} = {\mathbb {N}}_3^{\mathcal {C}_2}$;

• 2. ${\mathbb {N}}_3^{\mathcal {C}} = {\mathbb {N}}_3^{\mathcal {C}_{\cap }}$.

Finally, we discuss the equivalences of q-ROFNOs $N_4^{\mathcal {C}}, N_4^{\mathcal {C}_2}, N_4^{\mathcal {C}_{\cap }}$ and the equivalences of q-ROFNOs ${\mathbb {N}}_4^{\mathcal {C}}, {\mathbb {N}}_4^{\mathcal {C}_2}, {\mathbb {N}}_4^{\mathcal {C}_{\cap }}$ when the q-ROF overlap function which is used to define them satisfies (O6).

Proposition 30

Let $\mathcal {C}$ be a finite q-ROF covering and $N_4^{\mathcal {C}}, N_4^{\mathcal {C}_2}, N_4^{\mathcal {C}_{\cap }}$ be defined by a q-ROF t-norm $\mathscr {T}$, then

• 1. $N_4^{\mathcal {C}} = N_4^{\mathcal {C}_2}$;

• 2. $N_4^{\mathcal {C}} = N_4^{\mathcal {C}_{\cap }}$.

Proposition 31

Let $\mathcal {C}$ be a finite q-ROF covering and q-ROFNOs ${\mathbb {N}}_4^{\mathcal {C}}, {\mathbb {N}}_4^{\mathcal {C}_2}, {\mathbb {N}}_4^{\mathcal {C}_{\cap }}$ be defined by a q-ROF overlap function $\mathscr {O}$ satisfying (O6), then

• 1. ${\mathbb {N}}_4^{\mathcal {C}} = {\mathbb {N}}_4^{\mathcal {C}_2}$;

• 2. ${\mathbb {N}}_4^{\mathcal {C}} = {\mathbb {N}}_4^{\mathcal {C}_{\cap }}$.

Based on the above research, we conculde that given a finite q-ROF covering $\mathcal {C}$, a continuous q-ROF t-norm and its q-ROF $R_T$-implication, an q-ROF overlap function and its $R_O$-implication, there are sixteen different groups of Tq-ROFNOs listed in Table 1 and seventeen different groups of Oq-ROFNOs listed in Table 2.

Table 1 Tq-ROFNOs

Table 2 Oq-ROFNOs

5.2 A lattice of q-ROFNOs on finite q-ROF coverings

The partial order relations of different groups of q-ROFNOs in Tables 1 and 2 are studied in this section. We still assume that the q-ROF covering $\mathcal {C}$ is finite, q-ROF t-norm used to define t-norm-based q-ROFNOs is continuous and q-ROF overlap function used to define overlap function-based q-ROFNOs satisfies (O6).

The partial order relation $\preceq _L$ between different groups of q-ROFNOs is defined as follows: $N \preceq _L N' ({\mathbb {N}}\preceq _L {\mathbb {N}}')$ when and only when $N(\varepsilon )(\eta ) \preceq _L N'(\varepsilon )(\eta ) ({\mathbb {N}}(\varepsilon )(\eta ) \preceq _L {\mathbb {N}}'(\varepsilon )(\eta ))$ for $\varepsilon ,\eta \in U$. Two q-ROFNOs are said to be incomparable if neither $N' \preceq _L N ({\mathbb {N}}' \preceq _L {\mathbb {N}})$ nor $N \preceq _L N' ({\mathbb {N}} \preceq _L {\mathbb {N}}')$ holds. Note that q-ROFNOs are extensions of fuzzy neighborhood operators in D’eer et al. (2017) and Qi et al. (2023), so if two fuzzy neighborhood operators are incomparable, the q-ROFNOs are still incomparable. Therefore, only the partial order relations given in Figs. 2 and 3 need to be studied.

Firstly, we discuss the partial order relations between $N_1^{\mathcal {C}}, N_2^{\mathcal {C}}, N_3^{\mathcal {C}}$ and $N_4^{\mathcal {C}}$.

Proposition 32

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {T}$ be a continuous q-ROF t-norm used to defines $N_2^{\mathcal {C}}$ and $N_4^{\mathcal {C}}$ and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication used to define $N_1^{\mathcal {C}}$ and $N_3^{\mathcal {C}}$. Then

• 1. $N_1^{\mathcal {C}} \preceq _L N_2^{\mathcal {C}}$;

• 2. $N_1^{\mathcal {C}} \preceq _L N_3^{\mathcal {C}}$;

• 3. $N_2^{\mathcal {C}} \preceq _L N_4^{\mathcal {C}}$;

• 4. $N_3^{\mathcal {C}} \preceq _L N_4^{\mathcal {C}}$.

In light of Proposition 32, the following conclusions are maintained for Table 1.

Corollary 1

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {T}$ be a continuous q-ROF t-norm used to define q-ROF covering $\mathcal {C}_4$ and $N_2^{\mathcal {C}_j}$ and $N_4^{\mathcal {C}_j}$ and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication used to define define q-ROF covering $\mathcal {C}_3$ and $N_1^{\mathcal {C}_j}$ and $N_3^{\mathcal {C}_j}$. Then

• 1. For $\mathcal {C}$, $A1\preceq _L E\preceq _L H1$ and $A1\preceq _L F1 \preceq _L H1$ hold;

• 2. For $\mathcal {C}_1$, $A1\preceq _L E\preceq _L L$ and $A1\preceq _L B \preceq _L L$ hold;

• 3. For $\mathcal {C}_2$, $F2\preceq _L H2\preceq _L H1$ and $F2\preceq _L F1 \preceq _L H1$ hold;

• 4. For $\mathcal {C}_3$, $A1\preceq _L A2\preceq _L D$ and $A1\preceq _L C \preceq _L D$ hold;

• 5. For $\mathcal {C}_4$, $G\preceq _L I\preceq _L K$ and $G\preceq _L J \preceq _L K$ hold;

• 6. For $\mathcal {C}_{\cap }$, $A1\preceq _L M\preceq _L H1$ and $A1\preceq _L F1 \preceq _L H1$ hold.

As is known to all, the q-ROF overlap function $\mathscr {O}$ degenerates into a q-ROF t-norm when $\mathscr {O}$ satisfies (O8). Therefore the partial order relations in Proposition 32 are still maintained for ${\mathbb {N}}_1^{\mathcal {C}}, {\mathbb {N}}_2^{\mathcal {C}}, {\mathbb {N}}_3^{\mathcal {C}}, {\mathbb {N}}_4^{\mathcal {C}}$ when the q-ROF overlap function$\mathscr {O}$ used to define these q-ROFNOs satisfies (O8). A natural question is whether these partial order relations are still maintained when $\mathscr {O}$ satisfies (O6). The following proposition gives a positive answer to this question.

Proposition 33

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {O}$ be a q-ROF overlap function satisfying (O6) which is used to define ${\mathbb {N}}_2^{\mathcal {C}}$ and ${\mathbb {N}}_4^{\mathcal {C}}$, $\mathscr {I}_{O}$ be a q-ROF $R_O$-implication derived from $\mathscr {O}$ used to define ${\mathbb {N}}_1^{\mathcal {C}}$ and ${\mathbb {N}}_3^{\mathcal {C}}$. Then

• 1. ${\mathbb {N}}_1^{\mathcal {C}} \preceq _L {\mathbb {N}}_3^{\mathcal {C}}$;

• 2. ${\mathbb {N}}_2^{\mathcal {C}} \preceq _L {\mathbb {N}}_4^{\mathcal {C}}$.

In light of Proposition 33, the following conclusions are still maintained for Table 2.

Corollary 2

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {O}$ be a q-ROF overlap function satisfying (O6) which is used to define q-ROF covering $\hat{\mathcal {C}}_4$, ${\mathbb {N}}_2^{\mathcal {C}_j}$ and ${\mathbb {N}}_4^{\mathcal {C}_j}$, $\mathscr {I}_{O}$ be a q-ROF $R_O$-implication derived from $\mathscr {O}$ used to define q-ROF covering $\hat{\mathcal {C}}_3$ and ${\mathbb {N}}_1^{\mathcal {C}_j}$ and ${\mathbb {N}}_3^{\mathcal {C}_j}$, where ${\mathbb {N}}_2^{\hat{\mathcal {C}}_3}$, ${\mathbb {N}}_2^{\hat{\mathcal {C}}_4}$, ${\mathbb {N}}_4^{\hat{\mathcal {C}}_3}$, ${\mathbb {N}}_4^{\hat{\mathcal {C}}_4}$ are denoted as ${\mathbb {N}}_2^{\mathcal {C}_3}$, ${\mathbb {N}}_2^{\mathcal {C}_4}$, ${\mathbb {N}}_4^{\mathcal {C}_3}$, ${\mathbb {N}}_4^{\mathcal {C}_4}$, respectively. Then

• 1. For $\mathcal {C}$, ${\mathbb {A}}1\preceq _L {\mathbb {F}}1$ and ${\mathbb {E}}\preceq _L {\mathbb {H}}1$ hold;

• 2. For $\mathcal {C}_1$, ${\mathbb {A}}1\preceq _L {\mathbb {B}}$ and ${\mathbb {E}}\preceq _L {\mathbb {L}}$ hold;

• 3. For $\mathcal {C}_2$, ${\mathbb {F}}2\preceq _L {\mathbb {F}}1$ and ${\mathbb {H}}2\preceq _L {\mathbb {H}}1$ hold;

• 4. For $\hat{\mathcal {C}}_3$, ${\mathbb {A}}3\preceq _L \mathcal {C}$ and ${\mathbb {A}}2\preceq _L {\mathbb {D}}$ hold;

• 5. For $\hat{\mathcal {C}}_4$, ${\mathbb {I}}\preceq _L {\mathbb {K}}$ and ${\mathbb {G}}\preceq _L {\mathbb {J}}$ hold;

• 6. For $\mathcal {C}_{\cap }$, ${\mathbb {M}}\preceq _L {\mathbb {H}}1$ and ${\mathbb {A}}1\preceq _L {\mathbb {F}}1$ hold.

Next, in D’eer et al. (2017), it holds that $N_1^{\mathcal {C}} \le N_1^{\mathcal {C}_2}$ and $N_4^{\mathcal {C}_1} \le N_4^{\mathcal {C}}$. The extensions of these partial order relations are still maintained in q-ROF setting.

Proposition 34

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {T}$ be a continuous q-ROF t-norm used to define $N_4^{\mathcal {C}}$ and $N_4^{\mathcal {C}_1}$ and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication used to define $N_1^{\mathcal {C}}$ and $N_1^{\mathcal {C}_2}$. Then

• 1. $N_1^{\mathcal {C}} \preceq _L N_1^{\mathcal {C}_2}$;

• 2. $N_4^{\mathcal {C}_1} \preceq _L N_4^{\mathcal {C}}$.

Furthermore, the partial order relations in the above proposition are still maintained for ${\mathbb {N}}_1^{\mathcal {C}}, {\mathbb {N}}_1^{\mathcal {C}_2}, {\mathbb {N}}_4^{\mathcal {C}}, {\mathbb {N}}_4^{\mathcal {C}_1}$ when the q-ROF overlap function $\mathscr {O}$ used to define these q-ROFNOs satisfies (O8). The following proposition illustrate that these partial order relations are still maintained when $\mathscr {O}$ satisfies (O6).

Proposition 35

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {O}$ be a q-ROF overlap function satisfying (O6) which is used to define ${\mathbb {N}}_4^{\mathcal {C}}$ and ${\mathbb {N}}_4^{\mathcal {C}_1}$, $\mathscr {I}_{O}$ be a q-ROF $R_O$-implication derived from $\mathscr {O}$ used to define ${\mathbb {N}}_1^{\mathcal {C}}$ and ${\mathbb {N}}_1^{\mathcal {C}_2}$. Then

• 1. ${\mathbb {N}}_1^{\mathcal {C}} \preceq _L {\mathbb {N}}_1^{\mathcal {C}_2}$;

• 2. ${\mathbb {N}}_4^{\mathcal {C}_1} \preceq _L {\mathbb {N}}_4^{\mathcal {C}}$.

In D’eer et al. (2017), $N_3^{\mathcal {C}} \le N_1^{\mathcal {C}_4}, N_1^{\mathcal {C}_4} \le N_4^{\mathcal {C}}$ and $N_4^{\mathcal {C}} \le N_2^{\mathcal {C}_4}$ hold. In order to prove the extensions of these partial order relations in q-ROF setting are still maintained, the following lemma is discussed firstly.

Lemma 1

Let $\mathscr {T}$ be a continuous q-ROF t-norm and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication, then $\mathscr {I}_{T}(\varepsilon ,\eta )\preceq _L \mathscr {I}_{T}(\mathscr {T}(\varepsilon ,\theta ),\mathscr {T}(\eta ,\theta ))$ holds for $\varepsilon ,\eta ,\theta \in L$.

Proposition 36

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {T}$ be a continuous q-ROF t-norm used to define the q-ROF covering $\mathcal {C}_4$, $N_4^{\mathcal {C}}$ and $N_2^{\mathcal {C}_4}$, and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication used to define $N_3^{\mathcal {C}}$ and $N_1^{\mathcal {C}_4}$. Then

• 1. $N_3^{\mathcal {C}} \preceq _L N_1^{\mathcal {C}_4}$;

• 2. $N_1^{\mathcal {C}_4} \preceq _L N_4^{\mathcal {C}}$;

• 3. $N_4^{\mathcal {C}} \preceq _L N_2^{\mathcal {C}_4}$.

In D’eer et al. (2017), it holds that $N_4^{\mathcal {C}_3} \le N_4^{\mathcal {C}_1}$. The extension of this partial order relation still holds in q-ROF setting.

Proposition 37

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {T}$ be a continuous q-ROF t-norm used to define $N_4^{\mathcal {C}_3}$ and $N_4^{\mathcal {C}_1}$, and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication used to define the q-ROF covering $\mathcal {C}_3$. Then $N_4^{\mathcal {C}_3} \preceq _L N_4^{\mathcal {C}_1}$.

Then, we consider the partial order relation between $N_2^{\mathcal {C}_{\cap }}$ and $N_2^{\mathcal {C}_2}$ and the partial order relation between ${\mathbb {N}}_2^{\mathcal {C}_{\cap }}$ and ${\mathbb {N}}_2^{\mathcal {C}_2}$.

Proposition 38

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {T}$ be a continuous q-ROF t-norm used to define $N_2^{\mathcal {C}_{\cap }}$ and $N_2^{\mathcal {C}_2}$. Then $N_2^{\mathcal {C}_{\cap }} \preceq _L N_2^{\mathcal {C}_2}$.

Proposition 39

Let $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {O}$ be a q-ROF overlap function satisfying (O6) which is used to define ${\mathbb {N}}_2^{\mathcal {C}_{\cap }}$ and ${\mathbb {N}}_2^{\mathcal {C}_2}$. Then ${\mathbb {N}}_2^{\mathcal {C}_{\cap }} \preceq _L {\mathbb {N}}_2^{\mathcal {C}_2}$.

At last, since ${\mathbb {N}}_1^{\hat{\mathcal {C}}_3}$ is no longer equivalent to ${\mathbb {N}}_1^{\mathcal {C}}$ when the q-ROF overlap function satisfies (O6), the partial order relation between them is discussed as follows.

Proposition 40

Let U be a nonempty finite set, $\mathcal {C}$ be a finite q-ROF covering, $\mathscr {O}$ be a q-ROF overlap function satisfying (O6) and $\mathscr {I}_{O}$ be a q-ROF $R_O$-implication used to define ${\mathbb {N}}_1^{\mathcal {C}}$ and ${\mathbb {N}}_1^{\hat{\mathcal {C}}_3}$. Then ${\mathbb {N}}_1^{\mathcal {C}} \preceq _L {\mathbb {N}}_1^{\hat{\mathcal {C}}_3}$.

The results about Tq-ROFNOs obtained in Sect. 5.2 are summarized in Fig. 2, where the partial order $\preceq _L$ is shown to define a lattice on the set of Tq-ROFNOs of Table 1. Similarly, the results about Oq-ROFNOs obtained in Sect. 5.2 are summarized in Fig. 3, where the partial order $\preceq _L$ is shown to define a lattice on the set of Tq-ROFNOs of Table 2.

Fig. 2

Lattice of Tq-ROFNOs

Fig. 3

Lattice of Oq-ROFNOs

6 Neighborhood-related q-ROF covering-based rough set models

We still assume that the q-ROF covering $\mathcal {C}$ is finite, the q-ROF t-norm used to define q-ROFNOs and q-ROF coverings is continuous and the q-ROF overlap functions used to define Oq-ROFNOs and q-ROF coverings satisfy (O6) in this section. We establish two pairs of 24 kinds of t-norm-based neighborhood-related generalized q-ROF covering-based rough set models (TNRq-ROFCRS), two pairs of 24 kinds of overlap function-based neighborhood-related generalized q-ROF covering-based rough set models (ONRq-ROFCRS) and illustrate related properties. According the groups of the q-ROFNOs, TNRq-ROFCRS models in each pair are divided into sixteen groups and ONRq-ROFCRS models in each pair are divided into seventeen groups.

For convenience, t-norm-based the q-ROFNOs can be written as $N_i^{\mathcal {C}_j}$ and the overlap function-based q-ROFNOs can be written as ${\mathbb {N}}_i^{\mathcal {C}_j}$, where $i = 1,2,3,4,j = 0,1,2,3,4,5$, $N_i^{\mathcal {C}}$ and $N_i^{\mathcal {C}_{\cap }}$ are denoted as $N_i^{\mathcal {C}_0}$ and $N_i^{\mathcal {C}_5}$, ${\mathbb {N}}_i^{\mathcal {C}}, {\mathbb {N}}_i^{\mathcal {C}_{\cap }}$ ${\mathbb {N}}_i^{\hat{\mathcal {C}}_3}$ and ${\mathbb {N}}_i^{\hat{\mathcal {C}}_4}$ are denoted as ${\mathbb {N}}_i^{\mathcal {C}_0}, {\mathbb {N}}_i^{\mathcal {C}_5}, {\mathbb {N}}_i^{\mathcal {C}_3}$ and ${\mathbb {N}}_i^{\mathcal {C}_4}$, respectively. Next, we illustrate the concepts of TNRq-ROFCRS and ONRq-ROFCRS as follows.

Definition 39

Let U be a nonempty finite set, $\mathcal {C}_j$ be a finite q-ROF coverings, $\mathscr {T}$ be a continuous q-ROF t-norm and $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication of $\mathscr {T}$, $N_i^{\mathcal {C}_j}$ be t-norm-based q-ROFNO. For $X \in \mathscr {F}_q(U)$, the t-norm-based q-ROF lower approximation operators $\underline{\Phi ^1_{i,j}}(X), \underline{\Phi ^2_{i,j}}(X)$ and upper approximation operators $\overline{\Phi ^1_{i,j}}(X),\overline{\Phi ^2_{i,j}}(X)$ of X are defined respectively by

$$\begin{aligned} \begin{aligned} \underline{\Phi ^1_{i,j}}(X)(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), X(\theta ))), \\ \overline{\Phi ^1_{i,j}}(X)(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), X(\theta ))), \\ \underline{\Phi ^2_{i,j}}(X)(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), X(\theta ))), \\ \overline{\Phi ^2_{i,j}}(X)(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), X(\theta ))), \end{aligned} \end{aligned}$$

where $\varepsilon \in U$, $\bigvee$ and $\bigwedge$ represent $\vee _L$ and $\wedge _L$ in Eq.(1) respectively, and $i = 1,2,3,4$ and $j = 0,1,2,3,4,5$. $(\underline{\Phi ^1_{i,j}}(X),\overline{\Phi ^1_{i,j}}(X))$ is referred to as the first pair of t-norm-based neighborhood-related q-ROF approximation operators and $(\underline{\Phi ^2_{i,j}}(X), \overline{\Phi ^2_{i,j}}(X))$ is called the second pair of t-norm-based neighborhood-related q-ROF approximation operators.

Definition 40

Let U be a nonempty finite set, $\mathcal {C}_j$ be a finite q-ROF covering, $\mathscr {O}$ be a q-ROF overlap function satisfying (O6) and $\mathscr {I}_{O}$ be a q-ROF $R_O$-implication derived from $\mathscr {O}$, ${\mathbb {N}}_i^{\mathcal {C}_j}$ be overlap function-based q-ROFNOs. For any $X \in \mathscr {F}_q(U)$, the overlap function-based q-ROF lower approximation operators $\underline{\Psi ^1_{i,j}}(X), \underline{\Psi ^2_{i,j}}(X)$ and upper approximation operators $\overline{\Psi ^1_{i,j}}(X),\overline{\Psi ^2_{i,j}}(X)$ of X are defined respectively by

$$\begin{aligned} \begin{aligned} \underline{\Psi ^1_{i,j}}(X)(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), X(\theta ))), \\ \overline{\Psi ^1_{i,j}}(X)(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), X(\theta ))), \\ \underline{\Psi ^2_{i,j}}(X)(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), X(\theta ))), \\ \overline{\Psi ^2_{i,j}}(X)(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), X(\theta ))), \end{aligned} \end{aligned}$$

where $\varepsilon \in U$, $\bigvee$ and $\bigwedge$ represent $\vee _L$ and $\wedge _L$ in Eq. (1) respectively, $i = 1,2,3,4$ and $j = 0,1,2,3,4,5$, $(\underline{\Psi ^1_{i,j}}(X),\overline{\Psi ^1_{i,j}}(X))$ is referred to as the first pair of overlap function-based neighborhood-related q-ROF approximation operators and $(\underline{\Psi ^2_{i,j}}(X), \overline{\Psi ^2_{i,j}}(X))$ is called the second pair of overlap function-based neighborhood-related q-ROF approximation operators.

In light of above definitions, equalities of NRq-ROFCRS models are the same with the corresponding of q-ROFNOs used to define them. Therefore, TNRq-ROFCRS models of each pair can be divided into sixteen groups which are depicted in Table 3 and ONRq-ROFCRS models of each pair can be divided into seventeen groups which are depicted in Table 4. We write $(\underline{\Phi ^k_{i,j}}(X), \overline{\Phi ^k_{i,j}}(X))$ as $(\underline{\Phi ^k_{i,j}}, \overline{\Phi ^k_{i,j}})$ in Table 3 and $(\underline{\Psi ^k_{i,j}}(X), \overline{\Psi ^k_{i,j}}(X))$ as $(\underline{\Psi ^k_{i,j}}, \overline{\Psi ^k_{i,j}})$ in Table 4 for short, where $k=1,2$.

Table 3 The groups of TNRq-ROFCRS models

Table 4 The groups of ONRq-ROFCRS models

Then properties of NRq-ROFCRS models are investigated as follows.

Proposition 41

Let U be a nonempty finite set, $N_i^{\mathcal {C}_j}$ be q-ROFNOs based on a continuous q-ROF t-norm $\mathscr {T}$ and its q-ROF $R_T$-implication $\mathscr {I}_{T}$, $(\underline{\Phi ^1_{i,j}}(X), \overline{\Phi ^1_{i,j}}(X))$ be a pair of t-norm-based q-ROF approximation operators, where $i = 1,2,3,4$ and $j = 0,1,2,3,4,5$. Then, for $X_1, X_2 \in \mathscr {F}_q(U)$, the following statements hold.

• 1. $\underline{\Phi ^1_{i,j}}(U) = U, \underline{\Phi ^1_{i,j}}(\emptyset ) = \emptyset , \overline{\Phi ^1_{i,j}}(U) = U, \overline{\Phi ^1_{i,j}}(\emptyset ) = \emptyset$, where U represents the set of objects whose q-ROFN is $1_L$, $\emptyset$ represents the set of objects whose q-ROFN is $0_L$;

• 2. $\underline{\Phi ^1_{i,j}}(X_1) \subseteq X_1 \subseteq \overline{\Phi ^1_{i,j}}(X_1)$;

• 3. If $X_1 \subseteq X_2$, then $\underline{\Phi ^1_{i,j}}(X_1) \subseteq \underline{\Phi ^1_{i,j}}(X_2)$, $\overline{\Phi ^1_{i,j}}(X_1) \subseteq \overline{\Phi ^1_{i,j}}(X_2)$;

• 4. $\underline{\Phi ^1_{i,j}}(X_1) \bigcup \underline{\Phi ^1_{i,j}}(X_2) \subseteq \underline{\Phi ^1_{i,j}}(X_1 \bigcup X_2)$, $\underline{\Phi ^1_{i,j}}(X_1 \bigcap X_2) \subseteq \underline{\Phi ^1_{i,j}}(X_1) \bigcap \underline{\Phi ^1_{i,j}}(X_2)$, $\overline{\Phi ^1_{i,j}}(X_1) \bigcup \overline{\Phi ^1_{i,j}}(X_2) \subseteq \overline{\Phi ^1_{i,j}}(X_1 \bigcup X_2)$, $\overline{\Phi ^1_{i,j}}(X_1 \bigcap X_2) \subseteq \overline{\Phi ^1_{i,j}}(X_1) \bigcap \overline{\Phi ^1_{i,j}}(X_2)$;

• 5. $\underline{\Phi ^1_{i,j}}(\underline{\Phi ^1_{i,j}}(X_1)) = \underline{\Phi ^1_{i,j}}(X_1)$ and $\overline{\Phi ^1_{i,j}}(\overline{\Phi ^1_{i,j}}(X_1)) = \overline{\Phi ^1_{i,j}}(X_1)$.

Proposition 42

Let U be a nonempty finite set, $N_i^{\mathcal {C}_j}$ be q-ROFNOs based on a continuous q-ROF t-norm $\mathscr {T}$ and its q-ROF $R_T$-implication $\mathscr {I}_{T}$, $(\underline{\Phi ^2_{i,j}}(X), \overline{\Phi ^2_{i,j}}(X))$ be a pair of t-norm-based q-ROF approximation operators, where $i = 1,2,3,4$ and $j = 0,1,2,3,4,5$. Then for $X_1, X_2 \in \mathscr {F}_q(U)$, the following statements hold.

• 1. $\underline{\Phi ^2_{i,j}}(U) = U, \underline{\Phi ^2_{i,j}}(\emptyset ) = \emptyset , \overline{\Phi ^2_{i,j}}(U) = U, \overline{\Phi ^2_{i,j}}(\emptyset ) = \emptyset$, where U represents the set of objects whose q-ROFN is $1_L$, $\emptyset$ represents the set of objects whose q-ROFN is $0_L$;

• 2. $\underline{\Phi ^2_{i,j}}(X_1) \subseteq X_1 \subseteq \overline{\Phi ^2_{i,j}}(X_1)$;

• 3. If $X_1 \subseteq X_2$, then $\underline{\Phi ^2_{i,j}}(X_1) \subseteq \underline{\Phi ^2_{i,j}}(X_2)$, $\overline{\Phi ^2_{i,j}}(X_1) \subseteq \overline{\Phi ^2_{i,j}}(X_2)$;

• 4. $\underline{\Phi ^2_{i,j}}(X_1) \bigcup \underline{\Phi ^2_{i,j}}(X_2) \subseteq \underline{\Phi ^2_{i,j}}(X_1 \bigcup X_2), \underline{\Phi ^2_{i,j}}(X_1 \bigcap X_2) \subseteq \underline{\Phi ^2_{i,j}}(X_1) \bigcap \underline{\Phi ^2_{i,j}}(X_2)$, $\overline{\Phi ^2_{i,j}}(X_1) \bigcup \overline{\Phi ^2_{i,j}}(X_2) \subseteq \overline{\Phi ^2_{i,j}}(X_1 \bigcup X_2), \overline{\Phi ^2_{i,j}}(X_1 \bigcap X_2) \subseteq \overline{\Phi ^2_{i,j}}(X_1) \bigcap \overline{\Phi ^2_{i,j}}(X_2)$;

• 5. $\overline{\Phi ^2_{i,j}}(\underline{\Phi ^2_{i,j}}(X_1)) \subseteq X_1 \subseteq \underline{\Phi ^2_{i,j}}(\overline{\Phi ^2_{i,j}}(X_1))$.

Proposition 43

Let U be a nonempty finite set, ${\mathbb {N}}_i^{\mathcal {C}_j}$ be q-ROFNOs based on q-ROF overlap function $\mathscr {O}$ satisfing (O6) and its q-ROF $R_T$-implication $\mathscr {I}_{O}$, $(\underline{\Psi ^1_{i,j}}(X), \overline{\Psi ^1_{i,j}}(X))$ be a pair of overlap function-based q-ROF approximation operators, where $i = 1,2,3,4$ and $j = 0,1,2,3,4,5$. Then, for $X_1, X_2\in \mathscr {F}_q(U)$, the following statements hold.

• 1. $\underline{\Psi ^1_{i,j}}(\emptyset ) = \emptyset , \overline{\Psi ^1_{i,j}}(\emptyset ) = \emptyset$;

• 2. $\underline{\Psi ^1_{i,j}}(X_1) \subseteq X_1 \subseteq \overline{\Psi ^1_{i,j}}(X_1)$;

• 3. If $X_1 \subseteq X_2$, then $\underline{\Psi ^1_{i,j}}(X_1) \subseteq \underline{\Psi ^1_{i,j}}(X_2)$, $\overline{\Psi ^1_{i,j}}(X_1) \subseteq \overline{\Psi ^1_{i,j}}(X_2)$;

• 4. $\underline{\Psi ^1_{i,j}}(X_1) \bigcup \underline{\Psi ^1_{i,j}}(X_2) \subseteq \underline{\Psi ^1_{i,j}}(X_1 \bigcup X_2), \underline{\Psi ^1_{i,j}}(X_1 \bigcap X_2) \subseteq \underline{\Psi ^1_{i,j}}(X_1) \bigcap \underline{\Psi ^1_{i,j}}(X_2)$, $\overline{\Psi ^1_{i,j}}(X_1) \bigcup \overline{\Psi ^1_{i,j}}(X_2) \subseteq \overline{\Psi ^1_{i,j}}(X_1 \bigcup X_2), \overline{\Psi ^1_{i,j}}(X_1 \bigcap X_2) \subseteq \overline{\Psi ^1_{i,j}}(X_1) \bigcap \overline{\Psi ^1_{i,j}}(X_2)$;

• 5. $\underline{\Psi ^1_{i,j}}(\underline{\Psi ^1_{i,j}}(X_1)) = \underline{\Psi ^1_{i,j}}(X_1)$ and $\overline{\Psi ^1_{i,j}}(\overline{\Psi ^1_{i,j}}(X_1)) = \overline{\Psi ^1_{i,j}}(X_1)$.

Proposition 44

Let U be a nonempty finite set, ${\mathbb {N}}_i^{\mathcal {C}_j}$ be q-ROFNOs based on a q-ROF overlap function $\mathscr {O}$ satisfing (O6) and its q-ROF $R_T$-implication $\mathscr {I}_{O}$, $(\underline{\Psi ^2_{i,j}}(X), \overline{\Psi ^2_{i,j}}(X))$ be a pair of overlap function-based q-ROF approximation operators, where $i = 1,2,3,4$ and $j = 0,1,2,3,4,5$. Then, for $X_1, X_2 \in \mathscr {F}_q(U)$, the following statements hold.

• 1. $\underline{\Psi ^2_{i,j}}(U) = U, \underline{\Psi ^2_{i,j}}(\emptyset ) = \emptyset , \overline{\Psi ^2_{i,j}}(\emptyset ) = \emptyset$, where U represents the set of objects whose q-ROFN is $1_L$, $\emptyset$ represents the set of objects whose q-ROFN is $0_L$;

• 2. If $X_1 \subseteq X_2$, then $\underline{\Psi ^2_{i,j}}(X_1) \subseteq \underline{\Psi ^2_{i,j}}(X_2)$, $\overline{\Psi ^2_{i,j}}(X_1) \subseteq \overline{\Psi ^2_{i,j}}(X_2)$;

• 3. $\underline{\Psi ^2_{i,j}}(X_1) \bigcup \underline{\Psi ^2_{i,j}}(X_2) \subseteq \underline{\Psi ^2_{i,j}}(X_1 \bigcup X_2), \underline{\Psi ^2_{i,j}}(X_1 \bigcap X_2) \subseteq \underline{\Psi ^2_{i,j}}(X_1) \bigcap \underline{\Psi ^2_{i,j}}(X_2)$, $\overline{\Psi ^2_{i,j}}(X_1) \bigcup \overline{\Psi ^2_{i,j}}(X_2) \subseteq \overline{\Psi ^2_{i,j}}(X_1 \bigcup X_2), \overline{\Psi ^2_{i,j}}(X_1 \bigcap X_2) \subseteq \overline{\Psi ^2_{i,j}}(X_1) \bigcap \overline{\Psi ^2_{i,j}}(X_2)$;

• 4. $\overline{\Psi ^2_{i,j}}(\underline{\Psi ^2_{i,j}}(X_1)) \subseteq X_1 \subseteq \underline{\Psi ^2_{i,j}}(\overline{\Psi ^2_{i,j}}(X_1))$.

By the monotonicity of q-ROF t-norm and its q-ROF $R_T$-implication (q-ROF overlap function and its q-ROF $R_O$-implication), we conclude that partial order relations of $\overline{\Phi ^2_{i,j}}(X)$ ($\overline{\Psi ^2_{i,j}}(X)$) are the same with corresponding relations of q-ROF neiborhood operators $N_i^{\mathcal {C}_j}$ (${\mathbb {N}}_i^{\mathcal {C}_j}$) based on definition of NRq-ROFCRS models. However, partial order relations of $\underline{\Phi ^2_{i,j}}(X)$ ($\underline{\Psi ^2_{i,j}}(X)$) are inverse to corresponding relations of q-ROF neiborhood operators $N_i^{\mathcal {C}_j}$ (${\mathbb {N}}_i^{\mathcal {C}_j}$) which are used to define NRq-ROFCRS models. In light of the above analyses and properties of NRq-ROFCRS models, the partial order relations of $\underline{\Phi ^2_{i,j}}(X)$ and $\overline{\Phi ^2_{i,j}}(X)$ are decipted in Fig. 4 and the partial order relations of $\underline{\Psi ^2_{i,j}}(X)$ and $\overline{\Psi ^2_{i,j}}(X)$ are decipted in Figs. 5 and 6, respectively.

Fig. 4

Lattice of t-norm-based neighborhood-related q-ROF approximatin operators

Fig. 5

Lattice of overlap function-based q-ROF lower approximatin operators

Fig. 6

Lattice of overlap function-based q-ROF upper approximatin operators

7 MADM method

MADM is a process for making decisions over the feasible alternatives which are characterized by multiple (usually conflicting) attributes. Its theories and methods are widely used in economy, technology, engineering, management and so on. It is well known that TOPSIS method has become an important and effective tool in management decision making science and is usually used in MADM problem. We put forward a novel approach to solve MADM problem under q-ROF setting by means of TOPSIS method and NRq-ROFCRS models in this section.

A typical MADM problem under q-ROF setting can be described as follows: Let $U = \{x_1,x_2,\cdots ,x_n\}$ be a universe with n alternatives, $\mathcal {C} = \{\Gamma _1,\Gamma _2,\ldots ,\Gamma _m\}$ be a set with m attributes, $\Gamma _l(x_k) = (\mu _{k,l},\nu _{k,l}),(k = 1,2,\ldots ,n,l= 1,2,\ldots ,m)$ be q-ROFNs used to express decision makers’ preference information, where $0\le \mu _{k,l}^q+\nu _{k,l}^q\le 1$. The ultimate goal of MADM problem is to choose the best alternative in U upon decision makers’ preference information. In the following, by means of TOPSIS method and NRq-ROFCRS models proposed in Sect. 6, a novel weighted MADM methods are proposed to solve this problem. The weights in this method are defined by means of q-ROF approximate operators of $\Gamma _l$. The proceding of this method as follows.

Firstly, we construct a q-ROF covering $\mathcal {C}$ and a q-ROF set $\Gamma _j~(j=1,2,\ldots ,m)$ to express decision makers’ preference information of U. Note that each alternative $x_k$ has at least one attribute with the score (1, 0). Then, we can calculate neighborhood operators $N_i^{\mathcal {C}_j}(x)(i=1,2,3,4,j=0,1,2,3,4,5)$ for $x \in U$.

Secondly, by Definitions 39 and 40, the approximate operators $\underline{\Phi ^1_{i,j}}, \overline{\Phi ^2_{i,j}},\underline{\Phi ^2_{i,j}}, \overline{\Phi ^2_{i,j}}$ or $\underline{\Psi ^1_{i,j}},\overline{\Psi ^2_{i,j}},\underline{\Psi ^1_{i,j}}$,$\overline{\Psi ^2_{i,j}}$ of $\Gamma _l$ for each alternative can be computed.

Thirdly, we compute the weight of wach attribute by

$$\begin{aligned} W_l = \frac{\sum \nolimits _{k=1}^n ( |\underline{\Phi ^1_{i,j}}(\Gamma _l)(x_k) |+ |\underline{\Phi ^2_{i,j}}(\Gamma _l)(x_k)|)}{\sum \nolimits _{k=1}^n (|\overline{\Phi ^1_{i,j}}(\Gamma _l)(x_k) |+ |\overline{\Phi ^2_{i,j}}(\Gamma _l)|)(x_k) }, \end{aligned}$$

(2)

or

$$\begin{aligned} W_l = \frac{\sum \nolimits _{k=1}^n (|\underline{\Psi ^1_{i,j}}(\Gamma _j)(x_k) |+ |\underline{\Psi ^2_{i,j}}(\Gamma _j)(x_k)|)}{\sum \nolimits _{k=1}^n (|\overline{\Psi ^1_{i,j}}(\Gamma _j)(x_k) |+ |\overline{\Psi ^2_{i,j}}(\Gamma _j)(x_k)|) }, \end{aligned}$$

(3)

where $|Q |= \mu _Q + \nu _Q$, Q represents a q-ROFN.

Next, we construct the positive ideal solution $\Gamma ^{+}$ and the negative ideal solution $\Gamma ^{-}$ by the following formula

$$\begin{aligned} \Gamma ^{+}= & {} \{(\mu _{\Gamma _l^+},\nu _{\Gamma _l^+})\mid \mu _{\Gamma _l^+} = \max \{\mu _{\Gamma _l}(x_k)\}_{k=1}^n, \nu _{\Gamma _l^+} = \min \{ \nu _{\Gamma _l}(x_k)\}_{k=1}^n,l =1,2,\ldots ,m\}, \nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned} \Gamma ^{-}= & {} \{(\mu _{\Gamma _l^-},\nu _{\Gamma _l^-})\mid \mu _{\Gamma _l^-} = \min \{\mu _{\Gamma _l}(x_k)\}_{k=1}^n, \nu _{\Gamma _l^-} = \max \{ \nu _{\Gamma _l}(x_k)\}_{k=1}^n,l =1,2,\ldots ,m\}. \nonumber \\ \end{aligned}$$

(5)

It is obvious that $\Gamma ^{+} \in \mathscr {F}_q(U)$ and $\Gamma ^{-} \in \mathscr {F}_q(U)$.

Furthermore, the positive ideal distance $D^+$ and the negative ideal distance $D^-$ can be computed by

$$\begin{aligned} D^+(x_k)= & {} \left( \sum \limits _{l=1}^m W_l \left\| \mu _{\Gamma _l}(x_k) - \mu _{\Gamma ^+}\right\| ^q + \sum \limits _{l=1}^m W_l \left\| \nu _{\Gamma _l}(x_k) - \nu _{\Gamma ^+}\right\| ^q\right) ^{\frac{1}{q}}, \end{aligned}$$

(6)

$$\begin{aligned} D^-(x_k)= & {} \left( \sum \limits _{l=1}^m W_l \left\| \mu _{\Gamma _l}(x_k) - \mu _{\Gamma ^-}\right\| ^q + \sum \limits _{l=1}^m W_l \left\| \nu _{\Gamma _l}(x_k) - \nu _{\Gamma ^-}\right\| ^q\right) ^{\frac{1}{q}}. \end{aligned}$$

(7)

Therefore, we have $D(x_k) = (D^+(x_k),(D^-(x_k))$.

Finally, the sorting function can be computed by

$$\begin{aligned} \sigma (x_k) = S(D(x_k)), \end{aligned}$$

(8)

where $S(\mu ,\nu ) = \frac{\mu ^q+\nu ^q}{(1+\mu ^q*\nu ^q)^{1/q}}$. Then we can rank alternatives and choose the best alternative by using values of $\sigma (x_k)$.

The process of above method can be illustrated as Algorithm 1.

Algorithm 1

The algorithm of our method

8 Application and analyses

The performance of our method is illustrated in this section. Firstly, we elaborate on our method by a practical MADM problem. Then the effectiveness and rationality of our method are analyzed from many aspects. Finally a comparison with other existing q-ROFCRS rough set methods is made to illustrute the effectiveness of our proposed method.

8.1 Application

To demonstrate the effectiveness of our proposed method for MADM problem, we still consider the assessment and rank of appointment of new faculty position in universities in Hussain et al. (2019); Garg and Atef (2022). Assume that $U=\{x_1,x_2,x_3,x_4,x_5\}$ is a set of five candidates who fulfil the requirements for senior faculty positions at a university and $\mathcal {C}=\{\Gamma _1,\Gamma _2,\Gamma _3,\Gamma _4,\Gamma _5,\Gamma _6\}$ is a set of six attributes such as academic leadership qualities, ability to work under pressure, impact on research community, managerial skill, research productivity and contribution to the university. In order to appoint the most qualified and suitable person for the position, some experts judge candidates upon the six attributes and judgements are shown in Table 5.

To solve above MADM problem using our method presented in Sect. 7, we assume that $\mathscr {T}_P$ in Example 1 and its q-ROF $R_T$-implication are used to construct the TNRq-ROFRSC models, $\mathscr {O}_D$ and q-ROF $R_O$-implication in Example 7 are used to construct the ONRq-ROFRSC models. By Definitions 39 and 40, we conclude that the groups of the models are consistent with that of the neighborhood operators, therefore we still use $A1,A2,B,\cdots$ and ${\mathbb {A}}1,{\mathbb {A}}2,{\mathbb {A}}3,\ldots$ to represent the grouping results of our methods based on different TNRq-ROFRSC models and ONRq-ROFRSC models, respectively.

Table 5 The description of $(U,\mathcal {C})$

No loss of generality, we use the model A1 and the model ${\mathbb {A}}1$ as examples to show the process of our MADM as follows.

Step 1: According to scores provided by experts and definitions of approximation operators, we calculate approximate operators $\underline{\Phi ^1_{A1}}, \overline{\Phi ^1_{A1}},\underline{\Phi ^2_{A1}}, \overline{\Phi ^2_{A1}}$ or $\underline{\Psi ^1_{{\mathbb {A}}1}},\overline{\Psi ^1_{{\mathbb {A}}1}},\underline{\Psi ^2_{{\mathbb {A}}1}},\overline{\Psi ^2_{{\mathbb {A}}1}}$ of each attribute $\Gamma _l$ and results are shown in Tables 6 and 7.

Step 2: In terms of Eq. (2) or Eq. (3), we calculate the weight $W_l$ for each attribute $\Gamma _l$ and results are shown in Tables 8 and 9.

Step 3: The positive ideal solution $\Gamma ^{+}$ and the negative ideal solution $\Gamma ^{-}$ are calculated according to Eqs. (4) and (5) and results are depicted in Tables 10 and 11.

Step 4: By means of Eq. (6) and (7), the positive ideal distance $D^+$ and the negative ideal distance $D^-$ are calculated and results are displayed in Tables 12 and 13.

Step 5: In light of Eq.(8), the values of the sorting function are calculated for each alternative $x_k$ and results are shown in Tables 14 and 15.

According to the above process, the ranking of alternatives based on model $A_1$ and model ${\mathbb {A}}1$ can be obtained and results can be find in Tables 16 and 17, where the ranking results of other models are also presented. From Tables 16 and 17, we can conclude that the second candidate is the most qualified and suitable person for the position.

Table 6 The q-ROF t-norm-based lower approximation and upper approximation of attribute q-ROFS $\Gamma _l(x_k)$

Table 7 The q-ROF overlap function-based lower approximation and upper approximation of attribute q-ROFS $\Gamma _l(x_k)$

Table 8 The atribute weights based on A1 model

Table 9 The atribute weights based on ${\mathbb {A}}1$ model

Table 10 The ideal solutions based on A1 model

Table 11 The ideal solutions based on ${\mathbb {A}}1$ model

Table 12 The ideal distances based on A1 model

Table 13 The ideal distances based on ${\mathbb {A}}1$ model

Table 14 The values of $\sigma$ based on A1 model

Table 15 The values of $\sigma$ based on ${\mathbb {A}}1$ model

Table 16 Ranking results of alternatives with different TNRq-ROFRSC models with $q=3$

Table 17 Ranking results of alternatives with different ONRq-ROFCRS models with $q=3$

8.2 Analyses

Results of assessment problem of new faculty position obtained in Sect. 8.1 are analyzed to show the effectiveness and reasonableness of our method in this section.

8.2.1 The analyses among new models

According to the results shown in Tables 16 and 17, we conclude that although sorting results are highly similar and the optimal alternative selected by all models are consistent, using different ONRq-ROFCRS models in our method can result in slight differences in sorting results which do not occur for TNRq-ROFCRS models. The reason for this phenomenon is the majority of relationships between ONRq-ROFCRS models are incomparable which will result in inconsistent relationships between attribute weights for different models. The essence for the incomparability of most ONRq-ROFCRS models compared to TNRq-ROFCRS models is that the q-ROF overlap function is not associative and changes the boundary conditions compared with q-ROF t-norm, however, it doesn’t hinder ONRq-ROFCRS models from making similar decision results as TNRq-ROFCRS models. Therefore, for complex problems where the data to be processed cannot be arbitrarily combined, such as image processing, ONRq-ROFCRS models are more suitable, and the incomparable q-ROFNOs provide more choices for decision makers.

Comparing TNRq-ROFCRS models with ONRq-ROFCRS models, sorting results obtained by TNRq-ROFCRS models are more consistent according to Table 17. This does not mean that ONRq-ROFCRS models are invalid, nor does it mean that TNRq-ROFCRS models is superior to ONRq-ROFCRS models. For decision-makers who want to quickly obtain ranking results based on a model, any TNRq-ROFCRS model is a good choice. But for decision-makers who want to obtain different opinions, ONRq-ROFCRS models are better choices. Furthermore, it may be wiser to combine the results of TNRq-ROFCRS models and ONRq-ROFCRS models.

8.2.2 The analyses with different logical operators and different parameters q

From the previous analysis, we know that the sorting results of different models are slightly different. We speculate that the results of models of the same type defined by different logical operators may be also slightly different. To verify this conclusion, $\mathscr {T}_M$, $\mathscr {T}_P$, $\mathscr {T}_L$ and their q-ROF $R_T$-implications are used to construct the TNRq-ROFCRS models, and $\mathscr {O}_{m2}$, $\mathscr {O}_D$, $\mathscr {O}_2^V$ and their q-ROF $R_O$-implications are used to construct the ONRq-ROFCRS models in this subsection. Due to space limitations, only the results of models A1, ${\mathbb {A}}1$, H1 and ${\mathbb {H}}1$ models with different logical operators are shown in Figs. 7 and 8.

According to the results shown in Figs. 7 and 8, we conclude that results by NRq-ROFCRS models with different logical operators are slightly different, but best alternatives of different models are highly consistent. This means that results of our models do not vary significantly with different fuzzy logic operators, which further verifies the effectiveness and objectivity of our method. However, as can be seen from Fig. 8, ONRq-ROFCRS models with different fuzzy logic operators lead to bigger change in the sorting results compared with TNRq-ROFCRS models, this is due to the nature of the q-ROF overlap function and the q-ROF t-norm. Furthermore, different fuzzy logic operators can be selected according to the preference of decision makers to adapt to the application background in real life.

Fig. 7

Ranking results based on models A1 and ${\mathbb {A}}1$ with different logical operators

Fig. 8

Ranking results based on models H and ${\mathbb {H}}1$ with different logical operators

The impact of different parameters q on results of our models is also worth investigation. For q-ROFSs, by increasing the value of parameter q, the range of decision process can be widened and information distortion can be avoided. We speculate that the models based on different q of the same logical operator will also lead to slightly different results. In order to verify our suspicions, $\mathscr {T}_P$ with different rungs and their q-ROF $R_T$-implications are used to construct the TNRq-ROFRSC models, $\mathscr {O}_D$ with different rungs and their q-ROF $R_O$-implications are used to construct the ONRq-ROFRSC models. We only give the results based on models H1 and ${\mathbb {H}}1$ with different rungs here. The ranking results are shown in Figs. 9 and 10. As can be seen from Figs. 9 and 10, results of models with different q are slightly different, but best alternatives are still consistent, which verifies the stability and robustness of our method. Therefore, in practical application, experts can choose the appropriate parameter q according to the q-ROF information.

Fig. 9

Ranking results based on models H with different q

Fig. 10

Ranking results based on models ${\mathbb {H}}1$ with different q

8.2.3 The analyses based on cross-validation

The previous subsection has validated the effectiveness and stability of our method from the perspective of the influence by logical operators and parameters. Next, we further discuss the impact of data sets on the stability of our method, that is, the stability of our method is verified by the idea of cross validation.

From the previous analysis, we know that different models and logical operators have no significant impact on the performance of our method. Without loss of generality, the four most representative models A1, ${\mathbb {A}}_1$, H1, and ${\mathbb {H}}_1$ are used to analyze the performance of our method. And $\mathscr {T}_P$ with $q=3$ and its q-ROF $R_T$-implication are used to construct A1, H1 models and $\mathscr {O}_D$ with $q=3$ and its q-ROF $R_O$-implication are used to construct ${\mathbb {A}}_1, {\mathbb {H}}_1$ models in this subsection.

The following five sets $U_1 = \{x_1, x_2, x_4\}, U_2 = \{x_1, x_2, x_5\}$, $U_3 = \{x_5, x_1, x_2, x_4\}, U_4 = \{x_3, x_4, x_2, x_5\}$, $U_5 = \{x_1, x_3, x_4, x_2\}$ are sampled from the set $U = \{x_1, x_2, x_3, x_4, x_5\}$ and corresponding information are selected from Table 5. Note that each of these sets contains the optimal alternative $x_2$. The ranking results of the above five sets are shown in Table 18. As can be seen from the Table 18, the ranking results are similar to the results in Tables 16 and 17, and the optimal alternative is still $x_2$.

To objectively demonstrate the performance of our method, we use the concept sorting similarity in Qi et al. (2023). Based on the definition of sorting similarity, for model A1, the sorting similarity of $U_i (i=1,2,3,5)$ and U is $100\%$; for model H1, the sorting similarity of $U_i (i=1,2,3,4,5)$ and U is $100\%$; for model ${\mathbb {A}}_1$, the sorting similarity of $U_i (i=1,2,3,4,5)$ and U is $100\%$; for model ${\mathbb {H}}_1$, the sorting similarity of $U_i (i=1,2,3,4)$ and U is $100\%$. This means that data sets have a slight influence on our method, which may be due to the fact that the way we calculate weights objectively reflects the preference of decision makers. Thus our method is the effectiveness and stability.

Table 18 Ranking results based on different sets when $q=3$

8.3 Comparison with existing methods

To further verify the effectiveness of our method, comparisons between our methods with different models and the existing works based on q-ROFCRS are conducted in this section. We utilize the methods in Hussain et al. (2019), Garg and Atef (2022), Zhang et al. (2019) as benchmark methods for comparison. These methods can be seen as extensions of the TOPSIS method in the q-ROF covering approximation space. The method in Hussain et al. (2019) adopts to hybrid q-ROF with $\beta$ covering rough set and TOPSIS. The method in Garg and Atef (2022) is proposed by using q-ROF $\beta$-neighborhood and q-ROF complementary $\beta$-neighborhood. The method in Zhang et al. (2019) integrates TOPSIS method with the generalized IFCRS models which is defined by IF neighborhood operators. Comparing our method with methods in Hussain et al. (2019) and Garg and Atef (2022), our method does not require adjusting parameters to make our results more objective, as parameter’s adjustments can to some extent reflect the subjective wills of decision-makers. The main advantage of our method comparing with the method in Zhang et al. (2019) is that it provides a larger space and enables experts to have more freedom in assigning scores by adjusting the value of q. In this paper, to solve the MADM problem mentioned above, IF neighborhood operators of the method in Zhang et al. (2019) are replaced by q-ROFNOs proposed by us.

From the previous analysis, we know that different models have no significant impact on the performance of our method. Without loss of generality, three representative models A1, ${\mathbb {A}}_1$ and ${\mathbb {H}}_1$ are used to compare with three methods mentioned in the previous paragraph. The ranking results based on our three different models A1, ${\mathbb {A}}_1$, ${\mathbb {H}}_1$ and other methods (Hussain et al. 2019; Garg and Atef 2022; Zhang et al. 2019) are shown in Table 19. From Table 19, we can conclude that although results of different methods are slightly different, but the best alternative and the worst alternative are consistent.

Table 19 Ranking results of alternatives with different methods

In order to objectively evaluate the relationship between the ranking results obtained by different methods, we rely on the help of the Spearman rank correlation coefficient which is a statistical indicator used to measure the relationship between two variables (Myers et al. 2013). Moreover, the Spearman rank correlation coefficient is not based on the original data, but on the ranking of the data. In light of ranking results in Table 19, we can obtain the correlations among the results obtained by our models and the existing methods and the resuls are shown in Table 20, where M1 represents the method in Hussain et al. (2019), M2 represents the method in Garg and Atef (2022), M3 represents the method in Zhang et al. (2019), and $A1,{\mathbb {A}}_1, {\mathbb {H}}_1$ represent our method based on A1 model,${\mathbb {A}}_1$ model, ${\mathbb {H}}_1$ model, respectively.

As is well known, the closer the coefficient is to 1, the stronger the correlation between two variables. From Table 20, it can be concluded that except for the ranking results obtained by method in Garg and Atef (2022), there is a high correlation between the ranking results obtained by other methods, and the Spearman rank correlation coefficient between these methods pairwise is not less than 0.9. Furthermore, each method has at least one other method that is completely correlated to it. This further verifies the effectiveness of our method. However, the correlation coefficient between the ranking results obtained by method in Garg and Atef (2022) and other methods is at most 0.7, which does not indicate that method in Garg and Atef (2022) is invalid, as it obtains the same optimal alternative as other methods. In practical applications, the ranking results obtained by different methods are different, and the specific choice of method depends to some extent on the preferences of decision-makers.

Table 20 Ranking results of alternatives with different methods

9 Conclusions

The main focus of this paper is to extend the fuzzy covering-based rough set to the q-ROF environment inspired by the ideas in Qi et al. (2023). First of all, the q-ROF theory has been enriched by proposing q-ROF t-norm, q-ROF t-conorm, q-ROF overlap function, q-ROF implication and so on. Next, four t-norm based fuzzy neighborhood operators, four overlap function based fuzzy neighborhood operators and eight fuzzy coverings (D’eer et al. 2017; Qi et al. 2023) are extended to q-ROF setting. For a finite q-ROF covering, 24 Tq-ROFNOs are defined by four Tq-ROFNOs and six coverings $\mathcal {C}, \mathcal {C}_1,\mathcal {C}_2,\mathcal {C}_3, \mathcal {C}_4$ and $\mathcal {C}_{\cap }$, 24 Oq-ROFNOs are defined by four Oq-ROFNOs and six coverings $\mathcal {C}, \mathcal {C}_1,\mathcal {C}_2,\hat{\mathcal {C}}_3,\hat{\mathcal {C}}_4$ and $\mathcal {C}_{\cap }$ and relations of these neighborhood operators are discussed. We have conclude that there are sixteen groups of Tq-ROFNOs for a continuous q-ROF t-norm and seventeen groups of Oq-ROFNOs for a q-ROF overlap function satisfying (O6). In this setting, the partial order relations “$\preceq _L$" among sixteen groups of Tq-ROFNOs and among seventeen groups of Oq-ROFNOs are discussed respectively, and the lattice of Tq-ROFNOs and the lattice of Oq-ROFNOs are obtained. Then four types of NRq-ROFCRS models defined by q-ROF neighborhood operators have been investigated. Furthermore, a novel method via integrating NRq-ROFCRS models with the idea of TOPSIS is proposed. In our method, weights of attributes are calculated by neighborhood-related q-ROF approximation operators, which can objectively reflect the preference of decision makers and overcome their subjective influence on the ranking results. Finally, the effectiveness and reasonableness of our method are verified by assessment of new faculty position problem. By experimental analysis, we have concluded that different models, logical operators and parameters q have no significant impact on the performance of our method. Results of our method are no less than other existing methods.

Recently, Alcantud proposed complemental fuzzy sets that encompass the q-rung orthopair fuzzy sets and Sugeno intuitionistic fuzzy sets which generalize intuitionistic fuzzy sets in a novel manner (Alcantud 2023). Extending neighborhood-related covering-based rough set model to complementary fuzzy sets and Sugeno intuitionistic fuzzy sets comes to mind easily. The application of NRq-ROFCRS models in other fields, such as attribute reduction and three-way decision, is also our future line of research. Moreover, q-ROFS can’t be applied in situations where opinion is not only yes or no but there is some abstinence or refusal too. To deal with such situations, Mahmood et al. proposed the concept of spherical fuzzy sets and T-spherical fuzzy sets (Mahmood et al. 2019). Then medical diagnosis (Mahmood et al. 2019), multi-attribute decision-making problem (Ali et al. 2022) and multi-attribute group decision-making problem (Hussain et al. 2023) were discussed in the context of spherical fuzzy sets through the use of aggregation functions. Extending our work to spherical fuzzy sets and T-spherical fuzzy sets with multi-attribute decision making methodologies is also our future line of research.

Appendix

Proof of Proposition 1

We first need to prove that $\mathscr {T}\in L$ and $\mathscr {S}\in L$. In fact, $\left( \root q \of {T(\varepsilon ^q_1, \eta ^q_1)}\right) ^q + \left( \root q \of {S(\varepsilon ^q_2, \eta ^q_2)}\right) ^q = T(\varepsilon ^q_1, \eta ^q_1) + S(\varepsilon ^q_2, \eta ^q_2) \le 1-S(1-\varepsilon ^q_1, 1-\eta ^q_1) + S(\varepsilon ^q_2, \eta ^q_2)$, because $T(\rho ,\delta ) \le 1 - S(1-\rho , 1-\delta )$ for $\rho , \delta \in [0,1]$. And since $\varepsilon = (\varepsilon _1,\varepsilon _2) \in L, \eta = (\eta _1,\eta _2) \in L$ and the monotonicity of T and S, we have that $S(\varepsilon ^q_2, \eta ^q_2)\le S(1-\varepsilon ^q_1, 1-\eta ^q_1)$. Thus, $T(\varepsilon ^q_1, \eta ^q_1) + S(\varepsilon ^q_2, \eta ^q_2) \le 1$. This proves that $\mathscr {T}\in L$. It is similar to prove that $\mathscr {S}\in L$.

In addition, it’s easy to prove that $\mathscr {T}$ and $\mathscr {S}$ are commutative, associative, and monotonic based on the commutativity, associativity and monotonicity of T and S. Moreover, $\mathscr {T}(1_L, \varepsilon ) = (\root q \of {T(1, \varepsilon ^q_1)}, \root q \of {S(0, \varepsilon ^q_2)}) = (\varepsilon _1, \varepsilon _2) = \varepsilon$. Similarly, we can prove that $\mathscr {S}(0_L, \varepsilon ) = \varepsilon$. Therefore, $\mathscr {T}$ is a q-ROF t-norm and $\mathscr {S}$ is a q-ROF t-conorm. $\square$

Proof of Proposition 2

By Definition 17, for $z_i = (\mu _i,\nu _i) \in L$, we have that

$$\begin{aligned} \begin{aligned} \mathscr {I}_{T}(\varepsilon ,\eta )&= \sup \{z_i \in L \mid \mathscr {T}(\varepsilon ,z_i)\preceq _L \eta \},\\&= \sup \{(\mu _i,\nu _i) \in L \mid \root q \of {T(\varepsilon ^q_1,\mu ^q_i)} \le \eta _1, \root q \of {S(\varepsilon ^q_2,\nu ^q_i)}\ge \eta _2 \},\\&= \sup \{(\mu _i,\nu _i) \in L\mid T(\varepsilon ^q_1,\mu ^q_i) \le \eta ^q_1, S(\varepsilon ^q_2,\nu ^q_i)\ge \eta ^q_2 \}.\\ \end{aligned} \end{aligned}$$

By definitions of $I_{T}$ and $D_{S}$, we have that

$$\begin{aligned} \begin{aligned} T(\varepsilon ^q_1,\mu ^q_i) \le \eta ^q_1, S(\varepsilon ^q_2,\nu ^q_i)\ge \eta ^q_2&\Rightarrow I_{T}(\varepsilon ^q_1, \eta ^q_1)\ge \mu ^q_i, \text {and~~} D_{S}(\eta ^q_2, \varepsilon ^q_2) \le \nu ^q_i, \\&\Rightarrow \root q \of {I_{T}(\varepsilon ^q_1, \eta ^q_1)}\ge \mu _i, \root q \of {D_{S}(\eta ^q_2, \varepsilon ^q_2)} \le \nu _i, \\&~~~~~ \root q \of { 1- D_{S}(\eta ^q_2, \varepsilon ^q_2)} \ge \root q \of { 1- \nu ^q_i} \ge \mu _i. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \mathscr {I}_{T}(\varepsilon ,\eta ) \preceq _L \bigg (\min \bigg \{\root q \of {I_{T}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg \},\root q \of {D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg ). \end{aligned}$$

On the other hand,

$$\begin{aligned} \begin{aligned}&\mathscr {T}\bigg (\varepsilon ,\bigg (\min \bigg \{\root q \of {I_{T}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg \},\root q \of {D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg )\bigg )\\ {}&\quad \preceq _L\mathscr {T}\bigg (\varepsilon ,\bigg (\root q \of {I_{T}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg )\bigg )\\&\quad \preceq _L \bigg (\root q \of {T\bigg (\varepsilon ^q_1, I_{T}(\varepsilon ^q_1, \eta ^q_1))},\root q \of {S(\varepsilon ^q_2,D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg )\bigg )\\&\quad \preceq _L (\eta _1, \eta _2) = \eta . \end{aligned} \end{aligned}$$

Therefore, we have that

$$\begin{aligned} \bigg (\min \bigg \{\root q \of {I_{T}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg \}, \root q \of {D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg ) \preceq _L \mathscr {I}_{T}(\varepsilon ,\eta ). \end{aligned}$$

Thus, we conclude that

$$\begin{aligned} \mathscr {I}_{T}(\varepsilon ,\eta ) = \bigg (\min \bigg \{\root q \of {I_{T}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg \},\root q \of {D_{S}(\eta ^q_2,\varepsilon ^q_2)}\bigg ). \end{aligned}$$

$\square$

Proof of Proposition 3

We first need to prove that $\mathscr {O}\in L$. In fact, $\left( \root q \of {O(\varepsilon ^q_1, \eta ^q_1)}\right) ^q + \left( \root q \of {G(\varepsilon ^q_2, \eta ^q_2)}\right) ^q = O(\varepsilon ^q_1, \eta ^q_1) + G(\varepsilon ^q_2, \eta ^q_2) \le 1-G(1-\varepsilon ^q_1, 1-\eta ^q_1) + G(\varepsilon ^q_2, \eta ^q_2)$, because $O(\rho ,\delta ) \le 1 - G(1-\rho , 1-\delta )$ for all $\rho , \delta \in [0,1]$. And since $\varepsilon = (\varepsilon _1,\varepsilon _2) \in L, \eta = (\eta _1,\eta _2) \in L$ and the monotonicity of O and G, we have that $G(\varepsilon ^q_2, \eta ^q_2)\le G(1-\varepsilon ^q_1, 1-\eta ^q_1)$. Thus, $O(\varepsilon ^q_1, \eta ^q_1) + G(\varepsilon ^q_2, \eta ^q_2) \le 1$. This proves that $\mathscr {O}\in L$.

In addition, it’s easy to prove that $\mathscr {O}$ is commutative, monotonic and continuous based on the commutativity, monotonicity and continuity of O and G. Moreover, $\mathscr {O}(\varepsilon , \eta ) = (\root q \of {O(\varepsilon ^q_1, \eta ^q_1)}, \root q \of {G(\varepsilon ^q_2, \eta ^q_2)}) = 0_L = (0, 1)$ if and only if $O(\varepsilon ^q_1, \eta ^q_1) = 0$ and $G(\varepsilon ^q_2, \eta ^q_2)=1$. By the boundary condition of O and G, we obtain that $\varepsilon _1 = 0, \varepsilon _2 = 1$ or $\eta _1 = 0, \eta _2 = 1$, i.e., $\varepsilon =0_L$ or $\eta =0_L$. Similarly, we can prove that $\mathscr {O}(\varepsilon , \eta ) = 1_L$ if and only if $\varepsilon = 1_L$ and $\eta = 1_L$. Therefore, $\mathscr {O}$ is a q-ROF overlap function. $\square$

Proof of Proposition 4

By Definition 21, for $z_i = (\mu _i,\nu _i) \in L$, we have that

$$\begin{aligned} \begin{aligned} \mathscr {I}_{O}(\varepsilon ,\eta )&= \max \{z_i \in L \mid \mathscr {O}(\varepsilon ,z_i)\preceq _L \eta \},\\&= \max \bigg \{(\mu _i,\nu _i) \in L\mid \root q \of {O(\varepsilon ^q_1,\mu ^q_i)} \le \eta _1, \root q \of {G(\varepsilon ^q_2,\nu ^q_i)}\ge \eta _2 \bigg \},\\&= \max \bigg \{(\mu _i,\nu _i) \in L\mid O(\varepsilon ^q_1,\mu ^q_i) \le \eta ^q_1, G(\varepsilon ^q_2,\nu ^q_i)\ge \eta ^q_2 \bigg \}.\\ \end{aligned} \end{aligned}$$

By definitions of $I_{O}$ and $\mathscr {D}$, we have that

$$\begin{aligned} \begin{aligned} O(\varepsilon ^q_1,\mu ^q_i) \le \eta ^q_1, G(\varepsilon ^q_2,\nu ^q_i)\ge \eta ^q_2&\Rightarrow I_{O}(\varepsilon ^q_1, \eta ^q_1)\ge \mu ^q_i, \text {and~~} \mathscr {D}(\eta ^q_2, \varepsilon ^q_2) \le \nu ^q_i, \\&\Rightarrow \root q \of {I_{O}(\varepsilon ^q_1, \eta ^q_1)}\ge \mu _i, \root q \of {\mathscr {D}(\eta ^q_2, \varepsilon ^q_2)} \le \nu _i, \\&~~~~~ \root q \of { 1- \mathscr {D}(\eta ^q_2, \varepsilon ^q_2)} \ge \root q \of { 1- \nu ^q_i} \ge \mu _i. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \mathscr {I}_{O}(\varepsilon ,\eta ) \preceq _L \bigg (\min \bigg \{\root q \of {I_{O}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg \},\root q \of {\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg ). \end{aligned}$$

On the other hand,

$$\begin{aligned} \begin{aligned}&\mathscr {O}(\varepsilon ,\bigg (\min \bigg \{\root q \of {I_{O}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg \},\root q \of {\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)})\bigg )\\ {}&\quad \preceq _L\mathscr {O}\bigg (\varepsilon ,\bigg (\root q \of {I_{O}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg )\bigg )\\&\quad \preceq _L \bigg (\root q \of {O(\varepsilon ^q_1, I_{O}(\varepsilon ^q_1, \eta ^q_1))},\root q \of {G(\varepsilon ^q_2,{\mathscr {D}}(\eta ^q_2,\varepsilon ^q_2)})\bigg )\\&\quad \preceq _L (\eta _1, \eta _2) = \eta . \end{aligned} \end{aligned}$$

Therefore, we have that

$$\begin{aligned} \bigg (\min \bigg \{\root q \of {I_{O}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg \},\root q \of {\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg ) \preceq _L \mathscr {I}_{O}(\varepsilon ,\eta ). \end{aligned}$$

Thus, we conclude that

$$\begin{aligned} \mathscr {I}_{O}(\varepsilon ,\eta ) = \bigg (\min \bigg \{\root q \of {I_{O}(\varepsilon ^q_1,\eta ^q_1)},\root q \of {1-\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg \},\root q \of {\mathscr {D}(\eta ^q_2,\varepsilon ^q_2)}\bigg ). \end{aligned}$$

$\square$

Proof of Proposition 6

If $\Gamma (\varepsilon ) = 0_L$, it is obvious that $\inf \nolimits _{\Gamma \in \mathcal {C}} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = 1_L$. Hence

$$\begin{aligned} \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned}$$

Since $\widetilde{md}(\mathcal {C}, \varepsilon ) \subseteq \mathscr {C}(\mathcal {C}, \varepsilon )$, it holds that

$$\begin{aligned} \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) \le \inf \limits _{\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned}$$

It is clear that

$$\begin{aligned} \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \min \bigg (\inf \limits _{\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )), \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon ){\setminus } \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta ))\bigg ). \end{aligned}$$

According to Proposition 5, if $\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon ){\setminus } \widetilde{md}(\mathcal {C}, \varepsilon )$, there is a $\Gamma _1 \in \widetilde{md}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma _1 \subseteq \Gamma$ and $\Gamma _1(\varepsilon ) = \Gamma (\varepsilon )$. Therefore,

$$\begin{aligned} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \mathscr {I}_{T}(\Gamma _1(\varepsilon ),\Gamma (\eta )) \ge \mathscr {I}_{T}(\Gamma _1(\varepsilon ),\Gamma _1(\eta )) \end{aligned}$$

for $\eta \in U$. Hence, we have that

$$\begin{aligned} \inf \limits _{\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) \le \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon ){\setminus } \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned}$$

Therefore,

$$\begin{aligned} \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \inf \limits _{\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned}$$

In summary, we have that

$$\begin{aligned} \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \inf \limits _{\Gamma \in \widetilde{md}(\mathcal {C}, \varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) \end{aligned}$$

$\square$

Proof of Proposition 7

The proof is similar to the Proposition 6.

$\square$

Proof of Proposition 8

If $\Gamma (\varepsilon ) = 0_L$, it is obvious that $\sup \limits _{\Gamma \in \mathcal {C}} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) = 0_L$. Hence

$$\begin{aligned} \sup \limits _{\Gamma \in \mathcal {C}} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \sup \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned}$$

Since $\widetilde{MD}(\mathcal {C}, \varepsilon ) \subseteq \mathscr {C}(\mathcal {C}, \varepsilon )$, it holds that

$$\begin{aligned} \sup \limits _{\Gamma \in \widetilde{MD}(\mathcal {C}, x)} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \le \sup \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned}$$

It is clear that

$$\begin{aligned} \sup \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \max \bigg (\sup \limits _{\Gamma \in \widetilde{MD}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )), \sup \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon ){\setminus } \widetilde{MD}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta ))\bigg ). \end{aligned}$$

According to Proposition 5, if $\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon ){\setminus } \widetilde{MD}(\mathcal {C}, \varepsilon )$, there is a $\Gamma _1 \in \widetilde{MD}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma \subseteq \Gamma _1$ and $\Gamma _1(\varepsilon ) = \Gamma (\varepsilon )$. Therefore,

$$\begin{aligned} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \mathscr {T}(\Gamma _1(\varepsilon ),\Gamma (\eta )) \le \mathscr {T}(\Gamma _1(\varepsilon ),\Gamma _1(\eta )) \end{aligned}$$

for $\eta \in U$. Hence, we have that

$$\begin{aligned} \sup \limits _{\Gamma \in \widetilde{MD}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \ge \inf \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon ){\setminus } \widetilde{MD}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned}$$

Therefore,

$$\begin{aligned} \sup \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \sup \limits _{\Gamma \in \widetilde{MD}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned}$$

In summary, we have that

$$\begin{aligned} \sup \limits _{\Gamma \in \mathcal {C}} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \sup \limits _{\Gamma \in \mathscr {C}(\mathcal {C}, \varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) = \sup \limits _{\Gamma \in \widetilde{MD}(\mathcal {C}, x)} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \end{aligned}$$

$\square$

Proof of Proposition 9

The proof is similiar to the Proposition 6.

$\square$

Proof of Proposition 10

Since for $\varepsilon \in U, ~\Gamma \in \mathcal {C}$, $\mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\varepsilon )) = 1_L$. Hence

$$\begin{aligned} N_1^\mathcal {C}(\varepsilon )(\varepsilon )= & {} \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\varepsilon )) = 1_L, \\ N_3^\mathcal {C}(\varepsilon )(\varepsilon )= & {} \inf \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\varepsilon )) = 1_L, \end{aligned}$$

Thus, the reflexivity of $N_1^\mathcal {C}$ and $N_3^\mathcal {C}$ holds.

For any $\varepsilon \in U$, there is a $\Gamma \in \mathcal {C}$ which satisfies $\Gamma (\varepsilon ) = 1_L$. Hence $N_4^\mathcal {C}(\varepsilon )(\varepsilon ) \succeq _L \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\varepsilon )) = 1_L$, that is $N_4^\mathcal {C}$ is reflexive.

Additionally, for any $\varepsilon \in U$, there is a $\Gamma \in \mathcal {C}$ which satisfies $\Gamma (\varepsilon ) = 1_L$. Moreover, due to $\mathcal {C}$ is finite, there exists $\Gamma _1 \in \widetilde{md}(\mathcal {C},\varepsilon )$ which satisfied $\Gamma _1(\varepsilon ) = \Gamma (\varepsilon ) = 1_L$. Hence, $N_2^\mathcal {C}(\varepsilon )(\varepsilon ) \succeq _L \mathscr {T}(\Gamma _1(\varepsilon ),\Gamma _1(\varepsilon )) = 1_L$. Thus, $N_2^\mathcal {C}$ is reflexive. $\square$

Proof of Proposition 11

Due to $\mathscr {O}$ satisfies (O6), for $\varepsilon \in U, ~\Gamma \in \mathcal {C}$, $\mathscr {O}(\Gamma (\varepsilon ),1_L) \preceq _L \Gamma (\varepsilon )$. Hence, if $\Gamma (\varepsilon ) \preceq _L \Gamma (\eta )$, we have $\mathscr {I}_{O}(\Gamma (\varepsilon ),\Gamma (\eta )) = 1_L$. Therefore,

$$\begin{aligned} {\mathbb {N}}_1^\mathcal {C}(\varepsilon )(\varepsilon )= & {} \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{O}(\Gamma (\varepsilon ),\Gamma (\varepsilon )) = 1_L, \\ {\mathbb {N}}_3^\mathcal {C}(\varepsilon )(\varepsilon )= & {} \inf \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )} \mathscr {I}_{O}(\Gamma (\varepsilon ),\Gamma (\varepsilon )) = 1_L, \end{aligned}$$

Thus, the reflexivity of ${\mathbb {N}}_1^\mathcal {C}$ and ${\mathbb {N}}_3^\mathcal {C}$ holds.

For any $\varepsilon \in U$, there is a $\Gamma \in \mathcal {C}$ which satisfies $\Gamma (\varepsilon ) = 1_L$. Hence ${\mathbb {N}}_4^\mathcal {C}(\varepsilon )(\varepsilon ) \succeq _L \mathscr {O}(\Gamma (\varepsilon ),\Gamma (\varepsilon )) = 1_L$, that is ${\mathbb {N}}_4^\mathcal {C}$ is reflexive.

Additionally, for $\varepsilon \in U$, there exists $\Gamma \in \mathcal {C}$ which satisfies $\Gamma (\varepsilon ) = 1_L$. Moreover, due to $\mathcal {C}$ is finite, there exists $\Gamma _1 \in \widetilde{md}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma _1(\varepsilon ) = \Gamma (\varepsilon ) = 1_L$. Hence, ${\mathbb {N}}_2^\mathcal {C}(\varepsilon )(\varepsilon ) \succeq _L \mathscr {O}(\Gamma _1(\varepsilon ),\Gamma _1(\varepsilon )) = 1_L$. Thus, ${\mathbb {N}}_2^\mathcal {C}$ is reflexive. $\square$

Proof of Proposition 12

It is easy to prove by the fact that the q-ROF t-norm is commutative. $\square$

Proof of Proposition 13

It is proved immediately from the fact that the q-ROF overlap function is commutative. $\square$

Proof of Proposition 15

As for $N_1^\mathcal {C}$,

$$\begin{aligned} \begin{aligned}&\mathscr {T}(\inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )),\inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{T}(\Gamma (\eta ),\Gamma (\theta )))\\&\quad \preceq _L \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {T}( \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\theta )), \mathscr {I}_{T}(\Gamma (\eta ),\Gamma (\theta ))),\\&\quad \preceq _L \inf \limits _{\Gamma \in \mathcal {C}} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\theta )), \end{aligned} \end{aligned}$$

Hence $N_1^\mathcal {C}$ is $\mathscr {T}$-transitive. The $\mathscr {T}$-transitivity of $N_3^\mathcal {C}$ can be proved similarly. $\square$

Proof of Proposition 16

For $\varepsilon \in U$, there is a $\Gamma \in \mathcal {C}$ which satisfies $\Gamma (\varepsilon ) = 1_L$.

According to Proposition 5, there are $\Gamma _1 \in \widetilde{md}(\mathcal {C},\varepsilon )$ and $\Gamma _2 \in \widetilde{MD}(\mathcal {C},\varepsilon )$ such $\Gamma (\varepsilon ) = \Gamma _1(\varepsilon ) = \Gamma _2(\varepsilon ) = 1_L$. Hence $\mathcal {C}_1,\mathcal {C}_2$ are finite q-ROF subcoverings of $\mathcal {C}$.

Let $\Gamma \notin \mathcal {C}_{\cup }$, there is a a collection of $\mathcal {C}^{\prime } \subseteq \mathcal {C}{\setminus } \{\Gamma \}$ which satisfies $\Gamma (\varepsilon ) = \bigcup \mathcal {C}^{\prime }(\varepsilon ) = 1_L$. Since $\mathcal {C}$ is finite, there is a $\mathcal {C}^{\prime }_1 \subseteq \cup \mathcal {C}^{\prime }$ and $\Gamma ^{\prime } \in \mathcal {C}^{\prime }_1$ which satisfies $\Gamma ^{\prime }(\varepsilon ) = 1_L$. Hence there exists a $\Gamma ^{\prime } \in \mathcal {C}_{\cup }$ which satisfies $\Gamma ^{\prime }(\varepsilon ) = 1_L$. Therefore $\mathcal {C}_{\cup }$ is a finite q-ROF subcovering of $\mathcal {C}$. $\square$

Proof of Proposition 17

For any $\varepsilon \in U$, there exists a $\Gamma \in \mathcal {C}$ which satisfies $\Gamma (\varepsilon ) = 1_L$. Assume $\Gamma \notin \mathcal {C}_{\cap }$, there exists a collection of $\mathcal {C}^{\prime } \subseteq \mathcal {C}{\setminus } \{\Gamma \}$ which satisfies $\Gamma = \bigcap \mathcal {C}^{\prime }$. Hence, for all $\Gamma ^{\prime } \in \bigcap \mathcal {C}^{\prime }$, we have $\Gamma ^{\prime }(\varepsilon ) = 1_L$. Thus, there exists a $\Gamma ^{\prime } \in \mathcal {C}_{\cap }$ which satisfies $\Gamma ^{\prime }(\varepsilon ) = 1_L$. Therefore $\mathcal {C}_{\cap }$ is also a q-ROF subcovering of $\mathcal {C}$. $\square$

Proof of Proposition 18

For any $\Gamma \in \mathcal {C}_2$, there exists a $\varepsilon \in U$ which satisfies $\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )$. If $\Gamma \notin \mathcal {C}_{\cap }$, there exists a collection $\mathcal {C}^{\prime } \subseteq \mathcal {C}{\setminus } \{\Gamma \}$ which satisfies $\Gamma = \bigcap \mathcal {C}^{\prime }$. Since $\mathcal {C}$ is finite, there exists $\Gamma ^{\prime } \in \mathcal {C}^{\prime }$ which satisfies $\Gamma ^{\prime }(\varepsilon ) = \Gamma (\varepsilon )\succ _L0_L$ and $\Gamma \subseteq \Gamma ^{\prime }$. And due to $\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )$, we have $\Gamma \in \mathcal {C}_{\cap }$. $\square$

Proof of Proposition 19

The proof is similar to Proposition 12 in D’eer et al. (2017). $\square$

Proof of Proposition 22

• 1. For $\varepsilon \in U$, if $\Gamma \in \widetilde{md}(\mathcal {C}_1,\varepsilon ), \Gamma \in \mathcal {C}_1$ and $\Gamma (\varepsilon ) \succ _L 0$ hold. Since $\mathcal {C}_1$ is a q-ROF subcovering of $\mathcal {C}$, $\Gamma \in \mathcal {C}$ also holds. Then there is a $\Gamma '\in \widetilde{md}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma '(\varepsilon ) = \Gamma (\varepsilon )$ and $\Gamma '\subseteq \Gamma$. By the definition of $\mathcal {C}_1$, $\Gamma '\in \mathcal {C}_1$, then $\Gamma '= \Gamma$ since $\Gamma \in \widetilde{md}(\mathcal {C}_1,\varepsilon )$. Therefore, $\Gamma \in \widetilde{md}(\mathcal {C},\varepsilon )$ and $\widetilde{md}(\mathcal {C}_1,\varepsilon ) \subseteq \widetilde{md}(\mathcal {C},\varepsilon )$. Moreover, if $\Gamma \in \widetilde{md}(\mathcal {C},\varepsilon ), \Gamma \in \mathcal {C}_1$ and $\Gamma (\varepsilon ) \succ _L 0$ hold. Then there is $\Gamma '\in \widetilde{md}(\mathcal {C}_1,\varepsilon )$ which satisfies $\Gamma '(\varepsilon ) = \Gamma (\varepsilon )$ and $\Gamma '\subseteq \Gamma$. Since $\mathcal {C}_1$ is a q-ROF subcovering of $\mathcal {C}$, $\Gamma ' \in \mathcal {C}$ holds. Due to $\Gamma \in \widetilde{md}(\mathcal {C},\varepsilon )$, then $\Gamma '= \Gamma$. Hence $\Gamma \in \widetilde{md}(\mathcal {C}_1,\varepsilon )$ and $\widetilde{md}(\mathcal {C},\varepsilon ) \subseteq \widetilde{md}(\mathcal {C}_1,\varepsilon )$. To sum up, we obtain that $\widetilde{md}(\mathcal {C}_1,\varepsilon ) = \widetilde{md}(\mathcal {C},\varepsilon )$.

• 2. For $\varepsilon \in U$, if $\Gamma \in \widetilde{MD}(\mathcal {C}_2,\varepsilon ), \Gamma \in \mathcal {C}_2$ and $\Gamma (\varepsilon ) \succ _L 0$ hold. Since $\mathcal {C}_2$ is a q-ROF subcovering of $\mathcal {C}$, $\Gamma \in \mathcal {C}$ also holds. Then there is a $\Gamma '\in \widetilde{MD}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma '(\varepsilon ) = \Gamma (\varepsilon )$ and $\Gamma \subseteq \Gamma '$. By the definition of $\mathcal {C}_2$, $\Gamma '\in \mathcal {C}_2$, then $\Gamma '= \Gamma$ since $\Gamma \in \widetilde{MD}(\mathcal {C}_2,\varepsilon )$. Therefore, $\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )$ and $\widetilde{MD}(\mathcal {C}_2,\varepsilon ) \subseteq \widetilde{MD}(\mathcal {C},\varepsilon )$. Moreover, if $\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon ), \Gamma \in \mathcal {C}_2$ and $\Gamma (\varepsilon ) \succ _L 0$ hold. Then there is a $\Gamma '\in \widetilde{MD}(\mathcal {C}_2,\varepsilon )$ which satisfies $\Gamma '(\varepsilon ) = \Gamma (\varepsilon )$ and $\Gamma \subseteq \Gamma '$. Since $\mathcal {C}_2$ is a q-ROF subcovering of $\mathcal {C}$, $\Gamma ' \in \mathcal {C}$ holds. Due to $\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )$, then $\Gamma '= \Gamma$. Hence $\Gamma \in \widetilde{MD}(\mathcal {C}_2,\varepsilon )$ and $\widetilde{MD}(\mathcal {C},\varepsilon ) \subseteq \widetilde{MD}(\mathcal {C}_2,\varepsilon )$. To sum up, we obtain that $\widetilde{MD}(\mathcal {C}_2,\varepsilon ) = \widetilde{MD}(\mathcal {C},\varepsilon )$.

• 3. For $\varepsilon \in U$, if $\Gamma \in \widetilde{MD}(\mathcal {C}_{\cap },\varepsilon )$, $\Gamma (\varepsilon ) \succ _L 0$ and $\Gamma \in \mathcal {C}_{\cap } \subseteq \mathcal {C}$ hold since $\mathcal {C}_{\cap }$ is the subset of $\mathcal {C}$. Then there is a $\Gamma '\in \widetilde{MD}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma '(\varepsilon ) = \Gamma (\varepsilon )$ and $\Gamma \subseteq \Gamma '$. By the definition of $\mathcal {C}_2$, $\Gamma '\in \mathcal {C}_2\subseteq \mathcal {C}_{\cap }$ holds since $\mathcal {C}_2$ is the subset of $\mathcal {C}_{\cap }$ if $\mathcal {C}$ is finite, then $\Gamma '= \Gamma$ since $\Gamma \in \widetilde{MD}(\mathcal {C}_{\cap },\varepsilon )$. Therefore, $\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )$ and $\widetilde{MD}(\mathcal {C}_{\cap },\varepsilon ) \subseteq \widetilde{MD}(\mathcal {C},\varepsilon )$. Moreover, if $\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon ), \Gamma \in \mathcal {C}_2 \subseteq \mathcal {C}_{\cap }$ and $\Gamma (\varepsilon ) \succ _L 0$ hold. Then there is a $\Gamma '\in \widetilde{MD}(\mathcal {C}_{\cap },\varepsilon )$ which satisfies $\Gamma '(\varepsilon ) = \Gamma (\varepsilon )$ and $\Gamma \subseteq \Gamma '$. Since $\mathcal {C}_{\cap }$ is a q-ROF subcovering of $\mathcal {C}$, $\Gamma ' \in \mathcal {C}$ holds. Due to $\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )$, then $\Gamma '= \Gamma$. Hence $\Gamma \in \widetilde{MD}(\mathcal {C}_{\cap },\varepsilon )$ and $\widetilde{MD}(\mathcal {C},\varepsilon ) \subseteq \widetilde{MD}(\mathcal {C}_{\cap },\varepsilon )$. To sum up, we obtain that $\widetilde{MD}(\mathcal {C}_{\cap },\varepsilon ) = \widetilde{MD}(\mathcal {C},\varepsilon )$.

$\square$

Proof of Proposition 23

For $\varepsilon \in U$, let $\Gamma \in \widetilde{md}(\mathcal {C}_{\cap },\varepsilon ) \bigcap \mathcal {C}_2$. Assume $\Gamma \notin \widetilde{md}(\mathcal {C}_2,\varepsilon )$, then there is a $\Gamma ' \in \widetilde{md}(\mathcal {C}_2,\varepsilon ) \subseteq \mathcal {C}_2$ which satisfies $\Gamma '(\varepsilon ) = \Gamma (\varepsilon )$ and $\Gamma ' \subseteq \Gamma$. We obtain $\Gamma ' = \Gamma$, since $\mathcal {C}_2 \subseteq \mathcal {C}_{\cap }$ and $\Gamma \in \widetilde{md}(\mathcal {C}_{\cap },\varepsilon )$, which contradicts with the hypothesis. Therefore, $\Gamma \in \widetilde{md}(\mathcal {C}_2,\varepsilon )$. $\square$

Proof of Proposition 24

• 1. It is deduced immediately from Propsition 6 and (1) of Propsition 22.

• 2. By Proposition 15, $N_1^{\mathcal {C}}$ is $\mathscr {T}$-transitive. Therefore, we have that

  $$\begin{aligned} \mathscr {T}(N_1^{\mathcal {C}}(\varepsilon )(\eta ), N_1^{\mathcal {C}}(\theta )(\varepsilon )) = \mathscr {T}(N_1^{\mathcal {C}}(\theta )(\varepsilon ), N_1^{\mathcal {C}}(\varepsilon )(\eta )) \preceq _L N_1^{\mathcal {C}}(\theta )(\eta ) \end{aligned}$$

  for $\varepsilon , \eta , \theta \in U$. Thus, $N_1^{\mathcal {C}}(\varepsilon )(\eta ) \preceq _L \mathscr {I}_{T}(N_1^{\mathcal {C}}(\theta )(\varepsilon ), N_1^{\mathcal {C}}(\theta )(\eta )).$ Hence, $N_1^{\mathcal {C}}(\varepsilon )(\eta ) \preceq _L \inf \limits _{\theta \in U} \mathscr {I}_{T}(N_1^{\mathcal {C}}(\theta )(\varepsilon ), N_1^{\mathcal {C}}(\theta )(\eta )) = \inf \limits _{\Gamma \in \mathcal {C}_3} \mathscr {I}_{T}(\Gamma (\varepsilon ), \Gamma (\eta )) = N_1^{\mathcal {C}_3}(\varepsilon )(\eta )$. Assume that $\mathscr {I}_{T}$ be a q-ROF $R_T$-implication of a continuous q-ROF t-norm and $\varepsilon \in U$. Since $N_1^{\mathcal {C}}(\varepsilon ) \in \mathcal {C}_3$ by the definition of $\mathcal {C}_3$, for ${\eta } \in U$, we have $N_1^{\mathcal {C}_3}(\varepsilon )(\eta ) = \inf \limits _{\Gamma \in \mathcal {C}_3} \mathscr {I}_{T}(\Gamma (\varepsilon ), \Gamma (\eta )) \preceq _L \mathscr {I}_{T}(N_1^{\mathcal {C}}(\varepsilon )(\varepsilon ), N_1^{\mathcal {C}}(\varepsilon )(\eta )) = \mathscr {I}_{T}(1, N_1^{\mathcal {C}}(\varepsilon )(\eta )) = N_1^{\mathcal {C}}(\varepsilon )(\eta )$. Hence, $N_1^{\mathcal {C}} = N_1^{\mathcal {C}_3}$ holds.

• 3. For $\varepsilon \in U$, $N_1^{\mathcal {C}}(\varepsilon ) \subseteq N_1^{\mathcal {C}_{\cap }}(\varepsilon )$ since $\mathcal {C}_{\cap }$ is a subset of $\mathcal {C}$. textcolor[rgb]1.00,0.00,0.00For all $\eta \in U$, there is a $\Gamma \in \mathcal {C}$ that satisfies $N_1^{\mathcal {C}}(\varepsilon )(\eta ) = \mathscr {I}_{T}(\Gamma (\varepsilon ), \Gamma (\eta ))$. If $\Gamma \in \mathcal {C}_{\cap }$, then $N_1^{\mathcal {C}_{\cap }}(\varepsilon )(\eta ) = \inf \limits _{\Gamma \in \mathcal {C}_{\cap }} \mathscr {I}_{T}(\Gamma (\varepsilon ), \Gamma (\eta )) \preceq _L \mathscr {I}_{T}(\Gamma (\varepsilon ), \Gamma (\eta )) = N_1^{\mathcal {C}}(\varepsilon )(\eta )$. If $\Gamma \notin \mathcal {C}_{\cap }$, there exists a colleciton $\mathcal {C}^{'} \subseteq \mathcal {C}_{\cap }$ which satisfies $\Gamma = \bigcap \mathcal {C}^{'}$. Since $\mathcal {C}$ is finite, there also exists a $\Gamma ' \in \mathcal {C}^{'}$ which satisfies $\Gamma '(\eta ) = \Gamma (\eta )$ and $\Gamma \subseteq \Gamma '$. Therefore $\mathscr {I}_{T}(\Gamma (\varepsilon ), \Gamma (\eta )) = \mathscr {I}_{T}(\Gamma (\varepsilon ), \Gamma '(\eta ))\succeq _L \mathscr {I}_{T}(\Gamma '(\varepsilon ), \Gamma '(\eta ))$. Since $\Gamma ' \in \mathcal {C}_{\cap }$ and the infimum of $N_1^{\mathcal {C}}(\varepsilon )(\eta )$ is reached at $\Gamma$, we have $N_1^{\mathcal {C}}(\varepsilon )(\eta ) = \mathscr {I}_{T}(\Gamma '(\varepsilon ), \Gamma '(\eta ))$. Therefore, $N_1^{\mathcal {C}_{\cap }}(\varepsilon )(\eta ) = \inf \limits _{\Gamma \in \mathcal {C}_{\cap }} \mathscr {I}_{T}(\Gamma (\varepsilon ), \Gamma (\eta )) \preceq _L \mathscr {I}_{T}(\Gamma '(\varepsilon ), \Gamma '(\eta )) = N_1^{\mathcal {C}}(\varepsilon )(\eta )$, i.e. $N_1^{\mathcal {C}_{\cap }}(\varepsilon ) \subseteq N_1^{\mathcal {C}}(\varepsilon )$. Hence, $N_1^{\mathcal {C}} = N_1^{\mathcal {C}_{\cap }}$ holds.

$\square$

Proof of Proposition 25

• 1. It is deduced immediately from Propsition 7 and (1) of Propsition 22.

• 2. For all $\varepsilon \in U$, ${\mathbb {N}}_1^{\mathcal {C}}(\varepsilon ) \subseteq {\mathbb {N}}_1^{\mathcal {C}_{\cap }}(\varepsilon )$ since $\mathcal {C}_{\cap }$ is a subset of $\mathcal {C}$. For $\eta \in U$, there exists $\Gamma \in \mathcal {C}$ which satisfies ${\mathbb {N}}_1^{\mathcal {C}}(\varepsilon )(\eta )) = \mathscr {I}_{O}(\Gamma (\varepsilon ), \Gamma (\eta ))$. If $\Gamma \in \mathcal {C}_{\cap }$, then ${\mathbb {N}}_1^{\mathcal {C}_{\cap }}(\varepsilon )(\eta )) = \inf \limits _{\Gamma \in \mathcal {C}_{\cap }} \mathscr {I}_{O}(\Gamma (\varepsilon ), \Gamma (\eta )) \preceq _L \mathscr {I}_{O}(\Gamma (\varepsilon ), \Gamma (\eta )) = {\mathbb {N}}_1^{\mathcal {C}}(\varepsilon )(\eta ))$. If $\Gamma \notin \mathcal {C}_{\cap }$, there exists a colleciton $\mathcal {C}^{'} \subseteq \mathcal {C}_{\cap }$ which satisfies $\Gamma = \bigcap \mathcal {C}^{'}$. Since $\mathcal {C}$ is finite, there also exists $\Gamma ' \in \mathcal {C}^{'}$ which satisfies $\Gamma '(\eta ) = \Gamma (\eta )$ and $\Gamma \subseteq \Gamma '$. Therefore $\mathscr {I}_{O}(\Gamma (\varepsilon ), \Gamma (\eta )) = \mathscr {I}_{O}(\Gamma (\varepsilon ), \Gamma '(\eta ))\succeq _L \mathscr {I}_{O}(\Gamma '(\varepsilon ), \Gamma '(\eta ))$. Since $\Gamma ' \in \mathcal {C}_{\cap }$ and the infimum of ${\mathbb {N}}_1^{\mathcal {C}}(\varepsilon )(\eta ))$ is reached at $\Gamma$, ${\mathbb {N}}_1^{\mathcal {C}}(\varepsilon )(\eta )) = \mathscr {I}_{O}(\Gamma '(\varepsilon ), \Gamma '(\eta ))$. Therefore, ${\mathbb {N}}_1^{\mathcal {C}_{\cap }}(\varepsilon )(\eta ) = \inf \limits _{\Gamma \in \mathcal {C}_{\cap }} \mathscr {I}_{O}(\Gamma (\varepsilon ), \Gamma (\eta )) \preceq _L \mathscr {I}_{O}(\Gamma '(\varepsilon ), \Gamma '(\eta )) = {\mathbb {N}}_1^{\mathcal {C}}(\varepsilon )(\eta ))$, i.e., ${\mathbb {N}}_1^{\mathcal {C}_{\cap }}(\varepsilon ) \subseteq {\mathbb {N}}_1^{\mathcal {C}}(\varepsilon )$.

$\square$

Proof of Proposition 26

The proof is immediately obtained from (1) of Propsition 22. $\square$

Proof of Proposition 27

The proof is immediately obtained from Propsition (1) of Propsition 22. $\square$

Proof of Proposition 28

The proof is immediately obtained from Propsition (2) and (3) of Propsition 22. $\square$

Proof of Proposition 29

The proof is immediately obtained from Propsition (2) and (3) of Propsition 22. $\square$

Proof of Proposition 30

The proof is immediately obtained from Propsition (2) and (3) of Propsition 22. $\square$

Proof of Proposition 31

The proof is immediately obtained from Propsition (2) and (3) of Propsition 22. $\square$

Proof of Proposition 32

• 1. Assume that $N_2^{\mathcal {C}} \prec _L N_1^{\mathcal {C}}$ holds, i.e., $N_2^{\mathcal {C}}(\varepsilon )(\eta ) \prec _L N_1^{\mathcal {C}}(\varepsilon )(\eta )$ for $\varepsilon ,\eta \in U$. That is to say that

  $$\begin{aligned} \sup \limits _{\Gamma \in \widetilde{md}(\mathcal {C},\varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \prec _L \inf \limits _{\Gamma \in \widetilde{md}(\mathcal {C},\varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) \end{aligned}$$

  holds. Then it holds that $\mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \prec _L \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta ))$ for $\Gamma \in \widetilde{md}(\mathcal {C},\varepsilon )$. By q-ROF minimal description, there is a $\Gamma ^* \in \widetilde{md}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma ^*(\varepsilon ) = 1_L$ for $\varepsilon \in U$. Therefore $\mathscr {T}(\Gamma ^*(\varepsilon ),\Gamma ^*(\eta )) \prec _L \mathscr {I}_{T}(\Gamma ^*(\varepsilon ),\Gamma ^*(\eta )).$ Hence, $\Gamma ^*(\eta )\prec _L \Gamma ^*(\eta )$, which is a contradiction. Hence, we have $N_1^{\mathcal {C}} \preceq _L N_2^{\mathcal {C}}$.

• 2. It is easy to prove by the fact that $\widetilde{MD}(\mathcal {C},\varepsilon ) \subseteq \mathcal {C}$;

• 3. It is easy to prove by the fact that $\widetilde{md}(\mathcal {C},\varepsilon ) \subseteq \mathcal {C}$;

• 4. Assume that $N_4^{\mathcal {C}} \prec _L N_3^{\mathcal {C}}$ holds, i.e., $N_4^{\mathcal {C}}(\varepsilon )(\eta ) \prec _L N_3^{\mathcal {C}}(\varepsilon )(\eta )$ for $\varepsilon ,\eta \in U$. That is to say that

  $$\begin{aligned} \sup \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \prec _L \inf \limits _{K\in \widetilde{MD}(\mathcal {C},\varepsilon )} \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) \end{aligned}$$

  holds. Then for $\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )$, it holds that $\mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \prec _L \mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )).$ By q-ROF maximal description, there is a $\Gamma ^* \in \widetilde{MD}(\mathcal {C},\varepsilon )$ which satisfies $\Gamma ^*(\varepsilon ) = 1_L$ for $\varepsilon \in U$. Therefore $\mathscr {T}(\Gamma ^*(\varepsilon ),\Gamma ^*(\eta )) \prec _L \mathscr {I}_{T}(\Gamma ^*(\varepsilon ),\Gamma ^*(\eta )).$ Hence, $\Gamma ^*(\eta )\prec _L \Gamma ^*(\eta )$, which is a contradiction. Hence, we have $N_3^{\mathcal {C}} \preceq _L N_4^{\mathcal {C}}$.

$\square$

Proof of Proposition 33

• 1. It is easy to prove by the fact that $\widetilde{MD}(\mathcal {C},\varepsilon ) \subseteq \mathcal {C}$;

• 2. It is easy to prove by the fact that $\widetilde{md}(\mathcal {C},\varepsilon ) \subseteq \mathcal {C}$.

$\square$

Proof of Proposition 34

• 1. The proof is immediately obtained from the fact that $\mathcal {C}_2 \subseteq \mathcal {C}$;

• 2. The proof is immediately obtained from the fact that $\mathcal {C}_1 \subseteq \mathcal {C}$.

$\square$

Proof of Proposition 35

• 1. The proof is immediately obtained from the fact that $\mathcal {C}_2 \subseteq \mathcal {C}$;

• 2. The proof is immediately obtained from the fact that $\mathcal {C}_1 \subseteq \mathcal {C}$.

$\square$

Proof of Lemma 1

For all $\varepsilon ,\eta ,\theta \in L$,

$$\begin{aligned} \begin{aligned} \mathscr {I}_{T}(\varepsilon ,\eta )&= \sup \{z\mid \mathscr {T}(\varepsilon ,z)\preceq _L \eta \}\\&= \sup \{z \mid \mathscr {T}(\mathscr {T}(\varepsilon ,z),\theta )\preceq _L \mathscr {T}(\eta ,\theta )\}\\&= \sup \{z\mid \mathscr {T}(\mathscr {T}(\varepsilon ,\theta ),z)\preceq _L \mathscr {T}(\eta ,\theta )\}\\&= \sup \{z\mid z \preceq _L \mathscr {I}_{T}(\mathscr {T}(\varepsilon ,\theta ),\mathscr {T}(\eta ,\theta ))\}\\&\preceq _L \mathscr {I}_{T}(\mathscr {T}(\varepsilon ,\theta ),\mathscr {T}(\eta ,\theta )) \end{aligned} \end{aligned}$$

$\square$

Proof of Proposition 36

• 1. For $\varepsilon ,\eta \in U$,

  $$\begin{aligned} \begin{aligned} N_1^{\mathcal {C}_4}(\varepsilon )(\eta )&= \inf \limits _{\theta \in U}\mathscr {I}_{T}(N_4^{\mathcal {C}}(\theta )(\varepsilon ),N_4^{\mathcal {C}}(\theta )(\eta ))\\&= \inf \limits _{\theta \in U}\mathscr {I}_{T}(N_4^{\mathcal {C}}(\varepsilon )(\theta ),N_4^{\mathcal {C}}(\theta )(\eta ))\\&= \inf \limits _{\theta \in U}\mathscr {I}_{T}(\sup \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\theta )),N_4^{\mathcal {C}}(\theta )(\eta ))\\&= \inf \limits _{\theta \in U} \inf \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )}\mathscr {I}_{T}( \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\theta )),{\mathscr {T}(N_4^{\mathcal {C}}(\theta )(\eta )})\\&\succeq _L \inf \limits _{\theta \in U} \inf \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )}\sup \limits _{\Gamma '\in \mathcal {C}} \mathscr {I}_{T}( \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\theta )),\mathscr {T}(\Gamma '(\eta ),\Gamma '(\theta ))) \\&\succeq _L \inf \limits _{\theta \in U} \inf \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )}\mathscr {I}_{T}( \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\theta )),\mathscr {T}(\Gamma (\eta ),\Gamma (\theta )))\\&= \inf \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )} \inf \limits _{\theta \in U}\mathscr {I}_{T}( \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\theta )),\mathscr {T}(\Gamma (\eta ),\Gamma (\theta )))\\&\succeq _L \inf \limits _{\Gamma \in \widetilde{MD}(\mathcal {C},\varepsilon )}\mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )) = N_3^{\mathcal {C}}(\varepsilon )(\eta ). \end{aligned} \end{aligned}$$

  Hence, we obtain that $N_3^{\mathcal {C}} \preceq _L N_1^{\mathcal {C}_4}$.

• 2. Since $N_4^{\mathcal {C}}(\varepsilon ) \in \mathcal {C}_4$ by the definition of $\mathcal {C}_4$, we obtain that $N_1^{\mathcal {C}_4}(\varepsilon )(\eta ) = \inf \limits _{\Gamma \in \mathcal {C}_4} \mathscr {I}_{T}(\Gamma (\varepsilon ), \Gamma (\eta )) \preceq _L \mathscr {I}_{T}(N_4^{\mathcal {C}}(\varepsilon )(\varepsilon ), N_4^{\mathcal {C}}(\varepsilon )(\eta )) = \mathscr {I}_{T}(1, N_4^{\mathcal {C}}(\varepsilon )(\eta )) = N_4^{\mathcal {C}}(\varepsilon )(\eta )$ for $\eta \in U$. Hence, we obtain that $N_1^{\mathcal {C}_4} \preceq _L N_4^{\mathcal {C}}$.

• 3. For $\varepsilon ,\eta \in U$, if $N_4^{\mathcal {C}}(\varepsilon ) \in \widetilde{md}(\mathcal {C}_4,\varepsilon )$, $N_2^{\mathcal {C}_4}(\varepsilon )(\eta ) = \sup \limits _{\Gamma \in \widetilde{md}(\mathcal {C}_4,\varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \succeq _L \mathscr {T}(N_4^{\mathcal {C}}(\varepsilon )(\varepsilon ),N_4^{\mathcal {C}}(\varepsilon )(\eta )) = \mathscr {T}(1,N_4^{\mathcal {C}}(\varepsilon )(\eta )) = N_4^{\mathcal {C}}(\varepsilon )(\eta )$; if $N_4^{\mathcal {C}}(\eta ) \in \widetilde{md}(\mathcal {C}_4,\varepsilon )$, $N_2^{\mathcal {C}_4}(\varepsilon )(\eta ) = \sup \limits _{\Gamma \in \widetilde{md}(\mathcal {C}_4,\varepsilon )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \succeq _L \mathscr {T}(N_4^{\mathcal {C}}(\eta )(\varepsilon ),N_4^{\mathcal {C}}(\eta )(\eta )) = \mathscr {T}(N_4^{\mathcal {C}}(\varepsilon )(\eta ),1) = N_4^{\mathcal {C}}(\varepsilon )(\eta )$. If $N_4^{\mathcal {C}}(\varepsilon ) \notin \widetilde{md}(\mathcal {C}_4,\varepsilon )$ and $N_4^{\mathcal {C}}(\eta ) \notin \widetilde{md}(\mathcal {C}_4,\varepsilon )$, there exist $\theta _1 \in U$ and $\theta _2 \in U$ which satisfies $N_4^{\mathcal {C}}(\theta _1), N_4^{\mathcal {C}}(\theta _2)\in \widetilde{md}(\mathcal {C}_4,\varepsilon )$,i.e.,$N_4^{\mathcal {C}}(\theta _1)(\varepsilon ) = N_4^{\mathcal {C}}(\varepsilon )(\varepsilon ) = 1_L, N_4^{\mathcal {C}}(\theta _1)\subseteq N_4^{\mathcal {C}}(\varepsilon )$ and $N_4^{\mathcal {C}}(\theta _2)(\varepsilon ) = N_4^{\mathcal {C}}(\eta )(\varepsilon ), N_4^{\mathcal {C}}(\theta _2)\subseteq N_4^{\mathcal {C}}(\eta )$. Therefore, since $N_4^{\mathcal {C}}(\theta _2)(\eta )\succeq _L N_4^{\mathcal {C}}(\theta _2)(\theta _2)) = 1_L,$

  $$\begin{aligned} \begin{aligned} N_2^{\mathcal {C}_4}(\varepsilon )(\eta )&\succeq _L \max \{\mathscr {T}(N_4^{\mathcal {C}}(\theta _1)(\varepsilon ),N_4^{\mathcal {C}}(\theta _1)(\eta )),\mathscr {T}(N_4^{\mathcal {C}}(\theta _2)(\varepsilon ),N_4^{\mathcal {C}}(\theta _2)(\eta ))\}\\&= \max \{\mathscr {T}(1_L,N_4^{\mathcal {C}}(\theta _1)(\eta )),\mathscr {T}(N_4^{\mathcal {C}}(\eta )(\varepsilon ),1_L)\}\\&= \max \{N_4^{\mathcal {C}}(\theta _1)(\eta ), N_4^{\mathcal {C}}(\varepsilon )(\eta )\} \\&= N_4^{\mathcal {C}}(\varepsilon )(\eta ). \end{aligned} \end{aligned}$$

  Hence, we have $N_4^{\mathcal {C}} \preceq _L N_2^{\mathcal {C}_4}$.

$\square$

Proof of Proposition 37

For $\varepsilon ,\eta ,\theta \in U$, let $\Gamma ' \in \widetilde{md}(\mathcal {C},\theta )$ and $\Gamma '(\theta ) = 1_L$, then

$$\begin{aligned} \begin{aligned} \mathscr {T}(N_1^{\mathcal {C}}(\theta )(\varepsilon ),N_1^{\mathcal {C}}(\theta )(\eta ))&\preceq _L \inf \limits _{\Gamma \in \widetilde{md}(\mathcal {C},\theta )} \mathscr {T}(\mathscr {I}_{T}(\Gamma (\theta ),\Gamma (\varepsilon )),\mathscr {I}_{T}(\Gamma (\theta ),\Gamma (\eta ))) \\&\preceq _L \mathscr {T}(\mathscr {I}_{T}(\Gamma '(\theta ),\Gamma '(\varepsilon )),\mathscr {I}_{T}(\Gamma '(\theta ),\Gamma '(\eta )))\\&= \mathscr {T}(\mathscr {I}_{T}(1,\Gamma '(\varepsilon )),\mathscr {I}_{T}(1,\Gamma '(\eta ))) \\&= \mathscr {T}(\mathscr {I}_{T}(\Gamma '(\varepsilon ),\Gamma '(\eta ))\\&\preceq _L \sup \limits _{\Gamma \in \widetilde{md}(\mathcal {C},\theta )}\mathscr {T}(\mathscr {I}_{T}(\Gamma (\varepsilon ),\Gamma (\eta )). \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} N_4^{\mathcal {C}_3}(\varepsilon )(\eta )&= \sup \limits _{\theta \in U} \mathscr {T}(N_1^{\mathcal {C}}(\theta )(\varepsilon ),N_1^{\mathcal {C}}(\theta )(\eta )) \\&\preceq _L \sup \limits _{\theta \in U}\sup \limits _{\Gamma \in \widetilde{md}(\mathcal {C},\theta )} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta ))\\&= \sup \limits _{\Gamma \in \mathcal {C}_1} \mathscr {T}(\Gamma (\varepsilon ),\Gamma (\eta )) \\&= N_4^{\mathcal {C}_1}(\varepsilon )(\eta ). \end{aligned} \end{aligned}$$

$\square$

Proof of Proposition 38

For $\eta \in U$, assume $N_2^{\mathcal {C}_{\cap }}(\varepsilon )(\eta ) = \mathscr {T}(\Gamma '(\varepsilon ),\Gamma '(\eta ))$ with $\Gamma ' \in \widetilde{md}(\mathcal {C}_{\cap },\varepsilon )$. If $\Gamma ' \notin \mathcal {C}_2$, then for $\theta \in U$, there exists a $\Gamma _\theta \in \mathcal {C}_2$ which satisfies $\Gamma _\theta (\varepsilon ) = \Gamma '(\varepsilon )$ and $\Gamma '\subseteq \Gamma _\theta$. This means $\Gamma ' = \mathop {\bigcap }\limits _{\theta \in U} \Gamma _\theta$, this contradicts with $\Gamma ' \in \mathcal {C}_{\cap }$. Therefore, $\Gamma ' \in \mathcal {C}_2$ and $\Gamma ' \in \widetilde{md}(\mathcal {C}_2,\varepsilon )$ by Proposition 23. Thus, $N_2^{\mathcal {C}_{\cap }}(\varepsilon )(\eta ) \preceq _L N_2^{\mathcal {C}_2}(\varepsilon )(\eta )$. $\square$

Proof of Proposition 39

For $\eta \in U$, assume ${\mathbb {N}}_2^{\mathcal {C}_{\cap }}(\varepsilon )(\eta ) = \mathscr {O}(\Gamma '(\varepsilon ),\Gamma '(\eta ))$ with $\Gamma ' \in \widetilde{md}(\mathcal {C}_{\cap },\varepsilon )$. If $\Gamma ' \notin \mathcal {C}_2$, then for any $\theta \in U$, there exists a $\Gamma _\theta \in \mathcal {C}_2$ which satisfies $\Gamma _\theta (\varepsilon ) = \Gamma '(\varepsilon )$ and $\Gamma '\subseteq \Gamma _\theta$. This means $\Gamma ' = \mathop {\bigcap }\limits _{\theta \in U} \Gamma _\theta$, this contradicts with $\Gamma ' \in \mathcal {C}_{\cap }$. Therefore, $\Gamma ' \in \mathcal {C}_2$ and $\Gamma ' \in \widetilde{md}(\mathcal {C}_2,\varepsilon )$ by Proposition 23. Thus, ${\mathbb {N}}_2^{\mathcal {C}_{\cap }}(\varepsilon )(\eta ) \preceq _L {\mathbb {N}}_2^{\mathcal {C}_2}(\varepsilon )(\eta )$. $\square$

Proof of Proposition 40

Assume that ${\mathbb {N}}_1^{\mathcal {C}} \succ _L {\mathbb {N}}_1^{\hat{\mathcal {C}}_3}$, i.e., for any $\varepsilon , \eta \in U$, ${\mathbb {N}}_1^{\hat{\mathcal {C}}_3}(\varepsilon )(\eta )\prec _L {\mathbb {N}}_1^{\mathcal {C}}(\varepsilon )(\eta )$. Then

$$\begin{aligned} {\mathbb {N}}_1^{\hat{\mathcal {C}}_3}(\varepsilon )(\eta ) =\inf \limits _{\Gamma \in \hat{\mathcal {C}}_3} \mathscr {I}_{O}(\Gamma (\varepsilon ),\Gamma (\eta )) = \inf \limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_1^{\mathcal {C}}(\theta )(\varepsilon ),{\mathbb {N}}_1^{\mathcal {C}}(\theta )(\eta )) \prec _L{\mathbb {N}}_1^{\mathcal {C}}(\varepsilon )(\eta ). \end{aligned}$$

Since U is finite, there exists $\theta _0 \in U$ which satisfies

$$\begin{aligned} {\mathbb {N}}_1^{\hat{\mathcal {C}}_3}(\varepsilon )(\eta ) = \mathscr {I}_{O}({\mathbb {N}}_1^{\mathcal {C}}(\theta _0)(\varepsilon ),{\mathbb {N}}_1^{\mathcal {C}}(\theta _0)(\eta ))\prec _L{\mathbb {N}}_1^{\mathcal {C}}(\varepsilon )(\eta ). \end{aligned}$$

Since $\varepsilon$ is arbitrary, we can take $\varepsilon = \theta _0$, thus $\mathscr {I}_{O}({\mathbb {N}}_1^{\mathcal {C}}(\theta _0)(\theta _0),{\mathbb {N}}_1^{\mathcal {C}}(\theta _0)(\eta ))\prec _L{\mathbb {N}}_1^{\mathcal {C}}(\theta _0)(\eta )$. Hence, we obtain that $\mathscr {I}_{O}(1,{\mathbb {N}}_1^{\mathcal {C}}(\theta _0)(\eta ))\prec _L{\mathbb {N}}_1^{\mathcal {C}}(\theta _0)(\eta )$, which is in contradiction with $\mathscr {I}_{O}(1_L,x) \succeq _L \varepsilon$ when $\mathscr {O}$ satisfies (O6). $\square$

Proof of Proposition 41

• 1. For $\varepsilon \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \underline{\Phi ^1_{i,j}}(U)(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), U(\theta )))\\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), 1_L))\\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 1_L) \\&= \mathop {\bigvee }\limits _{\eta \in U} N_i^{\mathcal {C}_j}(\eta )(\varepsilon ) = 1_L. \end{aligned} \end{aligned}$$

  Thus $\underline{\Phi ^1_{i,j}}(U) = U$. And for $\varepsilon \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \underline{\Phi ^1_{i,j}}(\emptyset )(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \emptyset (\theta )))\\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), 0_L))\\&\preceq _L \mathop {{\bigvee }}\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\eta ), 0_L))\\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{T}(1_L, 0_L)) \\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 0_L) = 0_L. \end{aligned} \end{aligned}$$

  And since $\underline{\Phi ^1_{i,j}}(\emptyset )(\varepsilon ) \succeq _L 0_L$, we have that $\underline{\Phi ^1_{i,j}}(\emptyset ) = \emptyset$. For $\varepsilon \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \overline{\Phi ^1_{i,j}}(U)(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), U(\theta )))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), 1_L))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} N_i^{\mathcal {C}_j}(\eta )(\theta ) ) \\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 1_L)\\&= \mathop {\bigwedge }\limits _{\eta \in U} 1_L = 1_L. \end{aligned} \end{aligned}$$

  Thus $\overline{\Phi ^1_{i,j}}(U) = U$.

  $$\begin{aligned} \begin{aligned} \overline{\Phi ^1_{i,j}}(\emptyset )(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \emptyset (\theta )))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), 0_L))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 0_L ) \\&\preceq _L \mathscr {I}_{T} (N_i^{\mathcal {C}_j}(\varepsilon )(\varepsilon ), 0_L) = 0_L. \end{aligned} \end{aligned}$$

  And since $\overline{\Phi ^1_{i,j}}(\emptyset )(\varepsilon ) \succeq _L 0_L$, we obtain that $\overline{\Phi ^1_{i,j}}(\emptyset ) = \emptyset$.

• 2. For $\alpha ,\beta \in L$, it holds that

  $$\begin{aligned} \begin{aligned} \mathscr {T}(\alpha , \mathscr {I}_{T}(\alpha ,\beta ))&=\mathscr {T}(\alpha ,\sup \{z\in L\mid \mathscr {T}(\alpha ,z)\preceq _L \beta \})\\&=\sup \{\mathscr {T}(\alpha ,\beta )\mid \mathscr {T}(\alpha ,z) \preceq _L \beta \} \preceq _L \beta . \end{aligned} \end{aligned}$$

  Therefore, for $X_1 \in \mathscr {F}_q(U)$,

  $$\begin{aligned} \begin{aligned} \underline{\Phi ^1_{i,j}}(X_1)(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), X_1(\theta )))\\&\preceq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), X_1(\varepsilon )))\\&\preceq _L X_1(\varepsilon ). \end{aligned} \end{aligned}$$

  For $\varepsilon ,\eta \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \mathscr {I}_{T}(\varepsilon , \mathscr {T}(\varepsilon ,\eta ))&=\sup \{\theta \in L\mid \mathscr {T}(\varepsilon ,\theta )\preceq _L \mathscr {T}(\varepsilon ,\eta )\}\succeq _L \eta . \end{aligned} \end{aligned}$$

  Then,

  $$\begin{aligned} \begin{aligned} \overline{\Phi ^1_{i,j}}({X_1})(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), X_1(\theta )))\\&\succeq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(y)(\varepsilon ), \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), X_1(\varepsilon )))\\&\succeq _L X_1(\varepsilon ). \end{aligned} \end{aligned}$$

  Hence, $\underline{\Phi ^1_{i,j}}(X_1) \subseteq X_1 \subseteq \overline{\Phi ^1}_{i,j}(X_1)$.

• 3. We can obtain that $\underline{\Phi ^1_{i,j}}(X_1) \subseteq \underline{\Phi ^1_{i,j}}(X_2)$ and $\overline{\Phi ^1_{i,j}}(X_1) \subseteq \overline{\Phi ^1_{i,j}}(X_2)$ by the monotonicity of $\mathscr {T}$ and $\mathscr {I}_{T}$.

• 4. It is immediately proved by (3).

• 5. By (4), we obtain that $\underline{\Phi ^1_{i,j}}(\underline{\Phi ^1_{i,j}}(X_1)) \subseteq \underline{\Phi ^1_{i,j}}(X_1)$ and $\overline{\Phi ^1_{i,j}}(\overline{\Phi ^1_{i,j}}(X_1)) \supseteq \overline{\Phi ^1_{i,j}}(X_1)$. Next, we need to prove that $\underline{\Phi ^1_{i,j}}(\underline{\Phi ^1_{i,j}}(X_1)) \supseteq \underline{\Phi ^1_{i,j}}(X_1)$ and $\overline{\Phi ^1_{i,j}}(\overline{\Phi ^1_{i,j}}(X_1)) \subseteq \overline{\Phi ^1_{i,j}}(X_1)$. For $\varepsilon \in U$,

  $$\begin{aligned} \begin{aligned}&\underline{\Phi ^1_{i,j}}(\underline{\Phi ^1_{i,j}}(X_1))(\varepsilon ) = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \underline{\Phi ^1_{i,j}}(X_1)(\theta )))\\&\quad = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigvee }\limits _{\rho \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\rho )(\theta ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\rho )(\delta ), (X_1)(\delta )))))\\&\quad \succeq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))))\\&\quad \succeq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))\\&\quad = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta ))) = \underline{\Phi ^1_{i,j}}(X_1)(\varepsilon ). \end{aligned} \end{aligned}$$
  $$\begin{aligned} \begin{aligned}&\overline{\Phi ^1_{i,j}}(\overline{\Phi ^1_{i,j}}(X_1))(\varepsilon ) = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \overline{\Phi ^1_{i,j}}(X_1)(\theta )))\\&\quad = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigwedge }\limits _{\rho \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\rho )(\theta ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\rho )(\delta ), (X_1)(\delta )))))\\&\quad \preceq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))))\\&\quad \preceq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathop {\bigvee }\limits _{\delta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))\\&\quad = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta ))) = \overline{\Phi ^1_{i,j}}(X_1)(\varepsilon ). \end{aligned} \end{aligned}$$

  Hence, $\underline{\Phi ^1_{i,j}}(\underline{\Phi ^1_{i,j}}(X_1)) = \underline{\Phi ^1_{i,j}}(X_1)$ and $\overline{\Phi ^1_{i,j}}(\overline{\Phi ^1_{i,j}}(X_1)) = \overline{\Phi ^1_{i,j}}(X_1)$.

$\square$

Proof of Proposition 42

• 1. For $\varepsilon \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \underline{\Phi ^2_{i,j}}(U)(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), U(\theta )))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), 1_L))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 1_L) = 1_L. \end{aligned} \end{aligned}$$

  Thus $\underline{\Phi ^2_{i,j}}(U) = U$. For $\varepsilon \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \underline{\Phi ^2_{i,j}}(\emptyset )(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \emptyset (\theta )))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), 0_L))\\&\preceq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\eta ), 0_L))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{T}(1_L, 0_L)) \\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 0_L) = 0_L. \end{aligned} \end{aligned}$$

  And since $\underline{\Phi ^2_{i,j}}(\emptyset )(\varepsilon ) \succeq _L 0_L$, we obtain that $\underline{\Phi ^2_{i,j}}(\emptyset ) = \emptyset$.

  $$\begin{aligned} \begin{aligned} \overline{\Phi ^2_{i,j}}(U)(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), U(\theta )))\\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), 1_L))\\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} N_i^{\mathcal {C}_j}(\eta )(\theta )) \\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 1_L)\\&= \mathop {\bigvee }\limits _{\eta \in U} N_i^{\mathcal {C}_j}(\eta )(\varepsilon ) = 1_L. \end{aligned} \end{aligned}$$

  Thus $\overline{\Phi ^2_{i,j}}(U) = U$.

  $$\begin{aligned} \begin{aligned} \overline{\Phi ^2_{i,j}}(\emptyset )(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \emptyset (\theta )))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), 0_L))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 0_L) \\&\preceq _L \mathscr {I}_{T} (N_i^{\mathcal {C}_j}(\varepsilon )(\varepsilon ), 0_L) = 0_L. \end{aligned} \end{aligned}$$

  And since $\overline{\Phi ^2_{i,j}}(\emptyset )(\varepsilon ) \succeq _L 0_L$, $\overline{\Phi ^2_{i,j}}(\emptyset ) = \emptyset$ holds.

• 2. For $\varepsilon \in U$,

  $$\begin{aligned} \underline{\Phi ^2_{i,j}}(X_1)(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), X_1(\theta )))\\&\preceq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), X_1(\varepsilon )))\\&\preceq _L \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\varepsilon )(\varepsilon ), \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\varepsilon )(\varepsilon ), X_1(\varepsilon )))\\&\preceq _L \mathscr {I}_{T}(1, \mathscr {I}_{T}(1, X_1(\varepsilon ))) = X_1(\varepsilon ). \end{aligned}$$
  $$\begin{aligned} \overline{\Phi ^2_{i,j}}(U)(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), X_1(\theta )))\\&\succeq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(y)(\varepsilon ), \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), X_1(\varepsilon )))\\&\succeq _L \mathscr {T}(N_i^{\mathcal {C}_j}(\varepsilon )(\varepsilon ), \mathscr {T}(N_i^{\mathcal {C}_j}(\varepsilon )(\varepsilon ), X_1(\varepsilon )))\\&\succeq _L \mathscr {T}(1, \mathscr {T}(1, X_1(\varepsilon ))) = X_1(\varepsilon ). \end{aligned}$$

  Hence, $\underline{\Phi ^2_{i,j}}(X_1) \subseteq X_1 \subseteq \overline{\Phi ^2_{i,j}}(X_1)$.

• 3. We can obtain that $\underline{\Phi ^2_{i,j}}(X_1) \subseteq \underline{\Phi ^2_{i,j}}(X_2)$ and $\overline{\Phi ^2_{i,j}}(X_1) \subseteq \overline{\Phi ^2_{i,j}}(X_2)$ by the monotonicity of $\mathscr {T}$ and $\mathscr {I}_{T}$.

• 4. It is immediately proved by (3).

• 5. For $\varepsilon \in U$, it holds that

  $$\begin{aligned}{} & {} \overline{\Phi ^2_{i,j}}(\underline{\Phi ^2_{i,j}}(X_1))(\varepsilon ) = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \underline{\Phi ^2_{i,j}}(X_1)(\theta )))\\{} & {} \quad = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigwedge }\limits _{\rho \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\varepsilon )(\theta ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\rho )(\delta ), (X_1)(\delta )))))\\{} & {} \quad \preceq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))))\\{} & {} \quad \preceq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))\\{} & {} \quad = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta ))) = \underline{\Phi ^1_{i,j}}(X_1)(\varepsilon ). \end{aligned}$$

  Thus $\overline{\Phi ^2_{i,j}}(\underline{\Phi ^2}_{i,j}(X_1)) \subseteq \underline{\Phi ^1_{i,j}}(X_1)$. And by (2) of Proposition 41, we obtain that $\underline{\Phi ^1_{i,j}}(X_1) \subseteq X_1$. Hence $\overline{\Phi ^2_{i,j}}(\underline{\Phi ^2_{i,j}}(X_1)) \subseteq X_1$.

  $$\begin{aligned}{} & {} \underline{\Phi ^2_{i,j}}(\overline{\Phi ^2_{i,j}}(X_1))(\varepsilon ) = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \overline{\Phi ^2_{i,j}}(X_1)(\theta )))\\{} & {} \quad = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigvee }\limits _{\rho \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\varepsilon )(\theta ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\rho )(\delta ), (X_1)(\delta )))))\\{} & {} \quad \succeq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))))\\{} & {} \quad \succeq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathop {\bigvee }\limits _{\delta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))\\{} & {} \quad = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{T}(N_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {T}(N_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta ))) = \overline{\Phi ^1_{i,j}}(X_1)(\varepsilon ). \end{aligned}$$

  Thus, $\underline{\Phi ^2_{i,j}}(\overline{\Phi ^2_{i,j}}(X_1)) \supseteq \overline{\Phi ^1_{i,j}}(X_1)$. And by (2) of Proposition 41, we obtain that $\overline{\Phi ^1_{i,j}}(X_1) \subseteq X_1$. Hence, $X_1 \subseteq \underline{\Phi ^2_{i,j}}(\overline{\Phi ^2_{i,j}}(X_1))$. Therefor, $\overline{\Phi ^2_{i,j}}(\underline{\Phi ^2_{i,j}}(X_1)) \subseteq X_1 \subseteq \underline{\Phi ^2_{i,j}}(\overline{\Phi ^2_{i,j}}(X_1))$.

$\square$

Proof of Proposition 43

• 1. For $\varepsilon \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \underline{\Psi ^1_{i,j}}(\emptyset )(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \emptyset (\theta )))\\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), 0_L))\\&\preceq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\eta ), 0_L))\\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{O}(1_L, 0_L)) \\&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 0_L) = 0_L. \end{aligned} \end{aligned}$$

  And since $\underline{\Psi ^1_{i,j}}(\emptyset )(\varepsilon ) \succeq _L 0_L$, we obtain that $\underline{\Psi ^1_{i,j}}(\emptyset ) = \emptyset$. For $\varepsilon \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \overline{\Psi ^1_{i,j}}(\emptyset )(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \emptyset (\theta )))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), 0_L))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 0_L ) \\&\preceq _L \mathscr {I}_{O} ({\mathbb {N}}_i^{\mathcal {C}_j}(\varepsilon )(\varepsilon ), 0_L) = 0_L. \end{aligned} \end{aligned}$$

  And since $\overline{\Psi ^1_{i,j}}(\emptyset )(\varepsilon ) \succeq _L 0_L$, $\overline{\Psi ^1_{i,j}}(\emptyset ) = \emptyset$.

• 2. For $\alpha ,\beta \in L$,

  $$\begin{aligned} \begin{aligned} \mathscr {O}(\alpha , \mathscr {I}_{O}(\alpha ,\beta ))&=\{\mathscr {O}(\alpha ,\max \{z\in L\mid \mathscr {O}(\alpha ,z)\preceq _L \beta \})\}\\&=\max \{\mathscr {O}(\alpha ,z)\mid \mathscr {O}(\alpha ,z) \preceq _L \beta \} \preceq _L \beta . \end{aligned} \end{aligned}$$

  Therefore, for $X_1 \in \mathscr {F}_q(U)$,

  $$\begin{aligned} \begin{aligned} \underline{\Psi ^1_{i,j}}(X_1)(\varepsilon )&= \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), X_1(\theta )))\\&\preceq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), X_1(\varepsilon )))\\&\preceq _L X_1(\varepsilon ). \end{aligned} \end{aligned}$$

  For $\varepsilon ,\eta \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \mathscr {I}_{O}(\varepsilon , \mathscr {T}(\varepsilon ,\eta ))&=\max \{\theta \in L\mid \mathscr {O}(\varepsilon ,\theta )\preceq _L \mathscr {O}(\varepsilon ,\eta )\}\succeq _L \eta . \end{aligned} \end{aligned}$$

  Then

  $$\begin{aligned} \begin{aligned} \overline{\Psi ^1_{i,j}}(U)(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), X_1(\theta )))\\&\succeq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), X_1(\varepsilon )))\\&\succeq _L X_1(\varepsilon ). \end{aligned} \end{aligned}$$

  Hence, $\underline{\Psi ^1_{i,j}}(X_1) \subseteq X_1 \subseteq \overline{\Psi ^1_{i,j}}(X_1)$.

• 3. By the monotonicity of $\mathscr {O}$ and $\mathscr {I}_{O}$, we can obtain that $\underline{\Psi ^1_{i,j}}(X_1) \subseteq \underline{\Psi ^1_{i,j}}(X_2)$ and $\overline{\Psi ^1_{i,j}}(X_1) \subseteq \overline{\Psi ^1_{i,j}}(X_2)$.

• 4. It is immediately proved by (3).

• 5. By (4), we obtain that $\underline{\Psi ^1_{i,j}}(\underline{\Psi ^1_{i,j}}(X_1)) \subseteq \underline{\Psi ^1_{i,j}}(X_1)$ and $\overline{\Psi ^1_{i,j}}(\overline{\Psi ^1}_{i,j}(X_1)) \supseteq \overline{\Psi ^1_{i,j}}(X_1)$. Next, we need to prove that $\underline{\Psi ^1_{i,j}}(\underline{\Psi ^1_{i,j}}(X_1)) \supseteq \underline{\Psi ^1_{i,j}}(X_1)$ and $\overline{\Psi ^1_{i,j}}(\overline{\Psi ^1_{i,j}}(X_1)) \subseteq \overline{\Psi ^1_{i,j}}(X_1)$. For $\varepsilon \in U$,

  $$\begin{aligned}{} & {} \underline{\Psi ^1_{i,j}}(\underline{\Psi ^1_{i,j}}(X_1))(\varepsilon ) = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \underline{\Psi ^1_{i,j}}(X_1)(\theta )))\\{} & {} \quad = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigvee }\limits _{\rho \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\rho )(\theta ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\varepsilon )(\delta ), (X_1)(\delta )))))\\{} & {} \quad \succeq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))))\\{} & {} \quad \succeq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))\\{} & {} \quad = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta ))) = \underline{\Psi ^1_{i,j}}(X_1)(\varepsilon ). \end{aligned}$$
  $$\begin{aligned}{} & {} \overline{\Psi ^1_{i,j}}(\overline{\Psi ^1_{i,j}}(X_1))(\varepsilon ) = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \overline{\Psi ^1_{i,j}}(X_1)(\theta )))\\{} & {} \quad = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigwedge }\limits _{\varepsilon \in U} \mathscr {I}_{R_O}({\mathbb {N}}_i^{\mathcal {C}_j}(\rho )(\theta ), \mathop {{\bigvee }}\limits _{\delta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\rho )(\delta ), (X_1)(\delta )))))\\{} & {} \quad \preceq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))))\\{} & {} \quad \preceq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathop {\bigvee }\limits _{\delta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))\\{} & {} \quad = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta ))) = \overline{\Psi ^1_{i,j}}(X_1)(\varepsilon ). \end{aligned}$$

  Hence, $\underline{\Psi ^1_{i,j}}(\underline{\Psi ^1}_{i,j}(X_1)) = \underline{\Psi ^1_{i,j}}(X_1)$ and $\overline{\Psi ^1_{i,j}}(\overline{\Psi ^1_{i,j}}(X_1)) = \overline{\Psi ^1_{i,j}}(X_1)$.

$\square$

Proof of Proposition 44

• 1. For $\varepsilon \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \underline{\Psi ^2_{i,j}}(U)(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), U(\theta )))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), 1_L))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 1_L) = 1_L. \end{aligned} \end{aligned}$$

  Thus $\underline{\Psi ^2_{i,j}}(U) = U$. For $\varepsilon \in U$, it holds that

  $$\begin{aligned} \begin{aligned} \underline{\Psi ^2_{i,j}}(\emptyset )(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \emptyset (\theta )))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), 0_L))\\&\preceq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\eta ), 0_L))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathscr {I}_{O}(1_L, 0_L)) \\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 0_L) = 0_L. \end{aligned} \end{aligned}$$

  And since $\underline{\Psi ^2_{i,j}}(\emptyset )(\varepsilon ) \succeq _L 0_L$, we obtain that $\underline{\Psi ^2_{i,j}}(\emptyset ) = \emptyset$.

  $$\begin{aligned} \begin{aligned} \overline{\Psi ^2_{i,j}}(\emptyset )(\varepsilon )&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \emptyset (\theta )))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), 0_L))\\&= \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), 0_L) \\&\preceq _L \mathscr {I}_{O} ({\mathbb {N}}_i^{\mathcal {C}_j}(\varepsilon )(\varepsilon ), 0_L) = 0_L. \end{aligned} \end{aligned}$$

  And since $\overline{\Psi ^2_{i,j}}(\emptyset )(x) \succeq _L 0_L$, $\overline{\Psi ^2_{i,j}}(\emptyset ) = \emptyset$ holds.

• 2. By the monotonicity of $\mathscr {O}$ and $\mathscr {I}_{O}$, we can obtain that $\underline{\Psi ^2_{i,j}}(X_1) \subseteq \underline{\Psi ^2_{i,j}}(X_2)$ and $\overline{\Psi ^2_{i,j}}(X_1) \subseteq \overline{\Psi ^2_{i,j}}(X_2)$.

• 3. It is immediately proved by (3).

• 4. For $\varepsilon \in U$,

  $$\begin{aligned} \begin{aligned}&\overline{\Psi ^2_{i,j}}(\underline{\Psi ^2_{i,j}}(X_1))(\varepsilon ) = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \underline{\Psi ^2_{i,j}}(X_1)(\theta )))\\&\quad = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigwedge }\limits _{\rho \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\rho )(\theta ), \mathop {{\bigwedge }}\limits _{\delta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\rho )(\delta ), (X_1)(\delta )))))\\&\quad \preceq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))))\\&\quad \preceq _L \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\theta \in U} \mathop {{\bigwedge }}\limits _{\delta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))\\&\quad = \mathop {\bigvee }\limits _{\eta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\delta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta ))) = \underline{\Psi ^1_{i,j}}(X_1)(\varepsilon ). \end{aligned} \end{aligned}$$

  Thus, $\overline{\Psi ^2_{i,j}}(\underline{\Psi ^2_{i,j}}(X_1)) \subseteq \underline{\Psi ^1_{i,j}}(X_1)$. And by (2) of Proposition 43, it holds that $\underline{\Psi ^1_{i,j}}(X_1) \subseteq X_1$. Hence $\overline{\Psi ^2_{i,j}}(\underline{\Psi ^2_{i,j}}(X_1)) \subseteq X_1$.

  $$\begin{aligned}&\underline{\Psi ^2_{i,j}}(\overline{\Psi ^2_{i,j}}(X_1))(\varepsilon ) = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \overline{\Psi ^2_{i,j}}(X_1)(\theta )))\\&\quad = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigvee }\limits _{\rho \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\rho )(\theta ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\rho )(\delta ), (X_1)(\delta )))))\\&\quad \succeq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), \mathop {\bigvee }\limits _{\delta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\delta ), (X_1)(\delta )))))\\&\quad \succeq _L \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigwedge }\limits _{\theta \in U} \mathop {{\bigvee }}\limits _{\theta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), (X_1)(\theta )))\\&\quad = \mathop {\bigwedge }\limits _{\eta \in U} \mathscr {I}_{O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\varepsilon ), \mathop {\bigvee }\limits _{\beta \in U} \mathscr {O}({\mathbb {N}}_i^{\mathcal {C}_j}(\eta )(\theta ), (X_1)(\theta ))) = \overline{\Psi ^1_{i,j}}(X_1)(\varepsilon ). \end{aligned}$$

  Thus, $\underline{\Psi ^2_{i,j}}(\overline{\Psi ^2_{i,j}}(X_1)) \supseteq \overline{\Psi ^1_{i,j}}(X_1)$ And by (2) of Proposition 43, it holds that $\overline{\Psi ^1_{i,j}}(X_1)(\varepsilon ) \supseteq X_1$. Hence, $\underline{\Psi ^2_{i,j}}(\overline{\Psi ^2_{i,j}}(X_1)) \supseteq X_1$. Hence, $\overline{\Psi ^2_{i,j}}(\underline{\Psi ^2_{i,j}}(X_1)) \subseteq X_1 \subseteq \underline{\Psi ^2_{i,j}}(\overline{\Psi ^2_{i,j}}(X_1))$.

$\square$