Abstract
Rough sets (RSs) and fuzzy sets (FSs) are designed to tackle the uncertainty in the data. By taking into account the control or reference parameters, the linear Diophantine fuzzy set (LD-FS) is a novel approach to decision making (DM), broadens the previously dominant theories of the intuitionistic fuzzy set (IFS), Pythagorean fuzzy set (PyFS), and q-rung orthopair fuzzy set (q-ROFS), and allows for a more flexible representation of uncertain data. A promising avenue for RS theory is to investigate RSs within the context of LD-FS, where LD-FSs are approximated by an intuitionistic fuzzy relation (IFR). The major goal of this article is to create a novel method of roughness for LD-FSs employing an IFR over dual universes. The notions of lower and upper approximations of an LD-FS are established by using an IFR, and some axiomatic systems are carefully investigated in detail. Moreover, a link between LD-FRSs and linear Diophantine fuzzy topology (LDF-topology) has been established. Eventually, based on lower and upper approximations of an LD-FS, several similarity relations are investigated. Meanwhile, we apply the recommended model of LD-FRSs over dual universes for solving the DM problem. Furthermore, a real-life case study is given to demonstrate the practicality and feasibility of our designed approach. Finally, we conduct a detailed comparative analysis with certain existing methods to explore the effectiveness and superiority of the established technique.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Data uncertainty is critical for human DM and has grown extensively in the present era. It is not always beneficial to tackle real-world problems using traditional mathematical approaches due to the uncertainties and vagueness present in these problems. This pursuit gave rise to several fruitful theories addressing data uncertainty, such as the FS (Zadeh 1965), IFS (Atanssov 1986, 1989), PyFS (Yager 2013), q-ROFS (Yager 2017), LD-FS (Riaz and Hashmi 2019), and rough sets (RS) (Pawlak 1982).
The idea of FS theory (Zadeh 1965), proposed by Zadeh in 1965, plays a significant role in modern DM approaches and could provide ideal solutions in many application domains like data mining, knowledge discovery, information retrieval, and project management. In classical set theory, an element either belongs to or does not belong to a set. FS theory assists in allocating a specific membership grade (MG) from the range \(\left[ 0, 1\right] \). FS theory is a remarkable achievement, having broad applications in a wide range of industries (Ali et al. 2021; Bashir et al. 2019; Bellman and Zadeh 1970, Ibrahim et al. 2023, Jana and Pal 2023).
However, in many real-life situations, only the MG is not enough to describe the uncertain data. There is a need for non-membership grade (NMG), and they might be independent of each other, for instance, benefit and loss claims, inferiority and superiority, perfection and imperfection, affiliation, and non-affiliation, sick and healthy, educated and ill-educated, etc. To address this issue, a series of generalizations of FS theory were proposed over the past years (Atanssov 1986, 1989; Kupongsak and Tan 2006; Yager 2017; Zhu 2007). Among the various extensions of FS theory, IFS is generally believed to be an intuitively straightforward extension of FS theory proposed by Attanassov (Atanssov 1986, 1989). Due to the large space of IFS, a number of scholars focused on the study of IFSs (Coker 1997; Cornelis et al. 2004; Deschrijver and Kerre 2003).
In IFSs, there is a constraint that the sum of MG and NMG must not be greater than one. When MG and NMG are granted to some object by independent decision-makers, it becomes challenging to satisfy this constraint. Therefore, Yager projected the idea of PyFS (Yager 2013) and subsequently their generalization q-ROFS (Yager 2017), which has been proved useful to deal with uncertain information in DM procedures. Since the establishment of PyFS and q-ROFS, numerous authors have done additional research in relation to these paradigms (Ali 2018; Liu and Wang 2018; Peng 2019; Shaheen et al. 2021; Yager 2014; Khan and Wang 2023).
Sometimes, the theories of PyFS and q-ROFS also failed to capture uncertainty in the data. To overcome this issue, Riaz and Hashmi (Riaz and Hashmi 2019) pioneered a novel generalized version of FS known as LD-FS with the addition of reference parameters related to the MG and NMG, which opens a new avenue of further research in decision analysis. The LD-FS model is more informative and effective than IFSs, PyFSs, and q-ROFSs. The key advantage of the LD-FS model is that it has reference parameters. Due to these reference parameters, the MG and NMG have more space than IFSs, PFSs, and q-ROFSs. LD-FS has a lot of merits over the classical FSs and their extensions, particularly in DM with anonymity. Decision-makers can freely choose the MG and NMG without any limitations. The LD-FS theory has attracted the attention of several researchers. Almagrabi et al. (2021) offered a new approach to q-linear Diophantine fuzzy emergency decision support system for COVID-19. Ayub et al. (2022a, 2022b) linear Diophantine fuzzy RSs. Further, Ayub et al. (2021) initiated the idea of LD-FRs and their algebraic properties with applications in DM problems. Riaz et al. (2022) projected some linear Diophantine fuzzy aggregation operators with multi-criteria decision-making (MCDM) applications. Iampan et al. (2021) established linear Diophantine fuzzy Einstien aggregation operators with applications in DM. Kamacı (2021) proposed some linear Diophantine fuzzy algebraic structures. Mohammad et al. (2022) offered some linear Diophantine fuzzy similarity measures for application in DM problems. Riaz and Farid (2023) devised through linear Diophantine fuzzy soft-max aggregation operators with application to enhancing green supply chain. Some of the remarkable applications of LD-FSs, along with algebraic structures, can be found in Ali et al. (2021), Alnoor et al. (2022), Mahmood et al. (2021), Mohammad et al. (2022), Riaz et al. (2020).
Binary relations receive special attention in pure and applied mathematics and are often used in real life, especially in DM problems. The idea of a fuzzy relation (FR) was first articulated by Zadeh (1971). FRs have many applications in various fields, such as fuzzy modeling (Kim et al. 1997), fuzzy control (Jäkel et al. 2004), uncertain reasoning (Dubois and Prade 2012), neural networks (Kupongsak and Tan 2006), pattern recognition (Sun et al. 2018) and artificial intelligence (Schwartz et al. 1994). FRs and their properties can be found in Murali (1989). A detailed overview of FSs and their properties is given in Wang et al. (2009) by Wang et al. Atanassov (Atanassov 1984) introduced the notion of IFR. Many scholars have developed the theory and applications of IFRs. For instance, in Burillo and Bustince (1995a), Burillo and Bustince (1995b), Burillo and Bustince examined certain IFR features using the t-norm and t-conorm. Bustince (2000) developed different results for the construction of IFRs on a set with predetermined properties that allow us to build reflexive, symmetric, antisymmetric, perfect antisymmetric, and transitive IFRs from FRs with the same properties. Without utilizing t-norm or t-conorm, Deschrijver and Kerre (2003) defined the composition of IFRs. With the composition of IFRs specified in Deschrijver and Kerre (2003), Kumar and Gangwal (2021) established an application of IFR in medical diagnosis.
The theories of FSs, IFSs, PyFSs, and q-ROFSs provide us only the information associated with MG and NMG but do not give us the roughness of an information system. Pawlak invented the RS theory (Pawlak 1982) as an extension of classical set theory, which manipulates the uncertainty of the data through an indiscernibility relation. RS theory provides various beneficiary approaches for investigating solutions for DM problems that usually occur in medical sciences, image processing, data analysis, computer intelligence, robotics, and artificial intelligence, and so on.
The theory of RSs is based on an equivalence relation that specifies the indiscernibility relation between any two objects. Although RS theory has been applied successfully in multiple disciplines, certain drawbacks may limit its applications. These drawbacks could be the result of inaccurate data regarding the objects under consideration. Sometimes, in an incomplete information system, such as an equivalence relation is difficult to find. Therefore, some more general notions have been introduced. The concept of generalized RSs based on relations was proposed by Zhu (2007). She et al. (2017) employed logical operators in RS theory. Dubois and Prade (1990) constructed the fuzzy RS (FRS) by swapping out the crisp binary relations in the universe with FRs. For more about the fusion of RSs and their generalization with application, we refer to References (Ayub et al. 2022c, Bashir et al. 2021, Gul and Shabir 2020; Shabir and Shaheen 2016).
Most of the existing studies on RS theory are based on one universe. However, in reality, RS models based on a single universe could limit the application domain of RS theory. Two or multi-universes can describe reality more effectively and reasonably. In the present era, several researchers have realized this, and some efforts have been made based on two different universes. For instance, Pei and Xu (2004) and Yan et al. (2010) presented the RS model on dual universes. Li and Zhang (2008) investigated rough fuzzy approximations of two universes. Sun and Ma (2011) established the FRS model over two different universes and its applications. Yang et al. (2012) initiated the notion of the bipolar fuzzy rough set model on two different universes with applications. Liu et al. (2012) offered a graded RS model based on two universes and their properties. Sun et al. (2012) presented an approach to DM based on intuitionistic FRSs over two universes. Bilal and Shabir (2021) discussed approximations of PyFSs over dual universes by soft binary relations. Bilal et al. (2021) proposed rough q-ROFSs based on crisp binary relations over dual universes with applications in DM. Ayub et al. (2022b) pioneered linear Diophantine fuzzy rough sets and their applications using a linear Diophantine fuzzy relation. In addition, Ayub et al. (2022a) offered a new linear Diophantine fuzzy rough set model based on paired universes with multi-stage decision analysis.
Topology is a fascinating branch of mathematics that has many applications not only in mathematics but also in real life. Topological structures are a key tool for knowledge extraction and processing. To date, numerous researchers have studied the algebraic features of topology in the environment of FSs (Chang 1968; Ming 1985), IFSs (Coker 1997), and q-ROFSs (Tükraslan et al. 2021). Hence, studying the relationship between RSs and topology is an interesting research avenue. Skowron (1988) and Wiweger (1989) studied RSs in the environment of topological concepts. From binary relations, Lashin et al. (2005) generated a topology that is used to generalize the essential ideas in RS theory. Al-shami (2022) introduced a topological approach to generate new rough set models. Qin and Pei (2005) explored the topological properties of fuzzy RSs. Yang and Xu (2011) studied the topological properties of generalized approximation spaces. Wu and Zhou (2011) discussed intuitionistic fuzzy topologies based on intuitionistic fuzzy reflexive and transitive relations. Zhou et al. (2009) initiated the idea of intuitionistic fuzzy RSs and their topological structures. El-Bably and Al-Shami (2021) demonstrated some techniques to construct a topology from various types of neighborhoods. Riaz et al. (2019) proposed the soft rough topology with application in DM.
1.1 Motivation and research gap of this paper
The notion of LD-FS has become a popular mechanism among researchers for dealing with ambiguity and vagueness in information. Based on the review of the latest research survey on LD-FS theory, our primary motivations, research gaps, and the novelty of this article are illustrated in a nutshell as follows:
-
1.
The theories of FSs, IFSs, PyFSs, and q-ROFSs have various applications in different domains of real life, but all theories have their drawbacks associated with the MG and NMG. To overcome these deficiencies, Riaz and Hashmi (2019) offered a novel idea of LD-FS with the addition of reference parameters corresponding to the MG and NMG. The LD-FS model is a more robust mathematical tool and has a broader space of MG and NMG than the prevailing notions of FSs, IFSs, PyFSs, and q-ROFSs. However, less effort has been made to the appropriate fusion of RS theory and LD-FSs via dual universes. To fill this knowledge gap, in this article, we have constructed a novel idea of the LD-FRS model based on IFR over dual universes, which has powerful modeling capabilities.
-
2.
Recently, Ayub et al. (2022a, 2022b) offered the notion of roughness in LD-FSs on two different universes, where crisp lower and upper approximations were characterized by using an arbitrary linear Diophantine fuzzy relation and the \(\big (\langle s, t \rangle , \langle u, v \rangle \big )\)-level sets of linear Diophantine fuzzy relation respectively with applications in DM. However, to the best of our knowledge, no research has yet been offered on LD-FRSs where the lower and upper approximations are also LD-FSs. This motivation has driven the present authors to develop a very interesting LD-FRS model where the lower and upper approximations of an LD-FS are characterized by using an arbitrary IFR on two different universes are again LD-FSs. The use of IFR over two universes without any extra condition makes this model more flexible and robust rather than the use of a crisp binary relation or an equivalence relation.
-
3.
Moreover, the potential applications of the LD-FRS model to MCDM in the context of IFR dual universes are also missing. This research gap motivates the current research to develop a comprehensive approach for MCDM by using this novel LD-FRS model.
1.2 Aims and objectives of proposed work
To further expand the applications spectrum of LD-FSs and RS theory in decision analysis, this research proposal aims to achieve the following main objectives:
-
1.
To propose an innovative hybrid model of LD-FRS by combining LD-FS theory with RSs and IFR over dual universes.
-
2.
To analyze key properties of the LD-FRS model in depth with some concrete illustrations.
-
3.
To develop a relationship between the LD-FRS model and LDF-topological spaces.
-
4.
To describe some similarity relations of LD-FSs based on the lower and upper approximations.
-
5.
The proposed hybrid model is implemented in MCDM with a real-life case study.
-
6.
Conduct a detailed comparative analysis with some existing approaches to demonstrate the superiority and effectiveness of the devised model.
1.3 Framework of the paper
The organization of this paper is structured as follows:
-
1.
In Sect. 2, we concisely recall some basic ideas which are used throughout this article.
-
2.
In Sect. 3, the LD-FRS model is constructed, where the lower and upper approximations of an LD-FS are characterized by using an IFR on two different universes.
-
3.
In Sect. 4, a connection between the LD-FRS model and LDF-topology is established.
-
4.
Section 5 examines several similarity relations of LD-FSs based on their lower and upper approximations and their associated properties.
-
5.
In Sect. 6, based on the LD-FRS model, a novel MCGDM method is established and exhibited by a real-world example.
-
6.
In Sect. 7, we conduct a comparative analysis to illustrate the effectiveness and superiority of the established method.
-
7.
Section 8, depicts the concluding remarks of this study and elaborates on future perspectives.
2 Preliminaries
In this section, some basic ideas and properties of FS, IFS, PyFS, LD-FS, IFR, and RS ideas are briefly reviewed. Throughout this study, \(\mathscr {W}\), \(\mathscr {W}_1\), and \(\mathscr {W}_2\) are used to denote universal sets.
Definition 2.1
(Zadeh 1965) A FS \(\mathscr {F}\) on \(\mathscr {W}\) is a mapping \(\mathscr {F} : \mathscr {W} \longrightarrow [0,1]\), which assigns the MG to each object \(w \in \mathscr {W}\) in \(\mathscr {F}\).
Only the MG is often insufficient to convey the uncertainty in real-world scenarios. Therefore, Atanassov created the idea of IFS to fill this research gap.
Definition 2.2
(Atanssov 1986) An IFS over \(\mathscr {W}\) is a structure of the form:
where the maps \(\textbf{I}^{M}, \textbf{I}^{N} : \mathscr {W} \longrightarrow [0,1]\) specifies the MG and NMG, fulfilling the following requirement, respectively:
for all \(w\in \mathscr {W}\). Moreover, the degree of hesitation can be calculated as:
for each \(w\in \mathscr {W}\).
In many real-life situations, IFS cannot work when \(\textbf{I}^{M}(w) + \textbf{I}^{N}(w) > 1\). To overcome this issue, Yager (2013) projected the idea of PyFS.
Definition 2.3
(Yager 2013) A PyFS over \(\mathscr {W}\) is a structure having the form:
where \(\textbf{I}_p^{M}, \textbf{I}_p^{N} : \mathscr {W} \longrightarrow [0, 1]\) represents the MG and NMG and the inequality
holds for all \(w \in \mathscr {W}\). The degree of hesitation is given as:
The PyFS technique becomes limited in the scenario when the sum of the squares of MG and NMG is greater than unity. Hence, Yager (2017) launched the notion of q-ROFS.
Definition 2.4
(Yager 2017) A q-ROFS over \(\mathscr {W}\) is an object of the form:
where \(\hat{\textbf{I}}^{M}, \hat{\textbf{I}}^{N} : \mathscr {W} \longrightarrow [0, 1]\) signifies the MG and NMG for each \(w \in \mathscr {W}\) such that \(0 \le \big ( \hat{\textbf{I}}^{M} \big )^q (w) + \big ( \hat{\textbf{I}}^{N} \big )^q (w) \le 1; q \ge 1\) Furthermore, the hesitation degree is given as
Recently, Riaz and Hashmi (2019) introduced the idea of LD-FS, which is an efficient approach to handling uncertainties and eradicates all the limitations on MG and NMG of the FS, IFS, PyFS, and q-ROFS.
Definition 2.5
An LD-FS \(\mathscr {L}\) over \(\mathscr {W}\) is an expression of following form:
where \(\daleth ^{M}, \daleth ^{N}: \mathscr {W} \longrightarrow [0,1]\) are MG and NMG and \(\varpi ^{M}(w), \varpi ^{N}(w) \in [0,1]\) are corresponding reference parameters, respectively, with \(0 \le \varpi ^{M}(w) + \varpi ^{N}(w) \le 1\) and \(0 \le \varpi ^{M}(w) \daleth ^{M}(w) + \varpi ^{N}(w) \daleth ^{N}(w) \le 1\) for all \(w\in \mathscr {W}\). The degree of hesitation of any \(w\in \mathscr {W}\) is denoted and defined as:
From now onward, We will use \(\mathcal {LDFS}(\mathscr {W})\) for the collection of all LD-FSs over \(\mathscr {W}\). For sake of simplicity, we will use \(\mathscr {L} = \big (\langle \daleth ^{M}(w), \daleth ^{N}(w)\rangle , \langle \varpi ^{M}(w), \varpi ^{N}(w) \rangle \big )\) for an LD-FS over \(\mathscr {W}\).
Example 2.6
Selection criteria are used to determine the most qualified candidate among all candidates who meet minimum qualifications and are selected for an interview for a certain post. The selection criteria go beyond minimum qualifications and look at the quality, quantity, and relevance of the experience, education, knowledge, and other abilities each applicant has. Assume that the goal is to identify the most eligible applicant who meets the specified selection criteria and is also young. Let \(\mathscr {W} = \{x_1, x_2, x_3\}\) be a set of applicants chosen for an interview for a specific post. For the construction of an LD-FS, the reference parameters are considered as \(\alpha = \text {young}\) and \(\beta = \text {not young}\). Hence, the subsequent LD-FS is created:
In the structure of LD-FS \(\mathscr {L}\), \(\mathscr {L}(x_2) = \big ( \langle 0.7, 0.6 \rangle , \langle 0.8, 0.2 \rangle \big )\) indicates that for the applicant \(x_2\), the MG and NMG w.r.t. criteria are 0.7 and 0.6, and the degrees of reference parameters: young and not young are 0.8 and 0.2.
Some fundamental set theoretic operations on LDF-Ss are given as follows.
Definition 2.7
(Riaz and Hashmi 2019) Let \(\mathscr {L}_{1} = \big (\langle \daleth ^{M}_{1}(w), \daleth ^{N}_{1}(w) \rangle , \langle \varpi ^{M}_{1}(w), \varpi ^{N}_{1}(w) \rangle \big )\) and \(\mathscr {L}_{2} = \big (\langle \daleth ^{M}_{2}(w), \daleth ^{N}_{2}(w)\rangle , \langle \varpi ^{M}_{2}(w), \varpi ^{N}_{2}(w)\rangle \big )\) be two LD-FSs on \(\mathscr {W}\). Then for all \(w\in \mathscr {W}\), we have
-
(1)
\(\mathscr {L}_{1}\subseteq \mathscr {L}_{2} \Longleftrightarrow \daleth ^{M}_{1}(w)\le \daleth ^{M}_{2}(w),\daleth ^{N}_{1}(w)\ge \daleth ^{N}_{2}(w),\text { and }\varpi ^{M}_{1}(w)\le \varpi ^{M}_{2}(w),\varpi ^{N}_{1}(w)\ge \varpi ^{M}_{2}(w)\);
-
(2)
\(\mathscr {L}_{1}\cup \mathscr {L}_{2} = \big (\langle \daleth ^{M}_{1}(w)\vee \daleth ^{M}_{2}(w), \daleth ^{N}_{1}(w)\wedge \daleth ^{N}_{2}(w) \rangle , \langle \varpi ^{M}_{1}(w)\vee \varpi ^{M}_{2}(w), \varpi ^{N}_{1}(w)\wedge \varpi ^{N}_{2}(w) \rangle \big )\);
-
(3)
\(\mathscr {L}_{1}\cap \mathscr {L}_{2} = \big (\langle \daleth ^{M}_{1}(w)\wedge \daleth ^{M}_{2}(w), \daleth ^{N}_{1}(w)\vee \daleth ^{N}_{2}(w) \rangle , \langle \varpi ^{M}_{1}(w)\wedge \varpi ^{M}_{2}(w),\varpi ^{N}_{1}(w)\vee \varpi ^{N}_{2}(w) \rangle \big )\);
-
(4)
\(\mathscr {L}_{1}^{c} = \big (\langle \daleth ^{N}_{1}(w),\daleth ^{M}_{1}(w) \rangle , \langle \varpi ^{N}_{1}(w),\varpi ^{M}_{1}(w) \rangle \big )\);
-
(5)
$$\begin{aligned} \mathscr {L}_{1}\oplus \mathscr {L}_{2}&= \left( \begin{aligned}&\langle \daleth ^{M}_{1}(w) + \daleth ^{M}_{2}(w)- \daleth ^{M}_{1}(w) \daleth ^{M}_{2}(w), \daleth ^{N}_{1}(w) \daleth ^{N}_{1}(w) \rangle ,\\&\langle \varpi ^{M}_{1}(w) + \varpi ^{M}_{2}(w)-\varpi ^{M}_{1}(w) \varpi ^{M}_{2}(w), \varpi ^{N}_{1}(w) \varpi ^{N}_{2}(w) \rangle \end{aligned} \right) ; \end{aligned}$$
-
(6)
$$\begin{aligned} \mathscr {L}_{1}\otimes \mathscr {L}_{2}&= \left( \begin{aligned}&\langle \daleth ^{M}_{1}(w) \daleth ^{M}_{2}(w), \daleth ^{N}_{1}(w) + \daleth ^{N}_{2}(w)-\daleth ^{N}_{1}(w) \daleth ^{N}_{2}(w) \rangle ,\\&\langle \varpi ^{M}_{1}(w) \varpi ^{M}_{2}(w), \varpi ^{N}_{1}(w) + \varpi ^{N}_{2}(w)-\varpi ^{N}_{1}(w) \varpi ^{N}_{2}(w)\rangle \end{aligned} \right) . \end{aligned}$$
Definition 2.8
(Riaz and Hashmi 2019) An absolute LD-FS over \(\mathscr {W}\) is denoted and defined by \(\widetilde{1} = \big (\langle \daleth ^{M}_{\tilde{1}}(w), \daleth ^{N}_{\tilde{1}}(w)\rangle , \langle \varpi ^{M}_{\tilde{1}}(w), \varpi ^{N}_{\tilde{1}}(w) \rangle \big )\), where
Definition 2.9
(Riaz and Hashmi 2019) A null LD-FS over \(\mathscr {W}\) is denoted and defined by \(\widetilde{0} = \big (\langle \daleth ^{M}_{\tilde{0}}(w), \daleth ^{N}_{\tilde{0}}(w) \rangle , \langle \varpi ^{M}_{\tilde{0}}(w), \varpi ^{N}_{\tilde{0}}(w) \rangle \big )\), where
Definition 2.10
(Riaz and Hashmi 2019) Let \(\mathscr {L} = \big (\langle \daleth ^{M}(w), \daleth ^{N}(w)\rangle , \langle \varpi ^{M}(w),\varpi ^{N}(w) \rangle \big )\) be an LD-FS over \(\mathscr {W}\).
-
(1)
The score function of \(\mathscr {L}\) is given by the mapping \(\Omega : \mathcal {LDFS}(\mathscr {W}) \longrightarrow [-1,1]\) defined as:
$$\begin{aligned} \Omega ({\mathscr {L}}) = \frac{1}{2} \Big [\big (\daleth ^{M}(w)-\daleth ^{N}(w)\big ) + \big (\varpi ^{M}(w)-\varpi ^{N}(w)\big )\Big ]. \end{aligned}$$(11) -
(2)
The quadratic score function (QSF) of \(\mathscr {L}\) is defined by a mapping \(\boxtimes _{qs} : \mathcal {LDFS}(\mathscr {W}) \longrightarrow [0,1]\) as follows:
$$\begin{aligned} . \boxtimes _{qs}(\mathscr {L})=\frac{1}{2}\Big [\Big ((\daleth ^{M}(w)\big )^{2} - \big (\daleth ^{N}(w)\big )^{2}\Big ) + \Big (\big (\varpi ^{M}(w)\big )^{2} - \big (\varpi ^{N}(w)\big )^{2}\Big )\Big ] \end{aligned}$$(12) -
(3)
The expected score function (ESF) of \(\mathscr {L}\) is defined by a mapping \(\boxtimes _{es} : \mathcal {LDFS}(\mathscr {W}) \longrightarrow [0,1]\) as follows:
$$\begin{aligned} \boxtimes _{es}(\mathscr {L}) = \frac{1}{2}\Bigg [\frac{\big (\daleth ^{M}(w) - \daleth ^{N}(w)+1 \big )}{2} + \frac{\big (\varpi ^{M}(w) - \varpi ^{N}(w)+1\big )}{2}\Bigg ]. \end{aligned}$$(13)
Definition 2.11
(Riaz and Hashmi 2019) Let \(\mathscr {L}_{i} = \big (\langle \daleth ^{M}_{i}(w),\daleth ^{N}_{i}(w)\rangle , \langle \varpi ^{M}_{i}(w),\varpi ^{N}_{i}(w)\rangle \big )\) be a collection of LD-FSs over \(\mathscr {W}\), where \(i=1,2, \cdots ,m\). Assume that \(W = (\xi _1,\xi _2, \cdots ,\xi _m)\) is a weight vector such that \(0 \le \xi _{i} \le 1 \) and \(\sum ^{m}_{i=1}\xi _{i}=1\). Then, a map \(LDFWGA : \mathcal {LDFS}(\mathscr {W}) \longrightarrow \mathcal {LDFS}(\mathscr {W})\) defined as:
called linear Diophantine fuzzy geometric weighted aggregation operator (LDFGWA-operator).
Attanssov explored certain fundamental features and developed the idea of an IFR in Atanassov (1984).
Definition 2.12
(Atanassov 1984) An IFR \(\circledR \) from \(\mathscr {W}_1\) to \(\mathscr {W}_2\) is an object of the form:
where the mappings \(\circledR ^{M}, \circledR ^{N} : \mathscr {W}_1 \times \mathscr {W}_2 \longrightarrow [0,1]\) indicates the MG and NMG from \(\mathscr {W}_1\) to \(\mathscr {W}_2\), respectively such that \(0\le \circledR ^{M}(w_1,w_2) + \circledR ^{N}(w_1,w_2) \le 1\) for all \((w_1,w_2) \in \mathscr {W}_1 \times \mathscr {W}_2\). The degree of hesitation of \((w_1,w_2) \in \mathscr {W}_1\times \mathscr {W}_2\) can calculated as:
For the sake of simplicity, we’ll utilize \(\circledR = \big (\langle \circledR ^{M}(w_1,w_2), \circledR ^{N}(w_1,w_2) \rangle \big )\) for an IFR from \(\mathscr {W}_1\) to \(\mathscr {W}_2\). The collection of all IFRs from \(\mathscr {W}_1\) to \(\mathscr {W}_2\) will be represented by \(\mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_2)\).
Some basic set theoretic operations on IFRs are given as follows.
Definition 2.13
(Burillo and Bustince 1995a, b) Let \(\circledR _{1} = \big (\langle \circledR ^{M}_{1}(w_1,w_2), \circledR ^{N}_{1}(w_1,w_2)\rangle \big )\) and \(\circledR _{2} = \big (\langle \circledR ^{M}_{2}(w_1,w_2), \circledR ^{N}_{2}(w_1,w_2)\rangle \big )\) be two IFRs from \(\mathscr {W}_{1}\) to \(\mathscr {W}_{2}\). Then, for all \((w_1,w_2)\in \mathscr {W}_1\times \mathscr {W}_2\), we have
-
(1)
\(\circledR _{1}\subseteq \circledR _{2} \Leftrightarrow \circledR ^{M}_{1}(w_1,w_2)\le \circledR ^{M}_{2}(w_1,w_2) \text { and}\ \circledR ^{N}_{1}(w_1,w_2) \ge \circledR ^{N}_{2} (w_1,w_2)\);
-
(2)
\(\circledR _{1} \cup \circledR _{2} = \big (\langle \circledR ^{M}_{1}(w_1,w_2) \vee \circledR ^{M}_{2}(w_1,w_2), \circledR ^{N}_{1}(w_1,w_2) \wedge \circledR ^{N}_{2}(w_1,w_2)\rangle \big )\);
-
(3)
\(\circledR _{1} \cap \circledR _{2} = \big (\langle \circledR ^{M}_{1}(w_1,w_2) \wedge \circledR ^{M}_{2}(w_1,w_2), \circledR ^{N}_{1}(w_1,w_2) \vee \circledR ^{N}_{2}(w_1,w_2)\rangle \big )\);
-
(4)
\(\circledR _{1}^{c} = \big (\langle \circledR ^{N}_{1}(w_1,w_2), \circledR ^{M}_{1}(w_1,w_2)\rangle \big )\).
Definition 2.14
(Deschrijver and Kerre 2003) Let \(\circledR _{1} = \big (\langle \circledR ^{M}_{1}(w_1,w_2), \circledR ^{N}_{1}(w_1,w_2)\rangle \big ) \in \mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_2)\) and \(\circledR _{2} = \big (\langle \circledR ^{M}_{2}(w_1,w_2), \circledR ^{N}_{2}(w_1,w_2)\rangle \big ) \in \mathcal {IFS}(\mathscr {W}_2\times \mathscr {W}_3)\). Then, their composition is denoted by \(\circledR _1\tilde{\circ }\circledR _{2}\) and is defined as:
where,
for all \((w_1,w_3) \in \mathscr {W}_1 \times \mathscr {W}_3\).
Definition 2.15
(Burillo and Bustince 1995a, b) Let \(\circledR = \big (\langle \circledR ^{M}(w_1,w_2), \circledR ^{N}(w_1,w_2)\rangle \big )\) be an IFR on \(\mathscr {W}\). Then,
-
(1)
\(\circledR \) is said to be reflexive IFR, if \(\circledR ^{M}(w,w) = 1, \circledR ^{N}(w,w) = 0\) for all \(w\in \mathscr {W}\).
-
(2)
\(\circledR \) is called symmetric IFR, if \(\circledR ^{M}(w_1,w_2) = \circledR ^{M}(w_2,w_1)\) and \(\circledR ^{N}(w_1,w_2) = \circledR ^{N}(w_2,w_1)\).
-
(3)
\(\circledR \) is called transitive IFR, if \(\circledR ^{M}\tilde{\circ }\circledR ^{M}\subseteq \circledR ^{M}, \circledR ^{N}\tilde{\circ }\circledR ^{N}\supseteq \circledR ^{N}\).
-
(4)
\(\circledR \) is said to be an equivalence IFR, if \(\circledR \) is a reflexive, symmetric and transitive IFR over \(\mathscr {W}\).
Definition 2.16
(Burillo and Bustince 1995a, b) Let \(\circledR = \big (\langle \circledR ^{M}(a_i,b_j),\circledR ^{N}(a_i,b_j)\rangle \big ) \in \mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_2)\), where \(\mathscr {W}_1=\{a_1,a_2,..., a_m\}\) and \(\mathscr {W}_2=\{b_1,b_2,..., b_n\}\). Consider \(\circledR ^{M}(a_i,b_j) = \big (\circledR ^{M}_{ij} \big )_{m\times n}\), \(\circledR ^{N}(a_i,b_j) = \big (\circledR ^{N}_{ij} \big )_{m\times n}\) with \(0\le \circledR ^{M}_{ij}+\circledR ^{N}_{ij}\le 1\) for all i, j, where \(1\le i \le m\) and \(1\le j\le n\). Then the IFR \(\circledR \) can be represented in the form of the following matrix:
Remark 2.17
If \(|\mathscr {W}| = n\) and \(\circledR = \big \langle (\circledR ^{M}_{ij})_{n\times n},(\circledR ^{N}_{ij})_{n\times n} \big \rangle \). Let \(\circledR ^{M} = \big (\circledR ^{M}_{ij} \big )_{n\times n}\) and \(\circledR ^{N} = \big (\circledR ^{N}_{ij}\big )_{n\times n}\). Then,
-
(1)
\(\circledR \) is reflexive, if \(\circledR ^{M}_{ii}=1\), and \(\circledR ^{N}_{ii}=0\), where \(i=1,2,...,n\).
-
(2)
\(\circledR \) is symmetric, if \(\big (\circledR ^{M}\big )^{T} = \circledR ^{M}\) and \(\big (\circledR ^{N} \big )^{T} = \circledR ^{M}\).
Definition 2.18
(Pawlak 1982) Let \(\varrho \) be an equivalence relation on \(\mathscr {W}\). Then, the pair \((\mathscr {W}, \varrho )\) is referred to as an approximation space. For any subset \(\mathscr {Y}\) of \(\mathscr {W}\), the lower approximation \(\underline{\mathscr {Y}}_{\varrho }\) and the upper approximation \(\overline{\mathscr {Y}}^{\varrho }\) are respectively defined as:
where \([w]_{\varrho }\) represents the equivalence class of \(w \in \mathscr {W}\) induced by \(\varrho \). Moreover, the boundary region of \(\mathscr {Y}\) is defined as:
3 Linear Diophantine fuzzy sets approximations based on IFR over dual universes
In this section, we plan to introduce a novel idea of roughness in the context of LD-FSs, known as the LD-FRS model, where the lower and upper approximations are also LD-FSs. For this purpose, an arbitrary IFR over two distinct universes is used to define the lower and upper approximations of an LD-FS. The relevant axiomatic systems LD-FRS model are carefully explored in detail with some concrete examples.
Definition 3.1
Let \(\circledR = \big (\langle \circledR ^{M}(w_1,w_2), \circledR ^{N}(w_1,w_2)\rangle \big ) \in \mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_2)\). Then, the triplet \(\big (\mathscr {W}_1, \mathscr {W}_2, \circledR \big )\) is called an intuitionistic fuzzy approximation space (IFA-space). For an LD-FS \(\mathscr {L} = \big (\langle \daleth ^{M}(w_2),\daleth ^{N}(w_2)\rangle , \langle \varpi ^{M}(w_2),\varpi ^{N}(w_2)\rangle \big )\) over \(\mathscr {W}_2\), the lower and upper approximations are indicated and characterized as follows:
where
and
for all \(w_1\in \mathscr {W}_1\).
Definition 3.2
Using notations identical to those in the Definition 3.1, suppose that \(\big (\mathscr {W}_1, \mathscr {W}_2, \circledR \big )\) be an IFA-space and \(\mathscr {L} = \big (\langle \daleth ^{M}(w_1),\daleth ^{N}(w_1)\rangle , \langle \varpi ^{M}(w_1),\varpi ^{N}(w_1)\rangle \big )\) be an LD-FS over \(\mathscr {W}_1\). Then, the lower and upper approximations of \(\mathscr {L}\) are respectively characterized as follows:
where
and
for all \(w_2\in \mathscr {W}_2\).
Remark 3.3
Note that we have proved the results of the lower and upper approximations of an LD-FS \(\mathscr {L}\in \mathcal {LDFS}(\mathscr {W}_2)\) given in Definition 3.1. All the results from Theorem 3.5 to Theorem 5.5, along with algorithm 1 are valid for the lower and upper approximations of an LD-FS \(\mathscr {L}\in \mathcal {LDFS}(\mathscr {W}_1)\) given in Definition 3.2 and can be shown by adopting an identical way.
Lemma 3.4
Let \(a,b,c,d\in [0,1]\). Then,
-
(1)
\((a\vee b)\cdot (c\vee d)\ge a\cdot c \vee b\cdot d\);
-
(2)
\((a\wedge b)\cdot (c\wedge d)\le a\cdot c \wedge b\cdot d\);
-
(3)
\((1-a)\cdot (1-b)\le 1- a\cdot b\);
-
(4)
\(1-(1-a)\cdot (1-b)\ge 1-(1- a\cdot b) = a\cdot b \).
Proof
Straightforward. \(\square \)
Theorem 3.5
Let \(\big (\mathscr {W}_1, \mathscr {W}_2, \circledR \big )\) be an IFA-space. Then, \(\underline{(\mathscr {L})}_\circledR , \overline{(\mathscr {L})}^\circledR \in \mathcal {LDFS}(\mathscr {W}_1)\), where
\(\mathscr {L} = \big (\langle \daleth ^{M}(w_2),\daleth ^{N}(w_2)\rangle , \langle \varpi ^{M}(w_2),\varpi ^{N}(w_2)\rangle \big )\) is an LD-FS over \(\mathscr {W}_2\).
Proof
First we prove that \(\underline{(\mathscr {L})}_\circledR \). For this, we claim that:
and
According to the Definition 3.1, it follows that
since \(\mathscr {L}\in \mathcal {LDFS}(\mathscr {W}_2)\) and \(\circledR \in \mathcal {IFR}(\mathscr {W}_1\times \mathscr {W}_2)\).
Now, let \(w_1\in \mathscr {W}_1\). Then
Similarly, one can show that \(\overline{(\mathscr {L})}^\circledR \in \mathcal {LDFS}(\mathscr {W}_1)\). \(\square \)
To elaborate the idea proposed in Definition 3.1, we provide the following example.
Example 3.6
Let \(\mathscr {W}_1 = \{s_1,s_2,s_3\}\) and \(\mathscr {W}_2 = \{t_1,t_2,t_3\}\). Consider an IFR \(\circledR \in \mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_2)\) given as follows:
Consider an LD-FS \(\mathscr {L}\in \mathcal {LDFS}(\mathscr {W}_2)\) given in the following Table 1:
According to Definition 3.1, we get the lower approximation \(\underline{(\mathscr {L})}_\circledR \) and upper approximation \(\overline{(\mathscr {L})}^\circledR \) of \(\mathscr {L}\) respectively listed in Tables 2 and 3:
From Tables 2 and 3, We observed that: \(\underline{\varpi ^{M}}_{\circledR }(s_2)=0.60\nleq 0.51=\overline{\varpi ^{M}}^{\circledR }(s_3)\). Hence, \(\underline{(\mathscr {L})}_\circledR \nsubseteq \overline{(\mathscr {L})}^\circledR \) in general.
Theorem 3.7
If \(\circledR \in \mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_1)\) is reflexive and \(\mathscr {L}\in \mathcal {IFS}(\mathscr {W}_1)\), then:
-
(1)
\(\underline{(\widetilde{0})}_\circledR = \widetilde{0}\);
-
(2)
\(\overline{(\widetilde{1})}^\circledR = \widetilde{1}\);
-
(3)
\(\underline{(\mathscr {L})}_\circledR \subseteq \mathscr {L} \subseteq \overline{(\mathscr {L})}^\circledR \).
Proof
-
(1)
According to Definition 3.1 and reflexivity of \(\circledR \), we have
$$\begin{aligned} \underline{\daleth ^{M}_{\tilde{0}}}_{\circledR }(w_1) = \bigwedge _{w_2\in \mathscr {W}_1} \Big (\circledR ^{N}(w_1,w_2)\vee \daleth ^{M}_{\tilde{0}}(w_2) \Big ) \le \circledR ^{N}(w_1,w_1)\vee \daleth ^{M}_{\tilde{0}}(w_1) = 0. \end{aligned}$$Similarly, it can be shown that \(\underline{\varpi ^{M}_{\tilde{0}}}_{\circledR }(w_1) = 0\), \(\underline{\daleth ^{N}_{\tilde{0}}}_{\circledR }(w_1) = 1\) and \(\underline{\varpi ^{N}_{\tilde{0}}}_{\circledR }(w_1) = 1\). Hence, \(\underline{(\widetilde{0})}_\circledR = \widetilde{0}\).
-
(2)
As \(\circledR \) is reflexive, so
$$\begin{aligned} \overline{\daleth ^{M}_{\tilde{1}}}^{\circledR }(w_1) = \bigvee _{w_2\in \mathscr {W}_1} \Big (\circledR ^{M}(w_1,w_2) \wedge \daleth ^{M}_{\tilde{1}}(w_2)\Big ) \ge \circledR ^{M}(w_1,w_1) \wedge \daleth ^{M}_{\tilde{1}}(w_1) = 1. \end{aligned}$$In a similar way, one can show that \(\overline{\varpi ^{M}_{\tilde{1}}}^{\circledR }(w_1) = 1\), \(\overline{\daleth ^{N}_{\tilde{1}}}^{\circledR }(w_1) = 0\) and \(\overline{\varpi ^{N}_{\tilde{1}}}^{\circledR }(w_1) = 0\). Thus, \(\overline{(\widetilde{1})}^\circledR = \widetilde{1}\).
-
(3)
To show \(\underline{(\mathscr {L})}_\circledR \subseteq \mathscr {L}\), let \(w_1\in \mathscr {W}_1\). Then from Definition 3.1, it follows that
$$\begin{aligned} \underline{\daleth ^{M}}_{\circledR }(w_1)&= \bigwedge _{w_2\in \mathscr {W}_2} \Big (\circledR ^{N}(w_1,w_2) \vee \daleth ^{M}(w_2) \Big )\\&\le \circledR ^{N}(w_1,w_1)\vee \daleth ^{M}(w_1)\\&= 0 \vee \daleth ^{M}(w_1)\\&= \daleth ^{M}(w_1). \end{aligned}$$Similarly one can show that \(\underline{\varpi ^{M}}_{\circledR }(w_1)\le \varpi ^{M}(w_1)\), \(\underline{\daleth ^{N}}_{\circledR }(w_1)\ge \daleth ^{N}(w_1)\) and \(\underline{\varpi ^{N}}_{\circledR }(w_1)\ge \varpi ^{N}(w_1)\) which reveals that \(\underline{(\mathscr {L})}_\circledR \subseteq \mathscr {L}\).
For the next inclusion, let us assume that \(w_1\in \mathscr {W}_1\). Then,
$$\begin{aligned} \overline{\daleth ^{M}}^{\circledR }(w_1)&= \bigvee _{w_2\in \mathscr {W}_2} \Big (\circledR ^{M}(w_1,w_2)\wedge \daleth ^{M}(w_2)\Big )\\&\ge \circledR ^{M}(w_1,w_1)\wedge \daleth ^{M}(w_1)\\&= 1 \wedge \daleth ^{M}(w_1)\\&= \daleth ^{M}(w_1). \end{aligned}$$
Similarly, one can show that \(\overline{\varpi ^{M}}^{\circledR }(w_1)\ge \varpi ^{M}(w_1)\), \(\overline{\daleth ^{N}}^{\circledR }(w_1)\le \daleth ^{N}(w_1)\) and \(\overline{\varpi ^{N}}^{\circledR }(w_1)\le \varpi ^{N}(w_1)\). Therefore, \(\overline{(\mathscr {L})}^\circledR \supseteq \mathscr {L}\).
Hence, \(\underline{(\mathscr {L})}_\circledR \subseteq \mathscr {L} \subseteq \overline{(\mathscr {L})}^\circledR \). \(\square \)
Theorem 3.8
Suppose \(\circledR \in \mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_2)\) and \(\mathscr {L},\mathscr {L}_{1},\mathscr {L}_{2}\in \mathcal {LDFS}(\mathscr {W}_2)\). Then the following statements hold:
-
(1)
\(\overline{(\widetilde{0})}^\circledR = \widetilde{0}\);
-
(2)
\(\underline{(\widetilde{1})}_\circledR = \widetilde{1}\);
-
(3)
\(\underline{(\mathscr {L}^c)}_\circledR = \Big (\overline{(\mathscr {L})}^\circledR \Big )^c\);
-
(4)
\(\overline{(\mathscr {L}^c)}_\circledR = \Big (\underline{(\mathscr {L})}_\circledR \Big )^c\);
-
(5)
\(\mathscr {L}_{1}\subseteq \mathscr {L}_{2} \Rightarrow \underline{(\mathscr {L}_1)}_\circledR \subseteq \underline{(\mathscr {L}_2)}_\circledR \);
-
(6)
\(\mathscr {L}_{1}\subseteq \mathscr {L}_{2} \Rightarrow \overline{(\mathscr {L}_1)}^\circledR \subseteq \overline{(\mathscr {L}_2)}^\circledR \);
-
(7)
\(\overline{(\mathscr {L}_1 \cap \mathscr {L}_2)}^\circledR \subseteq \overline{(\mathscr {L}_1)}^\circledR \cap \overline{(\mathscr {L}_2)}^\circledR \);
-
(8)
\(\underline{(\mathscr {L}_1 \cap \mathscr {L}_2)}_\circledR = \underline{(\mathscr {L}_1)}_\circledR \cap \underline{(\mathscr {L}_2)}_\circledR \);
-
(9)
\(\underline{(\mathscr {L}_1 \cup \mathscr {L}_2)}_\circledR \supseteq \underline{(\mathscr {L}_1)}_\circledR \cup \underline{(\mathscr {L}_2)}_\circledR \);
-
(10)
\(\overline{(\mathscr {L}_1 \cup \mathscr {L}_2)}^\circledR = \overline{(\mathscr {L}_1)}^\circledR \cup \overline{(\mathscr {L}_2)}^\circledR \).
Proof
It can be obtained easily by Definition 3.1. \(\square \)
Theorem 3.9
Suppose that \(\circledR \in \mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_1)\) is reflexive and \(\mathscr {L}\in \mathcal {LDFS}(\mathscr {W}_1)\), then:
-
(1)
\(\underline{\Big (\underline{(\mathscr {L})}_\circledR \Big )}_\circledR \subseteq \underline{(\mathscr {L})}_\circledR \);
-
(2)
If \(\circledR \) is alo transitive, then the converse of part (1) is true;
-
(3)
\(\underline{(\mathscr {L})}_\circledR \subseteq \overline{\Big (\underline{(\mathscr {L})}_\circledR \Big )}^\circledR \);
-
(4)
\(\underline{\Big (\overline{(\mathscr {L})}^\circledR \Big )}_\circledR \subseteq \overline{(\mathscr {L})}^\circledR \);
-
(5)
\(\overline{(\mathscr {L})}_\circledR \subseteq \overline{\Big (\overline{(\mathscr {L})}^\circledR \Big )}^\circledR \);
-
(6)
If \(\circledR \) is also transitive, then the converse of part (5) is also true.
Proof
If \(\circledR \in \mathcal {IFS}(\mathscr {W}_1 \times \mathscr {W}_1)\) is reflexive, then the proofs of parts (1), (3), (4) and (5) can be obtained directly by part (3) of Theorem 3.7. We just verify the assertions of parts (2) and (6).
-
(2)
Let \(\circledR \) be transitive IFR and \(w_1 \in \mathscr {W}_1\). Then according to Definition 3.1, we have
$$\begin{aligned}&\underline{\big ({\underline{\daleth ^{M}}_{\circledR }}\big )}_{\circledR }(w_1)\\&\quad = \bigwedge _{w_2\in \mathscr {W}_1} \Big (\circledR ^{N}(w_1,w_2)\vee \underline{\daleth ^{M}}_{\circledR }(w_2) \Big )\\&\quad = \bigwedge _{w_2\in \mathscr {W}_1} \left[ \circledR ^{N}(w_1,w_2)\vee \Big \{\bigwedge _{w_3\in \mathscr {W}_1} \Big (\circledR ^{N}(w_2,w_3)\vee \daleth ^{M}(w_3) \Big ) \Big \} \right] \\&\quad = \bigwedge _{w_2\in \mathscr {W}_1}\bigwedge _{w_3\in \mathscr {W}_1} \bigg [\circledR ^{N}(w_1,w_2)\vee \Big (\circledR ^{N}(w_2,w_3)\vee \daleth ^{M}(w_3)\Big ) \bigg ]\\&\quad = \bigwedge _{w_2\in \mathscr {W}_1}\bigwedge _{w_3\in \mathscr {W}_1} \bigg [\Big (\circledR ^{N}(w_1,w_2)\vee \circledR ^{N}(w_2,w_3) \Big ) \vee \Big (\circledR ^{N}(w_1,w_2)\vee \daleth ^{M}(w_3)\Big ) \bigg ]\\&\quad \ge \bigwedge _{w_2\in \mathscr {W}_1} \bigwedge _{w_3\in \mathscr {W}_1} \bigg [\Big (\circledR ^{N}(w_1,w_2)\vee \circledR ^{N}(w_2,w_3)\Big ) \vee \daleth ^{M}(w_3) \bigg ]\\&\quad = \bigwedge _{w_3\in \mathscr {W}_1} \left[ \Bigg (\bigwedge _{w_2\in \mathscr {W}_1} \big (\circledR ^{N}(w_1,w_2)\vee \circledR ^{N}(w_2,w_3) \big )\Bigg ) \vee \daleth ^{M}(w_3) \right] \\&\quad \ge \bigwedge _{w_3\in \mathscr {W}_1} \bigg [\circledR ^{N}(w_1,w_3)\vee \daleth ^{M}(w_3) \bigg ], \text { since } \circledR \text { is transitive}\\&\quad = \underline{\daleth ^{M}}_{\circledR }(w_1).\\ \end{aligned}$$Likewise, we can show that \(\underline{\big ({\underline{\daleth ^{N}}_{\circledR }}\big )}_{\circledR }(w_1) \le \underline{\daleth ^{N}}_{\circledR }(w_1)\), \(\underline{\big ({\underline{\varpi ^{M}}_{\circledR }}\big )}_{\circledR }(w_1) \ge \underline{\varpi ^{M}}_{\circledR }(w_1)\) and \(\underline{\big ({\underline{\varpi ^{N}}_{\circledR }}\big )}_{\circledR }(w_1) \le \underline{\varpi ^{N}}_{\circledR }(w_1)\).
-
(6)
To verify \(\overline{\Big (\overline{(\mathscr {L})}^\circledR \Big )}^\circledR \subseteq \overline{(\mathscr {L})}_\circledR \), let us assume that \(\circledR \) is transitive and \(w_1\in \mathscr {W}_1\). Then, in the light of Definition 3.1, it follows that
$$\begin{aligned}&\overline{\big ({\overline{\daleth ^{M}}^{\circledR }}\big )}^{\circledR }(w_1)\\&\quad = \bigvee _{w_2\in \mathscr {W}_1} \Big (\circledR ^{M}(w_1,w_2)\wedge \overline{\daleth ^{M}}^{\circledR }(w_2) \Big )\\&\quad = \bigvee _{w_2\in \mathscr {W}_1} \left[ \circledR ^{M}(w_1,w_2) \wedge \Big \{\bigvee _{w_3\in \mathscr {W}_1} \Big (\circledR ^{M}(w_2,w_3)\wedge \daleth ^{M}(w_3) \Big ) \Big \} \right] \\&\quad = \bigvee _{w_2\in \mathscr {W}_1} \bigvee _{w_3\in \mathscr {W}_1} \bigg [\circledR ^{M}(w_1,w_2)\wedge \Big (\circledR ^{M}(w_2,w_3)\wedge \daleth ^{M}(w_3)\Big ) \bigg ]\\&\quad = \bigvee _{w_2\in \mathscr {W}_1} \bigvee _{w_3\in \mathscr {W}_1} \bigg [\Big (\circledR ^{M}(w_1,w_2)\wedge \circledR ^{M}(w_2,w_3) \Big ) \wedge \Big (\circledR ^{M}(w_1,w_2)\wedge \daleth ^{M}(w_3)\Big ) \bigg ]\\&\quad \le \bigvee _{w_2\in \mathscr {W}_1} \left[ \Big (\bigvee _{w_3\in \mathscr {W}_1} \big (\circledR ^{M}(w_1,w_2)\wedge \circledR ^{M}(w_2,w_3)\big ) \Big )\wedge \daleth ^{M}(w_3) \right] \\&\quad \le \bigvee _{w_2\in \mathscr {W}_1} \Big (\circledR ^{M}(w_1,w_3)\wedge \daleth ^{M}(w_3) \Big )\\&\quad = \overline{\daleth ^{M}}^{\circledR }(w_1). \end{aligned}$$By adopting the similar fashion, we can verify that \(\overline{\big ({\overline{\daleth ^{N}}^{\circledR }}\big )}^{\circledR }(w_1) \ge \overline{\daleth ^{N}}^{\circledR }(w_1)\), \(\overline{\big ({\overline{\varpi ^{M}}^{\circledR }}\big )}^{\circledR }(w_1) \le \overline{\varpi ^{M}}^{\circledR }(w_1)\) and \(\overline{\big ({\overline{\varpi ^{N}}^{\circledR }}\big )}^{\circledR }(w_1) \ge \overline{\varpi ^{N}}^{\circledR }(w_1)\).
This completes the proof. \(\square \)
4 Linear Diophantine fuzzy topology induced by IFR
This section is devoted to establishing a relationship between lower and upper approximations of an LD-FS and linear Diophantine fuzzy topological space (LDF-TS) via IFRs.
Definition 4.1
(Riaz and Hashmi 2019) Let \(\mho = \big \{\mathscr {L} : \mathscr {L}\in \mathcal {LDFS}(\mathscr {W}) \big \}\) be a collection of LD-FSs on \(\mathscr {W}\). Then, \(\mho \) is said to be an LDF-topology on \(\mathscr {W}\) if the following axioms hold:
-
(1)
\(\widetilde{0}, \widetilde{1} \in \mho \);
-
(2)
\(\mathscr {L}_{1}\cap \mathscr {L}_{2}\in \mho \) for any \(\mathscr {L}_{1},\mathscr {L}_{2}\in \mho \);
-
(3)
\(\cup _{i\in I}\mathscr {L}_{i}\in \mho \) for any \(\mathscr {L}_{i}\in \mho \).
Then pair \((\mho , \mathscr {W})\) is named as an LDF-TS.
Theorem 4.2
If \(\circledR \in \mathcal {LDFS}(\mathscr {W}_1\times \mathscr {W}_1)\) is reflexive, then
is an LDF-topology on \(\mathscr {W}_1\).
Proof
-
(1)
According to part (1) of Theorem 3.7 and part of (2) of Theorem 3.8, it follows that
$$\begin{aligned} \underline{(\widetilde{0})}_\circledR = \widetilde{0}\ \text {and}\ \underline{(\widetilde{1})}_\circledR = \widetilde{1}. \end{aligned}$$This indicates that \(\widetilde{0}, \widetilde{1} \in \mho \).
-
(2)
Let \(\mathscr {L}_{1},\mathscr {L}_{2}\in \mathcal {T}\). Then, \(\underline{(\mathscr {L}_1)}_\circledR = \mathscr {L}_1\) and \(\underline{(\mathscr {L}_2)}_\circledR = \mathscr {L}_2\). Thus, according to part (8) of Theorem 3.8, we have
$$\begin{aligned} \mathscr {L}_{1} \cap \mathscr {L}_{2} = \underline{(\mathscr {L}_1)}_\circledR \cap \underline{(\mathscr {L}_2)}_\circledR = \underline{(\mathscr {L}_1 \cap \mathscr {L}_2)}_\circledR \end{aligned}$$showing that \(\mathscr {L}_{1} \cap \mathscr {L}_{2} \in \mathcal {T}\).
-
(3)
Assume that \(\mathscr {L}_{i}\in \mathcal {T}\). Then, \(\underline{(\mathscr {L}_i)}_\circledR = \mathscr {L}_i\), \(i\in I\). By part (9) of Theorem 3.8, it implies that
$$\begin{aligned} \cup _{i\in I}\mathscr {L}_{i} = \cup _{i\in I} \underline{(\mathscr {L}_i)}_\circledR \subseteq \underline{(\cup _{i\in I}\mathscr {L}_{i})}_\circledR . \end{aligned}$$Since \(\circledR \) is reflexive IFR, so from part (3) of Theorem 3.7, it follows that \(\underline{(\cup _{i\in I}\mathscr {L}_{i})}_\circledR \subseteq \cup _{i\in I}\mathscr {L}_{i}\). Hence, \(\underline{(\cup _{i\in I}\mathscr {L}_{i})}_\circledR = \cup _{i\in I}\mathscr {L}_{i}\).
This proves that \(\mathcal {T}\) is an LDF-topology over \(\mathscr {W}_1\). \(\square \)
5 Similarity relations based on IFR
In this section, we establish a few binary relations between LD-FSs based on their lower and upper approximations known as linear Diophantine fuzzy similarity relations (LDF-SRs) and investigate their properties.
Definition 5.1
Let \(\circledR \in \mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_2)\) and \(\mathscr {L}_{1},\mathscr {L}_{2}\in \mathcal {LDFS}(\mathscr {W}_2)\). Define the relations  , \(\widetilde{\heartsuit }\) and \(\heartsuit \) on \(\mathscr {W}_2\) as follows:
, \(\widetilde{\heartsuit }\) and \(\heartsuit \) on \(\mathscr {W}_2\) as follows:
-
 if and only if \(\underline{(\mathscr {L}_{1})}_\circledR = \underline{(\mathscr {L}_{2})}_\circledR \).
if and only if \(\underline{(\mathscr {L}_{1})}_\circledR = \underline{(\mathscr {L}_{2})}_\circledR \). -
\(\mathscr {L}_{1}\widetilde{\heartsuit }\mathscr {L}_{2}\) if and only if \(\overline{(\mathscr {L}_{1})}^\circledR = \overline{(\mathscr {L}_{2})}^\circledR \).
-
\(\mathscr {L}_{1}\heartsuit \mathscr {L}_{2}\) if and only if \(\underline{(\mathscr {L}_{1})}_\circledR = \underline{(\mathscr {L}_{2})}_\circledR \) and \(\overline{(\mathscr {L}_{1})}^\circledR = \overline{(\mathscr {L}_{2})}^\circledR \).
These relations are generally known as the lower LDF-SR, upper LDF-SR, and LDF-SR, respectively.
Proposition 5.2
The relations  , \(\widetilde{\heartsuit }\) and \(\heartsuit \) on \(\mathscr {W}_2\) are equivalence relations on \(\mathcal {LDFS}(\mathscr {W}_2)\).
, \(\widetilde{\heartsuit }\) and \(\heartsuit \) on \(\mathscr {W}_2\) are equivalence relations on \(\mathcal {LDFS}(\mathscr {W}_2)\).
Proof
Straightforward. \(\square \)
Theorem 5.3
Let \(\circledR \in \mathcal {IFS}(\mathscr {W}_1\times \mathscr {W}_2)\). Then, the subsequent statements hold for each \(\mathscr {L}_{1}, \mathscr {L}_{2}, \mathscr {L}_{3}, \mathscr {L}_{4} \in \mathcal {LDFS}(\mathscr {W}_2)\).
-
(1)
\(\mathscr {L}_{1}\widetilde{\heartsuit }\mathscr {L}_{2}\) if and only if \(\mathscr {L}_{1}\widetilde{\heartsuit }(\mathscr {L}_{1}\cup \mathscr {L}_{2})\widetilde{\heartsuit }\mathscr {L}_{2}\);
-
(2)
If \(\mathscr {L}_{1}\widetilde{\heartsuit }\mathscr {L}_{2}\) and \(\mathscr {L}_{3}\widetilde{\heartsuit }\mathscr {L}_{4}\), then \((\mathscr {L}_{1}\cup \mathscr {L}_{3})\widetilde{\heartsuit }(\mathscr {L}_{2}\cup \mathscr {L}_{4})\);
-
(3)
If \(\mathscr {L}_{1}\subseteq \mathscr {L}_{2}\) and \(\mathscr {L}_{2}\widetilde{\heartsuit }\ \widetilde{0}\), then \(\mathscr {L}_{1}\widetilde{\heartsuit }\ \widetilde{0}\);
-
(4)
\((\mathscr {L}_{1}\cup \mathscr {L}_{2})\widetilde{\heartsuit }\ \widetilde{0}\) if and only if \(\mathscr {L}_{1}\widetilde{\heartsuit }\ \widetilde{0}\) and \(\mathscr {L}_{2}\widetilde{\heartsuit }\ \widetilde{0}\);
-
(5)
If \(\mathscr {L}_{1}\subseteq \mathscr {L}_{2}\) and \(\mathscr {L}_{1}\widetilde{\heartsuit }\ \widetilde{1}\), then \(\mathscr {L}_{2}\widetilde{\heartsuit }\ \widetilde{1}\);
-
(6)
If \((\mathscr {L}_{1}\cap \mathscr {L}_{2})\widetilde{\heartsuit }\ \widetilde{1}\), then \(\mathscr {L}_{1}\widetilde{\heartsuit }\ \widetilde{1}\) and \(\mathscr {L}_{2}\widetilde{\heartsuit }\ \widetilde{1}\).
Proof
-
(1)
Let \(\mathscr {L}_{1}\widetilde{\heartsuit }\mathscr {L}_{2}\). Then \(\overline{(\mathscr {L}_{1})}^\circledR = \overline{(\mathscr {L}_{2})}^\circledR \). According to part (10) of Theorem 3.8, we have
$$\begin{aligned} \overline{(\mathscr {L}_{1} \cup \mathscr {L}_{2})}^\circledR = \overline{(\mathscr {L}_{1})}^\circledR \cup \overline{(\mathscr {L}_{2})}^\circledR = \overline{(\mathscr {L}_{1})}^\circledR \cup \overline{(\mathscr {L}_{1})}^\circledR = \overline{(\mathscr {L}_{1})}^\circledR = \overline{(\mathscr {L}_{2})}^\circledR . \end{aligned}$$Hence, \(\mathscr {L}_{1}\widetilde{\heartsuit }(\mathscr {L}_{1}\cup \mathscr {L}_{2}) \widetilde{\heartsuit }\mathscr {L}_{2}\).
Converse follows by the transitivity of the relation \(\widetilde{\heartsuit }\).
-
(2)
Let \(\mathscr {L}_{1}\widetilde{\heartsuit }\mathscr {L}_{2}\) and \(\mathscr {L}_{3}\widetilde{\heartsuit }\mathscr {L}_{4}\). Then, \(\overline{(\mathscr {L}_{1})}^\circledR = \overline{(\mathscr {L}_{2})}^\circledR \) and \(\overline{(\mathscr {L}_{3})}^\circledR = \overline{(\mathscr {L}_{4})}^\circledR \). From part (10) of Theorem 3.8, it follows that
$$\begin{aligned} \overline{(\mathscr {L}_{1}\cup \mathscr {L}_{3})}^\circledR = \overline{(\mathscr {L}_{1})}^\circledR \cup \overline{(\mathscr {L}_{3})}^\circledR = \overline{(\mathscr {L}_{2})}^\circledR \cup \overline{(\mathscr {L}_{4})}^\circledR = \overline{(\mathscr {L}_{2}\cup \mathscr {L}_{4})}^\circledR . \end{aligned}$$Thus, \((\mathscr {L}_{1}\cup \mathscr {L}_{3})\widetilde{\heartsuit } (\mathscr {L}_{2} \cup \mathscr {L}_{4})\).
-
(3)
Assume that \(\mathscr {L}_{1}\subseteq \mathscr {L}_{2}\) and \(\mathscr {L}_{2}\widetilde{\heartsuit }\ \widetilde{0}\). Then, \(\overline{(\mathscr {L}_{2})}^\circledR = \overline{(\widetilde{0})}^\circledR \). In the light of part (6) of Theorem 3.8, we have \(\overline{(\mathscr {L}_{1})}^\circledR \subseteq \overline{(\mathscr {L}_{2})}^\circledR \). Thus, \(\overline{(\mathscr {L}_{1})}^\circledR \subseteq \overline{(\widetilde{0})}^\circledR \). But \(\overline{(\widetilde{0})}^\circledR \subseteq \overline{(\mathscr {L}_{1})}^\circledR \) always. Therefore, \(\overline{(\mathscr {L}_{1})}^\circledR = \overline{(\widetilde{0})}^\circledR \). Hence, \(\mathscr {L}_{1}\widetilde{\heartsuit }\ \widetilde{0}\).
-
(4)
Suppose that \((\mathscr {L}_{1}\cup \mathscr {L}_{2}) \heartsuit \ \widetilde{0}\). Then, \(\overline{(\mathscr {L}_{1} \cup \mathscr {L}_{2})}^\circledR = \overline{(\widetilde{0})}^\circledR \). Since \(\mathscr {L}_{1} \subseteq \mathscr {L}_{1} \cup \mathscr {L}_{2}\) and \(\mathscr {L}_{2} \subseteq \mathscr {L}_{1} \cup \mathscr {L}_{2}\). We have from part (3), \(\mathscr {L}_{1}\widetilde{\heartsuit }\ \widetilde{0}\) and \(\mathscr {L}_{2}\widetilde{\heartsuit }\ \widetilde{0}\).
Conversely, assume that \(\mathscr {L}_{1}\widetilde{\heartsuit }\ \widetilde{0}\) and \(\mathscr {L}_{2}\widetilde{\heartsuit }\ \widetilde{0}\). Then, \(\overline{(\mathscr {L}_{1})}^\circledR = \overline{(\widetilde{0})}^\circledR \) and \(\overline{(\mathscr {L}_{2})}^\circledR = \overline{(\widetilde{0})}^\circledR \). Therefore, \(\overline{(\mathscr {L}_{1}\cup \mathscr {L}_{2})}^\circledR = \overline{(\mathscr {L}_{1})}^\circledR \cup \overline{(\mathscr {L}_{2})}^\circledR = \overline{(\widetilde{0})}^\circledR \). Hence, \((\mathscr {L}_{1}\cup \mathscr {L}_{2})\widetilde{\heartsuit }\ \widetilde{0}\).
-
(5)
Let \(\mathscr {L}_{1}\subseteq \mathscr {L}_{2}\) and \(\mathscr {L}_{1}\widetilde{\heartsuit }\ \widetilde{1}\). Then, \(\overline{(\mathscr {L}_{1})}^\circledR = \overline{(\widetilde{1})}^\circledR \). According to part (6) of Theorem 3.8, \(\overline{(\mathscr {L}_{1})}^\circledR \subseteq \overline{(\mathscr {L}_{2})}^\circledR \). It implies that \(\overline{(\tilde{1})}^\circledR \subseteq \overline{(\mathscr {L}_{2})}^\circledR \) but \(\overline{(\mathscr {L}_{2})}^\circledR \subseteq \overline{(\widetilde{1})}^\circledR \) always. Therefore, \(\overline{(\widetilde{1})}^\circledR = \overline{(\mathscr {L}_{2})}^\circledR \). Hence, \(\mathscr {L}_{2}\widetilde{\heartsuit }\ \widetilde{1}\).
-
(6)
Assume that \((\mathscr {L}_{1}\cap \mathscr {L}_{2})\widetilde{\heartsuit }\ \widetilde{1}\). Since \(\mathscr {L}_{1}\cap \mathscr {L}_{2}\subseteq \mathscr {L}_{1}\) and \(\mathscr {L}_{1}\cap \mathscr {L}_{2}\subseteq \mathscr {L}_{2}\) and \((\mathscr {L}_{1}\cap \mathscr {L}_{2})\widetilde{\heartsuit }\ \widetilde{1}\). From part (5), \(\mathscr {L}_{1}\widetilde{\heartsuit }\ \widetilde{1}\) and \(\mathscr {L}_{2}\widetilde{\heartsuit }\ \widetilde{1}\).
This completes the proof. \(\square \)
Theorem 5.4
With the same assumptions as in the Theorem 5.3, the following properties hold:
-
(1)
 if and only if
if and only if  ;
; -
(2)
If
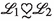 and
and  , then
, then  ;
; -
(3)
If \(\mathscr {L}_{1}\subseteq \mathscr {L}_{2}\) and
 , then
, then  ;
; -
(4)
 if and only if
if and only if  and
and 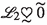 ;
; -
(5)
If \(\mathscr {L}_{1}\subseteq \mathscr {L}_{2}\) and
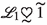 , then
, then  ;
; -
(6)
If
 , then
, then  and
and  .
.
Proof
The proof is analogous to the proof of Theorem 5.3. \(\square \)
Theorem 5.5
With the same assumptions as in the Theorem 5.3, the following properties hold:
-
(1)
\(\mathscr {L}_{1}\heartsuit \mathscr {L}_{2}\) if and only if \(\mathscr {L}_{1}\widetilde{\heartsuit }(\mathscr {L}_{1}\cup \mathscr {L}_{2}) \widetilde{\heartsuit }\mathscr {L}_{2}\) and
 ;
; -
(2)
If \(\mathscr {L}_{1}\heartsuit \mathscr {L}_{2}\) and \(\mathscr {L}_{3}\heartsuit \mathscr {L}_{4}\), then \((\mathscr {L}_{1}\cup \mathscr {L}_{3})\widetilde{\heartsuit }(\mathscr {L}_{2}\cup \mathscr {L}_{4})\) and
 ;
; -
(3)
If \(\mathscr {L}_{1}\subseteq \mathscr {L}_{2}\) and \(\mathscr {L}_{2}\heartsuit \ \widetilde{0}\), then \(\mathscr {L}_{1}\heartsuit \ \widetilde{0}\);
-
(4)
\((\mathscr {L}_{1}\cup \mathscr {L}_{2})\heartsuit \ \widetilde{0}\) if and only if \(\mathscr {L}_{1}\heartsuit \ \widetilde{0}\) and \(\mathscr {L}_{2}\heartsuit \ \widetilde{0}\);
-
(5)
If \(\mathscr {L}_{1}\subseteq \mathscr {L}_{2}\) and \(\mathscr {L}_{1}\heartsuit \ \widetilde{1}\), then \(\mathscr {L}_{2}\heartsuit \ \widetilde{1}\);
-
(6)
If \((\mathscr {L}_{1}\cap \mathscr {L}_{2})\heartsuit \ \widetilde{1}\), then \(\mathscr {L}_{1}\heartsuit \ \widetilde{1}\) and \(\mathscr {L}_{2}\heartsuit \ \widetilde{1}\).
Proof
This directly follows from Definition 5.1, Theorems 5.3 and 5.4. \(\square \)
6 Application of LD-FRS model in decision-making
DM is the process of choosing among several alternatives based on the available information and resources. It involves analyzing and evaluating information, considering multiple perspectives, and making informed and effective choices that align with an individual’s or organization’s goals and values. DM is an important skill that is necessary for personal and professional success. It is a crucial part of problem-solving and helps individuals and organizations navigate challenges and make progress. Effective DM requires good judgment and the ability to communicate and collaborate with others to gather additional information and seek input and feedback.
Several authors put forward different DM techniques in the framework of FSs (Bashir et al. 2019; Bellman and Zadeh 1970), IFS (Boran et al. 2009), PyFS (Zhang et al. 2019), q-ROFS (Liu and Wang 2018) and LD-FS (Ayub et al. 2021, 2022a, b, c; Almagrabi et al. 2021; Ayub et al. 2022b; Mohammad et al. 2022). Based on lower and upper approximations, we build an alternative strategy for MCDM in this section. Certain helpful examples in the agriculture industry are provided for the practical uses of these proposed algorithms.
Figure 1 depicts the flowchart representation of the proposed MCDM algorithm.
We provide the following example for usage in real-world scenarios and as an example.
Example 6.1
The agricultural sector is essential to the development of the national economy. Around \(38.5 \%\) of the labour force is employed by it, contributing \(19.2 \%\) to the GDP. More than \(65-70 \%\) of people rely on agriculture. Reduced arable land, climate change, water limitations, widespread population, and labour migration from rural to urban areas have all slowed agricultural development rates. Therefore, enhancing agricultural output necessitates the implementation of novel strategies. It can be crucial in promoting economic growth because of its strong forward and backward links with the secondary (industrial) and tertiary (services) sectors. However, this industry has faced several difficulties, including climate change, temperature variations, a water deficit, changes in precipitation patterns, and increased input prices.
To maintain a continuous supply of fundamental food goods at reasonable costs, the government regularly monitors major crops and develops policies and planning initiatives. The government’s top priority is to increase financial inclusion in the agricultural sector to increase productivity and exports and enable economic growth driven by rural development. Recognizing the value of agriculture, the government is concentrating on a set of pro-agriculture policies to maximize gains by enacting an agri-input regime to boost yields of significant rabi and khraif crops. What are the fundamental and essential aspects influencing the agriculture sector’s growth rate? Let’s use our suggested approach to resolve this issue.
Assume that \(\mathscr {W}_1 = \{f_1,f_2,f_3,f_4\}\) be a collection of some crops, where \(f_1=\ \)wheat, \(f_2=\ \)rice, \(f_3=\ \)corn and \(f_4=\ \)lentils. Consider some criterions for growth \(\mathscr {W}_2 = \{c_1,c_2,c_3\}\), where
-
\(c_1 = {\textbf {Fertility of land}}:\) The fertility of land affects crop growth by influencing nutrient availability, soil structure, pH levels, organic matter content, microbial activity, and water retention. Farmers use various practices to improve soil fertility and crop production, including fertilization, crop rotation, and soil amendments.
-
\(c_2 = {\textbf {Areography}}:\) The areography of the land consists of the factors, including elevation, slope, and orientation towards the sun can significantly impact crop growth.
-
\(c_3 = {\textbf {Weather condition}}:\) Weather conditions greatly influence crop growth, including temperature, precipitation, humidity, sunlight, wind, and extreme events.
To determine the best decision, we use our proposed methodology.
Step 1: Let us consider a decision matrix in terms of an IFR which describes the weighings of “satisfactory” and “non-satisfactory” for each of these crops corresponding to each criterion, given in the Table 4.
Consider an LD-FS of characteristics or attributes displayed in Table 5.
where MG and NMG talk about the fulfillment and dissatisfaction with the corresponding criteria and reference parameters \(\varpi ^{M}(c)\) denotes the "adequate criteria" and \(\varpi ^{N}(c)\) represents "inadequate criteria".
Step 2: Using the Definition 3.1, the lower and upper approximations of \(\mathscr {L}\) w.r.t. \(\circledR \) are respectively given in Tables 6 and 7.
Step 3: Using the ring product \(\otimes \), an LD-FS \(\Game =\underline{(\mathscr {L})}_\circledR \otimes \overline{(\mathscr {L})}^\circledR \) is given in the Table 8.
Step 4: According to the Definition 2.10, the score values \(\hslash _{i} = \Omega \big (\Game (w_{i})\big )\) are given in the Table 9.
Step 5: Since \(max\{\hslash _{i} : i=1,\cdots ,4\} = \hslash _{1} = 0.0100\), so the optimal alternative is \(f_1\). Moreover, the ranking among the alternatives of \(\mathscr {W}_1\) is given as follows:
The pictorial representation for the ranking of crops is shown in Fig. 2.
7 Discussion and comparative analysis
This section analyzes the advantages of the proposed strategy and conducts a comparative analysis from quantitative and qualitative aspects with existing approaches in the context of LD-FS theory to legitimate the superiority, authenticity, and validity of our designed LD-FRS approach.
7.1 Advantages of the proposed model
The expounded technique offers several advantages, which are outlined as follows:
-
1.
The proposed DM model is designed to deal with real-life DM problems based on an innovative hybrid approach of LD-FRSs. A hybrid model is always more efficient, powerful, and reliable for dealing with uncertain information.
-
2.
Some studies on the LD-FSs are devised in Almagrabi et al. (2021), Ayub et al. (2021), Iampan et al. (2021), Riaz and Hashmi (2019), but the roughness of the suggested approaches is not examined in these studies. Our approach integrates LD-FSs, RSs, and IFR to construct the lower and upper approximation operators of an LD-FS, which is the uniqueness and novelty of our study.
-
3.
The prevailing studies based on FSs, IFSs, PyFSs, and q-ROFSs cannot deal with reference parametrization. The suggested methodology offers freedom to the decision-makers to assign MG and NMG without any restriction. The dynamic characteristics of the reference parameters can effectively resolve MCDM scenarios.
7.2 Quantitative analysis
In LD-FSs, the ranking of objects is easy according to the method of Riaz et al. (2020). Since then, there have been various interesting models for ranking among objects that originated in the framework of LD-FSs (see Almagrabi et al. (2021), Ayub et al. (2021, 2022a, 2022b), Mohammad et al. (2022)). However, the situation is not straightforward in the case of LD-FRSs, where an LD-FS is approximated by an arbitrary IFR over two universes. However, Ayub et al. (2022a, 2022b) proposed various methods for ranking in case of LD-FRSs. But, these techniques are totally independent of each other and of the technique in this paper. In this work, we have introduced a new hybrid model of LD-FRSs, where the lower and upper approximations of an LD-FS have been defined by using an IFR over two universes.
In the following, through numerical experiments, we quantitatively compare our designed DM approach with certain existing DM techniques in the context of LD-FSs. In the view of DM methods introduced by Ayub et al. 2023, Boran et al. (2009) and Riaz and Hashmi (2019), we can determine the ranking results of alternatives, which are displayed in Table 10. Additionally, the ranking results are visually shown in Fig. 2.
Here, in Table 10, in the proposed studies (Ayub et al. 2023, Boran et al. 2009; Riaz and Hashmi 2019), the ranking order of the crops is the same, and each study provided \(f_1\) as a desirable alternative. As a result, the designed model is stable and trustworthy.
7.3 Qualitative comparison
We compare the qualitative aspects of the established approach and the proposed approaches in Zadeh (1965), Atanssov (1986), Yager (2013), Ali (2018), Riaz and Hashmi (2019), and Bilal and Shabir (2021). The comparison results are listed in Table 11. We perform qualitative comparisons from five aspects: MG, NMG, reference parametrization, the roughness of an information system (IS), and dual universes characteristic to demonstrate its superiority. The suggested approach contains all the listed characteristics, but the mentioned approaches do not have all of them, which can be shown in Table 11. Therefore, in many real-world DM problems, the suggested method is superior to the DM methods in IFS, PyFS, and q-ROFS settings.
7.4 Limitations
The performance of the developed LD-FRS model can be sensitive to its reference parameters \(\alpha \) and \(\beta \). The sensitivity of these parameters might be a shortcoming, as choosing inappropriate values might yield less reliable or biased results.
8 Conclusion and future perspective
The LD-FS model is one of the remarkable extensions of the FS, IFS, PyFS, and q-ROFS, which provide a tradeoff mechanism to cope with uncertain data in real-world DM problems. In this script, we proposed a robust hybrid LD-FRS model, which is a conglomeration of LD-FSs, RS theory, and IFRs. In the LD-FRS model, an arbitrary IFR over two universes has been employed to construct the lower and upper approximations of an LD-FS. Several relevant structural properties of the LD-FRS model have been examined in length with certain concrete illustrations. Additionally, a connection is made between the LD-FRS model and LDF-topology. Meanwhile, based on the lower and upper approximations of an LD-FS, some similarity relations among LD-FSs have been proposed. Subsequently, an application of MCDM in the framework of LD-FRS is provided to demonstrate the practicality and feasibility of the proposed method. A novel approach for MCDM has also been created by using the mechanism of proposed LD-FRSs, which is further implemented in a real-life case study. Finally, a detailed comparison of the developed model with some prevailing approaches is conducted to demonstrate its reliability and superiority.
We hope that the invented LD-FRS model will bring a new avenue in the research and development of paradigm of LD-FSs. For possible future research perspectives, see our suggestions as follows:
-
1.
Future studies will concentrate on creating innovative DM strategies for the proposed LD-FRS model, employing various approaches such as TOPSIS, VIKOR, ELECTRE, AHP, COPRAS, PROMETHEE, EDAS, MULTIMOORA, and ELECTRE methods to enhance the efficacy of MCDM.
-
2.
We will investigate the possible fusion of the LD-FRS model with other theories to get useful applications to management sciences and big data processing techniques.
-
3.
The suggested idea of the LD-FRS model can be expanded to the framework of multi-granulation RSs and covering-based RSs.
-
4.
The attribute reduction of the proposed LDF-RS model should be analyzed, and comprehensive experimental investigations and comparisons with prevailing methodologies should also be justified and explored.
-
5.
In addition, the hybridization of LD-FRS with complex LD-FSs (Kamacı 2022), q-LD-FSs (Almagrabi et al. 2021), and (p, q)-RLD-FSs (Panpho and Yiarayong 2023) will be a hot research topic in the near future.
Data availability
Not applicable.
References
Ali MI (2018) Another view on q-rung orthopair fuzzy sets. Int J Intell Syst 33(11):2139–2153
Ali J, Bashir Z, Rashid T (2021) Weighted interval-valued dual-hesitant fuzzy sets and its application in teaching quality assessment. Soft Comput 25:3503–3530
Ali Z, Mahmood T, Santos-García G (2021) Heronian mean operators based on novel complex linear Diophantine uncertain linguistic variables and their applications in multi-attribute decision making. Mathematics 9(21):2730
Almagrabi AO, Abdullah S, Shams M (2021) A new approach to q-linear Diophantine fuzzy emergency decision support system for COVID19. J Ambient Intell Humaniz Comput. https://doi.org/10.1007/s12652-021-03130-y
Alnoor A, Zaidan AA, Qahtan S, Alsattar HA, Mohammed RT, Khaw KW, Albahri AS (2022) Toward a sustainable transportation industry: oil company benchmarking based on the extension of linear Diophantine fuzzy rough sets and multicriteria decision-making methods. IEEE Trans Fuzzy Syst 31(2):449–459
Al-shami TM (2022) Topological approach to generate new rough set models. Complex Intell Syst 8(5):4101–4113
Atanassov KT (1984) Intuitionistic Fuzzy Relations. In: Antonov L (ed) III International School Automation and Scientiï Instrumentation. Varna, pp 56–57
Atanssov KT (1986) Intuintionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Atanssov KT (1989) More on intuintionistic fuzzy sets. Fuzzy Sets Syst 33:37–45
Ayub S, Shabir M, Riaz M, Aslam M, Chinram R (2021) Linear Diophantine fuzzy relations and their algebraic properties with decision making. Symmetry 13:945. https://doi.org/10.3390/sym13060945
Ayub S, Shabir M, Riaz M, Karaslan F, Marinkovic D, Vranjes D (2022a) Linear Diophantine fuzzy rough sets on paired universes with multi-stage decision analysis. Axioms 11(686):1–18. https://doi.org/10.3390/axioms11120686
Ayub S, Shabir M, Riaz M, Mahmood W, Bozanic D, Marinkovic D (2022b) Linear Diophantine fuzzy rough sets: a new rough set approach with decision making. Symmetry 14:525. https://doi.org/10.3390/sym14030525
Ayub S, Mahmood W, Shabir M, Koam ANA, Gul R (2022c) A study on soft multi-granulation rough sets and their applications. IEEE Access 10:115541–115554
Ayub S, Shabir M, Gul R (2023) Another approach to Linear Diophantine fuzzy rough sets on two universes and its application towards decision-making problem. Phys Scripta 98(10):105240
Bashir Z, Bashir Y, Rashid T, Ali J, Gao W (2019) A novel multi-attribute group decision-making approach in the framework of proportional dual hesitant fuzzy sets. Appl Sci 9(6):1232
Bashir Z, Mahnaz S, Abbas Malik MG (2021) Conflict resolution using game theory and rough sets. Int J Intell Syst 36(1):237–259
Bellman RE, Zadeh LA (1970) Decision-making in fuzzy environment. Manag Sci 4(17):141–164
Bilal MA, Shabir M (2021) Approximations of Pythagorean fuzzy sets over dual universes by soft binary relations. J Intell Fuzzy Syst 41:2495–2511
Bilal MA, Shbair M, Al-Kenani Ahmad N (2021) Rough q-rung orthopair fuzzy sets and their applications in decision-making. Symmetry 13:1–22
Boixder D, Jacas J, Recasens J (2000) Upper and lower approximations of fuzzy sets. Int J Gen Syst 29:555–568
Boran FE, Geniç S, Kurt M, Akay D (2009) A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst Appl 36:11363–11368
Burillo P, Bustince H (1995) Intuitionistic fuzzy relations (Part I). Mathw Soft Comput 2(1):5–38
Burillo P, Bustince H (1995) Intuitionistic fuzzy relations (Part II) Effect of Atanassov’s operators on the properties of the intuitionistic fuzzy relations. Mathw Soft Comput 2(2):117–148
Bustince H (2000) Construction of intuitionistic fuzzy relations with predetermined properties. Fuzzy Sets Syst 109:379–403
Chang CL (1968) Fuzzy topological spaces. J Math Anal Appl 24:182–189
Coker D (1997) An introduction of intuitionistic fuzzy topological spaces. Fuzzy Sets Syst 88:81–89
Cornelis C, Deschrijver G, Kerre EE (2004) Implication in intuintionistic fuzzy and interval-valued fuzzy set theory: Construction, classification, application. Int J Approx Reason 35(1):55–95
Davvaz B (2008) A short note on algebraic \(T-\)rough sets. Inf Sci 178:3247–3252
Deschrijver G, Kerre EE (2003) On the composition of intuitionistic fuzzy relations. Fuzzy Sets Syst 136:333–361
Dubois D, Prade H (1990) Fuzzy rough sets and rough fuzzy sets. Int J Gen Syst 17:191–209
Dubois D, Prade H (2012) Gradualness, uncertainty and bipolarity: making sense of fuzzy sets. Fuzzy Sets Syst 192:3–24
El-Bably MK, Al-Shami TM (2021) Different kinds of generalized rough sets based on neighborhoods with a medical application. Int J Biomath 14(08):2150086
Gul R, Shabir M (2020) Roughness of a set by \((\alpha ,\beta )-\)indiscernibility of Bipolar fuzzy relation. Comput Appl Math 39(160):1–22. https://doi.org/10.1007/s40314-020-01174-y
Iampan A, Garcia GS, Riaz M, Afrid HMA, Chinram R (2021) Linear Diophanine fuzzy Einstien aggregation operators for multi-criteria decision-making problems. J Math (Hindawi) 2021:1–31
Ibrahim HZ, Al-shami TM, Mhemdi A (2023) Applications of \(n^{th}\) power root fuzzy sets in multicriteria decision making. J Math 2023:14
Jäkel J, Mikut R, Bretthauer G (2004) Fuzzy control systems. In: Institute of Applied Computer Science, Forschungszentrum Karlsruhe GmbH, Germany, pp 1–31
Jana C, Pal M (2023) Interval-valued picture fuzzy uncertain linguistic dombi operators and their application in industrial fund selection. J Ind Intell 1(2):110–124
Kamacı H (2021) Linear Diophantine fuzzy algebraic structures. J Ambient Intell Humaniz Comput 12(11):10353–10373. https://doi.org/10.1007/s12652-020-02826-x
Kamacı H (2022) Complex linear Diophantine fuzzy sets and their cosine similarity measures with applications. Complex Intell Syst 8(2):1281–1305
Khan AA, Wang L (2023) Generalized and group-generalized parameter based fermatean fuzzy aggregation operators with application to decision-making. Int J Knowl Innov Stud 1:10–29
Kim E, Park M, Ji S, Park M (1997) A new approach to fuzzy modeling. IEEE Trans Fuzzy Syst 5(3):328–337
Kortelainen J (1994) On relationship between modified sets, topological spaces and rough sets. Fuzzy Sets Syst 61:91–95
Kumar S, Gangwal C (2021) A study of fuzzy relation and its application in medical diagnosis. Asian Res J Math 17(4):6–11
Kupongsak S, Tan J (2006) Application of fuzzy set and neural network techniques in determining food process control set points. Fuzzy Sets Syst 157(9):1169–1178
Lashin EF, Kozae AM, khadra AAA, Medhat T (2005) Rough set theory for topological spaces. Int J Approx Reason 40:35–43
Li TJ, Zhang WX (2008) Rough fuzzy approximations on two universes of discourse. Inf Sci 178(3):892–906
Liu P, Wang P (2018) Some q-rung orthopair fuzzy aggregation operators and their applications to multi-attribute DM. Int J Intell Syst 33:259–280
Liu C, Miao D, Zhang N (2012) Graded rough set model based on two universes and its properties. Knowl-Based Syst 33:65–72
Mahmood T, Ali Z, Aslam M, Chinram R (2021) Generalized Hamacher aggregation operators based on linear Diophantine uncertain linguistic setting and their applications in decision-making problems. IEEE Access 9:126748–126764
Ming HC (1985) Fuzzy topological spaces. J Math Anal Appl 110:141–178
Mohammad MMS, Abdullah S, Al-Shomrani MM (2022) Some linear diophantine fuzzy similarity measures and their application in decision making problem. IEEE Syst Man Cybern Soc Sect 10:29859–29877
Molodtsov D (1999) Soft set theory-first results. Comput Math Appl 37:19–31
Murali V (1989) Fuzzy equivalence relations. Fuzzy Sets Syst 30:155–163
Panpho P, Yiarayong P (2023) (p, q)-Rung linear Diophantine fuzzy sets and their application in decision-making. Comput Appl Math 42(8):324
Pawlak Z (1982) Rough sets. Int J Inf Comp Sci 11:341–356
Pei D, Xu ZB (2004) Rough set models on two universes. Int J Gen Syst 33(5):569–581
Peng X (2019) New Similarity measure and distance measure for Pythagorean fuzzy set. Complex Intell Syst 5:101–111
Qin KY, Pei Z (2005) On topological properties of fuzzy rough sets. Fuzzy Sets Syst 151:601–613
Riaz M, Farid HMA (2023) Enhancing green supply chain efficiency through linear Diophantine fuzzy soft-max aggregation operators. J Ind Intell 1(1):8–29
Riaz M, Hashmi MR (2019) Linear Diophantine fuzzy set and its applications towards multi-attribute decision-making problems. J Intell Fuzzy Syst 37:5417–5439
Riaz M, Davvaz B, Firdous A, Fakhar A (2019) Novel concepts of soft rough set topology with applications. J Intell Fuzzy Syst 36(4):3579–3590
Riaz M, Hashmi MR, Kulsoom H, Pamucar D, Chu YM (2020) Linear Diophantine fuzzy soft rough sets for the selection of sustainable material handling equipment. Symmetry 12:1–39
Riaz M, Farid HMA, Karaaslan F (2022) Linear Diophantine fuzzy aggregation operators with multi-criteria decision-making. J Comput Cogn Eng
Samanta SK, Mondal TK (2001) Intuitionistic fuzzy rough sets and rough intuitionistic fuzzy sets. J Fuzzy Math 9:561–582
Schwartz DG, Klir GJ, Lewis HW, Ezawa Y (1994) Applications of fuzzy sets in approximate reasoning. Proc IEEE 82(4):482–498
Shabir M, Shaheen T (2016) A new methodology for fuzzification of rough sets based on \(\alpha -\)indiscernibility. Fuzzy Sets Syst 16:1–19
Shaheen T, Ali MI, Toor H (2021) Why do we need q-rung orhopair fuzzy sets? Some evidence established via mass assignment. Int J Intell Syst 36:5493–5505
She Y, He X, Shi H, Qian Y (2017) A multiple-valued logic approach for multigranulation rough set model. Int J Approx Reason 82:270–284
Skowron A (1988) On topology in information systems. Bull Polish Acad Sci Math 36(7–8):477–479
Sun BZ, Ma WM (2011) Fuzzy rough set model on two different universes and its applications. Appl Math Model 35:1798–1809
Sun B, Ma W, Liu Q (2012) An approach to decision making based on intuitionistic fuzzy rough sets over two universes. J Oper Res Soc 64:1–11
Sun G, Guan X, Yi X, Zhou Z (2018) Grey relational analysis between hesitant fuzzy sets with applications to pattern recognition. Expert Syst Appl 92:521–532
Tang W, Wu J, Zheng D (2014) On fuzzy rough sets and their toplogical structuers. Hindawi Publ Coporat Math Probl Eng 2014:1–17 (ID: 546372)
Tükraslan E, Ünver M, Olgun M (2021) q-rung orthopair fuzzy topologial spaces. Lobachevskii J Math 42:470–478
Wang XZ, Ruan D, Kerre EE (2009) Mathematics of fuzziness-basic issues. Stud Fuzzin Soft Comput 245:1–227
Wiweger A (1989) On topological rough sets. Bull Polish Acad Sci Math 37(1–6):89–93
Wu W, Zhou L (2011) On intuitionistic fuzzy topologies based on intuitionistic fuzzy reflexive and transitive relations. Soft Comput 15:1183–1194
Yager RP (2013) Pythagorean fuzzy subsets. In: Proceedings of the IFSA World Congress and NAFIPS Anual Meeting, Edmonton, AB Canada, pp 57–61
Yager RP (2014) Pythagorean membership grades in multi-criteria decision marking. IEEE Trans Fuzzy Syst 22:958–965
Yager RP (2017) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25:1222–1230
Yan R, Zheng J, Liu J, Zhai Y (2010) Research on the model of rough set over dual-universes. Knowl-Based Syst 23(8):817–822
Yang L, Xu L (2011) Topological properties of generalized approximation spaces. Inf Sci 181(17):3570–3580
Yang HL, Li SG, Wang S, Wang J (2012) Bipolar fuzzy rough set model on two different universes and its applications. Knowl-Based Syst 35:94–101
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zadeh LA (1971) Similarity relations and fuzzy orderings. Inf Sci 3:177–200
Zhang WR (1994) Bipolar fuzzy sets and relations: a computational framework for cognitive modeling and multiagent decision analysis. In: proceedings of industrial fuzzy control and intelligent systems conference and the NASA joint technology workshop on neural networks and fuzzy logic and fuzzy information processing society biannual conference, San Antonio, Tex, USA, pp 305–309
Zhang Q, Hu J, Feng J, Liu A, Li Y (2019) New similarity measures of Pythagorean fuzzy sets and their applications. IEEE Access 7(3):138192–138202
Zhou L, Wu WZ, Zhang WX (2009) On intuitionistic fuzzy rough sets and their topological structures. Int J Gener Syst 6(38):589–616
Zhu W (2007) Generalized rough sets based on relations. Inf Sci 177(22):4997–5011
Acknowledgements
The authors extend their appreciation to the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R404), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia for funding this research work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Gul, R., Ayub, S., Shabir, M. et al. Roughness of linear Diophantine fuzzy sets by intuitionistic fuzzy relations over dual universes with decision-making applications. Comp. Appl. Math. 43, 346 (2024). https://doi.org/10.1007/s40314-024-02805-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-024-02805-4





 if and only if
if and only if  if and only if
if and only if  ;
;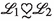 and
and  , then
, then  ;
; , then
, then  ;
; if and only if
if and only if  and
and 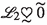 ;
;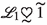 , then
, then  ;
; , then
, then  and
and  .
. ;
; ;
;

