1 Introduction

The variational inclusion problem (1) which is to

$$\begin{aligned} \text {find } \quad u\in H \quad \text { with } \quad 0\in (Au+Bu), \end{aligned}$$
(1)

where A and B are respectively, single and set valued mappings on a real Hilbert space H, has attracted the interest of many authors largely due to the fact that models arising from image restoration, machine learning and signal processing can be recast to fit the setting of (1). Problem (1) is called monotone inclusion problem, when A and B are monotone operators. In the literature, many authors have developed mathematical algorithms for approximating solutions of problem (1) when such solutions exist (see, e.g., Takahashi et al. 2012; Kitkuan et al. 2019; Yodjai et al. 2019; Abubakar et al. 2020a; Chidume et al. 2020a). Assuming existence of solutions, one of the early methods developed for approximating solutions of problem (1) is the forward-backward algorithm (FBA) introduced by Passty (1979). The FBA generates its iterates in the setting of problem (1) under maximal monotonicity requirement on A, B and \((A+B)\) by solving the recursive equation:

$$\begin{aligned} a_{n+1}=\big (I+\nu _nB\big )^{-1} \big (a_n-\nu _n Aa_n\big ), \end{aligned}$$
(2)

where \(\{\nu _n\}\subset (0,\infty )\). Weak convergence of the iterates generated by the FBA (2) has been obtained by many authors (see, e.g., Passty 1979). Passty (1979) noted that for the special case when B is the indicator function of a nonempty closed and convex set, Lions (Lions 1978) also established weak convergence of the iterates generated by (2). Over the years, some modifications have been made to the FBA to get strong convergence in the setting of real Hilbert spaces (see, e.g., Takahashi et al. 2012; Adamu et al. 2021; Phairatchatniyom et al. 2021). However, a Series Editor of Mathematics and Its Applications, Kluwer Academic Publishers, Hazewinkle, made the following remark “... many and probably most, mathematical objects and models do not naturally live in Hilbert space”, see, (Cioranescu et al. 2012) pg. viii. To further support his claim, interested readers may see, for example (Alber and Ryazantseva 2006; Shehu 2019) for some nontrivial and interesting examples of monotone operators and convex minimization problems in the setting of real Banach spaces.

There are two ways in which monotonicity on Hilbert spaces can be moved to Banach spaces. An extension of a monotone map A defined on a Hilbert space will be called accretive on a Banach space E if the mapping \(A: E \rightarrow 2^E\) satisfies the following condition:

$$\begin{aligned} \langle u-v,j_q(x-y) \rangle \ge 0, ~~\forall ~x,y \in E, ~ u\in Ax, ~v\in Ay,~j_q(x-y)\in J_q(x-y), \end{aligned}$$

where \(q>1\) and \(J_q\) is the duality mapping on E (interested readers may see, e.g., (Alber and Ryazantseva 2006) for explicit definition of \(J_q\) and some of its properties on certain Banach spaces). In the literature, extension of the inclusion problem (1) involving accretive operators have been considered by many researchers (see, e.g., Chidume et al. 2021a; Qin et al. 2020; Adamu et al. 2022a; Luo 2020).

The other extension of a monotone map A defined on a Hilbert space H is when the operator maps a Banach space E to subsets of its dual space, \(E^*\) and satisfies the following condition:

$$\begin{aligned} \langle x-y, u-v \rangle ,~~u\in Ax, ~v\in Ay, \end{aligned}$$

the name monotone is maintained. Many research efforts have been devoted toward extending the the inclusion problem (1) to involve monotone operators in the setting of Banach space. However, only a few success have been recorded (see, e.g., Shehu 2019; Kimura and Nakajo 2019; Cholamjiak et al. 2020). In 2019, in the setting of a real Banach space E that is 2-uniformly convex and uniformly smooth, Shehu (2019) established strong convergence of the iterates generated by algorithm (3) defined by:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1\in E,\\ y_n=(J+\nu _nB)^{-1}(Jx_n-\nu _nAx_n),\\ w_n=J^{-1}(Jy_n-\nu _n(Ay_n-Ax_n)),\\ x_{n+1}=J^{-1}(\alpha _n Jx_1 + (1-\alpha _n)Jw_n), \end{array}\right. } \end{aligned}$$
(3)

to a solution of problem (1) under the assumption that B is maximal monotone, A is monotone and L-Lipschitz continuous, \(\{\nu _n\}\) is a sequence of positive real numbers which satisfies some appropriate conditions, and \(\{\alpha _n\}\subset (0,1)\) with \( \lim _{n\rightarrow \infty } \alpha _n=0\) and \( \sum _{n=1}^\infty \alpha _n=\infty \).

Also, in the same year, under the same Banach space considered by Shehu (2019) and Kimura and Nakajo (2019) established strong convergence of the iterates generated by algorithm (4) defined by:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1\in C\subset E,~ u\in E,\\ x_{n+1}=\Pi _C (J+\nu _nB)^{-1}(\gamma _nJu+(1-\gamma _n)Jx_n-\nu _nAx_n), \end{array}\right. } \end{aligned}$$
(4)

In this work, we introduce a new projection free inertial Halpern-type algorithm in the setting of real Banach spaces that are uniformly smooth and 2-uniformly convex. We proved strong convergence of the iterates generated by our algorithm to a solution of problem (1). In addition, we used our algorithm in the recovery process of some degraded images and compared its performance with the algorithms (3) of Shehu (2019) and (4) of Kimura and Nakajo (2019). Finally, we give a numerical example in the classical Banach space \(l_3(\mathbb {R})\) to support our main Theorem and the Theorems of Shehu (2019), and Kimura and Nakajo (2019).

2 Preliminaries

In this section, we will introduce some notions and results established in Banach spaces that will be required in proving our main theorem. It is well-known that any normed linear space E with conjugate dual space, \(E^*\) has a duality map associated to it. In this work, we will need the normalized duality map \(J: E \rightarrow 2^{E^*} \) which one can find its explicit definition in, for example, (Alber and Ryazantseva 2006) and some of its nice properties on some normed spaces are given therein. Also, the well-known Alber’s functional \(\phi \) defined on a smooth space \(E\times E \rightarrow \mathbb {R}\) by

$$\begin{aligned} \phi (p,r):=\Vert p \Vert ^2-2\langle p,Jr\rangle +\Vert r \Vert ^2,~~\forall \, p,r\in E, \end{aligned}$$
(5)

which is central in estimations involving J on smooth spaces will be needed. As a consequence of this definition, the following are immediate for any \(p,r,z\in E \) and \(\tau \in [0,1]\)

  1. P1:

    \((\Vert p \Vert -\Vert r\Vert )^2 \le \phi (p,r)\le (\Vert p\Vert +\Vert r\Vert )^2,\)

  2. P2:

    \(\phi (p, J^{-1}(\tau Jr+(1-\tau )Jz)\le \tau \phi (p,r) + (1-\tau ) \phi (p,z), \)

  3. P3:

    \(\phi (p,r)=\phi (p,z)+\phi (z,r)+2\langle z-p,Jr-Jz\rangle ,\)

where J and \(J^{-1}\) are the normalized duality maps on E and \(E^*\), respectively (see, e.g., Nilsrakoo and Saejung 2011 for a proof of properties P1, P2 and P3). Also, we will need the mapping \(V: E\times E^* \rightarrow \mathbb {R}\) defined by

$$\begin{aligned} V(p,p^*):=\Vert p\Vert ^2-\langle p,p^*\rangle +\Vert p^*\Vert ^2,~~\forall ~p\in E,~p^*\in E^* \end{aligned}$$

in our estimations. Observe that \(V(p,p^*)=\phi (p,J^{-1}p^*)\). Thus, we shall use them interchangeably as the need arise in the course of the proof of our main theorem. In addition, the generalized projection defined by \(z=\Pi _C x \in C\) such that \(\phi (z,x)=\inf _{y\in C}\phi (y,x)\) where C is a nonempty closed and convex subset of a smooth, strictly convex and reflexive real Banach space will appear in our proof. Moreover, the resolvent operator for a set valued monotone operator that is maximal, \(B: E \rightarrow 2^{E^*}\), defined as \(J_\lambda ^B=\big (J+\lambda B)^{-1}J,\) for all \(\lambda >0\) on a smooth, reflexive and strictly convex Banach space, E will be used in our estimations.

Lemma 2.1

In Alber and Ryazantseva (2006), it was established that in a smooth, reflexive and strictly convex real Banach space, the generalized projection \(\Pi _C\) has the following property:

$$\begin{aligned} \langle z-y, Jx-Jz \rangle \ge 0, \end{aligned}$$

for any \(y\in C\), where \(x \in E\) and \(z=\Pi _C x\).

Lemma 2.2

On a smooth, reflexive and strictly convex Banach space, E with dual \(E^*\), the following inequality

$$\begin{aligned} V(p,p^*)+2\langle J^{-1}p^*-p,v^*\rangle \le V(p,p^*+v^*), \end{aligned}$$
(6)

was established in Alber and Ryazantseva (2006) for all \(p\in E\) and \(p^*,v^*\in E^{*}\).

Lemma 2.3

On a Banach space, E that is 2-uniformly smooth, it is shown in Xu (1991) that one can find \(\gamma >0\) such that

$$\begin{aligned} \Vert p+r\Vert ^2\le \Vert p\Vert ^2+2\langle r, Jp\rangle +\gamma \Vert r\Vert ^2, \end{aligned}$$

holds \(\forall ~p,r\in E\).

Lemma 2.4

(Kamimura and Takahashi 2002)

The Alber’s functional \(\phi \) has the property that \(\lim _{n\rightarrow \infty } \phi (u_n,v_n )= 0\) implies \(\lim _{n\rightarrow \infty }\Vert u_n-v_n \Vert = 0,\) whenever \(\{u_n\}\) or \(\{v_n\}\) is a bounded sequence in a Banach space that is smooth and uniformly convex.

Lemma 2.5

It was established in Nilsrakoo and Saejung (2011) that the Alber’s functional \(\phi \) has the following property:

$$\begin{aligned} \phi \left( u,J^{-1}[\tau Jp + (1-\tau )Jr]\right) \le \tau \phi (u,p)+(1-\tau )\phi (u,r)-\tau (1-\tau )g(\Vert Jp-Jr\Vert ) \end{aligned}$$

in a Banach space that is uniformly smooth E, for any \(\tau \in [0, 1],~ u \in E\) and p, r are in a bounded subset of E, for some convex, continuous and strictly increasing function g that is fixed at 0.

Lemma 2.6

For real sequences \(\{ m_n \}\), \(\{ \zeta _n \}\), \(\{ \mu _n \}\) and \(\{c_n\}\) that satisfy:

$$\begin{aligned} m_{n+1} \le (1-\zeta _n)m_n +\zeta _n \mu _n +c_n,~n\ge 0, \end{aligned}$$

where \(\{ m_n \}, \{c_n\}\subset [0,\infty )\) and, \(\sum _{n=0}^\infty c_n <\infty \) \( \{\zeta _n\}\subset [0,1]\) with the condition \(\sum _{n=0}^\infty \zeta _n=\infty , \) and \(\lim _{n\rightarrow \infty } \zeta _n=0\) and finally, \( \limsup _{n\rightarrow \infty } \mu _n \le 0\). It was shown in Hong-Kun (2002) that \(\lim _{n \rightarrow \infty } m_n=0 .\)

Lemma 2.7

Given a subsequence \(\{x_{n_j}\}\) of a nondecreasing sequence \( \{x_n\}\subset \mathbb {R}\) which satisfies \(x_{n_j}<x_{n_j+1}\) for all \(j\ge 1\). The following conclusions were established in Maingé (2010): there exists some nondecreasing index \(\{m_k\}_{k\ge 1}\subset \mathbb {N}\)

$$\begin{aligned} x_{m_k}\le x_{m_k+1} \quad \text { and } \quad x_k \le x_{m_k+1}. \end{aligned}$$

Lemma 2.8

For nonnegative sequences \(\{m_n\}, ~\{b_n\}\) and \(\{c_n\}\) that can be expressed as

$$\begin{aligned} m_{n+1} \le m_n +b_n(m_n-m_{n-1})+c_n,~\forall n \ge 1, \end{aligned}$$

if  \( \sum _{n=1}^\infty c_n < \infty \) and \(0 \le b_n \le b < 1\), for all \(n\ge 1\), in Alvarez (2004) the authors proved that

  • \(\displaystyle \sum _{n = 1}^\infty [m_n - m_{n-1}]_+ < + \infty ,\) where \([t]_+=\max \{t,0\}; \) and limit of \(\{m_n\}\) exists.

Lemma 2.9

In Kimura and Nakajo (2019) the authors established that for a set-valued maixmal monotone operator B and an \(\alpha \)-inverse strongly operator A in the setting of a 2-uniformly convex and uniformly smooth real Banach space, the operator \(T_\lambda v:= (J+\lambda B)^{-1}(Jv-\lambda Av),\) \(\lambda >0\) has the following properties:

  1. (i)

    \(F(T_\lambda )=(A+B)^{-1}0,\) where \(F(T_\lambda )\) denote the set of fixed points of \(T_\lambda \).

  2. (ii)

    \(\phi (u, T_\lambda v) \le \phi (u,v)-(\gamma -\lambda \beta ) \Vert v-T_\lambda v\Vert ^2-\lambda \Big (2\alpha -\frac{1}{\beta }\Big )\Vert Av-Au\Vert ^2,\)

for any \(\beta >0\), \(u\in F(T_\lambda )\), \(v\in E\) and \(\gamma \) is as defined in Lemma 2.3

Remark 1

Observe that given \(\alpha >0\), there exists \(\lambda _0>0\) such that \(\frac{\gamma }{\lambda _0}>\frac{1}{2\alpha }.\) Thus, one can choose \(\beta >0\) such that \(\frac{1}{2\alpha }<\beta < \frac{\gamma }{\lambda _0}\). Hence, from (ii) we have

$$\begin{aligned} \phi (u,T_\lambda v) \le \phi (u,v),~~\forall v\in E,~u\in (A+B)^{-1}0. \end{aligned}$$

Lemma 2.10

Given initial points \(r_0,r_1\) in a 2-uniformly convex and uniformly smooth real Banach space, E, the following estimate concerning the sequence \(v_n:=J^{-1}\big (Jr_n+\mu _n(Jr_n-Jr_{n-1})\big )\) was established in Adamu et al. (2022b)

$$\begin{aligned} \phi (w,v_n)&\le \phi (w,r_n)+\gamma \mu _n^2\Vert Jr_n-Jr_{n-1}\Vert ^2 +\mu _n\phi (r_n,r_{n-1}) \\&\quad + \mu _n \big ( \phi (w,r_n)-\phi (w,r_{n-1})\big ), \end{aligned}$$

where \( w\in E\), \(\{\mu _n\}\subset (0,1)\) and \(\gamma \) is as defined in Lemma 2.3. For completeness, we shall give the proof here.

Proof

Using property P3, we have

$$\begin{aligned} \phi (w,v_n)&=\phi (w,r_n)+\phi (r_n,v_n)+2\langle r_n-w,Jv_n-Jr_n \rangle \nonumber \\&=\phi (w,r_n)+\phi (r_n,v_n)+2\mu _n \langle r_n-w, Jr_n-Jr_{n-1} \rangle \end{aligned}$$
(7)
$$\begin{aligned}&=\phi (w,r_n)+\phi (r_n,v_n)+\mu _n\phi (r_n,r_{n-1})+\mu _n\phi (w,r_n)-\mu _n\phi (w,r_{n-1}). \end{aligned}$$
(8)

Also, by Lemma 2.3, one can estimate \(v_n\) as follows:

$$\begin{aligned} \phi (w,v_n)&=\phi \big ( w, J^{-1}(Jr_n+\mu _n(Jr_n-Jr_{n-1}))\big ) \nonumber \\&= \Vert w\Vert ^2+ \Vert Jr_n+\mu _n(Jr_n-Jr_{n-1})\Vert ^2-2\langle w, Jr_n+\mu _n(Jr_n-Jr_{n-1})\rangle \nonumber \\&= \Vert w\Vert ^2+ \Vert Jr_n+\mu _n(Jr_n-Jr_{n-1})\Vert ^2-2\langle w, Jr_n \rangle -2\mu _n \langle w, Jr_n-Jr_{n-1} \rangle \nonumber \\&\le \phi (w, r_n) +\gamma \mu _n^2\Vert Jr_n-Jr_{n-1}\Vert ^2+2\mu _n \langle r_n-w, Jr_n-Jr_{n-1} \rangle . \end{aligned}$$
(9)

Putting together equation (7) and inequality (9), we get

$$\begin{aligned} \phi (r_n,v_n) \le \gamma \mu _n^2\Vert Jr_n-Jr_{n-1}\Vert ^2. \end{aligned}$$

From (8), this implies that

$$\begin{aligned} \phi (w,v_n)&\le \phi (w,r_n)+\gamma \mu _n^2\Vert Jr_n-Jr_{n-1}\Vert ^2 +\mu _n\phi (r_n,r_{n-1}) \nonumber \\&\quad + \mu _n \big ( \phi (w,r_n)-\phi (w,r_{n-1})\big ). \end{aligned}$$
(10)

\(\square \)

3 Main result

Theorem 3.1

Let E be a 2-uniformly convex and uniformly smooth real Banach space with dual space, \(E^*\). Let \(A: E \rightarrow E^*\) be an \(\alpha \)-inverse strongly monotone and \(B: E \rightarrow 2^{E^*}\) be maximal monotone. Assume the solution set \(\Omega = (A+B)^{-1}0 \ne \emptyset \), given \(a_0, a_1, u \in E\), generate \(\{a_n\}\subset E\) by:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_n= J^{-1}\big ( Ja_n+\tau _n(Ja_n-Ja_{n-1})\big ), &{}\\ w_n= \big (J+\nu _nB\big )^{-1}(Jx_n-\nu _nAx_n), &{}\\ y_n= J^{-1}\big (\mu _nJu+(1-\mu _n)Jw_n\big ), &{} \\ a_{n+1}= J^{-1}\big (\varepsilon _nJx_n+(1-\varepsilon _n)Jy_n \big ), \end{array}\right. } \end{aligned}$$
(11)

where \(0<\tau _n\le \bar{\tau _n}\) and \( \bar{\tau _n}= {\left\{ \begin{array}{ll} \min \Big \{ \tau , \frac{\sigma _n}{\Vert Ja_n-Ja_{n-1}\Vert ^2}, \frac{\sigma _n}{\phi (a_n,a_{n-1})}\Big \}, &{} a_n\ne a_{n-1} , \\ \tau , &{} \text {otherwise}, \end{array}\right. }\)

\(\tau \in (0,1)\) and \(\{\sigma _n\}\subset (0,1)\) such that \(\sum _{n=1}^\infty \sigma _n<\infty \), \(0<\nu _n< 2\alpha \gamma \), with \(\gamma \) as defined in Lemma 2.3, \(\{\mu _n\} \subset (0,1)\) such that \( \lim _{n\rightarrow \infty } \mu _n=0\) and \( \sum _{n=1}^\infty \mu _n=\infty \), \(\{\varepsilon _n\}\subset (0,1)\) is nondecreasing. Then, \(\{a_n\}\) converges strongly to \(z\in \Omega \).

Proof

We begin the proof by showing that \(\{a_n\}\) is bounded. Let \(z\in \Omega \). Then, using P2, Remark 1 and Lemma 2.10, we obtain that

$$\begin{aligned} \phi (z,a_{n+1})&=\phi \big (z,J^{-1}(\varepsilon _nJx_n+(1-\varepsilon _n)Jy_n )\big ) \nonumber \\&\le \varepsilon _n \phi (z,x_n)+(1-\varepsilon _n)\phi (z,y_n) \nonumber \\&=\varepsilon _n \phi (z,x_n)+(1-\varepsilon _n)\phi \big (z,J^{-1}(\mu _nJu+(1-\mu _n)Jw_n)\big ) \nonumber \\&\le \varepsilon _n \phi (z,x_n) +(1-\varepsilon _n)\mu _n \phi (z,u)+ (1-\varepsilon _n)(1-\mu _n)\phi (z,w_n)\nonumber \\&\le \varepsilon _n \phi (z,x_n) +(1-\varepsilon _n)\mu _n \phi (z,u)+ (1-\varepsilon _n)(1-\mu _n)\phi (z,x_n)\nonumber \\&= (1-\varepsilon _n)\mu _n \phi (z,u)+ (1-(1-\varepsilon _n)\mu _n) \phi (z,x_n) \nonumber \\&\le (1-\varepsilon _n)\mu _n \phi (z,u) + (1-(1-\varepsilon _n)\mu _n)\Big ( \phi (z,a_n) +\tau _n\big (\phi (z,a_n)-\phi (z,a_{n-1})\big ) \nonumber \\& +\tau _n \phi (a_n,a_{n-1}) +\gamma \tau _n^2\Vert Ja_n-Ja_{n-1}\Vert ^2 \Big ) \nonumber \\&\le \max \Big \{\phi (z,u),\phi (z,a_n) +\tau _n\big (\phi (z,a_n)-\phi (z,a_{n-1})\big ) \nonumber \\& +\tau _n \phi (a_n,a_{n-1}) +\gamma \tau _n^2\Vert Ja_n-Ja_{n-1}\Vert ^2 \Big \}. \end{aligned}$$
(12)

If the maximum is \(\phi (z,u)\), we are done. Else, one can find an \(n_0\in \mathbb {N}\) such that for all \(n\ge n_0\),

$$\begin{aligned} \phi (z,a_{n+1})&\le \phi (z,a_n) +\tau _n\big (\phi (z,a_n)-\phi (z,a_{n-1})\big ) +\gamma \tau _n\Vert Ja_n-Ja_{n-1}\Vert ^2 \\&\quad +\tau _n \phi (a_n,a_{n-1}). \end{aligned}$$

By Lemma 2.8, \(\{\phi (z,a_n)\}\) has a limit. Hence, using P1, it is easy to deduce that \(\{a_n\}\) bounded. Thus, \(\{y_n\}\) and \(\{w_n\}\) are bounded.

Next, we show that \( \lim _{n\rightarrow \infty } a_n=z,\) where \(z=\Pi _\Omega u\) and \(\Pi \) is the generalized projection. Using Lemma 2.5 and Remark 1 we obtain the following estimate:

$$\begin{aligned} \phi (z,a_{n+1})&\le \varepsilon _n \phi (z,x_n)+ (1-\varepsilon _n)\phi (z,y_n)-\varepsilon _n(1-\varepsilon _n)g(\Vert Jx_n-Jy_n\Vert ) \nonumber \\&\le \varepsilon _n \phi (z,x_n)+ (1-\varepsilon _n)\mu _n\phi (z,u)+(1-\varepsilon _n)(1-\mu _n)\phi (z,w_n)\nonumber \\& -\varepsilon _n(1-\varepsilon _n)g(\Vert Jx_n-Jy_n\Vert ) \nonumber \\&\le \varepsilon _n\phi (z,x_n)+ (1-\varepsilon _n)\mu _n\phi (z,u)+(1-\varepsilon _n)(1-\mu _n) \phi (z,x_n)\nonumber \\& -\varepsilon _n(1-\varepsilon _n)g(\Vert Jx_n-Jy_n\Vert ) \nonumber \\&=(1-\varepsilon _n)\mu _n\phi (z,u) +(1-(1-\varepsilon _n)\mu _n)\phi (z,x_n) -\varepsilon _n(1-\varepsilon _n)g(\Vert Jx_n-Jy_n\Vert )\nonumber \\&=(1-\varepsilon _n)\mu _n \big (\phi (z,u)-\phi (z,x_n) \big ) + \phi (z,x_n) -\varepsilon _n(1-\varepsilon _n)g(\Vert Jx_n-Jy_n\Vert ) \nonumber \\&\le (1-\varepsilon _n)\mu _n \big (\phi (z,u)-\phi (z,x_n) \big ) + \phi (z,a_n) +\tau _n\big (\phi (z,a_n)-\phi (z,a_{n-1})\big ) \nonumber \\& +\gamma \tau _n\Vert Ja_n-Ja_{n-1}\Vert ^2 +\tau _n \phi (a_n,a_{n-1}) -\varepsilon _n(1-\varepsilon _n)g(\Vert Jx_n-Jy_n\Vert ) . \end{aligned}$$
(13)

Thus,

$$\begin{aligned} \varepsilon _n(1-\varepsilon _n)g(\Vert Jx_n-Jy_n\Vert )&\le (1-\varepsilon _n)\mu _n \big (\phi (z,u)-\phi (z,x_n) \big ) + \phi (z,a_n) -\phi (z,a_{n+1}) \nonumber \\& +\tau _n\big (\phi (z,a_n)-\phi (z,a_{n-1})\big ) +\gamma \tau _n\Vert Ja_n-Ja_{n-1}\Vert ^2 +\tau _n \phi (a_n,a_{n-1}). \end{aligned}$$
(14)

Since for any sequence in \(\mathbb {R}\), it is either monotone or one can construct a monotone subsequence from it, to complete the proof, we shall first assume there exists an \(n_0\in \mathbb {N}\) such that

$$\begin{aligned} \phi (z,a_{n+1}) \le \phi (z,a_n),~ \forall n\ge n_0. \end{aligned}$$

Then, from inequality (14), we deduce that

$$\begin{aligned} \lim _{n\rightarrow \infty } g(\Vert Jx_n-Jy_n\Vert )=0 ~\text { and thus, }~ \lim _{n \rightarrow \infty }\Vert Jx_n-Jy_n\Vert =0. \end{aligned}$$

Furthermore, observe that

$$\begin{aligned} \Vert Ja_n-Jx_n\Vert =\tau _n\Vert Ja_n-Ja_{n-1}\Vert ~\Rightarrow ~\lim _{n\rightarrow \infty } \Vert Ja_n-Jx_n\Vert =0. \end{aligned}$$

Therefore,

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert Jy_n-Ja_n\Vert =0 ~\text {and so,} ~~\lim _{n\rightarrow \infty } \Vert y_n-a_n\Vert =0. \end{aligned}$$
(15)

We will state here (without a proof to avoid unnecessary repetition) that the set of all weak limits of any subsequence of \(\{a_n\}\) is contained in \((A+B)^{-1}0\). The proof is standard, interested readers may see, e.g., page 10 of Kimura and Nakajo (2019) for this proof.

Let \(z^*\) be a weak limit of \(\{a_n\}\). Then one can find a subsequence \(\{a_{n_k}\}\subset \{a_n\}\) such that

$$\begin{aligned} \limsup _{n\rightarrow \infty } \langle a_n -z, Ju-Jz \rangle =\lim _{k \rightarrow \infty } \langle a_{n_k}-z, Ju-Jz \rangle =\langle z^*-z, Ju-Jz \rangle \le 0, \end{aligned}$$

since \(z=\Pi _\Omega u\). Thus, by (15) we deduce that

$$\begin{aligned} \limsup _{n\rightarrow \infty } \langle y_n-z, Ju-Jz \rangle \le 0. \end{aligned}$$
(16)

Now, have all the tools we need prove that \( \lim _{n\rightarrow \infty } a_n =\Pi _\Omega u\). Using Lemmas 2.5, 2.2 and 2.10, and Remark 1 we get

$$\begin{aligned} \phi (z,a_{n+1})&\le \varepsilon _n\phi (z,x_n)+(1-\varepsilon _n)\phi (z,y_n) \nonumber \\&= \varepsilon _n \phi (z,x_n)+(1-\varepsilon _n) V(z, \mu _nJu+(1-\mu _n)Jw_n) \nonumber \\&\le \varepsilon _n \phi (z,x_n)+(1-\varepsilon _n) \big ( V(z, \mu _nJu+(1-\mu _n)Jw_n-\mu _n(Ju-Jz))\nonumber \\& +2\mu _n\langle y_n-z, Ju-Jz \rangle \big )\nonumber \\&= \varepsilon _n \phi (z,x_n)+(1-\varepsilon _n) \phi (z,J^{-1}(\mu _nJz+(1-\mu _n)Jw_n)) \nonumber \\& +2(1-\varepsilon _n)\mu _n \langle y_n-z, Ju-Jz \rangle \nonumber \\&\le \varepsilon _n \phi (z,x_n)+(1-\varepsilon _n)(1-\mu _n) \phi (z,x_n) +2(1-\varepsilon _n)\mu _n \langle y_n-z, Ju-Jz \rangle \nonumber \\&=\big (1-(1-\varepsilon _n)\mu _n\big )\phi (z,x_n) +2(1-\varepsilon _n)\mu _n \langle y_n-z, Ju-Jz \rangle \nonumber \\&\le \big (1-(1-\varepsilon _n)\mu _n\big )\Big (\phi (z,a_n) +\tau _n\big (\phi (z,a_n)-\phi (z,a_{n-1})\big ) +\gamma \tau _n\Vert Ja_n-Ja_{n-1}\Vert ^2\nonumber \\& +\tau _n \phi (a_n,a_{n-1}) \Big ) +2(1-\varepsilon _n)\mu _n \langle y_n-z, Ju-Jz \rangle \end{aligned}$$
(17)
$$\begin{aligned}&\le \big (1-(1-\varepsilon _n)\mu _n\big ) \phi (z,a_n) +\gamma \tau _n\Vert Ja_n-Ja_{n-1}\Vert ^2 +\tau _n \phi (a_n,a_{n-1}) \nonumber \\& +2(1-\varepsilon _n)\mu _n \langle y_n-z, Ju-Jz \rangle \end{aligned}$$
(18)

By Lemma 2.6, we deduce from (18) that \( \lim _{n\rightarrow \infty }\phi (z,a_n)=0.\) Which implies that \( \lim _{n\rightarrow \infty } a_n=z\) as a consequence of Lemma 2.4.

If the assumption above is false for the sequence \(\{a_n\}\) then necessarily, one can find a subsequence \(\{a_{m_j}\}\subset \{a_n\}\) such that

$$\begin{aligned} \phi (z,a_{m_j+1}) >\phi (z,a_{m_j}),~~\forall j\in \mathbb {N}. \end{aligned}$$

By Lemma 2.7, we have that

$$\begin{aligned} \phi (z,a_{m_k})\le \phi (z,a_{m_k+1}) ~~\text {and}~~ \phi (z,a_k)\le \phi (z,a_{m_k+1}),~\forall k\in \mathbb {N}. \end{aligned}$$

From inequality (14), using this index \(\{m_k\}\subset \mathbb {N}\) we have

$$\begin{aligned} \varepsilon _{m_k}(1-\varepsilon _{m_k})g(\Vert Jx_{m_k}-Jy_{m_k}\Vert )&\le (1-\varepsilon _{m_k})\nu _{m_k} \big (\phi (z,u)-\phi (z,x_{m_k}) \big )\\&\quad + \phi (z,a_{m_k}) -\phi (z,a_{m_k+1}) +\tau _{m_k}\big (\phi (z,a_{m_k})-\phi (z,a_{n-1})\big )\\&\quad +\gamma \tau _{m_k}\Vert Ja_{m_k}-Ja_{n-1}\Vert ^2 {\textbf {}}+\tau _{m_k} \phi (a_{m_k},a_{m_k-1}). \end{aligned}$$

If follows using same argument as we did above that

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert y_{m_k}-a_{m_k}\Vert =0, ~\text { and } ~\limsup _{k\rightarrow \infty } \langle y_{m_k}-z, Ju-Jz \rangle \le 0. \end{aligned}$$

From inequality (17), we get

$$\begin{aligned} \phi (z,a_{m_k+1})&\le \big (1-(1-\varepsilon _{m_k})\mu _{m_k}\big )\Big (\phi (z,a_{m_k}) +\tau _{m_k}\big (\phi (z,a_{m_k})-\phi (z,a_{m_k-1})\big ) \nonumber \\& +\gamma \tau _{m_k}\Vert Ja_{m_k}-Ja_{m_k-1}\Vert ^2 +\tau _{m_k} \phi (a_{m_k},a_{m_k-1}) \Big ) \nonumber \\&+2(1-\varepsilon _{m_k})\mu _{m_k} \langle y_{m_k}-z, Ju-Jz \rangle \nonumber \\&\le \big (1-(1-\varepsilon _{m_k})\mu _{m_k}\big )\phi (z,a_{m_k}) +\tau _{m_k}\big (\phi (z,a_{m_k})-\phi (z,a_{m_k-1})\big ) \nonumber \\& +\gamma \tau _{m_k}\Vert Ja_{m_k}-Ja_{m_k-1}\Vert ^2 +\tau _{m_k} \phi (a_{m_k},a_{m_k-1}) \nonumber \\&+2(1-\varepsilon _{m_k})\mu _{m_k} \langle y_{m_k}-z, Ju-Jz \rangle . \end{aligned}$$
(19)

By Lemma 2.6, we deduce from (19) that \( \lim _{k\rightarrow \infty } \phi (z,a_{m_k})=0\). Thus,

$$\begin{aligned} \limsup _{k\rightarrow \infty } \phi (z,a_k) \le \lim _{k\rightarrow \infty } \phi (z,a_{m_k+1})=0. \end{aligned}$$

Therefore \( \limsup _{k\rightarrow \infty } \phi (z,a_k)=0\) and so, by Lemma 2.4, \( \lim _{k\rightarrow \infty } a_k=z\). This completes the proof. \(\square \)

4 An application and a numerical example

The goal of image recovery techniques is to restore an original image from a degraded observation of it. The convex optimization associated with image recovery problem is

$$\begin{aligned} \text {find } ~u\in H ~~\text { with }~~ u\in \mathop {\arg \min }\limits _{x \in H} f(x), \end{aligned}$$
(20)

where f is a convex differentiable functional on a real Hilbert space H. Since the solution may vary for any degraded image, problem (20) inherits ill-posedness. To restore well-posedness, regularization techniques are employed. That is, one can obtain a stable solution by introducing a regularization term in (20) to get the following problem:

$$\begin{aligned} \text {find } ~u\in H ~~\text { with }~~ u\in \mathop {\arg \min }\limits _{x \in H} \big (f(x)+ \nu g(x)\big ) , \end{aligned}$$

where \(\nu >0\) is a regularization parameter and g is a regularization function which maybe smooth or nonsmooth. In this work, we consider the classical image recovery problem which is modeled by

$$\begin{aligned} b =L x + w, \end{aligned}$$
(21)

where \( x, \,w\) and b are original image, noise and observed image, respectively, and L is a linear map. Problem (21) is ill-posed due to the nature of L. We will use the \(l_1\)-regularizer to solve problem (21) via the model

$$\begin{aligned} \mathop {\arg \min }\limits _{x \in \mathbb {R}^n} \Big ( \frac{1}{2}\Vert Lx-b\Vert ^2+\nu \Vert x\Vert _1\Big ). \end{aligned}$$
(22)

By setting \(Ax:=\nabla (\dfrac{1}{2}\Vert Lx-b\Vert ^2)=L^T(Lx-b)\) and \(Bx:=\partial (\nu \Vert x\Vert _1)\). Thus, a zero of \((Ax+Bx)\) is an equivalent solution of (22). Hence, we will use algorithm (3) of Shehu (2019), (4) of Kimura and Nakajo (2019) and our proposed algorithm (11) to find a solution of (22).

In our numerical experiments, we used the MATLAB blur function “P=fspecial(’motion’,30,40)” and added random noise. In algorithm (3) of Shehu (2019), we set \(x_1=L x + w\) and \(\nu _n= 0.0001\) and \(\alpha _n=\frac{1}{n+1}\), in algorithm (4) of Kimura and Nakajo (2019), we set \(\nu _n=0.00001\), \(\gamma _n=\frac{1}{n+1}\), u to be zeros, \(x_1=L x + w\). In our proposed algorithm (11) we choose \(\tau _n=0.95\), \(\nu _n=0.0001\) \(\mu _n=\frac{1}{10n+1}\) \(\varepsilon _n=\frac{n}{n+1}\), \(x_0\) to be zeros, \(u=x_1=L x + w\). Finally, we used a tolerance of \(10^{-5}\) and maximum number of iterations (n) to be 100, for all the algorithms. The original test images (Abubakar, Barbra, Abdulkarim) their degradation and restoration via algorithms (3), (4) and (11) are presented in Fig. 1.

Fig. 1
figure 1

Restoration process via algorithms (3), (4) and (11)

Full size image

Key to Fig. 1. In Fig. 1, the first column presents the original test images followed by the distortion via random noise and motion blur. In the third, fourth and fifth columns, the restored test images via algorithms (3), (4) and (11) are presented, respectively.

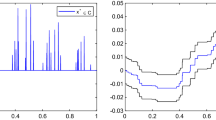
Observe that it will not be easy for one to tell which algorithm performed better in the restoration process from Fig. 1. To distinguish the performance of the algorithms, we use the signal to noise ratio (SNR). It is defined as:

$$\begin{aligned} \text {SNR}:= 10\log \frac{\Vert x\Vert ^2}{\Vert x-x_n\Vert }, \end{aligned}$$

where x is the test image and \(x_n\) is its estimate. Using SNR performance metric, the higher the SNR value for a restored image, the better the restoration process via the algorithm. In Table 1 and Fig. 2, we present the performances of algorithms (3), (4) and our proposed algorithm (11) in restoring the test images.

Table 1 SNR values for the restored Abubakar, Abdulkarim and Barbra images in Fig. 1
Full size table
Fig. 2
figure 2

Graphical illustrations of the SNR values present in Table 1

Full size image

Example 1

(An Example in \(l_{\frac{3}{2}}(\mathbb {R})\)) Consider the subspace of \(l_{\frac{3}{2}}(\mathbb {R})\) defined by

$$\begin{aligned} M_k(\mathbb {R}):=\{ x\in l_{\frac{3}{2}}(\mathbb {R}) : x=(x_1,x_2,x_3,\ldots , x_k,0, 0,0, \ldots ) \},~~\text { for some } k\ge 1. \end{aligned}$$

Let \(k=3\). Let \(A: M_3(\mathbb {R}) \rightarrow M_3^*(\mathbb {R})\) and \(B: M_3(\mathbb {R}) \rightarrow M_3^*(\mathbb {R})\) be defined by

$$\begin{aligned} Ax:=4x+(3,2,1, 0, 0, \ldots )\quad \text { and } \quad Bx:=2x. \end{aligned}$$

It is not difficult to verify that A is \(\frac{1}{4}\)-inverse strongly monotone and B is maximal monotone. Furthermore, observe that A is also 4-Lipschitz continuous. In addition, the solution set \(\Omega =\{ (-0.5,-0.333,-0.166, 0, 0, \ldots ) \}\). In algorithm (3) of Shehu (2019), we set \(\alpha _n=\frac{1}{10,000n+1}\), in algorithm (4) of Kimura and Nakajo (2019), we set \(\gamma _n=\frac{1}{10,000n+1}\), in our proposed algorithm (11), we set \(\tau =0.001\), \(\tau _n=\bar{\tau _n}\), \(\sigma _n=\frac{1}{(n+1)^3}\) and \(\mu _n=\frac{1}{10,000n+1}\). We set u to be zeros in \(M_3(\mathbb {R})\), \(a_0=(0,1,4,0,0,0, \ldots ),\) \(a_1=(4,0,2,0,0,0, \ldots )\). We set maximum number of iterations \(n=300\) and tolerance to be \(10^{-5}\). Finally, we study the behaviour of the algorithms as we vary the values of \(v_n\) (see, Table 2).

Table 2 Numerical results for Example 1
Full size table

5 Discussion

From the results of presented in Table 2, we observe that the choice of \(\nu _n=0.1\) gave the best approximation for algorithm (3) of Shehu (2019). While for algorithm (4) of Kimura and Nakajo (2019) the choice of \(\nu _n=0.3\) gave the best approximation. Finally, the choice of \(v_n=0.6\) or \(v_n=0.7\) gave the best approximation for our proposed algorithm (11). In this experiment, we saw that the step-size \(\nu _n\) has a great influence in approximating the solution for each algorithm. However, for the best choice of \(v_n\) with respect to each algorithm, our proposed algorithm (11) has the least number of iterations compared to algorithm (3) of Shehu (2019) and algorithm (4) of Kimura and Nakajo (2019).

6 Conclusion

This work presents a new inertial Halpern-type algorithm for solving problem (1) in certain Banach spaces. The proposed method was used in the restoration process of some distorted images. Furthermore, a numerical example in \(l_{\frac{3}{2}}(\mathbb {R})\) is presented to support the main theorem. Finally, the performance of the proposed algorithm is compared with that of some existing algorithms and from the simulations presented in Figs. 1 and 2, and Tables 1 and 2, the proposed algorithm appears to be competitive and promising.