An Augmented Lagrangian algorithm for nonlinear semidefinite programming applied to the covering problem

Abstract

In this work, we present an Augmented Lagrangian algorithm for nonlinear semidefinite problems (NLSDPs), which is a natural extension of its consolidated counterpart in nonlinear programming. This method works with two levels of constraints; one that is penalized and other that is kept within the subproblems. This is done to allow exploiting the subproblem structure while solving it. The global convergence theory is based on recent results regarding approximate Karush–Kuhn–Tucker optimality conditions for NLSDPs, which are stronger than the usually employed Fritz John optimality conditions. Additionally, we approach the problem of covering a given object with a fixed number of balls with a minimum radius, where we employ some convex algebraic geometry tools, such as Stengle’s Positivstellensatz and its variations, which allows for a much more general model. Preliminary numerical experiments are presented.

1 Introduction

Augmented Lagrangian methods for nonlinear semidefinite programming that consider quadratic penalty and modified barrier functions have already been introduced in Wu et al. (2013) and Kočvara and Stingl (2003), respectively. Convergence theories of both methods rely on constraint qualifications such as the constant positive linear dependence (CPLD), Mangasarian–Fromovitz constraint qualification (MFCQ), or non-degeneracy. The Augmented Lagrangian method introduced in the present work extends the results presented in Wu et al. (2013), Kočvara and Stingl (2003) using the sequential optimality condition introduced in Andreani et al. (2017b), that does not require the use of constraint qualifications.

Sequential optimality conditions (Andreani et al. 2011) have played a major role in extending and unifying global convergence results for several classes of algorithms for nonlinear programming and other classes of problems. In particular, we present a more general version of the algorithm from Andreani et al. (2017b) by allowing arbitrarily constrained subproblems in the Augmented Lagrangian framework. Namely, instead of penalizing all the constraints, we assume that the constraints can be divided in two sets: one set of constraints that will be penalized and other that will be kept as constraints for the subproblems. Allowing constrained subproblems is an important algorithmic feature due to the ability to explore good subproblem solvers. See Andreani et al. (2008a) and Birgin et al. (2018). We introduce this algorithm with a clear application in mind namely the so-called covering problem, where a new model based on convex algebraic geometry tools is introduced.

The covering problem consists of finding the centers and the minimal common radius of m balls whose union covers a given compact set. This problem has several applications, such as finding the optimal broadcast tower distribution over a region or the optimal allocation of Wi-Fi routers in a building, for example. Some specific cases have been attacked and solved in the last few decades non-algorithmically, but using results from linear algebra and discrete mathematics instead; for example, Gáspár and Tarnai (1995) presented minimal coverings of a square with up to ten circles. Their results were generalized for rectangles by Heppes and Melissen (1997), when they found the best coverings of a rectangle with up to five equal circles and also, under some conditions, with seven circles as well. Then, Melissen and Schuur 2000 extended those results for six and seven circles, following their previous work (Melissen and Schuur 1996). In the same year, Nurmela and Östergård (2000) presented numerical approximations of circle coverings for a square with up to 30 equal circles, improving some of the previous ones until then. Covering a unit circle with another set of n circles has been a matter of deep study for many years. Bezdek is responsible for proving coverings for $n=5$ and $n=6$ (in Bezdek 1979, 1983) and the result is somewhat trivial for $n\in \{1,2,3,4,7\}$. Then, coverings of a unit circle with other eight, nine, and ten circles were presented by Fejes Tóth (2005). Melissen and Nurmela have also provided coverings with up to 35 circles (see Melissen 1997; Nurmela 1998). Gáspár et al. (2014a, b) published a broad paper in which they discuss recently developed techniques used to pursuit a slight variation of the covering problem, where the radius is fixed.

Among the algorithmic approaches, we highlight the one introduced by Demyanov (1971), that approximates the compact set to be covered by a finite set of points (a process often called “discretization”) and then applies a point covering algorithm. Usually, the whole procedure leads to a min–max–min formulation, which needs further treatment, such as smoothing. Xavier and Oliveira 2005 employed the hyperbolic smoothing method to treat the min-max-min model for two-dimensional circle coverings, and in 2014, their work was extended to three-dimensional sphere coverings by Venceslau et al. (2014). They obtained satisfactory results in practice, but discretizing a set is a laborous task itself and the quality of the approximation bounds the quality of the solution.

Our approach is intended to be an alternative that aims to avoid discretizations, i.e., an exact formulation of the problem, where we characterize a feasible covering by means of auxiliary semidefinite variables relying on a Positivstellensatz theorem.

In our model, only equality constraints will be penalized, hence avoiding eigenvalue computations in evaluating the Augmented Lagrangian function, while the (linear) semidefinite constraints will be kept within the subproblems. Thus, eigenvalues are computed to project onto the semidefinite cone in the application of the Spectral Projected Gradient method (Birgin et al. 2000) for solving the subproblems. Numerical experiments are still very preliminary, as the complexity of the model increases rapidly with the increase of the degree of a polynomial needed in the formulation. However, we illustrate the generality of the model by solving the problem of covering a heart-shaped figure.

In Sect. 2, we give some preliminaries on sequential optimality conditions; in Sect. 3, we define our Augmented Lagrangian algorithm and prove its global convergence. In Sect. 4, we give our model to the covering problem. In Sect. 5, we show our numerical experiments, and in Sect. 6, we give some conclusions.

Notation: ${\mathbb {R}}$ is the set of real numbers, while ${\mathbb {R}}_+$ is the set of non-negative real numbers. ${\mathbb {S}}^{m}$ is the set of symmetric $m\times m$ matrices over ${\mathbb {R}}$. ${\mathbb {S}}^{m}_{+}$ (correspondently, ${\mathbb {S}}^{m}_{-}$) is the set of positive (negative) semidefinite $m\times m$ matrices over ${\mathbb {R}}$, and we denote $A\in {\mathbb {S}}^m_+$ ($A\in {\mathbb {S}}^m_{-}$) by $A\succeq 0$ ($A\preceq 0$). ${{\,\mathrm{tr}\,}}(A)$ denotes the trace of the matrix A. $\langle A, B\rangle :={{\,\mathrm{tr}\,}}(AB)$ is the standard inner product over ${\mathbb {S}}^{m}$, and $\Vert A\Vert :=\sqrt{\langle A,A\rangle }$ is the Frobenius norm on ${\mathbb {S}}^m$. $[a]_+:=\max \{0, a\},a\in {\mathbb {R}}$.

2 Preliminaries

In this section, we introduce the notation that will be adopted throughout the paper. We also formally present the nonlinear semidefinite programming problem, together with recently introduced optimality conditions. Let us consider the following problem:

$$\begin{aligned} \begin{aligned}&\underset{x \in {\mathbb {R}}^{n}}{\text {Minimize}}&f(x), \\&\text {subject to}&G(x) \preceq 0, \end{aligned} \end{aligned}$$

(1)

where $f: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}$ and $G: {\mathbb {R}}^{n}\rightarrow {\mathbb {S}}^{m}$ are continuously differentiable functions. The set ${\mathscr {F}}$ will denote the feasible set ${\mathscr {F}} := \{x\in {\mathbb {R}}^n\mid G(x)\preceq 0\}$. Throughout this paper, $G(x) \preceq 0$ will be called a semidefinite constraint and we will consider this simplified version of an NLSDP where the equality constraints are omitted without loss of generality. Given a matrix $A\in {\mathbb {S}}^m$, let $A=U\Lambda U^T$ be an orthogonal diagonalization of A, where $\Lambda ={{\textsf {diag}}}(\lambda _{1}^{U}(A), \dots ,\lambda _{m}^{U}(A) )$ is a diagonal matrix and $\lambda _{i}^{U}(A)$ is the eigenvalue of A at position i when A is orthogonally diagonalized by U. We omit U when the eigenvalues considered in the diagonalization of A are in ascending order, namely, $\lambda _1(A)\le \dots \le \lambda _m(A)$. The projection of A onto ${\mathbb {S}}^{m}_{+}$, denoted by $[A]_{+}$, is given by

$$\begin{aligned}{}[A]_{+}:=U {{\textsf {diag}}} ([\lambda _{1}^{U}(A)]_{+}, \dots , [\lambda _{m}^{U}(A)]_{+})U^{T}, \end{aligned}$$

and is independent of the choice of U. The derivative operator of the mapping $G: {\mathbb {R}}^{n} \rightarrow {\mathbb {S}}^{m}$ at a point $x \in {\mathbb {R}}^{n}$ is given by $DG(x): {\mathbb {R}}^{n} \rightarrow {\mathbb {S}}^{m}$, defined by

$$\begin{aligned} DG(x)h:= \displaystyle \sum _{i=1}^{n}G_{i}(x)h_{i}, \ h \in {\mathbb {R}}^{n}, \end{aligned}$$

where

$$\begin{aligned} G_{i}(x):=\displaystyle \frac{\partial G(x)}{\partial x_{i} } \in {\mathbb {S}}^{m},\quad i=1, \dots ,m \end{aligned}$$

are the partial derivative matrices with respect to $x_i$. In addition, its adjoint operator is given by $DG(x)^{*}: {\mathbb {S}}^{m} \rightarrow {\mathbb {R}}^{n}$ with

$$\begin{aligned} DG(x)^{*}\Omega := (\langle G_{1}(x), \Omega \rangle , \dots , \langle G_{n}(x), \Omega \rangle )^{T}, \end{aligned}$$

where $\Omega \in {\mathbb {S}}^{m}.$ We denote the Lagrangian function at $(x,\Omega ) \in {\mathbb {R}}^{n}\times {\mathbb {S}}^{m}_{+}$ by

$$\begin{aligned} L(x,\Omega ):= f(x)+\langle G(x) ,\Omega \rangle \end{aligned}$$

and the generalized Lagrangian function at $(x,\lambda ,\Omega ) \in {\mathbb {R}}^{n}\times {\mathbb {R}}_+\times {\mathbb {S}}^{m}_{+}$ by

$$\begin{aligned} L^{g}(x,\lambda ,\Omega ):= \lambda f(x)+\langle G(x) ,\Omega \rangle . \end{aligned}$$

In general, we use iterative algorithms for solving the nonlinear semidefinite programming problem (Kočvara and Stingl 2003, 2010; Huang et al. 2006; Wu et al. 2013; Luo et al. 2012; Yamashita and Yabe 2015). These algorithms must be able to identify good solution candidates for (1). By “good candidates”, we mean points that satisfy some necessary optimality condition. For instance, the Fritz John (FJ) necessary optimality condition states that whenever ${\bar{x}}\in {\mathbb {R}}^{n}$ is a local minimizer of (1), there exist the so-called Fritz John multipliers $(\lambda ,\Omega )\in {\mathbb {R}}_+\times {\mathbb {S}}^{m}_{+}$, with $\lambda +\Vert \Omega \Vert \ne 0,$ such that

$$\begin{aligned} \nabla _x L^{g}({\bar{x}},\lambda ,\Omega )=0 \text{ and } \langle \Omega , G({\bar{x}})\rangle =0. \end{aligned}$$

(2)

Note that, in the particular case of $\lambda =1$, the Fritz John condition coincides with the Karush–Kuhn–Tucker (KKT) condition for NLSDPs. Although Fritz John is a useful optimality condition, there are some disadvantages in its use, for instance, the multiplier associated with the objective function may vanish. In this case, the Fritz John condition would not be very informative, as it would not depend on the objective function. The possibility of the multiplier associated with the objective function vanishing can be avoided assuming that the Mangasarian–Fromovitz constraint qualification (MFCQ) holds (also called Robinson’s CQ in the context of NLSDPs). We say that ${\bar{x}}\in {\mathscr {F}}$ satisfies MFCQ if there exists a vector $h\in {\mathbb {R}}^{n}$, such that $G({\bar{x}})+DG({\bar{x}})h$ is negative definite (Bonnans and Shapiro 2000). Hence, the FJ optimality condition under the additional assumption that MFCQ holds implies that the KKT condition is satisfied. That is, under MFCQ, every Fritz John multiplier is also a Lagrange multiplier. In fact, one can prove that FJ is equivalent to the optimality condition “KKT or not-MFCQ”.

Most global convergence results for NLSDP methods assume that the problem satisfies MFCQ and proves that any feasible limit point of a sequence generated by the algorithm satisfies the KKT condition. That is, feasible limit points of sequences generated by it satisfy the FJ optimality condition. In this paper, we will present an Augmented Lagrangian algorithm with global convergence to an optimality condition strictly stronger than FJ. This optimality condition is the Approximate Karush–Kuhn–Tucker (AKKT) condition, which was defined for NLSDPs in Andreani et al. (2017b) and is well known in nonlinear programming (Andreani et al. 2011; Qi and Wei 2000). As the FJ condition, AKKT is an optimality condition without the need of assuming a constraint qualification. Instead of considering the punctual verification of the KKT condition at a point ${\bar{x}}$, one allows its approximate verification at a sequence $x^k\rightarrow {\bar{x}}$ with a corresponding (possibly unbounded) dual sequence $\{\Omega ^k\}\subset {\mathbb {S}}^m_+$.

The formal definition is as follows:

Definition 2.1

[AKKT, Andreani et al. (2017b)] The feasible point ${\bar{x}} \in {\mathscr {F}}$ of (1) satisfies the Approximate Karush–Kuhn–Tucker (AKKT) condition if there exist sequences $x^{k} \rightarrow {\bar{x}}$, $\{\Omega ^{k}\} \subset {\mathbb {S}}^{m}_{+}$ and $k_0\in {\mathbb {N}}$, such that

$$\begin{aligned}&\nabla f(x^{k})+ DG(x^{k})^{*}\Omega ^{k} \rightarrow 0, \end{aligned}$$

(3)

$$\begin{aligned}&\lambda ^U_{i}(G({\bar{x}}))<0 \Rightarrow \lambda ^{S_{k}}_{i}(\Omega ^{k})=0, \text{ for } \text{ all } i=1,\dots ,m \text{ and } k\geqslant k_0, \end{aligned}$$

(4)

where

$$\begin{aligned} G({\bar{x}})=U{{\textsf {diag}}}(\lambda ^{U}_{1}(G( {\bar{x}})), \dots ,\lambda ^{U}_{m}( G({\bar{x}})))U^{T} \end{aligned}$$

and

$$\begin{aligned} \Omega ^{k}=S_{k}{{\textsf {diag}}}(\lambda ^{S_{k}}_{1}( \Omega ^{k}), \dots ,\lambda _{m}^{S_{k}}(\Omega ^{k}))S_{k}^{T}, \end{aligned}$$

with U and $S_k$ orthogonal matrices, such that $S_k \rightarrow U$.

The importance of the AKKT condition in the nonlinear programming literature is due to the large amount of the first- and second-order algorithms that generate AKKT sequences, thus extending global convergence results under constraint qualifications strictly weaker than MFCQ (Andreani et al. 2008b, 2012a, b, 2016a, b, 2017a, c, 2018a, b; Birgin and Martínez 2014; Birgin et al. 2016, 2018, 2017; Dutta et al. 2013; Haeser 2018; Haeser and Melo 2015; Haeser and Schuverdt 2011; Martínez and Svaiter 2003; Minchenko and Stakhovski 2011; Tuyen et al. 2017).

The definition of AKKT for nonlinear semidefinite programming is not straightforward from the definition known in nonlinear programming. A key difference is that the approximate constraint matrix $G(x^k)$ and the Lagrange multiplier approximation $\Omega ^k$ must be approximately simultaneously diagonalizable (this is the role of $S_k\rightarrow U$ in the definition), which is necessary for pairing the corresponding eigenvalues.

To explain the relevance of Definition 2.1, let us say that an AKKT sequence $\{x^k\}$ is known, converging to an AKKT point ${\bar{x}}$, with a corresponding dual sequence $\{\Omega ^k\}$, generated by an algorithm. A usual global convergence result would be to say that ${\bar{x}}$ is an FJ point, by dividing (3) by $\Vert \Omega ^k\Vert$ and taking the limit. The corresponding FJ multiplier $(\lambda ,\Omega )$ may be such that $\lambda =0$ provided that $\{\Omega ^k\}$ is unbounded. To avoid this situation and arrive at a KKT point, one usually assumes that MFCQ holds. This is equivalent to saying that no FJ multiplier with $\lambda =0$ may exist. By employing the AKKT condition, one may allow the existence of FJ multipliers with $\lambda =0$ (that is, MFCQ may fail) while still being able to take the limit in (3) and proving that ${\bar{x}}$ is a KKT point (under a constraint qualification weaker than MFCQ). This is the case, for instance, when $\{\Omega ^k\}$ is bounded. Or, even in the unbounded case, one may be able to rewrite (3–4) with a different sequence $\{{\tilde{\Omega }}^k\}$ in place of $\{\Omega ^k\}$, allowing the proof that ${\bar{x}}$ is a KKT point. See Andreani et al. (2017b). Note that the FJ condition is meaningful with respect to the objective function (that is, implies KKT) only when the set of Lagrange multipliers is bounded (that is, MFCQ holds), while AKKT may imply KKT even when the set of Lagrange multipliers is unbounded. Note also that boundedness or unboundedness of the Lagrange multiplier set at ${\bar{x}}$ does not correspond, respectively, to the boundedness or unboundedness of the dual sequence $\{\Omega ^k\}$, as this sequence may be bounded even when the set of Lagrange multipliers is unbounded [see, for instance, Bueno et al. (2019); Haeser et al. (2017)].

We summarize by noting that the following properties give the main reasons for using AKKT in our global convergence results:

Theorem 2.2

(Andreani et al. 2017b) Let ${\bar{x}}$ be a local minimizer of (1). Then, ${\bar{x}}$ satisfies AKKT.

Theorem 2.3

(Andreani et al. 2017b) Let ${\bar{x}}$ be a feasible point of (1). If ${\bar{x}}$ satisfies AKKT, then ${\bar{x}}$ satisfies the FJ condition. The reciprocal is not true.

Usually, when proving that feasible limit points of a sequence generated by an algorithm satisfy AKKT, the sequences $\{x^k\}$ and $\{\Omega ^k\}$ are explicitly generated by the algorithm. Hence, one may safely use these sequences for stopping the execution of the algorithm. Given small tolerances $\epsilon _\mathrm{opt}>0$, $\epsilon _\mathrm{feas}>0$, $\epsilon _\mathrm{diag}>0$ and $\epsilon _\mathrm{compl}>0$, one may stop at iteration k when

$$\begin{aligned}&\Vert \nabla f(x^{k})+ DG(x^{k})^{*}\Omega ^{k} \Vert \le \epsilon _\mathrm{opt}, \end{aligned}$$

(5)

$$\begin{aligned}&\Vert [G(x^{k})]_{+} \Vert \le \epsilon _\mathrm{feas},\end{aligned}$$

(6)

$$\begin{aligned}&\Vert U_{k}-S_{k}\Vert \le \epsilon _\mathrm{diag},\end{aligned}$$

(7)

$$\begin{aligned}&\lambda ^{U_{k}}_{i}(G(x^k))<-\epsilon _\mathrm{compl} \Rightarrow \lambda ^{S_{k}}_{i}(\Omega ^{k})=0, i=1,\ldots ,m. \end{aligned}$$

(8)

For simplicity, we say that $x^k$ satisfies the $\epsilon$-KKT stopping criterion when (5)–(8) hold with $\epsilon _\mathrm{opt}=\epsilon _\mathrm{feas}=\epsilon _\mathrm{diag}=\epsilon _\mathrm{compl}=\epsilon \ge 0$. In this case, the point $x^k$ together with a corresponding $\Omega ^k, U_k$ and $S_k$ will be called an $\epsilon$-KKT point. A point that satisfies the stopping criterion with $\epsilon =0$ is precisely a KKT point, see Andreani et al. (2017b). Note that, from the compactness of the set of orthogonal matrices, we can take, if necessary, a subsequence of the orthogonal matrices’ sequence $\{U_{k}\}$ that converges to U and define it as the original sequence. Thus, the limit $\Vert U_{k}-S_{k}\Vert \rightarrow 0$ implies that $U_{k}\rightarrow U$ and $S_{k}\rightarrow U$. Since $\{\Omega ^{k}\}$ does not need to have a convergent subsequence, the inequality given by (7) expresses only a correspondence relation for pairing the eigenvalues of $G(x^{k})$ and $\Omega ^{k}$.

We refer the reader to Andreani et al. (2017b) for a detailed measure of the strength of AKKT, in comparison with FJ, together with a characterization of the situation in which an AKKT point is in fact a KKT point. Also, we note that the developments of this paper could be done with a different optimality condition presented in Andreani et al. (2017b) (Trace-AKKT), which gives a simpler stopping criterion than (5)–(8); however, an additional smoothness assumption on the function G would be needed, which we have decided to avoid for simplicity.

3 An Augmented Lagrangian algorithm

Let us consider the following problem:

$$\begin{aligned}&\underset{x \in {\mathbb {R}}^{n}}{\text {Minimize}} \quad f(x), \nonumber \\&\text {subject to} \quad \quad x \in {\mathscr {F}}_{u}\cap {\mathscr {F}}_{l}, \end{aligned}$$

(9)

where

$$\begin{aligned} {\mathscr {F}}_{u}:=\{x \in {\mathbb {R}}^{n}| \ G_{1}(x)\preceq 0\} \end{aligned}$$

is the set of constraints in the upper level and

$$\begin{aligned} {\mathscr {F}}_{l}:=\{x \in {\mathbb {R}}^{n}| \ G_{2}(x)\preceq 0\} \end{aligned}$$

the set of constraints in the lower level. We assume that $f: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}$, $G_{1}: {\mathbb {R}}^{n}\rightarrow {\mathbb {S}}^{m}$ and $G_{2}: {\mathbb {R}}^{n}\rightarrow {\mathbb {S}}^{{\overline{m}}}$ are all continuously differentiable functions.

The choice of which constraints will go to the upper level and which ones will stay in the lower level can be done arbitrarily. Nevertheless, the two-level minimization technique is used, in general, when some constraints are somewhat “easier” than the others. These constraints should be kept at the lower level, which will not be penalized. On the other hand, the difficult constraints will be maintained at the upper level; that is, they will be penalized with the use of the Powell–Hestenes–Rockafellar (PHR) Augmented Lagrangian function for NLSDPs. Since we do not restrict ourselves to which class of constraints will be kept at the lower level and which ones will be penalized, we will be considering a large class of Augmented Lagrangian algorithms. More details of this technique applied to nonlinear optimization problems can be found in Andreani et al. (2008a), Birgin and Martínez (2014), and Birgin et al. (2018). If the problem has, in addition, equality constraints, they may also be arbitrarily split in the upper and lower level sets, and the algorithm and its global convergence proof can be carried out with the necessary modifications. In particular, this is the technique which we used in our numerical experiments regarding the covering problem (more details in Sect. 5). Alternatively, one may incorporate an equality constraint $h(x)=0$ as the diagonal block:

$$\begin{aligned} \left( \begin{array}{ll}h(x)&{}0\\ 0&{}-h(x)\end{array}\right) \preceq 0. \end{aligned}$$

Note that the optimality condition AKKT is independent of the formulation, while the FJ optimality condition becomes trivially satisfied at all feasible points when an equality constraint is treated as a negative semidefinite block matrix (Andreani et al. 2017b). Next, we will present an Augmented Lagrangian method for NLSDPs based on the quadratic penalty function. This is an extension of the algorithm defined in Andreani et al. (2017b), where only unconstrained subproblems were considered. For more details about the Augmented Lagrangian method for NLSDPs, see Andreani et al. (2008a), Kočvara and Stingl (2003), Kočvara and Stingl (2010), Huang et al. (2006), Sun et al. (2006, 2008), Wu et al. (2013), and Yamashita and Yabe (2015).

Let us take a penalty parameter $\rho >0$. The Augmented Lagrangian function $L_\rho :{\mathbb {R}}^n\times {\mathbb {S}}^m\rightarrow {\mathbb {R}}$, a natural extension of the Augmented Lagrangian function for nonlinear programming, penalizes the constraints at the upper level and is defined below:

$$\begin{aligned} L_\rho (x, \Omega ):=f(x)+\displaystyle \frac{1}{2\rho } \left\{ \Vert [\Omega +\rho G_{1}(x) ]_{+} \Vert ^{2} - \displaystyle \Vert \Omega \Vert ^{2} \right\} . \end{aligned}$$

(10)

The gradient with respect to x of the Augmented Lagrangian function above is given by:

$$\begin{aligned} \nabla _{x} L_\rho (x, \Omega )= \nabla f(x)+ DG_{1}(x)^{*} \left[ \Omega +\rho G_{1}(x) \right] _{+}. \end{aligned}$$

The formal statement of the algorithm is as follows:

Note that, in Step 3 of the algorithm above, we take the Lagrange multiplier approximation for the next subproblem as the projection of the natural update of $\Omega ^k$ onto a “safeguarded box” as in Birgin and Martínez (2014). This means that when the penalty parameter is too large, the method reduces to the external penalty method. The penalty parameter is updated using the joint measure of feasibility and complementarity for the conic constraint defined by $V^k$. Note that $V^{k}=0$ implies the sequence $x^{k}$ is feasible and the complementarity condition holds. Therefore, if $\Vert V^k\Vert$ is sufficiently reduced, the algorithm keeps the previous penalty parameter unchanged and increases it otherwise. In Step 1, we assume that an unspecified algorithm for solving the subproblem (11) returns an $\epsilon _k$-KKT point at each iteration k, where $\epsilon _k$ is the tolerance for stopping the execution of the subproblem solver. Taking into account our global convergence results, a natural stopping criterion for Algorithm 1 is to stop when $x^k$ and the corresponding dual approximations satisfy $\epsilon$-KKT for the original problem (9), for some $\epsilon >0$.

Let us show that the algorithm tends to find feasible points. Namely, the following result shows that Algorithm 1 finds AKKT points of an infeasibility measure of the upper level constraints restricted to the lower level constraints.

Theorem 3.1

Let $\epsilon _{k}\rightarrow 0^+$. Assume that ${\bar{x}}\in {\mathbb {R}}^n$ is a limit point of a sequence $\{x^{k}\}$ generated by Algorithm 1. Then, ${\bar{x}}$ is an AKKT point of the infeasibility optimization problem:

$$\begin{aligned} \begin{aligned}&\underset{x \in {\mathbb {R}}^{n}}{ \text {Minimize}}&P(x):=\Vert [G_{1}(x)]_{+}\Vert ^2 \text{ subject } \text{ to } x \in {\mathscr {F}}_{l}. \end{aligned} \end{aligned}$$

(12)

Proof

Since $x^{k}$ is an $\epsilon _{k}$-KKT sequence, from (11), we have that

$$\begin{aligned} \Vert \nabla _x L_{\rho _{k}}(x^{k},\Omega ^{k})+DG_{2}(x^{k})^{*}{\underline{\Omega }}^{k}\Vert \le \epsilon _{k}, \end{aligned}$$

(13)

$$\begin{aligned} \Vert [G_{2}(x^{k})]_{+}\Vert \le \epsilon _{k},\end{aligned}$$

(14)

$$\begin{aligned} \Vert U_{k}-S_{k}\Vert \le \epsilon _{k},\end{aligned}$$

(15)

$$\begin{aligned} \lambda ^{U_{k}}_{i}( G_{2}(x^{k}))\le -\epsilon _{k} \Rightarrow \lambda ^{S_{k}}_{i}({\underline{\Omega }}^{k})=0. \end{aligned}$$

(16)

where $U_{k}$ and $S_{k}$ are orthogonal matrices that diagonalize $G_{2}(x^{k})$ and ${\underline{\Omega }}^{k}$, respectively. From (14), we have that ${\bar{x}} \in {\mathscr {F}}_{l}$. Now, let us consider two cases: the first when $\{\rho _{k}\}$ is unbounded and the second when $\{\rho _{k}\}$ is bounded. If the penalty parameter $\{\rho _{k}\}$ is unbounded, let us define

$$\begin{aligned} \delta ^{k}:=\nabla f(x^{k}) + DG_{1}(x^{k})^{*}[{\bar{\Omega }}^{k}+\rho _{k}G_{1}(x^{k})]_{+}+DG_{2}(x^{k})^{*}{\underline{\Omega }}^{k}. \end{aligned}$$

From (13), we have $\Vert \delta ^{k} \Vert \le \epsilon _{k}$. Dividing $\delta ^{k}$ by $\rho _{k}$:

$$\begin{aligned} \displaystyle \frac{\delta ^{k}}{\rho _{k}}=\displaystyle \frac{\nabla f(x^{k})}{\rho _{k}} + DG_{1}(x^{k})^{*}\left[ \displaystyle \frac{{\bar{\Omega }}^{k}}{\rho _{k}}+G_{1}(x^{k})\right] _{+}+ DG_{2}(x^{k})^{*}\frac{{\underline{\Omega }}^{k}}{\rho _{k}}, \end{aligned}$$

since $\displaystyle \frac{\delta ^{k}}{\rho _k}\rightarrow 0$ and $\nabla f(x^k)\rightarrow \nabla f({\bar{x}})$, we have that

$$\begin{aligned} DG_{1}(x^{k})^{*}\Omega _{1}^{k}+ DG_{2}(x^{k})^{*}\Omega _{2}^{k} \rightarrow 0, \end{aligned}$$

where $\Omega _{1}^{k}:=\left[ \displaystyle \frac{{\bar{\Omega }}^{k}}{\rho _{k}}+G_{1}(x^{k})\right] _{+}$ and $\Omega _{2}^{k}:=\displaystyle \frac{{\underline{\Omega }}^{k}}{\rho _{k}}.$ Furthermore, from (15) and from the compactness of the orthogonal matrices set, we can take a subsequence $\{U_{k}\}_{k\in {\mathbb {N}}}$ that converges to U and define it as the original sequence, such that $S_{k}\rightarrow U$ and $U_{k}\rightarrow U$. Then, if $\lambda ^{U}_{i}(G_{2}({\bar{x}}))<0$, we have that $\lambda ^{U_{k}}_{i}(G_{2}(x^{k}))<-\epsilon _{k}$ for all sufficiently large k, which implies, from (16), that $\lambda ^{S_{k}}_{i}(\Omega ^{k}_{2})=0.$ If the penalty parameter $\{\rho _{k}\}$ is bounded, that is, for $k\ge k_{0}$, the penalty parameter remains unchanged and then $V^{k} \rightarrow 0$. The sequence $\{{\bar{\Omega }}^{k}\}$ is bounded, then there is an ${\bar{\Omega }} \in {\mathbb {S}}^{m}_{+}$, such that

$$\begin{aligned} {\bar{\Omega }}=\displaystyle \lim {\bar{\Omega }}^{k}=\displaystyle \lim \left[ {\bar{\Omega }}^{k}+ \rho _{k_{0}} G_{1}(x^{k})\right] _{+}=\displaystyle \lim \Omega ^{k}=\left[ {\bar{\Omega }}+ \rho _{k_{0}} G_{1}({\bar{x}})\right] _{+}. \end{aligned}$$

Since ${\bar{\Omega }} \in {\mathbb {S}}^{m}_{+}$, we can take a diagonalization

$$\begin{aligned} {\bar{\Omega }}=[{\bar{\Omega }}+\rho _{k_{0}}G_{1}({\bar{x}})]_{+}=R{{\textsf {diag}}}([\lambda _{1}^{R}]_{+}, \dots , [\lambda _{m}^{R}]_{+} )R^{T}, \end{aligned}$$

with $RR^{T}=I$. Moreover

$$\begin{aligned} {\bar{\Omega }}+ \rho _{k_{0}}G_{1}({\bar{x}})=R{{\textsf {diag}}}(\lambda ^{R}_{1}, \dots , \lambda ^{R}_{m})R^{T}. \end{aligned}$$

In this way

$$\begin{aligned} G_ {1}({\bar{x}})=(1/\rho _{k_{0}}) R {{\textsf {diag}}}((\lambda ^{R}_{1}-[\lambda ^{R}_{1}]_{+}), \dots ,( \lambda ^{R}_{m}-[\lambda ^{R}_{m}]_{+}))R^{T}; \end{aligned}$$

thus, $G_{1}({\bar{x}}) \preceq 0$, and since ${\bar{x}} \in {\mathscr {F}}_{l}$, it follows that ${\bar{x}}$ is a global minimizer of the optimization problem (12) and, in particular, an AKKT point. $\square$

Let us now show that if, in addition, the limit point ${\bar{x}}$ is feasible for (9), then ${\bar{x}}$ is, in addition, an AKKT point for (9). In fact, $\{x^k\}$ is an associated AKKT sequence and $\{\Omega ^{k}\}$ is its corresponding dual sequence.

Theorem 3.2

Let $\epsilon _{k}\rightarrow 0^+$. Assume that ${\bar{x}}\in {\mathscr {F}}_{u}\cap {\mathscr {F}}_{l}$ is a feasible limit point of a sequence $\{x^{k}\}$ generated by Algorithm 1. Then, ${\bar{x}}$ is an AKKT point of problem (9).

Proof

Let ${\bar{x}} \in {\mathscr {F}}_{u}\cap {\mathscr {F}}_{l}$ be a limit point of a sequence $\{x^{k}\}$ generated by Algorithm 1. Let us assume without loss of generality that $x^k\rightarrow {\bar{x}}$. From Step 1 of the algorithm, we have that

$$\begin{aligned} \displaystyle \lim \limits _{k \rightarrow \infty } \nabla f(x^{k}) + DG_{1}(x^{k})^{*}\Omega ^{k}+DG_{2}(x^{k})^{*}{\underline{\Omega }}^{k} =0, \end{aligned}$$

where

$$\begin{aligned} \Omega ^{k}:= \left[ {\bar{\Omega }}^{k} + \rho _{k} G_{1}(x^{k}) \right] _{+}. \end{aligned}$$

Now, let us prove the complementarity condition in AKKT, both for the upper level and the lower level constraints. For this, we will use appropriate orthogonal matrices $S_{k}$, $R_{k}$, $U_{k}$, $Z_{k}$, R and U which diagonalize ${\underline{\Omega }}^{k}$, $\Omega ^{k}$, $G_{2}(x^{k})$, $G_{1}(x^{k})$, $G_{1}({\bar{x}})$, and $G_{2}({\bar{x}})$, respectively, such that $S_k\rightarrow U$ and $R_k\rightarrow R$. Note that, similarly to what was done in Theorem 3.1, $x^{k}$ is an $\epsilon _{k}$-KKT point for problem (11). Then, by Step 2 of Algorithm 1, we get that

$$\begin{aligned} \Vert \nabla _x L_{\rho _{k}}(x^{k},\Omega ^{k})+DG_{2}(x^{k})^{*}{\underline{\Omega }}^{k}\Vert \le \epsilon _{k}, \end{aligned}$$

(17)

$$\begin{aligned} \Vert [G_{2}(x^{k})]_{+}\Vert \le \epsilon _{k},\end{aligned}$$

(18)

$$\begin{aligned} \Vert U_{k}-S_{k}\Vert \le \epsilon _{k},\end{aligned}$$

(19)

$$\begin{aligned} \lambda ^{U_{k}}_{i}( G_{2}(x^{k}))\le -\epsilon _{k}\Rightarrow \lambda ^{S_{k}}_{i}({\underline{\Omega }}^{k})=0. \end{aligned}$$

(20)

If $\rho _{k} \rightarrow +\infty$, for the upper level constraints, since the sequence $\{{\bar{\Omega }}^{k}\}$ is bounded, we have that $\displaystyle \frac{{\bar{\Omega }}^{k}}{\rho _{k}}+G_{1}(x^{k})\rightarrow G_{1}({\bar{x}})$. Let us take a diagonalization

$$\begin{aligned} \frac{{\bar{\Omega }}^{k}}{\rho _{k}} + G_{1}(x^{k})=R_{k}{{\textsf {diag}}}(\lambda ^{k}_{1}, \dots , \lambda ^{k}_{m})R^{T}_{k}. \end{aligned}$$

Taking a subsequence if necessary, let us take a diagonalization

$$\begin{aligned} G_{1}({\bar{x}})=R{{\textsf {diag}}}(\lambda _{1}, \dots , \lambda _{m})R^{T}, \end{aligned}$$

where $R_{k} \rightarrow R$, $\lambda _{i}^{k}\rightarrow \lambda _{i}$ for all i. Then

$$\begin{aligned} \Omega ^{k}=[{\bar{\Omega }}^{k}+\rho _{k}G_{1}(x^{k})]_{+}=R_{k}{{\textsf {diag}}}(\rho _{k}[\lambda ^{k}_{1}]_{+}, \dots , \rho _{k}[\lambda ^{k}_{m}]_{+})R^{T}_{k}. \end{aligned}$$

Now, assume that $\lambda ^{R}_{i}( G_{1}({\bar{x}}))=\lambda _i<0$. Then, $\lambda _i^k<0$ for all sufficiently large k, which implies that $\lambda _i^{R_k}(\Omega ^k)=\rho _k[\lambda _i^k]_+=0$. Furthermore, from (19) and from the compactness of the orthogonal matrices set, we can take a subsequence $\{U_{k}\}_{k\in {\mathbb {N}}}$ that converges to U and define it as the original sequence, such that $S_{k}\rightarrow U$ and $U_{k}\rightarrow U$. For the lower level constraints, note that, if $\lambda ^{U}_{i}(G_{2}({\bar{x}}))<0$, we have $\lambda ^{U_{k}}_{i}(G_{2}(x^{k}))<-\epsilon _{k}$ for k large enough, and then by (20), it follows that $\lambda _{i}^{S_{k}}({\underline{\Omega }}^{k})=0$.

If $\{\rho _{k}\}$ is bounded, for the upper level constraints, analogously to what was done in Theorem 3.1, for $k\ge k_{0}$, we have that $V^{k} \rightarrow 0.$ Thus

$$\begin{aligned} {\bar{\Omega }}=\displaystyle \lim {\bar{\Omega }}^{k}=\displaystyle \lim \left[ {\bar{\Omega }}^{k}+ \rho _{k_{0}} G_{1}(x^{k})\right] _{+}=\displaystyle \lim \Omega ^{k}=\left[ {\bar{\Omega }}+ \rho _{k_{0}} G_{1}({\bar{x}})\right] _{+}. \end{aligned}$$

Writing the orthogonal decomposition of the matrix $\Omega ^{k}$, we have

$$\begin{aligned} \Omega ^{k}=[{\bar{\Omega }}^{k}+\rho _{k_{0}}G_{1}(x^{k})]_{+}=R_{k}{{\textsf {diag}}}([\lambda _{1}^{R_k}]_{+}, \dots , [\lambda _{m}^{R_k}]_{+} )R_{k}^{T}, \end{aligned}$$

and taking a subsequence if necessary

$$\begin{aligned} {\bar{\Omega }}=[{\bar{\Omega }}+\rho _{k_{0}}G_{1}({\bar{x}})]_{+}=R{{\textsf {diag}}}([\lambda ^{R}_{1}]_{+}, \dots , [\lambda ^{R}_{m}]_{+} )R^{T}, \end{aligned}$$

where $R_{k} \rightarrow R$, $\lambda _{i}^{R_k}\rightarrow \lambda ^{R}_{i}$ for all i. Moreover

$$\begin{aligned} {\bar{\Omega }}+ \rho _{k_{0}}G_{1}({\bar{x}})=R{{\textsf {diag}}}(\lambda ^{R}_{1}, \dots , \lambda ^{R}_{m})R^{T}. \end{aligned}$$

In this way

$$\begin{aligned} G_{1}({\bar{x}})=(1/\rho _{k_{0}}) R {{\textsf {diag}}}((\lambda ^{R}_{1}-[\lambda ^{R}_{1}]_{+}), \dots ,( \lambda ^{R}_{m}-[\lambda ^{R}_{m}]_{+}))R^{T}, \end{aligned}$$

and then, $\lambda ^{R}_{i}(G_{1}({\bar{x}}))=\displaystyle \frac{\lambda ^{R}_{i}-[\lambda ^{R}_{i}]_{+}}{\rho _{k_{0}}}$. If $\lambda ^{R}_{i}(G_{1}({\bar{x}}))<0$, we have that $\lambda ^{R}_{i}<[\lambda ^{R}_{i}]_{+}$; hence, $[\lambda ^{R}_{i}]_{+}=0$. Then, $\lambda ^{R_k}_{i}<0$ for all sufficiently large k, which implies that $\lambda _{i}^{R_{k}}(\Omega ^{k})=[\lambda _{i}^{R_k}]_{+}=0.$ Furthermore, from (19) and from the compactness of the orthogonal matrices set, we can take a subsequence $\{U_{k}\}_{k\in {\mathbb {N}}}$ that converges to U and define it as the original sequence, such that $S_{k}\rightarrow U$ and $U_{k}\rightarrow U$. Now, for the lower level constraints, note that, if $\lambda ^{U}_{i}(G_{2}({\bar{x}}))<0$, then $\lambda ^{U_{k}}_{i}(G_{2}(x^{k}))<-\epsilon _{k}$ for k large enough, which implies by (20), $\lambda _{i}^{S_{k}}({\underline{\Omega }}^{k})=0$. $\square$

Note that for proving the first theorem, concerning feasibility of limit points, one could relax the condition in (13) by replacing $\{\varepsilon _k\}$ by a bounded sequence $\{{\tilde{\epsilon }}_k\}$, not necessarily converging to zero, while keeping $\varepsilon _k\rightarrow 0^+$ in conditions (14–16). This allows including, without further analysis, an adaptive computation of ${{\tilde{\epsilon }}}_k:=\varphi (\Vert [G_1(x^{k-1})]_+\Vert )$, for some $\varphi (t)\rightarrow 0^+$ as $t\rightarrow 0^+$.

4 The covering problem

In this section, we present a new approach to a problem that consists of computing the smallest common radius for a collection of m closed balls, such that their union contains a given compact set, which is of the many special cases of the class of problems known as “covering problems”.

The problem can be modeled as an NLSDP of the following form:

$$\begin{aligned}&{\text {Minimize}} \quad f(r,c_1,\dots ,c_m,S_1,\dots ,S_p), \nonumber \\&\text {subject to} \quad H(r,c_1,\dots ,c_m,S_1,\dots ,S_p)=0, \nonumber \\&\,\, \quad \quad r\ge 0, \quad S_i\succeq 0, \quad i=1,\ldots ,p, \end{aligned}$$

(21)

-+ where $r\in {\mathbb {R}}, c_j\in {\mathbb {R}}^n, j=1,\dots ,m$, $S_i\in {\mathbb {S}}^N, i=1,\dots ,p$ and f and H are continuously differentiable functions, where H takes values on ${\mathbb {R}}^W$.

The nonlinear equality constraints defined by H will be penalized (upper level constraints), while the non-negativity constraint $r\ge 0$ and the conic constraints $S_i\succeq 0, i=1,\dots ,p$ will be kept in the subproblems (lower level constraints). Since the projection of $(r,S_1,\dots ,S_p)$ onto the lower level feasible set can be computed from a spectral decomposition of each variable, namely, $([r]_+,[S_1]_+,\dots ,[S_p]_+)$, we will solve each subproblem by the Spectral Projected Gradient (SPG) method (Birgin et al. 2000, 2014). In the nonlinear programming case, an Augmented Lagrangian method where subproblems are solved by the SPG method was previously considered in Diniz-Ehrhardt et al. (2004). We start by describing our model of the covering problem, by means of convex algebraic geometry tools, which is interesting in its own in the sense that it allows dealing with this difficult problem in its full generality, without resorting to discretizations.

Let $V\subset {\mathbb {R}}^n$ be a compact set to be covered by m balls. Let $c_1,\dots ,c_m \in {\mathbb {R}}^n$ be the centers and $\sqrt{r}$ the common radius of the balls, to be determined, where $r\geqslant 0$. We use the notation ${\mathbb {R}}[\mathbf{x }]:={\mathbb {R}}[x_1,\dots ,x_n]$ for the ring of real polynomials in n variables. The ith closed ball will be denoted by

$$\begin{aligned} B_i[c_i,r]:=\{x\in {\mathbb {R}}^n\mid p_i(x,c_i,r)\leqslant 0\}, \end{aligned}$$

where $p_i(x,c_i,r):=\Vert x-c_i\Vert _2^2-r\in {\mathbb {R}}[\mathbf{x }]$, for $i=1,\dots ,m$, and their union will be denoted by ${\mathscr {B}}[c_1,\dots ,c_m,r]$. More specifically, we intend to compute a solution to the following problem:

$$\begin{aligned}&\underset{c_i\in {\mathbb {R}}^n,r \in {\mathbb {R}}}{\text {Minimize}} r, \nonumber \\&\text {subject to} \, V\subseteq {\mathscr {B}}[c_1,\dots ,c_m,r], \nonumber \\&\quad \qquad r\geqslant 0. \end{aligned}$$

(22)

To rewrite this problem in a tractable form, we assume that there exists a set of v polynomials, namely $\{g_1,\dots ,g_v\}\subset {\mathbb {R}}[\mathbf{x }]$, such that

$$\begin{aligned} V=\{x\in {\mathbb {R}}^n\mid g_1(x)\geqslant 0,\dots ,g_v(x)\geqslant 0\}; \end{aligned}$$

that is, V is a closed basic semialgebraic set. Then, $V\subseteq {\mathscr {B}}[c_1,\dots ,c_m,r]$ if, and only if

$$\begin{aligned} {\mathscr {K}}[c_1,\dots ,c_m,r]:=\{x\in {\mathbb {R}}^n\mid p_i(x)> 0, g_j(x)\geqslant 0, \forall i, \forall j\}=\emptyset . \end{aligned}$$

The set ${\mathscr {K}}[c_1,\dots ,c_m,r]$ is the region of V not covered by ${\mathscr {B}}[c_1,\dots ,c_m,r]$. Note that the strict inequalities $p_i(x)>0$ can be replaced by $p_i(x)\geqslant 0$ and ${\overline{p}}(x):=\prod _{i=1}^{m} p_i(x)\ne 0$. To simplify the notation, let us define $q_i:=p_i$, for $i=1,\dots ,m$, and $q_{m+i}=g_i$, for $i=1,\dots ,v$, with $\eta :=m+v$. Hence

$$\begin{aligned} {\mathscr {K}}[c_1,\dots ,c_m,r]=\{x\in {\mathbb {R}}^n\mid q_i(x)\geqslant 0, {\overline{p}}(x) \ne 0, \forall i\in \{1,\dots ,\eta \}\}. \end{aligned}$$

(23)

Then, we can rewrite (22) as:

$$\begin{aligned}&\underset{c_i\in {\mathbb {R}}^n,r \in {\mathbb {R}}}{\text {Minimize}} r, \nonumber \\&\text {subject to} \,\, {\mathscr {K}}[c_1,\dots ,c_m,r]=\emptyset , \nonumber \\&\quad \qquad r\geqslant 0. \end{aligned}$$

(24)

At first glance, formulation (24) may not seem so pleasant, but fortunately, there are several results from the last few decades which manage to give infeasibility certificates for basic semialgebraic sets, in particular, for ${\mathscr {K}}[c_1,\dots ,c_m,r]$. Before introducing them, we recall two redundancy sets for the solutions of systems of polynomial inequalities. The set of all polynomials in n variables of degree at most 2d that can be written as a sum of squares (s.o.s.) of other polynomials will be denoted by $\Sigma _{n,2d}$, and $\Sigma _{n}:=\bigcup _{d\in {\mathbb {N}}} \Sigma _{n,2d}$.

Definition 4.1

The quadratic module generated by $q_1,\dots ,q_\eta$ is the set

$$\begin{aligned} {\textsf {qmodule}}(q_1,\dots ,q_\eta ):=\left\{ s_0+q_1s_1+\dots +q_\eta s_\eta \mid s_i\in \Sigma _n,\forall i\in \{1,\dots ,\eta \}\right\} . \end{aligned}$$

Definition 4.2

The preorder generated by $q_1,\dots ,q_\eta$ is the set

$$\begin{aligned} {\textsf {preorder}}(q_1,\dots ,q_\eta ):=\left\{ s_0+\sum _{i}q_is_i+\sum _{i\ne j}q_iq_js_{ij}+\sum _{i\ne j\ne k} q_iq_jq_ks_{ijk}+\dots \right\} , \end{aligned}$$

where each of the $2^{\eta }$ terms is free of squares and $s_i$, $s_{ij}$, etc. are all s.o.s. of polynomials. To put it briefly

$$\begin{aligned} {\textsf {preorder}}(q_1,\dots ,q_\eta )=\left\{ \sum _{\Lambda \subseteq \{1,\dots ,\eta \}}(s_\Lambda \prod _{i\in \Lambda } q_i)\mid s_\Lambda \in \Sigma _n,\forall \Lambda \subseteq \{1,\dots ,\eta \}\right\} . \end{aligned}$$

The next result, introduced in Stengle (1974), provides infeasibility certificates for ${\mathscr {K}}[c_1,\dots ,c_m,r]$.

Theorem 4.3

(Stengle’s Positivstellensatz) The set ${\mathscr {K}}[c_1,\dots ,c_m,r]$ is empty if, and only if, there exist $P\in {\textsf {preorder}}(q_1,\dots ,q_\eta )$ and an integer $b\ge 0$, such that

$$\begin{aligned} P+{\overline{p}}^{2b}=0. \end{aligned}$$

In Choi et al. (1995), it was proved that deciding whether a polynomial is an s.o.s. or not is intrinsically related to the possibility of finding a positive semidefinite matrix that represents it, in the following sense:

Theorem 4.4

(Gram representation) Define $N:=\left( {\begin{array}{c}n+d\\ d\end{array}}\right)$. A real polynomial s of degree 2d is an s.o.s. polynomial if, and only if, there exists a real symmetric $N\times N$ (Gram) matrix $S\succeq 0$, such that

$$\begin{aligned} s=[\mathbf{x }]_d^T S [\mathbf{x }]_d, \end{aligned}$$

where $[\mathbf{x }]_d:=(1,x_1,x_2,\dots ,x_n,x_1x_2,\dots ,x_n^d)^T$ is a (lexicographically) ordered array containing every monomial of degree at most d.

Thus, based on Parrilo (2003), for every fixed degree $d>0$ and $b\ge 0$, (24) can be written in the form:

$$\begin{aligned}&\underset{c_i\in {\mathbb {R}}^n,r \in {\mathbb {R}}}{\text {Minimize}} \, r, \nonumber \\&\text {subject to} \, {\textsf {coeffs}}\left( {\overline{p}}^{2b}+\sum _{\Lambda \subseteq \{1,\dots ,\eta \}}[\mathbf{x }]_d^T S_\Lambda [\mathbf{x }]_d \prod _{i\in \Lambda } q_i\right) =0, \nonumber \\&\quad \quad S_{\Lambda }\in {\mathbb {S}}^N_+,\forall \Lambda \subseteq \{1,\dots ,\eta \}, \nonumber \\&\quad \quad r\geqslant 0, \end{aligned}$$

(25)

where ${\textsf {coeffs}}(p)$ represents the vector of coefficients of the polynomial p. Formulation (25) is an NLSDP with $2^{\eta }$ matrix variables and, even if the fixed degrees do not lead to a Positivstellensatz certificate of emptyness for every feasible covering, they work for sufficiently large ones and thus bound the quality of the solution. In a similar fashion of Lasserre hierarchy for s.o.s. optimization, one can solve (25) starting from $d=1$ and then increasing it until the desired accuracy is obtained. This procedure is expected to stop in a few levels, even though the known bounds for d are unpracticably large. Technical details can be found in Lasserre (2010) and Laurent (2009).

Although the formulation presented above is the most desired one in terms of corresponding exactly to the true covering problem, it involves a very large number of variables and constraints. The difficulty appears due to the presence of the unusual requirement ${\overline{p}}(x)\ne 0$ in the definition of the set ${\mathscr {K}}[c_1,\dots ,c_m,r]$ in (23). In our experiments, we will deal with a simplified version of the problem where this requirement is dropped. The corresponding model is then much simpler. This situation corresponds to the problem of covering a compact set with open balls. That is, let us consider the problem of finding a minimal covering for V made of open balls with common radius, namely, define

$$\begin{aligned} B_i(c_i,r):=\{x\in {\mathbb {R}}^n\mid p_i(x,c_i,r)< 0\}, \quad i=1,\ldots ,m, \end{aligned}$$

and denote their union by ${\mathscr {B}}(c_1,\dots ,c_m,r)$. Then, $V\subseteq {\mathscr {B}}(c_1,\dots ,c_m,r)$ if, and only if, the set

$$\begin{aligned} {\mathscr {K}}(c_1,\dots ,c_m,r):=\{x\in {\mathbb {R}}^n\mid q_i(x)\geqslant 0, \forall i\in \{1,\dots ,\eta \}\} \end{aligned}$$

(26)

is empty. Of course, the problem

$$\begin{aligned}&\underset{c_i\in {\mathbb {R}}^n,r \in {\mathbb {R}}}{\text {Minimize}} \,r, \nonumber \\&\text {subject to} \, {\mathscr {K}}(c_1,\dots ,c_m,r)=\emptyset , \nonumber \\&\quad \quad r\geqslant 0 \end{aligned}$$

(27)

has no solution, but every strictly feasible covering of (24) is also feasible in (27). There is a simplified Positivstellensatz for this case, assuming an additional hypothesis over ${\mathscr {K}}(c_1,\dots ,c_m,r)$. The set ${\textsf {qmodule}}(q_1,\dots ,q_\eta )$ is said to be archimedean if there is a polynomial $p\in {\textsf {qmodule}}(q_1,\dots ,q_\eta )$, such that $\{x\in {\mathbb {R}}^n\mid p(x)\geqslant 0\}$ is compact or, equivalently, if there exists $M>0$, such that $b_M(x):=M-\Vert x\Vert _2^2\in {\textsf {qmodule}}(q_1,\dots ,q_\eta )$.

Theorem 4.5

(Putinar’s Positivstellensatz) Given $p\in {\mathbb {R}}[\mathbf{x }]$, suppose that ${\mathscr {K}}(c_1,\dots ,c_m,r)$ is a compact set and that ${\textsf {qmodule}}(q_1,\dots ,q_\eta )$ satisfies the archimedean property. If p(x) is positive on ${\mathscr {K}}(c_1,\dots ,c_m,r)$, then $p\in {\textsf {qmodule}}(q_1,\dots ,q_\eta ).$

See Putinar (1993) for details.

Corollary 4.6

Suppose that ${\mathscr {K}}(c_1,\dots ,c_m,r)$ is a compact set. Then, ${\mathscr {K}}(c_1,\dots ,c_m,r)$ is empty if, and only if, $-1\in {\textsf {qmodule}}(q_1,\dots ,q_\eta ,b_M)$, for some $M>0$, such that ${\mathscr {K}}(c_1,\dots ,c_m,r)\subseteq \{x\in {\mathbb {R}}\mid b_M(x)\geqslant 0\}$.

Proof

If there are $s_0,\dots ,s_\eta ,s_M\in \Sigma _n$, such that $s_0+q_1s_1+\dots +q_{\eta }s_{\eta }+b_Ms_M=-1$, then ${\mathscr {K}}(c_1,\dots ,c_m,r)$ must be empty. Otherwise, for any $x\in {\mathscr {K}}(c_1,\dots ,c_m,r)$:

$$\begin{aligned} 0\leqslant s_0(x)+q_1(x)s_1(x)+\dots +q_{\eta }(x)s_{\eta }(x)+b_M(x)s_M(x)< 0 \end{aligned}$$

would hold, as ${\mathscr {K}}(c_1,\dots ,c_m,r)=\{x\in {\mathbb {R}}^n\mid b_M(x)\geqslant 0, q_i(x)\geqslant 0,\forall i\in \{1,\dots ,\eta \}\}$. Conversely, if ${\mathscr {K}}(c_1,\dots ,c_m,r)$ is empty, the polynomial $p:x\mapsto p(x)=-1$ is strictly positive on ${\mathscr {K}}(c_1,\dots ,c_m,r)$; this is a vacuous truth. Then, $-1\in {\textsf {qmodule}}(q_1,\dots ,q_{\eta },b_M)$, given that the archimedean property is satisfied by ${\textsf {qmodule}}(q_1,\dots ,q_{\eta },b_M)$. $\square$

When V is defined by at least one polynomial $g_i$, such that $\{x\in {\mathbb {R}}^n\mid g_i(x)\geqslant 0\}$ is compact; for example, when V is a closed ball or a solid heart-shaped figure, then ${\mathscr {K}}(c_1,\dots ,c_m,r)$ is empty if, and only if, $-1\in {\textsf {qmodule}}(q_1,\dots ,q_{\eta })$. Moreover, similarly to Stengle’s theorem, Putinar’s result leads to a reformulation of (27) as an NLSDP of the following form:

$$\begin{aligned}&\underset{c_i\in {\mathbb {R}}^n,r \in {\mathbb {R}}}{\text {Minimize}} \, r, \nonumber \\&\text {subject to} \, {\textsf {coeffs}}(s_0+s_1q_1+\cdots + s_{\eta }q_{\eta }+1)=0, \nonumber \\&\quad \quad S_i\in {\mathbb {S}}^N_+,\forall i\in \{0,\ldots ,\eta \}, \nonumber \\&\quad \quad r\geqslant 0, \end{aligned}$$

(28)

where each polynomial $s_i$, with $i\in \{0,\ldots ,\eta \}$, is to be understood as the polynomial $s_i(x):=[\mathbf{x }]_d^T S_i [\mathbf{x }]_d$. The problem has $\eta +1$ matrix variables, which is much better than $2^{\eta }$ from (25). We expected that an algorithm that aims at solving (28) would find a good approximation to a solution of (25), and hence, this is the formulation which we use in our numerical experiments.

5 Numerical experiments

In this section, we give some implementation details for the application to the covering problem. We build the model based on Putinar’s Positivstellensatz described in (28) using the MATLAB package YALMIP [more details in Löfberg (2004)]. It has a structure made to represent semidefinite variables symbolically, called sdpvar, and a function to extract coefficients of polynomials even when they are symbolic. This is useful, because the polynomial variables $x_1,\ldots ,x_n$ are only used for ordering and grouping the problem variables. In general, finding a closed expression for each coefficient of the polynomials defined by the Positivstellensatz is not a simple task; also, we make use of a gradient-based (first order) method, which requires the partial derivatives of each coefficient with respect to the relevant variables, which we present below.

Define $X_{2d}:=[\mathbf{x }]_d[\mathbf{x }]_d^t$, and then, the partial derivatives of the coefficients of Putinar’s polynomial are given as follows:

• Derivative with respect to the radius:

  $$\begin{aligned} \frac{\partial }{\partial r}{\textsf {coeffs}}(s_0+s_1q_1+\dots + s_{\eta }q_{\eta }+1)={\textsf {coeffs}}\left( -\sum _{k=1}^{m} \langle S_k, X_{2d}\rangle \right) . \end{aligned}$$

• Derivatives with respect to the centers:

  $$\begin{aligned} \frac{\partial }{\partial c_{ij}}{\textsf {coeffs}}(s_0+s_1q_1+\dots + s_{\eta }q_{\eta }+1)={\textsf {coeffs}}(2(c_{ij}-x_j) \langle S_i, X_{2d}\rangle ), \end{aligned}$$

  for all $(i,j)\in \{1,\dots ,m\}\times \{1,\dots ,n\}$.

• Derivatives with respect to the Gram matrices:

  $$\begin{aligned} \frac{\partial }{\partial S_{k}^{(i,j)}}{\textsf {coeffs}}(s_0+s_1q_1+\dots + s_{\eta }q_{\eta }+1)={\textsf {coeffs}}(q_kX_{2d}^{(i,j)}), \end{aligned}$$

  for all $k\in \{0,\dots ,\eta \}$ and $(i,j)\in \{1,\dots ,N\}\times \{1,\dots ,N\}$, with $g_0:=1$.

The extracted coefficients are then written in the form H(y) and its jacobian matrix $J_H(y)$, where $y:=(r,c,S)^T$ is a vector of variables that stores $r,c_{ij}$ and $S_k^{(i,j)}$ in array form.

Next, we give some general numbers. Recall that $N=\left( {\begin{array}{c}n+d\\ d\end{array}}\right)$. Then, for the Putinar model, we have $\frac{N(N+1)}{2}(\eta +1)+nm+1$ real variables and one integer parameter d; the degree of Putinar’s polynomial is $d_P:=2d+\max _{i\in \{1,\dots ,\eta \}}\{\deg (q_i)\}$; so the number of nonlinear equality constraints is $\left( {\begin{array}{c}n+d_P\\ d_P\end{array}}\right)$. Note that only $mn+1$ variables are geometrically relevant (c and r), while the remaining ones (S) are feasibility certificates.

The nonlinear constraints $H(y)=0$ will be penalized, while the (convex) semidefinite constraints will be kept within the subproblems; that is, at each iteration, we solve the problem:

$$\begin{aligned}&\underset{y\in {\mathbb {R}}^N}{\text {Minimize}} \, L_{\rho ^k}(y,\lambda ^k):=f(y)+\displaystyle \frac{1}{2\rho ^k} \left\{ \Vert \lambda ^k+\rho ^k H(y) \Vert ^{2} \right\} , \nonumber \\&\text {subject to} \, S_i\succeq 0,\forall i\in \{0,\dots ,\eta \}, \nonumber \\&r\geqslant 0, \end{aligned}$$

(29)

where $y=(r,c,S)^T$ and $f(y)=r$. We employ the Spectral Projected Gradient (SPG) method (Birgin et al. 2000) for solving the Augmented Lagrangian subproblems (29) with its recommended parameters. Since the feasible region ${\mathscr {D}}$ of (29) is closed and convex, the above framework can be seen as a particular case of a standard Augmented Lagrangian algorithm with an abstract constraint from Birgin and Martínez (2014) and its convergence theory relies on a sequential optimality condition, described in Theorem 3.7 from the same reference, which holds at a feasible point $y^{\star }$ when there exist sequences $\{y^k\}_{k\in {\mathbb {N}}}\rightarrow y^{\star }$ and $\{\lambda ^k\}_{k\in {\mathbb {N}}}$, such that

$$\begin{aligned} ||\Pi _{{\mathscr {D}}}(y^k-\nabla L_\mathrm{up}(y^k,\lambda ^k))-y^k||\rightarrow 0, \end{aligned}$$

where $L_\mathrm{up}(y,\lambda ):=f(y)+\langle H(y),\lambda \rangle$ is the upper level Lagrangian of Problem (21). It is elementary to check that this condition, sometimes called Approximate Gradient Projection (AGP), implies on AKKT (from Definition 2.1) when the lower level feasible set has the particular structure of Problem (29). That is, in the covering application, we use the SPG method to exploit the simple structure of the non-negativity semidefinite constraints, allowing the analysis to be conducted by AGP, but our abstract algorithm is much more general, in the sense that it has its convergence guaranteed even in the absence of a convenient structure in the lower level, which makes AKKT interesting even in the presence of AGP. The simplicity of AKKT also makes it very natural in this context, in contrast with AGP, since it is not yet extended to the general NLSDP context due to the fact that it would be based on linearizing the constraint $G(y)\succeq 0$, but linear constraints do not guarantee stationarity of minimizers in NLSDP, as it occurs in nonlinear programming.

Let us now describe some details about the implementation.

• (1) Modeling part The inputs are the dimension n, the number of balls m, half of the fixed degree for the s.o.s. polynomials d, and the chosen version of the Positivstellensatz; in case of Stengle’s, choosing a degree b is also required. The code then writes the functions H(y) and $J_H(y)$ in the format of a Fortran subroutine supported by the Fortran implementation (Andreani et al. 2008a) of the Augmented Lagrangian with subproblems solved by SPG. This modeling code was done in MATLAB 2015a using YALMIP—version R20180926. We used BLAS/LAPACK version 3.8.0. We make use of the Fortran compiler gfortran 7.3.0 with the optimization flag -O3.

• (2) Solving part The initial penalty parameter is $\rho ^0=2$, and if the infeasibility in iteration k is larger than $\rho _\mathsf{frac}:=0.9$ times the infeasibility in iteration $k-1$, then the penalty parameter is multiplied by $\rho _\mathsf{mult}:=1.05$. Else, it remains unchanged. In our tests, we considered the initial Lagrange multiplier approximations for the equality constraints as $\lambda ^0:=0$. The maximum number of outer iterations is fixed as $\mathrm{OMAX}=2000$ and the sum of all SPG iterations is limited to $\mathrm{TMAX}=10^6$. The required decay of the objective function is $\varepsilon _\mathsf{obj}=10^{-8}$ and the desired feasibility is $\varepsilon _\mathsf{feas}=10^{-8}$. M is set to 10, as usual. The program stops when either one of these occurs:

  • The objective function has not decreased enough, that is $|f(y^k)-f(y^{k-1})|<\varepsilon _\mathsf{obj}$, for $N_\mathsf{stat}=5$ consecutive iterations, and feasibility is at least as required, that is, $\Vert H(y^k)\Vert _{\infty } <\varepsilon _\mathsf{feas}$;

  • The maximum number of outer iterations OMAX is reached;

  • The maximum number of SPG iterations TMAX is reached.

• (3) Computing a feasible initial covering: The initial point must also be provided by the user, in general, but in two dimensions, our choice consists on placing the initial centers $c_1^0,\dots ,c_m^0$ over the vertices of an m-sided regular polygon inscribed in the circle centered at the origin, with radius 0.5. The initial common radius for those circles is defined as $r^0:=1.0$. The initial point does not need to be feasible nor close to a minimizer, but feasibility certificates are computed (if they exist) by fixing $(r^0,c_1^0,\dots ,c_m^0)$ in y and solving the following problem:

  $$\begin{aligned}&\underset{S_i\in {\mathbb {S}}^N}{\text {Minimize}} \,\, \frac{1}{2}\Vert H(y)\Vert _2^2, \nonumber \\&\text {subject to} \,\, S_i\succeq 0,\forall i\in \{0,\dots ,\eta \}, \end{aligned}$$

  (30)

  where $y=(r,c,S)^T$. This is done using SPG itself, and since $H(y)={\textsf {coeffs}}(s_0+s_1q_1+\dots + s_{\eta }q_{\eta }+1)$ is now an affine function of the variables in the entries of $S_i$, the objective function of (30) is quadratic. Hence, this problem is expected to be easily solved. In all tests made, it has converged in a single iteration.

Our results are summarized below:

Table 1 Numerical results for Putinar’s Positivstellensatz

We cover the closed unit circle centered at the origin using three other circles. Due to rotation symmetry of the solution, we arbitrarily fix one coordinate of a circle to guarantee unicity of solution. The optimal radius is given by $r^{\star }=0.75$. In Table 1, we present a comparison between different degrees for this test case. Note that the model is sharper with respect to the covering problem the larger the degree 2d is, and hence, we expect to approach $r^*$ with the increase of the degree considered.

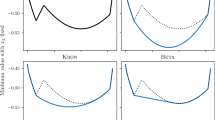
Unfortunately, the experiment results were less satisfactory than what we expected, because the highest degree from our tests, $2d=18$, demands some computational effort both for modeling and solving, but the computed approximation is still quite far from the optimum. By avoiding discretizations, we expected to obtain an arbitrarily close approximation for the actual solution in an acceptable amount of steps. This could not be verified in practice, even though there is no theoretical impeditive at all. The objective function decreases quickly and monotonically in the first few iterations, but slows down considerably after that (see Fig. 1); feasibility follows a similar pattern. The issue found is that subproblems are generally not being solved up to the desired tolerance for optimality at later iterations. This may be due to the inherent difficulty of the subproblems, where a second-order method should probably perform better. Also, the Augmented Lagrangian method seems to be very sensitive to the initial Lagrange multipliers approximation, which is not clear how to compute them at this moment. It could also be the case that the true degree 2d at the solution $r^*$ is much larger than what is computationally solvable.

We have also done extensive tests relaxing several stopping criteria for the SPG solver, allowing oversolving the subproblems and iterating until the maximum number of outer iterations OMAX is reached, and also covering other objects. In general, the results were not much better than what was obtained after stopping under the usual criteria. We also performed some experiments with PENLAB [see Fiala et al. (2013)] via YALMIP, which is a general Augmented Lagrangian method for nonlinear semidefinite programming, but the solver could not find even a feasible point. This might indicate that our model provides problems that are inherently hard to solve. Let us recall that our model is very general, as it allows problems in any dimension, shape of the object to be covered, and number of balls. We even do not need to use balls to cover the given object. Any basic semialgebraic set can be used in place of a ball. We achieve this generality while avoiding discretizations.

To exemplify the generality of the model, we present the following pictures illustrating the coverings obtained with three and seven circles (with squared radii equal to 0.6505 and 0.3051, respectively) of a heart-shaped object described by $\{(x,y)\in {\mathbb {R}}^2\mid (x^2+y^2-1)^3-x^2y^3\leqslant 0\}$ (Fig. 2).

Fig. 1

Radius per iteration, up to 157, degrees 4 to 16, up to down

Fig. 2

Solution found by an inexact restoration method for covering a heart-shaped object

Note that our model provides certificates of feasibility of the given solution and certificates of approximate optimality via the approximate Lagrange multipliers, while we do not know any other technique for dealing with such problem besides straightforward discretization. These experiments can be found in detail in Mito (2018), where an Inexact Restoration solver was implemented for the same model, but no proof of convergence was given.

6 Conclusions

We present an Augmented Lagrangian method for solving nonlinear semidefinite programming problems which allows constrained subproblems. Our global convergence proof is based on the AKKT optimality condition, which is strictly stronger than the usually employed Fritz John optimality condition (or, equivalently, “KKT or not-MFCQ”). This algorithm was designed to approach the covering problem by means of convex algebraic geometry tools, which provide a very general and versatile nonlinear semidefinite programming model. The dimension and the shape of the regions that build the covering are left as input for the user, even though those factors have a strong influence on the problem structure. Some of the previous algorithms that aimed to cover arbitrary regions were developed for two and three dimensions with sphere coverings using a min–max–min approach with hyperbolic smoothing; we offer an alternative for higher dimensions and our model gives freedom in the shape of the covering as well, not limited to balls. We point out that the min–max–min model performs better than ours in two and three dimensions, but our model is more general and, to the best of our knowledge, it is the first exact one. However, due to the size of the models and lack of information about good Lagrange multiplier estimates, or geometric insight about the feasibility certificates S, we are still not able to solve our model to a high accuracy. Further work should be done to compute these estimates and to presolve the constraints, hopefully avoiding its inherent difficulty. We advocate that the model is interesting in its own due to the use of somewhat heavy algebraic machinery, which is somewhat unusual. We believe that algebraic techniques can provide further insights for solving difficult optimization problems without resorting to discretizations, and we hope that our work may inspire further investigations in this direction.