A derivative-free trust-region algorithm for composite nonsmooth optimization

Abstract

The derivative-free trust-region algorithm proposed by Conn et al. (SIAM J Optim 20:387–415, 2009) is adapted to the problem of minimizing a composite function $\varPhi (x)=f(x)+h(c(x))$, where $f$ and $c$ are smooth, and $h$ is convex but may be nonsmooth. Under certain conditions, global convergence and a function-evaluation complexity bound are proved. The complexity result is specialized to the case when the derivative-free algorithm is applied to solve equality-constrained problems. Preliminary numerical results with minimax problems are also reported.

1 Introduction

We consider the composite nonsmooth optimization (NSO) problem

$$\begin{aligned} \min _{x\in \mathbb {R}^{n}} \varPhi (x)\equiv f(x)+h(c(x)), \end{aligned}$$

(1)

where $f:\mathbb {R}^{n}\rightarrow \mathbb {R}$ and $c:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ are continuously differentiable and $h:\mathbb {R}^{r}\rightarrow \mathbb {R}$ is convex. The formulation of (1) with $f=0$ includes problems of finding feasible points of nonlinear systems of inequalities (where $h(c)\equiv \Vert c^{+}\Vert _{p}$, with $c_{i}^{+}=\max \left\{ c_{i},0\right\}$ and $1\le p \le +\infty$), finite minimax problems (where $h(c)\equiv \max _{1\le i\le r}c_{i}$), and best $L_{1}$, $L_{2}$ and $L_{\infty }$ approximation problems (where $h(c)\equiv \Vert c\Vert _{p}$, $p=1,2,+\infty$). Another interesting example of problem (1) is the minimization of the exact penalty function

$$\begin{aligned} \varPhi (x,\sigma )=f(x)+\sigma \Vert c(x)\Vert , \end{aligned}$$

(2)

associated to the equality-constrained optimization problem

$$\begin{aligned}&\min \ f(x),\nonumber \\&\text {s.t.}\ c(x)=0. \end{aligned}$$

(3)

There are several derivative-based algorithms to solve problem (1), which can be classified into two main groups.¹ The first group consists of methods for general nonsmooth optimization, such as subgradient methods (Shor 1978), bundle methods (Lemaréchal 1978), and cutting plane methods (Kelly 1960). If the function $\varPhi$ satisfies suitable conditions, these methods are convergent in some sense. But they do not exploit the form of the problem, neither the convexity of $h$ nor the differentiability of $f$ and $c$. In contrast, the second group of methods is composed by methods in which the smooth substructure of the problem and the convexity of $h$ are exploited. Notable algorithms in this group are those proposed by Fletcher (1982a, b), Powell (1983), Yuan (1985a), Bannert (1994) and Cartis et al. (2011b).

An essential feature of the algorithms mentioned above is that they require a subgradient of $\varPhi$ or a gradient vector of $f$ and a Jacobian matrix of $c$ at each iteration. However, there are many practical problems where the derivative information is unreliable or unavailable (see, e.g., Conn et al. 2009a). In these cases, derivative-free algorithms become attractive, since they do not use (sub-)gradients explicitly.

In turn, derivative-free optimization methods can be distinguished into three groups. The first one is composed by direct-search methods, such as the Nelder–Mead method (Nelder and Mead 1965), the Hooke–Jeeves pattern search method (Hooke and Jeeves 1961) and the mesh adaptive direct-search (MADS) method (Audet and Dennis 2006). The second group consists of methods based on finite-differences, quasi-Newton algorithms or conjugate direction algorithms, whose examples can be found in Mifflin (1975), Stewart (1967), Greenstadt (1972) and Brent (1973). Finally, the third group is composed by methods based on interpolation models of the objective function, such as those proposed by Winfield (1973), Powell (2006) and Conn et al. (2009b).

Within this context, in this paper, we propose a globally convergent derivative-free trust-region algorithm for solving problem (1) when the function $h$ is known and the gradient vectors of $f$ and the Jacobian matrices of $c$ are not available. The design of our algorithm is strongly based on the derivative-free trust-region algorithm proposed by Conn et al. (2009b) for unconstrained smooth optimization, and on the trust-region algorithms proposed by Fletcher (1982a), Powell (1983), Yuan (1985a) and Cartis et al. (2011b) for composite NSO. To the best of our knowledge, this work is the first one to present a derivative-free trust-region algorithm with global convergence results for the composite NSO problem, in which the structure of the problem is exploited.² We also investigate the worst-case function-evaluation complexity of the proposed algorithm. Specializing the complexity result for the minimization of (2), we obtain a complexity bound for solving equality-constrained optimization problems. At the end, we also present preliminary numerical results for minimax problems.

The paper is organized as follows. In Sect. 2, some definitions and results are reviewed and provided. The algorithm is presented in Sect. 3. Global convergence is treated in Sect. 4, while worst-case complexity bounds are given in Sects. 5 and 6. Finally, the numerical results are presented in Sect. 7.

2 Preliminaries

Throughout this paper, we shall consider the following concept of criticality.

Definition 1

(Yuan 1985b, page 271) A point $x^{*}$ is said to be a critical point of $\varPhi$ given in (1) if

$$\begin{aligned} f(x^{*})+h(c(x^{*}))\le f(x^{*})+\nabla f(x^{*})^\mathrm{T}s+h(c(x^{*})+J_{c}(x^{*})s),\quad \forall s\in \mathbb {R}^{n}, \end{aligned}$$

(4)

where $J_{c}$ denotes the Jacobian of $c$.

Based on the above definition, for each $x\in \mathbb {R}^{n}$, define

$$\begin{aligned} l(x,s)\equiv f(x)+\nabla f(x)^\mathrm{T}s+h(c(x)+J_{c}(x)s),\quad \forall s\in \mathbb {R}^{n}, \end{aligned}$$

(5)

and, for all $r>0$, let

$$\begin{aligned} \psi _{r}(x)\equiv l(x,0)-\min _{\Vert s\Vert \le r} l(x,s). \end{aligned}$$

(6)

Following Cartis et al. (2011b), we shall use the quantity $\psi _{1}(x)$ as a criticality measure for $\varPhi$. This choice is justified by the lemma below.

Lemma 1

Let $\psi _{1}:\mathbb {R}^{n}\rightarrow \mathbb {R}$ be defined by (6). Suppose that $f:\mathbb {R}^{n}\rightarrow \mathbb {R}$ and $c:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ are continuously differentiable$,$ and that $h:\mathbb {R}^{r}\rightarrow \mathbb {R}$ is convex and globally Lipschitz. Then$,$

• (a) $\psi _{1}$ is continuous$;$

• (b) $\psi _{1}(x)\ge 0$ for all $x\in \mathbb {R}^{n};$ and

• (c) $x^{*}$ is a critical point of $\varPhi \Longleftrightarrow \psi _{1}(x^{*})=0$.

Proof

See Lemma 2.1 in Yuan (1985a). $\square$

Our derivative-free trust-region algorithm will be based on the class of fully linear models proposed by Conn et al. (2009b). To define such class of models, let $x_{0}$ be the initial iterate and suppose that the new iterates do not increase the value of the objective function $\varPhi$. Then, it follows that

$$\begin{aligned} x_{k}\in L(x_{0})\equiv \left\{ x\in \mathbb {R}^{n}\,:\,\varPhi (x)\le \varPhi (x_{0})\right\} ,\quad \text {for all }k. \end{aligned}$$

(7)

In this case, if the sampling to form the models is restricted to the closed balls $B[x_{k};\varDelta _{k}]$, and $\varDelta _{k}$ is supposed bounded above by a constant $\bar{\varDelta }>0$, then $\varPhi$ is only evaluated within the set

$$\begin{aligned} L_{enl}(x_{0})=\bigcup _{x\in L(x_{0})} B[x;\bar{\varDelta }]. \end{aligned}$$

(8)

Now, considering the sets $L(x_{0})$ and $L_{enl}(x_{0})$, we have the following definition.

Definition 2

(Conn et al. 2009b, Definition 3.1) Assume that $f:\mathbb {R}^{n}\rightarrow \mathbb {R}$ is continuously differentiable and that its gradient $\nabla f$ is Lipschitz continuous on $L_{enl}(x_{0})$. A set of model functions $M=\left\{ p:\mathbb {R}^{n}\rightarrow \mathbb {R}\,|\,p\in C^{1}\right\}$ is called a fully linear class of models if:

• 1. There exist constants $\kappa _{jf},\kappa _{f},\kappa _{lf}>0$ such that for any $x\in L(x_{0})$ and $\varDelta \in (0,\bar{\varDelta }]$ there exists a model function $p\in M$, with Lipschitz continuous gradient $\nabla p$ and corresponding Lipschitz constant bounded above by $\kappa _{lf}$, and such that

  $$\begin{aligned} \Vert \nabla f(y)-\nabla p(y)\Vert \le \kappa _{jf}\varDelta ,\quad \forall y\in B[x;\varDelta ], \end{aligned}$$

  (9)

  and

  $$\begin{aligned} |f(y)-p(y)|\le \kappa _{f}\varDelta ^{2},\quad \forall y\in B[x;\varDelta ]. \end{aligned}$$

  (10)

  Such a model $p$ is called fully linear on $B[x;\varDelta ]$.

• 2. For this class $M$, there exists an algorithm called “model-improvement” algorithm, that in a finite, uniformly bounded (with respect to $x$ and $\varDelta$) number of steps can either establish that a given model $p\in M$ is fully linear on $B[x;\varDelta ]$, or find a model $\tilde{p}\in M$ that is fully linear on $B[x;\varDelta ]$.

Remark 1

Interpolation and regression linear models of the form

$$\begin{aligned} p(y)=c+g^\mathrm{T}y \end{aligned}$$

(11)

are examples of fully linear models when the set of sample points is chosen in a convenient way (see Section 2.4 in Conn et al. 2009a). Furthermore, under some conditions, one can also prove that (interpolation or regression) quadratic models of the form

$$\begin{aligned} p(y)=c+g^\mathrm{T}y+\dfrac{1}{2}y^\mathrm{T}Hy\quad (H\in \mathbb {R}^{n\times n}\ \text {symmetric}) \end{aligned}$$

(12)

are fully linear models (see Section 6.1 in Conn et al. 2009a). On the other hand, Algorithms 6.3 and 6.5 in Conn et al. (2009a) are examples of model-improvement algorithms (see Sections 6.2 and 6.3 in Conn et al. 2009a).

Remark 2

Let $c:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ be continuously differentiable with Jacobian function $J_{c}$ Lipschitz continuous on $L_{enl}(x_{0})$. If $q_{i}:\mathbb {R}^{n}\rightarrow \mathbb {R}$ is a fully linear model of $c_{i}:\mathbb {R}^{n}\rightarrow \mathbb {R}$ on $B[x;\varDelta ]$ for each $i=1,\ldots ,r$, then there exist constants $\kappa _{jc},\kappa _{c},\kappa _{lc}>0$ such that the function $q\equiv (q_{1},\ldots ,q_{r}):\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ satisfies the inequalities

$$\begin{aligned} \Vert J_{c}(y)-J_{q}(y)\Vert \le \kappa _{jc}\varDelta ,\quad \forall y\in B[x;\varDelta ], \end{aligned}$$

(13)

and

$$\begin{aligned} \Vert c(y)-q(y)\Vert \le \kappa _{c}\varDelta ^{2},\quad \forall y\in B[x;\varDelta ]. \end{aligned}$$

(14)

Moreover, the Jacobian $J_{q}$ is Lipschitz continuous, and the corresponding Lipschitz constant is bounded by $\kappa _{lc}$. In this case, we shall say that $q$ is a fully linear model of $c$ on $B[x;\varDelta ]$ with respect to constants $\kappa _{jc}$, $\kappa _{c}$ and $\kappa _{lc}$.

The next lemma establishes that if a model $q$ is fully linear on $B[x;\varDelta ^{*}]$ with respect to some constants $\kappa _{jc}$, $\kappa _{c}$ and $\kappa _{lc}$, then it is also fully linear on $B[x;\varDelta ]$ for any $\varDelta \in [\varDelta ^{*},\bar{\varDelta }]$ with the same constants.

Lemma 2

Consider a function $c:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ satisfying the assumptions in Remark 2. Given $x\in L(x_{0})$ and $\varDelta ^{*}\le \bar{\varDelta },$ suppose that $q:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ is a fully linear model of $c$ on $B[x;\varDelta ^{*}]$ with respect to constants $\kappa _{jc},$ $\kappa _{c}$ and $\kappa _{lc}$. Assume also, without loss of generality$,$ that $\kappa _{jc}$ is no less than the sum of $\kappa _{lc}$ and the Lipschitz constant of $J_{c}$. Then$,$ $q$ is fully linear on $B[x;\varDelta ],$ for any $\varDelta \in [\varDelta ^{*},\bar{\varDelta }],$ with respect to the same constants $\kappa _{jc},\kappa _{c}$ and $\kappa _{lc}$.

Proof

It follows by the same argument used in the proof of Lemma 3.4 in Conn et al. (2009b). $\square$

From here, consider the following assumptions:

• A1 The functions $f:\mathbb {R}^{n}\rightarrow \mathbb {R}$ and $c:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ are continuously differentiable.

• A2 The gradient of $f$, $\nabla f:\mathbb {R}^{n}\rightarrow \mathbb {R}^{n}$, and the Jacobian of $c$, $J_{c}:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r\times n}$, are globally Lipschitz on $L_{enl}(x_{0})$, with Lipschitz constants $L_{f}$ and $L_{c}$, respectively.

• A3 The function $h:\mathbb {R}^{r}\rightarrow \mathbb {R}$ is convex and globally Lipschitz continuous, with Lipschitz constant $L_{h}$.

Given functions $p:\mathbb {R}^{n}\rightarrow \mathbb {R}$ and $q:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ continuously differentiable, for each $x\in \mathbb {R}^{n}$ define

$$\begin{aligned} \tilde{l}(x,s)=f(x)+\nabla p(x)^\mathrm{T}s+h(c(x)+J_{q}(x)s),\quad \forall s\in \mathbb {R}^{n}. \end{aligned}$$

(15)

and, for all $r>0$, let

$$\begin{aligned} \eta _{r}(x)\equiv \tilde{l}(x,0)-\min _{\Vert s\Vert \le r}\tilde{l}(x,s). \end{aligned}$$

(16)

The theorem below describes the relation between $\psi _{1}(x)$ and $\eta _{1}(x)$ when $p$ and $q$ are fully linear models of $f$ and $c$ around $x$.

Theorem 1

Suppose that A1–A3 hold. Assume that $p:\mathbb {R}^{n}\rightarrow \mathbb {R}$ is a fully linear model of $f$ with respect to constants $\kappa _{jf},\kappa _{f}$ and $\kappa _{lf},$ and that $q:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ is a fully linear model of $c$ with respect to constants $\kappa _{jc},\kappa _{c}$ and $\kappa _{lc},$ both on the ball $B[x;\varDelta ]$. Then$,$

$$\begin{aligned} |\psi _{1}(y)-\eta _{1}(y)|\le \kappa _{s}\varDelta ,\quad \forall y\in B[x;\varDelta ], \end{aligned}$$

(17)

with $\kappa _{s}=\kappa _{jf}+L_{h}\kappa _{jc}$.

Proof

Let $y\in B[x;\varDelta ]$. Since $p$ and $q$ are fully linear models of $f$ and $c$, respectively, on the ball $B[x;\varDelta ]$, it follows that

$$\begin{aligned} \Vert \nabla f(y)-\nabla p(y)\Vert \le \kappa _{jf}\varDelta \quad \text {and}\quad \Vert J_{c}(y)-J_{q}(y)\Vert \le \kappa _{jc}\varDelta . \end{aligned}$$

(18)

Consider $\tilde{s}\in B[0;1]$ such that

$$\begin{aligned} \min _{\Vert s\Vert \le 1} l(y,s)=l(y,\tilde{s}). \end{aligned}$$

(19)

Then, from A3, (18) and (19), it follows that

$$\begin{aligned} \psi _{1}(y)-\eta _{1}(y)&= \left( l(y,0)-\min _{\Vert s\Vert \le 1} l(y,s)\right) -\left( \tilde{l}(y,0)-\min _{\Vert s\Vert \le 1}\tilde{l}(y,s)\right) \nonumber \\&= \min _{\Vert s\Vert \le 1}\tilde{l}(y,s)-\min _{\Vert s\Vert \le 1} l(y,s) \nonumber \\&= \min _{\Vert s\Vert \le 1}\tilde{l}(y,s)-l(y,\tilde{s}) \nonumber \\&\le \tilde{l}(y,\tilde{s})-l(y,\tilde{s}) \nonumber \\&= \left( \nabla p(y)-\nabla f(y)\right) ^\mathrm{T}\tilde{s}+\left[ h(c(y)+J_{q}(y)\tilde{s})-h(c(y)+J_{c}(y)\tilde{s})\right] \nonumber \\&\le \Vert \nabla p(y)-\nabla f(y)\Vert +L_{h}\Vert J_{q}(y)-J_{c}(y)\Vert \nonumber \\&= \left( \kappa _{jf}+L_{h}\kappa _{jc}\right) \varDelta . \end{aligned}$$

(20)

Similarly, considering $\bar{s}\in B[0;1]$ such that

$$\begin{aligned} \min _{\Vert s\Vert \le 1}\tilde{l}(y,s)=\tilde{l}(y,\bar{s}), \end{aligned}$$

(21)

we obtain the inequality

$$\begin{aligned} \eta _{1}(y)-\psi _{1}(y)\le \left( \kappa _{jf}+L_{h}\kappa _{jc}\right) \varDelta . \end{aligned}$$

(22)

Hence, from (20) and (22), we conclude that (17) holds. $\square$

3 Algorithm

Considering the theory discussed above, in this section, we present an algorithm to solve (1) without derivatives. The algorithm is an adaptation of Algorithm 4.1 in Conn et al. (2009b) for unconstrained smooth optimization, and contains elements of the trust-region algorithms of Fletcher (1982a), Powell (1983), Yuan (1985a) and Cartis et al. (2011b) for composite NSO.

Algorithm 1 (Derivative-Free Trust-Region Algorithm for Composite NSO)

Step 0 :

Choose a class of fully linear models for $f$ and $c$ (e.g., linear interpolation models) and a corresponding model-improvement algorithm (e.g., Algorithm 6.3 in Conn et al. 2009a). Choose $x_{0}\in \mathbb {R}^{n}$, $\bar{\varDelta }>0$, $\varDelta _{0}^{*}\in (0,\bar{\varDelta }]$, $H_{0}\in \mathbb {R}^{n\times n}$ symmetric, $0\le \alpha _{0}\le \alpha _{1}<1$ (with $\alpha _{1}\ne 0$), $0<\gamma _{1}<1<\gamma _{2}$, $\epsilon _{c}>0$, $\mu >\beta >0$ and $\omega \in (0,1)$. Consider a model $p_{0}^{*}(x_{0}+d)$ for $f$ (with gradient at $d=0$ denoted by $g_{0}^{*}$) and a model $q_{0}^{*}(x_{0}+d)$ for $c$ (with Jacobian matrix at $d=0$ denoted by $A_{0}^{*}$). Set $k:=0$.

Step 1 :

Compute

$$\begin{aligned} \eta _{1}^{*}(x_{k})=l^{*}(x_{k},0)-l^{*}(x_{k},s_{k}), \end{aligned}$$

where

$$\begin{aligned} s_{k}=\arg \min _{\Vert s\Vert \le 1}l^{*}(x_{k},s), \end{aligned}$$

(23)

and

$$\begin{aligned} l^{*}(x_{k},s)=f(x_{k})+(g_{k}^{*})^\mathrm{T}s+h(c(x_{k})+A_{k}^{*}s). \end{aligned}$$

If $\eta _{1}^{*}(x_{k})>\epsilon _{c}$, then set $\eta _{1}(x_{k})=\eta _{1}^{*}(x_{k})$, $p_{k}=p_{k}^{*}$ ($g_{k}=g_{k}^{*}$), $q_{k}=q_{k}^{*}$ ($A_{k}=A_{k}^{*}$), $\varDelta _{k}=\varDelta _{k}^{*}$, and go to Step 3.

Step 2 :

Call the model-improvement algorithm to verify if the models $p_{k}^{*}$ and $q_{k}^{*}$ are fully linear on $B\left[ x_{k};\varDelta _{k}^{*}\right]$. If $\varDelta _{k}^{*}\le \mu \eta _{1}^{*}(x_{k})$ and the models $p_{k}^{*}$ and $q_{k}^{*}$ are fully linear on $B[x_{k};\varDelta _{k}^{*}]$, set $\eta _{1}(x_{k})=\eta _{1}^{*}(x_{k})$, $p_{k}=p_{k}^{*}$ ($g_{k}=g_{k}^{*}$), $q_{k}=q_{k}^{*}$ ($A_{k}=A_{k}^{*}$) and $\varDelta _{k}=\varDelta _{k}^{*}$. Otherwise, apply Algorithm 2 (described below) to construct a model $\tilde{p}_{k}(x_{k}+d)$ for $f$ (with gradient at $d=0$ denoted by $\tilde{g}_{k}$) and a model $\tilde{q}_{k}(x_{k}+d)$ for $c$ (with Jacobian matrix at $d=0$ denoted by $\tilde{A}_{k}$), both fully linear (for some constants which remain the same for all iterations of Algorithm 1) on the ball $B[x_{k};\tilde{\varDelta }_{k}]$, for some $\tilde{\varDelta }_{k}\in (0,\mu \tilde{\eta }_{1}(x_{k})]$, where $\tilde{\varDelta }_{k}$ and $\tilde{\eta }_{1}(x_{k})$ are given by Algorithm 2. In such case, set $\eta _{1}(x_{k})=\tilde{\eta }_{1}(x_{k})$, $p_{k}=\tilde{p}_{k}$ ($g_{k}=\tilde{g}_{k}$), $q_{k}=\tilde{q}_{k}$ ($A_{k}=\tilde{A}_{k}$) and

$$\begin{aligned} \varDelta _{k}=\min \left\{ \max \left\{ \tilde{\varDelta }_{k},\beta \tilde{\eta }_{1}(x_{k})\right\} ,\varDelta _{k}^{*}\right\} . \end{aligned}$$

(24)

Step 3 :

Let $D_{k}^{*}$ be the set of solutions of the subproblem

$$\begin{aligned} \min _{d\in \mathbb {R}^{n}}&\quad m_{k}(x_{k}+d)\equiv f(x)+g_{k}^\mathrm{T}d+ h\left( c(x_{k})+A_{k}d\right) +\frac{1}{2}d^\mathrm{T}H_{k}d \end{aligned}$$

(25)

$$\begin{aligned} \text {s.t.}&\quad \Vert d\Vert \le \varDelta _{k} \end{aligned}$$

(26)

Compute a step $d_{k}$ for which $\Vert d_{k}\Vert \le \varDelta _{k}$ and

$$\begin{aligned} m_{k}(x_{k})-m_{k}(x_{k}+d_{k})\ge \alpha _{2}\left[ m_{k}(x_{k})-m_{k}(x_{k}+d_{k}^{*})\right] , \end{aligned}$$

(27)

for some $d_{k}^{*}\in D_{k}^{*}$, where $\alpha _{2}\in (0,1)$ is a constant independent of $k$.

Step 4 :

Compute $\varPhi (x_{k}+d_{k})$ and define

$$\begin{aligned} \rho _{k}=\dfrac{\varPhi (x_{k})-\varPhi (x_{k}+d_{k})}{m_{k}(x_{k})-m_{k}(x_{k}+d_{k})}. \end{aligned}$$

If $\rho _{k}\ge \alpha _{1}$ or if both $\rho _{k}\ge \alpha _{0}$ and the models $p_{k}$ and $q_{k}$ are fully linear on $B[x_{k};\varDelta _{k}]$, then $x_{k+1}=x_{k}+d_{k}$ and the models are updated to include the new iterate into the sample set, resulting in new models $p_{k+1}^{*}(x_{k+1}+d)$ (with gradient at $d=0$ denoted by $g_{k+1}^{*}$) and $q_{k+1}^{*}(x_{k+1}+d)$ (with Jacobian matrix at $d=0$ denoted by $A_{k+1}^{*}$). Otherwise, set $x_{k+1}=x_{k}$, $p_{k+1}^{*}=p_{k}$ ($g_{k+1}^{*}=g_{k}$) and $q_{k+1}^{*}=q_{k}$ ($A_{k+1}^{*}=A_{k}$).

Step 5 :

If $\rho _{k}<\alpha _{1}$, use the model-improvement algorithm to certify if $p_{k}$ and $q_{k}$ are fully linear models on $B[x_{k};\varDelta _{k}]$. If such a certificate is not obtained, we declare that $p_{k}$ or $q_{k}$ is not certifiably fully linear (CFL) and make one or more improvement steps. Define $p_{k+1}^{*}$ and $q_{k+1}^{*}$ as the (possibly improved) models.

Step 6 :

Set

$$\begin{aligned} \varDelta _{k+1}^{*}\in \left\{ \begin{array}{ll} \left[ \varDelta _{k},\min \left\{ \gamma _{2}\varDelta _{k},\bar{\varDelta }\right\} \right] &{}\quad \text {if}\ \rho _{k}\ge \alpha _{1},\\ \left\{ \gamma _{1}\varDelta _{k}\right\} &{}\quad \text {if}\ \rho _{k}<\alpha _{1}\ \text {and}\ p_{k}\\ &{}\qquad \text {and}\ q_{k}\ \text {are fully linear},\\ \left\{ \varDelta _{k}\right\} &{} \quad \text {if}\ \rho _{k}<\alpha _{1}\ \text {and}\ p_{k}\\ &{}\qquad \text {or}\ q_{k}\ \text {is not CFL}. \end{array} \right. \end{aligned}$$

(28)

Step 7 :

Generate $H_{k+1}$, set $k:=k+1$ and go to Step 1.

Remark 3

The matrix $H_{k}$ in (25) approximates the second-order behavior of $f$ and $c$ around $x_{k}$. For example, as suggested by equation (1.5) in Yuan (1985b), one could use $H_{k}=\nabla ^{2}p_{k}(x_{k})+\sum _{i=1}^{r}\nabla ^{2}(q_{k})_{i}(x_{k})$. Moreover, if $h$ is a polyhedral function and $\Vert .\Vert =\Vert .\Vert _{\infty }$, then subproblem (25)–(26) reduces to a quadratic programming problem, which can be solved by standard methods.

In the above algorithm, the iterations for which $\rho _{k}\ge \alpha _{1}$ are said to be successful iterations; the iterations for which $\rho _{k}\in [\alpha _{0},\alpha _{1})$ and $p_{k}$ and $q_{k}$ are fully linear are said to be acceptable iterations; the iterations for which $\rho _{k}<\alpha _{1}$ and $p_{k}$ or $q_{k}$ is not certifiably fully linear are said to be model-improving iterations and; the iterations for which $\rho _{k}<\alpha _{0}$ and $p_{k}$ and $q_{k}$ are fully linear are said to be unsuccessful iterations.

Below we describe the Algorithm 2 used in Step 2, which is an adaptation of the Algorithm 4.2 in Conn et al. (2009b).

Algorithm 2 This algorithm is only applied if $\eta _{1}^{*}(x_{k})\le \epsilon _{c}$ and at least one of the following holds: the model $p_{k}^{*}$ or the model $q_{k}^{*}$ is not CFL on $B\left[ x_{k};\varDelta _{k}^{*}\right]$ or $\varDelta _{k}^{*}>\mu \eta _{1}^{*}(x_{k})$. The constant $\omega \in (0,1)$ is chosen at Step 0 of Algorithm 1.

Initialization: Set $p_{k}^{(0)}=p_{k}^{*}$, $q_{k}^{(0)}=q_{k}^{*}$ and $i=0$.

Repeat :

Set $i:=i+1$. Use the model-improvement algorithm to improve the previous models $p_{k}^{(i-1)}$ and $q_{k}^{(i-1)}$ until they become fully linear on $B\left[ x_{k};\omega ^{i-1}\varDelta _{k}^{*}\right]$ (by Definition 2, this can be done in a finite, uniformly bounded number of steps of the model-improvement algorithm). Denote the new models by $p_{k}^{(i)}$ and $q_{k}^{(i)}$. Set $\tilde{\varDelta }_{k}=\omega ^{i-1}\varDelta _{k}^{*}$, $\tilde{p}_{k}=p_{k}^{(i)}$, $\tilde{g}_{k}=\nabla \tilde{p}_{k}(x_{k})$, $\tilde{q}_{k}=q_{k}^{(i)}$ and $\tilde{A}_{k}=J_{\tilde{q}_{k}}(x_{k})$. Compute

$$\begin{aligned} \eta _{1}^{(i)}(x_{k})=\tilde{l}(x_{k},0)-\tilde{l}(x_{k},\tilde{s}_{k}), \end{aligned}$$

where

$$\begin{aligned} \tilde{s}_{k}=\arg \min _{\Vert s\Vert \le 1}\tilde{l}(x_{k},s), \end{aligned}$$

(29)

and

$$\begin{aligned} \tilde{l}(x_{k},s)\equiv f(x_{k})+(\tilde{g}_{k})^\mathrm{T}s+h(c(x_{k})+\tilde{A}_{k}s). \end{aligned}$$

Set $\tilde{\eta }_{1}(x_{k})=\eta _{1}^{(i)}(x_{k})$.

Until :

$\tilde{\varDelta }_{k}\le \mu \eta _{1}^{(i)}(x_{k})$.

Remark 4

When $h\equiv 0$, then Algorithms 1 and 2 are reduced to the corresponding algorithms in Conn et al. (2009b) for minimizing $f$ without derivatives.

Remark 5

If Step 2 is executed in Algorithm 1, then the models $p_{k}$ and $q_{k}$ are fully linear on $B[x_{k};\tilde{\varDelta }_{k}]$ with $\tilde{\varDelta }_{k}\le \varDelta _{k}$. Hence, by Lemma 2, $p_{k}$ and $q_{k}$ are also fully linear on $B[x_{k};\varDelta _{k}]$ (as well on $B[x_{k};\mu \eta _{1}(x_{k})]$).

4 Global convergence analysis

In this section, we shall prove the weak global convergence of Algorithm 1. Thanks to Theorem 1, it can be done by a direct adaptation of the analysis presented by Conn et al. (2009b). In fact, the proof of most of the results below follows by simply changing the criticality measures ($g_{k}$ and $\nabla f(x_{k})$ in Conn et al. (2009b) to $\eta _{1}(x_{k})$ and $\psi _{1}(x_{k})$, respectively). Thus, in these cases, we only indicate the proof of the corresponding result in Conn et al. (2009b).

The first result says that unless the current iterate is a critical point, Algorithm 2 will not loop infinitely in Step 2 of Algorithm 1.

Lemma 3

Suppose that A1–A3 hold. If $\psi _{1}(x_{k})\ne 0,$ then Algorithm 2 will terminate in a finite number of repetitions.

Proof

See the proof of Lemma 5.1 in Conn et al. (2009b). $\square$

The next lemma establishes the relation between $\eta _{r}(x)$ and $\eta _{1}(x)$.

Lemma 4

Suppose that A3 holds and let $r>0$. Then$,$ for all $x$

$$\begin{aligned} \eta _{r}(x)\ge \min \left\{ 1,r\right\} \eta _{1}(x). \end{aligned}$$

(30)

Proof

It follows as in the proof of Lemma 2.1 in Cartis et al. (2011b). $\square$

Lemma 5

Suppose that A3 holds. Then, there exists a constant $\kappa _{d}>0$ such that the inequality

$$\begin{aligned} m_{k}(x_{k})-m_{k}(x_{k}+d_{k})\ge \kappa _{d}\eta _{1}(x_{k})\min \left\{ \varDelta _{k},\dfrac{\eta _{1}(x_{k})}{1+\Vert H_{k}\Vert }\right\} . \end{aligned}$$

(31)

holds for all $k$.

Proof

From inequality (27) and Lemma 4, it follows as in the proof of Lemma 11 in Grapiglia et al. (2014). $\square$

For the rest of the paper, we consider the following additional assumptions:

• A4 There exists a constant $\kappa _{H}>0$ such that $\Vert H_{k}\Vert \le \kappa _{H}$ for all $k$.

• A5 The sequence $\left\{ \varPhi (x_{k})\right\}$ is bounded below by $\varPhi _\mathrm{low}$.

Lemma 6

Suppose that A1–A4 hold. If $p_{k}$ and $q_{k}$ are fully linear models of $f$ and $c,$ respectively$,$ on the ball $B[x_{k};\varDelta _{k}],$ then

$$\begin{aligned} \varPhi (x_{k}+d_{k})-m_{k}(x_{k}+d_{k})\le \kappa _{m}\varDelta _{k}^{2}, \end{aligned}$$

(32)

where $\kappa _{m}=(L_{f}+2\kappa _{jf}+L_{h}L_{c}+2L_{h}\kappa _{jc}+\kappa _{H})/2$.

Proof

In fact, from Assumptions A1–A4, it follows that

$$\begin{aligned} \varPhi (x_{k}+d_{k})-m_{k}(x_{k}+d_{k})&= f(x_{k}+d_{k})+h(c(x_{k}+d_{k}))-f(x_{k})-\nabla p_{k}(x_{k})^\mathrm{T}d_{k}\nonumber \\&-h(c(x_{k})+J_{q_{k}}(x_{k})d_{k})-\dfrac{1}{2}d_{k}^\mathrm{T}H_{k}d_{k}\nonumber \\&\le f(x_{k}+d_{k})-f(x_{k})\!-\!\nabla f(x_{k})^\mathrm{T}d_{k}+\left( \nabla f(x_{k})\!-\!\nabla p_{k}(x_{k})\right) ^\mathrm{T}d_{k}\nonumber \\&+h(c(x_{k}+d_{k}))-h(c(x_{k})+J_{q_{k}}(x_{k})d_{k})+ \dfrac{1}{2}\kappa _{H}\Vert d_{k}\Vert ^{2}\nonumber \\&\le \dfrac{L_{f}}{2}\varDelta _{k}^{2}+\kappa _{jf} \varDelta _{k}^{2}+L_{h}\Vert c(x_{k}+d_{k})-c(x_{k})-J_{c}(x_{k})d_{k}\Vert \nonumber \\&+L_{h}\Vert (J_{c}(x_{k})-J_{q_{k}}(x_{k}))d_{k} \Vert +\dfrac{1}{2}\kappa _{H}\varDelta _{k}^{2}\nonumber \\&\le \dfrac{1}{2}\left( L_{f}+2\kappa _{jf}+L_{h} L_{c}+2L_{h}\kappa _{jc}+\kappa _{H}\right) \varDelta _{k}^{2}. \end{aligned}$$

$\square$

The proof of the next lemma is based on the proof of Lemma 5.2 in Conn et al. (2009b).

Lemma 7

Suppose that A1–A4 hold. If $p_{k}$ and $q_{k}$ are fully linear models of $f$ and $c,$ respectively$,$ on the ball $B[x_{k};\varDelta _{k}],$ and

$$\begin{aligned} \varDelta _{k}\le \min \left\{ \dfrac{1}{1+\kappa _{H}}, \dfrac{\kappa _{d}(1-\alpha _{1})}{\kappa _{m}}\right\} \eta _{1}(x_{k}), \end{aligned}$$

(33)

then$,$ the $k$-th iteration is successful.

Proof

Since $\Vert H_{k}\Vert \le \kappa _{H}$ and $\varDelta _{k}\le \eta _{1}(x_{k})/(1+\kappa _{H})$, it follows from Lemma 5 that

$$\begin{aligned} m_{k}(x_{k})-m_{k}(x_{k}+d_{k})\ge \kappa _{d}\eta _{1}(x_{k})\varDelta _{k}. \end{aligned}$$

(34)

Then, by Lemma 6 and (33), we have

$$\begin{aligned} 1-\rho _{k}&= \dfrac{(m_{k}(x_{k})-m_{k}(x_{k}+d_{k})) -(\varPhi (x_{k})-\varPhi (x_{k}+d_{k}))}{m_{k}(x_{k})-m_{k}(x_{k}+d_{k})}\nonumber \\&= \dfrac{\varPhi (x_{k}+d_{k})-m_{k}(x_{k}+d_{k})}{m_{k}(x_{k}) -m_{k}(x_{k}+d_{k})}\nonumber \\&\le \dfrac{\kappa _{m}\varDelta _{k}}{\kappa _{d}\eta _{1}(x_{k})}\nonumber \\&\le 1-\alpha _{1}. \end{aligned}$$

(35)

Hence, $\rho _{k}\ge \alpha _{1}$, and consequently iteration $k$ is successful. $\square$

The next lemma gives a lower bound on $\varDelta _{k}$ when $\eta _{1}(x_{k})$ is bounded away from zero. Its proof is based on the proof of Lemma 5.3 in Conn et al. (2009b), and on the proof of the lemma on page 299 in Powell (1984).

Lemma 8

Suppose that A1–A4 hold and let $\epsilon >0$ such that $\eta _{1}(x_{k})\ge \epsilon$ for all $k=0,\ldots ,j,$ where $j\le +\infty$. Then$,$ there exists $\bar{\tau }>0$ independent of $k$ such that

$$\begin{aligned} \varDelta _{k}\ge \bar{\tau },\quad \text {for all}\ k=0,\ldots ,j. \end{aligned}$$

(36)

Proof

We shall prove (36) by induction over $k$ with

$$\begin{aligned} \bar{\tau }=\min \left\{ \beta \epsilon ,\varDelta _{0}^{*},\dfrac{\gamma _{1}\epsilon }{1+\kappa _{H}},\dfrac{\gamma _{1}\kappa _{d}(1-\alpha _{1})\epsilon }{\kappa _{m}}\right\} . \end{aligned}$$

(37)

From equality (24) in Step 2 of Algorithm 1, it follows that

$$\begin{aligned} \varDelta _{k}\ge \min \left\{ \beta \eta _{1}(x_{k}),\varDelta _{k}^{*}\right\} ,\quad \text {for all}\ k. \end{aligned}$$

(38)

Hence, since $\eta _{1}(x_{k})\ge \epsilon$ for $k=0,\ldots ,j$, we have

$$\begin{aligned} \varDelta _{k}\ge \min \left\{ \beta \epsilon , \varDelta _{k}^{*}\right\} ,\quad \text {for all}\ k=0,\ldots ,j. \end{aligned}$$

(39)

In particular, (39) implies that (36) holds for $k=0$.

Now, we assume that (36) is true for $k\in \left\{ 0,\ldots ,j-1\right\}$ and prove it is also true for $k+1$. First, suppose that

$$\begin{aligned} \varDelta _{k}\le \min \left\{ \dfrac{\epsilon }{1+\kappa _{H}},\dfrac{\kappa _{d}(1-\alpha _{1})\epsilon }{\kappa _{m}}\right\} . \end{aligned}$$

(40)

Then, by Lemma 7 and Step 5, the $k$-th iteration is successful or model improving, and so by Step 6 $\varDelta _{k+1}^{*}\ge \varDelta _{k}$. Hence, (39), the induction assumption and (37) imply that

$$\begin{aligned} \varDelta _{k+1}\ge \min \left\{ \beta \epsilon , \varDelta _{k+1}^{*}\right\} \ge \min \left\{ \beta \epsilon ,\varDelta _{k}\right\} \ge \min \left\{ \beta \epsilon ,\bar{\tau }\right\} =\bar{\tau }. \end{aligned}$$

(41)

Therefore, (36) is true for $k+1$. On the other hand, suppose that (40) is not true. Then, from (28), (39) and (37), it follows that

Hence, (36) holds for $k=0,\ldots ,j$. $\square$

Lemma 9

Suppose that A1–A5 hold. Then$,$

$$\begin{aligned} \lim _{k\rightarrow +\infty }\varDelta _{k}=0. \end{aligned}$$

(42)

Proof

See Lemmas 5.4 and 5.5 in Conn et al. (2009b). $\square$

The proof of the next result is based on the proof of Lemma 5.6 in Conn et al. (2009b).

Lemma 10

Suppose that A1–A5 hold. Then$,$

$$\begin{aligned} \liminf _{k\rightarrow +\infty }\eta _{1}(x_{k})=0. \end{aligned}$$

(43)

Proof

Suppose that (43) is not true. Then, there exists a constant $\epsilon >0$ such that

$$\begin{aligned} \eta _{1}(x_{k})\ge \epsilon ,\quad \text {for all}\ k. \end{aligned}$$

(44)

In this case, by Lemma 8, there exists $\bar{\tau }>0$ such that $\varDelta _{k}\ge \bar{\tau }$ for all $k$, contradicting Lemma 9.

The lemma below says that if a subsequence of $\left\{ \eta _{1}(x_{k})\right\}$ converges to zero, so does the corresponding subsequence of $\left\{ \psi _{1}(x_{k})\right\}$.

Lemma 11

Suppose that A1–A3 hold. Then$,$ for any sequence $\left\{ k_{i}\right\}$ such that

$$\begin{aligned} \lim _{i\rightarrow \infty }\eta _{1}(x_{k_{i}})=0, \end{aligned}$$

(45)

it also holds that

$$\begin{aligned} \lim _{i\rightarrow \infty }\psi _{1}(x_{k_{i}})=0. \end{aligned}$$

(46)

Proof

See Lemma 5.7 in Conn et al. (2009b). $\square$

Now, we can obtain the weak global convergence result.

Theorem 2

Suppose that A1–A5 hold. Then$,$

$$\begin{aligned} \liminf _{k\rightarrow +\infty }\psi _{1}(x_{k})=0. \end{aligned}$$

(47)

Proof

It follows directly from Lemmas10 and 11. $\square$

By Theorem 2 and Lemma 1(a), at least one accumulation point of the sequence $\left\{ x_{k}\right\}$ generated by Algorithm 1 is a critical point of $\varPhi$ (in the sense of Definition 1).

5 Worst-case complexity analysis

In this section, we shall study the worst-case complexity of a slight modification of Algorithm 1 following closely the arguments of Cartis et al. (2011a, b). For that, we replace (28) by the rule

$$\begin{aligned} \varDelta _{k+1}^{*}\in \left\{ \begin{array}{ll} \left[ \varDelta _{k},\min \left\{ \gamma _{2}\varDelta _{k},\bar{\varDelta }\right\} \right] &{} \quad \text {if}\ \rho _{k}\ge \alpha _{1},\\ \left\{ \gamma _{1}\varDelta _{k}\right\} &{} \quad \text {if}\ \rho _{k}<\alpha _{1}\ \text {and}\ p_{k}\\ &{}\qquad \text {and}\ q_{k}\ \text {are fully linear},\\ \left\{ \gamma _{0}\varDelta _{k}\right\} &{} \quad \text {if}\ \rho _{k}<\alpha _{1}\ \text {and}\ p_{k}\\ &{}\qquad \text {or}\ q_{k}\ \text {is not CFL}, \end{array} \right. \end{aligned}$$

(48)

where $0<\gamma _{1}<\gamma _{0}<1<\gamma _{2}$. Moreover, we consider $\epsilon _{c}=+\infty$ in Step 0. In this way, Step 2 will be called at all iterations and, consequently, the models $p_{k}$ and $q_{k}$ will be fully linear for all $k$.

Definition 3

Given $\epsilon \in (0,1]$, a point $x^{*}\in \mathbb {R}^{n}$ is said to be an $\epsilon$-critical point of $\varPhi$ if $\psi _{1}(x^{*})\le \epsilon$.

Let $\left\{ x_{k}\right\}$ be a sequence generated by Algorithm 1. Since the computation of $\psi _{1}(x_{k})$ requires the gradient $\nabla f(x_{k})$ and the Jacobian matrix $J_{c}(x_{k})$ [recall (5) and (6)], in the derivative-free framework we cannot test directly whether an iterate $x_{k}$ is $\epsilon$-critical or not. One way to detect $\epsilon$-criticality is to test $\eta _{1}(x_{k})$ based on the following lemma.

Lemma 12

Suppose that A1–A3 hold and let $\epsilon \in (0,1]$. If

$$\begin{aligned} \eta _{1}(x_{k})\le \dfrac{\epsilon }{(\kappa _{s}\mu +1)}\equiv \epsilon _{s}, \end{aligned}$$

(49)

then $x_{k}$ is an $\epsilon$-critical point of $\varPhi$.

Proof

Since the models $p_{k}$ and $q_{k}$ are fully linear on a ball $B[x_{k};\varDelta _{k}]$ with $\varDelta _{k}\le \mu \eta _{1}(x_{k})$, by Theorem 1, we have

$$\begin{aligned} |\psi _{1}(x_{k})-\eta _{1}(x_{k})|\le \kappa _{s}\varDelta _{k}\le \kappa _{s}\mu \eta _{1}(x_{k}). \end{aligned}$$

(50)

Consequently, from (49) and (50), it follows that

$$\begin{aligned} |\psi _{1}(x_{k})|\le |\psi _{1}(x_{k})-\eta _{1}(x_{k})|+|\eta _{1}(x_{k})|\le (\kappa _{s}\mu +1)\eta _{1}(x_{k})\le \epsilon , \end{aligned}$$

(51)

that is, $x_{k}$ is an $\epsilon$-critical point of $\varPhi$. $\square$

Another way to detect $\epsilon$-criticality is provided by Algorithm 2. The test is based on the lemma below.

Lemma 13

Suppose that A1–A3 hold and let $\epsilon \in (0,1]$. Denote by $i_{1}+1$ the number of times that the loop in Algorithm 2 is repeated. If

$$\begin{aligned} i_{1}\ge 1+log\left( \dfrac{\epsilon }{(\kappa _{s}+\mu ^{-1}) \bar{\varDelta }}\right) /log(\omega ), \end{aligned}$$

(52)

then the current iterate $x_{k}$ is an $\epsilon$-critical point of $\varPhi$.

Proof

Let $I_{1}=\left\{ i\in \mathbb {N}\,|\,0<i\le i_{1}\right\}$. Then, we must have

$$\begin{aligned} \mu \eta _{1}^{(i)}(x_{k})<\omega ^{i-1}\varDelta _{k}^{*}, \end{aligned}$$

(53)

for all $i\in I_{1}$. Since the models $p_{k}^{(i)}$ and $q_{k}^{(i)}$ were fully linear on $B[x_{k};\omega ^{i-1}\varDelta _{k}^{*}]$, it follows from Theorem 1 that

$$\begin{aligned} |\psi _{1}(x_{k})-\eta _{1}^{(i)}(x_{k})|\le \kappa _{s}\omega ^{i-1}\varDelta _{k}^{*}, \end{aligned}$$

(54)

for each $i\in I_{1}$. Hence,

$$\begin{aligned} |\psi _{1}(x_{k})|\le |\psi _{1}(x_{k})-\eta _{1}^{(i)}(x_{k})|+|\eta _{1}^{(i)}(x_{k})|\le (\kappa _{s}+\mu ^{-1})\omega ^{i-1}\varDelta _{k}^{*}\le (\kappa _{s}+\mu ^{-1})\omega ^{i-1}\bar{\varDelta },\nonumber \\ \end{aligned}$$

(55)

for all $i\in I_{1}$. On the other hand, since $\omega \in (0,1)$, by (52), we have

$$\begin{aligned}&i_{1}\ge 1+\log \left( \dfrac{\epsilon }{(\kappa _{s}+\mu ^{-1}) \bar{\varDelta }}\right) /\log (\omega ) \nonumber \\&\quad \Longrightarrow i_{1}-1\ge \log \left( \dfrac{\epsilon }{(\kappa _{s}+\mu ^{-1})\bar{\varDelta }}\right) /\log (\omega ) \nonumber \\&\quad \Longrightarrow (i_{1}-1)\log (\omega )\le \log \left( \dfrac{\epsilon }{(\kappa _{s}+\mu ^{-1})\bar{\varDelta }}\right) \nonumber \\&\quad \Longrightarrow \log (\omega ^{i_{1}-1})\le \log \left( \dfrac{\epsilon }{(\kappa _{s}+\mu ^{-1})\bar{\varDelta }}\right) \nonumber \\&\quad \Longrightarrow \omega ^{i_{1}-1}\le \dfrac{\epsilon }{(\kappa _{s}+\mu ^{-1})\bar{\varDelta }} \nonumber \\&\quad \Longrightarrow (\kappa _{s}+\mu ^{-1})\omega ^{i_{1}-1} \bar{\varDelta }\le \epsilon . \end{aligned}$$

(56)

Hence, from (55) and (56), it follows that $\psi _{1}(x_{k})\le \epsilon$, that is, $x_{k}$ is an $\epsilon$-critical point of $\varPhi$. $\square$

In what follows, the worst-case complexity is defined as the maximum number of function evaluations necessary for criterion (49) to be satisfied. For convenience, we will consider the following notation:

$$\begin{aligned} S&= \left\{ k\ge 0\,|\, k\ \text {successful}\right\} , \end{aligned}$$

(57)

$$\begin{aligned} S_{j}&= \left\{ k\le j\,|\,k\in S\right\} ,\quad \text {for each}\ j\ge 0, \end{aligned}$$

(58)

$$\begin{aligned} U_{j}&= \left\{ k\le j\,|\,k\notin S\right\} \quad \text {for each}\ j\ge 0, \end{aligned}$$

(59)

$$\begin{aligned} S'&= \left\{ k\in S\,|\,\eta _{1}(x_{k})>\epsilon _{s}= \epsilon _{s}(\epsilon )\right\} ,\quad \epsilon >0, \end{aligned}$$

(60)

where $S_{j}$ and $U_{j}$ form a partition of $\left\{ 1,\ldots ,j\right\}$, $|S_{j}|$, $|U_{j}|$ and $|S'|$ will denote the cardinality of these sets, and $\epsilon _{s}=\epsilon _{s}(\epsilon )$ is defined in (49). Furthermore, let $\tilde{S}$ be a generic index set such that

$$\begin{aligned} \tilde{S}\subseteq S', \end{aligned}$$

(61)

and whose cardinality is denoted by $|\tilde{S}|$.

The next lemma provides an upper bound on the cardinality $|\tilde{S}|$ of a set $\tilde{S}$ satisfying (61).

Lemma 14

Suppose that A3 and A5 hold. Given any $\epsilon >0,$ let $S'$ and $\tilde{S}$ be defined in (60) and (61), respectively. Suppose that the successful iterates $x_{k}$ generated by Algorithm 1 have the property that

$$\begin{aligned} m_{k}(x_{k})-m_{k}(x_{k}+d_{k})\ge \theta _{c}\epsilon ^{p},\quad \text {for all}\ k\in \tilde{S}, \end{aligned}$$

(62)

where $\theta _{c}$ is a positive constant independent of $k$ and $\epsilon ,$ and $p>0$. Then$,$

$$\begin{aligned} |\tilde{S}|\le \left\lceil \kappa _{p}\epsilon ^{-p}\right\rceil , \end{aligned}$$

(63)

where $\kappa _{p}\equiv \left( \varPhi (x_{0})-\varPhi _\mathrm{low}\right) \!/\!\left( \alpha _{1}\theta _{c}\right)$.

Proof

It follows as in the proof of Theorem 2.2 in Cartis et al. (2011a). $\square$

The next lemma gives a lower bound on $\varDelta _{k}$ when $\eta _{1}(x_{k})$ is bounded away from zero.

Lemma 15

Suppose that A1–A4 hold and let $\epsilon \in (0,1]$ such that $\eta _{1}(x_{k})\ge \epsilon _{s}$ for all $k=0,\ldots ,j,$ where $j\le +\infty$ and $\epsilon _{s}=\epsilon _{s}(\epsilon )$ is defined in (49). Then$,$ there exists $\tau >0$ independent of $k$ and $\epsilon$ such that

$$\begin{aligned} \varDelta _{k}\ge \tau \epsilon ,\quad \text {for all}\ k=0,\ldots ,j. \end{aligned}$$

(64)

Proof

It follows from Lemma 8. $\square$

Now, we can obtain an iteration complexity bound for Algorithm 1. The proof of this result is based on the proof of Theorem 2.1 and Corollary 3.4 in Cartis et al. (2011a).

Theorem 3

Suppose that A1–A5 hold. Given any $\epsilon \in (0,1],$ assume that $\eta _{1}(x_{0})>\epsilon _{s}$ and let $j_{1}\le +\infty$ be the first iteration such that $\eta _{1}(x_{j_{1}+1})\le \epsilon _{s},$ where $\epsilon _{s}=\epsilon _{s}(\epsilon )$ is defined in (49). Then$,$ Algorithm 1 with rule (48) and $\epsilon _{c}=+\infty$ takes at most

$$\begin{aligned} L_{1}^{s}\equiv \left\lceil \kappa _{c}^{s}\epsilon ^{-2}\right\rceil \end{aligned}$$

(65)

successful iterations to generate $\eta _{1}(x_{j_{1}+1})\le \epsilon _{s}$ and consequently $($by Lemma 12) $\psi _{1}(x_{j_{1}+1})\le \epsilon ,$ where

$$\begin{aligned} \kappa _{c}^{s}\equiv \left( \varPhi (x_{0})-\varPhi _\mathrm{low}\right) / (\alpha _{1}\theta _{c}),\quad \theta _{c}=\kappa _{d}\min \left\{ \tau , 1/(1+\kappa _{H})\right\} /(\kappa _{s}\mu +1)^{2}. \end{aligned}$$

(66)

Furthermore$,$

$$\begin{aligned} j_{1}\le \left\lceil \kappa _{w}\epsilon ^{-2}\right\rceil \equiv L_{1}, \end{aligned}$$

(67)

and Algorithm 1 takes at most $L_{1}$ iterations to generate $\psi _{1}(x_{j_{1}+1})\le \epsilon ,$ where

$$\begin{aligned} \kappa _{w}\equiv \left( 1-\dfrac{\log (\gamma _{2}^{-1})}{\log (\gamma _{2}^{-1})}\right) \kappa _{c}^{s}+ \dfrac{(\kappa _{s}\mu +1)\varDelta _{0}^{*}}{\tau \log (\gamma _{2}^{-1})}. \end{aligned}$$

(68)

Proof

The definition of $j_{1}$ in the statement of the theorem implies that

$$\begin{aligned} \eta _{1}(x_{k})>\epsilon _{s},\quad \text {for}\ k=0,\ldots ,j_{1}. \end{aligned}$$

(69)

Thus, by Lemma 5, Assumption A4, Lemma 15 and the definition of $\epsilon _{s}$ in (49), we obtain

$$\begin{aligned} m_{k}(x_{k})-m_{k}(x_{k}+d_{k})&\ge \kappa _{d}\epsilon _{s} \min \left\{ \varDelta _{k},\dfrac{\epsilon _{s}}{1+\kappa _{H}}\right\} \nonumber \\&\ge \dfrac{\kappa _{d}}{(\kappa _{s}\mu +1)^{2}}\epsilon \min \left\{ \tau \epsilon , \dfrac{\epsilon }{1+\kappa _{H}}\right\} \nonumber \\&= \dfrac{\kappa _{d}}{(\kappa _{s}\mu +1)^{2}}\min \left\{ \tau ,1/(1+\kappa _{H})\right\} \epsilon ^{2} \nonumber \\&= \theta _{c}\epsilon ^{2},\quad \text {for}\ k=1,\ldots ,j_{1}, \end{aligned}$$

(70)

where $\theta _{c}$ is defined by (66). Now, with $j=j_{1}$ in (58) and (59), Lemma 14 with $\tilde{S}=S_{j_{1}}$ and $p=2$ provides the complexity bound

$$\begin{aligned} |S_{j_{1}}|\le L_{1}^{s}, \end{aligned}$$

(71)

where $L_{1}^{s}$ is defined by (65).

On the other hand, from rule (48) and Lemma 15, it follows that

$$\begin{aligned} \varDelta _{k+1}^{*}&\le \gamma _{2}\varDelta _{k}\le \gamma _{2} \varDelta _{k}^{*},\quad \text {if}\ k\in S_{j_{1}},\\ \varDelta _{k+1}^{*}&\le \gamma _{0}\varDelta _{k}\le \gamma _{0} \varDelta _{k}^{*},\quad \text {if}\ k\in U_{j_{1}},\\ \varDelta _{k}^{*}&\ge \varDelta _{k}\ge \dfrac{\tau }{\kappa _{s}\mu +1} \epsilon ,\quad \text {for}\ k=0,\ldots ,j_{1}. \end{aligned}$$

Thus, considering $\omega _{k}\equiv 1/\varDelta _{k}^{*}$, we have

$$\begin{aligned} c_{1}\omega _{k}&\le \omega _{k+1},\quad \text {if}\ k\in S_{j_{1}}, \end{aligned}$$

(72)

$$\begin{aligned} c_{2}\omega _{k}&\le \omega _{k+1},\quad \text {if}\ k\in U_{j_{1}}, \end{aligned}$$

(73)

$$\begin{aligned} \omega _{k}&\le \bar{\omega }\epsilon ^{-1},\quad \text {for}\ k=0,\ldots ,j_{1}, \end{aligned}$$

(74)

where $c_{1}=\gamma _{2}^{-1}\in (0,1]$, $c_{2}=\gamma _{0}^{-1}>1$ and $\bar{\omega }=(\kappa _{s}\mu +1)/\tau$. From (72) and (73), we deduce inductively

$$\begin{aligned} \omega _{0}c_{1}^{|S_{j_{1}}|}c_{2}^{|U_{j_{1}}|}\le \omega _{j_{1}}. \end{aligned}$$

Hence, from (74), it follows that

$$\begin{aligned} c_{1}^{|S_{j_{1}}|}c_{2}^{|U_{j_{1}}|}\le \dfrac{\bar{\omega }\epsilon ^{-1}}{\omega _{0}}, \end{aligned}$$

(75)

and so, taking logarithm on both sides, we get

$$\begin{aligned} |U_{j_{1}}|\le \left[ -\dfrac{\log (c_{1})}{\log (c_{2})}|S_{j_{1}}|+ \dfrac{\bar{\omega }}{\omega _{0}\log (c_{2})}\epsilon ^{-1}\right] . \end{aligned}$$

(76)

Finally, since $j_{1}=|S_{j_{1}}|+|U_{j_{1}}|$ and $\epsilon ^{-2}\ge \epsilon ^{-1}$, the bound (67) is the sum of the upper bounds (71) and (76). $\square$

Remark 6

Theorem 3 also implies limit (47), which was established in Theorem 2. However, note that Theorem 2 was proved for $\epsilon _{c}>0$, while to prove Theorem 3 we needed the stronger assumption $\epsilon _{c}=+\infty$.

Corollary 1

Suppose that A1–A5 hold and let $\epsilon \in (0,1]$. Furthermore$,$ assume that the model-improving algorithm requires at most $K$ evaluations of $f$ and $c$ to construct fully linear models. Then, Algorithm 1 with rule (48) and $\epsilon _{c}=+\infty$ reaches an $\epsilon$-critical point of $\varPhi$ after at most

$$\begin{aligned} O\left( K\left[ |\log (\epsilon )|+|\log (\kappa _{u})|\right] \epsilon ^{-2}\right) \end{aligned}$$

(77)

function evaluations $($that is$,$ evaluations of $f$ and $c),$ where $\kappa _{u}=(\kappa _{s}+\mu ^{-1})\bar{\varDelta }$.

Proof

In the worst case, Algorithm 2 will be called in all iterations of Algorithm 1, and in each one of this calls, the number of repetitions in Algorithm 2 will be bounded above by

$$\begin{aligned} \left| \dfrac{\log \left( \dfrac{\epsilon }{\kappa _{u}}\right) }{\log (\omega )}\right| , \end{aligned}$$

(78)

such that the $\epsilon$-criticality criterion (52) in Lemma 13 is not satisfied. Since in each one of these repetitions the model-improving algorithm requires at most $K$ evaluations of $f$ and $c$ to construct fully linear models, it follows that each iteration of Algorithm 1 requires at most

$$\begin{aligned} K\left| \dfrac{\log \left( \dfrac{\epsilon }{\kappa _{u}}\right) }{\log (\omega )}\right| \end{aligned}$$

(79)

function evaluations. Hence, by Theorem 3, Algorithm 1 takes at most

$$\begin{aligned} K\left| \dfrac{\log \left( \dfrac{\epsilon }{\kappa _{u}}\right) }{\log (\omega )}\right| \kappa _{w}\epsilon ^{-2} \end{aligned}$$

(80)

function evaluations to reduce the criticality measure $\psi _{1}(x)$ below $\epsilon$. $\square$

Corollary 2

Suppose that A1–A5 hold and let $\epsilon \in (0,1]$. Furthermore$,$ assume that Algorithm 6.3 in Conn et al. (2009a) is used as model-improving algorithm. Then$,$ Algorithm 1 with rule (48) and $\epsilon _{c}=+\infty$ reaches an $\epsilon$-critical point of $\varPhi$ after at most

$$\begin{aligned} O\left( (n+1)\left[ |\log (\epsilon )|+|\log (\kappa _{u})|\right] \epsilon ^{-2}\right) \end{aligned}$$

(81)

function evaluations $($that is$,$ evaluations of $f$ and $c),$ where $\kappa _{u}=(\kappa _{s}+\mu ^{-1})\bar{\varDelta }$.

Proof

It follows from the fact that Algorithm 6.3 in Conn et al. (2009a) takes at most $K=n+1$ evaluations of $f$ and $c$ to construct fully linear models. $\square$

To contextualize the results above, it is worth to review some recent works on worst-case complexity in nonconvex and nonlinear optimization. Regarding derivative-based algorithms, Cartis et al. (2011b) have proposed a first-order trust-region method³ and a first-order quadratic regularization method for minimizing (1), for which they proved a worst-case complexity bound of $O\left( \epsilon ^{-2}\right)$ function evaluations to reduce $\psi _{1}(x_{k})$ below $\epsilon$. On the other hand, in the context of derivative-free optimization, Cartis et al. (2012) have proved a worst-case complexity bound of

$$\begin{aligned} O\left( (n^{2}+5n)\left[ 1+|\log (\epsilon )|\right] \epsilon ^{-\frac{3}{2}}\right) \end{aligned}$$

(82)

function evaluations for their adaptive cubic regularization (ARC) algorithm applied to unconstrained smooth optimization, where derivatives are approximated by finite differences. Furthermore, for the minimization of a nonconvex and nonsmooth function, Nesterov (2011) has proposed a random derivative-free smoothing algorithm for which he has proved a worst-case complexity bound of

$$\begin{aligned} O\left( n(n+4)^{2}\epsilon ^{-3}\right) \end{aligned}$$

(83)

function evaluations to reduce the expected squared norm of the gradient of the smoothing function below $\epsilon$. Finally, still in the nonsmooth case, Garmanjani and Vicente (2013) have proposed a class of smoothing direct-search methods for which they proved a worst-case complexity bound of

$$\begin{aligned} O\left( n^{\frac{5}{2}}\left[ |\log (\epsilon )|+\log (n)\right] \epsilon ^{-3}\right) \end{aligned}$$

(84)

function evaluations to reduce the norm of the gradient of the smoothing function below $\epsilon$.

Comparing the worst-case complexity bound (81) with the bounds of (82) and (83), we see that (81) is better in terms of the powers of $n$ and $\epsilon$. However, in such comparison, we must take into account that these worst-case complexity bounds were obtained for different criticality measures.

6 A derivative-free exact penalty algorithm

Let us now consider the equality-constrained optimization problem (3), where the objective function $f:\mathbb {R}^{n}\rightarrow \mathbb {R}$ and the constraint function $c:\mathbb {R}^{n}\rightarrow \mathbb {R}^{r}$ are continuously differentiable. One way to solve such problem consists of solving the related unconstrained problem

$$\begin{aligned} \min _{x\in \mathbb {R}^{n}} \varPhi (x,\sigma ), \end{aligned}$$

(85)

where

$$\begin{aligned} \varPhi (x,\sigma )\equiv f(x)+\sigma \Vert c(x)\Vert \end{aligned}$$

(86)

is an exact penalty function and $\Vert .\Vert$ is a polyhedral norm. More specifically, an exact penalty algorithm for problem (3) can be stated as follows.

Algorithm 3 (Exact Penalty Algorithm - see, e.g., Sun and Yuan 2006)

Step 0 :

Given $x_{0}\in \mathbb {R}^{n}$, $\sigma _{0}>0$, $\lambda >0$ and $\epsilon >0$, set $k:=0$.

Step 1 :

Find a solution $x_{k+1}$ of problem (85) with $\sigma =\sigma _{k}$ and starting at $x_{k}$ (or at $x_{0}$).

Step 2 :

If $\Vert c(x_{k+1})\Vert \le \epsilon$, stop. Otherwise, set $\sigma _{k+1}=\sigma _{k}+\lambda$, $k:=k+1$ and go to Step 1.

As mentioned in Sect. 1, problem (85) is a particular case of problem (1). For this problem, the criticality measure $\psi _{1}(x)$ becomes

$$\begin{aligned} \psi _{1}(x)=f(x)+\sigma \Vert c(x)\Vert -\min _{\Vert s\Vert \le 1}\left\{ f(x)+\nabla f(x)^\mathrm{T}s+\sigma \Vert c(x)+J_{c}(x)s\Vert \right\} \equiv \varPsi _{\sigma }(x),\nonumber \\ \end{aligned}$$

(87)

and we have the following result.

Theorem 4

Suppose that A1, A2 and A4 hold$,$ and assume that $\left\{ f(x_{k})\right\}$ is bounded below. Then$,$ for any $\epsilon \in (0,1]$, Algorithm 1 applied to problem (85) will generate a point $x(\sigma )$ such that

$$\begin{aligned} \varPsi _{\sigma }(x(\sigma ))\le \epsilon . \end{aligned}$$

(88)

Proof

It follows directly from Theorem 2 (or from Theorem 3 when (48) is used and $\epsilon _{c}=+\infty$). $\square$

By the above theorem, we can solve approximately subproblem (85) in Step 1 of Algorithm 3 by applying Algorithm 1. The result is the following derivative-free exact penalty algorithm.

Algorithm 4 (Derivative-Free Exact Penalty Algorithm)

Step 0 :

Given $x_{0}\in \mathbb {R}^{n}$, $\sigma _{0}>0$, $\lambda >0$ and $\epsilon >0$, set $k:=0$.

Step 1 :

Apply Algorithm 1 to solve subproblem (85) with $\sigma =\sigma _{k}$. Start at $x_{k}$ (or at $x_{0}$) and stop at an approximate solution $x_{k+1}$ for which

$$\begin{aligned} \varPsi _{\sigma _{k}}(x_{k+1})\le \epsilon , \end{aligned}$$

where $\psi _{\sigma _{k}}(x_{k+1})$ is defined in (87) with $\sigma =\sigma _{k}$ and $x=x_{k+1}$.

Step 2 :

If $\Vert c(x_{k+1})\Vert \le \epsilon$, stop. Otherwise, set $\sigma _{k+1}=\sigma _{k}+\lambda$, $k:=k+1$ and go to Step 1.

Definition 4

Given $\epsilon \in (0,1]$, a point $x\in \mathbb {R}^{n}$ is said to be a $\epsilon$-stationary point of problem (3) if there exists $y^{*}$ such that

$$\begin{aligned} \Vert \nabla f(x)+J_{c}(x)^\mathrm{T}y^{*}\Vert \le \epsilon . \end{aligned}$$

(89)

If, additionally, $\Vert c(x)\Vert \le \epsilon$, then $x$ is said to be a $\epsilon$-KKT point of problem (3).

The next result, due to Cartis et al. (2011b), establishes the relation between $\epsilon$-critical points of $\varPhi (.,\sigma )$ and $\epsilon$-KKT points of (3).

Theorem 5

Suppose that A1 holds and let $\sigma >0$. Consider minimizing $\varPhi (.,\sigma )$ by some algorithm and obtaining an approximate solution $x$ such that

$$\begin{aligned} \varPsi _{\sigma }(x)\le \epsilon , \end{aligned}$$

(90)

for a given tolerance $\epsilon >0$ $($that is$,$ $x$ is a $\epsilon$-critical point of $\varPhi (.,\sigma )).$ Then$,$ there exists $y^{*}(\sigma )$ such that

$$\begin{aligned} \Vert \nabla f(x)+J_{c}(x)^\mathrm{T}y^{*}(\sigma )\Vert \le \epsilon . \end{aligned}$$

(91)

Additionally$,$ if $\Vert c(x)\Vert \le \epsilon ,$ then $x$ is a $\epsilon$-KKT point of problem (3).

Proof

See Theorem 3.1 in Cartis et al. (2011b). $\square$

The theorem below provides a worst-case complexity bound for Algorithm 4.

Theorem 6

Suppose that A1, A2 and A4 hold. Assume that $\left\{ f(x_{k})\right\}$ is bounded below. If there exists $\bar{\sigma }>0$ such that $\sigma _{k}\le \bar{\sigma }$ for all $k,$ then Algorithm 4 $($where Algorithm 1 in Step 1 satisfies the assumptions in Corollary 1) terminates either with an $\epsilon$-KKT point or with an infeasible $\epsilon$-stationary point of (3) in at most

$$\begin{aligned} \dfrac{\bar{\sigma }K}{\lambda }\left| \dfrac{log\left( \dfrac{\epsilon }{\bar{\kappa }_{u}}\right) }{log(\omega )}\right| \left\lceil \bar{\kappa }_{w}\epsilon ^{-2}\right\rceil \end{aligned}$$

(92)

function evaluations$,$ where $\bar{\kappa }_{u}$ and $\bar{\kappa }_{w}$ are positive constants dependent of $\bar{\sigma },$ but are independent of the problem dimensions $n$ and $r$.

Proof

Using Corollary 1, it follows as in the proof of part (i) of Theorem 3.2 in Cartis et al. (2011b). $\square$

For constrained nonlinear optimization with derivatives, Cartis et al. (2011b) have proposed a first-order exact penalty algorithm, for which they have proved a worst-case complexity bound of $O(\epsilon ^{-2})$ function evaluations. Another complexity bound of the same order was obtained by Cartis et al. (2014) under weaker conditions for a first-order short-step homotopy algorithm. Furthermore, the same authors have proposed in Cartis et al. (2013) an short-step ARC algorithm, for which they have proved an improved worst-case complexity bound of $O\left( \epsilon ^{-3/2}\right)$ function evaluations. However, despite the existence of several derivative-free algorithms for constrained optimization (see, e.g., Bueno et al. 2013; Conejo et al. 2013, 2014; Diniz-Ehrhardt et al. 2011; Martínez and Sobral 2013), to the best of our knowledge, (92) is the first complexity bound for constrained nonlinear optimization without derivatives.

7 Numerical experiments

To investigate the computational performance of the proposed algorithm, we have tested a MATLAB implementation of Algorithm 1, called “DFMS”, on a set of 43 finite minimax problems from Luksǎn and Vlček (2000) and Di Pillo et al. (1993). Recall that the finite minimax problem is a particular case of the composite NSO problem (1) where $f=0$ and $h(c)=\max _{1\le i\le r}c_{i}$, namely

$$\begin{aligned} \min _{x\in \mathbb {R}^{n}}\varPhi (x)\equiv \max _{1\le i\le r} c_{i}(x). \end{aligned}$$

(93)

In the code DFMS, we approximate each function $c_{i}$ by a linear interpolation model of the form (11). The interpolation points around $x_{k}$ are chosen using Algorithm 6.2 in Conn et al. (2009a). As model-improvement algorithm, we employ Algorithm 6.3 in Conn et al. (2009a). Furthermore, as $h(c)=\max _{1\le i\le r}c_{i}$ is a polyhedral function, we consider $\Vert .\Vert =\Vert .\Vert _{\infty }$ and $H_{k}=0$ for all $k$. In this way, subproblems (23), (25), (26) and (29) are reduced to linear programming problems, which are solved using the MATLAB function linprog. Finally, we use (28) to update $\varDelta _{k}^{*}$.

First, with the purpose of evaluating the ability of the code DFMS to obtain accurate solutions for the finite minimax problem, we applied this code on the test set with a maximum number of function evaluations to be $2550$ and the parameters in Step 0 as $\bar{\varDelta }=50$, $\varDelta _{0}^{*}=1$, $\alpha _{0}=0$, $\alpha _{1}=0.25$, $\gamma _{1}=0.5$, $\gamma _{2}=2$, $\epsilon _{c}=10^{-4}$, $\mu =1$, $\beta =0.75$ and $\omega =0.5$. Within the budget of function evaluations, the code was terminated when any one of the criteria below was satisfied:

$$\begin{aligned} \varDelta _{k}<10^{-4}\quad \text {or}\quad \varPhi (x_{k})>0.98\varPhi (x_{k-10}),\qquad k>10. \end{aligned}$$

(94)

A problem was considered solved when the solution $\bar{x}$ obtained by DFMS was such that

$$\begin{aligned} \varPhi \text {-Error}\equiv \dfrac{|\varPhi (\bar{x})-\varPhi ^{*}|}{\max \left\{ 1,|\varPhi (\bar{x})|,|\varPhi ^{*}|\right\} }\le 10^{-2}, \end{aligned}$$

(95)

where $\varPhi ^{*}$ is the optimal function value provided by Luksǎn and Vlček (2000) and Di Pillo et al. (1993).

Problems and results are reported in Table 1, where “n”, “r” and “$n\varPhi$” represent the number of variables, the number of subfunctions and the number of function evaluations, respectively. Moreover, an entry “F” indicates that the code stopped due to some error.

Table 1 Numerical results for finite minimax problems

The results given in Table 1 show that DFMS was able to solve most of the problems in the test set (30 of them), with a reasonable number of function evaluations. The exceptions were problems 3, 13, 16–18, 20, 24, 32, 33 and 43, where criterion (95) was not satisfied, and problems 14, 36 and 42, in which the code stopped due to some error.

To investigate the potentialities and limitations of Algorithm 1, we also compare DFMS with the following codes:

• NMSMAX: a MATLAB implementation of the Nelder–Mead method (Nelder and Mead 1965), freely available from the Matrix Computation Toolbox;⁴ and

• NOMAD (version 3.6.2): a MATLAB implementation of the MADS algorithm (Le Digabel 2011), freely available from the OPTI Toolbox.⁵

We consider the data profile of Moré and Wild (2009). The convergence test for the codes is:

$$\begin{aligned} \varPhi (x_{0})-\varPhi (x)\ge \left( 1-\tau \right) \left( \varPhi (x_{0})-\varPhi _{L}\right) , \end{aligned}$$

(96)

where $\tau >0$ is a tolerance, $x_{0}$ is the starting point for the problem, and $\varPhi _{L}$ is computed for each problem as the smallest value of $\varPhi$ obtained by any solver within a given number $\mu _{\varPhi }$ of function evaluations. Since the problems in our test set have at most 50 variables, we set $\mu _{\varPhi }=2550$ so that all solvers can use at least 50 simplex gradients. The data profiles are presented for $\tau =10^{-k}$ with $k\in \left\{ 1,3,5,7\right\}$.

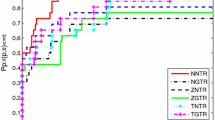
Despite the simplicity of our implementation of Algorithm 1, the data profiles in Figs. 1 and 2 suggest that DFMS is competitive with NMSMAX and NOMAD on finite minimax problems. This result is not so surprising, since DFMS exploits the structure of the finite minimax problem, which is not considered by codes NMSMAX and NOMAD.

Fig. 1

Data profiles for the finite minimax problems show the percentage of problems solved as a function of a computational budget of simplex gradients. Here, we have the graphs for tolerances $\tau =10^{-1}$ and $\tau =10^{-3}$

Fig. 2

Data profiles for the finite minimax problems show the percentage of problems solved as a function of a computational budget of simplex gradients. Here, we have the graphs for tolerances $\tau =10^{-5}$ and $\tau =10^{-7}$

8 Conclusions

In this paper, we have presented a derivative-free trust-region algorithm for composite NSO. The proposed algorithm is an adaptation of the derivative-free trust-region algorithm of Conn et al. (2009b) for unconstrained smooth optimization, with elements of the trust-region algorithms proposed by Fletcher (1982a), Powell (1983), Yuan (1985a) and Cartis et al. (2011b) for composite NSO. Under suitable conditions, weak global convergence was proved. Furthermore, considering a slightly modified update rule for the trust-region radius and assuming that the models are fully linear at all iterations, we adapted the argument of Cartis et al. (2011a, b) to prove a function-evaluation complexity bound for the algorithm reducing the criticality measure below $\epsilon$. This complexity result was then specialized to the case when the composite function is an exact penalty function, providing a worst-case complexity bound for equality-constrained optimization problems, when the solution is computed using a derivative-free exact penalty algorithm. Finally, preliminary numerical experiments were done, and the results suggest that the proposed algorithm is competitive with the Nelder–Mead algorithm (Nelder and Mead 1965) and the MADS algorithm (Audet and Dennis 2006) on finite minimax problems.

Future research includes the conducting of extensive numerical tests using more sophisticated implementations of Algorithm 1. Further, it is worth to mention that the mechanism used in Algorithm 2 for ensuring the quality of the models is the simplest possible, but not necessarily the most efficient. Perhaps, the self-correcting scheme proposed by Scheinberg and Toint (2010) can be extended to solve composite NSO problems.