Congestion Control in TCP/IP Routers Based on Sampled-Data Systems Theory

Abstract

A methodology for designing congestion controllers, based on active queue management (AQM), is presented here. The congestion control law is derived using sampled-data H_∞ systems theory. More precisely, a sampled-data state feedback that guarantees the stability of the closed-loop system and satisfies a H_∞ disturbance attenuation level is derived here, based on sufficient conditions expressed in terms of linear matrix inequalities. The effectiveness of the developed technique is validated on two examples.

1 Introduction

Network congestion in communication networks is being paid significant attention because of their wide range of applications, from Web servers to industrial control systems. In order to manage network congestion, active queue management (AQM) (Braden et al. 1998) techniques are frequently used, which aim to reduce packet drops and improve the overall network utilization. One of the most well-known AQM policies are random early detection (RED) (Floyd and Jacobson 1993), adaptive RED (ARED) (La et al. 2003) and nonlinear RED (NLRED) (Rastogi and Zaheer 2016). Moreover, the fundamentals of control theory have been used to analyze new AQM schemes, such as proportional integral (PI) (Hollot et al. 2002), proportional integral derivative (PID) (Zhang and Papachristodoulou 2014), adaptive PI (Zhang et al. 2003) and PI enhanced (PIE) (Pan et al. 2013). Also, in Bender (2013) it has proposed the use of a dynamic anti-windup gain matrix to improve the performance of a designed controller used to AQM in congested TCP/IP routers, and it was developed in El Fezazi et al. (2016). A sliding mode variable structure control (SMVS) scheme for TCP congestion control was developed in Ren et al. (2005). The new results on modeling and stabilization analysis of TCP/AQM system with single and multiple bottleneck topologies were proposed in Belamfedel et al. (2018).

This work concentrates on deriving an AQM based on sampled-data control theory. There are several approaches to model sampled-data control systems: One of them is the discrete-time approach (Zhang et al. 2001), based on transforming the continuous-time system into a discrete-time system. A second one is the impulsive systems modeling approach (Hu et al. 2003) that facilitates dealing with systems that have uncertain sampling intervals. The third one is the input delay approach proposed in Fridman et al. (2004), where the system is represented as a continuous-time system with a delayed control input.

A common problem that has been overlooked in most previous AQM proposals is the fact that the input saturates in all practical systems, creating unexpected oscillations, instabilities and performance degradations (El Fezazi et al. 2015; El Fezazi et al. 2017a; El Haoussi et al. 2007). In the AQM context, we can just cite the following papers that deal with input saturation: (El Fezazi et al. 2016; Lamrabet et al. 2017).

Another shortcoming of most previous AQM proposals is that in order to derive control laws, it is usually assumed that the control packets (sent from the controller to the actuator to implement the control algorithm) are transmitted perfectly, without any loss in the control data. However, control packets in practical systems would be lost due to communication interferences, congestions, power saving issues, etc. Furthermore, external disturbance appears in all practical systems and if they are ignored during the controller design, the stability of the practical closed-loop system cannot be guaranteed. It is known that the H_∞ control has an excellent ability to balance the performance of a system in the presence of external disturbance (Ardestani 2016; Cui et al. 2016; El Fezazi et al. 2017).

In summary, this paper concentrates on the problem of AQM in TCP/IP routers under sampled-data control in the presence of input saturation. The main objective of this article is to design a congestion controller for AQM in TCP/IP routers using H_∞ control ideas. The controller is designed based on an input delay approach: Sampled-data H_∞ controllers are characterized such that the closed-loop system is asymptotically stable, and a prescribed disturbance attenuation level γ is guaranteed. By using Jensen’s integral inequality together with Schur complement and constructing a new Lyapunov function, a new set of sufficient conditions are derived to guarantee the asymptotic stability of the closed-loop system; these conditions are expressed in terms of LMIs. The proposal will be illustrated by two numerical examples that make it possible to compare with previous works.

The remainder of this paper is structured as follows. The next section introduces the problem formulation and various preliminary concepts. Section 3 presents the main results in the form of theorems. The effectiveness of the proposed method is shown via two numerical examples in Sect. 4. Finally, conclusions are drawn in Sect. 5.

Notation

Throughout the paper, the superscript T^′ stands for matrix transposition, which denotes the n-dimensional Euclidean space with vector norm ∥.∥ and $R^{{\left( {n \times m} \right) }}$ the set of all n × m real matrices. For a matrix P, $\bar{\lambda }$(P) denotes its maximum eigenvalue. sat(u(t), $u_{0}$) = sign(u(t))min{|K(t)|,$u_{0}$ } denotes the saturation function, with $u_{0} > 0$ denoting the control amplitude bounds of u. For a vector $v\left( t \right)$ for t ∈ [− $t_{0}$, 0], ∥v∥ = $sup_{{t \in \left[ { - t_{0} ,0} \right]}}$ ∥v(t)∥.

2 Problem Formulation and Preliminaries

2.1 Network Dynamic Model Rⁿ

In order to derive congestion controllers for networks based on control theory, the following model is frequently used (Misra et al. 2000). This model is described by the following nonlinear delay differential equations:

$$ \begin{aligned} & \dot{W}\left( t \right) = \frac{1}{RTT\left( t \right)} - \frac{{W\left( t \right)W\left( {t - RTT\left( t \right)} \right)}}{{2RTT\left( {t - RTT\left( t \right)} \right)}}p\left( {t - RTT\left( t \right)} \right) \\ & \dot{q}\left( t \right) = - C\left( t \right) + \frac{N\left( t \right)}{RTT\left( t \right)}W\left( t \right) \\ & RTT\left( t \right) = \frac{q\left( t \right)}{C\left( t \right)} + T_{p} \\ \end{aligned} $$

(1)

where $W\left( t \right)$ is the average TCP window size (packets), q(t) is the average queue length (packets), RTT(t) is the round trip time (secs), C(t) is the available link capacity (packets/secs), $T_{\text{p}}$ is the propagation delay (secs), N(t) is the number of TCP sessions and p(t) is the probability of packet mark. It is assumed that W(t) ∈ [0,$W_{m}$] and q(t) ∈ [0,$q_{\text{m}}$] where $W_{\text{m}}$ and $q_{\text{m}}$ denote maximum window size and buffer capacity, respectively. The marking probability p belongs to the interval [0, 1]. For a given triplet of network parameters (N, C₀, T_p), and any triplet of initial conditions

$$ {\mathcal{L}} = \left( {W_{0} , q_{0} ,p_{0} } \right),\;{\text{let}} $$

$$ \varXi = \left\{ {{\mathcal{L}} : W_{0} = \frac{{R_{0} C_{0} }}{N}, q_{0} = C_{0} \left( {R_{0} - T_{p} } \right), p_{0} = \frac{2}{{W_{0}^{2} }}} \right\} $$

be the operating point.

It is assumed that the number of TCP sessions is constant N(t) = N, then defining δ$\varrho$ = $\varrho$ − $\varrho_{0}$ with $\varrho$ = W, q, p, C. We can obtain the linearized version of (1) as follows:

$$ \begin{aligned} \delta \dot{W}\left( t \right) & = \frac{ - N}{{RTT^{2} C_{0} }}\left( {\delta W\left( t \right) + \delta W\left( {t - RTT\left( t \right)} \right)} \right) \\ & \quad - \frac{1}{{RTT^{2} C_{0} }}\left( {\delta q\left( t \right) - \delta q\left( {t - RTT\left( t \right)} \right)} \right) \\ & \quad - \frac{{RTTC_{0}^{2} }}{{RTT^{2} C_{0} }} \delta p\left( {t - RTT\left( t \right)} \right) \\ & \quad + \frac{{RTT - T_{p} }}{{RTT^{2} C_{0} }}\left( {\delta C\left( t \right) - \delta C\left( {t - RTT\left( t \right)} \right)} \right) \\ \delta \dot{q}\left( t \right) &= \frac{N}{RTT}\delta W\left( t \right) - \frac{1}{RTT}\delta q\left( t \right) - \frac{{T_{p} }}{RTT}\delta C\left( t \right) \\ RTT\left( t \right) & = \frac{\delta q\left( t \right)}{{C_{0} }} + R_{0} \\ \end{aligned} $$

(2)

Rewriting (2) in state space form yields

$$ \begin{aligned} & \dot{x}\left( t \right) = Ax\left( t \right) + A_{d} x\left( {t - \tau \left( t \right)} \right) + Bu\left( {t - \tau \left( t \right)} \right) + B_{w} w\left( t \right) \\ & y\left( t \right) = C_{y} x\left( t \right) \\ \end{aligned} $$

(3)

in which

$$ \begin{aligned} & x\left( t \right) = \left[ {\begin{array}{*{20}c} {\delta W\left( t \right)} \\ {\delta q\left( t \right)} \\ \end{array} } \right], w\left( t \right) = \left[ {\begin{array}{*{20}c} {\delta C\left( t \right)} \\ {\delta C\left( {t - RTT\left( t \right)} \right)} \\ \end{array} } \right] \\ & A = \left[ {\begin{array}{*{20}c} {\frac{ - N}{{RTT^{2} C_{0} }}} & {\frac{ - 1}{{RTT^{2} C_{0} }}} \\ {\frac{N}{RTT}} & {\frac{ - 1}{RTT}} \\ \end{array} } \right], A_{d} = \left[ {\begin{array}{*{20}c} {\frac{ - N}{{RTT^{2} C_{0} }}} & {\frac{1}{{RTT^{2} C_{0} }}} \\ 0 & 0 \\ \end{array} } \right], \\ & B = \left[ {\begin{array}{*{20}c} {\frac{{ - RTTC_{0}^{2} }}{{N^{2} }}} \\ 0 \\ \end{array} } \right], B_{w} = \left[ {\begin{array}{*{20}c} {\frac{{RTT - T_{p} }}{{RTT^{2} C_{0} }}} & { - \frac{{RTT - T_{p} }}{{RTT^{2} C_{0} }}} \\ {\frac{{ - T_{p} }}{RTT}} & 0 \\ \end{array} } \right], \\ & u\left( t \right) = \delta p\left( t \right), y\left( t \right) = \frac{\delta q\left( t \right)}{{C_{0} }}, C_{y} = \left[ {\begin{array}{*{20}c} 0 & {\frac{1}{{C_{0} }}} \\ \end{array} } \right], \tau \left( t \right) = RTT\left( t \right) \\ \end{aligned} $$

2.2 Design of the H_∞ Congestion Controller

The congestion controller is implemented as a sampled-data system as follows:

$$ u\left( t \right) = Fx(t_{k} ),\;kT \le t < \left( {k + 1} \right)T, \left( {k = 0,1,2, \ldots } \right) $$

(4)

where F is the state gain to be designed, T is the sampling period and $t_{k} = kT$ is the sampling instants.

The relation between time delay and sampling period can be expressed as follows:

$$ \tau \left( t \right) = mT + \bar{\tau }, 0 \le \bar{\tau } < T,\tau \left( t \right) \le \tau_{m} = \left( {m + 1} \right)T $$

(5)

If m = 0, the time delay would be less than one sampling period, whereas in case of node failures or network faults, the time delay would be greater than one sampling period, but can be assumed to be a multiple of the sampling period: m ≥ 1, where m represents the number of successive packet dropout.

The control input $u\left( {t - \tau \left( t \right)} \right)$ has different formulations according to the fact that time delay is less than the sampling period $\left( {\tau \left( t \right) \le T} \right)$ or greater than the sampling period $\left( {\tau \left( t \right) \ge T} \right)$. The network models correspond to delays much greater than T, and in this case τ is assumed to verify (5), so

$$ \left( {k - m - 1} \right)T \le t{-}\tau \left( t \right) < \left( {k - m + 1} \right)T $$

(6)

which means that $\hbox{min} (t{-}\tau \left( t \right)) = t_{{\left( {k - m - 1} \right)}}$. Then, we have $u\left( {t - \tau \left( t \right)} \right) = Fx\left( {t_{k - m - 1} } \right)$. Further, we represent the sampling instance by a special time delay

$$ d_{k - m - 1} \left( t \right) = t - t_{k - m - 1} $$

(7)

which satisfies

$$ 0 \le d_{1} \le d_{k - m - 1} \left( t \right) \le d_{2} ,\dot{d}_{k - m - 1} \left( t \right) = 1 $$

(8)

where $d_{1}$ = (m + 1)T and $d_{2}$ = (m + 2)T.

Then, by using (4) and (7), the feedback controller can be rewritten as

$$ u\left( {t - \tau \left( t \right)} \right) = Fx\left( {t - d_{k - m - 1} \left( t \right)} \right) $$

(9)

By using controller (9), the system (3) can be written in the following

$$ \begin{aligned} & \dot{x}\left( t \right) = Ax\left( t \right) + A_{d} x\left( {t - \tau \left( t \right)} \right) + BFx\left( {t - d_{k - m - 1} \left( t \right)} \right) + B_{w} w\left( t \right) \\ & y\left( t \right) = C_{y} x\left( t \right) \\ \end{aligned} $$

(10)

The initial condition of system (3) is assumed to be given by

$$ \begin{aligned} & x\left( \theta \right)\,=\,\left( \theta \right),\theta \in \left[ { - d_{2} , 0} \right] \\ & d_{2}\,=\,\hbox{max} \left( {\tau ,d_{2} } \right) = \hbox{max} \left( {\left( {m + 1} \right)T,\left( {m + 2} \right)T} \right) = d_{2} \\ \end{aligned} $$

where (t) is a smooth vector-valued initial function.

Remark 1

It should be noted that the delay lower bound d₁ and the delay upper bound d₂ depend on the sampling period T.

Since the control signal u(t) is the variation in the packet mark probability around the operating point, it is reasonable to assume that the control law is subject to the following amplitude constraints

$$ \left| {u\left( t \right)} \right| \le u_{0} ,\;0 \le u_{0} , $$

(11)

and then, the saturated state feedback law has the following form

$$ u\left( t \right) = sat\left( {Fx\left( t \right), u_{0} } \right), $$

(12)

If we define the following function

$$ \psi \left( {Fx\left( t \right)} \right) = Fx\left( t \right) - sat\left( {Fx\left( t \right),u_{0} } \right), $$

and then, the closed-loop system from (3), (9) and (12) can be written as,

$$ \begin{aligned} & \dot{x}\left( t \right) = Ax\left( t \right) + A_{d} x\left( {t - \tau \left( t \right)} \right) + BFx\left( {t - d_{{k - m - 1}} \left( t \right)} \right) - B\psi \left( {Fx\left( {t - d_{{k - m - 1}} \left( t \right)} \right)} \right) + B_{w} w\left( t \right) \\ & y\left( t \right) = C_{y} x\left( t \right)~ \\ \end{aligned} $$

(13)

The disturbance vector $w\left( t \right)$ is assumed to be limited in energy, which is a reasonable assumption for practical problems,

$$ w\left( t \right)_{2}^{2} = \mathop \smallint \limits_{0}^{\infty } w\left( t \right)^{T} w\left( t \right){\text{d}}t < \infty $$

(14)

Based on the previous definitions and assumptions, we can state the objective of this paper in mathematical terms as finding a controller F such that the following performance index is satisfied:

$$ \frac{{y\left( t \right)_{2} }}{{w\left( t \right)_{2} }} = \frac{{\sqrt {\mathop \smallint \nolimits_{0}^{\infty } y\left( t \right)^{T} y\left( t \right){\text{d}}t } }}{{\sqrt {\mathop \smallint \nolimits_{0}^{\infty } w\left( t \right)^{T} w\left( t \right){\text{d}}t } }} < \sqrt \gamma $$

(15)

where $\gamma$ is a prescribed positive scalar.To state our results, we consider a matrix $G \in R^{1 \times 2}$ and define the following polyhedral set

$$ {\mathbf{\mathcal{S}}} = \left\{ {x\left( t \right) \in R^{2} ; \left| {\left( {F - G} \right)x\left( t \right)} \right| \le u_{0} } \right\} $$

The following useful lemmas will be used later in the paper.

Lemma 1

(Wang et al. 2006) If$x\left( t \right) \in {\mathbf{\mathcal{S}}}$, then the following relation

$$ \psi^{T} \left( {Fx\left( t \right)} \right)T\left[ {\psi \left( {Fx\left( t \right)} \right) - Gx\left( t \right)} \right] \le 0 $$

is verified for any diagonal positive matrix$T \in R^{1 \times 1}$.

Lemma 2

(Seuret and Gouaisbaut 2013). For any scalar b > a, positive matrix R and function x, the following inequality holds

$$ \mathop \smallint \limits_{a}^{b} \dot{x}^{T} \left( s \right)R\dot{x}\left( s \right){\text{d}}s \ge \frac{1}{b - a}(x\left( b \right) - x(a))^{T} R\left( {x\left( b \right) - x\left( a \right)} \right) + \frac{3}{b - a}\theta^{T} R\theta $$

where$\theta = x\left( b \right) + x\left( a \right) - \frac{2}{b - a}\mathop \smallint \limits_{a}^{b} x\left( s \right){\text{d}}s$

Finally, for a positive scalar β, the ellipsoid $D_{e }$ is defined as follows:

$$ D_{e } = \left\{ {x\left( t \right) \in {\Re }^{2} ;x^{T} \left( t \right)Px\left( t \right) \le \beta^{ - 1} } \right\} $$

3 Main Results

3.1 Sampled-Data H_∞ Performance

In this subsection, we present the stability criterion for the system (13) with an H_∞ disturbance attenuation level γ, which is derived by using the Lyapunov–Krasovskii functional method.

Theorem 1

For given scalars$\tau_{\text{m}} ,\;d_{2} ,\;\gamma > 0$and matrix F, the system (13) is asymptotically stable and satisfies the$H_{\infty }$performance (15), if there exist symmetric positive definite matrices$P,Q,R_{n} \left( {n = \, 1,2} \right)$and appropriately sized matrices$T_{0} ,\;G$such that

$$ \varGamma = \left[ {\begin{array}{*{20}c} \varPi & {\sqrt {\tau_{m} } \varPi_{1}^{T} R_{1} } & {\sqrt {d_{2} } \begin{array}{*{20}c} {\varPi_{1}^{T} R_{2} } & {\varPi_{2} } \\ \end{array} } \\ * & { - R_{1} } & { \begin{array}{*{20}c} 0 & { 0} \\ \end{array} } \\ {\begin{array}{*{20}c} * \\ * \\ \end{array} } & {\begin{array}{*{20}c} * \\ * \\ \end{array} } & { \begin{array}{*{20}c} {\begin{array}{*{20}c} { - R_{2} } & { 0} \\ \end{array} } \\ {\begin{array}{*{20}c} { *} & { - \gamma I} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] < 0 $$

(16)

where

$$ \begin{aligned} & \varPi_{1} = \left[ {A A_{d} BF - B B_{w} 0_{2 \times 5} } \right] \\ & \varPi_{2} = \left[ { C_{y} 0_{1 \times 12} } \right]^{T} , \\ \end{aligned} $$

and the elements of$\varPi$are defined by

$$ \begin{aligned} & \varPi_{11} = PA + A^{T} P + Q - \frac{4}{{\tau_{m} }}R_{1} - \frac{4}{{d_{2} }}R_{2} \\ & \varPi_{12} = PA_{d} - \frac{4}{{\tau_{m} }}R_{1} , \varPi_{13} = PBF - \frac{2}{{d_{2} }}R_{2} , \\ & \varPi_{14} = - PB, \varPi_{15} = PB_{w} ,\;, \varPi_{16} = \frac{6}{{\tau_{m}^{2} }}R_{1} ,\; \varPi_{17} = \frac{6}{{d_{2}^{2} }}R_{2} \\ & \varPi_{22} = - \left( {1 - d} \right)Q - \frac{4}{{\tau_{m} }}R_{1} , \varPi_{26} = \frac{6}{{\tau_{m}^{2} }}R_{1} \\ & \varPi_{33} = - \frac{4}{{d_{2} }}R_{2} , \varPi_{34} = G^{T} T_{0}^{T} , \varPi_{37} = \frac{6}{{d_{2}^{2} }}R_{2} \\ & \varPi_{44} = - 2T_{0} , \varPi_{55} = - I, \varPi_{66} = - \frac{12}{{\tau_{m}^{3} }}R_{1} ,\;\varPi_{77} = - \frac{12}{{d_{2}^{3} }}R_{2} \\ \end{aligned} $$

Proof

Let us consider the following Lyapunov function

$$ \begin{aligned} V\left( t \right) =\,& x^{T} \left( t \right)Px\left( t \right) + \mathop \smallint \limits_{t - \tau \left( t \right)}^{t} x^{T} \left( s \right)Qx\left( s \right){\text{d}}s \\ & \quad + \mathop \smallint \limits_{{ - \tau_{m} }}^{0} \mathop \smallint \limits_{t + \theta }^{t} \dot{x}^{T} \left( s \right)R_{1} \dot{x}\left( s \right){\text{d}}s{\text{d}}\theta \\ & \quad + \mathop \smallint \limits_{{ - d_{2} }}^{0} \mathop \smallint \limits_{t + \theta }^{t} \dot{x}^{T} \left( s \right)R_{2} \dot{x}\left( s \right){\text{d}}s{\text{d}}\theta \\ \end{aligned} $$

(17)

For a prescribed scalar γ, we define the following performance measure function:

$$ J\left( t \right) = \dot{V}\left( t \right) - w^{T} \left( t \right)w\left( t \right) + \frac{1}{\gamma }y^{T} \left( t \right)y\left( t \right) $$

(18)

Computing the derivative of the functional (17) along the trajectory of the system (13) and using Lemma 1, we have that

$$ \begin{aligned} J\left( t \right) \le & 2\dot{x}^{T} \left( t \right)Px\left( t \right) + x^{T}\left( t \right)Qx\left( t \right) - \left( {1 - d} \right)x^{T} \left( {t - \tau \left( t \right)} \right) \\ & \quad \times Qx\left( {t - \tau \left( t \right)} \right) + \tau_{m} \dot{x}^{T} \left( t \right)R_{1} \dot{x}\left( t \right) \\ & \quad - \mathop \smallint \limits_{{t - \tau_{m} }}^{t} \dot{x}^{T} \left( s \right)R_{1} \dot{x}\left( s \right)ds + d_{2} \dot{x}^{T} \left( t \right)R_{2} \dot{x}\left( t \right) \\ & \quad - \mathop \smallint \limits_{{t - d_{2} }}^{t} \dot{x}^{T} \left( s \right)R_{2} \dot{x}\left( s \right)ds - 2\psi^{T} (Fx(t - d_{k - m - 1} \left( t \right))) \\ & \quad \times T_{0} \left[ {\psi \left( {Fx\left( {t - d_{k - m - 1} \left( t \right)} \right)} \right) - Gx\left( {t - d_{k - m - 1} \left( t \right)} \right)} \right] \\ & \quad - w^{T} \left( t \right)w\left( t \right) + \frac{1}{\gamma }y^{T} \left( t \right)y\left( t \right) \\ \end{aligned} $$

(19)

From (5) and (8), it is clear that the following are true

$$ - \mathop \smallint \limits_{{t - \tau_{m} }}^{t} \dot{x}^{T} \left( s \right)R_{1} \dot{x}\left( s \right){\text{d}}s \le - \mathop \smallint \limits_{t - \tau \left( t \right)}^{t} \dot{x}^{T} \left( s \right)R_{1} \dot{x}\left( s \right){\text{d}}s $$

(20)

$$ - \mathop \smallint \limits_{{t - d_{2} }}^{t} \dot{x}^{T} \left( s \right)R_{2} \dot{x}\left( s \right){\text{d}}s \le - \mathop \smallint \limits_{{t - d_{k - m - 1} \left( t \right)}}^{t} \dot{x}^{T} \left( s \right)R_{2} \dot{x}\left( s \right){\text{d}}s $$

(21)

Furthermore, by applying Lemma 2 to (20) and (21), we get

$$ \begin{aligned} & - \mathop \smallint \limits_{t - \tau \left( t \right)}^{t} \dot{x}^{T} \left( s \right)R_{1} \dot{x}\left( s \right){\text{d}}s \\ &\quad \le - \frac{1}{{\tau_{m} }}\left( {x\left( t \right) - x\left( {t - \tau \left( t \right)} \right)} \right)^{T} R_{1} \\ &\qquad \times (x\left( t \right) - x\left( {t - \tau \left( t \right)} \right) - \frac{3}{{\tau_{m} }}_{1}^{T} R_{11} \\ \end{aligned} $$

(22)

$$ \begin{aligned} & - \mathop \smallint \limits_{{t - d_{k - m - 1} \left( t \right)}}^{t} \dot{x}^{T} \left( s \right)R_{2} \dot{x}\left( s \right){\text{d}}s \\ & \quad \le - \frac{1}{{d_{2} }}\left( {x\left( t \right) - x\left( {t - d_{k - m - 1} \left( t \right)} \right)} \right)^{T} R_{2} \\ & \quad \quad \times \left( {x\left( t \right) - x\left( {t - d_{k - m - 1} \left( t \right)} \right)} \right) - \frac{3}{{d_{2} }}_{2}^{T} R_{22} \\ \end{aligned} $$

(23)

where

$$ \begin{aligned} &_{1} = x\left( t \right) + x\left( {t - \tau \left( t \right)} \right) - \frac{2}{{\tau_{m} }}\mathop \smallint \limits_{t - \tau \left( t \right)}^{t} x\left( s \right)ds \\ &_{2} = x\left( t \right) + x\left( {t - d_{k - m - 1} \left( t \right)} \right) - \frac{2}{{d_{2} }}\mathop \smallint \limits_{{t - d_{k - m - 1} \left( t \right)}}^{t} x\left( s \right)ds \\ \end{aligned} $$

Now combining Eqs. (19)–(23), for every $x \in {\mathbf{\mathcal{S}}}$ we have

$$ \begin{aligned} J\left( t \right) \le & \xi^{T} \left( t \right)\left[ {\varPi + \tau_{m} \varPi_{1}^{T} R_{1} \varPi_{1} + d_{2} \varPi_{1}^{T} R_{2} \varPi_{1} } \right]\xi \left( t \right) \\ & \quad + \frac{1}{\gamma }\left( {C_{y} x\left( t \right))^{T} (C_{y} x\left( t \right)} \right) \\ \end{aligned} $$

(24)

where

$$ \begin{array}{*{20}l} {\xi^{T} \left( t \right) = \left[\vphantom{\int_{1}^{2}} {x^{T} \left( t \right) x^{T} \left( {t - \tau \left( t \right)} \right) x^{T} \left( {t - d_{k - m - 1} \left( t \right)} \right)} \right.} \hfill \\ {\quad \quad \quad \psi^{T} \left( {Fx\left( {t - d_{k - m - 1} \left( t \right)} \right)} \right)} \hfill \\ {\quad \quad \quad \left. {w^{T} \left( t \right) \mathop \smallint \limits_{t - \tau }^{t} x^{T} \left( s \right)ds \mathop \smallint \limits_{{t - d_{k - m - 1} \left( t \right)}}^{t} x^{T} \left( s \right)ds} \right]} \hfill \\ \end{array} $$

$\varPi$ and $\varPi_{1}$ are defined previously.

The inequality (24) can then be written as follows:

$$ J\left( t \right) \le \xi^{T} \left( t \right)\left[ {\varPi + \tau_{m} \varPi_{1}^{T} R_{1} \varPi_{1} + d_{2} \varPi_{1}^{T} R_{2} \varPi_{1} + \frac{1}{\gamma }\varPi_{2}^{T} \varPi_{2} } \right]\xi \left( t \right) $$

(25)

Since (16) holds, by Schur complement we obtain $J\left( t \right) < 0.$

When $w\left( t \right) = 0$, it can seen that $\dot{V}\left( t \right) < 0$ which implies the asymptotic stability of (13). Integrating $J\left( t \right)$ from 0 to $\infty$ yields

$$ \begin{aligned} \mathop \smallint \limits_{0}^{\infty } J\left( t \right) = & V\left( \infty \right) - V\left( 0 \right) - \mathop \smallint \limits_{0}^{\infty } w^{T} \left( t \right)w\left( t \right) \\ & \quad + \frac{1}{\gamma }\mathop \smallint \limits_{0}^{\infty } y^{T} \left( t \right)y\left( t \right){\text{d}}t < 0 \\ \end{aligned} $$

(26)

which implies that

$$ V\left( \infty \right) < V\left( 0 \right) + \mathop \smallint \limits_{0}^{\infty } (w^{T} \left( t \right)w\left( t \right) - \frac{1}{\gamma }y^{T} \left( t \right)y\left( t \right)){\text{d}}t $$

Under the zero initial condition $V \left( 0 \right) = 0$ and $V \left( \infty \right) = 0$, we have (15) which implies that the system (13) fulfills its restricted ${\mathcal{L}}_{2}$-gain from $w\left( t \right)$ to $y\left( t \right)$ which is smaller than γ. This completes the proof.

Remark 2

Some elements of the matrix inequality (16) contain the product of P and F or G and $T_{0}$. Thus, it follows that (16) is a bilinear matrix inequality that is difficult to solve with LMI toolbox. To solve (16), we can fix F and G, but this is not a practical solution, as they cannot be easily fixed a priori. Thus, our goal is to avoid the bilinearity in order to determine the matrices F and G; by solving an LMI condition, this is carried out in the next subsection.

3.2 Sampled-Data H_∞ Controller Design

This subsection is devoted to characterizing the controller gains F such that the system in (13) is asymptotically stable and the H_∞ performance index γ is guaranteed.

Theorem 2

For given scalars$\tau_{\text{m}} ,\;d_{2} ,\;\gamma > 0,$the system (13) is asymptotically stable and satisfies the H_∞norm performance, if there exist symmetric positive definite matrices$X,\tilde{Q},$and appropriately sized matrices$S,W,Y$such that

$$ \tilde{\varGamma } = \left[ {\begin{array}{*{20}l} \varPi \hfill & {\sqrt {\tau_{m} } \tilde{\varPi }_{1}^{T} } \hfill & {\sqrt {d_{2} } \tilde{\varPi }_{1}^{T} } \hfill & {\tilde{\varPi }_{2} } \hfill \\ * \hfill & { - X} \hfill & 0 \hfill & 0 \hfill \\ * \hfill & * \hfill & { - X} \hfill & 0 \hfill \\ * \hfill & * \hfill & * \hfill & { - \gamma I} \hfill \\ \end{array} } \right] < 0 $$

(27)

$$ \left[ {\begin{array}{*{20}c} X & {Y^{T} - W^{T} } \\ * & {\beta u_{0}^{2} } \\ \end{array} } \right] \ge 0 $$

(28)

where

$$ \begin{aligned} & \tilde{\varPi }_{1} = \left[ {\begin{array}{*{20}l} {AX} \hfill & {A_{d} X} \hfill & {BY} \hfill & { - BS} \hfill & {B_{w} } \hfill & {0_{2 \times 5} } \hfill \\ \end{array} } \right], \\ & \tilde{\varPi }_{2}^{T} = \left[ {\begin{array}{*{20}l} {C_{y} X} \hfill & {0_{1 \times 12} } \hfill \\ \end{array} } \right] \\ \end{aligned} $$

and the elements of$\tilde{\varPi }$are defined by

$$ \begin{aligned} & \tilde{\varPi }_{11} = AX + XA^{T} + \tilde{Q} - \frac{4}{{\tau_{m} }}X - \frac{4}{{d_{2} }}X \\ & \tilde{\varPi }_{12} = A_{d} X - \frac{4}{{\tau_{m} }}X,\tilde{\varPi }_{13} = BY - \frac{2}{{d_{2} }}X,\tilde{\varPi }_{14} = - BS \\ & \tilde{\varPi }_{15} = B_{w} ,\tilde{\varPi }_{16} = \frac{6}{{\tau_{m}^{2} }}X,\tilde{\varPi }_{17} = \frac{6}{{d_{2}^{2} }}X,\tilde{\varPi }_{26} = \frac{6}{{\tau_{m}^{2} }}X \\ & \tilde{\varPi }_{33} = - \frac{4}{{d_{2} }}X, \varPi_{34} = W^{T} \\ & \tilde{\varPi }_{37} = \frac{6}{{d_{2}^{2} }}X,\tilde{\varPi }_{44} = - 2S,\tilde{\varPi }_{55} = - I \\ & \tilde{\varPi }_{66} = - \frac{12}{{\tau_{m}^{3} }}X,\tilde{\varPi }_{77} = - \frac{12}{{d_{2}^{3} }}X \\ \end{aligned} $$

for every initial condition in$D_{e }$with,

$$ \left( {\bar{\lambda }\left( {X^{ - 1} } \right) + \tau_{m} \bar{\lambda }\left( {X^{ - 1} \tilde{Q}X^{ - 1} } \right)} \right)\left\| {} \right\|^{2} + \left( {\frac{{\tau_{m}^{2} }}{2}\bar{\lambda }\left( {X^{ - 1} } \right) + \frac{{d_{2}^{2} }}{2}\bar{\lambda }\left( {X^{ - 1} } \right)} \right) \left\| \cdot \right\|^{2} \le \beta^{ - 1} $$

(29)

Moreover, the controller gain can be calculated by $F = YX^{ - 1}$.

Proof

Pre- and post-multiplying both sides of (16) by ${\text{diag}}\left\{ {P^{ - 1} , P^{ - 1} , P^{ - 1} , T_{0}^{ - 1} , I, P^{ - 1} , P^{ - 1} , P^{ - 1} , P^{ - 1} , I} \right\}$ and denoting $X = P^{ - 1} = R_{1}^{ - 1} = R_{2}^{ - 1} ,\tilde{Q} = XQX,Y = FX,W = GX,S = T_{0}^{ - 1} .$ Thus, we can easily obtain the inequalities (27) of Theorem 2. On the other hand, the satisfaction of (28) guarantees that $\forall x \in D_{e} , x \in {\mathbf{\mathcal{S}}}.$ In fact, $D_{e} \subset \varvec{ }{\mathbf{\mathcal{S}}}$ is verified by the following conditions,

$$ \left[ {\begin{array}{*{20}c} P & {F^{T} - G^{T} } \\ * & {\beta \mu_{0}^{2} } \\ \end{array} } \right] \ge 0 $$

(30)

Pre- and post-multiplying (30) by $\Delta^{\prime } = {\text{diag}}\left\{ {P^{ - 1} ,I} \right\}$, we obtain the LMI (28).

Moreover, the satisfaction of (29) can be proven as follows. From the Lyapunov functional defined in (17), we have

$$ \begin{aligned} V\left( 0 \right) \le & x^{T} \left( 0 \right)Px\left( 0 \right) + \mathop \smallint \limits_{ - \tau \left( t \right)}^{0} x^{T} \left( s \right)Q_{1} x\left( s \right)ds \\ & \quad + \mathop \smallint \limits_{{ - \tau_{m} }}^{0} \mathop \smallint \limits_{\theta }^{0} x^{T} \left( s \right)R_{1} x\left( s \right)dsd\theta + \mathop \smallint \limits_{{ - d_{2} }}^{0} \mathop \smallint \limits_{\theta }^{0} \dot{x}^{T} \left( s \right)R_{2} \dot{x}\left( s \right)dsd\theta \\ & \quad \le \left( {\bar{\lambda }\left( P \right) + \tau \bar{\lambda }\left( {Q_{1} } \right)} \right)\left\| {} \right\|^{2} \\ & \quad + \left( { \frac{{\tau^{2} }}{2}\bar{\lambda }\left( {R_{1} } \right) + \frac{{d_{2}^{2} }}{2}\bar{\lambda }\left( {R_{2} } \right)} \right)\left\| \cdot \right\|^{2} = \varepsilon \\ \end{aligned} $$

Therefore, we have $x^{T} \left( t \right)Px\left( t \right) \le V\left( t \right) \le V\left( 0 \right) \le \varepsilon \le \beta^{ - 1}$ for all t ≥ 0. That is, the trajectories of the system do not leave the set $D_{e}$, for any initial functions ɸ($\theta )$ in $D_{e}$, which ensures that $x\left( t \right) \in {\mathbf{\mathcal{S}}}$. This concludes the proof.

Remark 3

In this paper, we consider just a long time-delay controller $(\tau \left( t \right) > T)$ as it is the most frequent case in congestion control. Nonetheless, the theoretical results for the short delay controller (when $\tau \left( t \right) \le T)$ can be straightforwardly deduced by setting $m = 0.$

Remark 4

It should be pointed that the main difference of the proposed congestion controller approach with previous AQM solutions for TCP/IP routers is that sampling is explicitly taken into account: Relation between time delay and sampling period is analyzed to derive the new control law.

Remark 5

In El Fezazi et al. (2017b), the authors transformed the continuous-time model into a discrete-time one, where not only the input but also other variables are sampled (state, disturbance and output). However, this solution requires perfect synchronization of the various samplers of the various variables, which is a shortcoming, as perfect synchronism is difficult to obtain in practice. Sampled-data approach was used in Lamrabet et al. (2019) to design an anti-windup compensator for time-delay systems subject to actuator saturation. We can also cite El Haiek et al. (2017) and Zabari et al. (2017). However, the application of these methods to the network (AQM) requires that all sampled variables must be transmitted in the same packet, which is a drawback for practical implementations.

Remark 6

In this paper, by incorporating LKF and Wirtinger integral inequality, some sufficient condition are established in terms of LMIs and thus can be effectively solved by using available LMI solvers. In order to obtain the simpler form of LMI, no free-weighting matrices are adopted, which reduce the computational complexity significantly.

4 Numerical Examples

In the following, two numerical examples are developed to illustrate the effectiveness of the proposed methodology.

Example 1

(El Fezazi et al. 2017) For this network, we assume that the operating point is defined by $N = 60,\;C_{0} = 3750,\;q_{0} = 175$ and $R_{0} = 0.2464$, so we can estimate the nominal window size, steady-state discard probability and propagation delay using $W_{0} = \frac{{R_{0} C_{0} }}{N}, p_{0} = \frac{2}{{W_{0}^{2} }}$ and $T_{p} = R_{0} - \frac{{q_{0} }}{{C_{0} }}$.

For the state feedback controller $F = 10^{ - 4} \left[ { - 5.379 - 0.093} \right]$ given in El Fezazi et al. (2017), when $m = 2$, solving the LMI conditions in Theorem 1 with the above parameter values, using MATLAB LMI toolbox, we can obtain a minimum allowable value of $\gamma$, which is 2.6 × 10⁻⁴, while it is 1.4 × 10⁻³ in El Fezazi et al. (2017a, b). From this example, it can be seen that Theorem 1 gives the best H_∞ performance.

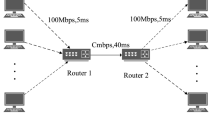
The sample-data controller (SDC) is now compared with the PI controller proposed in Floyd and Jacobson (1993) and with the RED controller in Hollot et al. (2002). For this comparison, we use the disturbance profile depicted in Fig. 1, and we set $u_{0} = p_{0}$. The queue length regulation and the drop probability are depicted in Figs. 2 and 3, respectively, with the above control gain and the sampling period $T = 0.01$. Parameters of the PI and RED controllers are listed in Table 1.

Fig. 1

Disturbance profile

Fig. 2

Queue length comparison. SDC, PI and RED

Fig. 3

Drop probability comparison. SDC, PI and RED

Table 1 Parameters of the AQM controllers

From Fig. 2, it can be seen that the variables effectively converge toward the desired operating point (defined by $q_{0}$ = 175 packets). However, we can clearly see that the queue size tracks the equilibrium point much faster when SDC is used (4 s), while the convergence time of PI and RED is over 10 s and 30 s, respectively. It can be concluded that the dynamic behavior of SDC is the best; the desired queue length is guaranteed. In fact, Fig. 3 shows that SDC curve converges to the desired value in a high speed (4 s). However, one can easily see that PI curve converges to the equilibrium point in a relative long time span after the simulation starts (over 15 s), while the RED curve fluctuates far away from the desired value significantly.

Example 2

In this second example, we study the disturbance attenuation properties via LMI toolbox of MATLAB. For this, we use the parameters from the example in Zheng and Nelson (2009):

• Case (1): high-speed network

$N = 1200,\;C_{0} = 25000,\;p_{0} = 0.0952 = u_{0}$ and $q_{0}$ = 500, so $W_{0}$ = 4.5833, RTT = 0.2199 and $T_{p}$= 0.1999. Using LMI tools of MATLAB, applying Theorem 2, with $m = 2$, and β = 1 we can obtain $\gamma = 0.0085$ and $F = \left[ { - 0. 0312 0.0000} \right]$.

• Case (2): low-speed network

$N = 120$, $C_{0}$ = $2500$, $p_{0} = 0.0288 = u_{0}$ and$q_{0} = 500$, so we have W₀ = 8.3333, RTT = 0.3999 and$T_{p}$= 0.1999. According to Theorem 2, with m = 2, and $\beta = 1$, a minimum attenuation level of $\gamma = 0.0105$ is obtained and $F = \left[ { - 0.0036 0.0000} \right]$.

For comparison purpose, we report the result of Zheng and Nelson (2009). By Theorem 1 of Zheng and Nelson (2009), it is obtained that $\gamma = 0.1719$ and $\gamma = 0.1783$, for Case (1) and (2), respectively. It can be seen that the proposed method achieves better attenuation than Zheng and Nelson (2009), which illustrates that the technique proposed in the paper is more effective.

We validate the performance of our proposed SDC via evaluating it through the network simulator NS3. The performance of SDC is compared with PIE, RED, NLRED and ARED for case (1). The queuing delay is controlled around the desired value 20 ms. Figure 4 presents the trade-off between goodput and queuing delay. We mention here that the ideal AQM should provide high goodput, small average queuing delay and small ellipse. The figure shows that all the AQMs have a well-average queuing delay. SDC provides the well performance since it has the best compromise between the average queuing delay and goodput, which demonstrate the superiority of our controller.

Fig. 4

SDC vs. PIE, RED, NLRED and RAED performance comparison

5 Conclusion

In this study, we have proposed a technique to design a congestion controller for networks based on TCP/IP, by using sampled-data control theory. The stability of the process is then ensured even in the presence of saturation nonlinearity, and an H_∞ norm performance is ensured for the attenuation of the effect of the disturbance input on the controlled output. The feedback controller can be constructed by solving a set of LMIs, which can be easily checked using off-the-shelf software. It is proved in the examples that the obtained result is less conservative than some ones in the existing literature.