A Model-Based Suboptimal Control to Improve Induction Motor Efficiency

Abstract

This paper proposes a control strategy for energy efficiency improvement of three-phase induction motors (TIM). The main control is based on the indirect field-oriented approach. A loss model-based controller is proposed in order to reduce the cooper and iron losses of TIM for different load values. A nonlinear equation based only on quadrature currents is derived and used to obtain suboptimal flux reference in steady-state conditions. Thus, for dynamic implementation (motor transient), a low-pass filter is included and designed based on the rotor time constant. MATLAB simulations are performed to test the proposed strategy for several operation conditions. To verify the approach in real situations, a 4hp motor drive platform was implemented using F28069 DSP. The effectiveness of the proposed model is demonstrated through simulations and experimental results.

1 Introduction

Induction motors (IM) are the most widely used machines in the industrial environment due to its known advantages, including robustness, reliability, low price and no maintenance. The control method most widespread and commercially applied is based on the concept of direct field-oriented (DFOC) or indirect field-oriented (IFOC) approach (Castaldi et al. 2005). According to Castaldi et al. (2005), IFOC is one of the most effective vector control techniques for induction motor drive due to the simplicity of design and implementation, resulting in a good torque and speed performance system.

Industrial applications with IM are divided into speed control and position control. Among those that require speed control, there are some that demand high dynamic performance. Vector control is essential in these applications. Thus, the research of the drive is especially directed toward development of speed controller, so that the dynamic performance of the motor is optimized (Thangaraj et al. 2011). The vector control technique allows a stable torque even when the machine is working at low speeds. This is possible by the decoupling of torque and flux currents, allowing these variables to be controlled independently (Souza et al. 2007). Despite the high cost of drive of induction motors, its high performance allows a significant reduction in energy consumption, especially in applications that require higher powers and in systems where the drive operates with speed variations. The call for energy conservation further justifies the use of such equipment. Moreover, the cost of drive can be reduced using sensorless techniques to control speed, position and torque, where mechanical sensors would be unnecessary (Diab 2014; Palácios et al. 2014).

When an IM operates at rated load and rated speed, its energy efficiency is high. However, for smaller loads, this efficiency drops drastically. Consequently, researches on induction motor drives have been developed in recent decades in order to improve energy efficiency of these drives. Moreover, the losses in motor stator, rotor and iron core are highly dependent on the control strategy, especially when the motor is operating at light loads (Uddin and Nam 2008).

Control strategies used in the literature to improve IM efficiency are based on search controller (SC), loss model-based controller (LMC) or a combination of both controllers (Raj et al. 2009). The SC approach is simple, consisting of successive approximations in the search for a minimum power consumption. This method has the advantage of not depending on any model. However, it presents convergence time delay and torque ripple. LMC techniques are fast, and torque ripple is reduced when compared with SC approaches. However, the good performance of this strategy depends on accurate motor and loss models.

The implementation of an efficiency controller based on LMC depends on the IM characteristics, such as resistances and inductances of both stator and rotor. In Ouadi et al. (2010), the efficiency control strategy uses an experimentally obtained relationship between the stator current and rotor flux. The current–flux curve provides the necessary amount of flux to keep the torque on the shaft for a given stator current. However, the implementation of the efficiency controller based on this approach usually occurs off-line, where a p.u. (per unit) curve is obtained for a given motor and it is extended for a general case. Thus, when motor parameter changes, the optimal curve is no longer valid.

A loss-minimizing torque control for IM is proposed by Stumper et al. (2013), where an optimal reference flux is deducted at steady state. Although the iron and copper losses of the motor have been used to obtain this model, the iron resistance is not considered in the motor model, which results in a less accurate loss model. For its implementation to dynamic operation of the loss model, a predictive control scheme that uses an exponential function is added.

In Uddin and Nam (2008), a different loss model control scheme is presented. This approach determines the optimal flux current for the efficiency optimization of the vector-controlled induction motor drive. In Takahashi and Noguchi (1986), another loss model is presented using the direct torque control (DTC) approach. The loss model presents an optimal stator flux algorithm for minimal power consumption. In Farasat and Karaman (2011), a LMC is presented to determine an optimal flux level for the efficiency optimization of the hybrid field-oriented and direct torque-controlled induction motor drive. In Qu et al. (2012), based on the corresponding steady-state loss function, a method is proposed for solving the loss-minimizing flux reference. Waheedabeevi et al. (2012) present a LMC to improve the efficiency and the power factor of field-oriented controlled induction motor, by calculating the optimal air gap flux. All these studies cited above adopt the model of motor power loss for optimization, and none of them present proposals for the IFOC control strategy.

In Scarmin et al. (2010), a combination of the SC and LMC techniques was unified and named by the author as Hybrid Adaptive Efficiency Controller (HAEC) for the IFOC strategy. In this work, the LMC technique uses the relationship between the stator current and rotor flux obtained experimentally and extended for a general case. This approach has good characteristics as the quick response from LMC technique and the optimal adaptive flux from SC technique. Moreover, this strategy can significantly improve energy consumption for light loads. In de Pelegrin et al. (2013), a LMC model for IFOC approach is presented, where the iron losses were ignored, and the results were not very accurate.

In this work, a loss model-based controller is presented to determine a flux reference for an IFOC approach where the copper and iron losses of the IM are minimized, without considering the core saturation (Stumper et al. 2013; Castaldi et al. 2005). This disregarding is adopted since the proposed approach aims to improve the energy efficiency at light loads. In these operating conditions, the motor works with magnetization flux below the rated one, then the core saturation becomes not relevant. In addition, Ouadi et al. (2010) shows an experimental result of core saturation behavior as a function of magnetizing current and observed that below the nominal flux, the behavior is essentially linear.

The main contribution of this work is the best accuracy of the LMC approach than that of ones used by Stumper et al. (2013), Scarmin et al. (2010) and Ouadi et al. (2010), because the iron losses are considered in the motor and loss models. For the implementation of the efficiency controller in dynamic conditions, a simple low-pass filter replaces the predictive controller proposed by Stumper et al. (2013). Experimental results are used to evaluate the dynamical operation of the whole control strategy, which includes the flux reference generator and IFOC controller.

2 System Description

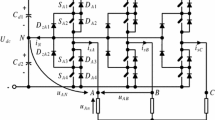
The simplified structure of the IM drive is presented in Fig. 1. The system is composed of an AC/DC rectifier module, a DC bus with LC filter, a DC/AC PWM inverter composed of IGBTs and a control module. This module consists of analog signal conditioning instrumentation and a floating point microcontroller. The IM is assembled on a fixed structure; its shaft is coupled to a torque transducer and a permanent magnet generator that operates as testing load. The generator is connected to scalable resistive loads in order to allow the motor to operate at different operation points. An absolute encoder is also coupled to the motor shaft to measure the rotor speed.

Fig. 1

IM drive system

2.1 Motor Model

The motor model can be obtained using Kirchoff’s laws applied to equivalent circuits of stator and rotor. The iron losses are also considered in motor modeling. However, as discussed in Sect. 1, the magnetic saturation is not considered in this modeling. The dynamical model can be divided into electrical and mechanical model as follows.

2.1.1 Electrical Model

In Levi (1995), the electrical model of a three-phase induction motor is presented for an arbitrary qd (quadrature-direct) reference frame. The equivalent circuit is shown in Fig. 2.

Fig. 2

IM equivalent circuit in arbitrary qd reference frame, which includes representation of the iron core loss

The electromagnetic equations are shown in (1), (2), (3) and (4).

Voltage equations:

$$\begin{aligned}&v_\mathrm{qs}=r_\mathrm{s} i_\mathrm{qs}+\omega \lambda _\mathrm{ds}+\dot{\lambda _\mathrm{qs}}\nonumber \\&v_\mathrm{ds}=r_\mathrm{s} i_\mathrm{ds}-\omega \lambda _\mathrm{qs}+\dot{\lambda _\mathrm{ds}\nonumber }\\&0=r_\mathrm{r} i_\mathrm{qr}+(\omega -\omega _\mathrm{r}) \lambda _\mathrm{dr}+\dot{\lambda _\mathrm{qr}}\nonumber \\&0=r_\mathrm{r} i_\mathrm{dr}-(\omega -\omega _\mathrm{r}) \lambda _\mathrm{qr}+\dot{\lambda _\mathrm{dr}} \end{aligned}$$

(1)

Flux equations:

$$\begin{aligned}&\lambda _\mathrm{qs}= L_\mathrm{ls}i_\mathrm{qs}+L_\mathrm{M} i_\mathrm{qm}\nonumber \\&\lambda _\mathrm{ds}= L_\mathrm{ls}i_\mathrm{ds}+L_\mathrm{M} i_\mathrm{dm}\nonumber \\&\lambda _\mathrm{qr}= L_\mathrm{lr}i_\mathrm{qr}+L_\mathrm{M} i_\mathrm{qm}\nonumber \\&\lambda _\mathrm{dr}= L_\mathrm{lr}i_\mathrm{dr}+L_\mathrm{M} i_\mathrm{dm} \end{aligned}$$

(2)

Current equations:

$$\begin{aligned}&i_\mathrm{qfe} = i_\mathrm{qs} + i_\mathrm{qr} - i_\mathrm{qm}\nonumber \\&i_\mathrm{dfe} = i_\mathrm{ds} + i_\mathrm{dr} - i_\mathrm{dm} \end{aligned}$$

(3)

Electromagnetic torque:

$$\begin{aligned} T_\mathrm{e}=\frac{3P}{4}\frac{L_\mathrm{M}}{L_\mathrm{r}}\left( \lambda _\mathrm{dr}(i_\mathrm{qs}-i_\mathrm{qfe}) -\lambda _\mathrm{qr}(i_\mathrm{ds}-i_\mathrm{dfe})\right) \end{aligned}$$

(4)

In Fig. 2 and Eqs. (1)–(4), $r_\mathrm{s}$ and $r_\mathrm{r}$ are the stator and rotor windings resistances per phase, $r_\mathrm{fe}$ is the iron resistance, $L_\mathrm{ls}$ and $L_\mathrm{lr}$ are the stator and rotor leakage inductances, $L_\mathrm{M}$ is the magnetizing inductance, $\omega _\mathrm{r}$ is the electrical rotor speed, $\omega$ is the speed of the arbitrary reference frame, $i_\mathrm{qs},\,i_\mathrm{ds},\,i_\mathrm{qr}$ and $i_\mathrm{dr}$ are currents in qd axis of stator and rotor, $i_\mathrm{qfe}$ and $i_\mathrm{dfe}$ are the iron currents in qd axis, $i_\mathrm{qm}$ and $i_\mathrm{dm}$ are the magnetizing currents in qd axis, $v_\mathrm{qs}$ and $v_\mathrm{ds}$ are voltages in dq axis of stator, $\lambda _\mathrm{q}$ and $\lambda _\mathrm{d}$ are the magnetic flux in qd axis of the stator and rotor, $T_\mathrm{e}$ is the electromagnetic torque, P is the number of poles, and $L_\mathrm{r}=L_\mathrm{lr}+LM$.

2.1.2 Mechanical Model

The mechanical model follows the Newton’s second law of motion according to

$$\begin{aligned} \dot{\omega _\mathrm{r}}=-\frac{D}{J} \omega _\mathrm{r} + \frac{P}{2J} T_\mathrm{e} - \frac{P}{2J}T_\mathrm{L} \end{aligned}$$

(5)

where J is the rotor inertia coefficient, D the viscous friction coefficient, and $T_\mathrm{L}$ the load torque.

2.2 System Controllers

The “Microprocessor-Based Controllers” module shown in Fig. 1 is detailed in Fig. 3, where $i_a,\,i_b$ and $i_c$ are the stator currents of the motor. For control purposes, the three-phase system is transformed into qd reference frame aligned with the rotor flux ($\lambda _\mathrm{qr}=0$). Based on the currents $i_\mathrm{qs}$ and $i_\mathrm{ds}$, the rotor flux $\lambda _\mathrm{dr}$ can be estimated, and the “Efficiency Controller” module generates the instantaneous suboptimal reference flux $\lambda _\mathrm{dri}^*$. The calculated flux is valid only in steady-state conditions. Consequently, during a dynamic transient, some adaptations are included. A first-order low-pass filter is used to smooth reference flux signal. With that, it is possible to avoid sudden variations in the reference flux. Otherwise, oscillations in motor currents could appear and lead the system to instability. Thus, to specify the time constant of this filter, a trade-off needs to be considered. The filter must be smooth to avoid oscillations and also must be fast enough to avoid loss efficiency of the LMC. According to Stumper et al. (2013), a low-pass filter in flux reference with time constant ($\tau$) approximately equal to the rotor time constant is appropriate to prevent current oscillations and a good trajectory for dynamic situations, i.e., ($\tau \backsimeq L_\mathrm{r} / r_\mathrm{r}$).

Fig. 3

Microprocessor-based controllers diagram

Considering the IM electric model referenced to the rotor flux and the system proposed by Almeida Souza et al. (2007), Fig. 4 presents the control structure used to perform current and voltage machine driving for a given speed reference and flux reference. In this figure, $\omega _\mathrm{r}^*$ is the reference speed, $\lambda _\mathrm{dr}^*$ is the rotor flux reference, and $i_\mathrm{qs}^*$ and $i_\mathrm{ds}^*$ are the reference currents.

Fig. 4

IFOC control

Considering the input variables and the reference speed $\omega _\mathrm{r}^*$, the IFOC approach uses PI controllers to generate output voltages $v_\mathrm{qs}$ and $v_\mathrm{ds}$, which are used to drive the motor using PWM modulation. The PI controller continuous-time transfer function, from error signal E(s) to controller output X(s), is given by

$$\begin{aligned} {{X(s) } \over {E(s) }} = K_p + {{K_i } \over s}. \end{aligned}$$

(6)

To discretize equation (6), backward Euler’s method is used, and therefore, $s = {{z - 1} \over {zT_\mathrm{s} }}$, where $T_\mathrm{s}$ is the sampling time. Substituting in Eq. (6),

$$\begin{aligned} {{X(z) } \over {E(z) }} = K_p + {{K_i T_\mathrm{s} z} \over {z - 1}}. \end{aligned}$$

(7)

The recursive difference equation of PI discrete-time controllers is obtained taking the inverse Z transform of Eq. (7):

$$\begin{aligned} x[k] = x[k - 1] + (K_p + K_i T_\mathrm{s} )e[k] - K_p e[k - 1]. \end{aligned}$$

(8)

The speed, flux and current discrete-time controllers are implemented using Eq. (8).

The methodology proposed by Shin et al. (2003) can be adopted to adjust the gains of the PI controllers, where the bandwidth is chosen to ensure stability of the closed loop system even under changes in motor parameters.

The IFOC uses the rotor flux estimation based on the mathematical model of the induction motor and allows the motor to operate with different load and speed profiles. In conventional approaches, the reference flux is the rated one.

In order to estimate rotor flux ($\lambda _\mathrm{dr}$) and flux speed ($\omega$), the equations of flux model (2), voltage model (1) and current model (3) are combined. Considering the qd reference system aligned with the rotor flux ($\lambda _\mathrm{qr}=0$), and $i_\mathrm{qm}\approx i_\mathrm{qs}+i_\mathrm{qr}$; $i_\mathrm{dm} \approx i_\mathrm{ds}+i_\mathrm{dr}$, flux estimative can be reduced to

$$\begin{aligned} 0 = \frac{L_\mathrm{M} r_\mathrm{r}}{L_\mathrm{r}} i_\mathrm{qs} - (\omega - \omega _\mathrm{r}) \lambda _\mathrm{dr} \end{aligned}$$

(9)

and

$$\begin{aligned} \dot{\lambda _\mathrm{dr}} = \frac{L_\mathrm{M} r_\mathrm{r}}{L_\mathrm{r}} i_\mathrm{ds} - \frac{r_\mathrm{r}}{L_\mathrm{r}} \lambda _\mathrm{dr}. \end{aligned}$$

(10)

Isolating $\omega$ in (9), the flux speed is given by

$$\begin{aligned} \omega =\omega _\mathrm{r}+\frac{L_\mathrm{M} r_\mathrm{r}}{L_\mathrm{r}} \frac{i_\mathrm{qs}}{\lambda _\mathrm{dr}}. \end{aligned}$$

(11)

For implementation, considering that the flux $\lambda _\mathrm{dr}$ in closed loop is near to the reference flux $\lambda _\mathrm{dr}^*$, the estimation of rotor flux speed $\omega$ is reduced to

$$\begin{aligned} \omega =\omega _\mathrm{r}+\frac{L_\mathrm{M} r_\mathrm{r}}{L_\mathrm{r}} \frac{i_\mathrm{qs}}{\lambda _\mathrm{dr}^*}. \end{aligned}$$

(12)

From (10), the recursive difference equation for rotor flux estimation $\lambda _\mathrm{dr}[k]$ from $i_\mathrm{ds}[k]$ can be derived using the backward Euler discretization method as

$$\begin{aligned} \lambda _\mathrm{dr}[k]=\left( 1- \frac{T_\mathrm{s} r_\mathrm{r}}{L_\mathrm{r}}\right) \lambda _\mathrm{dr}[k-1] + \frac{Ts L_\mathrm{M} r_\mathrm{r}}{L_\mathrm{r}} i_\mathrm{ds}[k]. \end{aligned}$$

(13)

3 Efficiency Controller

Most of the efficiency controllers used to generate flux or current references for IM drives are based on a loss model. Also, an alternative LMC approach is developed in this work to generate the flux reference to IFOC strategy, such that the driving losses are reduced.

3.1 Loss Model Control (LMC)

In the literature, there are several approaches of loss model-based efficiency controller. Some authors, such as Scarmin et al. (2010) and Ouadi et al. (2010), use loss models obtained experimentally for a specific motor and apply it as a general result to any other motors. Using experimental tests, curves with minimum power consumption in terms of an optimization parameter are obtained and interpolated by polynomial functions to define the loss model. Although the model works accurately for the analyzed motor, it can be verified that its usage to other motors does not have the same performance, since there are always differences in parameters from one motor to another. The proposed loss model will be applied to any other IM without significant optimality reduction.

Authors such as Takahashi and Noguchi (1986), Farasat and Karaman (2011) and Waheedabeevi et al. (2012) developed mathematical losses models considering parameter optimization, including iron and copper losses of the motor. All these models were developed in steady state, and none of them are applied with IFOC strategy.

Stumper et al. (2013) presents a similar approach to finding the optimum flux to minimize losses. However, its approach is focused on the torque control, and the loss model is less accurate, since the iron losses are not considered in motor model.

In this work, a loss model for the IFOC strategy is developed, which considers copper and iron losses of the motor.

3.2 Search Control (SC)

A simple search control approach is the Rosenbrock algorithm (Souza et al. 2007). In this approach, the reference flux $\lambda _\mathrm{dr}^*$ is changed in small steps in a given direction in order to search the optimum efficiency point, i.e., while the absorbed power from the grid is decreasing ($\varDelta P_\mathrm{in} [k] < 0$, with $\varDelta P_\mathrm{in}[k] = P_\mathrm{in}[k]-P_\mathrm{in}[k-1]$). When $\varDelta P_\mathrm{in}[k] > 0$, the search direction is reversed with a reduced step size. Figure 5 shows this method.

Fig. 5

Rosenbrock search control algorithm

In this work, the search control is also based on Rosenbrock algorithm and it is used for comparison with LMC techniques.

3.3 Proposed LMC Controller

This paper presents a suboptimal loss model approach to IFOC strategy. The proposed scheme optimizes rotor reference flux $\lambda _\mathrm{dr}^*$ in order to minimize the IM losses. Similarly to the works described before, the analysis considers IM steady-state characteristics. Moreover, in this paper, several operation points are analyzed.

The power losses $P_\mathrm{l}$ are given by

$$\begin{aligned} P_\mathrm{l}=P_\mathrm{cus}+P_\mathrm{cur}+P_\mathrm{fe} \end{aligned}$$

(14)

where $P_\mathrm{cus}$ are the cooper losses in stator, $P_\mathrm{cur}$ are the cooper looses in rotor, and $P_\mathrm{fe}$ are the iron losses. This equation can be written in terms of resistances and currents of the motor as

$$\begin{aligned} P_\mathrm{l}= & {} \frac{3}{2} \left[ r_\mathrm{s}(i_\mathrm{qs}^2+i_\mathrm{ds}^2)+r_\mathrm{r}(i_\mathrm{qr}^2+i_\mathrm{dr}^2)+ r_\mathrm{fe}(i_\mathrm{qfe}^2+i_\mathrm{dfe}^2)\right] . \end{aligned}$$

(15)

The objective is to determine an expression for $P_\mathrm{l}$ which depends only on the rotor flux $\lambda _\mathrm{dr}$ and constant parameters. For a given constant load on the motor, it can be noted that steady-state electric torque $T_\mathrm{e}$ also will be constant.

Considering the qd reference system aligned with the rotor flux ($\lambda _\mathrm{qr}=0$) and given the steady-state response, executing algebraic operations on the set of Eqs. (1), (2), (3) and (4) leads to

$$\begin{aligned}&i_\mathrm{qs}=\frac{4 T_\mathrm{e} L_\mathrm{r}}{3 P~ L_\mathrm{M}} \frac{1}{\lambda _\mathrm{dr}} + i_\mathrm{qfe} \end{aligned}$$

(16)

$$\begin{aligned}&i_\mathrm{ds}=\frac{1}{L_\mathrm{M}} \lambda _\mathrm{dr} + i_\mathrm{dfe} \end{aligned}$$

(17)

$$\begin{aligned}&i_\mathrm{qr}=-\frac{4 T_\mathrm{e} }{3 P} \frac{1}{\lambda _\mathrm{dr}} \end{aligned}$$

(18)

$$\begin{aligned}&i_\mathrm{dr}=0 \end{aligned}$$

(19)

$$\begin{aligned}&i_\mathrm{qfe}=\frac{\omega }{r_\mathrm{fe}} \frac{1}{\lambda _\mathrm{dr}} \end{aligned}$$

(20)

$$\begin{aligned}&i_\mathrm{dfe}=-\frac{4\omega L_\mathrm{lr} T_\mathrm{e}}{3 P ~ r_\mathrm{fe}} \frac{1}{\lambda _\mathrm{dr}} \end{aligned}$$

(21)

$$\begin{aligned}&\omega =\omega _\mathrm{r}+\frac{4 T_\mathrm{e} r_\mathrm{r}}{3 P} \frac{1}{\lambda _\mathrm{dr}^2}. \end{aligned}$$

(22)

Since the second term of (22) is the rotor slip $\omega _\mathrm{s}$ and in steady state $\omega _\mathrm{s} \ll \omega _\mathrm{r}$, then $\omega \approx \omega _\mathrm{r}$. Moreover, in steady state $i_\mathrm{s} \gg i_\mathrm{fe}$. Thus, the Eqs. (16), (17), (20) and (21) are reduced to

$$\begin{aligned}&i_\mathrm{qs}=\frac{4 T_\mathrm{e} L_\mathrm{r}}{3 P~ L_\mathrm{M}} \frac{1}{\lambda _\mathrm{dr}} \end{aligned}$$

(23)

$$\begin{aligned}&i_\mathrm{ds}=\frac{1}{L_\mathrm{M}} \lambda _\mathrm{dr} \end{aligned}$$

(24)

$$\begin{aligned}&i_\mathrm{qfe}=\frac{\omega _\mathrm{r}}{r_\mathrm{fe}} \frac{1}{\lambda _\mathrm{dr}} \end{aligned}$$

(25)

$$\begin{aligned}&i_\mathrm{dfe}=-\frac{4\omega _\mathrm{r} L_\mathrm{lr} ~ T_\mathrm{e}}{3 P~ r_\mathrm{fe}} \frac{1}{\lambda _\mathrm{dr}}. \end{aligned}$$

(26)

Substituting the current equations (23)–(26) into (15) leads to

$$\begin{aligned} P_\mathrm{l}= & {} \frac{3}{2}\left[ \left( \frac{4 T_\mathrm{e}}{3P}\right) ^2 \left( \frac{r_\mathrm{s} L_\mathrm{r}^2}{L_\mathrm{M}^2}+r_\mathrm{r}+\frac{\omega _\mathrm{r}^2 L_\mathrm{lr}}{r_\mathrm{fe}} \right) \frac{1}{\lambda _\mathrm{dr}^2} \right. \nonumber \\&\left. +\left( \frac{r_\mathrm{s}}{L_\mathrm{M}^2} +\frac{\omega _\mathrm{r}^2}{r_\mathrm{fe}}\right) \lambda _\mathrm{dr}^2\right] . \end{aligned}$$

(27)

Since $\frac{d^2 P_\mathrm{l}}{\mathrm{d}\lambda _\mathrm{dr}^2} > 0$, the optimal flux for minimum power losses can be obtained minimizing $P_\mathrm{l}$ with respect to the rotor flux ($d(P_\mathrm{l})/\mathrm{d}\lambda _\mathrm{dr} = 0$), and it is given by

$$\begin{aligned} \lambda _\mathrm{dr\_opt}^2=\frac{4 T_\mathrm{e}}{3P}\sqrt{\frac{r_\mathrm{s} r_\mathrm{fe} L_\mathrm{r}^2 + r_\mathrm{r} r_\mathrm{fe}L_\mathrm{M}^2+\omega _\mathrm{r}^2 L_\mathrm{lr}^2 L_\mathrm{M}^2}{r_\mathrm{s} r_\mathrm{fe} + L_\mathrm{M}^2 \omega _\mathrm{r}^2}} \end{aligned}$$

(28)

where the electrical torque $T_\mathrm{e}$ in steady state can be estimated by the following equation.

$$\begin{aligned} T_\mathrm{e}=\frac{3 P L_\mathrm{M}^2}{4 L_\mathrm{r}} i_\mathrm{qs}i_\mathrm{ds}. \end{aligned}$$

(29)

Substituting Eq. (29) into (28) yields a loss model which optimizes rotor flux as a function of the stator currents.

$$\begin{aligned} \lambda _\mathrm{dr\_opt}=K\sqrt{i_\mathrm{qs} i_\mathrm{ds} } \end{aligned}$$

(30)

where $K=\sqrt{\frac{L_\mathrm{M}^2}{L_\mathrm{r}}\sqrt{\frac{r_\mathrm{s} r_\mathrm{fe} L_\mathrm{r}^2 + r_\mathrm{r} r_\mathrm{fe}L_\mathrm{M}^2+\omega _\mathrm{r}^2 L_\mathrm{lr}^2 L_\mathrm{M}^2}{r_\mathrm{s} r_\mathrm{fe} + L_\mathrm{M}^2 \omega _\mathrm{r}^2}}}$.

Equation (30) is used to generate the reference flux $\lambda _\mathrm{dri}^*$, which is updated at each sampling time and leads the motor to operate on its minimal power point. Then, for discrete-time implementation, the optimal reference flux is obtained from

$$\begin{aligned} \lambda _\mathrm{dri}^*[k]=K\sqrt{i_\mathrm{qs}[k] i_\mathrm{ds}[k] }. \end{aligned}$$

(31)

A digital low-pass filter is used to smooth $\lambda _\mathrm{dri}^*[k]$ and generates the reference signal $\lambda _\mathrm{dr}^*$ to drive the IFOC module. The discrete-time low-pass filter is implemented using the backward Euler method and is given by

$$\begin{aligned} \lambda _\mathrm{dr}^*[k] = \left( 1- \frac{T_\mathrm{s}}{\tau }\right) \lambda _\mathrm{dr}^*[k-1]+\frac{T_\mathrm{s}}{\tau }\lambda _\mathrm{dri}^*[k] \end{aligned}$$

(32)

where $\tau$ is the time constant of low-pass filter, and its value is adopted as $\tau \backsimeq L_\mathrm{r} / r_\mathrm{r}$. This choice follows the considerations mentioned by Stumper et al. (2013).

The approach used in this work is similar to Stumper et al. (2013). However, in this work equation (30) includes the iron losses in a different way since they are obtained considering a more complete motor model. For the motor under study, a numerical evaluation shows a 3.65 % difference in K between both approaches. The practical evaluation of optimality of the K constant will be shown in the next section by comparison of the proposed strategy with the SC approach, which does not depend on motor parameters. The difference arises from the way how both models are obtained, since in Stumper et al. (2013) the motor model does not consider the core resistance.

Concerning the rotor speed measurement, although in this paper an absolute encoder is used, this optimization approach can also be implemented with sensorless control techniques. In some cases, small changes may be needed in the controllers’ gains and in the time constant of the reference flux low-pass filter. These changes are recommended since the system variables become more fluctuating due to the estimated variables dynamics.

4 Numerical Analysis

Table 1 shows the nominal parameters of the induction motor used in the numerical analysis and experimental evaluation, where $\omega _n$ is rated angular speed, $V_n$ is rated voltage, $I_n$ is rated current, $\eta$ is the efficiency, $P_n$ is rated power, and $\lambda _n$ is rated flux.

Table 1 IM parameters

From Figs. 6, 7, 8, 9, 10, 11 12, 13, 14 and 15, simulation results are presented. Figure 6 shows the IFOC performance for speed control and the respective behavior of stator currents in the qd system. In this case, the rated flux reference is used for simulation. The motor starts without load, and the rated load is applied at $t=7$ s. It can be observed that the speed controller tracks the reference in about 1 s. Also, it can be observed that the $i_\mathrm{ds}$ current remains constant to ensure that constant flux and $i_\mathrm{qs}$ varies according to the required torque.

Fig. 6

IFOC performance—speed control and stator currents

Fig. 7

Drive efficiency for full load and 30 % load

Fig. 8

Speed and load profiles used in the simulation and experimental analysis

Fig. 9

Optimal flux versus load ($\lambda _\mathrm{dr\_opt}$ without parameters variation)

Fig. 10

Power consumption versus flux for different load values

Fig. 11

Detail of power losses versus flux

Fig. 12

Power consumption from grid using the constant flux

Fig. 13

Power consumption from grid using the SC efficiency controller

Fig. 14

Power consumption from grid using the proposed LMC efficiency model

Fig. 15

Power consumption from grid using the HAEC model efficiency controller

On the other hand, Fig. 7 shows the motor efficiency for this case (Fig. 6) compared with a smaller load (30 % of the rated value). It can be verified that for any situation with smaller loads, the IM drive has lower efficiency.

For simulation and experimental analysis, the speed and load profiles are chosen to operate below the rated values, as shown in Fig. 8. These profiles are chosen since the motor efficiency is reduced when the motor is not under rated operation. In these situations, the efficiency controller aims to improve energy efficiency. To change the speed reference, a ramp profile is applied from $t=3$ s to $t=5$ s. The ramp is used since, due to its inertia, it is impossible to any motor to follow a step speed reference. This profile also guarantees a better machine magnetization than in step changes. It should be noted that during speed ramp, the load torque also has a ramp behavior due to the mechanical friction of the coupled generator. In experimental verification, this behavior was also checked by the torque transducer.

Figure 9 shows the curve $\lambda _\mathrm{dr\_opt}$ as a function of $T_\mathrm{L}$. In this case, the calculated reference flux is analyzed in terms of load variation for 104.7 rad/s (1000 rpm). It is observed that this relationship is nonlinear. The value of the optimal flux for test conditions is highlighted in this figure. The curves $\lambda _\mathrm{dr\_opt}A,\,\lambda _\mathrm{dr\_opt}$B and $\lambda _\mathrm{dr\_opt}$C are obtained for changes in motor parameters, which will be detailed in Sect. 4.2.

The consumed active power in terms of the rotor flux for different load values is shown in Fig. 10, also for 104.7 rad/s (1000 rpm) rotational speed. It can be seen that for each value of load, there is a minimum value of absorbed power as a function of rotor flux. Also, the minimum absorbed power to $T_\mathrm{L}=0.49$, 2.61, 5.04, 7.35 Nm is highlighted, which matches the optimal flux highlighted in Fig. 9.

Figure 11 presents details of the copper and iron losses when rotor flux varies in a point of operation. It is noted that the iron losses are smaller than cooper losses, so they have a minor influence on total losses.

Considering the load and speed profile in Fig. 8, simulations of power consumptions were performed using MATLAB for different flux references, and its results are presented in Figs. 12, 13, 14 and 15. Four cases were considered for described analysis, as follow:

• Reference flux constant ($\lambda _\mathrm{dr}^* = 0.23$ Wb).

• Reference flux optimized by the SC strategy.

• Reference flux optimized by the proposed loss model according to Eq. (30).

• Reference flux optimized by the HAEC model proposed by Scarmin et al. (2010).

In Fig. 13, the characteristic of the SC efficiency controller can be observed. At steady state, the SC controller achieves the same flux that the optimal value obtained from the proposed LMC controller. However, to achieve the optimal flux, the convergence time of SC approach is significantly higher than that of the proposed LMC model. Furthermore, oscillations are verified in the absorbed power due to step changes in flux reference, as shown in Fig. 13. Using the proposed LMC model, the absorbed power has no oscillations, as it is shown in Fig. 14. In Fig. 15 it can be noted that the HAEC controller combines the speed response of LMC approach with the accuracy of SC, but the response time is higher than that of the proposed LMC approach.

In all scenarios, corresponding to Figs. 12, 13, 14 and 15, the IFOC controller gains are kept the same.

4.1 Power Considerations

For the four cases of power consumption considered previously, the energy absorbed from the grid was calculated during the first 70 s and is summarized in Table 2.

Table 2 Energy consumption from the grid during 70 s

Analyzing the power consumption in Table 2 and graphical results in Figs. 12, 13, 14 and 15, some remarks can be verified:

• The constant flux reference has higher energy consumption at any situation;

• The LMC proposed controller has the best efficiency because the flux converges more quickly to optimal value;

• The HAEC controller has good efficiency; however, it is slightly less efficient than the LMC proposed model, since the SC term has higher convergence time.

The SC controller can achieve better efficiency than the proposed model in special situations. For example, if the load torque stays constant for long periods, the SC controller is always near the optimal value, since the proposed model depends on the accuracy of the obtained parameters and operating conditions. However, in situations where the load operation point changes frequently, the SC model will have a lower performance than the proposed model, not to mention that the SC controller produces torque ripples, consequently leading to poor quality in maintaining speed.

4.2 Sensitivity Analysis of the LMC Proposed Model Due to Parameters Variations

Although the motor parameters are usually obtained in experimental tests, these parameters can change due to environment conditions, such as temperature variation, and overload operation.

The parameters that are most affected by the temperature variation are the windings and iron resistances. The behavior of the resistance variation can be analyzed using the following expression (Moreno et al. 2001):

$$\begin{aligned} r=r_0\left[ 1+\alpha (T-T_0)\right] \end{aligned}$$

(33)

where $r_0$ is the known value of winding resistance ($\varOmega$), at temperature $T_0$ ($^\circ$C); r is the winding resistance ($\varOmega$), recalculated to the temperature T ($^\circ$C); $\alpha$ is the temperature coefficient (1/$^\circ$C). The typical values for $\alpha$ are 0.00389 for cooper, 0.00375 for aluminum and 0.005 for iron.

The rated resistances of the motor windings were measured at 20 $^\circ$C. On overload, the stator reaches up to 70 $^\circ$C and rotor up to 90 $^\circ$C. In this case, the new values for the resistors are recalculated using (33) as $r_\mathrm{r}=1.60\varOmega ,\,r_\mathrm{s}=2.05\varOmega$ and $r_\mathrm{fe}=775\varOmega$.

Another parameter change is the inductance due to core saturation. In Ganji et al. (1998), it is observed that an increasing magnetizing current reduces the dynamic inductance of the system. The variation in the inductance is around 15 % when the magnetizing current reaches 50 % above the rated value.

Using the error propagation theory (Barford 1985), Table 3 shows the sensitivity of the optimal flux due to variations of involved parameters individually. In this case, even with significant individual variations of the motor parameters the reference flux $\lambda _\mathrm{dr\_op}$ is only slightly affected.

Table 3 Optimal flux sensitivity due to individual parameters variation

In Table 4, the simultaneous variation of the motor parameters is considered and its effect in $\lambda _\mathrm{dr\_op}$.

Table 4 Optimal flux sensitivity due to simultaneous parameters variation

It is known in the literature that the error propagation theory considers the worst case of the involved parameters variation direction, which results in a higher error propagation. This propagation is summarized in the first row of Table 4 [union of ($r_\mathrm{s},\,r_\mathrm{r},\,r_\mathrm{fe},\,L_\mathrm{M},\,Llr$) (in theory)] and in the curve $\lambda _\mathrm{dr\_opt}$A in Fig. 9.

For the real electric motor case, in overload conditions, all windings tend to increase simultaneously their resistivity with an increase in temperature and, due the core saturation, decreases all inductances simultaneously. Therefore, the interference in the propagated error will be smaller, since the direction of parameters variation is known (Table 4—union of ($r_\mathrm{s},\,r_\mathrm{r},\,r_\mathrm{fe},\,L_\mathrm{M},\,Llr$) (in practice); curve $\lambda _\mathrm{dr\_opt}$C in Fig. 9).

When the motor is operating with an efficiency controller, the core saturation can be avoided, so only the resistances affect the propagated error (Table 4—only resistors (in practice); curve $\lambda _\mathrm{dr\_opt}$B in Fig. 9).

It is observed that the parameters that most influence the variation of the optimal flux are the resistance of the iron and the magnetizing inductance. However, in practice, these variations will be smaller, since the main objective is to optimize the energy efficiency of the motor at light loads, i.e., without overheating neither core saturation.

To improve even more the accuracy of the proposed loss model, online identification of winding resistances can be applied following the Verrelli et al. (2014) approach. Furthermore, temperature sensors are sometimes installed in the stator windings. However, since inserting sensors in the rotor is not feasible, the stator temperature can be used as a reference to estimate the rotor temperature (de Morais Sousa et al. 2013). Some motor factories such as WEG (2015) already produce small motors (approx. 1 kW) with thermocouples especially designed for such applications.

5 Experimental Setup and Results

In order to verify the numerical results in real situations, an experimental setup for induction motors driving has been built. The main modules that compose the experimental setup are: Semikron SKKH 42/08E Rectifier, Semikron SKM75GB063D IGBTs Inverter, a DC link LC filter ($L=2$ mH, $C=4700$ $\mu$F). Hall effect sensors are being used for current (LA55-P) and voltage (LV 25-600) measurements. The rotor speed of the motor is measured using an Hengstler AC58-12 bit gray output absolute encoder. The digital control algorithm is computed using a TMS320F28069 from Texas Instruments, which includes a 32-bit floating point core, 12-bit-3MSPS-12ch ADC converter and 16-bit-16ch-PWM generator.

Using a PWM output as a digital/analog (D/A) converter, the instantaneous reference speed is shown in Fig. 16. It is also observed that the controller action leads the motor to the desired speed in a short time without overshooting and with zero error in steady state. The delay of the motor speed to the reference speed is due to the use of a tachogenerator and a low-pass filter to obtain the motor speed signal on the oscilloscope.

Fig. 16

Reference speed (light blue) and rotor speed (dark blue) (Color figure online)

Figure 17 presents the three-phase currents of the stator. It is observed that the motor is turned on at 1 s and the next 3 s the rotor maintains zero speed. During this interval, the machine is magnetized.

Fig. 17

Three-phase stator currents of the motor

Figure 18 presents the experimental behavior of inverter input power and the rotor flux for 5.04 Nm load. Maintaining the motor operating with constant load, flux was changed from 0.19 to 0.68 Wb in eighteen equal intervals. The minimum input power 758.84 W was achieved with 0.54 Wb reference flux. For the same load, in Fig. 10 the optimal numerical reference flux is 0.517 Wb where the input power reaches its minimum value 662.9 W. It is observed that the numerical flux and experimental reference flux are very close. The difference for input power in both analyses is due to switching losses in the PWM inverter that were not considered in the theoretical model.

Fig. 18

Experimental input power (blue) and flux (magenta) for 5.04 Nm load (Color figure online)

Figure 19 shows the speed behavior when the load torque is changed according to load profile in Fig. 8. It is observed that the IFOC controller is able to track the motor speed reference for each required torque.

Fig. 19

Speed and torque response of the IFOC control strategy

The input power of DC bus for the three cases previously described is shown in Figs. 20, 21 and 22. The power curve for the constant reference flux ($\lambda _\mathrm{dr}^*=0.23$ Wb) is presented in Fig. 20. Figure 21 shows the power curve for reference flux optimized by the SC efficiency controller. The power curve for reference flux following the LMC proposed model is shown in Fig. 22.

Fig. 20

Analysis of the input power from DC bus with constant flux

Fig. 21

Analysis of the input power from DC bus with SC efficiency controller

Fig. 22

Analysis of the input power from DC bus with the LMC proposed model

It can be observed that the response of the absorbed power of these three cases has a similar behavior to the simulation ones. Since the inverter switching losses were not considered in the theoretical model, the power amplitude obtained in experimental results is slightly larger than that in the theoretical one. Therefore, this experimental result confirms the analysis of the proposed loss model.

6 Conclusion

This paper presented the development of a loss model-based control for energy improvement of three-phase induction motors. The strategy applies optimality concepts to derive a reference rotor flux expression for IFOC approach in order to obtain high efficiency even at light loads and low speed. This efficiency can be observed in steady state by comparing the proposed model with SC methods, where both reach the same optimal value. Although efficiency is verified at steady-state operation, the proposed model was performed in different operation conditions, presenting results with stable and fast transient response at the same time that it improves the overall drive efficiency. Considering variation of motor parameters, which are included in this paper, it is observed that the most significant changes for energy efficiency are iron resistance and magnetizing inductance. However, even with 26 % change in motor parameters, its effects are reduced in the proposed LMC (less than 6 %). To reduce even more this effect, an SC algorithm that does not depend on the motor model can be added to LMC. For real-time analysis, the proposed model was implemented on an experimental setup based on a 4hp motor and TMS320F28069 processor from Texas Instruments. The performance of the proposed model was tested in both simulation and experimental approaches considering different operating conditions. Numerical and experimental results show similar behavior, with significant improvement of energy efficiency, which demonstrates the proposed objective of the controller. Moreover, if the load or velocity profile changes are more frequent, the energy saving obtained with the proposed model will be even higher when compared with conventional approach of constant flux reference.