1 Introduction

Green’s function plays a significant role in the theoretical research and engineering application of many widely-used partial differential equations (PDEs), such as Poisson, Helmholtz and wave equations [35]. For one thing, Green’s function can help solve PDEs and develop PDE theory. Given Green’s function of the differential operator, the solutions of a class of PDE problems can be written explicitly in an integral form where Green’s function serves as the integral kernel [12, 18]. Thanks to this explicit representation of the PDE solution, Green’s function provides a powerful tool to study the analytical properties of PDEs. For the other, Green’s function also has applications in many physical and engineering fields such as quantum physics [13], electrodynamics [23] and geophysics [38].

Because of the importance of Green’s function, the computation of Green’s function, especially in general domains, has attracted more and more attention in the past several decades. Theoretically, in [19], the analytical expressions of Green’s function of the Poisson equation in some simple cases are given, while [27] discussed Green’s function of the Helmholtz equation in the interior or exterior of the unit disc. However, there is no analytical expression of Green’s function in general domains.

In the meanwhile, when it comes to computing Green’s function numerically, there are also mainly three difficulties. Firstly, solving Green’s functions is a high-dimensional problem. Compared with the original PDE, its dimension is doubled, which limits the application of traditional methods such as finite difference method (FDM) to solve Green’s function directly. Secondly, Green’s function is not smooth and has singular points, and thus more effort should be devoted to obtaining high-precision solutions. Thirdly, the domain of PDE may have a complex geometrical structure or is even unbounded, adding more difficulty to the computation of Green’s function.

Fortunately, the rapid development of neural networks and deep learning in recent years [17] open up new possibilities for computing Green’s function. Owing to its universal approximation ability [21], especially for high-dimensional functions, deep learning has made important progress in numerous fields such as image recognition [26], natural language processing [10] and many scientific computation problems. Note that Green’s function itself is the solution to a parametric PDE, we can consider using neural networks to solve this PDE.

In fact, tracing back to 1990 s, there were works considering using neural networks to solve PDEs [11, 28]. In recent years, with the emergence of more powerful tools in machine learning, such as automatic differentiation [3], more and more attention has been paid to this field. The most natural idea is to use neural networks to approximate the solutions of PDEs directly and use the residuals of the PDEs and the boundary conditions to construct loss functions for training, e.g., PINN [36], DGM [37]. There are also many works that put forward different forms of loss functions, such as Deep Ritz [40] using the variational form of the PDE and MIM [33] in which high-order PDEs are transformed to low-order systems. Except for the common choice of multilayer perceptron (MLP) as the network structure, in Deep Ritz method [40], the residual network (ResNet) structure is used while in [6] authors proposed multi-scale neural networks. In addition, there are also some works like Deep BSDE [39] where PDEs are solved by combining stochastic differential equations and neural networks which can avoid extra automatic differentiation of the networks.

In addition to solving a single equation, solving parametric equations and learning solution operators, i.e., the mapping from the parameter or the source item of PDEs to the corresponding solution has drawn extensive attention most recently. In [30], the Fourier neural operator (FNO) is proposed, where Fourier transformation is utilized to design the network architecture. In [32], another network structure composed of branch net and trunk net dealing with the PDE parameters and spatial coordinates respectively is proposed. Deep Green [16], and MOD-net [41] both use an analogous Green’s function approximated by a neural network to represent the solution operator of nonlinear PDEs, which maps the source item or boundary value to the solution.

However, some important issues that are not fully considered in these existing neural network-based methods, together with the complexity of Green’s function itself, hinder the direct application of these methods from solving Green’s function. Firstly, most of the works learning PDE solution operators are based on supervised learning, which requires a large amount of accurate solution data as the supervisory signal. The data are often obtained by solving PDE repeatedly, making the computational cost of preparing the training data very high. Besides, the learned solution operator usually performs badly outside the training set, and thus the generalization ability of these methods is limited by the coverage of the dataset. Secondly, some works use the neural network to directly approximate Green’s function. The singularity of Green’s function is not taken into account, and extra differentiation with respect to the network input is required, which may degenerate the accuracy of the approximation. Lastly, for some problems such as electromagnetic wave propagation, solving PDEs in an unbounded domain is critical. However, existing methods use a neural network to approximate the solution operator or Green’s function directly, which severely suffer from the difficulty of sampling in unbounded domains.

To address these issues and overcome the three difficulties in computing Green’s function mentioned above, in this paper, we design a novel neural network-based formulation to compute Green’s function directly. Firstly, we use the fundamental solution to decompose Green’s function into an explicit singular part and a smooth part such that the equation for Green’s function is reformulated into a smooth high-dimensional equation. Neural network-based methods are then designed to solve this high-dimensional PDE. In particular, we introduce two neural network formulations for this problem: derivative-based GreenNet method (DB-GreenNet) and boundary integral equation-based (BI-GreenNet) method. The idea of DB-GreenNet method is similar to PINN[36], DGM [37] and some other articles [5], which use the residual of equations and boundary conditions as the loss function, and directly approximate the objective function by a neural network. The derivative of the network with respect to network input appearing in the PDE residual is calculated by automatic differentiation. BI-GreenNet method is based on BINet [31], which is a method for solving parameterized PDEs. Based on potential layer theory, the PDE solution is transformed into the a boundary integral equation such that the PDE is automatically satisfied and no extra differentiation with respect to network input is needed. As is verified by our experiments, BI-GreenNet method not only outperforms the DB-GreenNet method, but also can compute Green’s function in unbounded domains.

Besides, the proposed neural network-based method can solve not only Green’s function of a single domain, but also that of interface problems. Interface problem refers to the problem in which an interface separates the computation domain into two parts, and the PDE parameters in the two parts are different, which widely appears in thermology [15], fluid mechanics [29], electrodynamics [23] and many other fields. Some jump conditions across the interface are required such that the solution is usually discontinuous and non-smooth, making it a non-trivial task to solve the interface problem. Therefore, solving Green’s function of the interface problem is also of great significance. Similarly, we can also derive the PDE for Green’s function of the interface problem and utilize the BI-GreenNet method to transform the PDE into a boundary integral equation.

In conclusion, the main contributions of our work are summarized as follows:

  • Firstly, we propose a novel neural network-based framework to learn Green’s function directly in an unsupervised manner, based on which the solution operator from the infinite-dimensional source term and boundary condition space to the solution space is also obtained.

  • Secondly, to override the singularity of Green’s function, we propose to decompose Green’s function into an explicit singular part and a smooth part solved by neural networks. Except for the natural idea of derivative-based neural network, we adopt the boundary integral-based network structure (BINet) such that the PDE is satisfied automatically and simple architecture of hidden layer network like MLP and ResNet is enough to fit the target function. It is also worth noting that under our framework, BINet can be flexibly replaced by other neural network-based solvers with specially designed architecture, which will be investigated in our future work.

  • Lastly, extensive experiments show that the proposed method can not only compute Green’s function in any bounded domain, but also works for interface problems. In particular, by utilizing the boundary integral equation, the BIE-based formulation can also solve Green’s function in unbounded domains. In addition, we also apply the learned Green’s function as the solution operator to solve a class of PDEs and also obtain solutions with reasonably high precision.

Our methods also have some limitations. The main limitation is that the requirements for the explicit expression of fundamental solutions hinder the application of our method in more complex PDEs. Besides, in BI-GreenNet, to accurately compute the integral on the boundary with singular kernels, high precision quadrature is required, which also limits the application of BI-GreenNet in computing Green’s function of too high dimensional problems.

The rest of this paper is organized as follows. In Sect. 2, we recall Green’s function and the basic theoretical foundation, potential theory of our method. In Sect. 3, we introduce our BI-GreenNet method for solving Green’s function. Extensive numerical experiments are shown in Sect. 4. At last, conclusion remarks are made in Sect. 5.

2 Preliminaries

2.1 Green’s Function

In this paper, for simplicity, we focus on the Dirichlet Green’s function, i.e., Dirichlet boundary condition is imposed on the boundary of the computation domain. Green’s function of other types can be easily handled with some small modifications. We consider both problems defined on a single domain, which can be further divided into interior problem and exterior problem, and the interface problem defined on two domains with different PDE parameters separated by an interface, as will be elaborated below.

Fig. 1
figure 1

Illustration of the computation domain

Full size image

2.1.1 Green’s Function on a Single Domain

As is shown in Fig. a, \(\Omega \subset \mathbb {R}^d\) is a bounded domain, \(\Omega ^c=\mathbb {R}^d\backslash \Omega \). The interior problem and the exterior problem are formulated as

  • Interior problem,

    $$\begin{aligned} \left\{ \begin{aligned} \mathcal {L}u(x)=f(x) \ \text {in} \ \Omega ,\\ u(x) = g(x) \ \text {on} \ \partial \Omega . \end{aligned} \right. \end{aligned}$$
    (2.1)

  • Exterior problem,

    $$\begin{aligned} \left\{ \begin{aligned}&\mathcal {L}u(x)=f(x) \ \text {in} \ \Omega ^c,\\ u(x) = g(x) \ \text {on} \ \partial \Omega&+\ \text {some boundary conditions at infinity}, \end{aligned} \right. \end{aligned}$$
    (2.2)

where \(\mathcal {L}\) is a differential operator. For brevity, we represent the equations in (2.1) and (2.2) as

$$\begin{aligned} \mathcal {L}u(x)=f(x)\ \text {in}\ \Omega ^*, \end{aligned}$$
(2.3)

where \(\Omega ^*=\Omega \) or \(\Omega ^c\) for the interior or the exterior problem, respectively.

In this paper, we focus on the Poisson equations and Helmholtz equations, i.e., \(\mathcal {L}=-\Delta \) or \(-\Delta -k^2\), where k is the wave number. Helmholtz equations are the expansion of wave equation in frequency domain. It is used to describe wave propagation and is widely used in electromagnetics [9] and acoustics [4]. Because it involves wave propagation, Helmholtz equation often appears in the problem in unbounded domain, and because of the instability of Helmholtz equation, its numerical solution has always been an important problem [2, 7].

For Eq. (2.3), we can use the corresponding Green’s function G(x) to give the analytical solution [14]

$$\begin{aligned} u(x)=\int _{\Omega ^*}G(x,y)f(y)dy+\int _{\partial \Omega }\frac{\partial G(x,y)}{\partial n_y}g(y)ds_y, \end{aligned}$$
(2.4)

where G(x, y) is a 2d-dimensional function satisfying

$$\begin{aligned} \left\{ \begin{aligned} \mathcal {L}_yG(x,y)=\delta (x-y),&\quad \forall \ x,y\in \Omega ^{*},\\ G(x,y)=0,&\quad \forall \ x\in \Omega ^{*}, \ y\in \partial \Omega . \end{aligned} \right. \end{aligned}$$
(2.5)

2.1.2 Green’s Function of the Interface Problem

As is shown in Fig. 1b, \(\Omega \subset \mathbb {R}^d\) can be either bounded or unbounded. An interface \(\Gamma _1\subset \mathbb {R}^{d-1}\) divides \(\Omega \) into two regions, i.e., inside (\(\Omega _1\)) and outside (\(\Omega _2)\) of the interface. The boundary of \(\Omega \) is denoted as \(\Gamma _2=\partial \Omega \).

The interface problem is then formulated as [8, 20]:

$$\begin{aligned} \left\{ \begin{aligned}&\mathcal {L}u=f,&\quad&\text {in} \ \Omega ,\\&[u]=g_1, \ \left[ \frac{1}{\mu }\frac{\partial u}{\partial n}\right] =g_2,&\quad&\text {on} \ \Gamma _1,\\&u=g_3,&\quad&\text {on} \ \Gamma _2, \end{aligned} \right. \end{aligned}$$
(2.6)

where \(\mathcal {L}\) is an operator with different parameters inside and outside the interface \(\Gamma _1\), n is the outward normal vector on the interface \(\Gamma _1\). The bracket \([\cdot ]\) denotes the jump discontinuity of the quantity approaching from \(\Omega _2\) minus the one from \(\Omega _1\). Moreover, some condition at infinity should be considered together for unbounded \(\Omega \) to make the interface problem well-posed, which will be specified in detail in the experiments.

Similar to the single domain case, we focus on

  • Poisson equations: \(\mathcal {L}u=-\nabla \cdot (\frac{1}{\mu }\nabla u)\), where \(\mu \) is a piecewise constant parameter such that \(\mu =\mu _1\) in \(\Omega _1\) and \(\mu =\mu _2\) in \(\Omega _2\);

  • Helmholtz equations: \(\mathcal {L}u=-\nabla \cdot (\frac{1}{\mu }\nabla u)-\varepsilon k^2u\), where \(\mu \) and \(\epsilon \) are also piecewise constant parameters such that \(\mu =\mu _1\), \(\varepsilon =\varepsilon _1\) in \(\Omega _1\) and \(\mu =\mu _2\), \(\varepsilon =\varepsilon _2\) in \(\Omega _2\).

Utilizing the corresponding Green’s function, the solution to the interface problem is given by

$$\begin{aligned} \begin{aligned} u(x)&=\int _{\Omega }G(x,y)f(y)dy+\int _{\Gamma _1}\left( \frac{1}{\mu }\frac{\partial G(x,y)}{\partial n_y}g_1(y)-G(x,y)g_2(y)\right) ds_y\\&\quad -\int _{\Gamma _2}\frac{1}{\mu }\frac{\partial G(x,y)}{\partial \nu _y}g_3(y)ds_y, \end{aligned} \end{aligned}$$
(2.7)

where \(\nu \) is the outward normal vector on \(\Gamma _2\) and G(x, y) satisfies

$$\begin{aligned} \left\{ \begin{aligned}&\mathcal {L}_y G(x,y)=\delta (x,y),&\quad&\forall \ x,y\in \Omega ,\\&[G(x,y)]=\left[ \frac{1}{\mu }\frac{\partial G(x,y)}{\partial n_y}\right] =0,&\quad&\forall \ x\in \Omega , \ y\in \Gamma _1,\\&G(x,y)=0,&\quad&\forall \ x\in \Omega , \ y\in \Gamma _2. \end{aligned} \right. \end{aligned}$$
(2.8)

2.2 Potential Theory

In this subsection, we briefly introduce the potential theory, the key to the boundary integral-based (BI-based) method, which will later be utilized to solve Green’s function. We first define the single and double layer potential operators corresponding to the differential operator \(\mathcal {L}_y\).

Definition 2.1

For any continuous function h defined on \(\Omega \times \partial \Omega \), the single layer potential is defined as

$$\begin{aligned} \mathcal {S}[h](x,y):=-\int _{\partial \Omega } G_0(y,z) h(x,z) d s_z, \end{aligned}$$
(2.9)

and the double layer potential is defined as

$$\begin{aligned} \mathcal {D}[h](x,y):=-\int _{\partial \Omega } \frac{\partial G_0(y,z) }{\partial n_z} h(x,z) d s_z. \end{aligned}$$
(2.10)

where \(n_z\) denotes outward normal of \(\partial \Omega \) at z, and \(G_0(x,y)\) is the fundamental solution corresponding to the differential operator \(\mathcal {L}_y\) satisfying

$$\begin{aligned} \mathcal {L}_yG_0(x,y)=\delta (x-y)\text { for all }x,y\in \mathbb {R}^d. \end{aligned}$$
(2.11)

Based on the layer potential theory of the Poisson equation and Helmholtz equation [25], we have the following theorem.

Theorem 2.2

The single and double layer potentials have the following properties.

(i) The single layer potential \(\mathcal {S}[h](x,y)\) and double layer potential \(\mathcal {D}[h](x,y)\) are well defined in \(\Omega ^*\times \Omega ^*\).

(ii) The single and double layer potentials satisfy equations (3.2) and (3.3), i.e.,

$$\begin{aligned} \begin{aligned} \mathcal {L}_y\mathcal {S}[h](x,y)=0,\\ \mathcal {L}_y\mathcal {D}[h](x,y)=0. \end{aligned} \end{aligned}$$
(2.12)

(iii) For \(y_0\in \partial \Omega \), and the boundary near \(y_0\) is smooth, we have

$$\begin{aligned} \begin{aligned} \mathop {\textit{lim}}\limits _{y\rightarrow y_0}\mathcal {S}[h](x,y)&= \mathcal {S}[h](x,y_0),\\ \mathop {\textit{lim}}\limits _{y\rightarrow y_0^\pm }\mathcal {D}[h](x,y)&= \mathcal {D}[h](x,y_0)\mp \frac{1}{2}h(x,y_0), \end{aligned} \end{aligned}$$
(2.13)

where \(y\rightarrow y_0^-\) and \(y\rightarrow y_0^+\) mean converging in \(\Omega \) and \(\Omega ^c\), respectively.

By Theorem 1 we can see the solution to the PDE \(\mathcal {L}_y u(x,y) =0\) can be written in a boundary integral form such that the PDE is satisfied automatically and we only need to solve the density function h to fit the boundary condition.

3 Neural Network for Green’s Function

3.1 Removing the Singularity

As mentioned above, Green’s function is a singular function. However, we can change the equation (2.5) into a smooth equation by using the fundamental solutions \(G_0\) of the original PDEs satisfying

$$\begin{aligned} \mathcal {L}_yG_0(x,y)=\delta (x-y)\text { for all }x,y\in \mathbb {R}^d, \end{aligned}$$
(3.1)

which also can be seen as Green’s function of the whole space \(\mathbb {R}^d\). For many important PDEs, fundamental solutions can be written explicitly. For the Poisson equation \(-\Delta u(x)=f(x)\) in \(\mathbb {R}^2\), the fundamental solution is \(G_0(x,y)=-\frac{1}{2\pi }\text {ln}\vert x-y\vert \), while the fundamental solution for the Helmholtz equation \(-\Delta u(x)-k^2u(x)=f(x)\) in \(\mathbb {R}^2\) is \(G_0(x,y)=\frac{i}{4}H_0^1(k\vert x-y\vert )\) where \(H^1_0\) is the Hankel function. The fundamental solutions of the high dimensional cases and more equations can be found in [22].

For Green’s function on a single domain, we set \(H(x,y)=G(x,y)-G_0(x,y)\), then H is a smooth function and satisfies the following equation

$$\begin{aligned} \left\{ \begin{aligned}&\mathcal {L}_y H(x,y)=0,&\quad \forall \ x,y\in \Omega ^{*},\\&H(x,y)=-G_0(x,y),&\quad \forall \ x\in \Omega ^{*}, \ y\in \partial \Omega . \end{aligned} \right. \end{aligned}$$
(3.2)

For Green’s function of the interface problem, the fundamental solution of the Poisson equation in \(\mathbb {R}^2\) is \(G_0(x,y)=-\frac{\mu (y)}{2\pi }\ln \vert x-y\vert \), while the fundamental solution of the Helmholtz equation in \(\mathbb {R}^2\) is \(G_0(x,y)=\frac{i}{4}\mu (y)H_0^1(k\sqrt{\varepsilon (y)\mu (y)}\vert x-y\vert )\). Set \(H(x,y)=G(x,y)-G_0(x,y)\), then H satisfies the following equation

$$\begin{aligned} \left\{ \begin{aligned}&\mathcal {L}_y H(x,y)=0,&\quad&\forall \ x,y\in \Omega ,\\&[H(x,y)]=-[G_0(x,y)],&\quad&\forall \ x\in \Omega , \ y\in \Gamma _1,\\&\left[ \frac{1}{\mu }\frac{\partial H(x,y)}{\partial n_y}\right] =-\left[ \frac{1}{\mu }\frac{\partial G_0(x,y)}{\partial n_y}\right] ,&\quad&\forall \ x\in \Omega , \ y\in \Gamma _1,\\&H(x,y)=-G_0(x,y),&\quad&\forall \ x\in \Omega , \ y\in \Gamma _2. \end{aligned} \right. \end{aligned}$$
(3.3)

After the singularity of the original equation is successfully eliminated, we will introduce how to use neural network to solve this problem by combining boundary integral method and neural network.

3.2 BI-GreenNet

3.2.1 Derivative-Based GreenNet (DB-GreenNet)

After removing the singularity, we transform the problem (2.5) and (2.8) into problem (3.2) and (3.3). Although the singularities have been removed, problem (3.2) and (3.3) are still of high dimension such that traditional methods are difficult to handle. A natural idea to solve these problems is based on the automatic differentiation technique [3]. Like the Deep Ritz [40] and PINN[36], for the interior problem in bounded domain, we use a neural network \(\tilde{H}(x,y;\theta )\) to approximate the function H(x, y) of the problems (3.2) and (3.3). The derivative \(\mathcal {L}_y\tilde{H}(x,y;\theta )\) can be calculated by automatic differentiation. For brevity, the loss function can be designed as the following form by combining the residuals of the PDE and the boundary condition

$$\begin{aligned} \begin{aligned} L(\theta ) = \sum _{i=1}^N \vert \mathcal {L}_y\tilde{H}(x_i^{\text {pde}},y_i^{\text {pde}};\theta )\vert ^2+\lambda \sum _{j=1}^M\vert \tilde{H}(x_j^{\text {bd}},y_j^{\text {bd}};\theta )+G_0(x_j^{\text {bd}},y_j^{\text {bd}})\vert ^2, \end{aligned}\nonumber \\ \end{aligned}$$
(3.4)

where \(\lambda \) is the given weight and \(\{x_i^{\text {pde}},y_i^{\text {pde}}\}_{i=1}^N\) are N points randomly sampled in \(\Omega \times \Omega \), while \(\{x_j^{\text {bd}},y_j^{\text {bd}}\}_{j=1}^M\) are M points randomly sampled in \(\Omega \times \partial \Omega \). After training, an approximation of Green’s function can be obtained by the sum of \(\tilde{H}(x,y;\theta )\) and the fundamental solution \(G_0(x,y)\). We refer to this formulation as derivative-based GreenNet (DB-GreenNet) method.

However, the derivative-based method is not stable since extra differentiation with respect to the network input is needed, and the experiment results in Sect. 4 show the poor accuracy of DB-GreenNet. More importantly, it can not deal with the exterior problems since it is difficult to sample in unbounded domains.

3.2.2 Boundary Integral-Based GreenNet (BI-GreenNet)

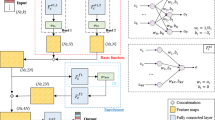
Due to the limitations of the derivative-based method, we try to combine the Boundary Integral Network (BINet) [31], a PDE solver that can achieve high accuracy and also can deal with the exterior problem in the unbounded domain, to compute Green’s function. Note that the partial differential equation \(\mathcal {L}_y H(x,y)=0\) in both (3.2) and (3.3) can be regarded as a parametric equation with x being the parameter. As is illustrated in Fig. , based on BINet, we can represent the smooth component H(x, y) in a boundary integral form such that the differential equation is satisfied automatically and only boundary conditions are to be fit. We call this fomulation boundary integral-based GreenNet (BI-GreenNet) method and we will describe in detail how this method is implemented for both the single domain problem and the interface problem.

Fig. 2
figure 2

The schematic of the boundary integral-based GreenNet (BI-GreenNet) method

Full size image

Single domain problem For the single domain problems, because we mainly consider the Dirichlet problem in this paper, we choose the double layer potential operator expression in our formulation. H(x, y) can then be written as the kernel integral form

$$\begin{aligned} H(x,y)=\mathcal {D}[h](x,y):=-\int _{\partial \Omega } \frac{\partial G_0(y,z) }{\partial n_z} h(x,z) d s_z, \end{aligned}$$
(3.5)

where \(G_0\) is the fundamental solution and the function \(h(x,y)\in \Omega ^*\times \partial \Omega \) is approximated by a hidden layer network \(\tilde{h}(x,y;\theta \), which can be selected as MLP or ResNet. The output of this network will satisfy Eq. (3.2) automatically, and we only need to fit the boundary condition, which the loss function is based on. This is also the reason that this method can handle the exterior PDE problem in unbounded domain. The loss function is

$$\begin{aligned} \begin{aligned} {L} = \sum _{i=1}^{N_1}\sum _{j=1}^{N_2}\vert \mathcal {D}[\tilde{h}](x_i,y_j)\mp \frac{1}{2}\tilde{h}(x_i,y_j;\theta )+G_0(x_i,y_j)\vert ^2, \end{aligned} \end{aligned}$$
(3.6)

where \(\{x_i\}_{i=1}^{N_1}\) are \(N_1\) points sampled in \(\Omega \), \(\{y_j\}_{j=1}^{N_2}\) are \(N_2\) points sampled on \(\partial \Omega \). It can be seen that compared with the derivative-based method, the dimension of the sampling space in the boundary integral method is less by 1 since \(\{y_j\}\) is only sampled on the boundary.

Another thing to note is the kernel function of the integral of the potential is singular, so we use the high accuracy quadrature rules in [24] and [1] for smooth boundary, and for the boundary of the polygon domain, we use Simpson’s quadrature rule directly. For convenience, we choose the points in the integration quadrature the same as the sampled points \(\{y_j\}\) on the boundary and are fixed throughout the training.

Interface problem For the interface problem, we use the single layer potential on \(\Gamma _1\) and the double layer potential on \(\Gamma _2\). H(x, y) can then be written as

$$\begin{aligned} H(x,y)= \left\{ \begin{aligned}&-\int _{\Gamma _1} G_0(y,z) h_1(x,z) d s_z,&\quad y\in \Omega _1,\\&-\int _{\Gamma _1} G_0(y,z) h_2(x,z) d s_z-\int _{\Gamma _2} \frac{\partial G_0(y,z)}{\partial \nu _z} h_3(x,z) d s_z,&\quad y\in \Omega _2, \end{aligned} \right. \nonumber \\ \end{aligned}$$
(3.7)

where \(h_1, h_2, h_3\) are approximated by three neural networks as \(\tilde{h}_1(x,z;\theta )\), \(\tilde{h}_2(x,z;\theta )\), \(\tilde{h}_3(x,z;\theta )\), respectively. Recall that in (3.3), three conditions on the boundary need to be satisfied, i.e., two jump conditions on \(\Gamma _1\) and one boundary condition on \(\Gamma _2\). Therefore, the loss function of the interface problem is a weighted summation of three loss functions

$$\begin{aligned} {L}=\lambda _{\text {jump1}} {L}_{\text {jump1}}+\lambda _{\text {jump2}} {L}_{\text {jump2}}+{L}_{\text {bd}}, \end{aligned}$$
(3.8)

where \(\lambda _{\text {jump1}}\) and \(\lambda _{\text {jump2}}\) are the corresponding weights. Denote \(\{x_i\}_{i=1}^{N_1}\) as the \(N_1\) points sampled in \(\Omega \), \(\{y_j\}_{j=1}^{N_2}\) as the \(N_2\) points sampled on \(\Gamma _1\), and \(\{w_k\}_{k=1}^{N_3}\) as the \(N_3\) points sampled on \(\Gamma _2\). The first jump condition \([H(x,y)]=-[G_0(x,y)]\) gives the loss

$$\begin{aligned} {L}_{\text {jump1}}= & {} \sum _{i=1}^{N_1}\sum _{j=1}^{N_2}\left| -\int _{\Gamma _1} G_0(y_j,z) \tilde{h}_2(x_i,z;\theta ) d s_z-\int _{\Gamma _2} \frac{\partial G_0(y_j,z)}{\partial \nu _z} \tilde{h}_3(x_i,z;\theta ) d s_z\right. \nonumber \\{} & {} \qquad \quad \ \left. +G_0(x_i,y_j^+)+\int _{\Gamma _1} G_0(y_j,z) \tilde{h}_1(x_i,z;\theta ) d s_z-G_0(x_i,y_j^-)\right| ^2, \end{aligned}$$
(3.9)

where \(y^+\) and \(y^-\) denote the outside and inside of \(\Gamma _1\), respectively. The second jump condition \(\left[ \frac{1}{\mu }\frac{\partial H(x,y)}{\partial n_y}\right] =-\left[ \frac{1}{\mu }\frac{\partial G_0(x,y)}{\partial n_y}\right] \) gives the loss

$$\begin{aligned} {L}_{\text {jump2}}= & {} \sum _{i=1}^{N_1}\sum _{j=1}^{N_2}\left| \frac{1}{\mu _2}\left[ -\int _{\Gamma _1} \frac{\partial G_0(y_j,z)}{\partial n_y} \tilde{h}_2(x_i,z;\theta ) d s_z+\frac{1}{2}\tilde{h}_2(x_i,y_j;\theta )\right. \right. \nonumber \\{} & {} \left. -\int _{\Gamma _2} \frac{\partial }{\partial n_y}\left( \frac{\partial G_0(y_j,z)}{\partial \nu _z}\right) \tilde{h}_3(x_i,z;\theta ) d s_z+\frac{\partial G_0(x_i,y_j^+)}{\partial n_y}\right] \nonumber \\{} & {} \left. +\frac{1}{\mu _1}\left[ \int _{\Gamma _1} \frac{\partial G_0(y_j,z)}{\partial n_y} \tilde{h}_2(x_i,z;\theta ) d s_z+\frac{1}{2}\tilde{h}_1(x_i,y_j;\theta )-\frac{\partial G_0(x_i,y_j^-)}{\partial n_y}\right] \right| ^2.\nonumber \\ \end{aligned}$$
(3.10)

The third loss is derived from the boundary condition \(H(x,y)=-G_0(x,y)\)

$$\begin{aligned} \begin{aligned} {L}_{\text {bd}}=&\sum _{i=1}^{N_1}\sum _{k=1}^{N_3}\left| -\int _{\Gamma _1} G_0(w_k,z) \tilde{h}_2(x_i,z;\theta ) d s_z-\int _{\Gamma _2} \frac{\partial G_0(w_k,z)}{\partial \nu _z} \tilde{h}_3(x_i,z;\theta ) d s_z\right. \\&\qquad \quad \ \left. +\frac{1}{2}\tilde{h}_3(x_i,w_k;\theta )+G_0(x_i,w_k)\right| ^2. \end{aligned} \end{aligned}$$
(3.11)

Remark: In this paper, we mainly consider the problem with one interface. In fact, the proposed method can be easily generalized to problems with multiple interfaces by setting different density functions on both sides of each interface and the boundary of the whole computational domain.

In conclusion, we summarize the algorithms of the DB-GreenNet and BI-GreenNet for the single domain and interface problem in Algorithms 1 and 2, respectively.

figure a
figure b

4 Numerical Results

In the implementation, we choose a ResNet structure neural network introduced in Deep Ritz method [40]. In order to estimate the accuracy of the numerical solution p, we used the relative \(L^2\) error \(\Vert p-p^{*}\Vert _2/\Vert p^{*}\Vert _2\), where \(p^*\) is the exact solution. In the experiments, we choose the Adam optimizer to minimize the loss function, and we training the neural network on a single GPU of Tesla V100.

4.1 Green’s Function of PDEs in Bounded Domains

In this subsection, we will use the GreenNet to compute Green’s functions of Poisson equations and Helmholtz equations with different shapes of domains, then we will also use Green’s function solved by our methods to solve the PDEs with different source functions.

4.1.1 The Poisson Equation in the Unit Disc

In this experiment, we consider Green’s function of the Poisson equation in the unit disc. From the notes[19], we can know Green’s function of the unit disc of the Poisson equation has the explicit expression,

$$\begin{aligned} G(x,y)=\frac{1}{2 \pi } \ln \frac{r}{r^{\prime } \rho }, \end{aligned}$$
(4.1)

where \(y\in S^1\) and \(y'=\frac{y}{\vert y\vert ^2}\), and \(r=\vert x-y\vert , \quad r^{\prime }=\vert x-y'\vert ,\rho =\vert y\vert .\) Then we can compare the exact Green’s function and the numerical Green’s function calculated by GreenNet.

In the training process, for the BI-GreenNet method, we choose a ResNet with 8 blocks and 100 neurons per layer and ReLU activate function. For every 500 epochs, 80 new x are randomly generated. After \(5\times 10^4\) epochs of training with learning rate \(1\times 10^{-5}\), we randomly generate 100 x and 800 y and compute the \(G(x_i,y_j)\) of these \(8\times 10^4\) points \((x_i,y_j)\) to obtain an average relative \(L_2\) error of Green’s function G(x, y) of \(4.66\times 10^{-3}\). For the DB-GreenNet method, we used the neural network of same size. For every 500 epochs, \(4\times 10^4\) new \((x_i,y_i)\in \Omega \times \Omega \) and \(1\times 10^4\) new \((x_j,y_j)\in \Omega \times \partial \Omega \) are randomly generated for the PDE loss and boundary condition loss respectively. Similarly, after \(5\times 10^4\) epochs, the relative \(L_2\) error of Green’s function G(x, y) is \(5.54\times 10^{-2}\). The comparison of relative \(L^2\) error can be seen in Table .

Table 1 Relative \(L^2\) error of Green’s function in Sect. 4.1
Full size table

Figure  shows the difference of y with fixed x between the exact Green’s function G(x, y) of the unit disc and Green’s function calculated by DB-GreenNet and BI-GreenNet methods. We can see the relative \(L^2\) error of BI-GreenNet method still small when x is close to the boundary. However, the error of derivative-based method increases significantly.

Fig. 3
figure 3

This figure shows the difference between the exact Green’s function G(x, y) of the unit disc and Green’s function calculated by DB-GreenNet and BI-GreenNet methods with fixed x. a and b are the results of \(x=(0.8427,0.4386)\). c and d are the results of \(x=(0.2923,0.0674)\)

Full size image

In addition, we also give some results to show the dependence of accuracy on the number of sampling points for Green’s function. First, We fixed number of sampling points in the domain to 80 or 160 and these interior points will be resampled for every 200 epochs in the training process. We choose different numbers of boundary sampling points, i.e., z in the density function h(x, z), and keep the same network structure and other hyperparameters. After 30000 epochs of training respectively, we calculate the relative error to the accurate Green’s function. Table  shows the relative error with different numbers of boundary sampling points. We can find within a certain range, more boundary sampling points gives higher accuracy. However, when the number of boundary sampling points exceeds a certain level, accuracy can not be further improved since the error is dominated by sampling points in the domain interior.

Table 2 Relative \(L^2\) error (\(\times 10^{-3}\)) of Green’s function with different number of sampling points on boundary
Full size table

We also fixed 1200 boundary sampling points and choose different numbers of sampling points in the domain, i.e., x of the density function h(x, z). These interior points will also be resampled randomly for every 200 epochs in the training process. Table  shows the relative error of Green’s function with different numbers of sampling points. It can be seen that the accuracy of the learned Green’s function increases with the number of interior sampling points. The reason is that more interior sampling points helps the neural network generalize better to new x. This is also reflected in Fig. , where the oscillation of the loss function alleviates for larger number of interior sampling points.

Fig. 4
figure 4

The loss functions of different numbers of interior sampling points

Full size image
Table 3 Relative \(L^2\) error of Green’s function with different number of sampling points in domain
Full size table

4.1.2 The Poisson Equation in the L-shaped Domain

In this experiment, we compute Green’s function of an L-shaped domain by BI-GreenNet method and use it to solve Poisson equations with different source functions in the same domain. We will compare with the results by finite difference method. We consider the following PDE problem,

$$\begin{aligned} \begin{aligned} -\Delta u(x) = f(x) \text { in }\Omega ,\\ u(x)=0\text { on }\partial \Omega . \end{aligned} \end{aligned}$$
(4.2)

The \(\Omega \) is an L-shaped domain and can be seen in Fig. . We use a BINet with 6 blocks and 80 neurons per layer as the hidden layer network. After training, we also obtain the accurate approximation of Green’s function G(x, y) of the L-shaped domain, and then we use integral

$$\begin{aligned} u(x) = \int _\Omega G(x,y)f(y)dy \end{aligned}$$
(4.3)

to calculate the numerical solution of the PDE problem (4.2). In this experiment, we consider a piecewise constant source term f. Specifically, we divided \(\Omega \) into 300 small rectangles and a constant in [\(-\)30, 30] is randomly given on each small rectangle, respectively. The examples of the function f can be seen in Fig. 5a and d. Figure 5 gives two example with randomly f, and shows that although the source function f is complex, our method can also get accurate solutions. The exact solutions are computed by finite difference method with the sufficiently small stepsize.

Fig. 5
figure 5

The exact solutions and numerical solutions of the problem (4.2) with different source terms f. The (a) and (d) are two examples of the source functions and (b), (e) and (c), (f) are corresponding exact solutions and numerical solutions respectively

Full size image

For comparison, we also used finite difference method (FDM) with two discrete stepsizes, 1/80 (=\(1.25\times 10^{-2}\)) and 1/160 (=\(6.25\times 10^{-3}\)) to solve this equation. The numbers of discrete points in \(\Omega \) are 19521 and 77441 respectively. We randomly generate 100 different source functions f and computed the relative \(L^2\) errors with these methods, the results are shown in Fig.  and Table . From these results, we can find that even if the number of parameters is less than the number of discrete points in the FDM method, our method can still achieve higher accuracy, and it should be noted that the parameters of BI-GreenNet are used to represent Green’s function, the solution operator from the source function to the solution function, not just a single solution, but the value of the discrete points of FDM method only represent the single solution. It can be seen that BI-GreenNet represent more complex information with fewer parameters and achieve higher accuracy in this experiment. In the meanwhile, because using our method to solve the equations for different source term functions does not need to retrain the network, but only needs integration, so in the practical implementation, the speed of solving the equations is also very fast.

Fig. 6
figure 6

The relative \(L^2\) error of the solution of the problem (4.2) with 100 different source terms f under the finite difference methods and BI-GreenNet method

Full size image
Table 4 The average of relative \(L^2\) error with 100 different source functions under the different methods of the problem (4.2) and the number of parameters with these methods
Full size table

4.1.3 The Helmholtz Equation in the Square

In this experiment, we consider Green’s function of the following equation

$$\begin{aligned} \begin{aligned} -\Delta u(x) - 4 u(x)&=f(x)\text { in }\Omega ,\\ u(x)&=0\text { on }\partial \Omega , \end{aligned} \end{aligned}$$
(4.4)

where \(\Omega =[-1,1]^2\). In this example, we will compare the performance of DB-GreenNet and BI-GreenNet on Helmholtz equation. The network structure and training details of the two methods are consistent with the first example. Because Green’s function of a Helmholtz equation is a complex number, we add an output of the network to represent the imaginary part. In this example, for some fixed \(x_i\), we can solve Eq. (3.2) about y as the ground truth, but as mentioned before, it should be noted that the equation has to be solved again for each x, so the computation cost is very expensive. Table 1 also shows the relative \(L^2\) error between ground truth and the numerical solution of Green’s function. We can find DB-GreenNet method failed. This is because the oscillation of Helmholtz solution will increase the difficulty for derivative-based method. The superiority of BI-GreenNet method over derivative-based method is shown here.

Next, we also show the ability on solving the Helmholtz equation in \(\Omega \) by Green’s function computed by BI-GreenNet method. We consider using Green’s function to solve the equations with different source terms f, where f belongs to the following set

$$\begin{aligned} \{((c_1^2+c_2^2)\pi ^2-4)f_1(c_1\pi x_1)f_2(c_2\pi x_2): c_1,c_2=1,\cdots ,5\}, \end{aligned}$$
(4.5)

where \(x=(x_1,x_2)\in \Omega \) and \(f_1(a),f_2(a)\in \{\pm \sin (a)\}\). It can be seen that f has 100 combinations. The histogram of Fig.  shows the distribution of the relative \(L^2\) error between the exact solutions and the solutions calculated by our Green’s function with different f. The relative \(L^2\) error of the solution of the equation is between \(1\times 10^{-2}\) and \(4.5\times 10^{-2}\), which shows the stability of solving the equation with Green’s function.

Fig. 7
figure 7

a is the distribution of relative \(L^2\) error of the solution of the PDE with 100 different source terms; b and c is the real part of the exact solution and the numerical solution with the source term \(f=(72\pi ^2-4)\cos (6\pi x_1+\pi /2)\sin (6\pi x_2)\); d is the absolute error between exact solution and numerical solution

Full size image

4.2 Green’s Function of PDEs in Unbounded Domains

The exterior PDE problems in unbounded domains are common in scattering problems and electromagnetic problems, which is closely related to the Helmholtz equation. Therefore, it will be very helpful for analyzing the properties of domains to study Green’s function of Helmholtz equation in unbounded domains. So in this subsection, we focus on Green’s functions of following Helmholtz equation problems

$$\begin{aligned} \begin{aligned} -\Delta u(x) - k^2 u(x)&=f(x)\text { in }\Omega ^c,\\ u(x)&=0\text { on }\partial \Omega ,\\ \lim _{\vert x\vert \rightarrow \infty }\left( \frac{\partial }{\partial r}-ik\right) u(x)&=o(\vert x\vert ^{-1/2}), \end{aligned} \end{aligned}$$
(4.6)

where k is the wavenumber and the limit of \(\vert x\vert \) is called the Sommerfeld condition. In this subsection, we consider two shapes that often appear in practical problems, the bow-tie domain and the U-shaped domain.

We will compare Green’s function calculated by BI-GreenNet method and the exact Green’s function. The exact Green’s function G(x, y) is derived by calculating the H(x, y) of the problem (3.2) through boundary integral method first. However, as mentioned before, Eq. (3.2) is a 4-dimensional problem, we can only solve this equation with some fixed points x. For the every given point x, it is required to solve the Helmholtz equation in an unbounded domain. Therefore, for a large number of different points x, the cost of obtaining H(x, y) is very large. Although our method solves Green’s functions in unbounded domains, we cannot show the results in whole domains, and the domains concerned in practical problems are often bounded, so we will analyze the accuracy and show the results in sufficiently large bounded domains.

4.2.1 The Helmholtz Equation Out of the Bow-tie Antenna

In this experiment, let us consider a more practical scenario, a receiving antenna electromagnetic simulation problem. Assume we have a bow-tie antenna of 1 in length and 1 in width, which is a type of broad-bandwidth antenna. Its structure is 2 dimensional, implemented on a printed circuit board. Therefore, for simplicity, we consider simulating the field within the 2-D space. The shape of the bow-tie antenna can be seen in Fig. . We consider Green’s function of Helmholtz equation out of the bow-tie domains, and in this experiment, we consider the wavenumber \(k=\pi -1/2\).

We also use the GreenNet formulation to compute Green’s function in the domain outside the bow-tie antenna. Because the domain is unbounded, we can only use the BI-GreenNet method. The neural network of this experiment has the similar architecture as the previous and the training process is also similar. We choose the ResNet architecture consisting of 8 blocks and 100 neurons per layer. We select 500 points equidistant on each edge of the boundary and randomly sample 100 points x out of the domain \(\Omega \) for calculating potential. After every 50 epochs of training, we will resample 100 points x. After training, we randomly sample the 100 x and select y at an interval of 0.1 in the domain \([-6,6]^2\backslash \Omega \). By computing the \(G(x_i,y_j)\) on these point pairs \((x_i,y_j)\) we can find the relative \(L^2\) error of Green’s function is \(4.05\times 10^{-2}\), which also achieves reasonably high accuracy in exterior problem. When the wave number increases and the domain of the PDE problem becomes more complex, a reasonably high-precision Green’s function approximation is still obtained. We randomly choose two points \(x=(-0.1163,-1.0780)\) and \(x=(0.3941,-0.1163)\), and show the results of G(x, y) in Fig. 8. We can see that compared with the exact solution, both the real part and the imaginary part have almost the same performance.

Fig. 8
figure 8

The first row show the results of G(x, y) with \(x=(-0.1163,-1.0780)\) and the second row show the it with \(x=(0.3941,-0.1163)\), a and f are the real part of the exact G(x, y). b and g are real parts of numerical G(x, y) respectively. c, d, h and i are corresponding imaginary part. e and j are the absolute errors between exact and numerical G(x, y)

Full size image

4.2.2 The Helmholtz Equation Out of a U-shape Domain

The U-shaped domain is also a common consideration area. In this experiment, we assume the wavenumber \(k=1\) and the setting of the domain is shown in Fig. . We also used the BI-GreenNet with a ResNet architecture network that has 8 blocks and 100 neurons per layer. We select 400 points equidistant on each edge of the boundary and randomly sample 150 points x out of the domain \(\Omega \) for calculating potential. After every 100 epochs of training, we will resample 150 points x.

After training, we randomly sample the 200 xs and select y at an interval of 0.4 in the domain \([-8,8]^2\backslash \Omega \). By computing the \(G(x_i,y_j)\) on these point pairs, the relative \(L^2\) error of Green’s function is \(2.06\times 10^{-2}\), which also achieves reasonably high accuracy. We choose two points \(x=(0.2,1.2)\) and \(x=(-1.9689 -2.0929)\) and show the G(x, y) of the two points in Fig. 9. We can also see that both the real part and the imaginary part are very close to the exact solution.

Fig. 9
figure 9

This figure shows the results of Green’s function out of the U-shaped domain. The first row are the results of G(x, y) with fixed \(x=(0.2,1.2)\) and the second row are the results of G(x, y) with fixed \(x=(-1.9689 -2.0929)\). The exact Green’s function is also shown for comparison

Full size image

4.3 Green’s Function of the Interface Problem

4.3.1 The Poisson Equation in a Square with Flower-shaped interface

Let \(\Omega \) be the square \(\{(x,y): \vert x\vert \le 1, \vert y\vert \le 1\}\), the interface \(\Gamma \) is parameterized by \((a\cos t-b\cos nt\cos t, a\sin t-b\cos nt\sin t)\) with \(t\in [0,2\pi ]\), which is a flower-shaped interface widely used in [34, 42]. We choose two set of parameters \((a,b,n)=(0.5,0.15,5)\) and \((a,b,n)=(0.5,0.1,8)\). For the first parameter, we choose \(\mu _1=1, \mu _2=2\) while for the second parameter, we take \(\mu _1=2, \mu _2=1\), as is shown in Fig. .

Fig. 10
figure 10

Illustration of the Poisson interface problem

Full size image

We impose Dirichlet boundary condition on \(\partial \Omega \) such that Green’s function to this problem satisfies (2.8) along with \(G(x,y)=0, \ \forall x\in \Omega , y\in \partial \Omega \). We sample 800 points on both \(\Gamma \) and \(\partial \Omega \) for boundary integral. In the training process, we choose a ResNet with 8 blocks with 100 neurons per layer. For every 500 epochs, 100 new x is randomly generated. After \(10^5\) epochs of training, we fix 100 newly generated x and compute the average relative \(L_2\) error of Green’s function G(x, y). Further more, for two fixed x in \(\Omega _1\) and \(\Omega _2\) respectively, we compare the exact Green’s function (obtained by traditional boundary integral method) and the numerical solution obtained by neural network.

The numerical results for the second set of parameters are given in Fig. . The average relative \(L_2\) error of Green’s function G(x, y) is \(1.85\times 10^{-2}\). For \(x=(-0.0960,0.2626)\in \Omega _1\), the relative \(L^2\) error of Green’s function is \(0.78\times 10^{-2}\), while for \(x=(0.8342,-0.4661)\in \Omega _2\), the relative \(L^2\) error is \(1.79\%\). The numerical results for the second set of parameters are given in Fig. . The average relative \(L_2\) error of Green’s function G(x, y) is \(3.34\times 10^{-2}\). For \(x=(-0.1512,-0.1410)\in \Omega _1\), the relative \(L^2\) error of Green’s function is \(0.81\times 10^{-2}\), while for \(x=(0.7288,0.2861)\in \Omega _2\), the relative \(L^2\) error is \(1.37\times 10^{-2}\). The results both show that the proposed method can solve Green’s function for the interface problem accurately.

Fig. 11
figure 11

Numerical results for the Poisson interface problem with \((a,b,n)=(0.5,0.15,5)\) and \(\mu _1=1, \mu _2=2\). a–c: exact solution, numerical solution and absolute error of Green’s function G(x, y) for \(x=(-0.0960,0.2626)\in \Omega _1\). d–f: exact solution, numerical solution and absolute error of Green’s function G(x, y) for \(x=(0.8342,-0.4661)\in \Omega _2\)

Full size image
Fig. 12
figure 12

Numerical results for the Poisson interface problem with \((a,b,n)=(0.5,0.1,8)\) and \(\mu _1=2, \mu _2=1\). a–c: exact solution, numerical solution and absolute error of Green’s function G(x, y) for \(x=(-0.1512,-0.1410)\in \Omega _1\). d–f: exact solution, numerical solution and absolute error of Green’s function G(x, y) for \(x=(0.7288,0.2861)\in \Omega _2\)

Full size image

4.3.2 The Helmholtz Equation in \(\mathbb {R}^2\) with Square Interface

In this experiment, we consider the interface problem of the Helmholtz Eq. (2.6) with the interface \(\Gamma \) = \(\{(x,y): \vert x\vert =1 \ \text {or} \ \vert y\vert =1\}\). On the interface 800 points are sampled for the boundary integral. Take \(\mu _1=2, \mu _2=1, \varepsilon _1=1, \varepsilon _2=4, k=2\) in the Helmholtz equation. The Sommerfeld condition is required at infinity, i.e., \(\lim _{\vert x\vert \rightarrow \infty }(\frac{\partial }{\partial r}-ik\sqrt{\varepsilon _2\mu _2})u(x)=o(\vert x\vert ^{-1/2})\), implying that \(\lim _{\vert y\vert \rightarrow \infty }(\frac{\partial }{\partial r}-ik\sqrt{\varepsilon _2\mu _2})G(x,y)=o(\vert x\vert ^{-1/2})\), which is automatically satisfied if H(x, y) is written in the boundary integral form. Therefore, only the two jump conditions need to be fit since the partial differential equation is already satisfied using the boundary integral representation.

The network and training hyperparameters are set the same as those in the Poisson interface problem. The average relative \(L_2\) error of Green’s function G(x, y) is \(4.63\times 10^{-2}\). For two fixed x, the exact Green’s function (obtained by traditional boundary integral method), numerical solution obtained by neural network and error is shown in Fig. , implying the effectiveness of the proposed method in computing Green’s function.

Fig. 13
figure 13

a–e are for \(x=(-0.8559,-0.8164)\in \Omega _1\) with relative \(L^2\) error \(3.98\times 10^{-2}\), while figure (f)–(j) are for \(x=(-1.4218,0.4312)\in \Omega _2\) with relative \(L^2\) error \(2.73\times 10^{-2}\). First and second column: the real part of the exact solution and the numerical solution; third and forth column: imaginary part of the exact solution and the numerical solution; fifth column: absolute error between exact solution and numerical solution

Full size image

Furthermore, after Green’s function is learnt by the neural network, to show the generalization ability of the proposed method in solving PDEs, we consider the homogeneous case of problem (2.6), i.e., \(f\equiv 0\), while the two jump conditions \(g_1\) and \(g_2\) are generated by the superposition of a class of parameterized function. Specifically, the exact solution to the interface problem is designed as

$$\begin{aligned} u(x,y)=\left\{ \begin{aligned}&\sum _{i=1}^I c_1(i)e^{j(k_1(i)x+k_2(i)y)\sqrt{\varepsilon _1\mu _1}},&\quad (x,y)\in \Omega _1,\\&\sum _{i=1}^I c_2(i)H_0^1(k\sqrt{\varepsilon _2\mu _2}\sqrt{(x-x_0(i))^2+(y-y_0(i))^2}),&\quad (x,y)\in \Omega _2,\\ \end{aligned} \right. \end{aligned}$$
(4.7)

where \(\{c_1,c_2,k_1,k_2,x_0,y_0\}\) is a set of randomly generated parameters satisfying \(k_1^2+k_2^2=k^2\) and \((x_0(i),y_0(i))\in \Omega _1, \ \forall i\). We set \(c_1,c_2\sim U[0,1]\), \(k_1=k\cos \theta , k_2=k\sin \theta \) with \(\theta \sim U[0,2\pi ]\), \(x_0,y_0\sim U[-0.8,0.8]\). \(g_1\) and \(g_2\) can be directly computed using the exact solution. Once Green’s function to this interface problem is obtained, the solution to the PDE can be directly computed by

$$\begin{aligned} u(x)=\int _{\Gamma }\left( \frac{1}{\mu }\frac{\partial G(x,y)}{\partial n_y}g_1(y)-G(x,y)g_2(y)\right) ds_y. \end{aligned}$$

We take \(I=3\) and randomly generate 100 sets of parameters, and solve the interface problem using the learned Green’s function. The histogram of the relative \(L^2\) errors of the numerical solutions to the 100 equations are shown in Fig. a, while the solution and corresponding error for one set of parameters are given in Fig. 14. It can be seen that all the relative \(L^2\) errors are below \(4\times 10^{-2}\). Therefore, not only can the proposed method accurately solve a class of PDEs accurately, but also this method has natural generalization ability over the PDE information. The parameters of the exact solution corresponding to Fig. 14b–f are given in Table .

Table 5 Parameter setting for Fig. 14b–f
Full size table
Fig. 14
figure 14

a: histogram of the relative \(L^2\) error of the 100 randomly generated equations. b–f are the exact solution and numerical solution of one specific equation generated. b and c: real part of the exact solution and the numerical solution; d and e: imaginary part of the exact solution and the numerical solution; f: absolute error between exact solution and numerical solution

Full size image

5 Conclusion

In this paper, a novel neural network-based method for learning Green’s function is proposed. By utilizing the fundamental solution to remove the singularity in Green’s function, the PDE required for Green’s function is reformulated into a smooth high-dimensional problem. Two neural network-based methods, DB-GreenNet and BI-GreenNet are proposed to solve this high-dimensional problem. The DB-GreenNet uses the neural network to directly approximate Green’s function and take the residual of the differential equation and the boundary conditions as the loss. The BI-GreenNet is based on the recently proposed BINet, in which the solution is written in a boundary integral form such that the PDE is automatically satisfied and only boundary terms need to be fit.

Extensive experiments are conducted and three conclusions can be drawn from the results. Firstly, the proposed method can effectively learn Green’s function of Poisson and Helmholtz equations in bounded domains, unbounded domains and domains with interfaces with reasonably high accuracy. Secondly, BI-GreenNet method outperforms DB-GreenNet method in the accuracy of Green’s function and the capability to handle problems in unbounded domains. Lastly, Green’s function obtained can be utilized to solve a class of PDEs accurately, and shows good generalization ability over the PDE data, including the source term and boundary conditions.

Although the proposed method exhibits great performance in computing Green’s function, the dependence on fundamental solutions hinders the application of this method in varying coefficient problems or equations without explicit fundamental solutions. Besides, in BI-GreenNet, the high precision quadrature required to accurately compute the singular integral on the boundary also limits the application of BI-GreenNet in computing Green’s function of too high dimensional problems. These will be further investigated in the future.