Reachability-Based Search for Tracking of Noncooperative Maneuvering Satellites in Data Sparse Environment

Abstract

A generic Bayesian framework is presented to track lost-in-space noncooperative maneuvering satellites. The developed framework predicts the reachability set for a lost-in-space satellite given bounds on maneuver parameters such as maneuver time and maneuver magnitude. Reachability sets are represented as a desired order polynomial series as a function of maneuver parameters. Recent advances in non-product quadrature methods are utilized to compute coefficients of this polynomial series in a computationally efficient manner. A major contribution of this work is to develop quadrature methods to generate samples for spherically uniform distribution for bounded magnitude maneuvers. Samples generated from this polynomial series are used for direct particle propagation in a traditional Bayesian filter rather than solving governing equations of motion for each sample point. An important component of the developed framework is a search strategy which exploits the reachability set calculations to task the sensor to increase the detection probability of the satellite. The samples generated from initial reachability sets are updated to systematically reduce the target search region based on actual detection of the target in a Bayesian framework. Numerical simulations are performed to show the efficacy of the developed ideas for tracking a lost-in-space satellite with the help of space based sensor. Performance of the proposed method varies widely based on factors such as the reachability set polynomial order, maneuver uncertainty bounds, sensor parameters (Field of view, measurement frequency, and detection probability), and initial conditions. For numerical experiments performed, the observer gained the custody of the maneuvering target in $100\%$ and $96\%$ of Monte Carlo (MC) simulations for the single maneuver and two maneuver cases, respectively.

1 Introduction

Space has become an increasingly congested environment over the last few decades, leading to difficulties in operationally tracking and maintaining the space catalog to enable maximum space situational awareness. These problems are greatly exacerbated when considering that noncooperative active satellites can make unknown maneuvers which lead to issues with tracking and data association. Maneuvering target tracking is a well-studied problem in the literature, with a history dating back to the 1970s [5, 11, 33]. The core objective of maneuvering target tracking is to extract meaningful information about the trajectory of the target based on observational data. In most tracking applications, this involves using real-time measurements to inform the dynamic model, as well as reconstruct or estimate the maneuver as it occurs. A comprehensive introduction to maneuvering target tracking is presented in a six part paper series[24,25,26,27,28,29] which covers literature up to the early 2000s. Methods for maneuvering target tracking in this category include decision-based methods [6, 12, 33] and multiple-model methods [3, 4, 10]. A variety of target tracking methods and algorithms exist which vary widely by application. There is a diverse body of existing methods in the literature for tracking maneuvering targets using real-time measurements [6, 7, 32, 37]; however, it is not within the scope of this paper to fully examine them. The authors emphasize here that all the literature cited above assume data-richness, such that measurements of the target are acquired during the target maneuver.

Methods using real-time measurements are useful in air and ground target tracking scenarios where it is reasonable to assume that measurements of the target are available throughout the entire trajectory. Unfortunately, due to the limited coverage and availability of sensor resources, satellite tracking applications frequently have large time delays between observations on the order of hours or days. In these data-sparse situations, unobserved maneuvers can drastically change the target trajectory to the point where a tasked sensor loses custody of the intended target entirely.

Detecting and reconstructing maneuvers in data-sparse situations has received some, albeit limited, coverage in the literature. Patera [36] addresses the problem of detecting maneuvers and other events (collisions, reentry, etc) in terms of statistically significant changes in orbital energy. An optimal control based method has also been developed to reconstruct finite maneuvers [19, 31, 39] connecting two measurements. The underlying technique for this method was first formulated in 1988 as the minimum model error method [34]. The minimum model error method treats the control as an unmodeled deviation from the dynamics, and minimizes this deviation such that the state estimate is statistically consistent with the observations. When applied to the satellite tracking problem, this method formulates the maneuver reconstruction process as a two point boundary value problem under the assumption of a minimum fuel control policy. Whenever the optimal control profile rises above the level of system noise, it is assumed that a maneuver has occurred. Although the minimum fuel maneuver is not necessarily a bad assumption, this method does not account for the many suboptimal trajectories that can explain the same observational data. Furthermore, the orbital energy method as well as the minimum model error method make the assumption that the target can be observed after making a maneuver. The problem addressed in this work is fundamentally different. The problem currently considered is to use sensor data in conjunction with dynamical model for target motion and bounds on maneuver parameters to seek and locate a target satellite which has been lost due to an unknown maneuver.

In this respect, the objective of this paper is to determine a set of sensing parameters to locate the target given apriori knowledge about the bounds on maneuver parameters (e.g. magnitude and time). This apriori knowledge is exploited in conjunction with dynamical model to compute a search area for the sensor at future times. The search area is defined by the reachability set of the target, and is synonymous with the target state pdf given by the mapping of target maneuver to state. The pdf represents all possible target states given a-priori knowledge on control bounds and measurement data, and the true target state will always lie within this set. If the tasked sensor is able to detect the target, then the measurement of the detected target is used to systematically reduce error in target state and maneuver estimates. In case of unsuccessful detection, the search area is updated and propagated to future times via reachability based methods. An important feature of this approach is that unsuccessful detection is also exploited to improve the future search and tracking of noncooperative satellites. The method presented in this paper creates a unified framework for search, detection, tracking, and maneuver estimation of a noncooperative target.

An important component of this framework is to compute the reachability sets of the target. Generally speaking, a reachability set is the domain of all possible future states of a system given a constrained control effort. There is some disagreement in the literature over the specific definition of a reachability set; some analytical methods consider only the reachable outer surface or reachable envelope of states given a constrained control input. In the authors previous works [14], reachability sets are defined by the entire domain of reachable states (i.e. pdf) given uncertainty in initial state, model parameters, and control input. This is the definition that will be adopted throughout this paper.

An optimal control formulation of the reachable envelope is given analytically in [18]; however, this formulation doesn’t provide information about the region inside the reachable envelope. Since then, there have been many analytical investigations into the application of reachability sets to impulsively maneuvering spacecraft [43, 45], and numerical objective map reachability analyses into proximity operations around asteroids [42]. Traditionally, numerical reachability set computation for high-dimensional systems require tensor-product quadature methods to evaluate the multi-dimensional integrals involved. This can render the problem computationally intractable.

Recently, the higher order sensitivity matrix (HOSM) method [14, 15] has been developed to address this problem. The HOSM method is analogous to polynomial chaos uncertainty propagation techniques, but utilizes higher order non-product quadrature schemes such as the conjugate unscented transform (CUT) method to effectively compute the multidimensional integrals involved in reachability set computation. Benefits of the non-product quadrature rules used in the HOSM method include higher accuracy than other popular methods like the unscented transform (UT) and sparse grid quadratures, and greatly reduced computational expense compared to alternative tensor product methods like Gauss–Hermite (GH). In this work, non-product quadrature rules are extended to the spherically uniform distribution for unknown maneuvers, and to mixed distributions for both unknown maneuver magnitude and maneuver time.

Once a target reachability set has been computed, a method for tasking sensors to search the set must be developed. A greedy in time maximum detection likelihood policy is implemented for this purpose. In practice, the maximum likelihood cost function for highly nonlinear dynamic and measurement models are evaluated using MC samples efficiently propagated via the reachability set model. The final component to the proposed framework is the measurement update step. A key contribution of the proposed method is the utilization of measurements of the reachability set rather than the target itself to provide better information on the remaining possible target locations. If the tasked sensor does not observe the target, the detection likelihood function is used to update the target search area. Conversely, if the target is located, an importance sampling with progressive correction (ISPC) procedure is used to accurately define the posterior.

The organization of the paper proceeds as follows. Section 2 provides a description of the data-sparse maneuvering target search method. Section 3 provides a summary of the higher order sensitivity matrix reachability set computation method, and discusses quadrature methods used in this problem. Sections 4 and 5 detail the sensor tasking and filtering/estimation components respectively. Section 6 provides numerical simulations and discussion of the applicability and limitations of this method, and Sect. 7 provides concluding remarks.

2 Problem Description

The objective of this problem is to locate a target that is able to make bounded unknown maneuvers at unknown times between observations. Given a sensor with limited field of view (FOV), the sensor parameters which provide the highest likelihood of detecting the target must be determined. After tasking the sensors, observational data must then be used to update the search region and track the target. This section will define the dynamic system, stochastic inputs, and sensor model for the noncooperative maneuvering satellite tracking problem.

2.1 Generic Target-Observer System

Assume a continuous-time dynamic system governing target and observer motion

$$\begin{aligned} \begin{aligned} \dot{\textbf{x}}_t&=\textbf{f}_t(\textbf{x}_t,t)+\textbf{g}_t(\textbf{u}_t,t)\\ \dot{\textbf{x}}_{ob}&=\textbf{f}_{ob}(\textbf{x}_{ob},t)+\textbf{g}_{ob}(\textbf{u}_{ob},t)\\ \end{aligned} \end{aligned}$$

(1)

where $\textbf{x}_t$ is the $(n_t\times 1)$ target state vector, $\textbf{u}_t$ is the $(l_t\times 1)$ target control vector, $\textbf{f}_t$ is the target dynamic model, and $\textbf{g}_t$ is the target control model. The observer is similarly assigned an $(n_{ob}\times 1)$ state $\textbf{x}_{ob}$, an $(l_{ob}\times 1)$ control $\textbf{u}_{ob}$, and dynamic and control models $\textbf{f}_{ob},\textbf{g}_{ob}$. The target control vector is approximated by a series of M impulsive maneuvers $\textbf{u}_{t,i}$ and maneuver times $t_i$ with known bounds

$$\begin{aligned} \begin{aligned} \textbf{u}_t=&\{\textbf{u}_{t,1},t_1,\textbf{u}_{t,2},t_2,\ldots \textbf{u}_{t,M},t_M\}\\ \dot{\textbf{x}}_t=&\textbf{f}_t(\textbf{x}_t,t)+\sum _{i=1}^M\textbf{g}_t(\textbf{u}_{t},t)\delta (t-t_i) \end{aligned} \end{aligned}$$

(2)

where $\delta (\cdot )$ is the dirac delta function. As will be discussed in Sect. 3, the dimension of $\textbf{u}_t$ imposes severe computational limitations on reachability set evaluation. Therefore, the proposed methodology is better suited for impulsive maneuvers use cases than continuous low thrust maneuvers which requires many independent random variables. The system flow for the target $\varvec{\chi }_t$ and the observer $\varvec{\chi }_{ob}$ can be written compactly as

$$\begin{aligned} \begin{aligned} \textbf{x}_{t,k+1}&=\varvec{\chi }_t(\textbf{x}_{t,0},\textbf{u}_{t},k+1)\\ \textbf{x}_{ob,k+1}&=\varvec{\chi }_{ob}(\textbf{x}_{ob,0},\textbf{u}_{ob},k+1)\\ \end{aligned} \end{aligned}$$

(3)

where k is the discrete-time index of the current time step $\mathbf {t_k}$. The combined system state is defined as the target state augmented by the observer state $\textbf{x}^T=\left[ \textbf{x}_t^T\ \textbf{x}_{ob}^T\right]$. Assume the sensor has field of view (FOV) constrained to a region defined by $\mathcal {C}_s(\textbf{x}_{k+1},\varvec{\theta }_{k+1})\le 0$ where $\varvec{\theta }_{k+1}$ is an $(l\times 1)$ vector of sensor parameters to be selected such that the target is detected. A piecewise detection likelihood function $\pi _d(\textbf{x}_{k+1},\varvec{\theta }_{k+1})$ can be defined with respect to the FOV constraints

$$\begin{aligned} \pi _d(\textbf{x}_{k+1},\varvec{\theta }_{k+1})=\left\{ \begin{array}{cl} \pi _d^\prime (\textbf{x}_{k+1},\varvec{\theta }_{k+1})&{}\text {if}\ \mathcal {C}_s(\textbf{x}_{k+1},\varvec{\theta }_{k+1})<0\\ 0&{}\text {otherwise}\end{array}\right. \end{aligned}$$

(4)

such that the target has a probability $\pi _d^\prime (\textbf{x}_{k+1},\varvec{\theta }_{k+1})\in [0,1]$ of being detected within the FOV. Given known bounds on the target maneuvers $\textbf{u}_{t,i}$, FOV constraints, and detection likelihood function, sensor parameters $\varvec{\theta }_{k+1}$ which maximize some target detection metric $J_d$ must be determined. It should be noted that the observer trajectory is assumed to be known in this work, however, one can optimize the trajectory of the observer along with sensing parameters. This work will consider scenarios under the simplifying assumptions of a single-observer, single-target, and greedy in time tasking approach.¹ The greedy in time assumption made here indicates that the sensor parameters $\varvec{\theta }_{k+1}$ may be independently optimized at each timestep rather than optimizing a sequence of sensor parameters $[\varvec{\theta }_{0}\ \varvec{\theta }_{1}\ldots \ \varvec{\theta }_{k+1}]$ for a finite time horizon. Under these simplifications, it is sufficient to define criteria $J_d$ as the expectation value of the detection likelihood function $\pi _d(\textbf{x}_{k+1},\varvec{\theta }_{k+1})$

$$\begin{aligned} \max _{\varvec{\theta }_{k+1}} J_d=E[\pi _d(\textbf{x}_{k+1},\varvec{\theta }_{k+1})]=\int \pi _d(\textbf{x}_{k+1},\varvec{\theta }_{k+1})\pi (\textbf{x}_{k+1})d\textbf{x} \end{aligned}$$

(5)

Assuming selection of $\varvec{\theta }_{k+1}$ provides a successful detection, the target measurement can be modeled by

$$\begin{aligned} \textbf{y}_{k+1}=\textbf{h}(\textbf{x}_{k+1})+\varvec{\nu }_{k+1} \end{aligned}$$

(6)

where $\textbf{y}_{k+1}$ is an $(m\times 1)$ measurement vector, $\textbf{h}$ is the measurement model, and $\varvec{\nu }_{k+1}\in \mathcal {N}(\textbf{0},\textbf{R}_{k+1})$ is zero mean Gaussian measurement noise. This measurement can be used in a classical filtering sense to update the target state and maneuver estimate. If there is not a successful detection, however, the target search region must be updated to inform future sensor tasking. The following section will outline the framework proposed to accomplish the objectives of this problem.

2.2 Overall Approach

The objective of this problem is to locate a target executing unknown maneuvers that has been lost by determining a set of sensor to search for the target. This problem is an extension of the classical filtering problem, where the sequence of maneuvers in time is unknown and observations are unavailable during the maneuver. It is assumed that the maneuvers have caused the target to deviate from its nominal trajectory to an extent where a limited FOV sensor cannot locate the target using traditional means.

The proposed method is a multipronged framework for determining the target search space, sensor tasking, and incorporation of measurement data for tracking/estimation. A Taylor series-based approach is used to compute the target pdf, i.e. reachability set, as a function of bounded stochastic maneuvers. This reachability set defines the search region over which an observer is tasked to maximize the likelihood of detecting the target. A Bayesian particle filtering framework is used to update the target pdf such that unsuccessful sensor tasking measurements systematically reduce the remaining reachable target states. The proposed framework depicted in Fig. 1, can be split into three main components

• 1. Reachability Set Computation

• 2. Sensor Tasking

• 3. Tacking/Estimation

Fig. 1

Reachability set search diagram

A core premise of this method is that the reachability set of the target is synonymous with the target state pdf resulting from stochastic maneuvers mapped through the dynamic system. Assume the system input $\textbf{z}$ is given by the known deterministic observer initial state $\textbf{x}_{ob,0}$ and control $\textbf{u}_{ob}$, in addition to the stochastic target initial state $\textbf{x}_{t,0}$ and maneuver sequence $\textbf{u}_{t,i},t_i$

$$\begin{aligned} \textbf{z}=\left[ \begin{array}{c} \textbf{z}_t\\ \textbf{z}_{ob}\end{array} \right] ,\ \ \begin{aligned} \textbf{z}_t^T=\left[ \textbf{x}_{t,0}^T\ \textbf{u}^T_{t,1}\ t_{1}\ \textbf{u}^T_{t,2}\ t_{2}\ \cdots \ \textbf{u}^T_{t,M}\ t_{M}\right] \\ \textbf{z}_{ob}^T=\left[ \textbf{x}_{ob,0}^T\ \textbf{u}^T_{ob}\right] \end{aligned} \end{aligned}$$

(7)

where M is the total number of target maneuvers. Assume the initial target state is defined by random variable $\textbf{x}_{t,0}$ with known pdf $\pi (\textbf{x}_{t,0})$. Traditionally, target maneuvers are represented by equivalent Gaussian process noise applied at each timestep; however, this does not intuitively make sense for the application currently considered. Instead, the maneuvers can be defined as impulsive zero-mean spherically uniform distributions up to maximum radius $\Delta V_{max}$, denoted by $\textbf{u}_{t,i}\in \mathcal {U}_s(0,\Delta V_{max})$, and maneuver times can be defined as linearly uniform between two time limits $t_{i}\in \mathcal {U}(t_a,t_b)$. Defining the maneuvers in this manner imposes assumptions only on the maximum maneuver magnitude, and considers any target attitude, maneuver magnitude, and maneuver time to be equally probable. Computing reachability sets using the statistics of this distribution will be discussed in Sect. 3.

For numerical accuracy, the stochastic part of the input vector is typically normalized to a zero mean vector $\varvec{\zeta }$

$$\begin{aligned} \varvec{\zeta }=\textbf{S}^{-1}\left( \textbf{z}_t-\varvec{\mu }\right) \end{aligned}$$

(8)

where $\textbf{S}$ is a block-diagonal scaling matrix dependent on the pdf normalization of each component of $\textbf{z}$, and $\varvec{\mu }$ is the augmented mean input vector. Table 1 summarizes the various input types and their associated means and the scaling components, which comprise the diagonal blocks of $\textbf{S}$. Using the normalized input vector, the system flow $\varvec{\chi }$ can be rewritten as

$$\begin{aligned} \textbf{x}_{k}=\varvec{\chi }(\varvec{\zeta },\textbf{z}_{ob},k) \end{aligned}$$

(9)

The system flow represents the mapping of stochastic inputs with joint distribution $\pi (\varvec{\zeta })$ onto the reachability set $\pi (\textbf{x}_k)$. Note that the selection of inputs to include in $\varvec{\zeta }$ is left to the discretion of the user based upon the application considered. The first problem in the proposed framework is to efficiently compute the target search area defined by the reachability set $\pi (\textbf{x}_k)$.

Table 1 Summary of input PDFs

3 Reachability Set Computation

Direct reachability set computation is notoriously expensive from a computational standpoint and involves the explicit evaluation of many MC samples to provide an accurate representation of the search space. This section outlines the basic concepts and equations of the HOSM, which enables very efficient polynomial approximation of a reachability set. Note that although the basic equations are provided here, a more detailed discussion can be found in Hall and Singla [15].

3.1 Taylor Series Expansion

Consider a d th order Taylor series expansion on Eq. (9)

$$\begin{aligned} \begin{aligned} \varvec{\chi }^{(d)}(\varvec{\zeta })&\approx \underbrace{\varvec{\chi }(0)}_{\text {Nominal Solution}}+\underbrace{\frac{\partial \varvec{\chi }(0)}{\partial \zeta _{\alpha _1}}\zeta _{\alpha _1}}_{{1^{st} Order Sensitivity}}+\underbrace{\frac{1}{2!}\frac{\partial ^2\varvec{\chi }(0)}{\partial \zeta _{\alpha _1}\partial \zeta _{\alpha _2}}\zeta _{\alpha _1}\zeta _{\alpha _2}}_{{2^{nd} Order Sensitivity}}\ldots \\&\quad +\underbrace{\frac{1}{d!}\frac{\partial ^d\varvec{\chi }(0)}{\partial \zeta _{\alpha _1}\partial \zeta _{\alpha _2}\ldots \partial \zeta _{\alpha _d}}\zeta _{\alpha _1}\zeta _{\alpha _2}\ldots \zeta _{\alpha _d}}_{\text {Higher Order Terms}}, \ \ \text {for }\ \alpha _1,\alpha _2,\ldots ,\alpha _d=1,2,\ldots ,n \end{aligned} \end{aligned}$$

(10)

where $\varvec{\zeta }$ is the normalized random input variable with known pdf. The objective of the HOSM method is to numerically compute a model analogous to the above Taylor series expansion rather than explicitly evaluating partial derivatives of $\varvec{\chi }$. Grouping the constant partial derivatives into sensitivity matrices $\textbf{C}_i$ and the $\zeta$ terms into sets of $i^{th}$ order basis functions $\varvec{\phi }_i$, the expansion can be rewritten as,

$$\begin{aligned} \varvec{\chi }(\varvec{\zeta })\approx \textbf{C}_0+\textbf{C}_1\varvec{\phi }_1+\textbf{C}_2\varvec{\phi }_2+\cdots \textbf{C}_d\varvec{\phi }_d \end{aligned}$$

(11)

These sensitivity matrices and basis functions can be grouped so that the target state is approximated by the compact polynomial model

$$\begin{aligned} \textbf{x}\approx \textbf{C}\varvec{\phi }(\varvec{\zeta }) \end{aligned}$$

(12)

where $\textbf{C}$ is an $(n\times L)$ matrix of coefficients, and $\varvec{\phi }$ is an $(L\times 1)$ vector of basis functions. A least squares minimization procedure is applied to the above approximation and the coefficients can computed using the normal equations given by

$$\begin{aligned} \begin{aligned} \textbf{C}&=\textbf{A}\textbf{B}^{-1}\\ A_{j,k}&=E[x_j\phi _k(\varvec{\zeta })],\ \ B_{k,l}=E[\phi _k(\varvec{\zeta })\phi _l(\varvec{\zeta })] \end{aligned} \end{aligned}$$

(13)

where $E[\cdot ]$ denotes the expectation value operator with respect to the input pdf $\pi (\varvec{\zeta })$. Note that if the basis functions $\phi _i's$ are orthogonal with respect to the pdf $\pi (\varvec{\zeta })$, $\textbf{B}$ becomes a diagonal matrix and the coefficients can be computed simply as

$$\begin{aligned} c_{j,k}=\frac{E[x_j\phi _k(\varvec{\zeta })]}{E[\phi _k(\varvec{\zeta })\phi _k(\varvec{\zeta })]} \end{aligned}$$

(14)

Additional details on the above procedure are provided in [15]. The problem now becomes a matter of accurately computing coefficients by evaluating the expectation integrals in (14). Expectation values in the denominator are purely polynomial, and are thus trivial to compute; however, the expectation values in the numerator are generic functions of the system flow. Quadrature methods can be used for this purpose.

All quadrature methods apply the same basic approach: approximate the function as a Taylor polynomial, and integrate that polynomial instead. The generic form of a quadrature rule is to approximate a polynomial integral as the finite sum of the function evaluated at specific points $\varvec{\zeta }^{(i)}$ multiplied by weights $w^{(i)}$

$$\begin{aligned} E[\chi _j(\varvec{\zeta })]\approx \sum _{i=1}^Nw^{(i)}\chi _j(\varvec{\zeta }^{(i)}) \end{aligned}$$

(15)

where the computational expense of the method is directly proportional to the number of points N required to evaluate. The key difference between various quadrature rules lies in how the points and weights are selected, and is intimately related to the Taylor series expansion as discussed in [13]. Substituting the Taylor series expansion (10) into (15) provides a following set of equations known as the moment constraint equations (MCEs).

$$\begin{aligned} \begin{aligned} E[1]&=\sum _{i=1}^Nw^{(i)}\\ E[\zeta _{\alpha _1}]&=\sum _{i=1}^Nw^{(i)}\zeta ^{(i)}_{\alpha _1}\\ E[\zeta _{\alpha _1}\zeta _{\alpha _2}]&=\sum _{i=1}^Nw^{(i)}\zeta ^{(i)}_{\alpha _1}\zeta ^{(i)}_{\alpha _2}\\&\vdots \\ E[\zeta _{\alpha _1}\zeta _{\alpha _2}\ldots \zeta _{\alpha _d}]&=\sum _{i=1}^Nw^{(i)}\zeta ^{(i)}_{\alpha _1}\zeta ^{(i)}_{\alpha _2}\ldots \zeta ^{(i)}_{\alpha _d}\\ \end{aligned} \end{aligned}$$

(16)

Extensive research has gone into devising quadrature rules which match the moments of Gaussian and uniform distributions; however, quadrature rules for the spherically uniform unknown maneuver model used in this work is a relatively unexplored problem. The following section will derive the moments of the spherically uniform distribution and discuss how quadrature sets may be determined to enable reachability coefficient computation.

3.2 Spherically Uniform Quadrature

Fig. 2

Spherical coordinate system

Unknown target maneuvers $\textbf{u}_{t,i}$ are characterized as zero-mean spherically uniform distributions with bounded magnitude, denoted by $\mathcal {U}_s(0,\Delta V_{max})$. To accurately compute the reachable space for such a maneuver, it is necessary to determine quadrature sets which match the MCEs up to a desired order d.

Consider the spherical coordinate system $(\alpha ,\phi ,r)$ given in Fig. 2 where $\alpha$ is the azimuth, $\phi$ is the co-latitude, and r is the radius. The transformation between Cartesian coordinates $(\zeta _1,\zeta _2, \zeta _3)$ and spherical coordinates is

$$\begin{aligned} \left\{ \begin{array}{c} \zeta _1\\ \zeta _2\\ \zeta _3\end{array}\right\} =\left\{ \begin{array}{c} r\sin (\phi )\cos (\alpha )\\ r\sin (\phi )\sin (\alpha )\\ r\cos (\phi )\end{array}\right\} ,\ \ \ \left\{ \begin{array}{c} \alpha \\ \phi \\ r\end{array}\right\} =\left\{ \begin{array}{c} tan^{-1}(\frac{\zeta _2}{\zeta _1})\\ cos^{-1}(\frac{\zeta _3}{r})\\ \sqrt{\zeta _1^2+\zeta _2^2+\zeta _3^2}\end{array}\right\} \end{aligned}$$

(17)

Assume there exist random variables $\alpha ,\phi ,r$ such that the pdf of a unit sphere is uniformly distributed in Cartesian space $\pi (\varvec{\zeta })=c$. The constant c must be determined such that the pdf integrates to one.

$$\begin{aligned} \int _\Omega \pi (\varvec{\zeta })d\varvec{\zeta }=1 \end{aligned}$$

(18)

where $\Omega$ is the support of a sphere, i.e. $r<1$. Firstly, notice that since the domain of the pdf is spherical, the bounds cannot be directly expressed in Cartesian space, therefore a transformation must be applied to map the differential volume element from Cartesian coordinates $d\varvec{\zeta }$ to spherical coordinates $drd\alpha d\phi$. This transformation is given by the determinant of the Jacobian of Cartesian variables with respect to spherical variables.

$$\begin{aligned} \begin{aligned} |J|=&\left| \begin{array}{ccc} \frac{\partial \zeta _1}{\partial r}&{}\frac{\partial \zeta _1}{\partial \alpha }&{}\frac{\partial \zeta _1}{\partial \phi }\\ \frac{\partial \zeta _2}{\partial r}&{}\frac{\partial \zeta _2}{\partial \alpha }&{}\frac{\partial \zeta _2}{\partial \phi }\\ \frac{\partial \zeta _3}{\partial r}&{}\frac{\partial \zeta _3}{\partial \alpha }&{}\frac{\partial \zeta _3}{\partial \phi } \end{array}\right| =r^2sin(\phi )\\ d\varvec{\zeta }=&\left| J\right| drd\alpha d\phi =r^2sin(\phi )drd\alpha d\phi \end{aligned} \end{aligned}$$

(19)

Using the differential volume element transformation, the constant c can be found by directly integrating the expression

$$\begin{aligned} \begin{aligned} 1&=c\int _0^\pi \int _0^{2\pi } \int _0^1 r^2 sin(\phi )drd\alpha d\phi \\ c&=\left[ \int _0^\pi \int _0^{2\pi } \int _0^1 r^2 sin(\phi )drd\alpha d\phi \right] ^{-1}=\frac{3}{4\pi } \end{aligned} \end{aligned}$$

(20)

where the constant c can be thought of as normalizing the sphere to unit volume. The expectation value operator with respect to the uniform spherical distribution can now be defined as

$$\begin{aligned} E[f(\varvec{\zeta })]=\frac{3}{4\pi }\int _0^\pi \int _0^{2\pi }\int _0^1 f(\varvec{\zeta })r^2 sin(\phi ) drd\alpha d\phi \end{aligned}$$

(21)

Expression (21) can be used to analytically evaluate the moments of the uniform spherical distribution with respect to cartesian space. These moments are evalutated and listed in Table 2. Note that since the uniformly spherical distribution is symmetric, the odd-order moments are all equal to zero.

Table 2 Moments of spherically uniform distribution

There are many quadrature methods that one might consider to match the moments of the spherically uniform distribution $(n=3)$. Perhaps the most well-known class of quadrature method, Gaussian quadrature rules, requires only N points to compute up to $d=2N-1$ order moments for systems where $n=1$, which is minimal for one dimensional systems [41]. Unfortunately, higher dimensional systems require a tensor product to be taken, which leads to exponential growth in the number of points. Furthermore, the Cartesian coordinates of the spherically uniform distribution are not statistically independent, i.e $E[\zeta _i^2\zeta _j^2]\ne E[\zeta _i^2]E[\zeta _j^2]$. This causes the tensor product of 1D points to incorrectly match moments, and thus be invalid.

The celebrated Unscented Transform (UT) [20,21,22] is a popular alternative to tensor product methods which avoids expontential growth in N with increasing dimension, and maintains positive weights. The UT symmetrically places points on the principal axes of the input $\varvec{\zeta }$ to match up to $3^{rd}$ order moments while incurring only linear growth in N with dimension. Consider matching up to $3^{rd}$ order moments of the uniform sphere using equally weighted $w_1$ points placed at a distance of $r_1$ on each principal axis. See Fig. 3 for a schematic of the UT for $n=3$. Since the points are symmetric, odd-order MCEs are automatically satisfied, and the even order equations are given by

Fig. 3

Unscented transformation points for n=3

$$\begin{aligned} E[1]=1=2nw_1,\ \ E[\zeta _i^2]=\frac{1}{5}=2w_1r_1^2 \end{aligned}$$

(22)

which leads to the simple solution

$$\begin{aligned} w_1=\frac{1}{2n}=\frac{1}{6},\ \ r_1=\sqrt{nE[\zeta _i^2]}=\sqrt{\frac{3}{5}} \end{aligned}$$

(23)

This solution matches up to 3rd order moments of $\varvec{\zeta }$ using only 6 points. Furthermore, notice that $r_1<1$ lies within the unit radius constraint for a spherical distribution and is therefore a valid solution. Support constraints $\varvec{\zeta }^{(i)}\in \Omega$ become very important when defining higher order quadrature sets. Notice that if a similar procedure is attempted for 5th order moments, the cross-dimension expectation value $E[\zeta _i^2\zeta _j^2]$ will never be replicated because at least one dimension will always have a zero component. Thus, an alternative method must be used.

The conjugate unscented transform (CUT) method is a higher order generalization of the UT method specifically designed with the cross-moment problem in mind. The CUT method leverages special symmetric axes to directly construct points in nD space, circumventing the need for a tensor product. The details of the CUT method are discussed thoroughly in Adurthi et al [2]; however, this section will outline application of CUT to the spherically uniform distribution.

Let us consider a set of points with distance $r_1$ and weight $w_1$ on the principal axes, and a set of points with distance $r_2$ and weight $w_2$ on the $c^{(3)}$ axis to saitsfy $5^{th}$ order MCEs. The $c^{(3)}$ axis is a symmetric axis which yields the set of points $\left\{ \textbf{Z}^{(3)}\right\} =\{[r_2\ r_2\ r_2],\ [-r_2\ r_2\ r_2],\ [r_2\ -r_2\ r_2],\ \ldots [-r_2\ -r_2\ -r_2]\}$ with all permutations of negative and positive scaling parameters. Note that there are a total of 6 points on the principal axes constrained such that $r_1\le 1$ and 8 points on the $c^{(3)}$ axis constrained such that $r_2\le \frac{1}{\sqrt{3}}$. Recalling that the symmetry automatically satisfies the odd-order moments, the even-order MCEs for the uniform sphere are given by

$$\begin{aligned} \begin{aligned} E[1]=1=&6w_1+8w_2\\ E[\zeta _i^2]=\frac{1}{5}=&2w_1r_1^2+8w_2r_2^2\\ E[\zeta _i^4]=\frac{3}{35}=&2w_1r_1^4+8w_2r_2^4\\ E[\zeta _i^2\zeta _j^2]=\frac{1}{35}=&8w_2r_2^4\\ \end{aligned} \end{aligned}$$

(24)

Analytically, these equations can be reduced to expressions for $w_1,\ w_2,\ r_1$

$$\begin{aligned} w_1=\frac{1}{35 r_1^4},\ w_2=\frac{1}{280r_2^4},\ r_1^2=\frac{2r_2^2}{7r_2^2-1} \end{aligned}$$

(25)

and a charateristic polynomial which is quadratic in $r_2^2$

$$\begin{aligned} r_2^4-\frac{42}{77}r_2^2+\frac{5}{77}=0 \end{aligned}$$

(26)

This equation leads to two positive solutions for the second scaling parameter

$$\begin{aligned} r_2=\left[ \sqrt{\frac{3}{11}+\frac{2}{77}\sqrt{14}},\sqrt{\frac{3}{11}-\frac{2}{77}\sqrt{14}}\right] \approx [0.6082,0.4190] \end{aligned}$$

(27)

It is cruical now to notice the role of constraints. The only feasible value $r_2\le \frac{1}{\sqrt{3}}$ is given by $r_2=0.4190$. Unfortunately, when substituting this solution for $r_2$ into the expression for $r_1$, a value of $r_1=1.2388$ is found, which lies outside of the unit radius constraint. Thus, there are no feasible solutions using this set of points.

This example highlights one of the most glaring difficulties with the CUT method. There is no guarantee that a selected set of CUT axes will satisfy the MCEs and support constraints, so selecting the axes is often a guess and check procedure. For example, consider adding a single central point $\varvec{\zeta }^{(0)}=[0,0,0]$ with weight $w_0$ to previously examined set. The only MCE that is influenced by this change is

$$\begin{aligned} E[1]=1=w_0+6w_1+8w_2 \end{aligned}$$

(28)

which yields the modified characteristic equation

$$\begin{aligned} r_2^4+\frac{42}{70w_0+77}r_2^2+\frac{5}{70w_0+77}=0 \end{aligned}$$

(29)

with solution

$$\begin{aligned} r_2=\left[ \sqrt{\frac{21+\sqrt{14(4-25w_0)}}{7(10w_0+11)}},\sqrt{\frac{21-\sqrt{14(4-25w_0)}}{7(10w_0+11)}}\right] \end{aligned}$$

(30)

Further analysis of this solution, shows that real solutions only exist for $w_0\le \frac{4}{25}$; however, selection of the central weight must still allow the unit radius constraint to be satisfied. Fig. 4 shows plots of $r_1$ and $r_2$ parameters vs. central weight $w_0$. The solid lines represent $r_1$, the dotted lines represent $r_2$, and red/blue lines represent coupled solutions (from either the plus or minus solution in (30)). It can be determined that the minimum central weight with a solution that satisfies the constraints is $w_0=0.0571$.

Fig. 4

CUT4 scaling parameters vs central weight

If $r_1$ is chosen to be fixed at the boundary value $r_1=1$, then the solution for the remaining parameters can be computed as $r_2=0.4472$, $w_0=0.1143$, $w_1=0.0286$, $w_2=0.0893$. This solution satisfies up to $5^{th}$ order moments using only $N=15$ points. Finding an analytical solution can be a tedious process even for $5^{th}$ order MCEs, and the complexity of extending analytical solutions to higher n and d can render analytical solutions impossible. Numerical solutions using CUT methodology can be found; however, selecting axes which satisfy the MCEs and support constraints while providing minimum N is very difficult.

The CUT method can be used if only a single unknown maneuver with known time is used as the input, however, the generic input considered in this work (7) is mixed rather than solely spherically uniform. This introduces another problem. All of the previously discussed methods implicitly assume fully-symmetric input, which is problematic when constructing non-product quadrature sets for a mixed distribution. The following section will discuss the method used in this work to determine quadrature sets for mixed distributions to enable reachability set propagation.

3.3 Quadrature for Mixed Distributions

The generic input $\varvec{\zeta }$ considered in this paper consists of a mix of Gaussian, uniform, and spherically uniform distributions. The traditional way of handling mixed distributions is to take the tensor product of lower dimensional fully-symmetric sets. For example, consider the input $\varvec{\zeta }=[\textbf{u}_{t,1}\in \mathcal {U}_s(0,1),t_1\in \mathcal {U}(-1,1)]$ for a known initial condition with unknown maneuver magnitude and maneuver time. Using the $(15\times 3)$ 5th order spherically uniform CUT set found in the previous section $\textbf{X}_1\in \mathcal {U}_s(0,1)$, and 5th order $(3\times 1)$ uniform Gauss-Legendre points $\textbf{X}_2\in \mathcal {U}(-1,1)$, a tensor product set can be computed as

$$\begin{aligned} \textbf{X}_{tens}=\textbf{X}_1\otimes \textbf{X}_2 \end{aligned}$$

(31)

where $\textbf{X}_{tens}$ is a $(45\times 4)$ set which replicates up to $5^{th}$ order moments. Although this method is valid, the tensor product is not minimal, so a non-product method is desired. To address this problem, a recently developed direct moment matching method known as designed quadrature (DQ) [23] is used.

A brief summary of the DQ algorithm is given here; however, a more detailed discussion can be found in [23]. The DQ algorithm is a recursive algorithm used to find a set of quadrature points and weights which satisfy a generic set of moments, then prunes out points to find a set with minimal number of points N. Recall that the computational expense of a quadrature method is directly proportional N. Therefore, despite an increased initial cost of finding a minimal quadrature set via recursive DQ, the efficiency of the resulting set for computing reachability sets is vastly improved.

The DQ algorithm does not impose any symmetric assumptions on $\varvec{\zeta }$ or require any explicit knowledge of $\pi (\varvec{\zeta })$. In fact, the only required information of $\varvec{\zeta }$ is the numeric value of the statistical moments of $\varvec{\zeta }$, and any constraints associated with the support $\Omega$. Since there are no symmetric conditions imposed on the quadrature set, odd-order moments must be included. Fortunately, moments are able to be easily computed analytically by separating the expectation values of independent mixed distibutions. Statistical moments for Gaussian and uniform distributions can be easily computed analytically and are provided in Tables 3 and 4 respectively.

Table 3 Moments of Gaussian distribution

Table 4 Moments of uniform distribution

For example, the cross-moments between spherically uniform dimension $\zeta _1$ and uniform dimension $\zeta _4$ can be computed as

$$\begin{aligned} E[\zeta _1^2\zeta _4^2]=E[\zeta _1^2]E[\zeta _4^2]=\frac{1}{5}\cdot \frac{1}{3}=\frac{1}{15} \end{aligned}$$

(32)

Given the numeric moment values and support constraints of the inputs, the DQ method will solve for a set that satisfies the constraints and MCEs up to a desired tolerance. DQ is an iterative procedure which minimizes the MCEs and support constraint penalty for fixed N using Gauss-Newton method, then prunes out points and repeats until a valid set cannot be found with fewer points. The four major components are

• 1. Penalization Define the cost function ${\tilde{\textbf{R}}}_{k}$ to be the squared error in MCEs augmented by support and weight constraint error penalties. This enables the cost function to be minimized using standard unconstrained minimization tools.

• 2. Gauss-Newton Iteration An iterative update step

  $$\begin{aligned} \textbf{d}_{k+1}=\textbf{d}_k-\Delta \textbf{d} \end{aligned}$$

  (33)

  is performed where $\textbf{d}$ is a vector of decision variables, i.e. quadrature point coordinates and weights. The unconstrained optimization problem at the $k^{th}$ iteration can be written

  $$\begin{aligned} \min _{\Delta \textbf{d}}\ ||\tilde{\textbf{R}}_{k+1}-\tilde{\textbf{J}}_{k+1}\Delta \textbf{d}||_2^2 \end{aligned}$$

  (34)

  where $\tilde{\textbf{J}}_{k+1}$ is the Jacobian of the cost function. The solution of this problem is found by solving for $\Delta \textbf{d}$ with a classical least squares solution.

  $$\begin{aligned} \Delta \textbf{d}=\left( \tilde{\textbf{J}}_k^T\tilde{\textbf{J}}_k\right) ^{-1}\tilde{\textbf{J}}_k^T\tilde{\textbf{R}}_k \end{aligned}$$

  (35)

• 3. Regularization The standard least squares solution is almost always poorly conditioned due to the sparse structure of the Jacobian, so an additional Tikhanov regularization procedure is required to get a reasonable solution. Regularization is done by including an additional term in the minimization

  $$\begin{aligned} \min _{\Delta \textbf{d}}\ ||\tilde{\textbf{R}}_{k+1}-\tilde{\textbf{J}}_{k+1}\Delta \textbf{d}||_2^2+\lambda ||\Delta \textbf{d}||_2^2 \end{aligned}$$

  (36)

  The solution to this modified least squares is found using singular value decomposition and including a modifying filter factor to the computation of $\Delta \textbf{d}$. See [23] for additional details

• 4. Initialization The DQ method requires an initial guess which can greatly impact the speed of finding a solution. In fact, initializing the DQ algorithm with a quadrature set determined from one of the previously discussed methods can prove benefical in terms off computation time. For example, initializing the DQ algorithm with the $(45\times 4)$ set $\textbf{X}_{tens}$, yields a final $(21\times 4)$ set $\textbf{X}_{DQ}$. Similar final results can be found via random initialization, however, initializing using a tensor product set reduces runtime of the DQ algorithm because the initial guess satisfies the cost function and the algorithm immediately begins pruning points. This illustrates how directly solving for a mixed distribution quadrature set in nD using DQ can provide significant computational savings when compared to traditional means. Since the mixed input considered in this problem consists of normalized distributions, a set can be solved once offline and used to determine the reachable space of a target in real time. See Sect. 6 for a comparison of the accuracy of reachability sets computed using the quadrature sets $\textbf{X}_{tens}$ and $\textbf{X}_{DQ}$.

The DQ method implemented here is slightly modified from the algorithm specified in [23]. A two-tiered optimization loop is used such that the first loop uses a weak tolerance $\epsilon _1$ to find a solution with N near the optimal $N^*$, then minimizes the solution to a strict tolerance $\epsilon _2$. If the strict tolerance is used throughout the minimization, the large majority of computational effort will go towards reducing error in a solution with $N>>N^*$. It is much more effective to use a lower tolerance first, then enforce the desired tolerance. Now that a method for computing the reachability set has been presented, a systematic method for tasking sensors must be determined.

4 Sensor Tasking

Assume at this stage a polynomial model has been found via HOSM method which can efficiently propagate the target reachability set, i.e. state pdf $\pi (\textbf{x})$, through the system dynamics. The question now becomes how to task sensors to search the reachability set. Recall the maximum detection likelihood objective posed in (5)

$$\begin{aligned} \max _{\varvec{\theta }} J_d=E[\pi _d(\textbf{x},\varvec{\theta })]=\int _\Omega \pi _d(\textbf{x},\varvec{\theta })\pi (\textbf{x})d\textbf{x} \end{aligned}$$

The observer for simulations in this work is assumed to be a space-based sensor with parameters $\varvec{\theta }$ defined as attitude angles with associated attitude unit vector $\hat{\textbf{a}}$. The detection likelihood function (4) can be defined in a number of ways. A simplistic detection likelihood function would simply be $\pi _d^\prime (\textbf{x},\varvec{\theta })=1$ which implies a $100\%$ probability of detecting targets within the FOV. Other options include geometric models which adjust the likelihood based on the position within the FOV, or physics based models which use basic principals to model the detection likelihood. Since the purpose of this paper is to provide a methodological framework rather than to provide realistic simulations, the detection likelihood function used in this paper is a toy geometric model with conical FOV constraints

$$\begin{aligned} \begin{aligned} \pi _d^\prime (\textbf{x},\varvec{\theta })=&\left( 1-\left( \frac{\gamma }{\gamma ^*}\right) ^2\right) exp\left[ -\frac{|\varvec{\rho }|}{|\rho _s|}\right] \\ {\mathcal {C}}_s(\textbf{x},\varvec{\theta })=&\gamma (\textbf{x},\varvec{\theta })-\gamma ^* \end{aligned} \end{aligned}$$

(37)

where $\gamma ^*$ is the FOV half-angle, $|\rho _s|$ is a scale distance, $\varvec{\rho }=\textbf{x}_t-\textbf{x}_{ob}$ is the range vector, and $\gamma$ is the angle between attitude vector and range vector. Angle $\gamma$ can be computed by

$$\begin{aligned} \gamma (\textbf{x},\varvec{\theta })=cos^{-1}\left( \frac{\varvec{\rho }\cdot \hat{\textbf{a}}}{|\varvec{\rho }|}\right) \end{aligned}$$

(38)

A schematic of the geometry between the observer FOV, target, and detection likelihood function is shown in Fig. 5. The problem now becomes how to evaluate the expected detection likelihood, i.e. cost function.

Fig. 5

Observer geometry

Due to the FOV constraints imposed on the detection probability function and the generic nonlinear pdf $\pi (\textbf{x})$, evaluation via quadrature methods is not a practical option. Thus, a MC evaluation is necessary. Typically this would require the explicit propagation of random samples throughout the dynamics; however, the polynomial model computed in the previous section enables rapid and accurate approximation of many thousands of samples to represent $\pi (\textbf{x})$. If N samples are randomly drawn from the normalized input vector $\varvec{\zeta }^{(i)}\in \pi (\varvec{\zeta })$ and assigned equal weights $w^{(i)}=\frac{1}{N}$, then the output state is approximated using the reachability coefficients

$$\begin{aligned} \textbf{x}^{(i)}\approx \textbf{C}\varvec{\phi }(\varvec{\zeta }^{(i)}) \end{aligned}$$

(39)

and the reachability set can be approximated as a finite sum

$$\begin{aligned} \pi (\textbf{x})\approx \sum _{i=1}^Nw^{(i)}\delta (\textbf{x}^{(i)}-\textbf{x}) \end{aligned}$$

(40)

where $\delta (\cdot )$ is the dirac delta function. Substituting (40) into (5) yields the MC approximated cost function

$$\begin{aligned} \max _{\varvec{\theta }} J_d=\sum _{i=1}^N w^{(i)}\pi _d(\textbf{x}^{(i)},\varvec{\theta }) \end{aligned}$$

(41)

In practice, the objective function is maximized by performing a grid search of $\varvec{\theta }$ and selecting the attitude which maximizes $J_d$. Due to the axial symmetry of the conic FOV and detection probability, only two attitude angles are required to describe the observer attitude. Note that there is a tradeoff here between computational efficiency and the optimality of the grid search.

An adaptive grid is used to avoid unnecessary computational costs. The grid is defined at each timestep by

$$\begin{aligned} \begin{aligned} \varvec{\theta }_1 =&[min(\theta (\textbf{x}^{(i)})), min(\theta (\textbf{x}^{(i)})) + \gamma ^*,min(\theta (\textbf{x}^{(i)})) + 2\gamma ^*, \ldots , max(\theta (\textbf{x}^{(i)}))]\\ \varvec{\theta }_2 =&[min(\phi (\textbf{x}^{(i)})), min(\phi (\textbf{x}^{(i)})) + \gamma ^*,min(\phi (\textbf{x}^{(i)})) + 2\gamma ^*, \ldots , max(\phi (\textbf{x}^{(i)}))]\\ \varvec{\Phi }=&\varvec{\theta }_{1}\otimes \varvec{\theta }_{2} \end{aligned} \end{aligned}$$

(42)

where $\varvec{\Phi }$ is the grid of angles, and $\theta ,\phi$ are the azimuth and colatitudes corresponding to the reachability samples respectively. In this manner the minimum and maximum azimuth and colatitude angles of the current target reachability set are used to bound the grid search and set nodes in increments of the FOV half-angle rather than fully grid searching all possible angles. After the optimal sensor parameters are selected, a measurement is taken and must be used to update the reachability set.

Note that in a generic multi-target multi-sensor tasking problem, an information metric may be used select sensor parameters. An example of this is the mutual information approach taken in Ref [1]. The following section discusses filtering measurements and estimating the target state and maneuver sequence using a particle filtering framework.

5 Filtering and Estimation

The traditional filtering problem involves fusion of target measurement data with propagated state uncertainty to most accurately describe the posterior target distribution. In contrast, the problem considered here is to use propagated state uncertainty to task sensors to detect the target. If the target is not detected, observations of vacant regions of the search area are used to update the search area at future times; however, if the target is detected, the objective is synonymous with the traditional filtering problem. Here, the prior and posterior update states will be denoted $\textbf{x}^-$ and $\textbf{x}^+$ respectively.

In data-rich applications, linearization such as the Extended Kalman Filter (EKF) are frequently sufficient to approximate nonlinear systems. The state can often be approximated as Gaussian in these applications; however, linear assumptions quickly break down in data-sparse applications due to the large interval between measurements. As a result, a particle filtering framework will be used to consider full density estimation of the target pdf. Particle filters are a subset of sequential Monte Carlo (SMC) techniques which are well suited for this purpose. SMC techniques are a popular class of methods which approximate a full pdf $\pi (\textbf{x})$ as an ensemble of discrete samples. A thorough introduction to SMC methods can be found in references [9, 38, 40]. Considering the MC ensemble representation of the prior given by (40), sensor parameters $\varvec{\theta }$ computed via maximum likelihood procedure given in Sect. 4, a measurement $\tilde{\textbf{y}}$ is taken. The prior pdf $\pi (\textbf{x}^-)$ can be updated to the posterior pdf $\pi (\textbf{x}^+)$ using the process of Bayesian inference. Bayes rule can be written as

$$\begin{aligned} \pi (\textbf{x}^+)=\frac{\pi (\textbf{x}^-)\pi (\tilde{\textbf{y}}|\textbf{x}^-)}{\int \pi (\textbf{x}^-)\pi (\tilde{\textbf{y}}|\textbf{x}^-)d\textbf{x}^-} \end{aligned}$$

(43)

where $\pi (\tilde{\textbf{y}}|\textbf{x}^-)$ is the measurement likelihood function. Notice that the denominator of Bayes rule is simply a normalization factor, so the update can instead be written as a proportionality

$$\begin{aligned} \pi (\textbf{x}^+)\propto \pi (\textbf{x}^-)\pi (\tilde{\textbf{y}}|\textbf{x}^-) \end{aligned}$$

(44)

Substituting (40) into (44), the measurement update can be written as a point-wise weight update

$$\begin{aligned} {\hat{w}}^{(i)+}\propto w^{(i)-}\pi (\tilde{\textbf{y}}|\textbf{x}^{(i)-}) \end{aligned}$$

(45)

where $\hat{w}^{(i)+}$ is an intermediate weight proportional to the prior weight. Recognizing that the denominator of Bayes rule is given by $\sum \hat{w}^{(i)+}$, the posterior weights are given by

$$\begin{aligned} w^{(i)+}=\frac{{\hat{w}}^{(i)+}}{\sum _{i=1}^N{\hat{w}}^{(i)+}} \end{aligned}$$

(46)

The prior samples are now shifted to the posterior samples $\varvec{\zeta }^{(i)+}=\varvec{\zeta }^{(i)-}$ and can be propagated to the next timestep.

The measurement likelihood function $\pi (\tilde{\textbf{y}}|\textbf{x}^{(i)-})$ plays an important role in the proposed search procedure and is closely related to the detection likelihood function. For simulation purposes, a random number is drawn on the interval [0, 1] and if it is less than the detection likelihood of the true target state $\pi _d(\textbf{x}^*_t,\varvec{\theta })$, the target is considered to have been located. If the target is detected, then the measurement likelihood is defined using zero mean Gaussian sensor noise $\mathcal {N}(0,\textbf{R})$ associated with the measurement model (6)

$$\begin{aligned} \pi (\tilde{\textbf{y}}|\textbf{x}^-)=\frac{1}{(2\pi )^{m/2}\sqrt{|\textbf{R}|}}exp{\left( \frac{-(\tilde{\textbf{y}}-\textbf{h}(\textbf{x}^-))^T\textbf{R}^{-1}(\tilde{\textbf{y}}-\textbf{h}(\textbf{x}^-))}{2}\right) } \end{aligned}$$

(47)

however, if the target is not detected, the measurement likelihood is defined to be the compliment of the detection probability

$$\begin{aligned} \pi (\tilde{\textbf{y}}|\textbf{x}^-)=1-\pi _d(\textbf{x}^-,\varvec{\theta }) \end{aligned}$$

(48)

In this manner, samples inside the observer FOV will have their weight reduced proportional to the detection likelihood if the target is not detected by measurement $\tilde{\textbf{y}}$.

Notice that any particle states with very low measurement likelihood $\pi (\tilde{\textbf{y}}|\textbf{x}^{(i)-})$ will have a posterior weight $w^{(i)+}$ near zero. In this situation, the particle $\textbf{x}^{(i)+}$ contributes very little to the approximation of the posterior, and as the particle filter update is repeated over multiple timesteps, the weight becomes concentrated in very few or even a single particle. This phenomenon is known as sample impoverishment or particle degeneracy and leads to a poor approximation of the target pdf. Resampling is an effective way to alleviate this issue. Ref [8] provides a concise summary and comparison of several popular resampling algorithms. The systematic resampling algorithm will be used in this paper for its efficiency and easy implementation. Note that since the system is propagated using the HOSM method, the normalized input samples $\varvec{\zeta }^{(i)}$ are redrawn from $\pi (\varvec{\zeta }^+)$ rather than directly from $\pi (\textbf{x}^+)$. Typically, a resampling condition is used to avoid costly resampling procedures at every timestep. Ref [30] characterizes this resampling condition using the Effective Sample Size (ESS) criterion

$$\begin{aligned} ESS=\left( \sum _{i=1}^N\left( w^{(i)}\right) ^2\right) ^{-1} \end{aligned}$$

(49)

The resampling condition is to resample only when ESS is less than a specific threshold $N_t$. The threshold $N_t=N/2$ is used in implementation of this paper.

Although resampling is an effective method for preventing particle degeneracy over multiple timesteps, if the prior distribution is very diffuse with respect to the likelihood function, problems with particle degeneracy may arise at a single timestep. This is frequently the case in the current application when a target with a large reachability set is detected by an observer with low sensor noise. For example, if a sensor has a range mesurement with noise standard deviation on the order of meters, and the closest particle in the reachability set has a range on the order of kilometers from the measured range, then the closest particle is thousands of standard deviations away from the expected measurement. The likelihood of such a particle is numerically zero, and thus, all of the particle weights will be set to zero and the filter will become singular.

This phenomenon is well understood in particle filters, and several methods have been developed to alleviate this practical implementation issue. This paper uses the importance sampling with progressive correction (ISPC) technique outlined in Ref [35] to update the reachability set when the target is detected. The idea behind ISPC is to include an expansion factor $\lambda _k$ in the likelihood function, and iteratively resample intermediate posterior distributions until the expansion factor converges to the true posterior. The modified likelihood function is given by

$$\begin{aligned} \pi ^\prime (\tilde{\textbf{y}}|\textbf{x}^-)=\frac{1}{(2\pi )^{m/2}\sqrt{|\textbf{R}|}}exp{\left( \frac{-(\tilde{\textbf{y}}-h(\textbf{x}^-))^T\textbf{R}^{-1}(\tilde{\textbf{y}}-h(\textbf{x}^-))}{2\lambda _k}\right) } \end{aligned}$$

(50)

such that for $\lambda _k>1$ the standard deviation of the likelihood function is artifically inflated. Ref[35] provides an adaptive choice for parameter $\lambda _k$ given by

$$\begin{aligned} \lambda _k=\frac{\max _{1\le i\le N}-(\tilde{\textbf{y}}-h(\textbf{x}^-))^T\textbf{R}^{-1}(\tilde{\textbf{y}}-h(\textbf{x}^-))}{2\log (\delta _{max})} \end{aligned}$$

(51)

where $\delta _{max}$ is a tunable parameter which influences the size of the progressive correction steps.

The final step in the maneuvering satellite search procedure is to estimate the target state and maneuver sequence. In fact, the HOSM method framework unifies the estimation of the target state and maneuver sequence into the same procedure. Since the samples in the maneuver space $\varvec{\zeta }^{(i)}$ are mapped to samples in the state space $\textbf{x}^{(i)}$ by the polynomial approximation (39), estimates can be computed simultaneously using

$$\begin{aligned} \left[ \begin{array}{c} E[\textbf{x}^+]\\ E[\varvec{\zeta }^+] \end{array}\right] =\sum _{i=1}^Nw^{(i)+}\left[ \begin{array}{c} \textbf{C}\varvec{\phi }(\varvec{\zeta }^{(i)+})\\ \varvec{\zeta }^{(i)+} \end{array}\right] \end{aligned}$$

(52)

Note that during the search phase, the point estimate of the target given above may be a poor estimate of the true target location due to the very diffuse target pdf. Typically, a point estimate of mean target state only becomes meaningful after the first target detection when the pdf contracts to the levels of sensor noise around the measurement. Additionally, it is important to note that since measurements are taken in the $\textbf{x}$ space, the reliability of maneuver estimates in the $\varvec{\zeta }$ space are highly dependent on the quality of the polynomial approximation (39). This will be discussed further in Sect. 6. The Bayesian particle filtering method can be summarized as following

• 1. Initialize Particles and Quadrature Points: Randomly sample N reachability set particles from the normalized maneuver distribution: $\varvec{\zeta }_{rs}^{(i)}\in \pi (\varvec{\zeta })$ and assign equal weights $w^{(i)}=\frac{1}{N}$, and initialize quadrature points computed via non-product quadrature method: $\varvec{\zeta }_q^{(i)}$

• 2. Propagate Directly propagate quadrature points: $\textbf{x}_{q,k+1}^{(i)}=\varvec{\chi }(\varvec{\zeta }_q^{(i)},\textbf{z}_{ob},k+1)$ to next measurement at $t_{k+1}$. Use $\textbf{x}_{q,k+1}^{(i)}$ to evaluate polynomial model coefficients via (13). Propagate reachability samples to $t_{k+1}$ using polynomial approximation: $\textbf{x}_{rs,k+1}^{(i)}\approx \textbf{C}_{k+1}\varvec{\phi }(\varvec{\zeta }_{rs}^{(i)})$. Since the quadrature points are designed to be minimal, approximating $\textbf{x}_{rs,k+1}^{(i)}$ in this manner can offer orders of magnitude of computational savings.

• 3. Determine Sensor Parameters Create a grid of sensor parameters $\varvec{\Phi }$. For each parameter combination, evaluate the cost function (41) using reachability samples $\textbf{x}^{(i)}_{rs,k+1}$ and select the parameters which maximize detection likelihood $\varvec{\theta }^*={{\,\mathrm{arg\,max}\,}}_{\Phi }\left[ J_d(\textbf{x},\varvec{\Phi })\right]$

• 4. Reachability Set Update Update the reachability set particle weights using (45) and (46). If target is detected, use likelihood function (47), if target is not detected, use likelihood function (48).

• 5. Resample If the target is detected for the first time, resample using ISPC algorithm, otherwise if resampling criterion $ESS<\frac{N}{2}$ is satisfied, resample $\varvec{\zeta }_{rs}^{(i)}$ using systematic resampling algorithm.

• 6. Estimate State and Maneuver Compute the current target state and maneuver estimates using (52). If desired, covariance estimates can be computed as well. Keep in mind that estimate covariance will be very large if the reachability set is still being searched. Return to step 2.

The above particle filtering framework in conjunction with maximum detection likelihood sensor tasking and the HOSM method enables a feasible framework for propagating and searching the reachability set of a noncooperative target satellite. Figure 6 summarizes each component of the proposed method, and the following section will present numerical simulations and discuss results.

Fig. 6

Noncooperative satellite search method

6 Numerical Results

This section validates the mixed-distribution quadrature method described in Sect. 3.3 used to propagate reachability sets, as well as provides simulation results for two examples of the full noncooperative satellite search method. The reachability set validation method provides a comparison of sets propagated using a tensor product method and using the DQ method. The two simulation test cases are 1) a single maneuver case, and 2) a two maneuver case. The first test case studies the effect of different order polynomial approximations on the overall performance of the developed framework.

The quadrature method validation section, propagates the reachability set for a target initially in an inclined LEO orbit, whereas both test cases consider a target initially in a slightly eccentric and slightly inclined Geosynchronous Earth Orbit (GEO). Additional test cases of the full search method, including a LEO orbit case, can be found in [16, 17]. The model $\textbf{f}(\textbf{x},t)$ used for all results is the nonlinear $J_2$-perturbed relative equations of motion defined in [44]. The equations of motion for the dynamic model are

$$\begin{aligned} \textbf{f}(\textbf{x},t)=\left\{ \begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\\ 2\dot{y}\omega _z+x\omega _z^2+y\alpha _z-z\omega _x\omega _z-r\eta ^2+\zeta s_i s_\theta +\eta ^2(r+x)+\zeta s_is_\theta \\ -2\dot{x}\omega _z+2\dot{z}\omega _x-x_k\alpha _z+y(\omega _z^2+\omega _x^2)+z\alpha _x+\zeta s_i c_\theta +\eta ^2y+\zeta s_i c_\theta \\ -2\dot{y}\omega _x-x\omega _x\omega _z-y\alpha _x+z\omega _x^2+\zeta c_i+\eta ^2z+\zeta c_i \end{array}\right\} \end{aligned}$$

(53)

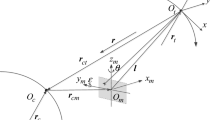
where $\omega _i$ terms are angular velocity of the rotating frame, $\alpha _i$ terms are the angular acceleration of the rotating frame, and $\zeta$,$\eta$ are constants related to the $J_2$ acceleration. The coordinate frame for this model is the relative RSW frame depicted in Fig. 9. The RSW coordinate frame is defined by $\hat{R}$ in the radial direction, $\hat{S}$ in the in-track direction and $\hat{W}$ in the orbit normal direction. The origin of the RSW frame is located at the nominal orbit of the target at $t_0$. The following section will provide a comparison of reachability sets computed with competing methods in the RSW frame with dynamic model $\textbf{f}(\textbf{x},t)$.

6.1 Comparison of Quadrature Methods

Consider the case of a single unknown maneuver magnitude and unknown maneuver time, with input vector $\textbf{z}_t=[\textbf{u}_{t,1},t_1]$. Two quadrature sets which match up to 5th order moments for this input were computed in Sect. 3.3. The first is a $(45\times 4)$ matrix $\textbf{X}_{tens}$ computed via tensor product of spherically uniform CUT points and uniform Gauss-Legendre points, and the second is a $(21\times 4)$ matrix $\textbf{X}_{DQ}$ constructed via the DQ algorithm.

The target is initially in an inclined LEO orbit with orbital elements given in Table 5, and is assumed to make a maneuver bounded by a magnitude of 5m/s $\textbf{u}_{t,1}\in \mathcal {U}_s(0,5m/s)$ and bounded maneuver time $t_1\in \mathcal {U}(0,P/2)$ where P is the orbital period $(P=5309.6 s)$.

Table 5 LEO initial orbital elements

Reachability set coefficents with respect to a second order polynomial basis are computed in intervals of 30 seconds throughout the first orbital period using each quadrature set $\textbf{X}_{tens}$ and $\textbf{X}_{DQ}$. 10,000 random Monte Carlo samples are then drawn from the input vector $\varvec{\zeta }_{mc}^{(i)}$ and exactly integrated through the dynamic model to target states $\textbf{x}_{mc,k}^{(i)}=\varvec{\chi }(\varvec{\zeta }_{mc}^{(i)},\textbf{z}_{ob},k)$ in the same 30 second intervals. The error between the exact MC sample evaluations and the polynomial approximation is computed for each quadrature method.

$$\begin{aligned} \begin{aligned} \epsilon _{tens,k}^{(i)}=&\textbf{x}_{mc,k}^{(i)}-\textbf{C}_{tens,k}\varvec{\phi }(\varvec{\zeta }_{mc}^{(i)})\\ \epsilon _{DQ,k}^{(i)}=&\textbf{x}_{mc,k}^{(i)}-\textbf{C}_{DQ,k}\varvec{\phi }(\varvec{\zeta }_{mc}^{(i)})\\ \end{aligned} \end{aligned}$$

(54)

The norm of position and velocity errors, $||\epsilon _r||_2,\ ||\epsilon _v||_2$ for each sample are computed and the RMS error value is computed over all samples

$$\begin{aligned} rms(||\epsilon ||_2)=\sqrt{\frac{1}{10000}\sum ||\epsilon ^{(i)}||_2} \end{aligned}$$

(55)

The RMS error of position and velocity is plotted for each method vs. time in Fig. 7.

Fig. 7

Approximation errors for reachability sets computed via tensor product and DQ methods

It is immediately obvious, that the errors for the DQ method and the tensor product method are nearly identical throughout the entirety of the simulation. This result demonstrates, that although the non-product DQ method has computational savings of $53\%$ compared to the product method ($N=21$ vs. $N=45$), there is no loss in accuracy. This is due to the fact that the same order of MCEs were satisfied for both sets regardless of the number of points used.

Figure 8 shows a position scatter plot of all 10,000 MC samples $\textbf{x}_{mc}^{(i)}$ at the final timestep, and the colorbar denotes the distribution of position errors thorughout the reachability set. Although this error analysis is only shown for a 2nd order basis, examples in [17] show that increasing the basis function order can significantly decrease the error in reachability set approximation. This fact is reflected in the following sections in the accuracy of target state and maneuver estimates for varying polynomial basis order. It has been demonstrated that the non-product DQ quadrature method has equivalent accuracy to a tensor product method, with significantly improved efficiency. The following sections demonstrate these efficient non-product quadrature methods can be used to enable the noncooperative maneuvering satellite search method.

Fig. 8

Scatterplot of reachability set position errors

6.2 Search Method Test Cases

This section describes the simulation parameters for the noncooperative satellite search method test cases and provide numerical results and analysis of each. Both test cases consider the observer to be a space-based satellite with the same dynamic equations of motion as the target. The observer is prescribed range $|\varvec{\rho }|$, range-rate $|\varvec{\dot{\rho }}|$, azimuth $\hat{\theta }_1$, and colatitude $\hat{\theta }_2$ measurements given by

$$\begin{aligned} \textbf{h}(\textbf{x})=\left[ \begin{array}{c} |\varvec{\rho }|\\ |\varvec{\dot{\rho }}|\\ \hat{\theta }_1\\ \hat{\theta }_2\end{array}\right] = \left\{ \begin{array}{c} \sqrt{\rho _1^2+\rho _2^2+\rho _3^2}\\ \frac{\varvec{\rho }\cdot \dot{\varvec{\rho }}}{\sqrt{\rho _1^2+\rho _2^2+\rho _3^2}}\\ \tan ^{-1}(\frac{\rho _2}{\rho _1})\\ \cos ^{-1}(\rho _3) \end{array}\right\} \end{aligned}$$

(56)

where all relative position and velocity coordinates are given in the RSW frame. The sensor parameters $\varvec{\theta }=[\theta _1\ \theta _2]^T$ specify the observer attitude, which can be converted into a unit vector $\hat{\textbf{a}}$ given by

$$\begin{aligned} \hat{\textbf{a}}=\left[ sin(\theta _2)cos(\theta _1)\ \ sin(\theta _2)sin(\theta _1)\ \ cos(\theta _1)\right] ^T \end{aligned}$$

(57)

such that $\gamma$ is the angle between $\hat{\textbf{a}}$ and $\varvec{\rho }$ and can be computed using (38).

Fig. 9

RSW coordinate system

The measurements are assigned Gaussian noise with covariance matrix $\textbf{R}=diag([25m,0.1m/s,0.1^\circ ,0.1^\circ ]^2)$. The observer is assigned a FOV with half angle $\gamma ^*=7.5^\circ$ and a scale distance $|\rho _s|=1000km$ for computing detection probability.

Note that the outcome of the simulation is dependent on the overall observability of the reachability set with respect to the observer detection zone. If the volume of the observer FOV is significantly less than the volume of the reachability set, then the observer may never be able to locate the target within the set; and conversely, if the observer FOV is larger than the reachable set, then the target will be detected within the first few timesteps. The parameters selected here correspond to a sensor with long range, but narrow FOV, and were chosen for moderate observability to demonstrate a range of outcomes.

Assume that half an orbital period elapses without observing the target such that maneuver time is defined as uniformly distributed between 0 and 12 hours, i.e. $t_i\in \mathcal {U}(0hr,12hr)$. Measurements are taken every 5 minutes ($\Delta t=300 sec$) starting from $t=12 hr$ through the end of the first orbital period $t_f=24 hr$. Also assume it is known that the target has a maximum maneuver capability of 5m/s such that unknown maneuvers are spherically uniform distributions $\textbf{u}_{t,i}\in \mathcal {U}_s(0,5m/s)$. The nominal target satellite orbit at $t=0$ is given by the orbital parameters and corresponding Earth Centered Inertial (ECI) coordinate state vector given in Tables 6 and 7.

Table 6 Initial target nominal orbital elements

Table 7 Initial target nominal state (ECI coordinates)

6.2.1 Test Case 1: Single Maneuver

This section will present the results for the single unknown maneuver test case. For this test case, the random target input vector is given by

$$\begin{aligned} \textbf{z}_t=[\textbf{u}_{t,1},t_1],\ \ \textbf{u}_{t,1}\in \mathcal {U}_s(0,5m/s),\ \ t_1\in {\mathcal {U}}(0,12hr) \end{aligned}$$

(58)

The nominal observer orbit at the start of the search $t=12hr$ is given by the relative RSW coordinate state vector given in Table 8.

Table 8 Observer state at t=12hr (RSW coordinates)

Quadrature sets which satisfy moment constraint equations up to $d=4,6,8,10$ order are computed and used to evaluate reachability set coefficients for polynomial models of $D=2,3,4,5$ order respectively. Refer to Sect. 3 for details on the computation of quadrature sets. The number of quadrature points and basis functions required for each model is given in Table 9. Once reachability set coefficients are computed, 10,000 samples $\varvec{\zeta }^{(i)}$ are drawn and evaluated using the polynomial model. The position of these samples in RSW coordinates at $t=12hr$ is shown in Fig. 10 for the 5th order polynomial model, where the colorbar depicts the maneuver time for a given sample.

Fig. 10

Test Case 1: 5th order polynomial reachability set at t = 12 h

Table 9 Test Case 1: summary of quadrature sets for single maneuver case (n=4)

Consider a single realization of the true target maneuver $\textbf{u}_{t,1}^*$ and maneuver time $t_1^*$ given by

$$\begin{aligned} \textbf{u}_{t,1}^*=[1.84,-2.54,2.30]^T(m/s),\ \ t^*_1=5396(s)(+12hr) \end{aligned}$$

(59)

Fig. 11 depicts the evolution of the target pdf in the initial target orbital plane (${\hat{R}},{\hat{S}}$) using a 5th order polynomial basis in 1 hour intervals. A subset of 100 samples are randomly selected and plotted over the contours of Fig. 11. The initial observer state and true target maneuver were specifically selected for this test case to demonstrate a few key takeaways. First and foremost, notice that the true target state is captured within the contours of the pdf at all times. The pdf contours represent all possible states and maneuvers histories that could explain the measurements up to the current time. Secondly, the geometry of the observer and the reachability set means that the target will not be in the observer’s FOV when initially searching the most likely region for the target (near the origin). This is done to demonstrate how the contours of the target pdf become more concentrated around the true target state as vacant regions of the reachability set are searched, and by 17 hours into the simulation the true target location is centered in the most probable region of the reachability set. The largest reduction in uncertainty during the search procedure is, by far, at the time of first detection $t_d$. Therefore, $t_d$, as well as state and maneuver estimate errors are important performance metrics. The detection time for the 5th order case is 18 hours and 25mins.

Fig. 11

Test Case 1: evolution of target PDF in orbital plane during search (5th order polynomial approximation)

The state and maneuver estimates at both the time of first detection $t_d$ as well as the final simulation time $t_f$ are computed for all polynomial models using (52). The target position and velocity estimate errors $\epsilon _r$ and $\epsilon _v$ respectively, are defined as

$$\begin{aligned} \epsilon _r=\frac{||E[\textbf{r}_{t}]-\textbf{r}_{t}^*||_2}{||\textbf{r}_0||_2},\ \ \epsilon _v=\frac{||E[\textbf{v}_{t}]-\textbf{v}_{t}^*||_2}{||\textbf{v}_0||_2} \end{aligned}$$

(60)

where $\textbf{r}_0$ and $\textbf{v}_0$ are used to normalize the errors by the initial Cartesian position and velocity. The maneuver estimate errors are given by

$$\begin{aligned} \epsilon _u=||E[\textbf{u}_{t,1}]-\textbf{u}_{t,1}^*||_2,\ \ \epsilon _t=|E[t_1]-t_1^*| \end{aligned}$$

(61)

These errors are tabulated for the initial detection time as well as the final time $t_f=24 hrs$ in Tables 10 and 11, respectively. Generally speaking, the error values for both the target state and maneuver estimate appear to decrease as the order of the polynomial model increases. There are some subtle numerical reasons why the state and maneuver estimate errors for this particular realization do not strictly decrease as polynomial order increases. One reason is that at $t_f$ the state estimate is largely a function of the assumed measurement error, not the reachability set error. A reason that the estimate errors do not correlate entirely with polynomial order at detection time $t_d$ may simply be random chance that certain order polynomials approximate the reachability set better at this particular input realization. In other words, on average over the entire reachability set higher order polynomials will approximate the set more accurately; however, there will always be locations in the set where a low order polynomial approximates the set better than a high order polynomial purely by chance. To this end, examining these results too closely will not provide a full picture, as only looking at a single realization of the true target maneuver doesn’t encompass the full domain of the reachability set.

Table 10 Test Case 1: target maneuver and state estimate error at $t_d$

Table 11 Test Case 1: target maneuver and state estimate error at $t_f$

Rather than considering a single realization of the true target maneuver, now consider the full simulation run 250 times with a new true target maneuver randomly sampled for each simulation. The simulation is run using the same 250 realizations for all polynomial models. Figure 12 shows histograms of the time of first detection $t_d$ for varying polynomial model orders. From Fig. 12, it can be observed that target target is detected quickly in the majority of the simulations; however some target maneuvers cause the target to be undetected for longer. The simulations are run long enough that $100\%$ of targets are detected, however increasing the polynomial order slightly reduces the time required to locate the target in these extreme cases. The target was detected in $95\%$ of simulations by $t=20.17$hr for the model order $D=2$, $t=19.58$hr for $D=3$, $t=19.17$hr for $D=4$, and $t=18.58$hr for $D=5$.

Fig. 12

Test Case 1: detection time for 250 simulations and varying d

Figures 13, and 14 show histograms of log estimate error in maneuver magnitude $\epsilon _u$, and maneuver time $\epsilon _t$ respectively for varying polynomial model orders. It can be readily seen that the maneuver magnitude and maneuver time estimate errors are reduced by increasing polynomial order. Since reduction of detection time is only very modestly improved by increased polynomial order, selection of the polynomial order to be used is dependent on the application considered. If the only requirement is to locate the target, perhaps a low order reachability set can be used to define the reachable space more efficiently; however, if maneuver reconstruction is required, higher accuracy reachability sets may be necessary to accurately estimate the maneuver. Table 12 summarizes the results of the 250 simulations by giving the mean error of the target state and maneuver estimates at the final time along with a $1\sigma$ plus or minus bounds.

Fig. 13

Test Case 1: maneuver estimate error $\epsilon _u$ for 250 simulations and varying d

Fig. 14

Test Case 1: maneuver time estimate error $\epsilon _t$ for 250 simulations and varying d

Table 12 Test Case 1: normalized target state and maneuver estimate error summary at $t_f$: mean error $\pm 1\sigma$

6.2.2 Test Case 2: Two Maneuvers

This section will present the results for a case with two unknown maneuvers. For this test case, the random target input vector is given by

$$\begin{aligned} \textbf{z}_t=[\textbf{u}_{t,1},t_1,\textbf{u}_{t,2},t_2,] \end{aligned}$$

(62)

where maneuver $\textbf{u}_{t,i}$ and maneuver time $t_i$ distributions are defined identically to the those in test case 1. The main difference in this test case is the dimension of the input and the total $\Delta V$ the target is allowed to make. Due to the curse of dimensionality, the number of points required to evaluate the reachability coefficients greatly exceeds that required for a 4-D input. In fact, 6th and 8th order quadrature points were unable to be found directly in eight dimensional space using the DQ algorithm, so a tensor product of lower dimensional sets had to be used as described in Sect. 3.3. Table 13 lists the number of basis functions and number of quadrature points required to compute reachability sets for varying polynomial model order.

Table 13 Test Case 2: summary of quadrature sets for two maneuver case (n = 8)

For brevity, only the results for the 4th order polynomial model will be shown. Figure 16 depicts the target reachability set in RSW coordinates using a 4th order polynomial model, where the colorbar indicates the average maneuver time. As is intuitively obvious, the larger total $\Delta V$ available to the target makes the physical size of the two maneuver reachability set considerably larger than the single maneuver set shown in Fig. 10. The evolution of the pdf for a single realization of the two maneuvers is shown in Fig. 15. The detection time for this realization was 15hr 45min.

Fig. 15

Test Case 2: evolution of target PDF in orbital plane during search (4th order polynomial approximation)

Fig. 16

Test Case 2: 4th order polynomial reachability set at t = 12 h

The 4th order polynomial model is used to run 250 full simulations with a new true target maneuver sequence randomly sampled for each iteration. The error in estimated maneuver magnitude $\epsilon _u$ and maneuver time $\epsilon _t$ for both unknown maneuvers at the final simulation time is given in Fig. 17. It is apparent from Fig. 17 that the maneuver estimates have greater error than the respective 4th order models in the single maneuver test case (Figs. 13, 14). This is to be expected for several reasons. Firstly, the physically larger size of the reachability set will cause errors in the polynomial approximation to increase, thereby increasing error in the mapping between maneuvers and target states. Furthermore, the second maneuver creates the possibility for multiple maneuver sequences to acheive the same target trajectory. In this situation, it is impossible for the particle filter to disambiguate between possible maneuver histories and the filter may converge around an incorrect solution.

Fig. 17

Test Case 2: maneuver estimate errors for 250 simulations

Despite the increased error in maneuver estimate and larger search region, using the proposed method the observer satellite was able to locate the target satellite in $96\%$ of the 250 simulations run (i.e. 10 unfound targets). There are several reasons why some targets were not detected in this simulation. Firstly, the parameters of the observation zone and detection probability were kept the same as the single maneuver case, and due to the larger search region, portions of the reachability set further away from the observer were unable to be searched adequately. Secondly, the final simulation time was kept constant at 24hr so it may be the case that the observer simply didn’t have enough time to find the target in extreme cases.

Simulations where the target was not detected were removed from state and maneuver estimate calculations. The error in position $\epsilon _r$ and velocity $\epsilon _v$ estimate at the final time are computed using the normalization given by (60). The average state and maneuver estimate errors at the final simulation time plus or minus $1\sigma$ is shown in Table 14. The average error in both maneuver and state estimates were higher for this case than the compareable 4th order estimate errors in test case 1. This is to be expected due to the higher dimensionality and larger physical size of the reachability set.

Table 14 Test Case 2: normalized target state and maneuver estimate error summary at $t_f$ for 4th order polynomial model: mean error $\pm 1\sigma$

7 Conclusions

This paper presents a systematic search method for detecting a satellite that has been lost due to unknown maneuvers. A novel characterization of unknown maneuvers defines the target search space, and a maximum detection likelihood approach is used to task sensors. Sensor observations of vacant regions of the search space are used to reduce uncertainty in target state, and inform future sensor tasking. In fact, the reachability set represents the set of all possible states and maneuver histories that can be explained by the measurments up to a given time. The true target state will always be a subset of this search space given that the bounds on input uncertainty are not violated. The proposed method provides a unified framework for search, detection, tracking, and maneuver estimation of a noncooperative target.

The applicability of the proposed method is largely dependent on the observability of the problem. Sensors with large FOV relative to the target reachability set will easily locate the target, whereas a sensor with small FOV relative to a physically large reachable set may only have limited observability. Generalization of the single-sensor single-target sensor tasking cases examined here to the generic sensor tasking problem as well as enabling active control of mobile sensors may prove beneficial for increasing observability of the reachability set.

Polynomial model order of the reachability set approximation is a flexible design parameter left to the discretion of the user. Higher order polynomial models offer better target state and maneuver estimation accuracy at the expense of increased computational cost. If the only objective is to locate the target, without regard for accurate maneuver reconstruction, using low order polynomials to model the reachable space can provide similar detection time performance. Additionally, increasing the assumed number of maneuvers the target imposes strongly prohibitive computational burdens on the proposed method. The current research work is focused on the computationally efficient extension of this approach for low-thrust continuous maneuvers.