Effective Stacking Fault Energy in Face-Centered Cubic Metals

Abstract

As a typical configuration in plastic deformations, dislocation arrays possess a large variation of the separation of the partial dislocation pairs in face-centered cubic (fcc) metals. This can be manifested conveniently by an effective stacking fault energy (SFE). The effective SFE of dislocation arrays is described within the elastic theory of dislocations and verified by atomistic simulations. The atomistic modeling results reveal that the general formulae of the effective SFE can give a reasonably satisfactory prediction for all dislocation types, especially for edge dislocation arrays. Furthermore, the predicted variation of the effective SFE is consistent with several previous experiments, in which the measured SFE is not definite, changing with dislocation density. Our approach could provide better understandings of cross-slip and the competition between slip and twinning during plastic deformations in fcc metals.

1 Introduction

It is widely accepted that in face-centered cubic (fcc) metals, a perfect dislocation < 110 >/2 could dissociate into two Shockley partials < 112 >/6 with a slice of stacking fault (SF) in between them [1]. The formation of SFs will bring about an additional energy called stacking fault energy (SFE), which is a primary factor in controlling cross-slip [2], the transition from slip to twinning [3] and so on. As a result, it significantly impacts several elementary processes, such as work-hardening [4, 5], the synchronous improvement of strength and ductility [6, 7], creep deformation [8, 9], the evolution of dislocation configurations in fatigue [10, 11], and the twinning-induced plasticity (TWIP) effect in some austenitic steels [12, 13]. Therefore, it is very important to ascertain the SFE with sufficient accuracy.

When an isolated < 110 >/2 dislocation dissociates freely into two Shockley partial dislocations, the separation of the two partial dislocations (termed by d) is inversely proportional to the SFE (termed by γ₀), as predicted by the elasticity theory of dislocations. However, d could be affected by several other factors. It has been proved that d will change with the external loading [14, 15]. Furthermore, dislocation density can also cause a dramatic variation of the dissociation separation d [13]. However, the density of dislocations only reflects their number per volume, but not their local configurations. Besides, dislocation arrays are often observed in the deformed material with relatively low SFE in association with cross-slip, dislocation multiplications and pile-ups [16,17,18,19,20]. In this configuration, dislocations usually have stronger interaction within an array rather than between arrays with consideration of dislocation spacing. However, the d variation with dislocation arrays has never been fully interpreted so far, and its importance received little attention in many related experimental observations and theories [11, 20]. In order to reveal the variation of d for dislocation arrays, the effective SFE for dislocation arrays is proposed and formulated within the framework of the elasticity theory of dislocations, and then systematical atomistic simulations are preformed to verify the accuracy of these formulae. In addition, several previous experimental observations [11, 20] are re-examined with our approach.

2 Theoretical Consideration

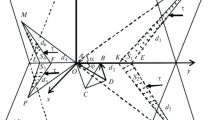
First of all, the effective SFE is derived within the framework of the isotropic elasticity theory of dislocations. Figure 1 shows an array of dislocations $\varvec{b} = {{\left[ {1\overline{1} 0} \right]} \mathord{\left/ {\vphantom {{\left[ {1\overline{1} 0} \right]} 2}} \right. \kern-0pt} 2}$ with spacing D, and each of them is dissociated into two Shockley partials $\varvec{b}_{1} = {{\left[ {1\overline{2} 1} \right]} \mathord{\left/ {\vphantom {{\left[ {1\overline{2} 1} \right]} 6}} \right. \kern-0pt} 6}$ and $\varvec{b}_{2} = {{\left[ {2\overline{1} \overline{1} } \right]} \mathord{\left/ {\vphantom {{\left[ {2\overline{1} \overline{1} } \right]} 6}} \right. \kern-0pt} 6}$ separated by a SF with d. In general, the Burger vector b lies along x (x||b). The dislocation line direction l makes an angle θ with x, and z is perpendicular to both b and l.

Fig. 1

Simulated dissociation of an dislocation ${{\left[ {1\overline{1} 0} \right]} \mathord{\left/ {\vphantom {{\left[ {1\overline{1} 0} \right]} 2}} \right. \kern-0pt} 2}$ array with θ = 90° in Ag, where the red atoms represent the $\varvec{b}_{1} = {{\left[ {1\overline{2} 1} \right]} \mathord{\left/ {\vphantom {{\left[ {1\overline{2} 1} \right]} 6}} \right. \kern-0pt} 6}$,the blue ones $\varvec{b}_{2} = {{\left[ {2\overline{1} \overline{1} } \right]} \mathord{\left/ {\vphantom {{\left[ {2\overline{1} \overline{1} } \right]} 6}} \right. \kern-0pt} 6}$ and the gray ones stacking fault zone. See the text for parameters

The force balance at the two partial dislocations indicated by b₁ and b₂ in Fig. 1 can be given below:

$$\left[ {\left( {\varSigma_{{\varvec{b}_{ 1} }} \cdot \varvec{b}_{\text{1}} } \right) \times \varvec{l}} \right] \cdot \varvec{m} - \gamma_{0} + F_{\text{r}} - F_{\text{l}} = 0,$$

(1)

$$\left[ {\left( {\varSigma_{{\varvec{b}_{ 2} }} \cdot \varvec{b}_{2} } \right) \times \varvec{l}} \right] \cdot \varvec{m} + \gamma_{0} - F_{\text{r}} - F_{\text{l}} = 0,$$

(2)

where $\varSigma_{{\varvec{b}_{ 1} }}$ and $\varSigma_{{\varvec{b}_{2} }}$ represent the stress tensors arising from the partial dislocation arrays b₁ and b₂, respectively (the two selected partial dislocations have to be removed). The unit vectors l= (cos θ, − sin θ, 0) and m=(sin θ, cos θ, 0). The force F_l is the possible lattice resistance in association with dislocation glide. The force F_r is the repulsive interaction between the two selected partials b₁ and b₂, which can be given according to Ref. [1]:

$$F_{\text{r}} = \frac{{w_{\text{i}} }}{\pi d},$$

(3)

where $w_{\text{i}} = {{\left[ {Gb_{\text{p}}^{2} \left( {2 - \nu - 2\nu \cos 2\theta } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {Gb_{\text{p}}^{2} \left( {2 - \nu - 2\nu \cos 2\theta } \right)} \right]} {\left[ {8\left( {1 - \nu } \right)} \right]}}} \right. \kern-0pt} {\left[ {8\left( {1 - \nu } \right)} \right]}},$ and b_p is the magnitude of the Burgers vector of the partial dislocation; G and ν are the shear modulus and Poisson’s ratio, respectively.

It is apparent that in Eqs. (1) and (2) z=0, and thus only σ _xz and σ _yz are nonzero according to the isotropic elasticity theory of dislocations [1]. In Eq. (1), the nonzero stresses can be given as:

$$\sigma_{xz,r}^{{b_{1} }} = \frac{1}{2D}\left( {\frac{1}{{\tan \left( {{{\pi d} \mathord{\left/ {\vphantom {{\pi d} D}} \right. \kern-0pt} D}} \right)}} - \frac{1}{{{{\pi d} \mathord{\left/ {\vphantom {{\pi d} D}} \right. \kern-0pt} D}}}} \right)\left( {\frac{{Gb_{{2{\text{e}}}} \sin \theta }}{1 - \nu } + Gb_{{2{\text{s}}}} \cos \theta } \right),$$

(4)

$$\sigma_{yz,r}^{{b_{1} }} = \frac{1}{2D}\left( {\frac{1}{{\tan \left( {{{\pi d} \mathord{\left/ {\vphantom {{\pi d} D}} \right. \kern-0pt} D}} \right)}} - \frac{1}{{{{\pi d} \mathord{\left/ {\vphantom {{\pi d} D}} \right. \kern-0pt} D}}}} \right)\left( {\frac{{Gb_{{2{\text{e}}}} \cos \theta }}{1 - \nu } - Gb_{{2{\text{s}}}} \sin \theta } \right).$$

(5)

In Eq. (2), they are:

$$\sigma_{xz,r}^{{b_{2} }} = - \frac{1}{2D}\left( {\frac{1}{{\tan \left( {{{\pi d} \mathord{\left/ {\vphantom {{\pi d} D}} \right. \kern-0pt} D}} \right)}} - \frac{1}{{{{\pi d} \mathord{\left/ {\vphantom {{\pi d} D}} \right. \kern-0pt} D}}}} \right)\left( {\frac{{Gb_{{ 1 {\text{e}}}} \sin \theta }}{1 - \nu } + Gb_{{ 1 {\text{s}}}} \cos \theta } \right),$$

(6)

$$\sigma_{yz,r}^{{b_{2} }} = - \frac{1}{2D}\left( {\frac{1}{{\tan \left( {{{\pi d} \mathord{\left/ {\vphantom {{\pi d} D}} \right. \kern-0pt} D}} \right)}} - \frac{1}{{{{\pi d} \mathord{\left/ {\vphantom {{\pi d} D}} \right. \kern-0pt} D}}}} \right)\left( {\frac{{Gb_{{ 1 {\text{e}}}} \cos \theta }}{1 - \nu } - Gb_{{ 1 {\text{s}}}} \sin \theta } \right),$$

(7)

where b_1e and b_1s (b_2e and b_2s) are the magnitudes of edge components and screw components of b₁ (b₂), respectively.

Adding Eqs. (1) to (2), we have:

$$F_{\text{l}} =0.$$

(8)

This indicates that the partial dislocations are in balance, without any tendency of motion. Correspondingly, their separation d can be easily obtained by subtracting Eq. (1) from (2):

$$d = \frac{D}{\pi }\arctan \left[ {{{w_{i} } \mathord{\left/ {\vphantom {{w_{i} } {\left( {D\gamma_{0} } \right)}}} \right. \kern-0pt} {\left( {D\gamma_{0} } \right)}}} \right].$$

(9)

When analyzing the forces at any pair of partial dislocations b₁ and b₂ in Fig. 1, it is convenient to propose an effective SFE γ_e equivalent to the total attractive force during the dissociation of the dislocation b, in balance with F_r in Eqs. (1) and (2), that is:

$$\gamma_{\text{e}} = F_{\text{r}} = \frac{{w_{\text{i}} }}{\pi d}.$$

(10)

Equation (10) indicates that the effective SFE γ _e , rather than the intrinsic SFE γ₀, is inversely proportional to the SF width d in dislocation arrays. This is often neglected in the previous studies [11, 20], as discussed later. γ_e can be calculated straightforwardly by Eq. (10) when d is known. This will be utilized to measure γ_e in the following atomistic simulations. However, it is worth noting that the calculated γ_e strongly depends on the w_i parameter, which varies from the isotropic to anisotropic elasticity theories. In fact, as seen from Eqs. (9) and (10), the effective SFE γ_e in dislocation arrays can also be calculated when D is given:

$$\gamma_{\text{e}} = \frac{{{{w_{\text{i}} } \mathord{\left/ {\vphantom {{w_{\text{i}} } D}} \right. \kern-0pt} D}}}{{\arctan \left[ {{{w_{\text{i}} } \mathord{\left/ {\vphantom {{w_{\text{i}} } {\left( {D\gamma_{0} } \right)}}} \right. \kern-0pt} {\left( {D\gamma_{0} } \right)}}} \right]}}.$$

(11)

When D approaches infinity, Eq. (11) becomes the same as Eq. (10–15) in Chapter 10 in Ref. [1] for an isolated dislocation. At this point, γ_e is equal to γ₀. It is clearly seen from Eq. (11) that dislocations in arrays cannot be simply treated as isolated dislocations because of the dependence of γ_e on D, as presented in the following simulations.

3 Simulation Methods

The atomistic modeling techniques have been previously described in details in Refs. [21, 22], but its main features are presented here for clarity. The coordinate system of the simulation box contains three axes, x||$\left[ {1\overline{1} 0} \right]$, y||$\left[ {11\overline{2} } \right]$ and z||$\left[ {111} \right]$, which are the same as that given in Fig. 1. And then a dislocation with Burgers vector $\varvec{b} = {{\left[ {1\overline{1} 0} \right]} \mathord{\left/ {\vphantom {{\left[ {1\overline{1} 0} \right]} 2}} \right. \kern-0pt} 2}$ is created in the center of the simulation box with dimensions L _x , L _y and L _z . Periodic boundary conditions are applied along the x and y directions, which can generate the straight dislocation array as displayed in Fig. 1. It is obvious that D = L _x for θ = 90° (an edge dislocation array), and D = L _y for θ = 0° (a screw dislocation array). The relaxation is thought to be completed when the force on each atom falls below 10⁻⁶ eV Å⁻¹.In this work, a large L _z is chosen to exclude the influence of the free boundary condition along z. γ₀ is calculated as Vitek did [23]. And two embedded-atom-method (EAM) potentials are selected for Cu [24] and Ag [25], respectively. Table 1 lists some parameters that are calculated with these potentials.

Table 1 Material properties of the simulated Cu and Ag, and a TWIP steel. See the text for parameters

In atomistic modeling, it is crucial to localize dislocation cores because γ_e is calculated from the core separation d, as seen from Eq. (10). Differential displacements represent the displacement difference between two neighbor atoms relative to the reference lattice along the Burgers vector [26]. It is a powerful tool to reveal dislocation cores at atomic-scale resolution and then accurately determine d (as indicated by d_DD in Fig. 2). Unfortunately, it cannot run automatically. In contrast, the γ-parameter on the basis of the Nye tensor [27, 28] also has high resolution, while it can be easily implemented in the simulation code. This method gives a smaller SF width (d _γ ), as indicated in Fig. 2, than the differential displacement method, but they could become identical when the γ-parameter approach is coupled with the excess energy analysis (our criteria are: (1) the excess energy > 0.058 eV and (2) the γ-parameter > 0.015 $b_{\text{p}}^{ - 2}$).

Fig. 2

Partial dislocations after dissociation of a screw dislocation array with θ = 0° in Ag. Both the differential displacements (arrows) and the γ-parameter distribution (color map) are superimposed on $\left( {1\overline{1} 0} \right)$, where atoms are displayed with circles. The triads of arrows with a closed loop identify the position of the two partials, while the local extrema of the γ-parameter locate these core positions. The separations revealed by these two methods are indicated by d_DD and d_γ, respectively

4 Results and Discussion

A series of D are selected to measure the corresponding d in Cu and Ag. Then, the simulation results for edge dislocation arrays are compared with the predictions of Eq. (11) (θ = 90°) as shown in Fig. 3. It is obvious that they agree with each other for both Cu and Ag. In addition, as mentioned above, when D approaches infinity γ_e becomes a constant γ₀ in Fig. 3. It is seen from Fig. 3 that the smaller γ₀, the larger the variation of γ_e with D will be. When D decreases from 73 to 5 nm (the corresponding dislocation density ρ, about equal to 1/D², increases from 1.7 × 10¹⁴/m² to 3.6 × 10¹⁶/m²), γ_e varies from 47 to 89 mJ/m² for Cu, and from 20 to 54 mJ/m² for Ag. Interestingly, it is noticed that the experimentally measured SFE changes from 41 to 85 mJ/m² for Cu and from 16 to 32 mJ/m² for Ag as reviewed by Reed and Schramm [29] (here only the TEM data are considered because of their relatively high accuracy), which are consistent with our simulation results. Therefore, the dislocation configurations could probably cause the dispersion of the experimental data about γ_e. This needs further experimental inspections.

Fig. 3

Variation of γ_e with D for edge dislocation arrays in Cu and Ag. Squares (solid line) and circles (dashed line) denote the simulation data (the prediction from Eq. (11) with w_i) in Cu and Ag, respectively

Since the $\gamma_{\text{e}} - D$ relation described by Eq. (11) changes with dislocation characters (θ) and other variables (G, b_p and v), it is convenient to utilize its scaled form:

$$\frac{{\gamma_{\text{e}} }}{{\gamma_{0} }} = \frac{\eta }{\arctan \left( \eta \right)},$$

(12)

where $\eta = {{w_{\text{i}} } \mathord{\left/ {\vphantom {{w_{\text{i}} } {\left( {D\gamma_{0} } \right)}}} \right. \kern-0pt} {\left( {D\gamma_{0} } \right)}}.$ The curve predicted by Eq. (12) is shown in Fig. 4, from which it is seen that the characteristic value γ_e for any dislocation array is much different from γ₀. The simulation data for edge dislocation arrays in Fig. 3 are scaled and superimposed in Fig. 4. As expected, Eq. (12) gives a precise prediction of the variation of the simulation data. In contrast, the difference is somewhat large for screw dislocation arrays in Fig. 4. This could be attributed to the isotropic elasticity approximation. When the anisotropic elasticity is considered, the $\gamma_{\text{e}} - D$ relation can also be described by Eqs. (10), (11) and (12), but w_i has to be replaced by $w_{\text{a}} = {{\left( {3K_{\text{s}} - K_{\text{e}} } \right)b_{\text{p}}^{ 2} } \mathord{\left/ {\vphantom {{\left( {3K_{\text{s}} - K_{\text{e}} } \right)b_{\text{p}}^{ 2} } 8}} \right. \kern-0pt} 8}$, where K_s and K_e can be calculated according to Ref. [1], as listed in Table 1. In this case, the curve for Eq. (12) remains unchanged in Fig. 4. In contrast, the γ_e values derived from Eq. (10) will change for the measured d in simulations when w _i is replaced with w_a. As seen from Fig. 4, for screw dislocation arrays, the anisotropic parameter w_a provides a better estimation of γ_e than w_i by comparison with the curve from Eq. (12).

Fig. 4

Variation of the scaled effective SFE γ_e/γ₀ with η. Squares and circles denote the simulation results in Fig. 3. Diamonds and upper triangles represent the simulation results of screw dislocation arrays for Ag based on isotropic and anisotropic theory, respectively. Down triangles are the experimental results for a TWIP steel

The experimentally measured γ_e changing with η for TWIP steels [13] can be calculated (here we assume $D = {1 \mathord{\left/ {\vphantom {1 {\sqrt \rho }}} \right. \kern-0pt} {\sqrt \rho }}$) and superimposed in Fig. 4. It is apparent that Eq. (12) can capture the trend of the γ_e-η variation for TWIP steels. The deviation between them could be partially attributed to that the dislocation density cannot account for the local dislocation configurations, as mentioned above. Therefore, besides dislocation density [13], the local dislocation configurations should also be characterized to determine the onset of deformation twinning in TWIP steels [12, 13]. However, there are few experimental results in previous studies for comparison with our formulae, and thus, further systematic experimental observations are needed.

As we discussed above, it is worth emphasizing that the effective SFE γ_e dominates the SF size rather than γ₀ for dislocation arrays. However, this point has not received much attention in earlier work. For example, since γ₀ decreases sharply with the increase in Al content in Cu–Al alloys, it is generally thought that it becomes difficult to operate cross-slip [2, 11]. This is not the case, however, at least for dislocation arrays. Instead, these arrays could enhance γ_e rapidly and then facilitate cross-slip. In Cu–Al alloys, Li et al. recently proposed a unified factor $(\alpha = {{48\pi \gamma_{0} y_{\text{s}} } \mathord{\left/ {\vphantom {{48\pi \gamma_{0} y_{\text{s}} } {(3Gb^{2} }}} \right. \kern-0pt} {(3Gb^{2} }})$, where y_s denotes the annihilation distance, while the other parameters are the same as defined in this work) that is proportional to γ₀ to evaluate the dislocation evolution in fatigue. However, γ₀ should be revised by γ_e because dislocation arrays are assumed to be the dominant microstructure in their theory. Besides, the simulations of Chassagne et al. [20] indicated that screw dislocations could cross-slip or cross over twin boundary. This could be quantified by the critical applied shear stress which depends on γ₀ for an isolated dislocation. However, it is seen from their experimental observations (Fig. 8 in Ref. [20]) that screw dislocations are usually grouped into arrays. Therefore, it is reasonable to choose γ _e rather than γ₀ in Eq. (4) in Ref. [20] when correlating their criterion with experimental results.

5 Conclusion

In summary, the effective SFE for dislocation arrays is quantitatively analyzed within the framework of the elasticity theory of dislocations, and its general formula is verified by atomistic simulations. It is found that the effective SFE of dislocation arrays is much different from that of isolated dislocations, and thus it has to be considered when analyzing cross-slip and pile-ups of dislocations. In more general case, dislocation configurations (arrays) could dominate many dislocation behaviors in fcc alloys and this can be the subject of future work.