1 Introduction

20Cr–24Ni–6Mo super-austenitic stainless steel (SASS), which possesses excellent corrosion and stress-corrosion resistance and elevated-temperature strength than those of types 304L and 316L stainless steels, has been considered as potential materials used for reactor core components [1, 2]. However, because it contains high content of alloying elements (> 50%), it possesses high deformation resistance and poor thermal conductivity, which results in severe difficulties in hot working. In particular, adiabatic heating due to poor thermal conductivity during deformation can greatly alter the behavior of dynamic recovery (DRV) and dynamic recrystallization (DRX), leading to more difficult control of the hot working processes. Therefore, precise understanding of microstructural evolution and flow behavior can be of significance for the optimization of hot working processes.

So far, some investigations about deformation behavior and the microstructure of this kind of alloy have been carried out. Nemat-Nasser et al. [3] investigated the hot deformation mechanisms of this alloy at temperatures from 77 to 1000 K over the strain rates from 0.001 to 8000 s−1. They found that this alloy could display good ductility at low temperatures and high strain rates; however, adiabatic shear bands were developed when strains exceeded about 0.4 at high strain rates and at the temperature of 77 K. They also found that its microstructure was more sensitive to the changes of temperatures than strain rates. Under the same experimental conditions, Abed and Voyiadjis [4] developed a plastic flow model for both isothermal and adiabatic plastic deformation by using the concept of thermal activation energy along with the dislocation interactions. The results showed that both thermal and a thermal flow stresses were plastic strain dependent, the microstructural evolution mainly altered by thermal history, and the dynamic strain aging at certain temperatures was strain rate dependent. Serrated flow behavior was investigated at temperatures from 773 to 973 K at strain rates from 3.3 × 10−3 to 3.3 × 10−3 s−1. The regime of dynamic strain aging reflected by the serrated flow curves was discussed in detail, and the critical strains were determined [5]. Most of works about deformation behavior and microstructure of this alloy were focused on relatively low temperatures (≤ 1000 K). Therefore, hot deformation behavior and microstructure of this alloy at elevated temperatures (≥ 1223 K) and different strain rates deserve to be systematically studied.

In industrial manufacturing, hot working plays a crucial role in controlling the shape, microstructure, and mechanical properties, in which the material shows complex metallurgical phenomena such as work hardening, flow instability, DRV, and DRX [6]. The effects of these metallurgical phenomena are often reflected in the flow curves. The flow stress is important not only for optimizing its final microstructure and mechanical properties but also for numerical simulation. However, the accuracy of the flow curves obtained from the hot compression tests is degraded by the deformation heating due to poor thermal conductivity and the friction between the specimens and dies [7]. During hot deformation, a significant proportion of the plastic work is converted into heat when the specimen is subjected to large plastic deformation [8]. When the deformation heat cannot be dissipated into the surrounding environment timely, the deformation temperature in the specimen would increase, which is called adiabatic heating, and result in flow softening of the material. In particular, adiabatic heating is significant for the studied alloy due to its poor thermal conductivity. In this case, the hot deformation is under non-isothermal condition, and the obtained flow stress is lower than the actual flow stress for the desired test temperature under isothermal condition [9]. However, the parameters used to establish the constitutive equation were obtained from the experimental flow curves. This would lead to some errors in the determination of constitutive equations to predict the flow behavior under isothermal condition. Hence, the adiabatic heating correction of the flow stress is needed for a reliable constitutive analysis [10]. Besides, interfacial friction between the specimen and die in compression tests cannot be eliminated by applying the appropriate lubricant. Therefore, the deformation becomes inhomogeneous and barreled-like shape specimens are formed and lead to the flow stress increases. Barreling coefficient B, developed by Roebuck et al. [11], could be used to evaluate whether the effect of friction in the compression was ignored. If the value of B was exceeded 1.1, friction corrected for the obtained data must be taken into account. In conclusion, the true stress–strain data directly obtained from hot compression tests are not suitable for immediate constitutive analysis unless the adiabatic heating and frictional effects are considered.

In the present work, the flow behavior and microstructure evolution of 20Cr–24Ni–6Mo SASS at elevated temperatures (950–1150 °C) and different strain rates (0.01–10 s−1) were analyzed and discussed by considering the effect of adiabatic heating. Strain-dependent constitutive modeling to predict flow behavior of the studied alloy was established based on the modified flow stress. Detailed correction procedures of adiabatic heating and frictional effect were discussed and presented. Also, a comparison was made between the experimental data and the predicted data to verify the accuracy of the established constitutive modeling.

2 Experimental

Table 1 shows the chemical composition of 20Cr–24Ni–6Mo SASS used in this work. The cylindrical specimens with 8 mm in diameter and 15 mm in height were prepared from hot-rolled plates.

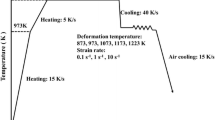
Table 1 Chemical composition of investigated alloy (wt%)
Full size table

Figure 1 shows the single-phase austenitic microstructure with some annealing twins in the starting material. A Gleeble-3500 thermal–mechanical simulator was utilized to perform the hot compression tests at constant strain rates. Specimens were reheated to 1200 °C at a heating rate of 10 °C s−1, held for 5 min, and cooled down to deformation temperatures at the rate of 10 °C s−1, in which complete solid solution could have been obtained. After soaking for 20 s at the deformation temperature, continuous hot compression with the reduction of 46% was carried out at strain rates of 0.01, 0.1, 1, and 10 s−1 in the temperature range from 950 to 1150 °C (at intervals of 50 °C). After hot compression, the specimens were water quenched within 1 s in order to preserve the high-temperature microstructures. In an effort to minimize the effect of friction between the specimens and dies during hot compression, the specimens ends were coated with graphite powders and Ta foil.

Fig. 1
figure 1

Initial microstructure of 20Cr–24Ni–6Mo SASS steel

Full size image

The water-quenched specimens were cut along the longitudinal direction for microstructure observations. The metallographic specimens were prepared using standard mechanical grinding and polishing, followed by electrolytic etching with a solution containing 60% nitric acid and 40% water at 6 V direct current for 40–50 s to reveal the deformed microstructure.

3 Results and Discussion

3.1 Flow Curves

Figure 2 shows the flow curves obtained at different deformation conditions. It is well known that work hardening makes the flow stress increase, while work softening from DRV and DRX makes the flow stress decrease. When work-hardening mechanism plays a leading role in the deformation process, flow stress is characterized by a rising trend with increasing strain. When DRV mechanism plays a dominant role in the deformation process, flow stress is characterized by a rising trend at early stage of deformation and then followed by a steady state. Moreover, when DRX plays a leading role in the deformation process, flow stress increases to a peak value and then gradually decreases to a steady value; at this point, full DRX microstructure could be obtained. In Fig. 2a, all flow curves exhibit a distinct peak followed by a decrease to a steady state in flow stress with increasing strain except at 950 °C, indicating DRX behavior was completed when the deformation temperature is higher than 950 °C. In Fig. 2b–d, flow curves obtained from these deformation conditions exhibit the similar characteristics. The flow stress slowly increases to peak value and followed by inconspicuous declining trend, indicating the main softening mechanism was DRV, and DRX maybe a little or not yet happened. In these flow curves, peak stress platform was broadened, which implies that the recrystallization was sluggish during hot deformation [12]. In terms of the whole deformation process, at the early stage of deformation, dislocation density and the interaction effect between dislocations increase with the increase of strain, leading to the increase of deformation resistance. With the increase of deformation, the degree of dislocation recovery increases gradually and then work softening is almost equal to work hardening. After peak stress, the dynamic restoration, i.e., DRV and DRX, becomes predominant due to the decline of dislocation density and the increase of DRX. From Fig. 2, it is also observed that the effects of deformation temperature and strain rate were momentous to deformation behavior. The flow stress increases with the increase of strain rate and the decrease of deformation temperature. The peak stress and corresponding strain decline with the decrease of strain rate and the increase of deformation temperature, indicate that pronounced work hardening can easily occur at lower strain rates and higher temperatures [13]. Higher temperature could provide lager driving force for the dynamic restoration and thus accelerate the grain boundary migration and dislocation movement. Lower strain rate could supply enough time for the nucleation and growth of new DRX grains and dislocation annihilation.

Fig. 2
figure 2

Experimental flow curves under different deformation temperatures with strain rates: a 0.01 s−1; b 0.1 s−1; c 1 s−1; d 10 s−1

Full size image

3.2 Microstructure Evolution During Hot Deformation

Figure 3 shows the microstructure evolution of the deformed specimens after compressed to 0.6 at 950 °C. It can be seen that original equiaxed grains were elongated, and initial grain boundaries and twin boundaries were somewhat distorted. Serrated and bulgy grain boundaries were developed and evolved into new DRX grains along these prior grain boundaries at 0.01 s−1, as shown in Fig. 3a. When the strain rate is up to 0.1 s−1, very few DRX grains could be observed at grain boundary. This is because higher strain rate provides shorter time for the recovery of dislocation and the nucleation of DRX. However, when the strain rate is up to 10 s−1, more DRX grains were observed than that at 0.1 s−1, which was inconsistent with the regular stated at 0.1 s−1.

Fig. 3
figure 3

Hot deformation micrographs of specimens under different strain rates at 950 °C: a 0.01 s−1; b 0.1 s−1; c 10 s−1

Full size image

Figure 4 shows the microstructure evolution of the deformed specimens after compressed to 0.6 at 1050 and 1150 °C. At the deformation temperature 1050 °C, DRX behavior was not finished at lower strain rate 0.01 s−1, but was almost completed at higher strain rate 10 s−1. At the deformation temperature 1150 °C, DRX behavior has been finished no matter at lower strain rate or at higher rate, indicating DRX behavior was not sensitive to strain rate when the specimen deformed at 1150 °C. Moreover, it can be found that the flow behaviors reflected by the actual microstructural evolution and the flow curve were different. For example, the flow curve at 1050 °C and 10 s−1 showed no steady state after peak value, indicating DRX happened but was not finished. However, the microstructure exhibited almost full recrystallization has been obtained at this deformation condition.

Fig. 4
figure 4

Hot deformation micrographs of specimens: a 1050 °C, 0.01 s−1; b 1050 °C, 10 s−1; c 1150 °C, 0.01 s−1; d 1150 °C, 10 s−1

Full size image

In general, the DRX process is more likely to be found at lower strain rates rather than at higher strain rates. However, microstructure evolution of this alloy was not conformed to the conventional regular. Similar result was also found in Ref. [14]. Main reasons can be divided into two categories. The first class is that higher strain rate can result in higher driving force for the grain nucleation during DRX, and the shorter deformation time can retain more deformation heating. Both of them are beneficial to the dynamic restoration [15]. The second class is that higher strain rate cannot provide enough time for the adiabatic heating dissipation into the surrounding environment timely which cause the deformation temperature to increase and accelerate the DRX process.

3.3 Adiabatic Heating and Friction Effects on Flow Curves

It is noted that adiabatic heating and friction effects on the flow stress are simultaneous during hot deformation. While performing the correction of adiabatic heating and friction effects, the correction order should be considered. However, it is indicated that the influence of the correction order (first adiabatic heating then friction, or first friction then adiabatic heating) on the flow stress was very slight and therefore the correction order can be neglected [8]. In this work, the correction order of adiabatic heating first and then friction was adopted.

3.3.1 Adiabatic Heating

For the alloys with poor thermal conductivity, adiabatic temperature rise cannot be easily removed from the specimen during hot deformation even though the specimen always exchanges energy with the surrounding environment. The actual temperature of the specimen can be calculated as follows [4, 9]:

$$\left\{ {\begin{array}{*{20}l} {T = T_{0} + \Delta T} \hfill \\ {\Delta T = \frac{\eta }{{\rho C_{\text{p}} }}\int_{0}^{\varepsilon } {\sigma {\text{d}}\varepsilon } } \hfill \\ \end{array} } \right.,$$
(1)

where T 0 is the initial temperature, ρ is the material density, C p is the specific heat, σ is the flow stress, ε is the strain, and η is the Taylor–Quinney factor being calculated as follows:

$$\eta = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad \dot{\varepsilon } \le 10^{ - 3} {\text{ s}}^{ - 1} } \hfill \\ {(0.316)\lg \dot{\varepsilon } + 0.95} \hfill & {\quad 10^{ - 3} {\text{ s}}^{ - 1} < \dot{\varepsilon } < 1. 0 {\text{ s}}^{ - 1} } \hfill \\ {0.95} \hfill & {\quad \dot{\varepsilon } \ge 1. 0 {\text{ s}}^{ - 1} } \hfill \\ \end{array} } \right.,$$
(2)

where \(\dot{\varepsilon }\) is strain rate. For the experimental steel, ρ is 8.06 g cm−3 and the values of C p under different temperatures are listed in Table 2.

Table 2 Values of specific heat of 20Cr–24Ni–6Mo SASS
Full size table

In order to research ΔT during whole deformation process, several representative strains in the range of 0.1–0.6 with an interval 0.05 were employed to calculate values of ΔT via Eq. (1) which can be solved numerically or can be integrated without introducing any noticeable errors by either using the mean value theorem or the simple Euler method [4].

Figure 5 shows the relationship between ΔT and ε after hot compression at the strain rate of 10 and 0.01 s−1 in the temperature range from 950 to 1150 °C. It can be seen that there existed an almost linear relationship between ΔT and ε at a given strain rate and deformation temperature. It can also be seen that ΔT increased with decreasing temperature and increasing strain rate and strain, with the largest ΔT being more than 47 at 950 °C with the strain rate of 10 s−1.

Fig. 5
figure 5

Variation of temperature rise with strain for specimens deformed at strain rates of a 10 s−1; b 0.01 s−1

Full size image

The adiabatic heating leads the hot deformation to be non-isothermal instead of being isothermal. The isothermal flow stress σ iso can be determined by using the following relationship [16]:

$$\sigma_{\text{iso}} (\varepsilon ,\dot{\varepsilon },T) = \sigma_{0} (\varepsilon ,\dot{\varepsilon },T) - \left. {\frac{{\partial \sigma_{0} (T)}}{\partial T}} \right|_{{\varepsilon ,\dot{\varepsilon }}} \Delta T,$$
(3)

where σ 0 is the flow stress without the correction of adiabatic heating. By using the method described above, isothermal flow stress can be obtained.

For a given strain, strain rate and initial temperature T 0, the uncorrected flow stress for adiabatic conditions can be expressed as a function of the isothermal flow stress:

$$\sigma_{0} (\varepsilon ,\dot{\varepsilon },T_{0} ) = \sigma_{\text{iso}} (\varepsilon ,\dot{\varepsilon },T_{0} + \Delta T).$$
(4)

Applying a first-order Taylor expansion of the σ iso in Eq. (3) about the point T 0, a new function can be obtained:

$$\sigma_{\text{iso}} (\varepsilon ,\dot{\varepsilon },T_{0} ) = \sigma_{0} (\varepsilon ,\dot{\varepsilon },T_{0} ) - \left. {\frac{{\partial \sigma_{\text{iso}} (T_{0} )}}{{\partial T_{0} }}} \right|_{{\varepsilon ,\dot{\varepsilon }}} \Delta T,$$
(5)

where \(\partial \sigma_{\text{iso}} (T_{0} )/\left. {\partial T_{0} } \right|_{{\varepsilon ,\dot{\varepsilon }}}\) is the rate of the flow softening due to adiabatic heating at T 0.

To acquire the isothermal flow stress, data of σ 0 at different T 0 and T i , where T i  = T 0 + ΔT, are plotted in Fig. 6 according to Eq. (5). Figure 6a shows the linear relationship between temperature and true stress, σ iso is linear decreasing with the T 0 increasing, and it can be acquired easily based on Eq. (5). Figure 6b shows that the relationship between the temperature and true stress did not obey a linear trend in some circumstances. In this case, linear processing is not suitable for the determination of σ iso, because some errors may be introduced. Hence, polynomial fitting method was used to process data, and by repeating the same procedures as described above, σ iso at any strain rate, strain and temperature can be obtained.

Fig. 6
figure 6

Schematic diagrams of processing methods for adiabatic heating correction: a linear relationship; b nonlinear relationship between temperature and true stress

Full size image

Figure 7 shows the comparison of the original experimental flow curves and the adiabatic heating corrected flow curves. It is observed that the difference between the two groups of curves was more significant at higher strain levels and lower deformation temperatures. This can be attributed to the fact that more deformation heat was accumulated with increasing strain level, consequently causing greater thermal softening during deformation. At lower temperature, it is more difficult to deform the material and thus more plastic work is converted into heat. In addition, the difference is more pronounced at higher strain rate. This is because more deformation heat was generated in unit time, and the time for deformation heat to dissipate was reduced at higher strain rate. Therefore, the difference was increased with the increase of strain rate.

Fig. 7
figure 7

Comparison of original experimental flow curves and adiabatic heating corrected flow curves at strain rates of a 10 s−1; b 0.01 s−1

Full size image

3.3.2 Friction Corrected

Figure 8 shows the typical appearances of the specimen after deformation, and it can be seen that barreled-like shape formed and the terminal size of the specimens after deformation are of inconformity, proving that frictional effect existed and was not the same for each specimen.

Fig. 8
figure 8

Typical appearance of the specimens after deformation

Full size image

As discussed in introduction, the value of barreling coefficient B is defined as:

$$B = h_{\text{f}} d_{\text{f}}^{2} /(h_{0} d_{0}^{2} ),$$
(6)

where h 0 and d 0 are the initial height and diameter of the specimen, respectively; h f is the final height, and d f is the diameter measured at the mid-length of the specimen after deformed. In this work, all values of B are presented in Table 3.

Table 3 Values of barreling coefficient B of investigated specimens
Full size table

It can be seen that all values of B were exceeded 1.1; hence, the correction of friction for the obtained data should be taken into account. A classical equation to correct the effect of friction has been used as follows [7]:

$$\bar{\sigma } = \frac{\sigma }{{1 + (2/3\sqrt 3 )m(r_{0} /h_{0} ){ \exp }(3\varepsilon /2)}},$$
(7)

where \(\bar{\sigma }\) is the friction corrected flow stress, r 0 is the initial radius, and m is the friction factor.

In Eq. (7), σ would be substituted by σ iso for further analysis. Determination of m is vital for the accuracy of corrected flow stress data. Based on the method developed by Ebrahimi and Najafizadeh [17], the friction factor can be calculated by the following equation:

$$m = \frac{{(R_{1} /h )b}}{(4 /\sqrt 3 ) - (2b / 3\sqrt 3 )},$$
(8)

where b is the barrel parameter, and R 1 and h are the average radius and height of specimen after deformation.

$$b = 4\frac{{(R_{\text{M}} /R_{\text{T}} )b}}{{R_{1} }} \cdot \frac{h}{{h_{0} - h}},$$
(9)
$$R_{1} = r_{0} (h_{0} /h)^{ 1 / 2} ,$$
(10)

where R M and R T are the maximum and top radius of the specimens after deformation. Figure 9 shows the true stress–strain curves corrected by adiabatic heating and friction. It is observed that the effect of friction was significant at test conditions, especially at higher strain rates. The effect of friction was enhanced with the increase of strain.

Fig. 9
figure 9

Comparison of adiabatic heating corrected and adiabatic heating and friction corrected flow curves at strain rates of a 10 s−1; b 0.01 s−1

Full size image

3.4 The Establishment of Constitutive Modeling

The relationship among flow stress, temperature, and strain rate can be expressed by the Arrhenius-type equation, especially at elevated temperatures. Zener–Hollomon parameter (Z-parameter) represents the combined effects of the temperature and strain rate on hot deformation behavior, which can be established through constitutive equations of hyperbolic sine function [18, 19]. These equations can be expressed by the following equations:

$$Z = \dot{\varepsilon }\exp (Q / (RT)) = f(\sigma ),$$
(11)
$$\dot{\varepsilon } = \left\{ {\begin{array}{*{20}l} {A\sigma^{{n_{1} }} \exp [ - Q/(RT)]} \hfill & {\quad \alpha \sigma < 0.8} \hfill \\ {A\exp (\beta \sigma )\exp [ - Q/(RT)]} \hfill & {\quad \alpha \sigma > 1.2} \hfill \\ {A[\sinh (\alpha \sigma )]^{n} \exp [ - Q/(RT)]} \hfill & {\quad {\text{for}}\,{\text{all}}\,\,\sigma } \hfill \\ \end{array} } \right.,$$
(12)

where Z is the Zener–Hollomon parameter, R is the universal gas constant (8.314 J mol−1 K−1), Q is the deformation activation energy for hot deformation, and A, n 1, n, α, and β are the material constants, α = β/n 1.

In Eq. (12), the power law description of flow stress is conventionally employed for relatively low stress, and the exponential law description is suitable for high stress, and the hyperbolic sine law can be used for a wide range of deformation conditions [20].

3.4.1 Determination of Material Constants

Material constants should be confirmed based on the flow curves before the constitutive equations are established. It is widely known that there exists a functional relationship between strain and material constant in the constitutive equations. Therefore, the material constants at various representative strains can be calculated to find suitable values for constitutive equations. As an example, the computational procedure of material constants at the strain 0.45 is illustrated below. The relationship between flow stress and strain rate is formulated as follows:

$$\left\{ {\begin{array}{*{20}l} {\dot{\varepsilon } = A\sigma^{{n_{1} }} \exp [ - Q/(RT)] = B_{1} \sigma^{{n_{1} }} } \hfill & {\alpha \sigma < 0.8} \hfill \\ {\dot{\varepsilon } = A\exp (\beta \sigma )\exp [ - Q/(RT)] = B^{\prime}\exp (\beta \sigma )} \hfill & {\alpha \sigma > 1.2} \hfill \\ \end{array} } \right.,$$
(13)

where B 1 and B′ are material constants, which are dependent on deformation temperatures.

By taking natural logarithm on Eq. (13), the following equations can be obtained:

$$\left\{ {\begin{array}{*{20}l} {\ln \sigma = \frac{1}{{n_{1} }}\ln \dot{\varepsilon } - \frac{1}{{n_{1} }}\ln B_{1} } \hfill \\ {\sigma = \frac{1}{\beta }\ln \dot{\varepsilon } - \frac{1}{\beta }\ln B^{{\prime }} } \hfill \\ \end{array} } \right.,$$
(14)

Then, substitute the values of flow stress and strain rate under the strain of 0.45 into Eq. (14). By using linear regression for the data points, the values of n 1 and β can be calculated from the reciprocal slope of lines in ln σ versus \(\ln \dot{\varepsilon }\) and σ versus \(\ln \dot{\varepsilon }\) plots in Fig. 10a, b, respectively. The mean value of n 1 and β is calculated to be 7.5204 and 0.0322. The value of α = β/n 1 = 0.004283 can be obtained. Stress multiplier α is an additional adjustable constant which brings ασ into the correct range to make the constant T curves in \(\ln \dot{\varepsilon }\) versus ln[sinh(ασ)] plots linear and parallel [23].

Fig. 10
figure 10

Evaluation of values of a n 1 by plotting \(\ln \sigma\) versus \(\ln \dot{\varepsilon }\); b β by plotting \(\sigma\) versus \(\ln \dot{\varepsilon }\); c n by plotting \(\ln [\sinh (\alpha \sigma )]\) versus \(\ln \dot{\varepsilon }\); d Q by plotting \(\ln [\sinh (\alpha \sigma )]\) versus 10,000/T; e \(\ln A\) by plotting \(\ln Z\) versus \(\ln [\sinh (\alpha \sigma )]\) at strain of 0.45

Full size image

By taking partial differentiation on the equation for all the flow stress in Eq. (12), the deformation activation energy Q can be expressed as:

$$Q = 10,000R\left\{ {\frac{{\partial \ln \dot{\varepsilon }}}{\partial [\sinh (\alpha \sigma )]}} \right\}_{T} \left\{ {\frac{\partial \ln [\sinh (\alpha \sigma )]}{\partial (10,000/T)}} \right\}.$$
(15)

Substitute the values of strain rate, deformation temperature, and flow stress at the strain 0.45 into Eq. (15). By using linear regression for the data points, values of n and Q can be calculated from the reciprocal slope of lines in ln[sinh(ασ)] versus \(\ln \dot{\varepsilon }\) and ln[sinh(ασ)] versus 10,000/T plots in Fig. 10c, d, respectively. The mean values of n and Q are calculated to be 5.458 and 463.26 kJ mol−1.

Substituting the equation for all the flow stress in Eqs. (12) into (11) yields:

$$Z = A[\sinh (\alpha \sigma )]^{n} ,$$
(16)

Taking the natural logarithm on Eq. (16) gives:

$$\ln Z = \ln A + n\ln [\sinh (\alpha \sigma )],$$
(17)

Substituting the values of α, n, Q, and other deformation variables into Eq. (17), the plot of lnZ versus ln[sinh(ασ)] shown in Fig. 10e can be used to obtain the value of lnA, which was found to be 39.973. Employing the same procedures described above, the values of α, n, Q, and lnA at any strain level in the range of 0.1–0.6 with an interval of 0.05 can be obtained.

3.4.2 Compensation for Deformation Strain

Figure 11 shows the variations of α, n, Q, and lnA with true strain. Polynomial fitting was used, and eighth-order polynomial fitting represents a good fit for the effect of strain on material constants, as shown in Eq. (18). The corresponding polynomial coefficients are given in Table 4.

$$\left\{ {\begin{array}{*{20}l} {\alpha = C_{1} \varepsilon - C_{2} \varepsilon^{2} + C_{3} \varepsilon^{3} - C_{4} \varepsilon^{4} + C_{5} \varepsilon^{5} - C_{6} \varepsilon^{6} } \hfill \\ {n = D_{1} \varepsilon - D_{2} \varepsilon^{2} + D_{3} \varepsilon^{3} - D_{4} \varepsilon^{4} + D_{5} \varepsilon^{5} - D_{6} \varepsilon^{6} } \hfill \\ {Q = E_{1} \varepsilon - E_{2} \varepsilon^{2} + E_{3} \varepsilon^{3} - E_{4} \varepsilon^{4} + E_{5} \varepsilon^{5} - E_{6} \varepsilon^{6} } \hfill \\ {\ln A = F_{1} \varepsilon - F_{2} \varepsilon^{2} + F_{3} \varepsilon^{3} - F_{4} \varepsilon^{4} + F_{5} \varepsilon^{5} - F_{6} \varepsilon^{6} } \hfill \\ \end{array} } \right..$$
(18)
Fig. 11
figure 11

Relationships between a \(\alpha\); b \(n\); c \(Q\); d ln A and true strain \(\varepsilon\)

Full size image
Table 4 Polynomial coefficients of α, n, Q, and ln A for investigated alloy
Full size table

As can be seen in Fig. 11a, the value of α is in the range from 0.004075 to 0.004468 MPa−1. In most cases, 0.012 MPa−1 is a “traditional value” for SASSs. However, it has been suggested that α values are altered for different materials and deformation conditions [21,22,23]. In Fig. 11b, the value of n decreases with the increase of strain and reaches a steady state at the strain from 0.55 to 0.6, reflecting that better workability could be obtained at relatively high strain. It is also noted that as α increases, n decreases in the literature [24]. The activation energy Q exhibits a similar trend with that of n. The value of Q varies in the range from 463 to 598 kJ mol−1. These values are bigger than that for self-diffusion in γ-iron, which is about 280 kJ mol−1, indicating that the deformation mechanism is dominated by the DRX instead of diffusion or DRV [13]. As compared to other austenitic stainless steels, 304 is 400 kJ mol−1, 316L is 414 kJ mol−1, 904L is 463 kJ mol−1, Sanicro 28 is 495–660 kJ mol−1, and SMO 254 is 577 kJ mol−1 [13, 20,21,22]. It is noted that the Q value for 20Cr–24Ni–6Mo is close to those of Sanicro 28 and SMO 254 and higher than others, indicating that the deformation for this alloy is rather difficult. The truth should be clarified that there exists some deviation in the deformation activation energy because of the nature of the linear regression method applied to solve the Q value.

According to Eq. (16), the constitutive modeling that relates the flow stress to the Z-parameter is expressed as:

$$\sigma = \frac{1}{\alpha }\left[ {\sinh^{ - 1} \left( {\frac{Z}{A}} \right)^{1/n} } \right].$$
(19)

Based on the definition of the inverse hyperbolic sine function, equivalent equation can be expressed as:

$$\sigma = \frac{1}{\alpha }\ln \left\{ {\left( {\frac{Z}{A}} \right)^{1/n} + \left[ {\left( {\frac{Z}{A}} \right)^{2/n} + 1} \right]^{1/2} } \right\}.$$
(20)

3.4.3 Verification of the Developed Constitutive Modeling

In order to evaluate the accuracy of the established constitutive modeling, Fig. 12 shows the comparison among experimental data, modified data, and predicted data. It is clearly seen that the predicted data are in good agreement with the experimental data at some certain deformation conditions; however, the predicted data are matched well with modified data at all deformation conditions except at 950 °C and 0.01 s−1 in Fig. 12a.

Fig. 12
figure 12

Comparison between modified data and predicted data at strain rates of a 0.01 s−1; b 0.1 s−1; c 1 s−1; d 10 s−1

Full size image

3.4.4 Analysis of Deviation at 950 °C and 0.01 s−1 of the Developed Constitutive Modeling

In Fig. 12a, it can be seen that the predicted data at 950 °C and 0.01 s−1 are lower than the modified data when the true strain is in the range from 0.1 to 0.45. Moreover, the difference gradually narrowed with the increase of strain level. The specific reasons for the worst agreement should be discussed. Figure 13 shows the magnifying microstructures of the specimens compressed to 0.6 at 950 °C at different strain rates. Discrete precipitates along grain boundary were detected only at 0.01 s−1. Transmission electronic microscopy (TEM) was used to analyze the composition and the structure of these precipitates, as shown in Fig. 13d–f. EDX result showed that these precipitates were rich in Cr and Mo. Combined with selected area electronic diffraction (SAED) result, there precipitates were identified as σ phase with a bct structure. It is noted that long time exposure of austenitic stainless steels to elevated temperatures may cause decomposition of the austenite matrix to result in the formation of various types of intermetallic compounds [25]. When the deformation temperature is in a sensitive range for the intermetallic compounds and the deformation time is relatively long, plenty of precipitates would be generated and change the deformation behavior. For instance, fine precipitates generated in the initial deformation stage could impede the movement of the grain boundaries and cause the deformation resistance to radically increase. In addition, fine precipitates would inhibit the recovery and recrystallization of the deformed structure. With the increment of deformation, fine precipitates were coarsened and the effect of inhibition to the movement of grain boundaries was weakened so that the corresponding increment of flow stress caused by precipitates was reduced. Moreover, adiabatic heating was accumulated with the increase of strain level and dislocation mobility was enhanced, causing the increment of flow stress reduced. Some studies suggested that the actual deformation strain rates were inconformity to the desired strain rates during hot deformation process and the modified method of strain rates compensation was adopted and satisfied results were obtained [26]. In addition, the calculation of material constants by using polynomial fitting method also has a certain impact on the results.

Fig. 13
figure 13

SEM microstructures of specimens deformed at 950 °C with strain rates of a 0.01 s−1; b 0.1 s−1; c 10 s−1; d precipitate morphology by TEM at 950 °C, 0.01 s−1, and corresponding results of e EDX, f SAED (GB grain boundary)

Full size image

4 Conclusions

  1. 1.

    Flow behavior exhibited from the flow curve was inconformity with the actual microstructure evolution because of the existence of adiabatic heating and friction, especially at higher strain, higher strain rate, and lower temperature. The adiabatic heating during hot deformation results in the transition from isothermal deformation to non-isothermal deformation.

  2. 2.

    DRX behavior was changed with the change of deformation conditions. DRX behavior was completed at any strain rate when the specimen deformed at 1150 °C, indicating that DRX behavior was more sensitive to deformation temperature than strain rate at 1150 °C.

  3. 3.

    When the specimen deformed at 1050 °C, incomplete DRX was found at the lowest strain rate 0.01 s−1, and full DRX was completed at the highest strain rate 10 s−1. This is because adiabatic heating was more pronounced at higher strain rate at 1050 °C.

  4. 4.

    When the specimen deformed at 950 °C and 0.01 s−1, plenty of σ phases were observed and those precipitates inhibited the DRX behavior.

  5. 5.

    The activation energy of this alloy in hot deformation at different strains was in the range from 463 to 598 kJ mol−1. The result indicates that the deformation of the studied alloy was more difficult than other common austenitic stainless steels.

  6. 6.

    Constitutive equations based on the modified flow curves were established to predict flow behavior well at the all deformation conditions except at 950 °C in 0.01 s−1. The main reason is the large amount of precipitations generated during hot deformation, causing the dramatic increase of deformation resistance.