1 Introduction

Titanium alloy developments were instrumental in the advancement of gas turbine technology over the latter half of the twentieth century [1]. Compared to the steels, titanium alloys have the superior strength-to-weight ratio, high operating temperatures, and corrosion resistance [2]. However, since 1972, engineers have confronted to the so-called cold dwell effect of titanium alloys, which refers to the reduction of the number of cycles to failure for dwell periods at maximum stress during stress-controlled cyclic loading at room temperature [3].

In the past four decades, significant efforts and progresses have been made to study dwell-fatigue and pure fatigue behavior of titanium alloys to find out how the material responds to dwell time. The prior research on titanium alloys attributes dwell sensitivity to many deleterious mechanisms. These mechanisms involved many factors, such as time-dependent strain accumulation [4–6], microstructure and micro-texture influences [1, 7–9], stress ratio effects [10, 11], internal hydrogen content [12, 13] and environmental effects [14, 15], crystallographic orientation dependence [5, 16], interactions between creep and fatigue [17]. However, there is no consensus on the basic cause of the dwell-fatigue sensitivity of titanium alloys. Up to now, the problem remains open both from scientific and engineering points of view.

Most of researchers have found that the dwell-fatigue lives with the dwell period at peak stress for titanium alloys were clearly reduced. For the titanium alloy IMI834, the dwell-fatigue lives were shorter with the increase of periods especially under the high stress level [10]. As reported in Ref. [19], the dwell-fatigue growth rates of the titanium alloy Ti-6Al-4V are clearly increased with the increase of the dwell periods, and the different microstructures had different sensitivity to the dwell periods. Also, there was a work [7] focused on the pure fatigue and dwell-fatigue crack growth rates of the titanium alloy Ti-6242. It was found that the long crack growth is similar for both dwell-fatigue and pure fatigue, and the dwell-fatigue crack growth rates are shown to be much greater than the pure fatigue in the short crack growth regime. It is concluded that the differences in the short regime are attributed to possible creep effects that give rise to a mean stress effect in the case of dwell-fatigue. From the tests of the pure fatigue and dwell-fatigue crack growth rate for β-forged Ti-6242, it was observed that the crack initiation results from coalescence of shear-induced cavities nucleated at α/β interfaces in large colonies of α laths nearly parallel to the loading axis. The introduction of dwell periods at the peak stress will result in an increase in the crack growth rate in air as well as in vacuum [3, 20–23]. To probe the mechanism of the dwell-fatigue on IMI685, the tests with different hydrogen contents were employed [4, 5, 14, 18]. It was concluded that there is an increase in life with increasing hydrogen content, and hydrogen content influenced deformation characteristic in the high stress region but did not affect fracture behavior in the lower stress region.

Furthermore, from the viewpoint of engineering, improvement of the prediction equations should be developed to explain the phenomenon of the dwell effect on the fatigue crack growth rate and life estimation. Typically, the linear accumulation model is used to consider the common interaction of the fatigue and creep during dwell time. The dwell-fatigue problem is separated to cycles with a triangular wave form and a constant load (dwell load). If such a separation is possible, the crack growth rate can be calculated by the addition of two terms: the crack growth rate (da/dN)tiang of a test with a triangular wave form and the crack growth rate da/dt in a constant load test at the stress intensity factor K max, corresponding the maximum load and the hold time Δt. So Saxena [44] proposed a model to predict the creep-fatigue crack growth rate by the linear summation. This model was used to study creep-fatigue crack growth behavior of some high strength alloys [45, 46]. But the linear summation is a simplified crack growth evaluation method which has been applicable to some structural integrity assessment procedure but the reasonability of the equation form has not been sufficiently validated.

In this work, a modified model of cold dwell-fatigue crack growth rate are proposed based on the unified fatigue life prediction method which was reported in previous works [24–26]. The effect of the dwell time at the maximum stress and the effect of the maximum stress are included in the dwell-fatigue crack growth rate model. The modified model is used to predict the crack growth rates and lives of the pure fatigue and the dwell-fatigue for three near α titanium alloys (IMI834, IMI685, Ti-6242) and one α + β titanium alloy (Ti-6Al-4V) under constant-amplitude loading at room temperature. The effects of microstructure, dwell time, hydrogen content, stress ratio and different stress levels are analyzed for several titanium alloys. And the prediction results are compared with the experimental results to validate the model.

2 Methods of Analysis

2.1 General Constitutive Relation for Fatigue Crack Growth

Recently, a unified fatigue life prediction method (UFLP) was proposed by Cui and Huang [24] based on fatigue crack growth theory. The UFLP introduced an unstable fracture condition into the crack growth rate curve and defines a ‘virtual strength’ σ v to replace the yield stress in the McEvily model [27]. Later on, Wang et al. [26] proposed an extended model based on the research results of Li et al. [25] that the McEvily model with a fixed slope of 2 was not in good agreement with experimental results for some materials. In this extended model, the parameter m was adopted to represent the slope of the fatigue crack growth rate curve for different materials. The stress intensity factors at opening level ΔK op and K opmax were introduced in the McEvily model and were replaced by Newman’s function in the extended model. Then, the general constitutive relation in the improved crack growth rate model is given as follows:

$$ {{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}N}}} \right. \kern-0pt} {{\text{d}}N}} = {{A_{1} \left[ {K_{\hbox{max} } \left( {1 - R} \right) - \left( {1 - {\text{e}}^{\text{ka}} } \right)\left( {K_{\text{opmax}} - RK_{\hbox{max} } } \right) - \varDelta K_{\text{effth}} } \right]^{{m_{1} }} } \mathord{\left/ {\vphantom {{A_{1} \left[ {K_{\hbox{max} } \left( {1 - R} \right) - \left( {1 - {\text{e}}^{\text{ka}} } \right)\left( {K_{\text{opmax}} - RK_{\hbox{max} } } \right) - \varDelta K_{\text{effth}} } \right]^{{m_{1} }} } {\left[ {1 - \left( {{{K_{ \hbox{max} } } \mathord{\left/ {\vphantom {{K_{ \hbox{max} } } {K_{\text{c}} }}} \right. \kern-0pt} {K_{\text{c}} }}} \right)^{{n_{1} }} } \right]}}} \right. \kern-0pt} {\left[ {1 - \left( {{{K_{ \hbox{max} } } \mathord{\left/ {\vphantom {{K_{ \hbox{max} } } {K_{\text{c}} }}} \right. \kern-0pt} {K_{\text{c}} }}} \right)^{{n_{1} }} } \right]}}, $$
(1)

where

$$ K_{\hbox{max} } = \left\{ {\pi r_{\text{e}} \left[ {\sec \left( {{{\pi \sigma_{\hbox{max} } } \mathord{\left/ {\vphantom {{\pi \sigma_{\hbox{max} } } {2\sigma_{\text{V}} }}} \right. \kern-0pt} {2\sigma_{\text{V}} }}} \right) + 1} \right]} \right\}^{0.5} \left[ {1 + Y\left( a \right)\left( {{a \mathord{\left/ {\vphantom {a {2r_{\text{e}} }}} \right. \kern-0pt} {2r_{\text{e}} }}} \right)^{0.5} } \right]\sigma_{\hbox{max} } , $$
(2)
$$ K_{\hbox{min} } = \left\{ {\pi r_{\text{e}} \left[ {\sec \left( {{{\pi \sigma_{\hbox{min} } } \mathord{\left/ {\vphantom {{\pi \sigma_{\hbox{min} } } {2\sigma_{\text{V}} }}} \right. \kern-0pt} {2\sigma_{\text{V}} }}} \right) + 1} \right]} \right\}^{0.5} \left[ {1 + Y\left( a \right)\left( {{a \mathord{\left/ {\vphantom {a {2r_{\text{e}} }}} \right. \kern-0pt} {2r_{\text{e}} }}} \right)^{0.5} } \right]\sigma_{\hbox{min} } . $$
(3)

2.2 Modified Model for Short Fatigue Crack Growth

The problem of short fatigue crack growth becomes a topic of interest in recent years since the study of Pearson [28] who observed that the linear elastic fracture mechanics failed to correlate the crack growth rate of the short cracks (0.006–0.5 mm) with that of long crack. Since then, many works [29–37] have been carried out to investigate the behavior of short fatigue crack growth and prediction of the fatigue lives based on fracture mechanics.

For long cracks with crack length in excess of 1 mm, linear elastic conditions are applied and the crack is assumed to grow when the quantity ΔK reaches its threshold value ΔK th. However, this criterion is no longer applicable for the cracks shorter than 1 mm, and there is a gradual transition to the fatigue strength as the controlling criterion for the fatigue crack growth in the range of very short cracks [38].

After the correction of the crack tip plasticity [39] and short crack threshold [40], the general constitutive relation in Eq. (1) was further modified for both short and long fatigue cracks with the regions of crack initiation, threshold region, stable crack growth and unstable fracture, which can be expressed as follows [24–26]:

$$ {{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}N}}} \right. \kern-0pt} {{\text{d}}N}} = {{A_{1} \left\{ {\varDelta K - \left( {\varDelta K_{\text{thR}} - \varDelta K_{\text{th - s}} } \right)\left[ {1 - {\text{e}}^{{ - k\left( {a - d} \right)}} } \right] - \varDelta K_{\text{th - s}} } \right\}^{{m_{1} }} } \mathord{\left/ {\vphantom {{A_{1} \left\{ {\varDelta K - \left( {\varDelta K_{\text{thR}} - \varDelta K_{\text{th - s}} } \right)\left[ {1 - {\text{e}}^{{ - k\left( {a - d} \right)}} } \right] - \varDelta K_{\text{th - s}} } \right\}^{{m_{1} }} } {\left[ {1 - \left( {{{K_{\hbox{max} } } \mathord{\left/ {\vphantom {{K_{\hbox{max} } } {K_{\text{cf}} }}} \right. \kern-0pt} {K_{\text{cf}} }}} \right)^{{n_{1} }} } \right]}}} \right. \kern-0pt} {\left[ {1 - \left( {{{K_{\hbox{max} } } \mathord{\left/ {\vphantom {{K_{\hbox{max} } } {K_{\text{cf}} }}} \right. \kern-0pt} {K_{\text{cf}} }}} \right)^{{n_{1} }} } \right]}}, $$
(4)

where,

$$ a = a^{\prime}F, $$
(5)
$$ F = 0.5\left[ {\sec \left( {{{\pi \sigma_{\hbox{max} } } \mathord{\left/ {\vphantom {{\pi \sigma_{\hbox{max} } } {2\sigma_{\text{fl}} }}} \right. \kern-0pt} {2\sigma_{\text{fl}} }}} \right) + 1} \right], $$
(6)
$$ d = {{\left( {{{\varDelta K_{\text{th - s}} } \mathord{\left/ {\vphantom {{\varDelta K_{\text{th - s}} } {Y\varDelta \sigma_{\text{R}} }}} \right. \kern-0pt} {Y\varDelta \sigma_{\text{R}} }}} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {{{\varDelta K_{\text{th - s}} } \mathord{\left/ {\vphantom {{\varDelta K_{\text{th - s}} } {Y\varDelta \sigma_{\text{R}} }}} \right. \kern-0pt} {Y\varDelta \sigma_{\text{R}} }}} \right)^{2} } \pi }} \right. \kern-0pt} \pi }, $$
(7)
$$ \varDelta K_{\text{th}} = \varDelta K_{\text{th - s}} + \varDelta K_{\text{th - cl}} , $$
(8)
$$ \varDelta K_{\text{th - cl}} = \left( {\varDelta K_{\text{thR}} - \varDelta K_{\text{th - s}} } \right)\left[ {1 - {\text{e}}^{{ - k\left( {a - d} \right)}} } \right]. $$
(9)

2.3 Constitutive Relation for Dwell-Fatigue Crack Growth

The dwell-fatigue crack growth rate is usually calculated as a linear summation of the pure fatigue and dwell conditions [41–43]. In addition, some experimental results show that the crack growth rate of dwell condition generally linearly increases with the increase of the dwell time, t [41–43]. And the dwell-fatigue life of some titanium alloys is very sensitive to the maximum stress, which is usually smaller than pure fatigue life if the maximum stress σ max is higher, but close to pure fatigue life when the maximum stress σ max is lower. Therefore, [(σ max−σ R )/(σ y−σ R )]κ is introduced in the present modified model taking into account the effect of maximum stress. Then concerned about all this, the short fatigue crack growth rate model in Eq. (4) is further modified to dwell-fatigue crack growth rate model, as expressed in the following,

$$ \begin{aligned} {{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}N}}} \right. \kern-0pt} {{\text{d}}N}} = & A_{1} {{\left\{ {\varDelta K - \left( {\varDelta K_{\text{thR}} - \varDelta K_{\text{th - s}} } \right)\left[ {1 - {\text{e}}^{{ - k\left( {a - d} \right)}} } \right] - \varDelta K_{\text{th - s}} } \right\}^{{m_{1} }} } \mathord{\left/ {\vphantom {{\left\{ {\varDelta K - \left( {\varDelta K_{\text{thR}} - \varDelta K_{\text{th - s}} } \right)\left[ {1 - {\text{e}}^{{ - k\left( {a - d} \right)}} } \right] - \varDelta K_{\text{th - s}} } \right\}^{{m_{1} }} } {\left[ {1 - \left( {{{K_{\hbox{max} } } \mathord{\left/ {\vphantom {{K_{\hbox{max} } } {K_{\text{c}} }}} \right. \kern-0pt} {K_{\text{c}} }}} \right)^{{n_{1} }} } \right]}}} \right. \kern-0pt} {\left[ {1 - \left( {{{K_{\hbox{max} } } \mathord{\left/ {\vphantom {{K_{\hbox{max} } } {K_{\text{c}} }}} \right. \kern-0pt} {K_{\text{c}} }}} \right)^{{n_{1} }} } \right]}} \\ \quad & + A_{2} t_{\text{hold}} \left[ {{{\left( {\sigma_{\hbox{max} } - \sigma_{R} } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{\hbox{max} } - \sigma_{R} } \right)} {\left( {\sigma_{y} - \sigma_{R} } \right)}}} \right. \kern-0pt} {\left( {\sigma_{y} - \sigma_{R} } \right)}}} \right]^{\kappa } {{\varDelta K^{{m_{2} }} } \mathord{\left/ {\vphantom {{\varDelta K^{{m_{2} }} } {\left[ {1 - \left( {{{K_{\hbox{max} } } \mathord{\left/ {\vphantom {{K_{\hbox{max} } } {K_{\text{c}} }}} \right. \kern-0pt} {K_{\text{c}} }}} \right)^{{n_{2} }} } \right]}}} \right. \kern-0pt} {\left[ {1 - \left( {{{K_{\hbox{max} } } \mathord{\left/ {\vphantom {{K_{\hbox{max} } } {K_{\text{c}} }}} \right. \kern-0pt} {K_{\text{c}} }}} \right)^{{n_{2} }} } \right]}}. \\ \end{aligned} $$
(10)

3 Prediction Results and Discussion

In this section, the modified model of Eq. (10) will be used to predict the crack growth rates and the lives under the pure fatigue and dwell-fatigue conditions for three near α titanium alloys and one α + β titanium alloy under constant-amplitude load including the titanium alloys IMI834 and IMI685 with different microstructures, dwell periods and hydrogen contents, the titanium alloy Ti-6242 with long and short fatigue cracks, titanium alloy Ti-6Al-4V with different microstructures. And the predictions will be validated by comparing with the corresponding experimental results which are derived from Refs. [4, 7, 10, 14, 15, 18, 20].

3.1 Fatigue Life of the Titanium Alloys

Experimental results of smooth-bar specimens of the titanium alloys IMI834 and IMI685 will be used for validation of Eq. (10) in dwell-fatigue life prediction. The titanium alloy IMI834 for the experiments [10, 15] has two different types of microstructure, the bimodal microstructure (bar stock material, σ y = 850 MPa, σ b = 1180 MPa) and elongated primary α grain microstructure (disk material, σ y = 860 MPa, σ b = 1046 MPa). The experiments [4, 14] of IMI834 were conducted under R = 0.1 with dwell time of 120 s in each cycle. The titanium alloy IMI685 for the experiments [4, 14] was under two conditions, one containing 40 ppm hydrogen (40 × 10−6, in mass fraction) (σ b = 907 MPa) and tested under cyclic loading (R = 0.05) with dwell time of 300 s, and the other containing 60 ppm hydrogen (60 × 10−6, in mass fraction) (σ b = 976 MPa) and tested under cyclic loading (R = 0.1) with dwell time of 120 s.

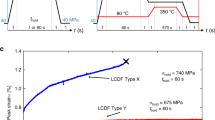
Equation (10) is used to predict the dwell-fatigue life of alloy IMI834 with elongated primary α grain microstructure under cyclic loading (R = 0.1) with different dwell time of 15 s, 120 s and 300 s. The experimental data for the condition of 120 s dwell time will be first applied to determine model parameters in Eq. (10) by optimal fitting method, as listed in Table 1. Then, all of the parameters were used to predict the cases of 15 s and 300 s dwell time. The prediction results of alloy IMI834 with the dwell time of 120 s accordingly compared with their corresponding experimental results, as shown in Fig. 1. It can be seen that the predicted results are in agreement well with the experimental data [10]. And the results show that the dwell-fatigue lives are evidently lower than the pure fatigue lives for the bimodal microstructure and the elongated primary alpha grain microstructure under higher stress level. The discrepancy between them is reduced with the decrease of the stress level. The dwell-fatigue life approximately reaches the pure fatigue life at 800 MPa for the bimodal microstructure. But for the titanium alloy IMI834 with the elongated primary alpha grain microstructure, the dwell-fatigue life merges with the pure fatigue life at 700 MPa. So the disappearance of the effect depends on microstructure largely.

Table 1 Predicted parameters for the titanium alloys IMI834 and IMI685
Full size table
Fig. 1
figure 1

Comparison between the predicted results and experimental data [10, 15] of pure fatigue and dwell-fatigue lives of titanium alloy IMI834

Full size image

The dwell time sensitivity of the titanium alloy IMI834 with the elongated primary alpha grain microstructure is presented in Fig. 2. It can be seen from the test data [10, 15] that the alloy IMI834 with elongated primary alpha grain microstructure is very sensitive to the dwell time. It is clear that the pure fatigue life decreases with increasing dwell time. But the reduction magnitude decreases as the applied stress level falls and disappears until the pure fatigue and dwell-fatigue life curves coincide. The predicted results using Eq. (10) agree well with the test data [15] under the dwell time of 120 s and 300 s but small than the test data under the dwell time of 15 s. Furthermore, to clearly illustrate the life variations with dwell time, more comparisons between the test data and prediction results of for the alloy IMI834 with elongated primary alpha grain microstructure at 880 MPa and R = 0.1 are shown in Fig. 3. It is evident that the reverse trend occurs between the dwell time and lives and Eq. (10) is able to predict the tendency of the dwell time effect.

Fig. 2
figure 2

Comparison between the prediction results and the experimental data [10, 15] of pure fatigue and dwell-fatigue lives for the alloy IMI834 with elongated primary alpha grain microstructure under different dwell time

Full size image
Fig. 3
figure 3

Comparison between the prediction results and the test data [10] for dwell-fatigue life of the alloy IMI834 with elongated primary alpha grain microstructure

Full size image

Similarly, the behavior of the dwell-fatigue crack growth for the titanium alloy IMI685 under different conditions is predicted by the modified model and compared with experimental data [4, 14]. The model parameters in Eq. (10) are listed in Table 1. The pure fatigue lives and the dwell-fatigue lives of alloy IMI685 with different hydrogen contents are shown in Fig. 4. It is evident the pure fatigue lives are affected by the hydrogen content, and the test data of the alloy with higher hydrogen content (60 ppm), has the lower pure fatigue lives. Equation (10) can well predict the behavior of the pure fatigue of IMI685 alloys with the hydrogen contents 40 ppm and 60 ppm. Moreover, the dwell time 300 s and 120 s significantly reduces the fatigue lives for the IMI685 alloys with different hydrogen contents at the maximum load. But the discrepancy between the dwell-fatigue and the pure fatigue is reduced with decreasing the maximum stress. The predicted results by the modified model agree well the experimental results [4, 14].

Fig. 4
figure 4

Comparison between the prediction results and test data [4, 14] of pure fatigue and dwell-fatigue lives for titanium alloy IMI685 with different hydrogen contents under different conditions

Full size image

In conclusion, by using the parameter t in Eq. (10), the dwell time effect can be reasonably reflected and predicted for two kinds of titanium alloys, IMI834 and IMI685. The experimental results presented in Refs. [4, 10, 14, 15] clearly indicate this phenomenon that the discrepancy between the dwell-fatigue lives and the pure fatigue lives is reduced as the maximum stress decreases, and the curve of the dwell-fatigue lives will merge with the curve of the pure fatigue lives when the maximum stress reaches a certain value. In addition, the parameter κ in the modified model is an important parameter to explain the applied stress level effect.

3.2 Fatigue Crack Propagation Rate of the Titanium Alloy

Experimental results of the titanium alloys Ti-6242 and Ti-6Al-4V [7, 19, 21] are applied in this section to validate Eq. (10) in prediction of dwell-fatigue crack growth rates. The yield strength and the ultimate strength of Ti-6242 are 927 MPa and 1044 MPa, respectively [21]. Long crack growth rates of the pure fatigue and the dwell-fatigue of the alloys are predicted under stress ratio R = 0.1 and dwell time 80 s. Short crack growth rates of the pure fatigue and the dwell-fatigue of the alloys are predicted considering three types of microstructure of equiaxed microstructure, elongated microstructure and colony microstructure for dwell time of 60 s at the maximum stress 0.8σy and at stress ratio R = 0.1. Similarly, the behavior of dwell-fatigue crack growth rate of α + β titanium alloy Ti-6Al-4V is also predicted by Eq. (10). Three Ti-6Al-4V alloys were subjected to different orientation annealing processes, as reported in Ref. [19]: One was TL orientation annealed at 700 °C (σ y = 1009 MPa, σ b = 1034 MPa); the other two were TS orientation annealed at 700 °C (σ y = 938 MPa, σ b = 1005 MPa) and TL orientation duplex annealed at 985 °C and 700 °C (σ y = 938 MPa, σ b = 1005 MPa), respectively. The model parameters for Ti-6242 and Ti-6Al-4V alloys are listed in Table 2.

Table 2 Predicted parameters for the titanium alloys Ti-6242 and Ti-6Al-4V
Full size table

The long crack growth rates of titanium alloy Ti-6242 at stress ratio 0.1 are shown in Fig. 5. It can be found that the predicted results agree well with the experimental data [21] for the pure fatigue and dwell-fatigue of Ti-6242. Moreover, the tendency shows that the crack growth resistance of Ti-6242 under dwell-fatigue is lower than that under pure fatigue. And the dwell-fatigue crack growth rates are about 4 times faster than the that of pure fatigue in all ΔK ranges.

Fig. 5
figure 5

Comparison between the prediction results and test data [21] of long crack growth rate for titanium alloy Ti-6242 under the conditions of R = 0.1 and dwell time of 80 s

Full size image

The comparison between the test data [7] and the prediction results by Eq. (10) for the short fatigue crack growth rate of the titanium alloy Ti-6242 with three different microstructures is shown in Fig. 6. It is shown that the test data [7] have great discrepancy in the lower ΔK below 5 MPa m0.5 but tends to be stable with increasing ΔK. The short fatigue crack growth rate of the test data in lower ΔK is much faster than the long fatigue crack the threshold. The phenomenon is widely observed in the short fatigue crack growth rate tests [29]. And the comparison shows that the crack growth data are underestimated by Eq. (10) in lower ΔK but agree well with the experimental results [7] in higher ΔK. Both the test data and predicted results show that the crack growth rate of the titanium alloy with equiaxed microstructure is the highest among the three microstructures. But the discrepancy between the equiaxed microstructure and the elongated microstructure becomes small in higher stress intensity factor range. The results illustrate the influence of the microstructure on the fatigue crack growth rate of the material, especially in lower stress intensity factor range. To sum up, Eq. (10) can be used to predict the behavior of the short fatigue crack growth for titanium alloy Ti-6242.

Fig. 6
figure 6

Comparison between the prediction results and test data [7] of short crack growth rate for titanium alloy Ti-6242 with different types of microstructure under the conditions of R = 0.1 and σ max = 0.8 σ y

Full size image

Figure 7 shows the comparison between the test data [7] and the prediction results for the short dwell-fatigue crack growth rate of titanium alloy Ti-6242 with the three microstructures at the stress ratio R = 0.1 and dwell time 60 s. Compared with Fig. 6, results show that the dwell-fatigue crack growth rates of titanium alloy with three different microstructures are higher than the corresponding pure fatigue crack growth data. But the dwell time sensitivity is different for the three microstructures. Both the test data and the predicted results show that the colony microstructure will bring the largest discrepancy between the dwell-fatigue and pure fatigue crack growth rate. And the other two microstructures have similar dwell time sensitivity. This comparison displays that the prediction results agree well with the test data [7] in all ΔK ranges. And Eq. (10) can reasonably predict the behavior of the dwell-fatigue crack growth of Ti-6242 with the three different microstructures.

Fig. 7
figure 7

Comparison between the prediction results and test data [7] of short crack growth rate for titanium alloy Ti-6242 with different types of microstructure under the conditions of R = 0.1, t hold = 60 s and σ max = 0.8 σ y

Full size image

The comparisons between the prediction results and the test data [19] for TL orientation annealed Ti-6Al-4V alloy are shown in Fig. 8, where different dwell time are considered. Similarly, several times larger crack growth rate is also observed by the introduction of dwell time at the maximum stress into pure fatigue. And the prediction results by Eq. (10), for pure fatigue and dwell-fatigue with dwell time 5 and 45 min coincide well with test data. But it is observed that the test data of the dwell-fatigue growth rate under dwell time 15 min are similar to that with the dwell time 5 min, which may result from test error.

Fig. 8
figure 8

Comparison between the prediction results and test data [19] of crack growth rate for TL orientation annealed Ti-6Al-4V alloy under the conditions of R = 0.1 and different dwell time

Full size image

Figure 9 shows the comparison between the prediction results and the test data [19] for TS orientation annealed Ti-6Al-4V alloy. Both the test data and prediction results illustrate that the dwell-fatigue crack growth rate increases with the dwell time. The prediction results of crack growth rate cohere with the test data for pure fatigue and dwell-fatigue with dwell time 5 min and 45 min. The prediction results of the dwell-fatigue crack growth rate with dwell time 5 min and 45 min are, respectively, 8–18 times and 42–106 times larger than the prediction results of pure fatigue crack growth rate. Under the same ΔK, the discrepancy of the test data between the dwell-fatigue and pure fatigue crack growth rate is 7.49–16 times and 50–100 times for dwell time 5 min and 45 min, respectively.

Fig. 9
figure 9

Comparison between the prediction results and test data [19] of crack growth rate for TS orientation annealed Ti-6Al-4V alloy under the conditions of R = 0.1 and different dwell time

Full size image

The comparison between the prediction results and the test data [19] for TL orientation duplex annealed Ti-6Al-4V alloy is shown in Fig. 10. Similar trends are observed. The prediction results of the crack growth rate with dwell time 5 min is almost 1.9–4 times larger than pure fatigue crack growth rate. Under the same ΔK, the test data of dwell-fatigue crack growth rate is almost 1.5–4.11 times larger than pure fatigue crack growth rate. When the dwell time reaches 45 min, the discrepancy of crack growth between the dwell-fatigue and pure fatigue grows to 5–16 times, according to prediction by Eq. (10), and 4.8–9 times observed from tests [19].

Fig. 10
figure 10

Comparison between the prediction results and test data [19] of crack growth rate for TL orientation duplex annealed Ti-6Al-4V alloy under the conditions of R = 0.1 and different dwell time

Full size image

In general, the dwell-fatigue crack growth rate shows that titanium alloy Ti-6Al-4V is very sensitive to the dwell time, but the sensitivity to the dwell time is different for the alloy under different annealing process. TS orientation annealed alloy is the most sensitive to the dwell time, and then TL orientation annealed one.

4 Conclusions

A modified model of cold dwell-fatigue crack growth is proposed in the present work based on the unified fatigue life prediction method. In this modified model, the effects of the dwell time and maximum stress level are included. The model can be successfully used to predict the behavior of pure fatigue and dwell-fatigue for four kinds of titanium alloys analyzed in this paper and the following conclusions are drawn:

  1. 1.

    The elastic–plastic behavior of short cracks in the vicinity of crack tips is considered in the modified model, which can reasonably predict the pure fatigue and the dwell-fatigue lives of the smooth-bar specimens of titanium alloys.

  2. 2.

    By introducing the parameter of dwell time t, the modified model is able to explain the dwell time effect on the dwell-fatigue lives and crack growth rates.

  3. 3.

    The prediction results show that the discrepancy between the dwell-fatigue lives and the pure fatigue lives will be reduced when the maximum stress decreases, and similar phenomena were observed from tests. In addition, the parameter κ in the modified model is an important parameter to explain the applied stress level effect on the dwell-fatigue lives of titanium alloys.

  4. 4.

    The modified model is capable of predicting dwell time sensitivity of titanium alloys with different microstructures.