Application of fracture mechanics to welds with crack origin at the weld toe: a review Part 1: Consequences of inhomogeneous microstructure for materials testing and failure assessment

Abstract

This two-part paper provides an overview on the state-of-the-art in the application of engineering fracture mechanics to weldments. This, of course, cannot be exhaustive but is limited to butt and fillet welds with crack initiation at weld toes. In the present first part, the authors briefly focus on the susceptibility of welds to cracks and other defects. Following this, they discuss in more detail the consequences of material inhomogeneity across the weld for fracture mechanics. Inhomogeneity causes scatter in fracture toughness and strength mismatch effects both of which have to be considered in fracture toughness testing, crack driving force determination, and fracture assessment of welded components. Part 2 of the paper series will add a discussion on welding residual stresses and questions of applying fracture mechanics to residual as well as total lifetime estimation of welds under cyclic loading.

1 Introduction

Compared with that in homogeneous structures, the application of fracture mechanics to weldments has to take into account a number of specific features. Besides an increased susceptibility to cracks and other defects in some cases, these are (a) a pronounced inhomogeneity of the microstructure across the weld, (b) potential strength mismatch, and (c) welding residual stresses. With respect to the overall fatigue life, (d) multiple crack initiation and propagation along the weld toe have to be added. Here, the first two aspects (a) and (b) will be discussed while (c) and (d) will be the topic of the second part of this two-paper series [1].

2 Susceptibility to cracks and other defects

Cracks and defects have to be distinguished between (a) large cracks and defects which require a classical damage tolerance analysis, and (b) small cracks and defects which are relevant for the total fatigue life and strength (safe life philosophy). The two kinds of analyses are schematically illustrated in Fig. 1. In classical damage tolerance, a so-called long crack, the size of which is usually in the order of millimeters, is presumed and, based on this, the residual lifetime of the component is determined. The crack or crack-like discontinuity (e.g., lack of fusion) can be one that has been detected in service or it can be assumed to be existing based on the detection limit of the non-destructive testing method applied in quality control after manufacturing or in regular inspection during service. Typical cracks and defects of this size are shown in Fig. 2. Note that the aim of proper manufacturing and quality control is to avoid such kind of flaws.

Fig. 1

Total vs. residual lifetime (“safe life” versus common “damage tolerance” philosophies). Schematic illustration

Fig. 2

Large cracks and crack-like defects in a weldment which require classical damage tolerance analysis. According to [2]

In contrast, small discontinuities and crack-like defects such as those shown in Fig. 3 can be responsible for limiting the total fatigue lifetime and fatigue strength of weldments in the sense of an S–N curve analysis. The emphasis is on “can be” because particularly not any high-quality weld contains defects such as those shown in Fig. 3. What is, however, always typical is a notch effect of the weld toe or other geometrical discontinuities, except these are removed by machining. The application of fracture mechanics to total fatigue life and strength will be addressed in part 2 of this paper [1].

Fig. 3

Typical defects which can be generated in manual arc welding. According to [3]

Fatigue cracks will usually initiate at macroscopic stress risers such as designed notches and holes. Figure 4 shows crack initiation sites along the toe of a butt weld of S355NL steel [4]. The small initial cracks have been visualized by heat tinting at about one-third of the total lifetime. While there were no undercuts at the toe, it was found that most cracks initiated at surface roughness dimples next to the toe (Fig. 5). These were leftovers from the hot rolling process of the base plates. Cracks were also initiated at welding ripple edges and in the weld seam at some distance from and parallel to the toe. Note, however, that the latter tended to arrest or to quickly coalesce with the main crack.

Fig. 4

Crack initiation pattern along the toe of a butt weld. a Weld ripple pattern; b schematic illustration of early crack propagation (according to [5]); c crack initiation sites found by heat tinting in [4]

Fig. 5

Base plate surface roughness close to the weld toe in a specimen of the same series as in [4]. According to [6]

Referring to [7], the authors mentioned in a previous review paper [8] that even in the absence of typical weld defects, non-metallic inclusions introduced in the manufacturing process of the original base and weld metal material could act as crack initiation sites at macroscopic notches such as weld toes (cf. also [9]). Figure 6 shows statistical size distributions of such inclusions in the areas around the weld toes of butt welds of the S355NL welds.

Fig. 6

Non-metallic inclusions in the toe areas of a butt weld of S355NL steel in a specimen of the same series as in [4]. a Metallographic section; b histogram of the area equivalent diameters of the inclusions; c extreme value statistics of these. According to [4]

3 Microstructural inhomogeneity across the weld

3.1 General picture

During cooling, welds go through a complex process of local “heat treatment” and microstructure formation. Since the material experiences quite different cooling rates at various positions (centerline of the weld, HAZ, etc.), cooling takes place along different time-temperature-transition (TTT) curves. Finally, different microstructures will exist at different positions such as those illustrated in Fig. 7. When instead of a single-pass a multiple pass weld is generated, complexity even increases due to additional re-heating and annealing phases. Examples for microstructures in the HAZ, compared with the base plate, are shown for two steels (S355NL and S960QL) in Fig. 8.

Fig. 7

Schematic representation of the heat-affected zone (HAZ) microstructure of a carbon–manganese steel weld, from left to right: single-pass, two-pass, and three-pass welds. According to [10]

Fig. 8

Metallographic views of the microstructures near the weld toes for welded joints made of steels S355NL and S960QL. According to [11]

It is no surprise that the various microstructures are characterized by quite different material properties both in terms of their deformation, i.e., their stress–strain behavior, and of their fracture toughness. Besides isolated brittle zones (usually within the coarse-grained HAZ), there are also medium-range gradients across the weldment as revealed by a look at the hardness distribution pattern in Fig. 9. These gradients, besides the stochastic effects of the brittle zones, control the strain pattern under applied loading such that there will be strain concentration zones at transitions from harder (i.e., higher strength) to softer (i.e., lower strength) areas. Note that these strain concentrations will also influence potential crack tip loading which depends on the strains or the energy rather than on the stresses. In other words, the inhomogeneous microstructure across the weldment will show a stochastic and a systematic effect on the mechanical behavior of the component.

Fig. 9

Hardness distributions across the welds of fusion welded S355NL and S960QL steels. According to [11]

3.2 Consequences with respect to monotonic fracture toughness

Usually, although not in any case, fatigue cracks will develop at the weld toe.¹ As a consequence, the early stages of crack propagation take place in the HAZ. An example is shown in Fig. 10. It can also be seen that the crack later grew out of this zone but not until it had reached a depth of about 2 mm. This means that total fatigue life considerations generally have to be based on HAZ properties in such cases (see [1]).

Fig. 10

Fatigue crack initiation and growth from the toe of a butt weld of S355NL steel. According to [4]

This is the reason why the fracture toughness of HAZ material frequently is in the focus of fracture mechanics material testing. The way this is done is described in detail in [8] and shall not be repeated here in full length since not much has changed since this publication. The essential points are pre- and post-test metallographic investigations in order to guarantee that the crack tip position is really in the HAZ. After etching the sample blanks, the notches are machined, e.g., with electrodischarging, and it is only then that the outer contours of the specimens are finally machined. Notch positioning, of course, is possible only at the outer surfaces of the specimens. Therefore, post-test metallographic investigation is needed after the test such as that illustrated in Fig. 11. The aim of this is to check whether the crack along its front (i.e., in thickness direction) has sampled enough HAZ microstructure for the test to be representative. According to the existing test standards for welds [12, 13], a lower bound HAZ toughness is expected when the crack tip was found to be no more than 0.5 mm distant from the HAZ boundary within the central 75% of the specimen thickness. Experience with multipass welds in thick section structural steels with a yield strength of around 350 MPa has also shown that the crack front should sample either 15% or at least 7 mm of HAZ microstructure again within the central 75% of the specimen thickness [12].

Fig. 11

Post-test sectioning to identify the microstructure at the fatigue crack tip: a through-thickness notched (B × 2B) specimen; b surface notched (B × B) specimen (these terms will be explained in section 2.4 of [1]). According to [12]

Excursus: weakest link considerations

At this point, another aspect comes into play: the weakest link statistical model. The weakest link philosophy in the context of fracture toughness testing has been elaborated for the ductile-to-brittle transition of steels with bcc lattice [14] (see Fig. 12). Under applied loading, a stress peak develops some 10 μm ahead of the crack tip which is further shifted into the ligament with load increase and crack extension (Fig. 12b). Across the ligament, there are stochastically distributed “weak links,” i.e., microstructural features, e.g., carbides or carbide clusters, such that the global failure of the specimen (or component) occurs when the stress peak reaches the position of this (like a chain that fails when its weakest link brakes). The “weakest link” is the flaw at the position closest to the crack front. Since the weak links are stochastically distributed across the ligament and since their overall number is rather limited, the position of the weakest link with respect to the crack front is different from specimen to specimen, and so is the work needed to shift the stress peak in the ligament and consequently also the fracture toughness. The scatter band is usually of an order of a magnitude or even more.

Fig. 12

Fracture toughness statistics in the ductile to brittle transition range as explained by the weakest-link model. a Transition including the scatter band; b weakest link model; c statistical size effect based on the weakest link model

The weakest link model allows for two conclusions

• (a) Since a longer crack front will increase the probability of a weak link to be close to the crack front, the scatter band will be “squeezed” to the lower bound in that case. That means, there is a statistical size effect when the thickness of the specimen is identical with the crack front length (Fig. 12c).

• (b) The lower bound can be reached by one or a few specimens with large crack front lengths or, alternatively, by a larger number of specimens with smaller crack front lengths.

Coming back to weldment testing, the same principles can be applied with the weak links being the local brittle zones in a HAZ. What is of most interest in our context is conclusion (b) which means that the demand to sample a large portion of HAZ by the crack front in a few specimens can be relaxed by testing a larger number of specimens. This is illustrated in Fig. 13.

Fig. 13

Required number of fracture mechanics tests vs. total length of coarse-grained HAZ sampled by the crack front. According to [10]

In any case, the determination of the fracture toughness of the HAZ requires a certain number of specimens. In the 2005 version of “BS 7910” [15] (Annex L: “Fracture toughness determination for welds”), this was specified as ≥ 12 for structural steels with yield strengths up to 450 MPa, except it could be shown that the HAZ material shows upper shelf behavior. The 2013 update [16] more generally speaks about a “larger number” of tests “dependent on the type of statistical analysis.”

This is usually realized by a 3-parameter Weibull distribution as it is applied in the ductile-to-brittle transition range, e.g., [17]. In Eq. (1):

$$ P=1-\exp \left\{-{\left[\frac{\left({K}_{mat}-{K}_{\mathrm{min}}\right)}{K_0-{K}_{\mathrm{min}}}\right]}^m\right\} $$

(1)

which is based on the VTT Master curve approach, e.g., [18], P is the fracture probability; K_mat the fracture toughness in terms of the K-factor, which is formally obtained from the critical J-integral, J_mat by:

$$ {K}_{mat}=\sqrt{J_{mat}\cdot E/\left(1-{\nu}^2\right)} $$

(2)

and K₀, K_min, and m are the scale, shift, and shape parameters of the distribution. In the frame of the Master curve concept, two of these fit parameters are replaced by fixed values: m = 4 and ${K}_{\mathrm{min}}=20\ \mathrm{MPa}\sqrt{m}$. The advantage of this approach is a substantial reduction of the necessary number of test specimens. However, since it is based on empirical evidence, there are also restrictions with respect to the application range, namely to ferritic steels with yield strengths between 275 and 825 MPa. The method has been proven to be applicable within these limits.

Note that this frequently will be a problem for welds, e.g., the HAZs of the steel welds of S355NL and S960QL of Figs. 8 and 9 both showed a martensitic–bainitic microstructure although the base plate of S355NL was ferritic-pearlitic. In principle, one could use Eq. (1) with K₀, K_min, and m being free-fit parameters, but this would eliminate the advantage of the limited number of specimens; therefore, this option is not realistic. A compromise which the authors have realized in another context [19] is to keep m = 4 but replace K_min by another value. Note, however, that this procedure is not covered by a test standard for now.

Another problem of HAZ testing is the considerable inhomogeneity of the microstructure even across the HAZ itself which is additionally superimposed by the medium-range material gradient mentioned in section 3.1. In terms of statistics, that means that the toughness data of the scatter band belong to different samples. The principle is schematically illustrated in Fig. 14 where a two-material system is considered. If the data points are mixed, i.e., if they are treated as one sample, it is obvious that the Master curve does not fit material 1 or material 2 in a correct way. What is particularly important is that the lower tail for (the more brittle) material 1 is non-conservatively described.

Fig. 14

Schematic illustration of the effect of inhomogeneous material on the statistical distribution of fracture toughness

What is obviously needed is some procedure for “demixing” the input data set. This can be realized by two methods: a bimodal Master curve and a lower tail Master curve as they have been proposed in [20]. While the first one describes the toughness distribution at the upper and lower tails, the last one only allows the description of the lower tail. The method has become part of the revised “BS 7910” [16] and is described in detail in Annex L of this document as well as in [8, 21] of the authors. This shall not be repeated here in detail. Only the basic principle will be explained. This uses a census criterion, i.e., a maximum toughness value above which the data are discarded. What is, however, retained is the total number of the specimens tested since these form the basis of the fracture probability in the statistical analysis. Now, the census criterion is stepwise decreased. As long as there is still an effect of the mixed sample, the lower tail of the distribution curve will be shifted to lower values with each subsequent step. When the latter becomes stable, the analysis is stopped and the resulting lower tail distribution can be used for the assessment.

A few short notes shall be added

• (a) It should have become clear that the Master curve concept as it currently stands is not only effortful when applied to HAZ toughness, it also shows deficits. This is one reason why older and more simple approaches are also still in use, e.g., the 2005 version of “BS 7910” [15] (Annex K: “Reliability, partial safety factors, number of tests and reserve factors”) contained simplified rules for specifying a lower bound toughness for data sets of no more than 15 results. This was based on [22] and provided the use of the lowest of 3 to 5 test results, the second lowest of 6 to 10 test results, and the third lowest of 11 to 15 test results as design values. However, care was advised with respect to HAZ testing. In the 2013 version [16], this approach is not included anymore. A critical review on the issue has recently been provided in [23] where a warning is formulated. The rules have been obtained and shown to be conservative in the context of the so-called CTOD design curve concept of the old “BS 6493” document [24]. However, when applied along with newer, more accurate flaw assessment procedures, they may give non-conservative results. For some background information on the approaches and procedures, see [25].

• (b) As an alternative to the testing of HAZ microstructure in real welds, specimens consisting of thermally simulated HAZ microstructure can be used. No guidance on the generation of those specimens will be provided here (see, however, [11], where the technology has been realized with respect to the S355NL and S960QL welds which serve as illustration examples in this paper). Note that other material parameters such as the cyclic stress–strain curve, the crack propagation characteristics da/dN − ΔK, or the fatigue crack propagation threshold ΔK_th can be determined with such specimens much better or in the first place.

• (c) The different microstructure of a HAZ compared with the base metal can also cause a change in the failure mechanism from upper shelf to ductile-brittle transition characteristics (Fig. 12). This happened for both demonstration examples: the S355NL and S960QL welds in this paper. For the first one, this is shown in Fig. 15. As can also be seen, the Master curve provides a rather poor fit of the experimental data which is, however, not really surprising because the martensitic–bainitic microstructure of the HAZ is not covered by the method.

  Fig. 15

  

  Fracture toughness of S355NL steel. a Base metal: upper shelf characteristics (monotonic R curve and resistance against stable crack initiation). b HAZ: ductile-to-brittle-transition characteristics (Weibull distribution of toughness—Master curve approach/open symbols). According to [11]

• (d) A typical feature in HAZ (and more generally weld) testing is so-called pop-in behavior [26]. The basic characteristics of this and an example are shown in Fig. 16. A pop-in is characterized by a discontinuity in the load-displacement record in a fracture mechanics test, i.e., the load temporarily decreases or stays constant for increasing displacement (Fig. 16a). The reasons of such discontinuities can be (i) crack initiation at local brittle zones followed by crack arrest in the surrounding more ductile material or (ii) other causes such as splits or delaminations perpendicular to the fatigue crack plane, coalescence between multiple cracks or cracks with other flaws such as slag inclusions, and pores.

  Fig. 16

  

  Pop-in behavior in the load-displacement record of a fracture mechanics test. a Types according to [26]. b Example: laser beam weld of a titanium alloy. According to [27]

A crucial point is to figure out whether a pop-in event has to be judged as relevant to component behavior or not. In the first case, toughness determination is based on this point and not on the complete load-displacement curve, e.g., when a critical J-integral is to be determined, the energy, i.e., the area below the curve, is restricted to the onset of the pop-in event. Neglecting a relevant pop-in can have disastrous consequences because the load-carrying capacity of the component can be significantly overestimated. Note that the guidelines for establishing pop-in events in weldments are stricter than those for non-weld applications in that a load drop of ≥ 1% is regarded as significant unless the non-existence of local brittle fracture propagation can be demonstrated by means of fractography or metallography [12, 13]. The reason for tightening the guideline is uncertainty about the extent of the local brittle zone sampled by the crack front which could have been larger if the crack tip had been displaced a slight distance away depending on the crack depth generated in the test. For a more detailed discussion, see also [8].

3.3 Strength mismatch and its consequences

3.3.1 General remarks

In section 3.1, it has been mentioned that the inhomogeneity of the microstructure across the weld, besides stochastic effects, also causes a medium-range gradient of the material properties. As could be seen in Fig. 9 for the demonstration examples, the hardness varies significantly between the base plates, the weld metals, and the HAZs, and even within these and between the two cap passes. Since hardness and strength correlate with each other, a similar effect is to be expected with respect to the local yield and tensile strength and, of course also with respect to the ductility. Figure 17 shows the corresponding cyclic stress–strain curves. The highest strengths are stated for those regions in the HAZs which also showed the largest hardness. Simultaneously, the ductility at these points (in terms of the elongation at break) is the lowest [11].

Fig. 17

Stabilized cyclic stress–strain curves at different positions at the weld for S355NL and S960Ql steel. According to [11]

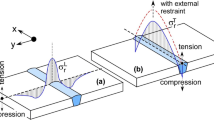
Strength mismatch also controls the strain pattern across the section in that, for a given applied load, the strains are higher for lower strength material sections and vice versa. Figure 18 schematically illustrates what that means with respect to weldments containing cracks. Remember that the crack tip loading corresponds to the local strain and not to the applied stress. In the figure, a crack is shown in the centerline of an even-, and over- and an undermatched weld (from left to right). Even-matching means that the base plate and the weld show the same strength, overmatching that of the weld is higher than that of the base plate, and undermatching that the base plate shows a higher strength.

Fig. 18

Plastic deformation pattern at a crack tip when affected by strength mismatch: schematic view. According to Annex P of [16]

Not surprising, in the overmatched weld, plasticity develops predominantly in the lower strength base plate with a strain concentration zone at the border between the two materials, i.e., at the fusion line, while the crack tip is shielded. Now, imagine that the position of the crack had not been in the center of the weld but at the fusion line as usually happens since this is the position of the weld toe. In that case, the crack driving force would have been increased compared with the even-matching case. And since this is also the position of the HAZ with its local brittle zones, two detrimental factors had combined, namely a high crack driving force and a low fracture resistance of the material. This shows that the simple rule of moderate overmatching will be of benefit because it shields the weld from being wrong and counterproductive. Coming to the right-hand side of Fig. 18, we find the situation just the other way around. Because of undermatching, the strain is now concentrated in the weld with the consequence of an increased crack driving force of the crack at that position.

In fusion welds, a moderate overmatching of some 10% is usually the aim. For welding processes with highly focused energy input such as laser and electron beam welding, the overmatching can be much larger. On the other hand, there might be also undermatching when the welding process “resets” the hardening of a metastable material or when there exists no welding filler material of the same or higher strength than the base material. Examples are aluminum alloys and ultrahigh-strength steels (see, e.g., Fig. 19).

Fig. 19

Hardness profiles of a a laser beam–welded aluminum alloy (undermatching) and b a laser beam–welded steel (overmatching). According to [27, 28]

Besides the type (i.e., over- or under-) and the degree of mismatch and the location of the crack with respect to the different material sections, two further parameters play a role: the crack length referred to the plate width (W − a), and the strip width (H) of the weld. This is shown in Fig. 20. It turned out that the “composite” parameter (W − a)/H provides a suitable measure for the following considerations [29]. These assume through-thickness cracks in plates and rectangular cross sections of the weld strips. Both are certainly significant restrictions compared with reality. Nevertheless, it will turn out that the conclusions can be used in a wider frame.

Fig. 20

Geometrical parameters of a mismatch configuration and the crack which are important in the context of strength mismatch

Preliminary proposals, on how the weld strip width could be defined for other than rectangular weld cross sections, are provided in Fig. 21. Note, however, that these still lack comprehensive validation.

Fig. 21

Definition of the weld strip width 2H or H in cases where the weld does not have a simple prismatic shape. a According to “ETM GTP” [30]; b proposal of [31]. The equivalent value H_eq is defined on the basis of the shortest distance between the crack tip and the fusion line along the slip lines emanating from the crack tip

Commonly, strength mismatch is treated by a two-material system consisting of the weld and the base plate such that the mismatch factor M is defined by:

$$ M={\sigma}_{YW}/{\sigma}_{YB} $$

(3)

with σ_YW and σ_YB being the yield strengths of the weld and the base metal. However, already, a look at Figs. 9 and 17 reveals that things are more complex in that the HAZ as a third material section shows a strength different from that of the base plate and weld, and even this is not constant but shows variations and gradients across its section and also between the lower and upper cap passes. In such cases, the solutions shown below could be applied just for two adjacent sections, i.e., the HAZ and the base metal instead of the weld and base metal. When it was stated above that the mismatch factor definition is based on the yield strengths of the materials, it has to be added that the ETM strength mismatch version [29] and, based on this, documents such as “BS 7910” [16] or R6 Rev. 4 [32] also provide mismatch relevant strain hardening exponents at higher analysis options.

3.3.2 The effect of strength mismatch on fracture toughness

Strength mismatch will influence the fracture toughness of the weld or HAZ in different ways. First, (i) for the same applied stress, the crack driving force in the specimen (or in the component) is different when compared with that in the homogenous (even-matched) case; (ii) there is an effect on local stress triaxiality with the consequence of different constraint conditions; and (iii) there might be crack path deviation such that the crack extends into adjacent material sections with different toughness properties than those of the material that should actually be investigated.

The strength mismatch effect on the crack driving force in fracture mechanics specimens can be taken into account by modifying the shape function η_p in the equation for the J-integral.

$$ J=\frac{K^2}{E}+{\eta}_p\frac{U}{B\left(W-a\right)} $$

(4)

In Fig. 22, the solutions of [30] are reproduced which have been obtained by simulations in [33]. Further solutions are provided in [34,35,36]. Figure 23 shows an example of formal application of the modified η_p to a monotonic crack resistance curve. Note that a mismatch influence on the crack driving force does not necessarily mean also an effect on fracture toughness. This has to be checked in material testing. Note further that documents such as [13, 30] contain limits with respect to the mismatch ratio M below of which no mismatch correction is required (cf. also [8]).

Fig. 22

Plastic η factors (η_p) of welded specimens with strength mismatch (according to [30]). Results obtained in [33]

Fig. 23

Example of a formally strength mismatch corrected R-curve using the η_p factor solution according to Fig. 22

In Fig. 24, the effect of strength mismatch on stress triaxiality is shown for two cases where the latter, deviating from the common definition, is given as the ratio of the hydrostatic stress and the yield strength of the material considered. As can be seen in Fig. 24a, the stress triaxiality in the undermatched M(T) plate with a center crack in the weld, above a certain (W − a)/H ratio, reaches a value typical for deeply cracked bending geometries. Note that a high stress triaxiality corresponds to a high constraint and, as a consequence, to a low fracture toughness.

Fig. 24

Effect of strength mismatch on stress triaxiality. aM(T) geometry, plane strain conditions. b Stress triaxiality at the crack tip and at the position where the maximum stress occurs. According to [29]

In Fig. 24b, the stress triaxiality at the crack tip is compared with those at the position of the highest local stress under extreme undermatching conditions (i.e., the base plate remains elastic). The second peak stress and stress triaxiality at some distance away from the crack tip (usually at the fusion line) can cause crack path deviation which is also found in experiments (e.g., [27]). In such a case, the situation becomes quite complex. Since the plastic strain is still more concentrated at the crack tip than anywhere else in the weld, the result will be a competition of the two spots.

In section 3.2, the effect of brittle zones on toughness was discussed in the frame of the weakest link concept. Note that this can occur in combination with strength mismatch caused by crack path deviation. Assume the initial crack tip to be located in rather brittle HAZ material. In some cases, the weak links, i.e., the brittle zones, will be close to the crack front and the specimens will immediately fail. Others, with the weak links more distant from the crack front will not fail but the crack will deviate and grow into a more ductile region with a tougher microstructure. Finally, the overall toughness scatter will be controlled by a mixture of different material conditions [37]. An example which the authors interpret this way is given in Fig. 24. Since the toughness of the specimens which immediately failed is the lowest, this should be used for component assessment [38] (Fig. 25).

Fig. 25

Scatter band of toughness in terms of the critical CTOD δ₅ as a function of the crack front length (specimen thickness) and overmatched power beam weld, according to [39]. The authors explain the pattern by a combined effect of the weakest link mechanism and strength mismatch–driven crack path deviation

The statistical effect of strength mismatch also shows up in the statistical distribution of the fracture toughness. An example is provided in Fig. 26 [40] (see also [41]).

Fig. 26

Effect of strength mismatch in the vicinity of the notch tip on the fracture toughness in terms of the critical CTOD. a Crack in the higher strength material; b crack in the lower strength material. According to [40]

3.3.3 The effect of strength mismatch on the crack driving force of the component

The effect of strength mismatch on the crack driving force has already been briefly addressed in the sections above. In the following, it shall be discussed how this is realized in component assessment with the focus being set on analytical methodology. Only the failure assessment diagram (FAD) approach and this only in its simplest format will be the topic here; for a more detailed discussion, the reader is referred to the book and the review paper of the authors in [21, 25].

The basic principle is that the crack driving force is first determined as a linear elastic stress intensity factor K and then corrected for ligament plasticity by a function f(L_r). In the FAD approach, this is realized by the basic equation:

$$ {K}_r=\frac{K}{K_{mat}}=f\left({L}_r\right) $$

(5)

with K_mat being a general term of the fracture toughness, e.g., it can be the resistance against stable crack initiation (see J_0.2;BL and J_0.2 in Fig. 15a formally transferred to K_mat by Eq. (2)). In that K is normalized to the toughness of the material, f(L_r) not only provides a correction function for ligament yielding but is also a limit curve against failure (Fig. 27).

Fig. 27

Failure assessment diagram (FAD) approach. a Determination of the critical applied load; b determination of the critical crack size

The failure assessment is based on the position of a design point (L_r, K_r) for the component to be evaluated relative to the FAD line. As long as the path of the design point (red curves) does not leave the (blue) area inside the FAD, the component is safe; if it turns to outside, it is potentially unsafe. Various options with stepwise decreased conservatism are given for the f(L_r) function in documents such as “BS 7910” [16] and R6, Rev. 4 [32]; for a workbook on these, see [21]. As an example, Option 1 of “BS 7910” gives a set of equations for materials which do not exhibit a yield discontinuity (Lüder’s plateau):

$$ f\left({L}_r\right)={\left[1+0.5\cdot {L}_r^2\right]}^{\hbox{-} 1/2}\cdot \left[0.3+0.7\cdot \exp \left(-\mu \cdot {L}_r^6\right)\right] for\kern0.5em 0\le {L}_r\le 1 $$

(6)

with

$$ \mu =\min \left\{\begin{array}{c}0.001\left(E/{R}_{p0.2}\right)\\ {}0.6\kern4.75em \end{array}\right. $$

(7)

and f(L_r) = f(L_r = 1) ⋅ L_r^{(N − 1)/2N} for

$$ 1\le {L}_r\le {L_r}^{\mathrm{max}} $$

(8)

The strain hardening coefficient N is conservatively determined by:

$$ N=0.3\cdot \left[1-\left({R}_{p0.2}/{R}_m\right)\right] $$

(9)

and the plastic collapse limit L_r^max (the vertical line in Fig. 26) by:

$$ {L_r}^{max}=0.5\cdot \left[\left({R}_{p0.2}+{R}_m\right)/{R}_{eL}\right] $$

(10)

The ligament yielding parameter L_r is given by alternative but equivalent options as:

$$ {L}_r=\frac{F}{F_Y}=\frac{\sigma_{ref}}{\sigma_Y}=\frac{\sigma_{app}}{\sigma_0} $$

(11)

No detailed discussion on these options shall be provided here (see, again [21, 25]). What is important with respect to strength mismatch is that a mismatch relevant L_r is defined in that the yield or limit load F_Y is replaced by a mismatch-corrected value F_YM. An example is provided in Fig. 28. Compendia for F_Y (or σ_ref) equations for a large number of geometries are given in [29] and, based on this, in [16, 32]. As an example, the yield load for the center-cracked plate in tension (Fig. 27) is simply determined by:

Fig. 28

Strength mismatch–corrected yield or limit load F_YM as referred to its base plate equivalent F_YB. According to [29]

$$ {F}_Y=2B\left(W-a\right)\cdot {\sigma}_{\mathrm{Y}} $$

(12)

for plane stress conditions. The base metal yield load (F_YB) in Fig. 27 refers to the yield strength σ_Y of the base metal.

In section 3.3.1, it was mentioned that the assessment tools for strength mismatch, despite a number of shortcomings such as simple two-material systems and prismatic weld strips, can be used for drawing conclusions in a wider frame. This might be exercised with Fig. 28. Assume overmatching with a narrow weld strip (small H ➔ large (W − a)/H) such as for laser or electron beam welds of steel (e.g., Fig. 19b). In this case, the ratio F_YM/F_YB approaches 1, i.e., it is acceptable to use the base metal yield load F_YB for the assessment and no consideration of mismatch is necessary. If H is, however, wide and/or the crack is large, there is a limit at about (W − a)/H = 1 below of which F_YM/F_YB approaches the mismatch ratio M which means that an all-weld metal yield load can be used, i.e., Eq. (12) is applied in conjunction with the yield strength of the weld metal.

3.3.4 Specifying the mismatch ratio

Providing information on the mismatch ratio of a weld, i.e., on the yield strengths (and stress–strain curves) of the material sections involved, is a problem of its own.

The simplest but also least accurate option is to estimate the yield strength (and the ultimate tensile strength) from hardness. Solutions for this are provided in the test standards [12, 13]. According to ISO 15653 [13], the following expressions can be used:

$$ Base\ metal:\kern0.5em {R}_{p0.2B}=3.28\kern0.50em HV10\hbox{--} -221 for160< HV10<495 $$

(13)

$$ {R}_{mB}=3.3\ HV10-8 for100< HV10<400 $$

(14)

$$ Weld\ metal:\kern0.5em {R}_{p0.2W}=2.35\ HV10+62 for170< HV10<330 $$

(15)

$$ {R}_{mW}=3.0\ HV10+22.1 for170< HV10<330 $$

(16)

with the strength values in MPa.

A second option uses sub-size tensile specimens small enough to be cut out of a real weld. The principle is illustrated in Fig. 29. Usually the specimens are extracted by electro-discharge machining (EDM). Since the specimens have rectangular cross sections which show a necking pattern different from those of round cross sections, they cannot be used beyond ultimate tensile strength. If this is needed, more elaborate techniques have to be applied so that a circular cross section is obtained by subsequent machining [43]. Careful final grinding might be necessary in order to avoid surface effects.

Fig. 29

Extraction and schematic test equipment for subsize tensile specimens; according to [42]

Sometimes, the extraction of subsize specimens can be a problem too, when e.g. a weld strip or the HAZ is very narrow. Note that the use of microsized specimens which are even much smaller than those of Fig. 29, e.g., generated by a FIP technique, might not be an alternative when the test cross sections of these represent local properties of the microstructure rather than averaged properties of the material composite as it would be obtained at macroscopic cross sections.

In such a case, a combination of measurement and (numerical) simulation can be effective. For example, in [44] and, more recently in [45], shape-optimized axisymmetric notched cylindrical tensile specimens with the notch root being located in the material of interest are used. During the test, the diameter reduction at that section is measured as a function of the applied load. A finite element simulation can be performed with the true stress–strain curve chosen such that the experimental data are met. Note that the authors have also provided parametrized analytical equations for solving the problem. A similar philosophy is followed in [46] where the author used local distortion data determined by digital imaging at the surface of flat specimens containing a laser beam weld as the input data.

4 Summary

A review has been provided on fracture mechanics-related aspects of welds with potential crack initiation sites at the weld toes. In the present first part of this two-paper series, the focus was on one hand on the susceptibility of welds to cracks and other defects, and on the other hand on the consequences of material inhomogeneity across the weld for fracture toughness testing, crack driving force determination, and fracture assessment. In that context, it was distinguished between stochastic effects of more or less randomly distributed weak links mainly in the HAZ and systematic effects of material gradients from the weld via the HAZ to the base plate and also across the plate thickness. Hints have been given for the treatment of “weakest link” and strength mismatch effects in test evaluation and assessment.